The free surface and flow field structure generated by the uniform acceleration (with dimensionless acceleration  $\unicode[STIX]{x1D70E}$ ) of a rigid plate, inclined at an angle
$\unicode[STIX]{x1D70E}$ ) of a rigid plate, inclined at an angle 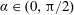 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$ to the exterior horizontal, as it advances (
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$ to the exterior horizontal, as it advances ( 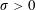 $\unicode[STIX]{x1D70E}>0$ ) or retreats (
$\unicode[STIX]{x1D70E}>0$ ) or retreats ( 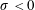 $\unicode[STIX]{x1D70E}<0$ ) from an initially stationary and horizontal strip of inviscid incompressible fluid under gravity, are studied in the small-time limit via the method of matched asymptotic expansions. This work generalises the case of a uniformly accelerating plate advancing into a fluid as studied by Needham et al. (Q. J. Mech. Appl. Maths, vol. 61 (4), 2008, pp. 581–614). Particular attention is paid to the innermost asymptotic regions encompassing the initial interaction between the plate and the free surface. We find that the structure of the solution to the governing initial boundary value problem is characterised in terms of the parameters
$\unicode[STIX]{x1D70E}<0$ ) from an initially stationary and horizontal strip of inviscid incompressible fluid under gravity, are studied in the small-time limit via the method of matched asymptotic expansions. This work generalises the case of a uniformly accelerating plate advancing into a fluid as studied by Needham et al. (Q. J. Mech. Appl. Maths, vol. 61 (4), 2008, pp. 581–614). Particular attention is paid to the innermost asymptotic regions encompassing the initial interaction between the plate and the free surface. We find that the structure of the solution to the governing initial boundary value problem is characterised in terms of the parameters  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and 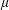 $\unicode[STIX]{x1D707}$ (where
$\unicode[STIX]{x1D707}$ (where 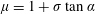 $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$ ), with a bifurcation in structure as
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$ ), with a bifurcation in structure as 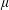 $\unicode[STIX]{x1D707}$ changes sign. This bifurcation in structure leads us to question the well-posedness and stability of the governing initial boundary value problem with respect to small perturbations in initial data in the innermost asymptotic regions, the discussion of which will be presented in the companion paper Gallagher et al. (J. Fluid Mech. vol. 841, 2018, pp. 146–166). In particular, when
$\unicode[STIX]{x1D707}$ changes sign. This bifurcation in structure leads us to question the well-posedness and stability of the governing initial boundary value problem with respect to small perturbations in initial data in the innermost asymptotic regions, the discussion of which will be presented in the companion paper Gallagher et al. (J. Fluid Mech. vol. 841, 2018, pp. 146–166). In particular, when 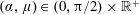 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$ , the free surface close to the initial contact point remains monotone, and encompasses a swelling jet when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{+}$ , the free surface close to the initial contact point remains monotone, and encompasses a swelling jet when 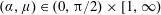 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times [1,\infty )$ or a collapsing jet when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times [1,\infty )$ or a collapsing jet when 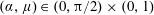 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$ . However, when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$ . However, when 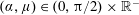 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$ , the collapsing jet develops a more complex structure, with the free surface close to the initial contact point now developing a finite number of local oscillations, with near resonance type behaviour occurring close to a countable set of critical plate angles
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times \mathbb{R}^{-}$ , the collapsing jet develops a more complex structure, with the free surface close to the initial contact point now developing a finite number of local oscillations, with near resonance type behaviour occurring close to a countable set of critical plate angles 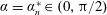 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }\in (0,\unicode[STIX]{x03C0}/2)$ (
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }\in (0,\unicode[STIX]{x03C0}/2)$ ( 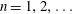 $n=1,2,\ldots$ ).
$n=1,2,\ldots$ ).