Article contents
On the large difference between Benjamin’s and Hanratty’s formulations of perturbed flow over uneven terrain
Published online by Cambridge University Press: 24 May 2019
Abstract
Flow over an uneven terrain is a complex phenomenon that requires a chain of approximations in order to be studied. In addition to modelling the intricacies of turbulence if present, the problem is classically first linearized about a flat bottom and a locally parallel flow, and then asymptotically approximated into an interactive representation that couples a boundary layer and an irrotational region through an intermediate inviscid but rotational layer. The first of these steps produces a stationary Orr–Sommerfeld equation; since this is a one-dimensional problem comparatively easy for any computer, it would seem appropriate today to forgo the second sweep of approximation and solve the Orr–Sommerfeld problem numerically. However, the results are inconsistent! It appears that the asymptotic approximation tacitly restores some of the original problem’s non-parallelism. In order to provide consistent results, Benjamin’s version of the Orr–Sommerfeld equation needs to be modified into Hanratty’s. The large difference between Benjamin’s and Hanratty’s formulations, which arises in some wavenumber ranges but not in others, is here explained through an asymptotic analysis based on the concept of admittance and on the symmetry transformations of the boundary layer. A compact and accurate analytical formula is provided for the wavenumber range of maximum laminar shear-stress response. We highlight that the maximum turbulent shear-stress response occurs in the quasi-laminar regime at a Reynolds-independent wavenumber, contrary to the maximum laminar shear-stress response whose wavenumber scales with a power of the boundary-layer thickness. A numerical computation involving an eddy-viscosity model provides a warning against the inaccuracy of such a model. We emphasize that the range 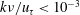 $k\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}<10^{-3}$ of the spectrum remains essentially unexplored, and that the question is still open whether a fully developed turbulent regime, similar to the one predicted by an eddy-viscosity model, ever exists for open flow even in the limit of infinite wavelength.
$k\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}<10^{-3}$ of the spectrum remains essentially unexplored, and that the question is still open whether a fully developed turbulent regime, similar to the one predicted by an eddy-viscosity model, ever exists for open flow even in the limit of infinite wavelength.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 5
- Cited by

