Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bandi, M. M.
2018.
Tension grips the flow.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
1.
Sur, Samrat
Masoud, Hassan
and
Rothstein, Jonathan P.
2019.
Translational and rotational motion of disk-shaped Marangoni surfers.
Physics of Fluids,
Vol. 31,
Issue. 10,
Lanzerotti, M.
Brakke, K.
Allen, K.
and
Hartke, J.
2019.
Bursting of molten steel thick films in a steel plate illuminated by a high energy laser.
Applied Physics Letters,
Vol. 115,
Issue. 4,
Gao, Song
Pan, Song
Wang, Huaicheng
and
Tian, Xinliang
2020.
Shape Deformation and Drag Variation of a Coupled Rigid-Flexible System in a Flowing Soap Film.
Physical Review Letters,
Vol. 125,
Issue. 3,
Wan, Dongmei
Xiang, Hengsheng
and
Xu, Haitao
2020.
A laminar-jet-discharging method for measuring the interfacial tension of deformable surfaces.
Measurement Science and Technology,
Vol. 31,
Issue. 3,
p.
035302.
Korlimarla, Aparna
and
Vorobieff, Peter
2020.
Evolution of a quasi-two-dimensional shear layer in a soap film flow.
Physics of Fluids,
Vol. 32,
Issue. 12,
Jafari Kang, Saeed
Sur, Samrat
Rothstein, Jonathan P.
and
Masoud, Hassan
2020.
Forward, reverse, and no motion of Marangoni surfers under confinement.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Yoo, Sangwook
Lee, Cheongho
and
Chin, Seongah
2021.
Physically Based Soap Bubble Synthesis for VR.
Applied Sciences,
Vol. 11,
Issue. 7,
p.
3090.
Xia, Yuxian
Qiu, Xiang
and
Qian, Yuehong
2021.
Lattice Boltzmann Method for Marangoni forcing soap film.
International Journal of Modern Physics C,
Vol. 32,
Issue. 05,
p.
2150065.
Mariot, Sandrine
Pasquet, Marina
Klein, Vincent
Restagno, Frédéric
and
Rio, Emmanuelle
2021.
A new setup for giant soap films characterization.
The European Physical Journal E,
Vol. 44,
Issue. 4,
Yi, Zhengming
Ding, Weijiang
and
Lv, Wei
2022.
Quantitative measurement of a landed soap bubble during its drainage.
Applied Optics,
Vol. 61,
Issue. 11,
p.
3190.
Zhu, Wancheng
Zhang, Xiufeng
Liu, Shuyuan
Wei, Chenhui
Wang, Jiangmei
and
Liu, Heyang
2022.
An experimental apparatus for supercritical CO2 fracturing of shale: System design and application tests.
Journal of Natural Gas Science and Engineering,
Vol. 103,
Issue. ,
p.
104656.
Pasquet, Marina
Restagno, Frédéric
Cantat, Isabelle
and
Rio, Emmanuelle
2023.
Thickness profiles of giant soap films.
Physical Review Fluids,
Vol. 8,
Issue. 3,
Tiwari, Akhilesh S.
and
Kumar, Sanjay
2023.
Effect of acoustic perturbation on the transition of vortex street in a flowing soap film.
Physics of Fluids,
Vol. 35,
Issue. 2,
Kim, Ildoo
2023.
The effect of menisci on vortex streets on soap film flows.
Physics of Fluids,
Vol. 35,
Issue. 4,
Wang, Shangning
Li, Yilong
Zhang, Yijia
Qiu, Shuyi
Li, Xuesong
and
Xu, Min
2024.
Liquid film burst caused by perpendicularly blowing gas jet.
Experimental Thermal and Fluid Science,
Vol. 157,
Issue. ,
p.
111228.
Zhao, Yu
and
Xu, Haitao
2024.
Laser-induced thermocapillary flows on a flowing soap film.
Physical Review Fluids,
Vol. 9,
Issue. 2,
Che, Lixuan
Hu, Xiaoguang
Xu, Hechen
Liu, Yuanbo
Lv, Cunjing
Kang, Zhan
Wu, Mengxi
Wen, Rongfu
Wu, Huaping
Cui, Jiayi
Li, Kun
Qi, Guangliang
Luo, Yangjun
Ma, Xuehu
Sun, Feiyi
Li, Ming
and
Liu, Junshan
2024.
Soap Film Transfer Printing for Ultrathin Electronics.
Small,
Vol. 20,
Issue. 15,
Conlin, Nicholas
Even, Hannah
Wei, Nathaniel J
Balantrapu, N Agastya
and
Hultmark, Marcus
2024.
Lagrangian particle tracking in the atmospheric surface layer.
Measurement Science and Technology,
Vol. 35,
Issue. 9,
p.
095803.
Liang, Yu
Alkindi, Ahmed
Alzeyoudi, Khalid
Liu, Lili
Ali, Mohamed
and
Masmoudi, Nader
2024.
Experimental investigation of three-dimensional Rayleigh–Taylor instability of a gaseous interface.
Journal of Fluid Mechanics,
Vol. 994,
Issue. ,
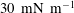 $30~\text{mN}~\text{m}^{-1}$
. A simple adsorption model with only two parameters describes our observations reasonably well. With our measurements, we are also able to estimate the Gibbs elasticity of our soap film.
$30~\text{mN}~\text{m}^{-1}$
. A simple adsorption model with only two parameters describes our observations reasonably well. With our measurements, we are also able to estimate the Gibbs elasticity of our soap film.