1 Introduction
Motivated by the need to model flow filtration and isotope separation, the quest for a similarity solution in the context of viscous, rotational and incompressible motion through porous channels and tubes may be traced back to the pioneering work of Berman (Reference Berman1953). Following Hiemenz (Reference Hiemenz1911) in the use of a linear variation of the streamfunction with respect to the axial distance from the headwall, Berman’s similarity transformation of the Navier–Stokes equations led to a fourth-order ordinary differential equation that could be solved either asymptotically or numerically over different ranges of the cross-flow Reynolds number. In fact, the first explicit solution presented by Berman (Reference Berman1953) related to the planar flow in a two-dimensional channel with porous walls and a small suction Reynolds number. The latter was based on the wall suction velocity, the kinematic viscosity and the channel’s half height. Owing to its relevance to a variety of phenomenological problems, including biological flows, Berman’s formulation gave rise to a plethora of complementary investigations. Two major research directions followed, and these focused either on the development of additional solutions for various flow configurations (Sellars Reference Sellars1955; Berman Reference Berman1958; Proudman Reference Proudman1960; Terrill & Shrestha Reference Terrill and Shrestha1965; Terrill & Thomas Reference Terrill and Thomas1969) or on the uniqueness or stability issues of such solutions under specific ranges of the cross-flow Reynolds number (Zaturska, Drazin & Banks Reference Zaturska, Drazin and Banks1988; Watson et al. Reference Watson, Banks, Zaturska and Drazin1990; Cox Reference Cox1991; Lu Reference Lu1994; Cox & King Reference Cox and King1997; Lu Reference Lu1997).
Independently of these studies, other relevant work in the context of membrane separation and paper manufacture may be attributed to Taylor (Reference Taylor1956), particularly in his presentation of analytical expressions for the inviscid motion in porous channels, wedges, cones and tubes. The latter was also reconstructed by Culick (Reference Culick1966) as a practical, rotational model for the mean flow field in axisymmetric rocket motors, thus leading to the so-called Taylor–Culick profile. The resulting injection-based formulation compared favourably with Berman’s large-Reynolds-number solution and was shown to adequately represent the non-reactive internal motion in solid rocket motors according to both laboratory experiments (Yamada, Goto & Ishikawa Reference Yamada, Goto and Ishikawa1976; Dunlap et al. Reference Dunlap, Blackner, Waugh, Brown and Willoughby1990; Gazanion, Chedevergne & Casalis Reference Gazanion, Chedevergne and Casalis2014) and computations (Sabnis, Gibeling & McDonald Reference Sabnis, Gibeling and McDonald1989; Apte & Yang Reference Apte and Yang2003; Venugopal, Moser & Najjar Reference Venugopal, Moser and Najjar2008). By forcing the flow to enter the chamber perpendicularly to the sidewall, the Taylor–Culick model exhibited a realistic axial velocity that could satisfy the no-slip requirement at the sidewall despite its strictly inviscid character. As shown by Chedevergne, Casalis & Majdalani (Reference Chedevergne, Casalis and Majdalani2012), this simple model compared very well with direct numerical simulations of a circular-port chamber except in the close vicinity of the headwall, where the inevitable development of a viscous boundary layer could not be accounted for.
The continued interest in Taylor–Culick type formulations may be attributed to its suitability as a base flow representation in modelling combustion instability phenomena and related pressure oscillations in rocket systems. In this vein, one may cite several studies that explore the linear instability behaviour of hydrodynamic perturbations (Casalis, Avalon & Pineau Reference Casalis, Avalon and Pineau1998; Griffond & Casalis Reference Griffond and Casalis2000; Chedevergne, Casalis & Féraille Reference Chedevergne, Casalis and Féraille2006; Abu-Irshaid, Majdalani & Casalis Reference Abu-Irshaid, Majdalani and Casalis2007; Chedevergne et al. Reference Chedevergne, Casalis and Majdalani2012; Boyer, Casalis & Estivalèzes Reference Boyer, Casalis and Estivalèzes2013), acoustic energy balance formulations (Fabignon et al. Reference Fabignon, Dupays, Avalon, Vuillot, Lupoglazoff, Casalis and Prévost2003; Flandro & Majdalani Reference Flandro and Majdalani2003; Majdalani, Flandro & Fischbach Reference Majdalani, Flandro and Fischbach2005; Majdalani, Fischbach & Flandro Reference Majdalani, Fischbach and Flandro2006; Fischbach, Majdalani & Flandro Reference Fischbach, Majdalani and Flandro2007; Flandro, Fischbach & Majdalani Reference Flandro, Fischbach and Majdalani2007), vortico-acoustic wave approximations (Majdalani & Flandro Reference Majdalani and Flandro2002; Majdalani Reference Majdalani2009), particle mean flow effects (Féraille & Casalis Reference Féraille and Casalis2003) and rocket performance characteristics (Saad, Sams & Majdalani Reference Saad, Sams and Majdalani2006; Sams, Majdalani & Saad Reference Sams, Majdalani and Saad2007).
In the spirit of improving the practicality and relevance of Taylor–Culick formulations to realistic rocket systems, several extensions have been systematically pursued in the past two decades. These have been warranted by the need to incorporate the effects of grain regression (Majdalani, Vyas & Flandro Reference Majdalani, Vyas and Flandro2002, Reference Majdalani, Vyas and Flandro2009), port variability (Kurdyumov Reference Kurdyumov2006), wall tapering (Saad et al. Reference Saad, Sams and Majdalani2006; Sams et al. Reference Sams, Majdalani and Saad2007), axisymmetric headwall injection (Majdalani & Saad Reference Majdalani and Saad2007), viscosity (Majdalani & Akiki Reference Majdalani and Akiki2010) and potential flow steepening (Saad & Majdalani Reference Saad and Majdalani2010). For the effects of compressibility, two general approaches have been successfully advanced. The first relied on a similarity reduction of the Navier–Stokes equations into an integral formulation that could suitably account for the slow axial pressure variations that occurred in long chambers (Balakrishnan, Liñan & Williams Reference Balakrishnan, Liñan and Williams1992; Akiki & Majdalani Reference Akiki and Majdalani2016). Although the resulting equations had to be solved numerically along different streamlines, the integral framework enabled us to capture the effects of arbitrary sidewall mass injection. The second approach applied a Rayleigh–Janzen expansion technique while assuming a constant wall injection speed to extract closed-form analytical expressions for the compressible Taylor–Culick profiles in both axisymmetric (Majdalani Reference Majdalani2007) and two-dimensional planar configurations (Maicke & Majdalani Reference Maicke and Majdalani2008).
Since most former studies have focused on circular grain configurations, the purpose of this study is to extend the Taylor–Culick flow description to more practical propellant grain perforations that comprise stars, multi-fins, wagon-wheels, dog-bones or dendrites. To do so requires the incorporation of a radial deviation from a fixed chamber radius. The concept of perturbing the injection velocity or the location of the injection site has, in fact, been previously explored by Balachandar, Buckmaster & Short (Reference Balachandar, Buckmaster and Short2001). Their work led to important physical insight into the streamwise evolution of axial vorticity along with the subdivision of the fluid domain into an inviscid annulus that extended radially inwards into a viscous core. Furthermore, for a radial deviation of
![]() $\unicode[STIX]{x1D700}$
, the analysis showed that the cross-flow Reynolds number could not exceed
$\unicode[STIX]{x1D700}$
, the analysis showed that the cross-flow Reynolds number could not exceed
![]() $1/\unicode[STIX]{x1D700}$
in their linear perturbation range. A subsequent study by Kurdyumov (Reference Kurdyumov2006) presented a mathematical model that could be solved numerically for a variable cross-section, thus confirming the evolution of axial vorticity in the presence of viscous effects. It also helped to characterize the behaviour of the pressure distribution and its deviation from the traditional Taylor–Culick value. Along similar lines, a closed-form analytical solution was developed by Van Horn & Majdalani (Reference Van Horn and Majdalani2014) for a non-circular star-shaped grain under incompressible, inviscid and rotational conditions. However, the latter dismissed the effects of the tangential velocity at the basis of their analysis, thus leading to a second-order asymptotic approximation that remained limited to a modest number of lobes,
$1/\unicode[STIX]{x1D700}$
in their linear perturbation range. A subsequent study by Kurdyumov (Reference Kurdyumov2006) presented a mathematical model that could be solved numerically for a variable cross-section, thus confirming the evolution of axial vorticity in the presence of viscous effects. It also helped to characterize the behaviour of the pressure distribution and its deviation from the traditional Taylor–Culick value. Along similar lines, a closed-form analytical solution was developed by Van Horn & Majdalani (Reference Van Horn and Majdalani2014) for a non-circular star-shaped grain under incompressible, inviscid and rotational conditions. However, the latter dismissed the effects of the tangential velocity at the basis of their analysis, thus leading to a second-order asymptotic approximation that remained limited to a modest number of lobes,
![]() $m$
, being constrained by
$m$
, being constrained by
![]() $\unicode[STIX]{x1D700}<1/m$
.
$\unicode[STIX]{x1D700}<1/m$
.
In what follows, a similarity solution will be applied to the viscous Navier–Stokes equations, along with a judiciously constructed perturbation expansion to derive a higher-order description of the incompressible flow field in a porous tube with uniform wall injection. The first objective will be to achieve a second-order formulation that extends the range of applicability of the ensuing model to sufficiently large values of the cross-flow Reynolds number, namely, to levels that correspond to practical rocket simulations and cold flow experiments. The second objective will be to provide a solution that can be reproduced with relative ease.
The paper is organized as follows. First, the problem formulation is presented along with the governing equations, including the proposed geometric configuration, the wavy surface definition, and the mapped coordinate system that will be necessary to shift the wall boundary conditions to a virtually fixed location. Second, after recovering Berman’s fourth-order differential equation at leading order, an asymptotic expansion of the asymmetric problem is pursued to the second order in
![]() $\unicode[STIX]{x1D700}$
. Third, a comparison to numerical simulations produced from a nonlinear Navier–Stokes solver is performed while varying the cross-flow Reynolds number,
$\unicode[STIX]{x1D700}$
. Third, a comparison to numerical simulations produced from a nonlinear Navier–Stokes solver is performed while varying the cross-flow Reynolds number,
![]() $Re$
, radial deviation amplitude,
$Re$
, radial deviation amplitude,
![]() $\unicode[STIX]{x1D700}$
, and number of lobes,
$\unicode[STIX]{x1D700}$
, and number of lobes,
![]() $m$
. Lastly, the limitations of this framework are presented and discussed along with several recommendations for future use.
$m$
. Lastly, the limitations of this framework are presented and discussed along with several recommendations for future use.
2 Solution methodology
2.1 Geometry and governing equations
Our geometric configuration consists of a semi-infinite porous cylinder that is closed at the headwall while admitting a uniformly distributed sidewall injection. Considering any real function
![]() $\unicode[STIX]{x1D6FC}$
with zero mean, the cross-section is determined by the tangentially evolving radius,
$\unicode[STIX]{x1D6FC}$
with zero mean, the cross-section is determined by the tangentially evolving radius,
![]() $r_{w}=a(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})$
, where
$r_{w}=a(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})$
, where
![]() $a$
is fixed and
$a$
is fixed and
![]() $\unicode[STIX]{x1D700}$
is a parameter. As shown in figure 1, the fluid is injected perpendicularly to the wavy surface at a constant speed
$\unicode[STIX]{x1D700}$
is a parameter. As shown in figure 1, the fluid is injected perpendicularly to the wavy surface at a constant speed
![]() $U_{w}$
. In view of this geometry, the steady incompressible Navier–Stokes equations are considered with all spatial coordinates, time, velocity and pressure variables made dimensionless using
$U_{w}$
. In view of this geometry, the steady incompressible Navier–Stokes equations are considered with all spatial coordinates, time, velocity and pressure variables made dimensionless using
![]() $a$
,
$a$
,
![]() $a/U_{w}$
,
$a/U_{w}$
,
![]() $U_{w}$
and
$U_{w}$
and
![]() $\unicode[STIX]{x1D70C}U_{w}^{2}$
, respectively. The corresponding cross-flow Reynolds number may be written as
$\unicode[STIX]{x1D70C}U_{w}^{2}$
, respectively. The corresponding cross-flow Reynolds number may be written as
![]() $Re=U_{w}a/\unicode[STIX]{x1D708}$
, where
$Re=U_{w}a/\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D708}$
denotes the kinematic viscosity. Then using
$\unicode[STIX]{x1D708}$
denotes the kinematic viscosity. Then using
![]() $\boldsymbol{u}=(u_{\bar{r}},u_{\bar{\unicode[STIX]{x1D703}}},u_{\bar{z}})$
and
$\boldsymbol{u}=(u_{\bar{r}},u_{\bar{\unicode[STIX]{x1D703}}},u_{\bar{z}})$
and
![]() $p$
for the velocity and pressure, our system of equations reduces to
$p$
for the velocity and pressure, our system of equations reduces to
where the overbar in
![]() $\bar{\unicode[STIX]{x1D6FB}}$
denotes differentiation with respect to the unmodified dimensionless variables
$\bar{\unicode[STIX]{x1D6FB}}$
denotes differentiation with respect to the unmodified dimensionless variables
![]() $(\bar{r},\bar{\unicode[STIX]{x1D703}},\bar{z})$
.
$(\bar{r},\bar{\unicode[STIX]{x1D703}},\bar{z})$
.
2.2 Mapping to a circular cross-section
To simplify the application of the boundary conditions at the sidewall, and thus avoid the need for Taylor-series expansions about a fixed radius, it is helpful to map the dimensionless spatial coordinates
![]() $(\overline{r},\overline{\unicode[STIX]{x1D703}},\overline{z})$
in such a manner to relocate the wall boundary conditions to a spatially invariant point. This may be accomplished through the coordinate transformation:
$(\overline{r},\overline{\unicode[STIX]{x1D703}},\overline{z})$
in such a manner to relocate the wall boundary conditions to a spatially invariant point. This may be accomplished through the coordinate transformation:
The vector basis
![]() $(\boldsymbol{e}_{r},\boldsymbol{e}_{\unicode[STIX]{x1D703}},\boldsymbol{e}_{z})$
defined in figure 1 remains unchanged. Although this substitution affects the form of the radial and tangential derivatives, the wall surface can now be specified using
$(\boldsymbol{e}_{r},\boldsymbol{e}_{\unicode[STIX]{x1D703}},\boldsymbol{e}_{z})$
defined in figure 1 remains unchanged. Although this substitution affects the form of the radial and tangential derivatives, the wall surface can now be specified using
![]() ${\mathcal{A}}(r)=r-1=0$
. The corresponding normal unit vector,
${\mathcal{A}}(r)=r-1=0$
. The corresponding normal unit vector,
![]() $\boldsymbol{n}=n_{r}\boldsymbol{e}_{r}+n_{\unicode[STIX]{x1D703}}\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
, becomes
$\boldsymbol{n}=n_{r}\boldsymbol{e}_{r}+n_{\unicode[STIX]{x1D703}}\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
, becomes
and so the wall-normal injection condition simplifies to
![]() $\boldsymbol{u}=-\boldsymbol{n}$
at
$\boldsymbol{u}=-\boldsymbol{n}$
at
![]() $r=1$
. Naturally, this substitution gives rise to a more complex form of the Navier–Stokes equations, which is detailed in appendix A.
$r=1$
. Naturally, this substitution gives rise to a more complex form of the Navier–Stokes equations, which is detailed in appendix A.
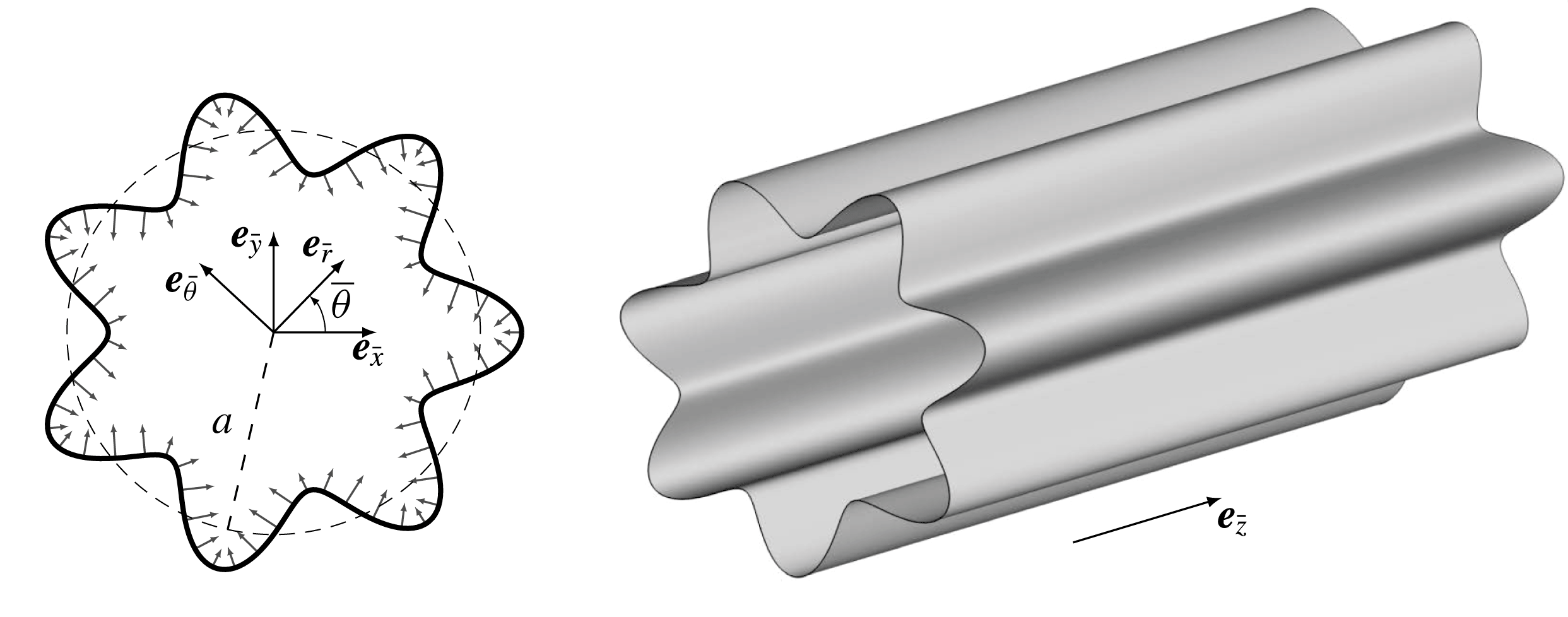
Figure 1. Sketch of the geometric configuration and coordinate systems corresponding to a non-circular, wavy cross-section with
![]() $\unicode[STIX]{x1D6FC}=\cos (m\unicode[STIX]{x1D703})$
. The sketch corresponds to
$\unicode[STIX]{x1D6FC}=\cos (m\unicode[STIX]{x1D703})$
. The sketch corresponds to
![]() $m=7$
lobes and a 20 % radial deviation in
$m=7$
lobes and a 20 % radial deviation in
![]() $\unicode[STIX]{x1D700}$
.
$\unicode[STIX]{x1D700}$
.
2.3 On the minimum perturbation order
In their elegant analysis of the axisymmetric flow in a porous tube, Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) establish a framework in which small perturbations of the form
![]() $\unicode[STIX]{x1D700}\cos (m\unicode[STIX]{x1D703})$
may be imposed at the sidewall. By examining the asymptotic behaviour of the ensuing solution as
$\unicode[STIX]{x1D700}\cos (m\unicode[STIX]{x1D703})$
may be imposed at the sidewall. By examining the asymptotic behaviour of the ensuing solution as
![]() $r\rightarrow 0$
, a viscous core is shown to be present near the centreline. Accordingly, viscous effects dominate on the scale of
$r\rightarrow 0$
, a viscous core is shown to be present near the centreline. Accordingly, viscous effects dominate on the scale of
![]() $r=O(1/\sqrt{Re})$
for wall perturbations of
$r=O(1/\sqrt{Re})$
for wall perturbations of
![]() $O(\unicode[STIX]{x1D700})$
. Furthermore, as we enter the viscous core region, the axial vorticity, which accompanies the evolution of a finite tangential velocity, appears at
$O(\unicode[STIX]{x1D700})$
. Furthermore, as we enter the viscous core region, the axial vorticity, which accompanies the evolution of a finite tangential velocity, appears at
![]() $O(\unicode[STIX]{x1D700}Re)$
. Consequently, the linear perturbative analysis remains valid as long as
$O(\unicode[STIX]{x1D700}Re)$
. Consequently, the linear perturbative analysis remains valid as long as
![]() $\unicode[STIX]{x1D700}Re\ll 1$
. To overcome this practical limitation, Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) introduce a nonlinear patch on the scale of
$\unicode[STIX]{x1D700}Re\ll 1$
. To overcome this practical limitation, Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) introduce a nonlinear patch on the scale of
![]() $r=O(\sqrt{\unicode[STIX]{x1D700}})$
. This viscous correction leads to a solution that extends the range of applicability to
$r=O(\sqrt{\unicode[STIX]{x1D700}})$
. This viscous correction leads to a solution that extends the range of applicability to
![]() $\unicode[STIX]{x1D700}Re\gg 1$
, where the axial vorticity increases to
$\unicode[STIX]{x1D700}Re\gg 1$
, where the axial vorticity increases to
![]() $O(1)$
. A similar conclusion may be reached in our analysis, which requires second-order perturbations of
$O(1)$
. A similar conclusion may be reached in our analysis, which requires second-order perturbations of
![]() $O(\unicode[STIX]{x1D700}^{2})$
to adequately capture the nonlinear interactions that evolve at previous orders. Moreover, a second-order approximation will be warranted to satisfy mass conservation requirements by virtue of the angular dependence being of the harmonic form,
$O(\unicode[STIX]{x1D700}^{2})$
to adequately capture the nonlinear interactions that evolve at previous orders. Moreover, a second-order approximation will be warranted to satisfy mass conservation requirements by virtue of the angular dependence being of the harmonic form,
![]() $\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
.
$\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$
.
The approach that we follow is therefore compatible with Balachandar’s framework, as it seeks to derive a second-order viscous solution for a periodically distorted cross-section. In this process, however, an effort will be made to secure the no-slip condition in all three spatial directions, including the axial and tangential velocities at the sidewall, thus leading to a uniformly valid solution that extends from
![]() $r=0$
to 1 inclusively.
$r=0$
to 1 inclusively.
To justify the need to carry out a second-order approximation, it may be instructive to revisit the mass flow rate evaluation at the sidewall. We start by remarking that, for an identical mean radius, the circumference of the cross-section corresponding to a wavy wall, such as a star-shaped grain configuration, will always exceed that of its counterpart with a fixed circular radius. Then, recognizing that
![]() $\unicode[STIX]{x1D6FC}$
is a periodic function with a vanishing mean value, the mass surplus can be estimated using an asymptotic expansion of
$\unicode[STIX]{x1D6FC}$
is a periodic function with a vanishing mean value, the mass surplus can be estimated using an asymptotic expansion of
![]() ${\dot{m}}_{w}(z)$
, namely,
${\dot{m}}_{w}(z)$
, namely,
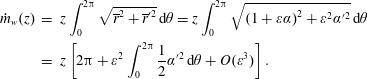 $$\begin{eqnarray}\displaystyle {\dot{m}}_{w}(z) & = & \displaystyle z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\overline{r}^{2}+\overline{r}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}=z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & = & \displaystyle z\left[2\unicode[STIX]{x03C0}+\unicode[STIX]{x1D700}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\,\text{d}\unicode[STIX]{x1D703}+O(\unicode[STIX]{x1D700}^{3})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\dot{m}}_{w}(z) & = & \displaystyle z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\overline{r}^{2}+\overline{r}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}=z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & = & \displaystyle z\left[2\unicode[STIX]{x03C0}+\unicode[STIX]{x1D700}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\,\text{d}\unicode[STIX]{x1D703}+O(\unicode[STIX]{x1D700}^{3})\right].\end{eqnarray}$$
The resulting equality confirms that the first-order corrections have no bearing on the injected mass flow rate. In particular, the axial velocity, which contributes to the mass injection, cannot by itself secure the mass balance without taking into account its interactions at the second order. Moreover, a second-order representation will enable us to extend the validity of the model to larger deviation amplitudes with
![]() $\unicode[STIX]{x1D700}^{2}\ll 1$
, while simultaneously aiding in improving the permissible range of Reynolds numbers to
$\unicode[STIX]{x1D700}^{2}\ll 1$
, while simultaneously aiding in improving the permissible range of Reynolds numbers to
![]() $\unicode[STIX]{x1D700}Re\gg 1$
, as predicted by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001).
$\unicode[STIX]{x1D700}Re\gg 1$
, as predicted by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001).
2.4 Asymptotic expansion
Given the above considerations, the velocity and pressure fields,
![]() $(\boldsymbol{u},p)$
, may be decomposed using
$(\boldsymbol{u},p)$
, may be decomposed using
where superscripts denote successive asymptotic orders. This two-term approximation may be substituted back into the Navier–Stokes equations, expressed through (A 1), and then further linearized using binomial expansions of
![]() $(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})^{-1}$
terms. These operations enable us to identify and segregate three sets of equations that appear at
$(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})^{-1}$
terms. These operations enable us to identify and segregate three sets of equations that appear at
![]() $O(1)$
,
$O(1)$
,
![]() $O(\unicode[STIX]{x1D700})$
and
$O(\unicode[STIX]{x1D700})$
and
![]() $O(\unicode[STIX]{x1D700}^{2})$
, consecutively. A similar expansion may be applied to the wall injection boundary condition (2.3), thus leading to
$O(\unicode[STIX]{x1D700}^{2})$
, consecutively. A similar expansion may be applied to the wall injection boundary condition (2.3), thus leading to
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}(\vphantom{u_{r}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)=-{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=-1+{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}),\\ u_{\unicode[STIX]{x1D703}}(\vphantom{u_{\unicode[STIX]{x1D703}}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)={\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}(\vphantom{u_{r}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)=-{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=-1+{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}),\\ u_{\unicode[STIX]{x1D703}}(\vphantom{u_{\unicode[STIX]{x1D703}}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)={\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}).\end{array}\right\}\end{eqnarray}$$
When translated to the asymptotic velocity corrections, these expressions give rise to an assortment of conditions that must be imposed at successively increasing orders, namely,
 $$\begin{eqnarray}\left.\begin{array}{@{}rclrclrcl@{}}u_{r}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -1, & \quad u_{\unicode[STIX]{x1D703}}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{z}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{\unicode[STIX]{x1D703}}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime 2}/2, & \quad u_{\unicode[STIX]{x1D703}}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rclrclrcl@{}}u_{r}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -1, & \quad u_{\unicode[STIX]{x1D703}}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{z}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{\unicode[STIX]{x1D703}}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime 2}/2, & \quad u_{\unicode[STIX]{x1D703}}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0.\end{array}\right\}\end{eqnarray}$$
The solution to the three sets of equations and their associated boundary conditions will be described in §§ 2.5–2.7.
Furthermore, to justify the use of the upcoming similarity transformation, it will be helpful to examine the mass conservation requirement. By equating the radial mass flow rate
![]() ${\dot{m}}_{w}(z)$
, which originates from the sidewall over a length of tubing that extends from the headwall to a point
${\dot{m}}_{w}(z)$
, which originates from the sidewall over a length of tubing that extends from the headwall to a point
![]() $z$
, to the axial mass flow rate
$z$
, to the axial mass flow rate
![]() ${\dot{m}}_{cross}(z)$
, crossing section
${\dot{m}}_{cross}(z)$
, crossing section
![]() $z$
, one arrives at the following equality:
$z$
, one arrives at the following equality:
A sufficient condition for
![]() $u_{z}$
to satisfy the previous relation (2.8) is to assume a linear variation with respect to
$u_{z}$
to satisfy the previous relation (2.8) is to assume a linear variation with respect to
![]() $z$
, as foretold by Hiemenz (Reference Hiemenz1911). To make further headway, only separable product solutions are sought, thus turning the linear dependence on
$z$
, as foretold by Hiemenz (Reference Hiemenz1911). To make further headway, only separable product solutions are sought, thus turning the linear dependence on
![]() $z$
into a necessary condition. Procedurally, this enables us to specify the axial velocity corrections,
$z$
into a necessary condition. Procedurally, this enables us to specify the axial velocity corrections,
![]() $u_{z}^{(0)}$
,
$u_{z}^{(0)}$
,
![]() $u_{z}^{(1)}$
and
$u_{z}^{(1)}$
and
![]() $u_{z}^{(2)}$
, with a linear dependence on
$u_{z}^{(2)}$
, with a linear dependence on
![]() $z$
.
$z$
.
2.5 Leading-order analysis
In the absence of angular wall deformation (
![]() $\unicode[STIX]{x1D700}=0$
), the classical problem of an injection-driven motion in a circular cylinder is restored. Being independent of
$\unicode[STIX]{x1D700}=0$
), the classical problem of an injection-driven motion in a circular cylinder is restored. Being independent of
![]() $\unicode[STIX]{x1D703}$
, one recovers
$\unicode[STIX]{x1D703}$
, one recovers
![]() $u_{\unicode[STIX]{x1D703}}^{(0)}=0$
and
$u_{\unicode[STIX]{x1D703}}^{(0)}=0$
and
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}f=0$
for any scalar function
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}f=0$
for any scalar function
![]() $f$
. In this situation, Berman’s formulation may be employed with a streamfunction
$f$
. In this situation, Berman’s formulation may be employed with a streamfunction
![]() $\unicode[STIX]{x1D713}(r,z)=zF(r)$
, where
$\unicode[STIX]{x1D713}(r,z)=zF(r)$
, where
![]() $F(r)$
represents the characteristic mean flow function (Berman Reference Berman1953). The leading-order solution may be subsequently retrieved from Berman’s fourth-order nonlinear ordinary differential equation:
$F(r)$
represents the characteristic mean flow function (Berman Reference Berman1953). The leading-order solution may be subsequently retrieved from Berman’s fourth-order nonlinear ordinary differential equation:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\left[\left({\displaystyle \frac{F}{r}}\right)\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }-\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{2}\right]^{\prime }-{\displaystyle \frac{1}{Re}}\left[{\displaystyle \frac{1}{r}}\left(r\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }\right)^{\prime }\right]^{\prime }=0,\\ \displaystyle \lim _{r\rightarrow 0}\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }=\displaystyle \lim _{r\rightarrow 0}{\displaystyle \frac{F}{r}}=F^{\prime }(1)=0,\quad F(1)=1.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\left[\left({\displaystyle \frac{F}{r}}\right)\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }-\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{2}\right]^{\prime }-{\displaystyle \frac{1}{Re}}\left[{\displaystyle \frac{1}{r}}\left(r\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }\right)^{\prime }\right]^{\prime }=0,\\ \displaystyle \lim _{r\rightarrow 0}\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }=\displaystyle \lim _{r\rightarrow 0}{\displaystyle \frac{F}{r}}=F^{\prime }(1)=0,\quad F(1)=1.\end{array}\right\}\end{eqnarray}$$
In the above, the boundary conditions may be ascribed to axisymmetry and wall-normal injection. In hindsight, the solutions obtained by Taylor (Reference Taylor1956) and Culick (Reference Culick1966) correspond to Berman’s formulation in the limit of
![]() $Re\rightarrow \infty$
. In fact, the Taylor–Culick profile begins to resemble Berman’s solution for
$Re\rightarrow \infty$
. In fact, the Taylor–Culick profile begins to resemble Berman’s solution for
![]() $Re>100$
. Nonetheless, as we aim to extend the validity of the viscous model to a generic non-axisymmetric configuration, we continue to employ Berman’s model and retain its dependence on the cross-flow Reynolds number. Thus, for a given
$Re>100$
. Nonetheless, as we aim to extend the validity of the viscous model to a generic non-axisymmetric configuration, we continue to employ Berman’s model and retain its dependence on the cross-flow Reynolds number. Thus, for a given
![]() $Re$
, (2.9) may be solved numerically for
$Re$
, (2.9) may be solved numerically for
![]() $F(r)$
, and so the three velocity components and pressure at order
$F(r)$
, and so the three velocity components and pressure at order
![]() $O(1)$
may be deduced directly from
$O(1)$
may be deduced directly from
where both
![]() $P_{0}$
and
$P_{0}$
and
![]() $\unicode[STIX]{x1D705}_{0}$
represent undetermined integration constants that may be obtained from Berman’s expression in the modified coordinate system
$\unicode[STIX]{x1D705}_{0}$
represent undetermined integration constants that may be obtained from Berman’s expression in the modified coordinate system
![]() $(r,\unicode[STIX]{x1D703},z)$
.
$(r,\unicode[STIX]{x1D703},z)$
.
2.6 First-order analysis
The system of linear equations (A 1) is written at the order
![]() $O(\unicode[STIX]{x1D700})$
and rearranged into (C 1). Guided by the wall-normal injection conditions requiring the appearance of
$O(\unicode[STIX]{x1D700})$
and rearranged into (C 1). Guided by the wall-normal injection conditions requiring the appearance of
![]() $\unicode[STIX]{x1D6FC}$
and its derivative, a solution is sought using separation of variables. Note that no additional axial pressure gradient is required for product solutions, since the mass flow surplus (2.4) is of second order. The solution then simply reads
$\unicode[STIX]{x1D6FC}$
and its derivative, a solution is sought using separation of variables. Note that no additional axial pressure gradient is required for product solutions, since the mass flow surplus (2.4) is of second order. The solution then simply reads
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(1)}\ & =\ & v_{r}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(1)}\ & =\ & v_{\unicode[STIX]{x1D703}}^{}(r)\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D703}),\\ u_{z}^{(1)}\ & =\ & zv_{z}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ p^{(1)}\ & =\ & q^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(1)}\ & =\ & v_{r}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(1)}\ & =\ & v_{\unicode[STIX]{x1D703}}^{}(r)\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D703}),\\ u_{z}^{(1)}\ & =\ & zv_{z}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ p^{(1)}\ & =\ & q^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
The substitution of these expressions into (C 1) gives rise to a
![]() $\unicode[STIX]{x1D703}$
-dependent system in which every equation can be collapsed into the form of
$\unicode[STIX]{x1D703}$
-dependent system in which every equation can be collapsed into the form of
![]() $\unicode[STIX]{x1D719}(\vphantom{\unicode[STIX]{x1D719}}\vphantom{r}r)=-\unicode[STIX]{x1D6FC}^{\prime \prime }(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})$
, where
$\unicode[STIX]{x1D719}(\vphantom{\unicode[STIX]{x1D719}}\vphantom{r}r)=-\unicode[STIX]{x1D6FC}^{\prime \prime }(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})$
, where
![]() $\unicode[STIX]{x1D719}$
denotes an operator that may be constructed from the aforementioned functions and their derivatives. Naturally, without any loss of generality in the space of real functions, harmonic variations of the form
$\unicode[STIX]{x1D719}$
denotes an operator that may be constructed from the aforementioned functions and their derivatives. Naturally, without any loss of generality in the space of real functions, harmonic variations of the form
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})=\cos (m\unicode[STIX]{x1D703})$
are retained,
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})=\cos (m\unicode[STIX]{x1D703})$
are retained,
![]() $m$
being a constant. Since
$m$
being a constant. Since
![]() $m$
represents the number of lobes along a fixed circular circumference, it will be referred to hereafter as the circular wavenumber. The underlying consequence of this choice for
$m$
represents the number of lobes along a fixed circular circumference, it will be referred to hereafter as the circular wavenumber. The underlying consequence of this choice for
![]() $\unicode[STIX]{x1D6FC}$
is that the mass flow conservation can be expressed at the third order using
$\unicode[STIX]{x1D6FC}$
is that the mass flow conservation can be expressed at the third order using
For the reader’s convenience, the
![]() $\unicode[STIX]{x1D703}$
-dependent system of equations is provided in (C 2). The system consists of one first-order and three second-order ordinary differential equations. The corresponding injection conditions, which stem from (2.7), lead to
$\unicode[STIX]{x1D703}$
-dependent system of equations is provided in (C 2). The system consists of one first-order and three second-order ordinary differential equations. The corresponding injection conditions, which stem from (2.7), lead to
![]() $v_{\unicode[STIX]{x1D703}}^{}(1)=1$
and
$v_{\unicode[STIX]{x1D703}}^{}(1)=1$
and
![]() $v_{r}^{}(1)=v_{z}^{}(1)=0$
. In order to achieve closure, four additional constraints are still necessary, and these may be specified at
$v_{r}^{}(1)=v_{z}^{}(1)=0$
. In order to achieve closure, four additional constraints are still necessary, and these may be specified at
![]() $r=0$
by introducing Taylor-series expansions of the different functions with respect to
$r=0$
by introducing Taylor-series expansions of the different functions with respect to
![]() $r$
in (C 3). After some effort, we arrive at
$r$
in (C 3). After some effort, we arrive at
![]() $v_{r}^{\prime }(0)=-F^{\prime \prime }(0)/2$
and
$v_{r}^{\prime }(0)=-F^{\prime \prime }(0)/2$
and
![]() $v_{r}^{}(0)=v_{\unicode[STIX]{x1D703}}^{}(0)=v_{z}^{}(0)=0$
, with the additional realization that
$v_{r}^{}(0)=v_{\unicode[STIX]{x1D703}}^{}(0)=v_{z}^{}(0)=0$
, with the additional realization that
![]() $m^{2}\neq (0,1)$
, to avoid a mathematically incongruent outcome. In practice, we are only interested in cross-sections with
$m^{2}\neq (0,1)$
, to avoid a mathematically incongruent outcome. In practice, we are only interested in cross-sections with
![]() $m\geqslant 3$
.
$m\geqslant 3$
.
With the advent of a sufficient number of boundary conditions, a collocation method, such as the one described by Canuto et al. (Reference Canuto, Hussaini, Quarteroni and Zang1988), may be used to discretize the system of equations and recover the first-order velocity and pressure corrections.
2.7 Second-order analysis
To make further headway, we proceed to decompose the second-order corrections using the following classical forms:
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & u_{r,0}^{(2)}(r)+u_{r,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -mu_{\unicode[STIX]{x1D703},2}^{(2)}(r)\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & z[u_{z,0}^{(2)}(r)+u_{z,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703})],\\ p_{}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}z^{2}+p_{0}^{(2)}(r)+p_{2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & u_{r,0}^{(2)}(r)+u_{r,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -mu_{\unicode[STIX]{x1D703},2}^{(2)}(r)\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & z[u_{z,0}^{(2)}(r)+u_{z,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703})],\\ p_{}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}z^{2}+p_{0}^{(2)}(r)+p_{2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
On the right-hand side of the resulting momentum equations at
![]() $O(\unicode[STIX]{x1D700}^{2})$
, terms that depend on the two previous orders, which are caused by nonlinear interactions, may be explicitly seen (appendix C). Computing this second-order correction will therefore enable us to capture the nonlinearities alluded to by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) when
$O(\unicode[STIX]{x1D700}^{2})$
, terms that depend on the two previous orders, which are caused by nonlinear interactions, may be explicitly seen (appendix C). Computing this second-order correction will therefore enable us to capture the nonlinearities alluded to by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) when
![]() $\unicode[STIX]{x1D700}Re$
is no longer a small quantity. The resulting set of seven linear equations can be subsequently consolidated into two concise and independent systems: the first assortment consists of four linear equations that prescribe
$\unicode[STIX]{x1D700}Re$
is no longer a small quantity. The resulting set of seven linear equations can be subsequently consolidated into two concise and independent systems: the first assortment consists of four linear equations that prescribe
![]() $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
, as given by (D 1), and the second entails three linear equations that control
$(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
, as given by (D 1), and the second entails three linear equations that control
![]() $(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$
, as given by (D 2). Being independent, these two systems may be solved separately. Moreover, since
$(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$
, as given by (D 2). Being independent, these two systems may be solved separately. Moreover, since
![]() $u_{\unicode[STIX]{x1D703}}^{(2)}$
only appears in the first system, each set leads to a well-posed problem with the same number of equations and unknowns, except for the constant
$u_{\unicode[STIX]{x1D703}}^{(2)}$
only appears in the first system, each set leads to a well-posed problem with the same number of equations and unknowns, except for the constant
![]() $\unicode[STIX]{x1D705}$
. Its determination will be described separately.
$\unicode[STIX]{x1D705}$
. Its determination will be described separately.
The boundary conditions associated with
![]() $\boldsymbol{u}_{2}^{(2)}$
may be readily obtained from (2.7), specifically at the wall and the centreline, using the
$\boldsymbol{u}_{2}^{(2)}$
may be readily obtained from (2.7), specifically at the wall and the centreline, using the
![]() $r\rightarrow 0$
Taylor-series expansions introduced previously. These produce
$r\rightarrow 0$
Taylor-series expansions introduced previously. These produce
With the boundary conditions in hand, the computation of
![]() $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
may be achieved easily using a discrete collocation, for instance.
$(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
may be achieved easily using a discrete collocation, for instance.
Unlike
![]() $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
, the three linear equations for
$(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$
, the three linear equations for
![]() $(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$
may be carefully reduced into a single third-order ordinary differential equation that depends solely on
$(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$
may be carefully reduced into a single third-order ordinary differential equation that depends solely on
![]() $u_{r,0}^{(2)}$
. This equation is given by (D 3). The undetermined pressure constant
$u_{r,0}^{(2)}$
. This equation is given by (D 3). The undetermined pressure constant
![]() $\unicode[STIX]{x1D705}$
, which appears on the right-hand side of (D 3), has a direct influence on
$\unicode[STIX]{x1D705}$
, which appears on the right-hand side of (D 3), has a direct influence on
![]() $u_{z,0}^{(2)}(1)$
. Since
$u_{z,0}^{(2)}(1)$
. Since
![]() $\unicode[STIX]{x1D705}$
appears as a forcing term in a linear relation, the connection between
$\unicode[STIX]{x1D705}$
appears as a forcing term in a linear relation, the connection between
![]() $u_{z,0}^{(2)}(1)$
and
$u_{z,0}^{(2)}(1)$
and
![]() $\unicode[STIX]{x1D705}$
proves to be linear. At the outset, a unique value for
$\unicode[STIX]{x1D705}$
proves to be linear. At the outset, a unique value for
![]() $\unicode[STIX]{x1D705}$
may be retrieved for a given set of input parameters in order to secure
$\unicode[STIX]{x1D705}$
may be retrieved for a given set of input parameters in order to secure
![]() $u_{z,0}^{(2)}(1)=0$
. For the reader’s convenience, its values for different ranges of
$u_{z,0}^{(2)}(1)=0$
. For the reader’s convenience, its values for different ranges of
![]() $Re$
and
$Re$
and
![]() $m$
are provided in table 1.
$m$
are provided in table 1.
Table 1. Calculated values of the pressure constant
![]() $\unicode[STIX]{x1D705}$
for different values of
$\unicode[STIX]{x1D705}$
for different values of
![]() $m$
and
$m$
and
![]() $Re$
.
$Re$
.

2.8 Characterization at successive orders and wavenumbers
In summary, the velocity and pressure fields may be expressed using
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}=-{\displaystyle \frac{F}{r}}+\unicode[STIX]{x1D700}v_{r}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{r,0}^{(2)}+u_{r,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right],\\ u_{\unicode[STIX]{x1D703}}=-m\unicode[STIX]{x1D700}v_{\unicode[STIX]{x1D703}}^{}\sin (m\unicode[STIX]{x1D703})-m\unicode[STIX]{x1D700}^{2}u_{\unicode[STIX]{x1D703},2}^{(2)}\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}=z\left\{{\displaystyle \frac{F^{\prime }}{r}}+\unicode[STIX]{x1D700}v_{z}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{z,0}^{(2)}+u_{z,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right]\right\},\\ p=P_{0}-{\displaystyle \frac{\unicode[STIX]{x1D705}_{0}}{2}}z^{2}-{\displaystyle \frac{F^{2}}{2r^{2}}}-{\displaystyle \frac{F^{\prime }}{rRe}}+\unicode[STIX]{x1D700}q^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[p_{0}^{(2)}+p_{2}^{(2)}\cos (2m\unicode[STIX]{x1D703})-{\displaystyle \frac{\unicode[STIX]{x1D705}}{2}}z^{2}\right].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}=-{\displaystyle \frac{F}{r}}+\unicode[STIX]{x1D700}v_{r}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{r,0}^{(2)}+u_{r,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right],\\ u_{\unicode[STIX]{x1D703}}=-m\unicode[STIX]{x1D700}v_{\unicode[STIX]{x1D703}}^{}\sin (m\unicode[STIX]{x1D703})-m\unicode[STIX]{x1D700}^{2}u_{\unicode[STIX]{x1D703},2}^{(2)}\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}=z\left\{{\displaystyle \frac{F^{\prime }}{r}}+\unicode[STIX]{x1D700}v_{z}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{z,0}^{(2)}+u_{z,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right]\right\},\\ p=P_{0}-{\displaystyle \frac{\unicode[STIX]{x1D705}_{0}}{2}}z^{2}-{\displaystyle \frac{F^{2}}{2r^{2}}}-{\displaystyle \frac{F^{\prime }}{rRe}}+\unicode[STIX]{x1D700}q^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[p_{0}^{(2)}+p_{2}^{(2)}\cos (2m\unicode[STIX]{x1D703})-{\displaystyle \frac{\unicode[STIX]{x1D705}}{2}}z^{2}\right].\end{array}\right\}\end{eqnarray}$$
To illustrate the behaviour of the solution, we confine our attention to a polar slice that extends between
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $2\unicode[STIX]{x03C0}/m$
. In figure 2, we examine the sensitivity of the solution for
$2\unicode[STIX]{x03C0}/m$
. In figure 2, we examine the sensitivity of the solution for
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
at increasing asymptotic orders using characteristic values of
$u_{z}$
at increasing asymptotic orders using characteristic values of
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=7$
. Only the radial variation is captured here, which may be accomplished by plotting the solution along a spoke at
$m=7$
. Only the radial variation is captured here, which may be accomplished by plotting the solution along a spoke at
![]() $\unicode[STIX]{x1D703}=0$
and a fixed value of
$\unicode[STIX]{x1D703}=0$
and a fixed value of
![]() $z$
. The radial velocity, which is featured on the left-hand side of the graph at three increasing orders of
$z$
. The radial velocity, which is featured on the left-hand side of the graph at three increasing orders of
![]() $\unicode[STIX]{x1D700}$
, confirms that even the first-order approximation,
$\unicode[STIX]{x1D700}$
, confirms that even the first-order approximation,
![]() $u_{r}^{(1)}$
, is considerably dissimilar from the leading-order solution. This disparity implies that the radial displacement of the sidewall leads to a significant distortion of the mean flow field compared to the circular configuration. However, these results also suggest that the second-order correction,
$u_{r}^{(1)}$
, is considerably dissimilar from the leading-order solution. This disparity implies that the radial displacement of the sidewall leads to a significant distortion of the mean flow field compared to the circular configuration. However, these results also suggest that the second-order correction,
![]() $u_{r}^{(2)}$
, only weakly affects the overall radial velocity. Although similar observations may be inferred for the tangential velocity, they are omitted here for the sake of brevity.
$u_{r}^{(2)}$
, only weakly affects the overall radial velocity. Although similar observations may be inferred for the tangential velocity, they are omitted here for the sake of brevity.
In contrast, by turning our attention to the axial velocity variation on the right-hand side, it may be seen that the second-order correction leads to a non-negligible shift in
![]() $u_{z}$
, especially as the centreline is approached, where the first-order contribution is nil by virtue of
$u_{z}$
, especially as the centreline is approached, where the first-order contribution is nil by virtue of
![]() $u_{z}^{(1)}(0)=0$
. The need for a second-order correction is therefore pivotal. In fact, the discrepancy near the centreline between Berman’s leading-order solution and that at
$u_{z}^{(1)}(0)=0$
. The need for a second-order correction is therefore pivotal. In fact, the discrepancy near the centreline between Berman’s leading-order solution and that at
![]() $O(\unicode[STIX]{x1D700}^{2})$
may be attributed to the mass flow rate increase reported in (2.4). Recalling that the mass flow rate entails an integration over
$O(\unicode[STIX]{x1D700}^{2})$
may be attributed to the mass flow rate increase reported in (2.4). Recalling that the mass flow rate entails an integration over
![]() $\unicode[STIX]{x1D703}$
, the contribution of the first-order correction
$\unicode[STIX]{x1D703}$
, the contribution of the first-order correction
![]() $u_{z}^{(1)}$
multiplied by the periodic function
$u_{z}^{(1)}$
multiplied by the periodic function
![]() $\cos (m\unicode[STIX]{x1D703})$
vanishes identically. However, the contribution of the second-order correction
$\cos (m\unicode[STIX]{x1D703})$
vanishes identically. However, the contribution of the second-order correction
![]() $u_{z}^{(2)}$
, which involves a
$u_{z}^{(2)}$
, which involves a
![]() $\unicode[STIX]{x1D703}$
-independent term (
$\unicode[STIX]{x1D703}$
-independent term (
![]() $u_{z,0}^{(2)}$
), leads to a finite contribution. Based on this simple comparison and mathematical verification, it may be concluded that the first-order correction affects all three velocity components, thus leading to marked differences from the circular configuration. As for the second-order correction, it proves to be essential to properly capture the behaviour of the axial velocity, especially near the centreline, and therefore helps to secure the principle of mass conservation.
$u_{z,0}^{(2)}$
), leads to a finite contribution. Based on this simple comparison and mathematical verification, it may be concluded that the first-order correction affects all three velocity components, thus leading to marked differences from the circular configuration. As for the second-order correction, it proves to be essential to properly capture the behaviour of the axial velocity, especially near the centreline, and therefore helps to secure the principle of mass conservation.
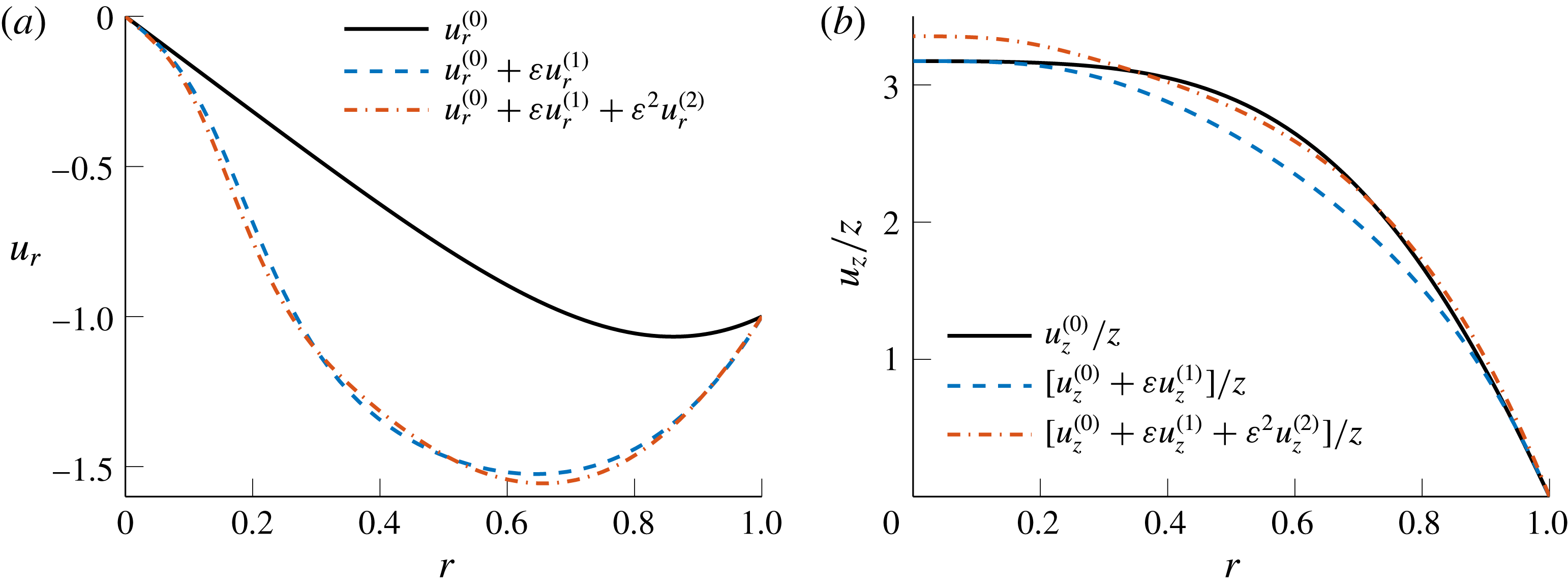
Figure 2. Influence of the corrections of different orders on the asymptotic approximations for (a)
![]() $u_{r}$
and (b)
$u_{r}$
and (b)
![]() $u_{z}/z$
at
$u_{z}/z$
at
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=7$
.
$m=7$
.

Figure 3. Influence of the circular wavenumber
![]() $m$
on (a)
$m$
on (a)
![]() $u_{\unicode[STIX]{x1D703}}$
along a spoke with
$u_{\unicode[STIX]{x1D703}}$
along a spoke with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$
and (b)
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$
and (b)
![]() $u_{z,0}^{(2)}$
at the centreline with
$u_{z,0}^{(2)}$
at the centreline with
![]() $\unicode[STIX]{x1D703}=0$
. Here
$\unicode[STIX]{x1D703}=0$
. Here
![]() $\unicode[STIX]{x1D700}=0.1$
and
$\unicode[STIX]{x1D700}=0.1$
and
![]() $Re=100$
.
$Re=100$
.
To better understand the effect of
![]() $m$
on the second-order approximation, both
$m$
on the second-order approximation, both
![]() $u_{\unicode[STIX]{x1D703}}$
and the centreline value of
$u_{\unicode[STIX]{x1D703}}$
and the centreline value of
![]() $u_{z}$
are depicted in figure 3 at
$u_{z}$
are depicted in figure 3 at
![]() $\unicode[STIX]{x1D700}=0.1$
and
$\unicode[STIX]{x1D700}=0.1$
and
![]() $Re=100$
. The tangential velocity is featured in figure 3(a) along a spoke with
$Re=100$
. The tangential velocity is featured in figure 3(a) along a spoke with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$
and
![]() $m=5$
, 6, 7, 8 and 9. Interestingly, the effect of the injection condition in (2.7) on the magnitude of
$m=5$
, 6, 7, 8 and 9. Interestingly, the effect of the injection condition in (2.7) on the magnitude of
![]() $u_{\unicode[STIX]{x1D703}}$
may be captured at the sidewall, where
$u_{\unicode[STIX]{x1D703}}$
may be captured at the sidewall, where
![]() $|u_{\unicode[STIX]{x1D703}}|$
increases incrementally with
$|u_{\unicode[STIX]{x1D703}}|$
increases incrementally with
![]() $m$
. The maximum values of
$m$
. The maximum values of
![]() $u_{\unicode[STIX]{x1D703}}$
also shift outwards towards the sidewall with successive increases in
$u_{\unicode[STIX]{x1D703}}$
also shift outwards towards the sidewall with successive increases in
![]() $m$
.
$m$
.
It is also useful to explore the sensitivity of the centreline value of
![]() $u_{z}^{(2)}(0)$
to variations in
$u_{z}^{(2)}(0)$
to variations in
![]() $m\in [3,12]$
in figure 3(b). Since
$m\in [3,12]$
in figure 3(b). Since
![]() $u_{z,2}^{(2)}(0)=0$
, it is sufficient to illustrate the behaviour of
$u_{z,2}^{(2)}(0)=0$
, it is sufficient to illustrate the behaviour of
![]() $u_{z,0}^{(2)}(0)$
in order to infer the underlying trend. Although the relation between
$u_{z,0}^{(2)}(0)$
in order to infer the underlying trend. Although the relation between
![]() $u_{z,0}^{(2)}(0)$
and
$u_{z,0}^{(2)}(0)$
and
![]() $m$
remains concealed in (D 2), the corresponding curve suggests the existence of a monotonically increasing quadratic polynomial of the form
$m$
remains concealed in (D 2), the corresponding curve suggests the existence of a monotonically increasing quadratic polynomial of the form
![]() $u_{z,0}^{(2)}(0)=c_{0}+c_{1}m+c_{2}m^{2}$
, whose coefficients in figure 3(b) are
$u_{z,0}^{(2)}(0)=c_{0}+c_{1}m+c_{2}m^{2}$
, whose coefficients in figure 3(b) are
![]() $c_{0}=-1.242$
,
$c_{0}=-1.242$
,
![]() $c_{1}=-0.1875$
and
$c_{1}=-0.1875$
and
![]() $c_{2}=0.817$
. Despite the appearance of
$c_{2}=0.817$
. Despite the appearance of
![]() $m^{2}$
in the equations explicitly, determining the quadratic solution analytically for any
$m^{2}$
in the equations explicitly, determining the quadratic solution analytically for any
![]() $Re$
and
$Re$
and
![]() $\unicode[STIX]{x1D700}$
proves to be a daunting task. Nonetheless, based on this characteristic graph, it may be ascertained that the role of
$\unicode[STIX]{x1D700}$
proves to be a daunting task. Nonetheless, based on this characteristic graph, it may be ascertained that the role of
![]() $u_{z,0}^{(2)}(0)$
can be significant, especially at increasing values of
$u_{z,0}^{(2)}(0)$
can be significant, especially at increasing values of
![]() $m$
. Although not shown, we also find that the effect of increasing the Reynolds number on
$m$
. Although not shown, we also find that the effect of increasing the Reynolds number on
![]() $u_{z,0}^{(2)}(0)$
is negligible in comparison to
$u_{z,0}^{(2)}(0)$
is negligible in comparison to
![]() $m$
.
$m$
.
As for flow rotationality, figure 4 displays isocontours of the tangential component of the steady-state vorticity
![]() $\unicode[STIX]{x1D6FA}_{z}$
in an arbitrary
$\unicode[STIX]{x1D6FA}_{z}$
in an arbitrary
![]() $\left(r,z\right)$
plane; also provided is a comparison of the streamlines for the present solution side by side with Berman’s. Based on this graph, it may be seen that the star-shaped configuration leads to deeper penetrating streamlines than the circular case. Specifically, the solid lines, which correspond to the present formulation, consistently approach the chamber axis more rapidly than the dashed lines of the non-wavy solution.
$\left(r,z\right)$
plane; also provided is a comparison of the streamlines for the present solution side by side with Berman’s. Based on this graph, it may be seen that the star-shaped configuration leads to deeper penetrating streamlines than the circular case. Specifically, the solid lines, which correspond to the present formulation, consistently approach the chamber axis more rapidly than the dashed lines of the non-wavy solution.

Figure 4. Isocontours of the tangential component of the rotational vorticity in an
![]() $\left(r,z\right)$
plane along with the corresponding streamlines according to the present formulation (solid lines). Also shown are the streamlines obtained for Berman’s model in a circular cross-section (dashed lines). Here we use
$\left(r,z\right)$
plane along with the corresponding streamlines according to the present formulation (solid lines). Also shown are the streamlines obtained for Berman’s model in a circular cross-section (dashed lines). Here we use
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=7$
.
$m=7$
.
3 Comparison to Navier–Stokes simulations
To further illustrate the behaviour of the non-circular profile and more accurately define its domain of applicability, a comparison is now undertaken between the results obtained from the present semi-analytical formulation and those predicted by a Navier–Stokes solver. To this end, the Navier–Stokes solver is introduced first along with its computational characteristics. Second, the sensitivity of the flow computations to variations in the three main parameters,
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $Re$
and
$Re$
and
![]() $m$
, are explored and compared to our second-order approximations.
$m$
, are explored and compared to our second-order approximations.
3.1 Solver description
Our numerical simulations are performed using a compressible Navier–Stokes solver called CHARME, which belongs to the multi-solver suite CEDRE developed by the French Aerospace Laboratory (ONERA). A detailed overview of the code’s functionality is provided by Refloch et al. (Reference Refloch, Courbet, Murrone, Villedieu, Laurent, Gilbank, Troyes, Tessé, Chaineray and Dargaud2011), while examples of its computational capabilities, which include laminar flow simulations and verifications of linear stability analyses of rocket internal flow fields, are furnished by Chedevergne et al. (Reference Chedevergne, Casalis and Majdalani2012) and Boyer et al. (Reference Boyer, Casalis and Estivalèzes2013). In these studies, an excellent agreement is reported between theory and computations, thus showcasing the solver’s effectiveness in capturing the mean flow development as well as the unsteady hydrodynamic instabilities that evolve in a rocket chamber. As usual, the latter may be idealized as a porous tube with uniform wall injection, which is consistent with the geometric configuration used presently. As for the code, a second-order discretization stencil is implemented for spatial interpolation, while Euler’s fluxes are computed using a Roe scheme. Throughout these simulations, the length and mean radius of the porous tube are kept constant at
![]() $8a$
and
$8a$
and
![]() $a=1$
cm, respectively. Although the value of
$a=1$
cm, respectively. Although the value of
![]() $a$
may be modified, the aspect ratio is held constant. Furthermore, the wall injection speed
$a$
may be modified, the aspect ratio is held constant. Furthermore, the wall injection speed
![]() $U_{w}$
is adjusted to calculate the targeted Reynolds numbers while ensuring that it remains sufficiently small to promote low compressibility levels. At the headwall, a slip condition that is compatible with our model is applied to avoid the development of an undesirable boundary layer. In the domain exit plane at
$U_{w}$
is adjusted to calculate the targeted Reynolds numbers while ensuring that it remains sufficiently small to promote low compressibility levels. At the headwall, a slip condition that is compatible with our model is applied to avoid the development of an undesirable boundary layer. In the domain exit plane at
![]() $z=8a$
, a pressure outlet condition is imposed. The code is fully three-dimensional and the assumption of linear axial variation is not forced. Then, using a three-dimensional unstructured mesh with approximately four million total elements, 600 cells are selected to construct the axial grid along the sidewall, whereas 150 cells are distributed radially along the diameter. Although the mesh size can generally depend on
$z=8a$
, a pressure outlet condition is imposed. The code is fully three-dimensional and the assumption of linear axial variation is not forced. Then, using a three-dimensional unstructured mesh with approximately four million total elements, 600 cells are selected to construct the axial grid along the sidewall, whereas 150 cells are distributed radially along the diameter. Although the mesh size can generally depend on
![]() $Re$
,
$Re$
,
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $m$
, the present discretization size is confidently chosen because of its demonstrated effectiveness in previous studies of analogous flow fields (Chedevergne et al.
Reference Chedevergne, Casalis and Majdalani2012; Boyer et al.
Reference Boyer, Casalis and Estivalèzes2013). In what follows, the term ‘model’ will be used to denote second-order asymptotic results obtained from the present framework, whereas ‘CFD’ will refer to numerical (computational fluid dynamics) simulations acquired from the nonlinear Navier–Stokes solver.
$m$
, the present discretization size is confidently chosen because of its demonstrated effectiveness in previous studies of analogous flow fields (Chedevergne et al.
Reference Chedevergne, Casalis and Majdalani2012; Boyer et al.
Reference Boyer, Casalis and Estivalèzes2013). In what follows, the term ‘model’ will be used to denote second-order asymptotic results obtained from the present framework, whereas ‘CFD’ will refer to numerical (computational fluid dynamics) simulations acquired from the nonlinear Navier–Stokes solver.
3.2 On the linearity of the axial velocity with respect to
 $z$
$z$
Inspired by Berman’s solution and the mass conservation relation (2.8), the axial velocity component can be assumed to be linear with respect to the axial coordinate
![]() $z$
. In order to verify that the CFD solution will indeed mimic this linear behaviour, figure 5 is used to compare our model to the computed solution for
$z$
. In order to verify that the CFD solution will indeed mimic this linear behaviour, figure 5 is used to compare our model to the computed solution for
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=7$
. To magnify the possible departures from the expected linearity, the leading-order contribution of
$m=7$
. To magnify the possible departures from the expected linearity, the leading-order contribution of
![]() $O(1)$
, i.e. Berman’s solution, is subtracted from the axial velocity component
$O(1)$
, i.e. Berman’s solution, is subtracted from the axial velocity component
![]() $u_{z}$
, thus leaving only first- and second-order corrections. Based on this comparison, it is clear that the computed axial velocity remains linear with respect to
$u_{z}$
, thus leaving only first- and second-order corrections. Based on this comparison, it is clear that the computed axial velocity remains linear with respect to
![]() $z$
up to approximately
$z$
up to approximately
![]() $z=7$
using
$z=7$
using
![]() $r=0.3$
. Beyond this location, it is possible for the outlet pressure condition to slightly influence the axial development of the flow field. Apart from this outlet effect, it may be argued that the Navier–Stokes solver in figure 5 helps to validate the assumption of a linear variation with respect to
$r=0.3$
. Beyond this location, it is possible for the outlet pressure condition to slightly influence the axial development of the flow field. Apart from this outlet effect, it may be argued that the Navier–Stokes solver in figure 5 helps to validate the assumption of a linear variation with respect to
![]() $z$
. Moreover, the visual agreement in the resulting slopes confirms that the simulation accurately reproduces the radial and tangential evolutions of the modelled flow. In fact, additional comparisons only reinforce this behaviour. In the interest of simplicity, subsequent results will be displayed halfway through the chamber at
$z$
. Moreover, the visual agreement in the resulting slopes confirms that the simulation accurately reproduces the radial and tangential evolutions of the modelled flow. In fact, additional comparisons only reinforce this behaviour. In the interest of simplicity, subsequent results will be displayed halfway through the chamber at
![]() $z=4$
.
$z=4$
.
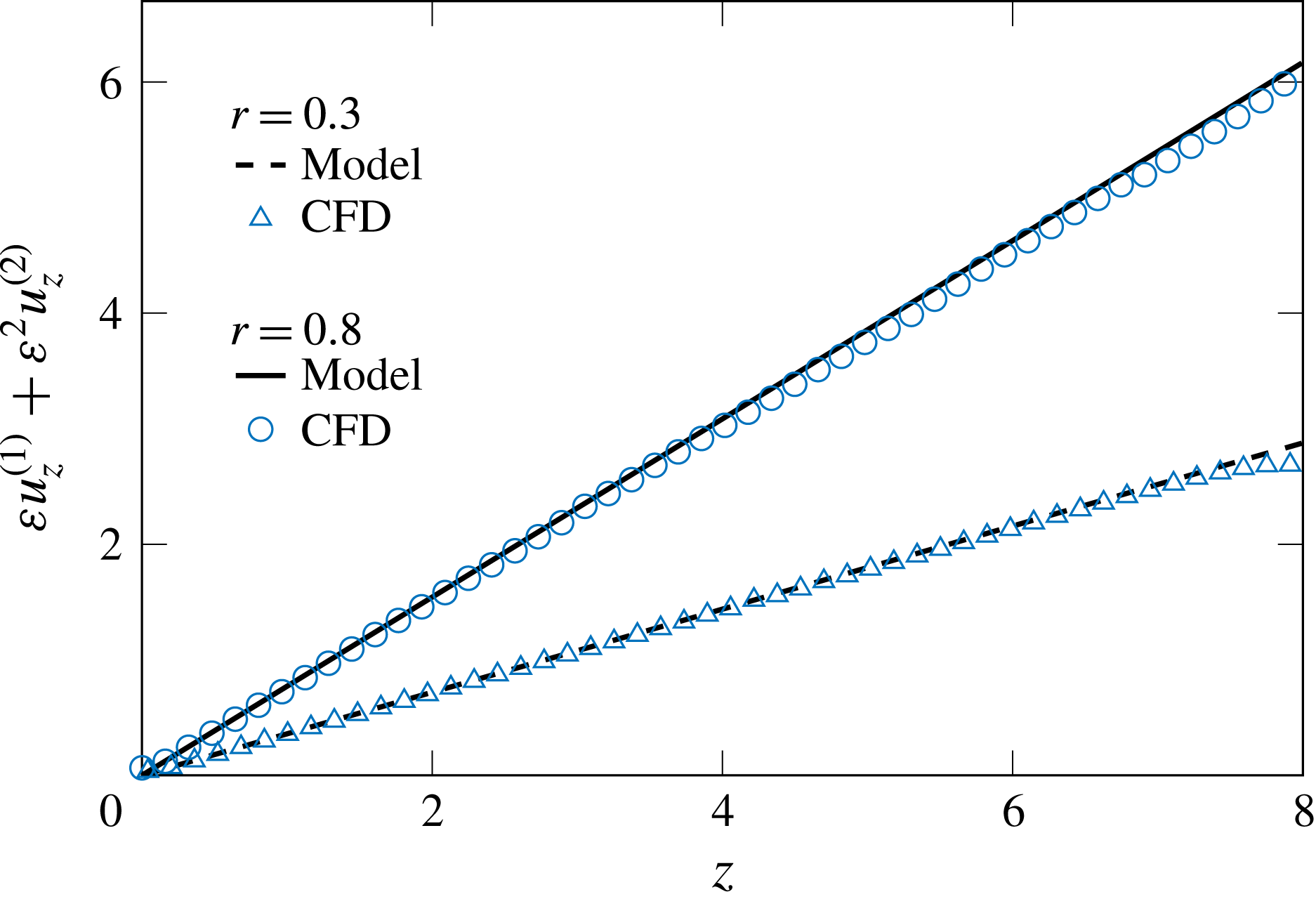
Figure 5. Evolution along the domain of the axial velocity
![]() $\unicode[STIX]{x1D700}u_{z}^{(1)}+\unicode[STIX]{x1D700}^{2}u_{z}^{(2)}$
at two radial locations of
$\unicode[STIX]{x1D700}u_{z}^{(1)}+\unicode[STIX]{x1D700}^{2}u_{z}^{(2)}$
at two radial locations of
![]() $r=(0.3,0.8)$
in the
$r=(0.3,0.8)$
in the
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
plane for
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
plane for
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=7$
.
$m=7$
.

Figure 6. Isocontours of the radial, tangential and axial velocity components based on (a) nonlinear Navier–Stokes computations and (b) linear asymptotics at
![]() $O(\unicode[STIX]{x1D700}^{2})$
. Using
$O(\unicode[STIX]{x1D700}^{2})$
. Using
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
and
$z=4$
and
![]() $m=7$
, the spokes depicting extrema are identified with dashed lines at their corresponding angular locations.
$m=7$
, the spokes depicting extrema are identified with dashed lines at their corresponding angular locations.
3.3 Flow characterization based on both asymptotics and computations
To take advantage of the periodicity in the angular direction, flow field comparisons are reproduced in a polar slice that extends from
![]() $\unicode[STIX]{x1D703}=0$
to
$\unicode[STIX]{x1D703}=0$
to
![]() $2\unicode[STIX]{x03C0}/m$
. Note that the mesh used in conjunction with the Navier–Stokes simulations does not rely on periodic conditions; the tangential coordinate
$2\unicode[STIX]{x03C0}/m$
. Note that the mesh used in conjunction with the Navier–Stokes simulations does not rely on periodic conditions; the tangential coordinate
![]() $\unicode[STIX]{x1D703}$
extends over the full range of
$\unicode[STIX]{x1D703}$
extends over the full range of
![]() $[0,2\unicode[STIX]{x03C0}]$
. We begin in figure 6 with the isocontours of the three velocity components using
$[0,2\unicode[STIX]{x03C0}]$
. We begin in figure 6 with the isocontours of the three velocity components using
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
and
$z=4$
and
![]() $m=7$
. Despite the linearization that affects the second-order asymptotic framework, an excellent agreement may be noted between the isocontours generated from the numerical simulations and those obtained from the asymptotic model for all three radial, tangential and axial velocity components.
$m=7$
. Despite the linearization that affects the second-order asymptotic framework, an excellent agreement may be noted between the isocontours generated from the numerical simulations and those obtained from the asymptotic model for all three radial, tangential and axial velocity components.
By turning our attention first to the tangential velocity, it may be confirmed that its maximum absolute values occur at
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
and
![]() $3\unicode[STIX]{x03C0}/(2m)$
taken along the sidewall because of surface waviness; as for its sign, it depends on whether the flow is situated above or below the meridian line at
$3\unicode[STIX]{x03C0}/(2m)$
taken along the sidewall because of surface waviness; as for its sign, it depends on whether the flow is situated above or below the meridian line at
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, where the tangential velocity vanishes identically. The tangential velocity also vanishes at the domain delimiting lower and upper spoke lines located at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, where the tangential velocity vanishes identically. The tangential velocity also vanishes at the domain delimiting lower and upper spoke lines located at
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $2\unicode[STIX]{x03C0}/m$
, where the radial velocity
$2\unicode[STIX]{x03C0}/m$
, where the radial velocity
![]() $u_{r}$
matches the wall-normal velocity in both direction and magnitude. At those specific sites, both axial and tangential velocities vanish, thus leaving the flow to enter the chamber radially inwards towards the centreline (i.e. with no directional distortion). Naturally,
$u_{r}$
matches the wall-normal velocity in both direction and magnitude. At those specific sites, both axial and tangential velocities vanish, thus leaving the flow to enter the chamber radially inwards towards the centreline (i.e. with no directional distortion). Naturally,
![]() $|u_{\unicode[STIX]{x1D703}}|$
diminishes while moving inwards away from the sidewall, or when moving tangentially towards the meridian lines as well as the upper and lower domain delimiting lines. In anticlockwise fashion,
$|u_{\unicode[STIX]{x1D703}}|$
diminishes while moving inwards away from the sidewall, or when moving tangentially towards the meridian lines as well as the upper and lower domain delimiting lines. In anticlockwise fashion,
![]() $u_{\unicode[STIX]{x1D703}}$
switches from negative to positive values as we cross from
$u_{\unicode[STIX]{x1D703}}$
switches from negative to positive values as we cross from
![]() $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/m$
to
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/m$
to
![]() $\unicode[STIX]{x03C0}/m<\unicode[STIX]{x1D703}<2\unicode[STIX]{x03C0}/m$
. Moreover, given that the tangential velocity is induced by small deviations from a circular cross-section, it remains smaller than its radial and axial counterparts, being asymptotically driven by
$\unicode[STIX]{x03C0}/m<\unicode[STIX]{x1D703}<2\unicode[STIX]{x03C0}/m$
. Moreover, given that the tangential velocity is induced by small deviations from a circular cross-section, it remains smaller than its radial and axial counterparts, being asymptotically driven by
![]() $O(\unicode[STIX]{x1D700})$
surface displacements, unlike the radial and axial velocities, which are chiefly induced by the mass injection mechanism.
$O(\unicode[STIX]{x1D700})$
surface displacements, unlike the radial and axial velocities, which are chiefly induced by the mass injection mechanism.
At this juncture, it may be helpful to recall that, in the absence of surface waviness, the isocontours of the axisymmetric axial velocity lead to concentric circles that exhibit a maximum value along the centreline. In the present configuration, the isocontours of
![]() $u_{z}$
stretch radially outwards along the meridian line of
$u_{z}$
stretch radially outwards along the meridian line of
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, where the chamber radius happens to be the shortest. Naturally, the area contraction in flow cross-section at this angular position induces a local increase in the axial velocity. Conversely, these isocontours shift radially inwards at the upper and lower boundaries where local wall expansions lead to an increase in the flow cross-section and, therefore, a corresponding reduction in
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, where the chamber radius happens to be the shortest. Naturally, the area contraction in flow cross-section at this angular position induces a local increase in the axial velocity. Conversely, these isocontours shift radially inwards at the upper and lower boundaries where local wall expansions lead to an increase in the flow cross-section and, therefore, a corresponding reduction in
![]() $u_{z}$
.
$u_{z}$
.
In fact, continuity may be used to partly explain the trends observed in the isocontours of the radial velocity. Upon close inspection of the corresponding graphs, it may be ascertained that
![]() $u_{r}$
vanishes along the centreline, where
$u_{r}$
vanishes along the centreline, where
![]() $u_{z}$
reaches its peak value, and that it increases in regions of axial velocity deficit. This behaviour may be attributed to the flow turning mechanism that affects the wall-injected stream, specifically as it negotiates a
$u_{z}$
reaches its peak value, and that it increases in regions of axial velocity deficit. This behaviour may be attributed to the flow turning mechanism that affects the wall-injected stream, specifically as it negotiates a
![]() $90^{\circ }$
turn before merging axially with the core flow. At
$90^{\circ }$
turn before merging axially with the core flow. At
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, owing to the stretched axial velocity isocontours, the radial velocity deceleration towards the centreline is more rapid than at the
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
, owing to the stretched axial velocity isocontours, the radial velocity deceleration towards the centreline is more rapid than at the
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $2\unicode[STIX]{x03C0}/m$
borderlines, where the flow may be seen to be radially expanded. Another characteristic of
$2\unicode[STIX]{x03C0}/m$
borderlines, where the flow may be seen to be radially expanded. Another characteristic of
![]() $u_{r}$
, which has been well documented in the literature, corresponds to its velocity overshoot compared to its wall value (Saad & Majdalani Reference Saad and Majdalani2010). Despite the unitary speed of
$u_{r}$
, which has been well documented in the literature, corresponds to its velocity overshoot compared to its wall value (Saad & Majdalani Reference Saad and Majdalani2010). Despite the unitary speed of
![]() $|u_{r}|=1$
at the sidewall,
$|u_{r}|=1$
at the sidewall,
![]() $|u_{r}|$
undergoes first an increase in absolute value due to the sudden radial pinching of the circumferential area that is normal to the injected flow, and which does not permit the flow to develop a sufficient
$|u_{r}|$
undergoes first an increase in absolute value due to the sudden radial pinching of the circumferential area that is normal to the injected flow, and which does not permit the flow to develop a sufficient
![]() $u_{z}$
component to adequately transport the mass axially. The resulting increase in
$u_{z}$
component to adequately transport the mass axially. The resulting increase in
![]() $|u_{r}|$
may be noted in the peak contour points in figure 6, namely, those that materialize at some intermediate positions between the wall and the centreline. Naturally, when the flow is pinched, the locus of these extrema moves closer to the centreline.
$|u_{r}|$
may be noted in the peak contour points in figure 6, namely, those that materialize at some intermediate positions between the wall and the centreline. Naturally, when the flow is pinched, the locus of these extrema moves closer to the centreline.
As alluded to earlier, another byproduct of waviness and viscosity may be the production of axial vorticity, which is absent in the strictly axisymmetric Taylor–Culick model (Balachandar et al.
Reference Balachandar, Buckmaster and Short2001). To illustrate the corresponding behaviour, isocontours of axial vorticity, namely,
![]() $\unicode[STIX]{x1D6FA}_{z}$
, are displayed in figure 7 for
$\unicode[STIX]{x1D6FA}_{z}$
, are displayed in figure 7 for
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
and
$z=4$
and
![]() $m=7$
. Using the variable coordinate transformation at the wall,
$m=7$
. Using the variable coordinate transformation at the wall,
![]() $\unicode[STIX]{x1D6FA}_{z}$
may be expressed as
$\unicode[STIX]{x1D6FA}_{z}$
may be expressed as
Note that this vorticity component vanishes for the axisymmetric case. In order to improve the velocity gradients and thus the vorticity, the spatial integration scheme within the Navier–Stokes solver is increased to the third order in figure 7. Graphically, one may infer that the Navier–Stokes computations tend to agree qualitatively with the second-order asymptotic solution, especially in the two bulk regions where the axial vorticity is largest. Nonetheless, discrepancies may also be seen at the sidewall near
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
and
![]() $3\unicode[STIX]{x03C0}/(2m)$
. The bulk vorticity regions that develop in this configuration are consistent with those detailed by Kurdyumov (Reference Kurdyumov2006). Furthermore, the dissimilarities observed near the sidewall may be attributed to the practical limitations associated with asymptotic expansions. They may also be ascribed to the compounded effects of numerical errors that accrue during the evaluation of velocity gradients within the Navier–Stokes solver.
$3\unicode[STIX]{x03C0}/(2m)$
. The bulk vorticity regions that develop in this configuration are consistent with those detailed by Kurdyumov (Reference Kurdyumov2006). Furthermore, the dissimilarities observed near the sidewall may be attributed to the practical limitations associated with asymptotic expansions. They may also be ascribed to the compounded effects of numerical errors that accrue during the evaluation of velocity gradients within the Navier–Stokes solver.

Figure 7. Isocontours of the axial vorticity based on (a) nonlinear Navier–Stokes computations and (b) linear asymptotics at
![]() $O(\unicode[STIX]{x1D700}^{2})$
. Here
$O(\unicode[STIX]{x1D700}^{2})$
. Here
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
and
$z=4$
and
![]() $m=7$
.
$m=7$
.
3.4 Sensitivity to various Reynolds numbers, radial deviations and wavenumbers
To further explore the effects of varying the Reynolds number, radial deviation amplitude and circular wavenumber on the flow development, the sensitivity of the three velocity components to these parameters may be quantified by comparing the second-order corrections to the individual computations taken along different polar angles. Guided by the isocontours of figure 6, both
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{z}$
seem to display interesting structures along angular cuts taken at
$u_{z}$
seem to display interesting structures along angular cuts taken at
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $\unicode[STIX]{x03C0}/m$
, whereas
$\unicode[STIX]{x03C0}/m$
, whereas
![]() $u_{\unicode[STIX]{x1D703}}$
may be best featured at
$u_{\unicode[STIX]{x1D703}}$
may be best featured at
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
. We therefore proceed to evaluate the three velocity components along their most representative inclination angles and showcase their outcomes in figures 8–10 using both asymptotics and computations.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
. We therefore proceed to evaluate the three velocity components along their most representative inclination angles and showcase their outcomes in figures 8–10 using both asymptotics and computations.
As we seek to better understand the role of
![]() $\unicode[STIX]{x1D700}$
on the axial velocity, the second-order corrections obtained asymptotically are compared to those computed in figure 8(a) using
$\unicode[STIX]{x1D700}$
on the axial velocity, the second-order corrections obtained asymptotically are compared to those computed in figure 8(a) using
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
,
$z=4$
,
![]() $m=7$
and two values of
$m=7$
and two values of
![]() $\unicode[STIX]{x1D700}$
that correspond to
$\unicode[STIX]{x1D700}$
that correspond to
![]() $0.01$
and
$0.01$
and
![]() $0.1$
. Results are deliberately displayed along a constant
$0.1$
. Results are deliberately displayed along a constant
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
spoke where the largest deviations from the axisymmetric motion may be realized. To further magnify differences, the exact Berman solution that is recovered at leading order is subtracted from both solutions, and the outcome is divided by
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
spoke where the largest deviations from the axisymmetric motion may be realized. To further magnify differences, the exact Berman solution that is recovered at leading order is subtracted from both solutions, and the outcome is divided by
![]() $\unicode[STIX]{x1D700}$
, thus leaving us with
$\unicode[STIX]{x1D700}$
, thus leaving us with
![]() $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
. In view of the dual magnification levels that are implemented, it may be argued that the agreement between computations and asymptotics is satisfactory, especially in the ability of the model to capture both sidewall and centreline variations with
$[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
. In view of the dual magnification levels that are implemented, it may be argued that the agreement between computations and asymptotics is satisfactory, especially in the ability of the model to capture both sidewall and centreline variations with
![]() $\unicode[STIX]{x1D700}$
rather consistently. The most noticeable discrepancies remain small and mostly confined to the annular region that extends approximately between
$\unicode[STIX]{x1D700}$
rather consistently. The most noticeable discrepancies remain small and mostly confined to the annular region that extends approximately between
![]() $r\approx 0.4$
and 0.7.
$r\approx 0.4$
and 0.7.
In fact, because of the magnification effect, these discrepancies actually fall within the numerical uncertainty that accompanies our simulations. The reasons are these. Since the mesh is uniformly discretized along the
![]() $z$
direction, the accuracy of
$z$
direction, the accuracy of
![]() $u_{z}/z$
directly depends on the finite gap between two axial positions. Furthermore, the disparities can stem either from higher-order terms that are not accounted for in the asymptotic formulation, or from the diffusive nature of the second-order discretization scheme that is adopted in the Navier–Stokes solver.
$u_{z}/z$
directly depends on the finite gap between two axial positions. Furthermore, the disparities can stem either from higher-order terms that are not accounted for in the asymptotic formulation, or from the diffusive nature of the second-order discretization scheme that is adopted in the Navier–Stokes solver.

Figure 8. Comparison between (a) the axial velocity correction at
![]() $Re=100$
,
$Re=100$
,
![]() $z=4$
and
$z=4$
and
![]() $\unicode[STIX]{x1D700}=(0.01,0.1)$
along a constant
$\unicode[STIX]{x1D700}=(0.01,0.1)$
along a constant
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
spoke, and (b) the radial velocity correction at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$
spoke, and (b) the radial velocity correction at
![]() $\unicode[STIX]{x1D700}=0.01$
,
$\unicode[STIX]{x1D700}=0.01$
,
![]() $z=4$
and
$z=4$
and
![]() $Re=(100,1000)$
along a constant
$Re=(100,1000)$
along a constant
![]() $\unicode[STIX]{x1D703}=0$
spoke. Here we use both Navier–Stokes computations (symbols) and second-order asymptotics (lines) for
$\unicode[STIX]{x1D703}=0$
spoke. Here we use both Navier–Stokes computations (symbols) and second-order asymptotics (lines) for
![]() $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
and
$[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
and
![]() $u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$
with
$u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$
with
![]() $m=7$
crests.
$m=7$
crests.
As for the influence of the Reynolds number on the radial velocity, it is illustrated in figure 8(b) using
![]() $\unicode[STIX]{x1D700}=0.01$
,
$\unicode[STIX]{x1D700}=0.01$
,
![]() $m=7$
and two values of
$m=7$
and two values of
![]() $Re$
that correspond to 100 and 1000, respectively. Choosing a relatively small value of
$Re$
that correspond to 100 and 1000, respectively. Choosing a relatively small value of
![]() $\unicode[STIX]{x1D700}$
enables us to compute the flow field with a large Reynolds number. Here, too, we display only the second-order correction in the radial velocity,
$\unicode[STIX]{x1D700}$
enables us to compute the flow field with a large Reynolds number. Here, too, we display only the second-order correction in the radial velocity,
![]() $u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$
, by subtracting the leading-order contribution. The agreement that is achieved between the numerical simulations and the asymptotic formulation is gratifying to note, especially as the Reynolds number is set at 1000.
$u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$
, by subtracting the leading-order contribution. The agreement that is achieved between the numerical simulations and the asymptotic formulation is gratifying to note, especially as the Reynolds number is set at 1000.
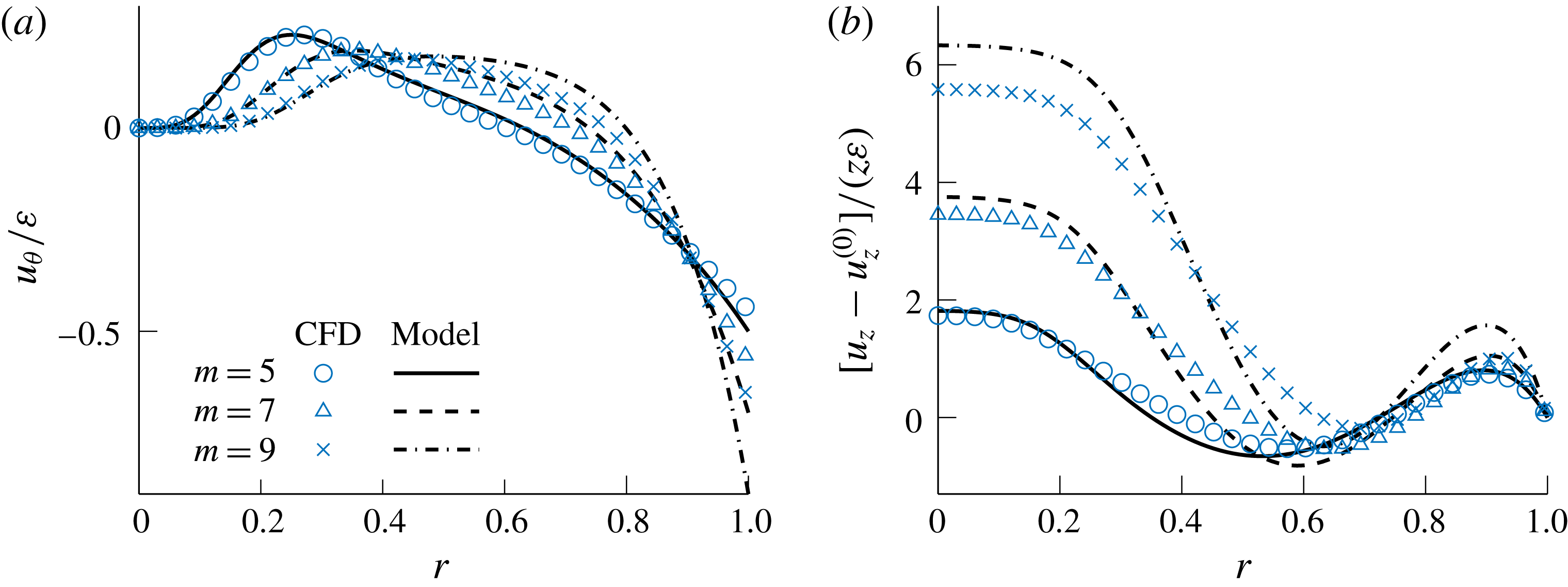
Figure 9. Sensitivity of the tangential and axial velocities to variations in
![]() $m$
using both computations (symbols) and second-order asymptotics; here we take
$m$
using both computations (symbols) and second-order asymptotics; here we take
![]() $\unicode[STIX]{x1D700}=0.1$
and
$\unicode[STIX]{x1D700}=0.1$
and
![]() $Re=100$
. Results are shown along constant angular spokes of (a)
$Re=100$
. Results are shown along constant angular spokes of (a)
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
for the tangential velocity
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
for the tangential velocity
![]() $u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$
and (b)
$u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$
and (b)
![]() $\unicode[STIX]{x1D703}=0$
for the axial velocity
$\unicode[STIX]{x1D703}=0$
for the axial velocity
![]() $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
.
$[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$
.
In figure 9(a), the sensitivity of the tangential velocity on the circular wavenumber is characterized by showcasing
![]() $u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$
along a polar angle of
$u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$
along a polar angle of
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
using
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
using
![]() $\unicode[STIX]{x1D700}=0.1$
,
$\unicode[STIX]{x1D700}=0.1$
,
![]() $Re=100$
and
$Re=100$
and
![]() $m=5$
, 7 and 9. The skipping of even values of
$m=5$
, 7 and 9. The skipping of even values of
![]() $m$
reduces visual clutter by helping to distinguish between the remaining curves, especially since the use of
$m$
reduces visual clutter by helping to distinguish between the remaining curves, especially since the use of
![]() $m=4$
, 6 and 8 leads to nearly identical trends. It is also guided by practical reasons, such as the preferred grain perforations in industry, which are invariably designed with an odd number of star points, crests or lobes, with the hope that such arrangements would help to mitigate the development of acoustic instabilities. Here, too, the agreement between computations and the modelled solution appears to be excellent in the core region. However, small differences begin to appear when the wavenumber is increased or when the sidewall is approached. We also remark that at
$m=4$
, 6 and 8 leads to nearly identical trends. It is also guided by practical reasons, such as the preferred grain perforations in industry, which are invariably designed with an odd number of star points, crests or lobes, with the hope that such arrangements would help to mitigate the development of acoustic instabilities. Here, too, the agreement between computations and the modelled solution appears to be excellent in the core region. However, small differences begin to appear when the wavenumber is increased or when the sidewall is approached. We also remark that at
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
, the contribution of second-order terms to the tangential velocity become negligible because of the
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
, the contribution of second-order terms to the tangential velocity become negligible because of the
![]() $\sin (2m\unicode[STIX]{x1D703})$
term that appears in the definition of
$\sin (2m\unicode[STIX]{x1D703})$
term that appears in the definition of
![]() $u_{\unicode[STIX]{x1D703}}^{(2)}$
. As one may surmise from (2.13), the minor disparities that are detected near the sidewall may be attributed to the omission of third-order terms in the asymptotic expansion of the injection velocity. Asymptotically, one must have
$u_{\unicode[STIX]{x1D703}}^{(2)}$
. As one may surmise from (2.13), the minor disparities that are detected near the sidewall may be attributed to the omission of third-order terms in the asymptotic expansion of the injection velocity. Asymptotically, one must have
where the quantity
![]() $\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D6FC}^{2}-\frac{1}{2}\unicode[STIX]{x1D6FC}^{\prime 2})\unicode[STIX]{x1D700}^{3}$
reduces to
$\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D6FC}^{2}-\frac{1}{2}\unicode[STIX]{x1D6FC}^{\prime 2})\unicode[STIX]{x1D700}^{3}$
reduces to
![]() $m^{3}\unicode[STIX]{x1D700}^{3}/2$
at
$m^{3}\unicode[STIX]{x1D700}^{3}/2$
at
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
; this third-order correction actually matches the gap between the computational and second-order asymptotic values at the wall, which widens with successive increases in
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$
; this third-order correction actually matches the gap between the computational and second-order asymptotic values at the wall, which widens with successive increases in
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D700}$
.
$\unicode[STIX]{x1D700}$
.

Figure 10. Isocontours of (a) the radial velocity
![]() $u_{r}$
for
$u_{r}$
for
![]() $m=5$
, (b) the radial velocity
$m=5$
, (b) the radial velocity
![]() $u_{r}$
for
$u_{r}$
for
![]() $m=7$
, (c) the tangential velocity
$m=7$
, (c) the tangential velocity
![]() $u_{\unicode[STIX]{x1D703}}$
for
$u_{\unicode[STIX]{x1D703}}$
for
![]() $m=7$
and (d) the axial velocity
$m=7$
and (d) the axial velocity
![]() $u_{z}$
for
$u_{z}$
for
![]() $m=7$
using
$m=7$
using
![]() $\unicode[STIX]{x1D700}=0.2$
and
$\unicode[STIX]{x1D700}=0.2$
and
![]() $Re=100$
.
$Re=100$
.
The sensitivity of the axial velocity on the circular wavenumber is illustrated in figure 9(b) along a different polar angle, namely
![]() $\unicode[STIX]{x1D703}=0$
, at the same Reynolds number and deviation values. Here, Berman’s contribution
$\unicode[STIX]{x1D703}=0$
, at the same Reynolds number and deviation values. Here, Berman’s contribution
![]() $u_{z}^{(0)}$
is subtracted from the total axial velocity component in order to showcase the correction only, as done previously in figure 8. Consistently with the behaviour observed in the tangential velocity comparison, the agreement between computations and the modelled solution appears to be quite satisfactory for
$u_{z}^{(0)}$
is subtracted from the total axial velocity component in order to showcase the correction only, as done previously in figure 8. Consistently with the behaviour observed in the tangential velocity comparison, the agreement between computations and the modelled solution appears to be quite satisfactory for
![]() $m=5$
, although it slowly deteriorates as
$m=5$
, although it slowly deteriorates as
![]() $m$
is increased. As before, the overshoot of the model near
$m$
is increased. As before, the overshoot of the model near
![]() $r\approx 0.9$
may be attributed to the diffusivity of the Navier–Stokes solver; the accuracy of the simulation along the axis remains limited by the finite discretization in the axial direction. Since the absolute value of the axial velocity along the axis
$r\approx 0.9$
may be attributed to the diffusivity of the Navier–Stokes solver; the accuracy of the simulation along the axis remains limited by the finite discretization in the axial direction. Since the absolute value of the axial velocity along the axis
![]() $|u_{z}^{(2)}(0)|$
increases with
$|u_{z}^{(2)}(0)|$
increases with
![]() $m$
, so does the uncertainty associated with the axial mesh discretization, thus leading to a growing disparity between the simulations and the modelled solution. Furthermore, it may be helpful to note that the displayed velocity components are divided by
$m$
, so does the uncertainty associated with the axial mesh discretization, thus leading to a growing disparity between the simulations and the modelled solution. Furthermore, it may be helpful to note that the displayed velocity components are divided by
![]() $\unicode[STIX]{x1D700}$
to better differentiate among the curves. Nonetheless, the noted discrepancies remain small compared to the total velocity magnitude
$\unicode[STIX]{x1D700}$
to better differentiate among the curves. Nonetheless, the noted discrepancies remain small compared to the total velocity magnitude
![]() $\boldsymbol{u}$
.
$\boldsymbol{u}$
.
Before leaving this discussion, it may be instructive to note that, in the foregoing work, the product
![]() $\unicode[STIX]{x1D700}Re$
has been consistently smaller than 10. Nonetheless, comparisons could have been undertaken for values that reach
$\unicode[STIX]{x1D700}Re$
has been consistently smaller than 10. Nonetheless, comparisons could have been undertaken for values that reach
![]() $\unicode[STIX]{x1D700}Re\approx 30$
. Above this level, the Navier–Stokes solver will have difficulty converging onto a steady periodic solution. An example of the model’s validity for
$\unicode[STIX]{x1D700}Re\approx 30$
. Above this level, the Navier–Stokes solver will have difficulty converging onto a steady periodic solution. An example of the model’s validity for
![]() $\unicode[STIX]{x1D700}Re=20$
is provided in figure 10, where isocontours of the velocity are displayed at two different values of
$\unicode[STIX]{x1D700}Re=20$
is provided in figure 10, where isocontours of the velocity are displayed at two different values of
![]() $m$
. By comparing the upper and lower sections of the graph, the ability of the model to mirror the computed solution seems gratifying, except in what concerns the negative peak magnitudes of
$m$
. By comparing the upper and lower sections of the graph, the ability of the model to mirror the computed solution seems gratifying, except in what concerns the negative peak magnitudes of
![]() $u_{r}$
in the model, which overshoot their computed values. The axial velocity in figure 10(d) also exhibits different lobe shapes when comparing the modelled solution to its simulation at the same contour levels.
$u_{r}$
in the model, which overshoot their computed values. The axial velocity in figure 10(d) also exhibits different lobe shapes when comparing the modelled solution to its simulation at the same contour levels.
4 Conclusion
In this study, the Navier–Stokes equations are applied to the asymmetric problem that arises in the context of an injection-driven mean flow motion in a porous tube with a wavy non-circular cross-section. After mapping the radial coordinate to a fixed boundary, the equations of motion are transformed and shown to recover Berman’s fourth-order differential equation in the absence of surface distortion. To make further headway, an asymptotic expansion is pursued in the deviation amplitude,
![]() $\unicode[STIX]{x1D700}$
, which stands for the maximum radial displacement in a unit circle. This enables us to derive the system of equations that prescribe the stationary motion both at the first and second orders in
$\unicode[STIX]{x1D700}$
, which stands for the maximum radial displacement in a unit circle. This enables us to derive the system of equations that prescribe the stationary motion both at the first and second orders in
![]() $\unicode[STIX]{x1D700}$
. Then using judiciously imposed similarity transformations, the first-order system is reduced to four ordinary differential equations that can be solved straightforwardly. Along similar lines, the second-order system is transformed into an assortment of seven ordinary differential equations that can be solved with equal ease. The second-order formulation is subsequently shown to provide a practical similarity-based, asymptotic approximation to the problem at hand. Comparisons to nonlinear numerical simulations serve to verify the accuracy of the solution and to confirm the necessity of carrying out the analysis at least to second order. In this vein, we find that the axial velocity component is strongly affected by the second-order correction, which also plays a key role in securing mass conservation, especially in long chambers. From a fundamental standpoint, a high-order approximation not only extends our range of applicability to larger values of the Reynolds number and deviation amplitudes, it also helps to capture the axial vorticity that evolves in the chamber, as well as the viscous patch that develops along the centreline. Moreover, the semi-analytical solution enables us to assess the sensitivity of the flow field to variations in the cross-flow Reynolds number, the deviation amplitude and the circular wavenumber, which is specified by the number of lobes or crests in an actual grain perforation.
$\unicode[STIX]{x1D700}$
. Then using judiciously imposed similarity transformations, the first-order system is reduced to four ordinary differential equations that can be solved straightforwardly. Along similar lines, the second-order system is transformed into an assortment of seven ordinary differential equations that can be solved with equal ease. The second-order formulation is subsequently shown to provide a practical similarity-based, asymptotic approximation to the problem at hand. Comparisons to nonlinear numerical simulations serve to verify the accuracy of the solution and to confirm the necessity of carrying out the analysis at least to second order. In this vein, we find that the axial velocity component is strongly affected by the second-order correction, which also plays a key role in securing mass conservation, especially in long chambers. From a fundamental standpoint, a high-order approximation not only extends our range of applicability to larger values of the Reynolds number and deviation amplitudes, it also helps to capture the axial vorticity that evolves in the chamber, as well as the viscous patch that develops along the centreline. Moreover, the semi-analytical solution enables us to assess the sensitivity of the flow field to variations in the cross-flow Reynolds number, the deviation amplitude and the circular wavenumber, which is specified by the number of lobes or crests in an actual grain perforation.
The inception of a viscous second-order mean flow model as a substitute to the Taylor–Culick profile opens up a parallel line of research inquiry into the stability and performance of rocket chambers in the presence of wall distortion. Although numerous stability investigations of the Taylor–Culick profile exist, with and without particle mean flow interactions, the corresponding problems in non-circular grain configurations remain relatively unexplored. In a circular motor, for example, the role of the tangential vorticity component on stability is relatively well understood. However, in the presence of asymmetry and surface distortions, the impact of axial vorticity on instability remains an open question. Given the deeply modified vorticity structures in a non-circular configuration, it will be interesting to explore the effects of deviation amplitudes and wavenumbers on flow instability. It is also hoped that these and other research questions will be addressed in future work.
Acknowledgements
The first three authors wish to thank CNES, the French Space Agency, Herakles, the European solid rocket manufacturer, and ONERA, the French Aerospace Laboratory. This work is based on the doctoral work of the first author, M.B., under sponsorship from both CNES and ONERA. The last author, J.M., was sponsored partly by Auburn University, through the Hugh and Loeda Francis Chair of Excellence, and partly by the National Science Foundation.
Appendix A
This appendix provides the resulting system of equations after substituting (2.2) into (2.1). When multiplied by the strictly positive quantity
![]() $(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})$
, one is left with
$(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})$
, one is left with
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}} & & u_{r}\unicode[STIX]{x2202}_{r}u_{r}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{2}}{r}}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{r}\\ & & \quad =-\unicode[STIX]{x2202}_{r}p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{r},\\ & & u_{r}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}u_{r}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{\unicode[STIX]{x1D703}}\\ & & \quad ={\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x2202}_{r}p-{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{\unicode[STIX]{x1D703}},\\ & & u_{r}\unicode[STIX]{x2202}_{r}u_{z}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{z}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{z}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{z}\\ & & \quad =-(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})\unicode[STIX]{x2202}_{z}\,p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{z},\\ & & \unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{u_{r}}{r}}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})\unicode[STIX]{x2202}_{z}u_{z}=0,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}} & & u_{r}\unicode[STIX]{x2202}_{r}u_{r}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{2}}{r}}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{r}\\ & & \quad =-\unicode[STIX]{x2202}_{r}p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{r},\\ & & u_{r}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}u_{r}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{\unicode[STIX]{x1D703}}\\ & & \quad ={\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x2202}_{r}p-{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{\unicode[STIX]{x1D703}},\\ & & u_{r}\unicode[STIX]{x2202}_{r}u_{z}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{z}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{z}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})u_{z}\unicode[STIX]{x2202}_{z}u_{z}\\ & & \quad =-(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})\unicode[STIX]{x2202}_{z}\,p+{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{Re}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{e}_{z},\\ & & \unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{u_{r}}{r}}-{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}+(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})\unicode[STIX]{x2202}_{z}u_{z}=0,\end{array}\right\}\end{eqnarray}$$
where the expression for
![]() $\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
is detailed in appendix B.
$\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
is detailed in appendix B.
Appendix B
This appendix details the scalar representation of the Laplacian
![]() $\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
in view of the coordinate transformation
$\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
in view of the coordinate transformation
This substitution entails, for any scalar function
![]() $f$
,
$f$
,
In cylindrical coordinates, the Laplacian of a vector
![]() $\boldsymbol{u}$
may be expanded into
$\boldsymbol{u}$
may be expanded into
 $$\begin{eqnarray}\bar{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{u}=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x2202}_{\overline{r}}^{2}u_{r}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{r}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{r}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{r}-{\displaystyle \frac{2}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{u_{r}}{\overline{r}^{2}}}\\ \unicode[STIX]{x2202}_{\overline{r}}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{2}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{\overline{r}^{2}}}\\ \unicode[STIX]{x2202}_{\overline{r}}^{2}u_{z}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{z}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{z}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{z}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{u}=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x2202}_{\overline{r}}^{2}u_{r}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{r}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{r}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{r}-{\displaystyle \frac{2}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{u_{r}}{\overline{r}^{2}}}\\ \unicode[STIX]{x2202}_{\overline{r}}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{2}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{\overline{r}^{2}}}\\ \unicode[STIX]{x2202}_{\overline{r}}^{2}u_{z}+{\displaystyle \frac{1}{\overline{r}^{2}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D703}}}^{2}u_{z}+\unicode[STIX]{x2202}_{\overline{z}}^{2}u_{z}+{\displaystyle \frac{1}{\overline{r}}}\unicode[STIX]{x2202}_{\overline{r}}u_{z}\end{array}\right).\end{eqnarray}$$
When converted into the
![]() $(r\text{,}~\unicode[STIX]{x1D703}\text{,}~z)$
coordinate system, the three components of
$(r\text{,}~\unicode[STIX]{x1D703}\text{,}~z)$
coordinate system, the three components of
![]() $\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
may be expressed in vector form using
$\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$
may be expressed in vector form using
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}=\left(\begin{array}{@{}c@{}}A_{r}\\ A_{\unicode[STIX]{x1D703}}\\ A_{z}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}=\left(\begin{array}{@{}c@{}}A_{r}\\ A_{\unicode[STIX]{x1D703}}\\ A_{z}\end{array}\right),\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle A_{r} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{r}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{r}+\unicode[STIX]{x2202}_{z}^{2}u_{r}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle -\,{\displaystyle \frac{2}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{u_{r}}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{r},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{r} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{r}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{r}+\unicode[STIX]{x2202}_{z}^{2}u_{r}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{r}+{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle -\,{\displaystyle \frac{2}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{u_{r}}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{r},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{\unicode[STIX]{x1D703}} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{z}^{2}u_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{r}u_{r}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{2}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{\unicode[STIX]{x1D703}} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{\unicode[STIX]{x1D703}}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x2202}_{z}^{2}u_{\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{r}u_{r}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{2}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}-{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{z} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{z}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{z}+\unicode[STIX]{x2202}_{z}^{2}u_{z}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{z}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{z}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{z} & = & \displaystyle {\displaystyle \frac{1}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\right]\unicode[STIX]{x2202}_{r}^{2}u_{z}+{\displaystyle \frac{1}{r^{2}\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{z}+\unicode[STIX]{x2202}_{z}^{2}u_{z}\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{1}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}\left[1+{\displaystyle \frac{(\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime })^{2}}{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}}}-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}}\right]\unicode[STIX]{x2202}_{r}u_{z}-{\displaystyle \frac{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{r\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{3}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{r}u_{z}.\qquad\end{eqnarray}$$
Appendix C
This appendix contains the equations related to the determination of
![]() $O(\unicode[STIX]{x1D700})$
terms. The initial system at
$O(\unicode[STIX]{x1D700})$
terms. The initial system at
![]() $O(\unicode[STIX]{x1D700})$
reads:
$O(\unicode[STIX]{x1D700})$
reads:
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{r}^{(1)}+u_{r}^{(1)}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{r}^{(1)}\\ \quad =-\unicode[STIX]{x2202}_{r}p^{(1)}+{\displaystyle \frac{1}{Re}}\left[\unicode[STIX]{x2202}_{r}^{2}u_{r}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{r}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(1)}-{\displaystyle \frac{2}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}^{(1)}-{\displaystyle \frac{u_{r}^{(1)}}{r^{2}}}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{r}^{2}u_{r}^{(0)}\right.\\ \qquad -\left.{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}+{\displaystyle \frac{2\unicode[STIX]{x1D6FC}}{r^{2}}}u_{r}^{(0)}\right],\\ u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r}}u_{r}^{(0)}u_{\unicode[STIX]{x1D703}}^{(1)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{\unicode[STIX]{x1D703}}^{(1)}\\ \quad =-{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}p^{(1)}+\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x2202}_{r}p^{(0)}+{\displaystyle \frac{1}{Re}}\left[\vphantom{{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{(1)}}{r^{2}}}}\unicode[STIX]{x2202}_{r}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{2}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}^{(1)}\right.\\ \qquad -\left.{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{(1)}}{r^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D6FC}^{\prime }}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}\right],\\ u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{z}^{(1)}+u_{r}^{(1)}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{z}^{(1)}+u_{z}^{(1)}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}+\unicode[STIX]{x1D6FC}u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}\\ \quad =-\unicode[STIX]{x2202}_{z}p^{(1)}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{z}p^{(0)}\vphantom{{\displaystyle \frac{1}{Re}}\left[-{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}\right]}+{\displaystyle \frac{1}{Re}}\left[\unicode[STIX]{x2202}_{r}^{2}u_{z}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{z}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{z}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(1)}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{r}^{2}u_{z}^{(0)}\right.\\ \qquad -\left.{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}\right]\\ \unicode[STIX]{x2202}_{r}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x2202}_{z}u_{z}^{(1)}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{r}^{(1)}+u_{r}^{(1)}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{r}^{(1)}\\ \quad =-\unicode[STIX]{x2202}_{r}p^{(1)}+{\displaystyle \frac{1}{Re}}\left[\unicode[STIX]{x2202}_{r}^{2}u_{r}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{r}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(1)}-{\displaystyle \frac{2}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}^{(1)}-{\displaystyle \frac{u_{r}^{(1)}}{r^{2}}}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{r}^{2}u_{r}^{(0)}\right.\\ \qquad -\left.{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}+{\displaystyle \frac{2\unicode[STIX]{x1D6FC}}{r^{2}}}u_{r}^{(0)}\right],\\ u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r}}u_{r}^{(0)}u_{\unicode[STIX]{x1D703}}^{(1)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{\unicode[STIX]{x1D703}}^{(1)}\\ \quad =-{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}p^{(1)}+\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x2202}_{r}p^{(0)}+{\displaystyle \frac{1}{Re}}\left[\vphantom{{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{(1)}}{r^{2}}}}\unicode[STIX]{x2202}_{r}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}^{(1)}+{\displaystyle \frac{2}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}^{(1)}\right.\\ \qquad -\left.{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}^{(1)}}{r^{2}}}-{\displaystyle \frac{2\unicode[STIX]{x1D6FC}^{\prime }}{r}}\unicode[STIX]{x2202}_{r}u_{r}^{(0)}\right],\\ u_{r}^{(0)}\unicode[STIX]{x2202}_{r}u_{z}^{(1)}+u_{r}^{(1)}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}+u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{z}^{(1)}+u_{z}^{(1)}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}+\unicode[STIX]{x1D6FC}u_{z}^{(0)}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}\\ \quad =-\unicode[STIX]{x2202}_{z}p^{(1)}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{z}p^{(0)}\vphantom{{\displaystyle \frac{1}{Re}}\left[-{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}\right]}+{\displaystyle \frac{1}{Re}}\left[\unicode[STIX]{x2202}_{r}^{2}u_{z}^{(1)}+{\displaystyle \frac{1}{r^{2}}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}^{2}u_{z}^{(1)}+\unicode[STIX]{x2202}_{z}^{2}u_{z}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(1)}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{r}^{2}u_{z}^{(0)}\right.\\ \qquad -\left.{\displaystyle \frac{2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FC}^{\prime \prime }}{r}}\unicode[STIX]{x2202}_{r}u_{z}^{(0)}\right]\\ \unicode[STIX]{x2202}_{r}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}u_{r}^{(1)}+{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x2202}_{z}u_{z}^{(1)}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x2202}_{z}u_{z}^{(0)}=0.\end{array}\right\}\end{eqnarray}$$
Thus the system of equations that controls
![]() $v_{r}^{}\text{,}~v_{\unicode[STIX]{x1D703}}^{}\text{,}~v_{z}^{}$
and
$v_{r}^{}\text{,}~v_{\unicode[STIX]{x1D703}}^{}\text{,}~v_{z}^{}$
and
![]() $q^{}$
may be rearranged into:
$q^{}$
may be rearranged into:
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}} & & -{\displaystyle \frac{1}{Re}}v_{r}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{r}^{\prime }+\left[\left(-{\displaystyle \frac{F}{r}}\right)^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}Re}}\right]v_{r}^{}+q^{\prime }-{\displaystyle \frac{2m^{2}}{r^{2}Re}}v_{\unicode[STIX]{x1D703}}^{}\\ & & \quad ={\displaystyle \frac{1}{rRe}}\left(2F^{\prime \prime }-{\displaystyle \frac{m^{2}+2}{r}}F^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}F\right),\\ & & -{\displaystyle \frac{1}{Re}}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{\unicode[STIX]{x1D703}}^{\prime }+{\displaystyle \frac{1}{r^{2}}}\left(-F+{\displaystyle \frac{m^{2}+1}{Re}}\right)v_{\unicode[STIX]{x1D703}}^{}+{\displaystyle \frac{1}{r}}q^{}-{\displaystyle \frac{2}{r^{2}Re}}v_{\unicode[STIX]{x1D703}}^{}\\ & & \quad =\left(-{\displaystyle \frac{F^{2}}{2r^{2}}}\right)^{\prime }+{\displaystyle \frac{1}{rRe}}\left(-F^{\prime \prime }+{\displaystyle \frac{3}{r}}F^{\prime }-{\displaystyle \frac{2}{r^{2}}}F\right),\\ & & -{\displaystyle \frac{1}{Re}}v_{z}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{z}^{\prime }+{\displaystyle \frac{1}{r}}\left(2F^{\prime }+{\displaystyle \frac{m^{2}}{rRe}}\right)v_{z}^{}+\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }v_{r}^{}\\ & & \quad =\left(-{\displaystyle \frac{F}{r}}\right)\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }-{\displaystyle \frac{1}{rRe}}\left(3F^{\prime \prime \prime }-{\displaystyle \frac{m^{2}+3}{r}}F^{\prime \prime }+{\displaystyle \frac{m^{2}+3}{r^{2}}}F^{\prime }\right),\\ & & v_{r}^{\prime }+{\displaystyle \frac{1}{r}}v_{r}^{}-{\displaystyle \frac{m^{2}}{r}}v_{\unicode[STIX]{x1D703}}^{}+v_{z}^{}=-{\displaystyle \frac{F^{\prime }}{r}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}} & & -{\displaystyle \frac{1}{Re}}v_{r}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{r}^{\prime }+\left[\left(-{\displaystyle \frac{F}{r}}\right)^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}Re}}\right]v_{r}^{}+q^{\prime }-{\displaystyle \frac{2m^{2}}{r^{2}Re}}v_{\unicode[STIX]{x1D703}}^{}\\ & & \quad ={\displaystyle \frac{1}{rRe}}\left(2F^{\prime \prime }-{\displaystyle \frac{m^{2}+2}{r}}F^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}F\right),\\ & & -{\displaystyle \frac{1}{Re}}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{\unicode[STIX]{x1D703}}^{\prime }+{\displaystyle \frac{1}{r^{2}}}\left(-F+{\displaystyle \frac{m^{2}+1}{Re}}\right)v_{\unicode[STIX]{x1D703}}^{}+{\displaystyle \frac{1}{r}}q^{}-{\displaystyle \frac{2}{r^{2}Re}}v_{\unicode[STIX]{x1D703}}^{}\\ & & \quad =\left(-{\displaystyle \frac{F^{2}}{2r^{2}}}\right)^{\prime }+{\displaystyle \frac{1}{rRe}}\left(-F^{\prime \prime }+{\displaystyle \frac{3}{r}}F^{\prime }-{\displaystyle \frac{2}{r^{2}}}F\right),\\ & & -{\displaystyle \frac{1}{Re}}v_{z}^{\prime \prime }-{\displaystyle \frac{1}{r}}\left(F+{\displaystyle \frac{1}{Re}}\right)v_{z}^{\prime }+{\displaystyle \frac{1}{r}}\left(2F^{\prime }+{\displaystyle \frac{m^{2}}{rRe}}\right)v_{z}^{}+\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }v_{r}^{}\\ & & \quad =\left(-{\displaystyle \frac{F}{r}}\right)\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }-{\displaystyle \frac{1}{rRe}}\left(3F^{\prime \prime \prime }-{\displaystyle \frac{m^{2}+3}{r}}F^{\prime \prime }+{\displaystyle \frac{m^{2}+3}{r^{2}}}F^{\prime }\right),\\ & & v_{r}^{\prime }+{\displaystyle \frac{1}{r}}v_{r}^{}-{\displaystyle \frac{m^{2}}{r}}v_{\unicode[STIX]{x1D703}}^{}+v_{z}^{}=-{\displaystyle \frac{F^{\prime }}{r}},\end{array}\right\}\end{eqnarray}$$
with the auxiliary boundary conditions
Appendix D
This appendix summarizes the equations needed to determine the
![]() $O(\unicode[STIX]{x1D700}^{2})$
corrections. First, the linear equations for
$O(\unicode[STIX]{x1D700}^{2})$
corrections. First, the linear equations for
![]() $u_{r,2}^{(2)}\text{,}~u_{\unicode[STIX]{x1D703},2}^{(2)}\text{,}~u_{z,2}^{(2)}$
and
$u_{r,2}^{(2)}\text{,}~u_{\unicode[STIX]{x1D703},2}^{(2)}\text{,}~u_{z,2}^{(2)}$
and
![]() $p_{2}^{(2)}$
may be written as
$p_{2}^{(2)}$
may be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{r,2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,2}^{(2)\prime }+\left(u_{r}^{(0)\prime }+{\displaystyle \frac{4m^{2}+1}{r^{2}Re}}\right)u_{r,2}^{(2)}-{\displaystyle \frac{4m^{2}}{r^{2}Re}}u_{\unicode[STIX]{x1D703},2}^{(2)}+p_{2}^{(2)\prime }\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{v_{r}^{}v_{r}^{\prime }}{2}}-{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}\left(u_{r}^{(0)\prime }-{\displaystyle \frac{v_{r}}{r}}+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)+{\displaystyle \frac{1}{2Re}}\left[u_{r}^{(0)\prime \prime }\left(1-m^{2}\right)-v_{r}^{\prime \prime }+{\displaystyle \frac{1-4m^{2}}{r}}u_{r}^{(0)\prime }\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{3m^{2}-1}{r}}v_{r}^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{r}^{}-{\displaystyle \frac{2m^{2}}{r}}\left(v_{\unicode[STIX]{x1D703}}^{\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)-{\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{r,2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,2}^{(2)\prime }+\left(u_{r}^{(0)\prime }+{\displaystyle \frac{4m^{2}+1}{r^{2}Re}}\right)u_{r,2}^{(2)}-{\displaystyle \frac{4m^{2}}{r^{2}Re}}u_{\unicode[STIX]{x1D703},2}^{(2)}+p_{2}^{(2)\prime }\nonumber\\ \displaystyle & & \displaystyle \quad ={\displaystyle \frac{v_{r}^{}v_{r}^{\prime }}{2}}-{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}\left(u_{r}^{(0)\prime }-{\displaystyle \frac{v_{r}}{r}}+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)+{\displaystyle \frac{1}{2Re}}\left[u_{r}^{(0)\prime \prime }\left(1-m^{2}\right)-v_{r}^{\prime \prime }+{\displaystyle \frac{1-4m^{2}}{r}}u_{r}^{(0)\prime }\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{3m^{2}-1}{r}}v_{r}^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{r}^{}-{\displaystyle \frac{2m^{2}}{r}}\left(v_{\unicode[STIX]{x1D703}}^{\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)-{\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{\unicode[STIX]{x1D703},2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{\unicode[STIX]{x1D703},2}^{(2)\prime }+\left({\displaystyle \frac{u_{r}^{(0)}}{r}}+{\displaystyle \frac{4m^{2}+1}{r^{2}Re}}\right)u_{\unicode[STIX]{x1D703},2}^{(2)}-{\displaystyle \frac{4}{r^{2}Re}}u_{r,2}^{(2)}+{\displaystyle \frac{2}{r}}p_{2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{\unicode[STIX]{x1D703}}^{\prime }}{2}}-{\displaystyle \frac{1}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{r}^{}+{\displaystyle \frac{m^{2}}{2r}}(v_{\unicode[STIX]{x1D703}}^{})^{2}+{\displaystyle \frac{1}{2}}q^{\prime }-{\displaystyle \frac{1}{2}}p^{(0)\prime }+{\displaystyle \frac{1}{2Re}}\left(-v_{\unicode[STIX]{x1D703}}^{\prime \prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{\unicode[STIX]{x1D703}}^{}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{3m^{2}-1}{r}}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-{\displaystyle \frac{2}{r}}v_{r}^{\prime \prime }-{\displaystyle \frac{2}{r^{2}}}v_{r}^{}+{\displaystyle \frac{4}{r}}u_{r}^{(0)}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{\unicode[STIX]{x1D703},2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{\unicode[STIX]{x1D703},2}^{(2)\prime }+\left({\displaystyle \frac{u_{r}^{(0)}}{r}}+{\displaystyle \frac{4m^{2}+1}{r^{2}Re}}\right)u_{\unicode[STIX]{x1D703},2}^{(2)}-{\displaystyle \frac{4}{r^{2}Re}}u_{r,2}^{(2)}+{\displaystyle \frac{2}{r}}p_{2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{\unicode[STIX]{x1D703}}^{\prime }}{2}}-{\displaystyle \frac{1}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{r}^{}+{\displaystyle \frac{m^{2}}{2r}}(v_{\unicode[STIX]{x1D703}}^{})^{2}+{\displaystyle \frac{1}{2}}q^{\prime }-{\displaystyle \frac{1}{2}}p^{(0)\prime }+{\displaystyle \frac{1}{2Re}}\left(-v_{\unicode[STIX]{x1D703}}^{\prime \prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{\unicode[STIX]{x1D703}}^{}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{3m^{2}-1}{r}}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-{\displaystyle \frac{2}{r}}v_{r}^{\prime \prime }-{\displaystyle \frac{2}{r^{2}}}v_{r}^{}+{\displaystyle \frac{4}{r}}u_{r}^{(0)}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{z,2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,2}^{(2)\prime }+\left(2u_{z}^{(0)}+{\displaystyle \frac{4m^{2}}{r^{2}Re}}\right)u_{z,2}^{(2)}+u_{z}^{(0)\prime }u_{r,2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime \prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}-u_{z}^{(0)}v_{z}^{}-{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }+{\displaystyle \frac{m^{2}}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{z}^{}+{\displaystyle \frac{1}{2Re}}\left[\vphantom{{\displaystyle \frac{1-4m^{2}}{r}}}u_{z}^{(0)\prime \prime }\left(1-m^{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.v_{z}^{\prime \prime }+{\displaystyle \frac{1-4m^{2}}{r}}u_{z}^{(0)\prime }+{\displaystyle \frac{3m^{2}-1}{r}}v_{z}^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}v_{z}^{}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{u_{z,2}^{(2)\prime \prime }}{Re}}+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,2}^{(2)\prime }+\left(2u_{z}^{(0)}+{\displaystyle \frac{4m^{2}}{r^{2}Re}}\right)u_{z,2}^{(2)}+u_{z}^{(0)\prime }u_{r,2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime \prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}-u_{z}^{(0)}v_{z}^{}-{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }+{\displaystyle \frac{m^{2}}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{z}^{}+{\displaystyle \frac{1}{2Re}}\left[\vphantom{{\displaystyle \frac{1-4m^{2}}{r}}}u_{z}^{(0)\prime \prime }\left(1-m^{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.v_{z}^{\prime \prime }+{\displaystyle \frac{1-4m^{2}}{r}}u_{z}^{(0)\prime }+{\displaystyle \frac{3m^{2}-1}{r}}v_{z}^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}v_{z}^{}\right].\end{eqnarray}$$
In the above, the lower-order terms that capture nonlinear interactions are collected on the right-hand side of the momentum equations.
Second, the defining equations for
![]() $u_{r,0}^{(2)}\text{,}~u_{z,0}^{(2)}$
and
$u_{r,0}^{(2)}\text{,}~u_{z,0}^{(2)}$
and
![]() $p_{0}^{(2)}$
may be consolidated into
$p_{0}^{(2)}$
may be consolidated into
 $$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{1}{Re}}u_{r,0}^{(2)\prime \prime }+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,0}^{(2)\prime }+\left(u_{r}^{(0)\prime }+{\displaystyle \frac{1}{r^{2}Re}}\right)u_{r,0}^{(2)}+p_{0}^{(2)\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{r}^{\prime }}{2}}+{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}\left(u_{r}^{(0)\prime }-{\displaystyle \frac{v_{r}}{r}}+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)+{\displaystyle \frac{1}{2Re}}\left[u_{r}^{(0)\prime \prime }\left(1+m^{2}\right)-v_{r}^{\prime \prime }+{\displaystyle \frac{u_{r}^{(0)\prime }}{r}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.{\displaystyle \frac{m^{2}+1}{r}}v_{r}^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{r}^{}+{\displaystyle \frac{2m^{2}}{r}}\left(v_{\unicode[STIX]{x1D703}}^{\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)-{\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{1}{Re}}u_{r,0}^{(2)\prime \prime }+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{r,0}^{(2)\prime }+\left(u_{r}^{(0)\prime }+{\displaystyle \frac{1}{r^{2}Re}}\right)u_{r,0}^{(2)}+p_{0}^{(2)\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =-{\displaystyle \frac{v_{r}^{}v_{r}^{\prime }}{2}}+{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}\left(u_{r}^{(0)\prime }-{\displaystyle \frac{v_{r}}{r}}+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)+{\displaystyle \frac{1}{2Re}}\left[u_{r}^{(0)\prime \prime }\left(1+m^{2}\right)-v_{r}^{\prime \prime }+{\displaystyle \frac{u_{r}^{(0)\prime }}{r}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.{\displaystyle \frac{m^{2}+1}{r}}v_{r}^{\prime }+{\displaystyle \frac{m^{2}+1}{r^{2}}}v_{r}^{}+{\displaystyle \frac{2m^{2}}{r}}\left(v_{\unicode[STIX]{x1D703}}^{\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}}{r}}\right)-{\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{1}{Re}}u_{z,0}^{(2)\prime \prime }+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{z,0}^{(2)\prime }+2u_{z}^{(0)}u_{z,0}^{(2)}+u_{z}^{(0)\prime }u_{r,0}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}-u_{z}^{(0)}v_{z}^{}+{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }-{\displaystyle \frac{m^{2}}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{z}^{}+{\displaystyle \frac{1}{2Re}}\left[\vphantom{{\displaystyle \frac{m^{2}}{r^{2}}}}u_{z}^{(0)\prime \prime }\left(1+m^{2}\right)-v_{z}^{\prime \prime }\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{u_{z}^{(0)\prime }}{r}}-{\displaystyle \frac{m^{2}+1}{r}}v_{z}^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}v_{z}^{}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -{\displaystyle \frac{1}{Re}}u_{z,0}^{(2)\prime \prime }+\left(u_{r}^{(0)}-{\displaystyle \frac{1}{rRe}}\right)u_{z,0}^{(2)\prime }+2u_{z}^{(0)}u_{z,0}^{(2)}+u_{z}^{(0)\prime }u_{r,0}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}-u_{z}^{(0)}v_{z}^{}+{\displaystyle \frac{m^{2}}{2}}v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }-{\displaystyle \frac{m^{2}}{2r}}v_{\unicode[STIX]{x1D703}}^{}v_{z}^{}+{\displaystyle \frac{1}{2Re}}\left[\vphantom{{\displaystyle \frac{m^{2}}{r^{2}}}}u_{z}^{(0)\prime \prime }\left(1+m^{2}\right)-v_{z}^{\prime \prime }\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.{\displaystyle \frac{u_{z}^{(0)\prime }}{r}}-{\displaystyle \frac{m^{2}+1}{r}}v_{z}^{\prime }+{\displaystyle \frac{m^{2}}{r^{2}}}v_{z}^{}\right].\end{eqnarray}$$
Here, again, the continuity relation may be combined with the radial momentum equation to express
![]() $u_{z,0}^{(2)}$
and
$u_{z,0}^{(2)}$
and
![]() $p_{0}^{(2)}$
in terms of
$p_{0}^{(2)}$
in terms of
![]() $u_{r,0}^{(2)}$
and its derivatives. This manipulation leads to a single third-order ordinary differential equation for
$u_{r,0}^{(2)}$
and its derivatives. This manipulation leads to a single third-order ordinary differential equation for
![]() $u_{r,0}^{(2)}$
, specifically,
$u_{r,0}^{(2)}$
, specifically,
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{u_{r,0}^{(2)\prime \prime \prime }}{Re}}+\left({\displaystyle \frac{2}{rRe}}-u_{r}^{(0)}\right)u_{r,0}^{(2)\prime \prime }-\left(2u_{z}^{(0)}+{\displaystyle \frac{u_{r}^{(0)}}{r}}+{\displaystyle \frac{1}{r^{2}Re}}\right)u_{r,0}^{(2)\prime }+\left({\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}-{\displaystyle \frac{2u_{z}^{(0)}}{r}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.u_{z}^{(0)\prime }+{\displaystyle \frac{1}{r^{3}Re}}\right)u_{r,0}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}+{\displaystyle \frac{u_{r}^{(0)}v_{z}^{\prime }}{2}}+{\displaystyle \frac{m^{2}}{2}}\left(v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}v_{z}}{r}}-u_{r}^{(0)}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-2u_{z}^{(0)}v_{\unicode[STIX]{x1D703}}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\displaystyle \frac{1}{2Re}}\left[\left(1+m^{2}\right)u_{z}^{(0)\prime \prime }-2v_{z}^{\prime \prime }+{\displaystyle \frac{u_{z}^{(0)\prime }}{r}}-{\displaystyle \frac{m^{2}+2}{r}}v_{z}^{\prime }+m^{2}\left({\displaystyle \frac{v_{z}}{r^{2}}}+v_{\unicode[STIX]{x1D703}}^{\prime \prime \prime }+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}^{\prime \prime }}{r}}\right)\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{u_{r,0}^{(2)\prime \prime \prime }}{Re}}+\left({\displaystyle \frac{2}{rRe}}-u_{r}^{(0)}\right)u_{r,0}^{(2)\prime \prime }-\left(2u_{z}^{(0)}+{\displaystyle \frac{u_{r}^{(0)}}{r}}+{\displaystyle \frac{1}{r^{2}Re}}\right)u_{r,0}^{(2)\prime }+\left({\displaystyle \frac{u_{r}^{(0)}}{r^{2}}}-{\displaystyle \frac{2u_{z}^{(0)}}{r}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.u_{z}^{(0)\prime }+{\displaystyle \frac{1}{r^{3}Re}}\right)u_{r,0}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D705}-{\displaystyle \frac{v_{r}^{}v_{z}^{\prime }}{2}}-{\displaystyle \frac{(v_{z}^{})^{2}}{2}}+{\displaystyle \frac{u_{r}^{(0)}v_{z}^{\prime }}{2}}+{\displaystyle \frac{m^{2}}{2}}\left(v_{\unicode[STIX]{x1D703}}^{}u_{z}^{(0)\prime }-{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}v_{z}}{r}}-u_{r}^{(0)}v_{\unicode[STIX]{x1D703}}^{\prime \prime }-2u_{z}^{(0)}v_{\unicode[STIX]{x1D703}}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\displaystyle \frac{1}{2Re}}\left[\left(1+m^{2}\right)u_{z}^{(0)\prime \prime }-2v_{z}^{\prime \prime }+{\displaystyle \frac{u_{z}^{(0)\prime }}{r}}-{\displaystyle \frac{m^{2}+2}{r}}v_{z}^{\prime }+m^{2}\left({\displaystyle \frac{v_{z}}{r^{2}}}+v_{\unicode[STIX]{x1D703}}^{\prime \prime \prime }+{\displaystyle \frac{v_{\unicode[STIX]{x1D703}}^{\prime \prime }}{r}}\right)\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$













