Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-29T17:21:43.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 1. Drift and diffusion flux closures

Published online by Cambridge University Press:  22 May 2019

Sarma L. Rani Open the ORCID record for Sarma L. Rani [Opens in a new window] ,
Vijay K. Gupta  and
Donald L. Koch Open the ORCID record for Donald L. Koch [Opens in a new window]
Sarma L. Rani*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Alabama in Huntsville, Huntsville, AL 35899, USA
Vijay K. Gupta
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Alabama in Huntsville, Huntsville, AL 35899, USA
Donald L. Koch
Affiliation:
Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: sarma.rani@uah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this two-part study, we present the development and analysis of a stochastic theory for characterizing the relative positions of monodisperse, low-inertia particle pairs that are settling rapidly in homogeneous isotropic turbulence. In the limits of small Stokes number and Froude number such that 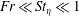$Fr\ll St_{\unicode[STIX]{x1D702}}\ll 1$, closures are developed for the drift and diffusion fluxes in the probability density function (p.d.f.) equation for the pair relative positions. The theory focuses on the relative motion of particle pairs in the dissipation regime of turbulence, i.e. for pair separations smaller than the Kolmogorov length scale. In this regime, the theory approximates the fluid velocity field in a reference frame following the primary particle as locally linear. In this part 1 paper, we present the derivation of closure approximations for the drift and diffusion fluxes in the p.d.f. equation for pair relative positions $\boldsymbol{r}$. The drift flux contains the time integral of the third and fourth moments of the ‘seen’ fluid velocity gradients along the trajectories of primary particles. These moments may be analytically resolved by making approximations regarding the ‘seen’ velocity gradient. Accordingly, two closure forms are derived specifically for the drift flux. The first invokes the assumption that the fluid velocity gradient along particle trajectories has a Gaussian distribution. In the second drift closure, we account for the correlation time scales of dissipation rate and enstrophy by decomposing the velocity gradient into the strain-rate and rotation-rate tensors scaled by the turbulent dissipation rate and enstrophy, respectively. An analytical solution to the p.d.f. 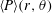$\langle P\rangle (r,\unicode[STIX]{x1D703})$ is then derived, where 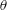$\unicode[STIX]{x1D703}$ is the spherical polar angle. It is seen that the p.d.f. has a power-law dependence on separation $r$ of the form 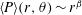$\langle P\rangle (r,\unicode[STIX]{x1D703})\sim r^{\unicode[STIX]{x1D6FD}}$ with 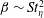$\unicode[STIX]{x1D6FD}\sim St_{\unicode[STIX]{x1D702}}^{2}$ and 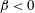$\unicode[STIX]{x1D6FD}<0$, analogous to that for the radial distribution function of non-settling pairs. An explicit expression is derived for 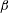$\unicode[STIX]{x1D6FD}$ in terms of the drift and diffusion closures. 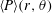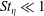The $\langle P\rangle (r,\unicode[STIX]{x1D703})$ solution also shows that, for a given $r$, the clustering of $St_{\unicode[STIX]{x1D702}}\ll 1$ particles is only weakly anisotropic, which is in conformity with prior observations from direct numerical simulations of isotropic turbulence containing settling particles.

JFM classification

Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 450 - 476
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Chemical Engineering, University of Missouri, Columbia, MO 65211, USA.

References

Ayala, O., Rosa, B. & Wang, L.-P. 2008a Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10, 075016.Google Scholar
Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2008b Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10 (7), 075015.Google Scholar
Bartlett, J. T. 1966 The growth of cloud droplets by coalescence. Q. J. R. Meteorol. Soc. 92 (391), 93–104.Google Scholar
Bragg, A. D. & Collins, L. R. 2014a New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16 (5), 055013.Google Scholar
Bragg, A. D. & Collins, L. R. 2014b New insights from comparing statistical theories for inertial particles in turbulence: II. Relative velocities. New J. Phys. 16 (5), 055014.Google Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Dhariwal, R., Rani, S. L. & Koch, D. L. 2017 Stochastic theory and direct numerical simulations of the relative motion of high-inertia particle pairs in isotropic turbulence. J. Fluid Mech. 813, 205–249.Google Scholar
Druzhinin, O. A. 1995 Dynamics of concentration and vorticity modification in a cellular flow laden with solid heavy particles. Phys. Fluids 7, 2132–2142.Google Scholar
Druzhinin, O. A. & Elghobashi, S. 1999 On the decay rate of isotropic turbulence laden with microparticles. Phys. Fluids 11, 602–610.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Ferry, J., Rani, S. L. & Balachandar, S. 2003 A locally implicit improvement of the equilibrium Eulerian method. Intl J. Multiphase Flow 29, 869–891.Google Scholar
Fouxon, I., Park, Y., Harduf, R. & Lee, C. 2015 Inhomogeneous distribution of water droplets in cloud turbulence. Phys. Rev. E 92 (3), 033001.Google Scholar
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 65 (1), 1–57.Google Scholar
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112 (21), 214501.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Parishani, H., Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2015 Effects of gravity on the acceleration and pair statistics of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 27 (3), 033304.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rani, S. L. & Balachandar, S. 2003 Evaluation of the equilibrium Eulerian approach for the evolution of particle concentration in isotropic turbulence. Intl J. Multiphase Flow 29, 1793–1816.Google Scholar
Rani, S. L. & Balachandar, S. 2004 Preferential concentration of particles in isotropic turbulence: a comparison of the Lagrangian and the equilibrium Eulerian approaches. Powder Technol. 141, 109–118.Google Scholar
Rani, S. L., Dhariwal, R. & Koch, D. L. 2014 A stochastic model for the relative motion of high Stokes number particles in isotropic turbulence. J. Fluid Mech. 756, 870–902.Google Scholar
Rani, S. L., Dhariwal, R. & Koch, D. L. 2019 Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 2. Comparison of theory and DNS. J. Fluid Mech. 871, 477–488.Google Scholar
Ray, B. & Collins, L. R. 2011 Preferential concentration and relative velocity statistics of inertial particles in Navier–Stokes turbulence with and without filtering. J. Fluid Mech. 680, 488–510.Google Scholar
Reade, W. C. & Collins, L. R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12 (10), 2530–2540.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2003 Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 15, 1776–1787.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2007 Refinement of the probability density function model for preferential concentration of aerosol particles in isotropic turbulence. Phys. Fluids 19 (11), 113308.Google Scholar