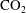1 Introduction
For many years, scientists have focused on the study of drop coalescence, both experimentally (see e.g. Wu, Cubaud & Ho Reference Wu, Cubaud and Ho2004; Case & Nagel Reference Case and Nagel2008) and numerically (see e.g. Eggers, Lister & Stone Reference Eggers, Lister and Stone1999), since this process is fundamental to many applications, such as inkjet printing and foam stability (Andrieu et al. Reference Andrieu, Beysens, Nikolayev and Pomeau2002; Kapur & Gaskell Reference Kapur and Gaskell2007). The research on droplet coalescence driven by surface tension done by Menchaca-Rocha, Martínez-Dávalos & Núñez (Reference Menchaca-Rocha, Martínez-Dávalos and Núñez2001) showed that the coalescence mechanism of droplets is extraordinarily similar to that of bubbles. Indeed, the study of bubble coalescence has attained more interest as it affects mass transfer towards bubbles, i.e. bubble growth is highly affected by the presence of coalescence events (Stover, Tobias & Denn Reference Stover, Tobias and Denn1997). Besides, bubble coalescence has a tremendous influence in the thinning and break-up of liquid films (Marrucci Reference Marrucci1969; Oolman & Blanch Reference Oolman and Blanch1986) and even alters the flavour of champagne (Liger-Belair, Seon & Antkowiak Reference Liger-Belair, Seon and Antkowiak2012). The fact that bubbles emerge in many catalytic reactions with the purpose of energy conversion (see e.g. Somorjai & Li Reference Somorjai and Li2010) and in many electrolytic processes (Verhaart, de Jonge & van Stralen Reference Verhaart, de Jonge and van Stralen1979) intrigues and motivates scientists to investigate how these bubbles behave in such conditions, and more concretely, how they interact with surrounding bubbles, including, of course, eventual coalescence and detachment processes, which in many applications are favoured, as attaching bubbles can hinder electrolytic and catalytic reactions.
In general, the coalescence of neighbouring growing bubbles is not always granted, as the presence of electrolytes (Craig, Ninham & Pashley Reference Craig, Ninham and Pashley1993; Boström et al.
Reference Boström, Craig, Albion, Williams and Ninham2003) and the viscosity of the surrounding liquid (Crabtree & Bridgwater Reference Crabtree and Bridgwater1971; Chesters & Hofman Reference Chesters and Hofman1982) play a significant role, since the potentially coalescing bubbles need to push away the liquid layer in between them so that the coalescence event can occur (Munro et al.
Reference Munro, Anthony, Basaran and Lister2015). Stover et al. (Reference Stover, Tobias and Denn1997) worked on the coalescence of 50–
![]() $600~\unicode[STIX]{x03BC}\text{m}$
bubbles under a constant velocity flow, focusing on the oscillating frequency and damping time. Thoroddsen et al. (Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
) also worked on this subject, using bigger air bubbles in ethyl alcohol with an improved time resolution, allowing a more precise study of the early evolution and comparison of their results with their work about droplet coalescence (Thoroddsen, Takehara & Etoh Reference Thoroddsen, Takehara and Etoh2005b
). On the other hand, Bremond et al. (Reference Bremond, Arora, Dammer and Lohse2006) studied the growth of two cavitation bubbles and their coalescence in an inertia-dominated process. In our case, we focus on bubbles quasi-statically growing by diffusion, such that they take many minutes to grow and touch each other so that coalescence is dominated by capillarity. We precisely study the beginning of the coalescence and compare its results to previous research, improving both the experimental and the theoretical approach. We also study the capillary waves propagating along the surface of the coalescing bubbles, especially the velocity and dominant mode of the wave packet. The viscosity of the involved fluids is of relevance during this propagation, since the higher vibration modes are damped as the wave propagates along the bubble surface. To conclude, we comment on the detachment mechanism caused by energy liberation and buoyancy-driven upwards acceleration, as well as the bubble oscillation with its Minnaert frequency during its rising.
$600~\unicode[STIX]{x03BC}\text{m}$
bubbles under a constant velocity flow, focusing on the oscillating frequency and damping time. Thoroddsen et al. (Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
) also worked on this subject, using bigger air bubbles in ethyl alcohol with an improved time resolution, allowing a more precise study of the early evolution and comparison of their results with their work about droplet coalescence (Thoroddsen, Takehara & Etoh Reference Thoroddsen, Takehara and Etoh2005b
). On the other hand, Bremond et al. (Reference Bremond, Arora, Dammer and Lohse2006) studied the growth of two cavitation bubbles and their coalescence in an inertia-dominated process. In our case, we focus on bubbles quasi-statically growing by diffusion, such that they take many minutes to grow and touch each other so that coalescence is dominated by capillarity. We precisely study the beginning of the coalescence and compare its results to previous research, improving both the experimental and the theoretical approach. We also study the capillary waves propagating along the surface of the coalescing bubbles, especially the velocity and dominant mode of the wave packet. The viscosity of the involved fluids is of relevance during this propagation, since the higher vibration modes are damped as the wave propagates along the bubble surface. To conclude, we comment on the detachment mechanism caused by energy liberation and buoyancy-driven upwards acceleration, as well as the bubble oscillation with its Minnaert frequency during its rising.
2 Description of the experiments and computation of the boundary integral code
Bubble coalescence is challenging to record in a well-controlled way; for example, when bubbles are chemically produced in a fast reaction, some instabilities in the bubble surroundings are created which hinder the record of their coalescence. The case of fast-growing bubbles, in which the associated advective liquid flow may influence the coalescence process, or that of inertial bubbles hitting each other due to gravity, are also difficult to record. We use the set-up described in Enríquez et al. (Reference Enríquez, Hummelink, Bruggert, Lohse, Prosperetti, van der Meer and Sun2013) to nucleate and grow bubbles. We can produce
![]() $\text{CO}_{2}$
bubbles quasi-statically growing in a diffusive regime and then study the coalescence with enough spatial and time accuracy. We use a small rectangular hydrophilic silicon chip with two hydrophobic pits, which are the bubble nucleation sites, as depicted in figure 1. We introduce the chip in a sealed tank filled with a
$\text{CO}_{2}$
bubbles quasi-statically growing in a diffusive regime and then study the coalescence with enough spatial and time accuracy. We use a small rectangular hydrophilic silicon chip with two hydrophobic pits, which are the bubble nucleation sites, as depicted in figure 1. We introduce the chip in a sealed tank filled with a
![]() $\text{CO}_{2}$
-water saturated solution at pressure
$\text{CO}_{2}$
-water saturated solution at pressure
![]() $P_{0}$
and temperature
$P_{0}$
and temperature
![]() $T$
. Afterwards, we decrease the pressure to
$T$
. Afterwards, we decrease the pressure to
![]() $P_{s}<P_{0}$
by opening a control valve, turning the solution supersaturated according to Henry’s law. Consequently, bubbles start growing until they touch and coalesce. The strong pinning conditions at the hydrophobic pits and the small ratio between the viscosities of the gas and the liquid (Munro et al.
Reference Munro, Anthony, Basaran and Lister2015) grant that the growing bubbles will push away the liquid layer in between them, guaranteeing coalescence. Finally, the coalesced bubble detaches from the substrate and a new couple of bubbles start growing. In every experiment, temperature and pressure are set to
$P_{s}<P_{0}$
by opening a control valve, turning the solution supersaturated according to Henry’s law. Consequently, bubbles start growing until they touch and coalesce. The strong pinning conditions at the hydrophobic pits and the small ratio between the viscosities of the gas and the liquid (Munro et al.
Reference Munro, Anthony, Basaran and Lister2015) grant that the growing bubbles will push away the liquid layer in between them, guaranteeing coalescence. Finally, the coalesced bubble detaches from the substrate and a new couple of bubbles start growing. In every experiment, temperature and pressure are set to
![]() $T=20.5\pm 0.5\,^{\circ }\text{C}$
,
$T=20.5\pm 0.5\,^{\circ }\text{C}$
,
![]() $P_{0}=9.2\pm 0.05$
bar and
$P_{0}=9.2\pm 0.05$
bar and
![]() $P_{s}=7.75\pm 0.05$
bar, thus achieving a supersaturation
$P_{s}=7.75\pm 0.05$
bar, thus achieving a supersaturation
![]() $\unicode[STIX]{x1D701}=(c_{0}-c_{s})/c_{s}\approx 0.18$
(where
$\unicode[STIX]{x1D701}=(c_{0}-c_{s})/c_{s}\approx 0.18$
(where
![]() $c_{0}$
indicates the gas concentration in the liquid at saturation and
$c_{0}$
indicates the gas concentration in the liquid at saturation and
![]() $c_{s}$
at supersaturation), which is small enough to neglect advective effects influencing the bubble growth (as explained in e.g. Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014)).
$c_{s}$
at supersaturation), which is small enough to neglect advective effects influencing the bubble growth (as explained in e.g. Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014)).
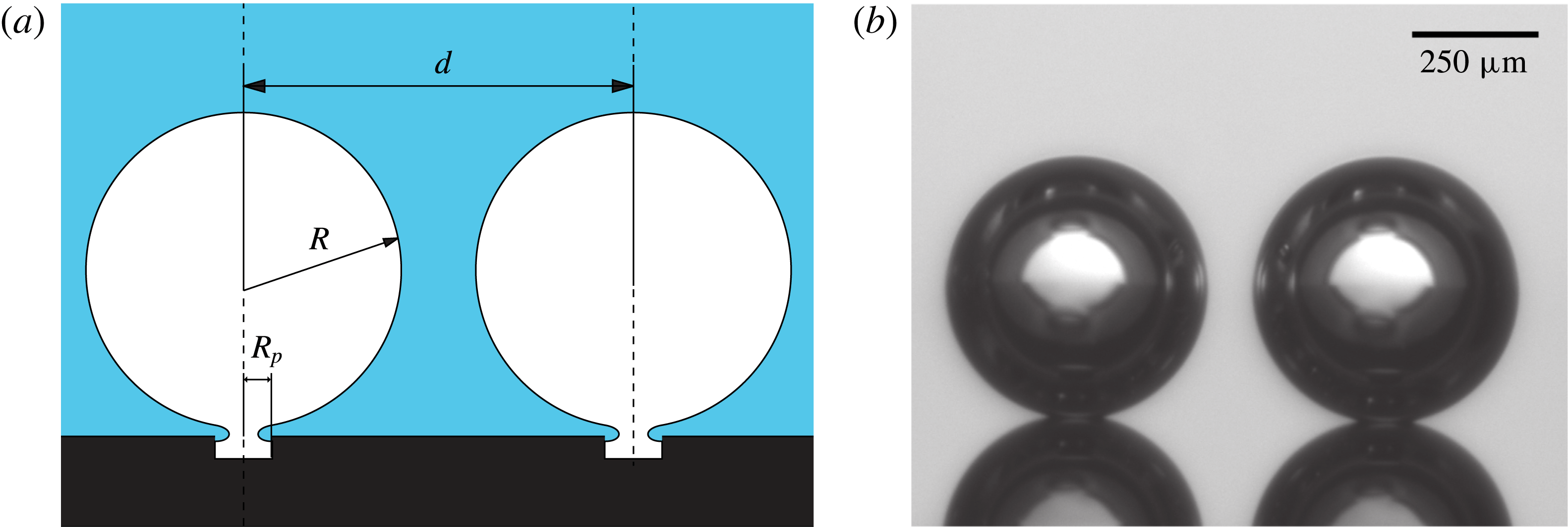
Figure 1. (a) Sketch of two gas bubbles diffusively growing before coalescence. The attaching geometry is based on the study done by Moreno Soto et al. (Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017). (b) Image recorded from experiments.
For the coalescence process, we use a Photron SAX high speed camera to record images at
![]() $66\,462$
fps of
$66\,462$
fps of
![]() $272\times 768$
pixel resolution, which corresponds to
$272\times 768$
pixel resolution, which corresponds to
![]() $15.05~\unicode[STIX]{x03BC}\text{s}$
between two images and
$15.05~\unicode[STIX]{x03BC}\text{s}$
between two images and
![]() $5.5~\unicode[STIX]{x03BC}\text{m}$
per pixel. Figure 2 shows several snapshots of the coalescence of two
$5.5~\unicode[STIX]{x03BC}\text{m}$
per pixel. Figure 2 shows several snapshots of the coalescence of two
![]() $300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles with a surface tension coefficient of
$300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles with a surface tension coefficient of
![]() $\unicode[STIX]{x1D70E}=58.7~\text{mN}~\text{m}^{-1}$
(Lubetkin & Akhtar Reference Lubetkin and Akhtar1996), mixture density
$\unicode[STIX]{x1D70E}=58.7~\text{mN}~\text{m}^{-1}$
(Lubetkin & Akhtar Reference Lubetkin and Akhtar1996), mixture density
![]() $\unicode[STIX]{x1D70C}=1014.5~\text{kg}~\text{m}^{-3}$
(Hebach, Oberhof & Dahmen Reference Hebach, Oberhof and Dahmen2004) and viscosity coefficient
$\unicode[STIX]{x1D70C}=1014.5~\text{kg}~\text{m}^{-3}$
(Hebach, Oberhof & Dahmen Reference Hebach, Oberhof and Dahmen2004) and viscosity coefficient
![]() $\unicode[STIX]{x1D707}=0.964~\text{mN}~\text{s}~\text{m}^{-2}$
(Frank, Kuipers & van Swaaij Reference Frank, Kuipers and van Swaaij1996). The radii of the two bubbles at the moment of coalescence has been considered to be the same, even if they are slightly different due to small perturbations during their growth. However, the ratio of the two bubbles’ radii is always between 0.95 and 1.05.
$\unicode[STIX]{x1D707}=0.964~\text{mN}~\text{s}~\text{m}^{-2}$
(Frank, Kuipers & van Swaaij Reference Frank, Kuipers and van Swaaij1996). The radii of the two bubbles at the moment of coalescence has been considered to be the same, even if they are slightly different due to small perturbations during their growth. However, the ratio of the two bubbles’ radii is always between 0.95 and 1.05.

Figure 2. Snapshots of the coalescence of two
![]() $300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles pinned to
$300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles pinned to
![]() $50~\unicode[STIX]{x03BC}\text{m}$
radius pits. The images (a–o) are separated by
$50~\unicode[STIX]{x03BC}\text{m}$
radius pits. The images (a–o) are separated by
![]() $75~\unicode[STIX]{x03BC}\text{s}$
, images (o–t) by
$75~\unicode[STIX]{x03BC}\text{s}$
, images (o–t) by
![]() $150~\unicode[STIX]{x03BC}\text{s}$
and images (t–y) by
$150~\unicode[STIX]{x03BC}\text{s}$
and images (t–y) by
![]() $300~\unicode[STIX]{x03BC}\text{s}$
. Three main stages can be identified: neck formation between the two bubbles, images (a–d); propagation of the capillary waves along the upper and lower half-surface of the coalescing bubble and their final convergence at its side, images (e–j); and final detachment, upwards jumping, rising and oscillation with the Minnaert frequency, images (k–y).
$300~\unicode[STIX]{x03BC}\text{s}$
. Three main stages can be identified: neck formation between the two bubbles, images (a–d); propagation of the capillary waves along the upper and lower half-surface of the coalescing bubble and their final convergence at its side, images (e–j); and final detachment, upwards jumping, rising and oscillation with the Minnaert frequency, images (k–y).
To help analyse and compare the experimental results, we also simulate the bubble coalescence using an axisymmetric boundary integral (BI) code (see e.g. Og̃uz & Prosperetti Reference Og̃uz and Prosperetti1993; Power & Wrobel Reference Power and Wrobel1995; Bergmann et al.
Reference Bergmann, van der Meer, Gekle, van der Bos and Lohse2009; Gekle et al.
Reference Gekle, Gordillo, van der Meer and Lohse2009) under the assumption of zero viscosity. The simulation obtains information from the coalescence event in an easy way without the difficulties associated with performing experiments. Besides, higher-order waves can be studied in more detail. Aiming for simplification, some assumptions need to be made. We start the simulation when the bubbles are already connected through a thin neck at the symmetry axis (vertical line at a distance
![]() $d/2$
from each bubble, i.e. through the contact point at coalescence) to avoid the initial coalescence singularity (Og̃uz & Prosperetti Reference Og̃uz and Prosperetti1989; Duchemin et al.
Reference Duchemin, Popinet, Josserand and Zaleski2002; Munro et al.
Reference Munro, Anthony, Basaran and Lister2015; Zhang et al.
Reference Zhang, Thoraval, Thoroddsen and Taborek2015; Anthony et al.
Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017). Different initial values of the connecting neck have been used, showing an extremely fast convergence to the actual initial experimentally measured neck radius (Anthony et al.
Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017). Because we want to keep an axisymmetric configuration for simplicity, the wall is left out of the numerical configuration. Obviously, this is an oversimplification of the experimental situation. However, in this way, the simulation provides symmetric results along a horizontal axis which goes through the centre of the bubbles and along the symmetry axis. Results are thus accurate on the upper halves of the bubbles, since the presence of the pinning points in the experiments breaks the symmetry, as can be detected from image 2(d) on. Other codes, such as the free-surface Navier–Stokes code developed by Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos and Núñez2001) and the fully implicit arbitrary Lagrangian–Eulerian (ALE) method developed by Anthony et al. (Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017), generated similar results.
$d/2$
from each bubble, i.e. through the contact point at coalescence) to avoid the initial coalescence singularity (Og̃uz & Prosperetti Reference Og̃uz and Prosperetti1989; Duchemin et al.
Reference Duchemin, Popinet, Josserand and Zaleski2002; Munro et al.
Reference Munro, Anthony, Basaran and Lister2015; Zhang et al.
Reference Zhang, Thoraval, Thoroddsen and Taborek2015; Anthony et al.
Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017). Different initial values of the connecting neck have been used, showing an extremely fast convergence to the actual initial experimentally measured neck radius (Anthony et al.
Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017). Because we want to keep an axisymmetric configuration for simplicity, the wall is left out of the numerical configuration. Obviously, this is an oversimplification of the experimental situation. However, in this way, the simulation provides symmetric results along a horizontal axis which goes through the centre of the bubbles and along the symmetry axis. Results are thus accurate on the upper halves of the bubbles, since the presence of the pinning points in the experiments breaks the symmetry, as can be detected from image 2(d) on. Other codes, such as the free-surface Navier–Stokes code developed by Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos and Núñez2001) and the fully implicit arbitrary Lagrangian–Eulerian (ALE) method developed by Anthony et al. (Reference Anthony, Kamat, Thete, Munro, Lister, Harris and Basaran2017), generated similar results.
Considering the gas–liquid properties, the liquid flow around the bubble is assumed to be irrotational, incompressible and inviscid. The gas inside the bubble behaves as an ideal gas with a polytropic exponent
![]() $n=1.338$
(Moran & Shapiro Reference Moran and Shapiro2006) corresponding to the experimental conditions. The initial conditions in the simulation are matched to those in one of the experiments, i.e. distance between bubbles
$n=1.338$
(Moran & Shapiro Reference Moran and Shapiro2006) corresponding to the experimental conditions. The initial conditions in the simulation are matched to those in one of the experiments, i.e. distance between bubbles
![]() $d=600~\unicode[STIX]{x03BC}\text{m}$
, pressure at supersaturated conditions
$d=600~\unicode[STIX]{x03BC}\text{m}$
, pressure at supersaturated conditions
![]() $P_{s}=7.75~\text{bar}$
, temperature
$P_{s}=7.75~\text{bar}$
, temperature
![]() $T=20.5\,^{\circ }\text{C}$
, surface tension coefficient
$T=20.5\,^{\circ }\text{C}$
, surface tension coefficient
![]() $\unicode[STIX]{x1D70E}=58.7~\text{mN}~\text{m}^{-1}$
and liquid (water) and gas (
$\unicode[STIX]{x1D70E}=58.7~\text{mN}~\text{m}^{-1}$
and liquid (water) and gas (
![]() $\text{CO}_{2}$
) densities
$\text{CO}_{2}$
) densities
![]() $\unicode[STIX]{x1D70C}_{l}=1012.6~\text{kg}~\text{m}^{-3}$
and
$\unicode[STIX]{x1D70C}_{l}=1012.6~\text{kg}~\text{m}^{-3}$
and
![]() $\unicode[STIX]{x1D70C}_{g}=12.8~\text{kg}~\text{m}^{-3}$
, respectively. The simulation has been run up to the point where the capillary waves propagating on the upper and lower half of the bubble converge at the opposite apex from the coalescence point, since we reach a singularity. Note that both outer (water) and inner (
$\unicode[STIX]{x1D70C}_{g}=12.8~\text{kg}~\text{m}^{-3}$
, respectively. The simulation has been run up to the point where the capillary waves propagating on the upper and lower half of the bubble converge at the opposite apex from the coalescence point, since we reach a singularity. Note that both outer (water) and inner (
![]() $\text{CO}_{2}$
) fluid are independently modelled in the BI simulations (Gekle et al.
Reference Gekle, Gordillo, van der Meer and Lohse2009). A video which contains the one-to-one comparison between experiments and simulation can be found in the supplementary material available at https://doi.org/10.1017/jfm.2018.277.
$\text{CO}_{2}$
) fluid are independently modelled in the BI simulations (Gekle et al.
Reference Gekle, Gordillo, van der Meer and Lohse2009). A video which contains the one-to-one comparison between experiments and simulation can be found in the supplementary material available at https://doi.org/10.1017/jfm.2018.277.
3 Analysis of results
3.1 Diffusive bubble growth
We use several samples with different distances between the pits (
![]() $d=300,400,500$
and
$d=300,400,500$
and
![]() $600~\unicode[STIX]{x03BC}\text{m}$
) and different pit radii (
$600~\unicode[STIX]{x03BC}\text{m}$
) and different pit radii (
![]() $10$
and
$10$
and
![]() $50~\unicode[STIX]{x03BC}\text{m}$
). We record the growth of successive bubble pairs with a LaVision camera at 2 fps, so that we can confirm their diffusion-driven growth. The theoretical evolution of the radius
$50~\unicode[STIX]{x03BC}\text{m}$
). We record the growth of successive bubble pairs with a LaVision camera at 2 fps, so that we can confirm their diffusion-driven growth. The theoretical evolution of the radius
![]() $R(t)$
of a single quasi-statically growing isolated bubble is given by the Epstein–Plesset equation (Epstein & Plesset Reference Epstein and Plesset1950):
$R(t)$
of a single quasi-statically growing isolated bubble is given by the Epstein–Plesset equation (Epstein & Plesset Reference Epstein and Plesset1950):
where
![]() $D=1.76\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
(Frank et al.
Reference Frank, Kuipers and van Swaaij1996; Diamond & Akinfiev Reference Diamond and Akinfiev2003; Liger-Belair et al.
Reference Liger-Belair, Prost, Parmentier, Jeandet and Nuzillard2003; Cussler Reference Cussler2009; Lu et al.
Reference Lu, Guo, Chou, Burruss and Li2013) is the diffusivity of
$D=1.76\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
(Frank et al.
Reference Frank, Kuipers and van Swaaij1996; Diamond & Akinfiev Reference Diamond and Akinfiev2003; Liger-Belair et al.
Reference Liger-Belair, Prost, Parmentier, Jeandet and Nuzillard2003; Cussler Reference Cussler2009; Lu et al.
Reference Lu, Guo, Chou, Burruss and Li2013) is the diffusivity of
![]() $\text{CO}_{2}$
in water. Equation (3.1) has been solved and the results agree with the experiments adding a term which accounts for the effect of the silicon chip on which the bubbles are growing (Enríquez et al.
Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). The approximate solution for the dimensionless bubble radius
$\text{CO}_{2}$
in water. Equation (3.1) has been solved and the results agree with the experiments adding a term which accounts for the effect of the silicon chip on which the bubbles are growing (Enríquez et al.
Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). The approximate solution for the dimensionless bubble radius
![]() $\unicode[STIX]{x1D716}=R/R_{p}$
reads
$\unicode[STIX]{x1D716}=R/R_{p}$
reads
 $$\begin{eqnarray}\unicode[STIX]{x1D716}=\left(\sqrt{\frac{\unicode[STIX]{x1D701}c_{s}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{g}}}+\left(\frac{1}{2}+\sqrt{\frac{\unicode[STIX]{x1D701}c_{s}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{g}}}\right)^{1/2}\right)x\equiv S^{\ast }x,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}=\left(\sqrt{\frac{\unicode[STIX]{x1D701}c_{s}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{g}}}+\left(\frac{1}{2}+\sqrt{\frac{\unicode[STIX]{x1D701}c_{s}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{g}}}\right)^{1/2}\right)x\equiv S^{\ast }x,\end{eqnarray}$$
where
![]() $R_{p}$
is the pit radius and
$R_{p}$
is the pit radius and
![]() $x=\sqrt{((2D\unicode[STIX]{x1D701}c_{s})/(\unicode[STIX]{x1D70C}_{g}R_{p}^{2}))t}$
the square root of the dimensionless time.
$x=\sqrt{((2D\unicode[STIX]{x1D701}c_{s})/(\unicode[STIX]{x1D70C}_{g}R_{p}^{2}))t}$
the square root of the dimensionless time.

Figure 3. Temporal evolution of the dimensionless radius
![]() $\unicode[STIX]{x1D716}(t)=R(t)/R_{p}$
for two bubbles growing next to each other. The separation between the pits is indicated by the length
$\unicode[STIX]{x1D716}(t)=R(t)/R_{p}$
for two bubbles growing next to each other. The separation between the pits is indicated by the length
![]() $d$
. Both bubbles show the same evolution and only one is represented for clarity. (a) Evolution of the dimensionless bubble radius
$d$
. Both bubbles show the same evolution and only one is represented for clarity. (a) Evolution of the dimensionless bubble radius
![]() $\unicode[STIX]{x1D716}$
before coalescence. The black line (corresponding to the same black curve in b) represents the theoretical Epstein and Plesset solution for a single bubble attached to a horizontal wall given by (3.2), based on Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). (b) Evolution of the derivative of the bubble radius. The experimental points show a horizontal behaviour, corresponding to the expected competitive diffusive growth: see The curve corresponding to
$\unicode[STIX]{x1D716}$
before coalescence. The black line (corresponding to the same black curve in b) represents the theoretical Epstein and Plesset solution for a single bubble attached to a horizontal wall given by (3.2), based on Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). (b) Evolution of the derivative of the bubble radius. The experimental points show a horizontal behaviour, corresponding to the expected competitive diffusive growth: see The curve corresponding to
![]() $d=600~\unicode[STIX]{x03BC}\text{m}$
differs from the others because the coalescence occurs in the very early stages of the bubble growth, thus the mass transfer is settling to diffusion after the explosive initial growth right after nucleation.
$d=600~\unicode[STIX]{x03BC}\text{m}$
differs from the others because the coalescence occurs in the very early stages of the bubble growth, thus the mass transfer is settling to diffusion after the explosive initial growth right after nucleation.
Because the two neighbouring growing bubbles compete for the dissolved gas, their growth is influenced by the distance
![]() $d$
separating them (Enríquez Paz y Puente Reference Enríquez Paz y Puente2015). However, the corresponding concentration boundary layers growing around each bubble as
$d$
separating them (Enríquez Paz y Puente Reference Enríquez Paz y Puente2015). However, the corresponding concentration boundary layers growing around each bubble as
![]() $\sqrt{\unicode[STIX]{x03C0}Dt}$
merge in one concentration layer from which both bubbles absorb gas from the very early stages of the bubbles growth. Therefore, the influence of the distance
$\sqrt{\unicode[STIX]{x03C0}Dt}$
merge in one concentration layer from which both bubbles absorb gas from the very early stages of the bubbles growth. Therefore, the influence of the distance
![]() $d$
is negligible except for the very beginning of the process. In figure 3, we represent the evolution of the bubble radii for different distances
$d$
is negligible except for the very beginning of the process. In figure 3, we represent the evolution of the bubble radii for different distances
![]() $d$
between the pinning holes (which is equal to twice the coalescence radius,
$d$
between the pinning holes (which is equal to twice the coalescence radius,
![]() $d=2R_{coal}$
) and compare this to the theoretical radius evolution, equation (3.2). Indeed, the radius evolution is proportional to the square root of time, as expected for a diffusive growth: see figure 3(a). However, the nominal value of the slope
$d=2R_{coal}$
) and compare this to the theoretical radius evolution, equation (3.2). Indeed, the radius evolution is proportional to the square root of time, as expected for a diffusive growth: see figure 3(a). However, the nominal value of the slope
![]() $\text{d}\unicode[STIX]{x1D716}/\text{d}x$
is lower than the theoretical one (Liger-Belair et al.
Reference Liger-Belair, Sternenberg, Brunner, Robillard and Cilindre2015) and independent of
$\text{d}\unicode[STIX]{x1D716}/\text{d}x$
is lower than the theoretical one (Liger-Belair et al.
Reference Liger-Belair, Sternenberg, Brunner, Robillard and Cilindre2015) and independent of
![]() $d$
(Enríquez Paz y Puente Reference Enríquez Paz y Puente2015), caused by the influence of each bubble growing next to a neighbouring one and the rapid merging of the two concentration boundary layers (Zhu et al.
Reference Zhu, Verzicco, Zhang and Lohse2018). In figure 3(b), we plot the theoretical dimensionless radius derivative
$d$
(Enríquez Paz y Puente Reference Enríquez Paz y Puente2015), caused by the influence of each bubble growing next to a neighbouring one and the rapid merging of the two concentration boundary layers (Zhu et al.
Reference Zhu, Verzicco, Zhang and Lohse2018). In figure 3(b), we plot the theoretical dimensionless radius derivative
![]() $(1/S^{\ast })\,\text{d}\unicode[STIX]{x1D716}/\text{d}x=1$
(following the representation depicted in Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014)) and compare it with the experimental derivative. The experimental data fall below the theoretically predicted diffusive growth for a single bubble growing on a substrate, which agrees with the expected behaviour for two neighbouring bubbles. Thus we confirm that the growth of both bubbles is driven by diffusion right before their coalescence. Note that long-time depletion effects (Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017) have not been observed during the diffusive growth of the bubble pairs, since the bubbles coalesce and detach before the onset of natural convection (Enríquez et al.
Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). The area around the pits in which the new bubble pair will grow is also refreshed with new solution as the coalesced bubble detaches and rises. Whereas the damping time of the originated flow is below one second (Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017), the new bubble pair needs approximately 10 s to renucleate afterwards and many minutes to grow until coalescence occurs, so the mass transfer enhancement caused by the refreshing flow plays no significant role on their growth.
$(1/S^{\ast })\,\text{d}\unicode[STIX]{x1D716}/\text{d}x=1$
(following the representation depicted in Enríquez et al. (Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014)) and compare it with the experimental derivative. The experimental data fall below the theoretically predicted diffusive growth for a single bubble growing on a substrate, which agrees with the expected behaviour for two neighbouring bubbles. Thus we confirm that the growth of both bubbles is driven by diffusion right before their coalescence. Note that long-time depletion effects (Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017) have not been observed during the diffusive growth of the bubble pairs, since the bubbles coalesce and detach before the onset of natural convection (Enríquez et al.
Reference Enríquez, Sun, Lohse, Prosperetti and van der Meer2014). The area around the pits in which the new bubble pair will grow is also refreshed with new solution as the coalesced bubble detaches and rises. Whereas the damping time of the originated flow is below one second (Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017), the new bubble pair needs approximately 10 s to renucleate afterwards and many minutes to grow until coalescence occurs, so the mass transfer enhancement caused by the refreshing flow plays no significant role on their growth.
3.2 Evolution of the neck between bubbles at the beginning of the coalescence
As seen in figure 2(a–d), the early coalescence is characterised by the neck formation between the bubbles. By integrating the axisymmetric Navier–Stokes equations from a quiescent point far away up to the neck radius, similar to the derivation of the Rayleigh–Plesset equation (Plesset & Prosperetti Reference Plesset and Prosperetti1977), we can model the evolution of the neck radius
![]() $r_{n}$
, geometrically defined in figure 4(a), as
$r_{n}$
, geometrically defined in figure 4(a), as
where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}\approx \unicode[STIX]{x1D70C}$
is the density difference between the liquid and the gas,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}\approx \unicode[STIX]{x1D70C}$
is the density difference between the liquid and the gas,
![]() $g$
is the gravitational constant and
$g$
is the gravitational constant and
![]() $\unicode[STIX]{x0394}P$
is the Laplace pressure. We calculate the Reynolds
$\unicode[STIX]{x0394}P$
is the Laplace pressure. We calculate the Reynolds
![]() $Re={\dot{r}}_{n}d/2\unicode[STIX]{x1D708}$
and Froude
$Re={\dot{r}}_{n}d/2\unicode[STIX]{x1D708}$
and Froude
![]() $Fr=\sqrt{2{\dot{r}}_{n}^{2}/gd}$
numbers, comparing inertia with viscosity and gravity, respectively. We find that both
$Fr=\sqrt{2{\dot{r}}_{n}^{2}/gd}$
numbers, comparing inertia with viscosity and gravity, respectively. We find that both
![]() $Re$
and
$Re$
and
![]() $Fr$
are larger than
$Fr$
are larger than
![]() $100$
, thus the inertial stress
$100$
, thus the inertial stress
![]() $\unicode[STIX]{x1D70C}(\text{d}r_{n}/\text{d}t)^{2}$
is dominant in (3.3), such that we can neglect viscosity and gravity effects. Besides, surface tension dominates over viscosity, since the Ohnesorge number
$\unicode[STIX]{x1D70C}(\text{d}r_{n}/\text{d}t)^{2}$
is dominant in (3.3), such that we can neglect viscosity and gravity effects. Besides, surface tension dominates over viscosity, since the Ohnesorge number
![]() $Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70E}R_{coal}}$
is always of the order of
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70E}R_{coal}}$
is always of the order of
![]() ${\sim}10^{-3}$
. It is important to mention that up to 10 ns after the bubbles touch, the evolution of the neck is ruled by viscosity, crossing over to an inertia-dominated process, as demonstrated by Paulsen, Burton & Nagel (Reference Paulsen, Burton and Nagel2011). The cross-over time is dependent on the viscosity of the liquids and gases involved in the coalescence, i.e. the higher the viscosity of the fluids involved, the later the cross-over will occur (Paulsen et al.
Reference Paulsen, Burton, Nagel, Appathurai, Harris and Basaran2012). Our work focuses however on the capillary–inertia mechanics of the neck evolution.
${\sim}10^{-3}$
. It is important to mention that up to 10 ns after the bubbles touch, the evolution of the neck is ruled by viscosity, crossing over to an inertia-dominated process, as demonstrated by Paulsen, Burton & Nagel (Reference Paulsen, Burton and Nagel2011). The cross-over time is dependent on the viscosity of the liquids and gases involved in the coalescence, i.e. the higher the viscosity of the fluids involved, the later the cross-over will occur (Paulsen et al.
Reference Paulsen, Burton, Nagel, Appathurai, Harris and Basaran2012). Our work focuses however on the capillary–inertia mechanics of the neck evolution.

Figure 4. Graphical definition of (a) the neck radius
![]() $r_{n}$
and (b) the horizontal spacing between the two bubbles
$r_{n}$
and (b) the horizontal spacing between the two bubbles
![]() $\unicode[STIX]{x1D6FF}(r_{n})$
measured in the equivalent configuration before coalescence.
$\unicode[STIX]{x1D6FF}(r_{n})$
measured in the equivalent configuration before coalescence.
Thoroddsen et al. (Reference Thoroddsen, Takehara and Etoh2005b
) suggested a Laplace pressure definition based on the neck radius
![]() $r_{n}$
and the horizontal spacing between the two bubbles
$r_{n}$
and the horizontal spacing between the two bubbles
![]() $\unicode[STIX]{x1D6FF}(r_{n})$
measured in the equivalent non-deformable configuration according to the model in figure 4(b):
$\unicode[STIX]{x1D6FF}(r_{n})$
measured in the equivalent non-deformable configuration according to the model in figure 4(b):
Combining equations (3.3) and (3.4), and non-dimensionalising with the half-distance between pits
![]() $d/2$
and the capillary time
$d/2$
and the capillary time
![]() $\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
, the ordinary differential equation (ODE) for the dimensionless neck radius
$\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
, the ordinary differential equation (ODE) for the dimensionless neck radius
![]() $\tilde{r}_{n}=2r_{n}/d$
becomes
$\tilde{r}_{n}=2r_{n}/d$
becomes
where
![]() $C$
is a dimensionless fitting constant of order 1,
$C$
is a dimensionless fitting constant of order 1,
![]() $\tilde{\unicode[STIX]{x1D6FF}}=2\unicode[STIX]{x1D6FF}/d$
and
$\tilde{\unicode[STIX]{x1D6FF}}=2\unicode[STIX]{x1D6FF}/d$
and
![]() $\tilde{t}=t/\unicode[STIX]{x1D70F}$
. From geometry, we obtain
$\tilde{t}=t/\unicode[STIX]{x1D70F}$
. From geometry, we obtain
![]() $\tilde{\unicode[STIX]{x1D6FF}}(\tilde{r}_{n})=2(1-\sqrt{1-\tilde{r}_{n}^{2}})$
for the dimensionless horizontal spacing, which results in a differential equation for
$\tilde{\unicode[STIX]{x1D6FF}}(\tilde{r}_{n})=2(1-\sqrt{1-\tilde{r}_{n}^{2}})$
for the dimensionless horizontal spacing, which results in a differential equation for
![]() $\tilde{r}_{n}$
that can be numerically solved. Although Thoroddsen et al. (Reference Thoroddsen, Takehara and Etoh2005b
) used
$\tilde{r}_{n}$
that can be numerically solved. Although Thoroddsen et al. (Reference Thoroddsen, Takehara and Etoh2005b
) used
![]() $\unicode[STIX]{x1D6FF}$
as the length scale estimate in the Laplace pressure definition (3.4), we find better agreement using the half-spacing between the two bubbles instead, which actually corresponds to an equivalent radius of curvature of the evolving neck in the axial direction. With this modification, the ODE for
$\unicode[STIX]{x1D6FF}$
as the length scale estimate in the Laplace pressure definition (3.4), we find better agreement using the half-spacing between the two bubbles instead, which actually corresponds to an equivalent radius of curvature of the evolving neck in the axial direction. With this modification, the ODE for
![]() $\tilde{r}_{n}(t)$
becomes
$\tilde{r}_{n}(t)$
becomes
 $$\begin{eqnarray}\frac{\text{d}\tilde{r}_{n}}{\text{d}\tilde{t}}=C\sqrt{\left(\frac{1}{1-\sqrt{1-\tilde{r}_{n}^{2}}}-\frac{1}{\tilde{r}_{n}}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}\tilde{r}_{n}}{\text{d}\tilde{t}}=C\sqrt{\left(\frac{1}{1-\sqrt{1-\tilde{r}_{n}^{2}}}-\frac{1}{\tilde{r}_{n}}\right)}.\end{eqnarray}$$
Another approach with the square root of time is often proposed for the case of drops (Case & Nagel Reference Case and Nagel2008; Paulsen et al. Reference Paulsen, Carmigniani, Kannan, Burton and Nagel2014):
where
![]() $B$
is a dimensionless fitting parameter. During the early coalescence,
$B$
is a dimensionless fitting parameter. During the early coalescence,
![]() $\unicode[STIX]{x1D6FF}\ll r_{n}$
and
$\unicode[STIX]{x1D6FF}\ll r_{n}$
and
![]() $\unicode[STIX]{x1D6FF}\ll d/2$
, conditions such that
$\unicode[STIX]{x1D6FF}\ll d/2$
, conditions such that
![]() $\unicode[STIX]{x1D6FF}$
can be approximated as
$\unicode[STIX]{x1D6FF}$
can be approximated as
![]() $\unicode[STIX]{x1D6FF}=2r_{n}^{2}/d$
, and therefore,
$\unicode[STIX]{x1D6FF}=2r_{n}^{2}/d$
, and therefore,
![]() $\unicode[STIX]{x0394}P=\unicode[STIX]{x1D70E}d/2r_{n}^{2}$
. Introducing these new definitions into (3.3) after neglecting viscosity and gravity, we obtain
$\unicode[STIX]{x0394}P=\unicode[STIX]{x1D70E}d/2r_{n}^{2}$
. Introducing these new definitions into (3.3) after neglecting viscosity and gravity, we obtain
When solving this ODE, we recover equation (3.7), which is valid for the early coalescence and is only a particular case of the general equation (3.6). Indeed, Thoroddsen et al. (Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
) pointed out that this law is valid for
![]() $2r_{n}/d<0.45$
.
$2r_{n}/d<0.45$
.

Figure 5. (a) Evolution of the dimensionless neck radius
![]() $r_{n}/(d/2)$
for different bubble radii at the moment of coalescence
$r_{n}/(d/2)$
for different bubble radii at the moment of coalescence
![]() $R_{coal}=d/2$
and comparison with the Thoroddsen model (3.6) and Paulsen model (3.7), together with the results from the BI code. Time has been non-dimensionalised by the capillary time
$R_{coal}=d/2$
and comparison with the Thoroddsen model (3.6) and Paulsen model (3.7), together with the results from the BI code. Time has been non-dimensionalised by the capillary time
![]() $\unicode[STIX]{x1D70F}$
. Inset: the same data on a double logarithmic plot for a better appreciation of the early coalescence. (b) The same evolution as in (a) but with the vertical axis compensated with the dimensionless time. Here we can appreciate with higher detail the discrepancies between experiments and the model with the square root of time, equation (3.7), which no longer agree after
$\unicode[STIX]{x1D70F}$
. Inset: the same data on a double logarithmic plot for a better appreciation of the early coalescence. (b) The same evolution as in (a) but with the vertical axis compensated with the dimensionless time. Here we can appreciate with higher detail the discrepancies between experiments and the model with the square root of time, equation (3.7), which no longer agree after
![]() $t/\unicode[STIX]{x1D70F}=0.2$
, whereas the model (3.6) is more realistic and precisely fits the experimental data even at high values of the neck radius. The BI results show excellent agreement with experiments, despite the initial coalescence singularity.
$t/\unicode[STIX]{x1D70F}=0.2$
, whereas the model (3.6) is more realistic and precisely fits the experimental data even at high values of the neck radius. The BI results show excellent agreement with experiments, despite the initial coalescence singularity.
We measure the evolution of the neck radius for many coalescences with different values of the bubble radius. To compare the experimental results, we use the measured values for the upper part of the neck formed between the bubbles. Results for the lower neck are only considered for the very early coalescence, since the presence of the pits to which the bubbles attach breaks the symmetric neck evolution and impedes a free propagation of the deforming wave. The experimental results are compared to the theoretical models (3.6) and (3.7) in figure 5, as well as to the results obtained from the BI code. As expected, the square root scaling law (3.7) no longer accurately fits to the experimental data after
![]() $2r_{n}/d\approx 0.45$
. Nevertheless, the capillary–inertial model, equation (3.6), precisely matches the experimental data at all times for a best fitting constant
$2r_{n}/d\approx 0.45$
. Nevertheless, the capillary–inertial model, equation (3.6), precisely matches the experimental data at all times for a best fitting constant
![]() $C=0.85$
. In the literature, a fitting value of
$C=0.85$
. In the literature, a fitting value of
![]() $C=1.06$
in (3.5) for bubbles can be found (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
), whereas a value
$C=1.06$
in (3.5) for bubbles can be found (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
), whereas a value
![]() $C=0.80$
follows for the case of drops (Thoroddsen et al.
Reference Thoroddsen, Takehara and Etoh2005b
). The difficulty in matching the experimental data to the theory originates from the choice of the initial time. Indeed, the first snapshot where we can see the bubble surface moving does not correspond to the exact beginning of the coalescence, which actually starts shortly before. To find time zero, we solved the ODE (3.6) with
$C=0.80$
follows for the case of drops (Thoroddsen et al.
Reference Thoroddsen, Takehara and Etoh2005b
). The difficulty in matching the experimental data to the theory originates from the choice of the initial time. Indeed, the first snapshot where we can see the bubble surface moving does not correspond to the exact beginning of the coalescence, which actually starts shortly before. To find time zero, we solved the ODE (3.6) with
![]() $\tilde{r}_{n}(\tilde{t}=0)=0$
. Then, we shift the time of the experimental plot so that both theory and experiments agree. The results from the BI code precisely agree with the experimental data and with the theoretical model given by (3.6), which corroborates both our modifications of the original model proposed by Thoroddsen et al. (Reference Thoroddsen, Takehara and Etoh2005b
) and the results from our experiments.
$\tilde{r}_{n}(\tilde{t}=0)=0$
. Then, we shift the time of the experimental plot so that both theory and experiments agree. The results from the BI code precisely agree with the experimental data and with the theoretical model given by (3.6), which corroborates both our modifications of the original model proposed by Thoroddsen et al. (Reference Thoroddsen, Takehara and Etoh2005b
) and the results from our experiments.
In addition, we measure the time evolution of the neck radius of curvature in the axial direction
![]() $R_{c}(t)$
: see figure 6. For the calculation of this radius of curvature, we fit a circle at the bridge formed between the bubbles at the position
$R_{c}(t)$
: see figure 6. For the calculation of this radius of curvature, we fit a circle at the bridge formed between the bubbles at the position
![]() $r_{n}$
, whose radius is by definition the neck curvature (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
), as represented in figure 6(a). We investigate that the radius of curvature is also affected by the presence of the pinning points: see figure 6(b). As expected, the early evolution is similar for both curves, but after
$r_{n}$
, whose radius is by definition the neck curvature (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
), as represented in figure 6(a). We investigate that the radius of curvature is also affected by the presence of the pinning points: see figure 6(b). As expected, the early evolution is similar for both curves, but after
![]() $t\approx 0.1~\text{ms}$
, the upper radius of curvature grows much faster than the bottom one due to the presence of the substrate and the pinning spots, which do not let the lower half-surface freely deform. As mentioned before, the same phenomenon occurs for the evolution of the neck radius.
$t\approx 0.1~\text{ms}$
, the upper radius of curvature grows much faster than the bottom one due to the presence of the substrate and the pinning spots, which do not let the lower half-surface freely deform. As mentioned before, the same phenomenon occurs for the evolution of the neck radius.

Figure 6. (a) Evolution of the neck and its best-fit circle. The cross markers correspond to the contour of the top part of the coalescing bubble. Each contour from the bottom to the top of the figure is separated by
![]() $15~\unicode[STIX]{x03BC}\text{s}$
and the first contour on the bottom corresponds to the first recorded shape of the coalescing bubbles. The radius of the best-fit circle corresponds to the neck curvature. (b) Time evolution of the top and bottom radii of curvature for
$15~\unicode[STIX]{x03BC}\text{s}$
and the first contour on the bottom corresponds to the first recorded shape of the coalescing bubbles. The radius of the best-fit circle corresponds to the neck curvature. (b) Time evolution of the top and bottom radii of curvature for
![]() $300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles. The time when the two necks start growing differently corresponds approximately to figure 2(c).
$300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles. The time when the two necks start growing differently corresponds approximately to figure 2(c).

Figure 7. (a) Time evolution of the dimensionless radius of curvature
![]() $R_{c}/(d/2)$
for different bubble radii at coalescence
$R_{c}/(d/2)$
for different bubble radii at coalescence
![]() $R_{coal}$
. Inset: the same data on a double logarithmic scale, for a better appreciation of the early coalescence. (b) Evolution of the radius of curvature
$R_{coal}$
. Inset: the same data on a double logarithmic scale, for a better appreciation of the early coalescence. (b) Evolution of the radius of curvature
![]() $R_{c}(t)$
against that of the neck radius
$R_{c}(t)$
against that of the neck radius
![]() $r_{n}(t)$
. It can be observed that the non-deformable model, in which any point on the bubble surface remains unaltered until it is reached by the perturbation, does not follow the experimental data. For both panels (a) and (b), the prediction given by the BI code accurately matches the experiments.
$r_{n}(t)$
. It can be observed that the non-deformable model, in which any point on the bubble surface remains unaltered until it is reached by the perturbation, does not follow the experimental data. For both panels (a) and (b), the prediction given by the BI code accurately matches the experiments.
Results concerning this radius of curvature are presented in figure 7. Figure 7(a) shows the time evolution of the radius of curvature. For the early coalescence, the curvature seems to follow a linear evolution if the radius of curvature is non-dimensionalised by the bubble radius at the start of the coalescence, accounting for any geometrical effect that may originate from the different
![]() $R_{coal}=d/2$
(Hernández-Sánchez et al.
Reference Hernández-Sánchez, Lubbers, Eddi and Snoeijer2012). The radius of curvature also shows a linear dependence with the neck radius (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
) during the early stages of the coalescence process (figure 7
b), increasing drastically as the neck radius approaches the value of the bubble radius. Both curves collapse into one universal behaviour, i.e. the capillary time
$R_{coal}=d/2$
(Hernández-Sánchez et al.
Reference Hernández-Sánchez, Lubbers, Eddi and Snoeijer2012). The radius of curvature also shows a linear dependence with the neck radius (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Ootsuka2005a
) during the early stages of the coalescence process (figure 7
b), increasing drastically as the neck radius approaches the value of the bubble radius. Both curves collapse into one universal behaviour, i.e. the capillary time
![]() $\unicode[STIX]{x1D70F}$
is still relevant for the curvature evolution. Again, the BI code accurately matches the experimental results. The precision in the calculation of the radius of curvature is strongly affected by the bubble radius, with the last experimental values being extremely dependent on the selected points in the neck to which the curvature circle is fitted. Thus, the higher
$\unicode[STIX]{x1D70F}$
is still relevant for the curvature evolution. Again, the BI code accurately matches the experimental results. The precision in the calculation of the radius of curvature is strongly affected by the bubble radius, with the last experimental values being extremely dependent on the selected points in the neck to which the curvature circle is fitted. Thus, the higher
![]() $2R_{c}/d$
, the higher the inaccuracy in the calculation of the curvature radius.
$2R_{c}/d$
, the higher the inaccuracy in the calculation of the curvature radius.
If we assume that any point on the bubble surface remains unaltered until the perturbing wave reaches it, we can relate the radius of curvature to the neck radius as follows:
However, the discrepancies between this limit and the experiments observed in figure 7(b) show that, indeed, the bubble surface at a certain point is deformed by the perturbing wave even before it reaches that spot. However, once more, the BI code provides an extremely good prediction of the radius of curvature related to the neck radius.
3.3 Propagation of the deformation wave
After the neck is formed between the two bubbles, the deformation travels along the bubble surface until the upper and lower waves converge at the opposite apex of the bubbles from the coalescence point, a shape reminiscent of a lemon, as shown in figure 2(g). We note that even though the lower deforming wave travels through the pits (figure 2
c–e), the coalescing bubble does not detach. Indeed, detachment occurs once the deformation moves backwards and goes through the pit position once more (figure 2
k,l). Despite surface tension dominating over viscosity during the wave propagation,
![]() $Oh\sim 10^{-3}$
, a satellite pinch-off after the perturbing upper and lower waves meet at the side of the coalescing bubbles has not been observed, in contrast to the results documented by Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008) and Zhang et al. (Reference Zhang, Thoraval, Thoroddsen and Taborek2015). We associate the differences with the geometrical configuration of our system: the presence of the pits alters the perturbing wave propagation along the lower half-surface of the bubbles and breaks the axisymmetry of the process.
$Oh\sim 10^{-3}$
, a satellite pinch-off after the perturbing upper and lower waves meet at the side of the coalescing bubbles has not been observed, in contrast to the results documented by Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008) and Zhang et al. (Reference Zhang, Thoraval, Thoroddsen and Taborek2015). We associate the differences with the geometrical configuration of our system: the presence of the pits alters the perturbing wave propagation along the lower half-surface of the bubbles and breaks the axisymmetry of the process.
We focus on the surface deformation and how the collapsing waves travel along the bubble surface. Some results about capillary waves on a water–gas interface were discussed in Liberzon, Shemer & Barnea (Reference Liberzon, Shemer and Barnea2006) and Gekle et al. (Reference Gekle, van der Bos, Bergmann, van der Meer and Lohse2008), but with different geometries. Capillary waves have also been reported during the partial coalescence of droplets (Gilet et al. Reference Gilet, Mulleners, Lecomte, Vandewalle and Dorbolo2007). For a plane surface, the general dispersion relation for a single surface wave is (see e.g. Rayleigh (Reference Rayleigh1879) and Lamb (Reference Lamb1895, pp. 448–451))
with
![]() $\unicode[STIX]{x1D714}$
the angular frequency and
$\unicode[STIX]{x1D714}$
the angular frequency and
![]() $k$
the wavenumber. Capillarity is dominant over gravity if
$k$
the wavenumber. Capillarity is dominant over gravity if
![]() $(\unicode[STIX]{x1D70E}/g\unicode[STIX]{x1D70C})\cdot k^{2}\gg 1$
, i.e. the wavelength
$(\unicode[STIX]{x1D70E}/g\unicode[STIX]{x1D70C})\cdot k^{2}\gg 1$
, i.e. the wavelength
![]() $\unicode[STIX]{x1D706}\ll 15.5~\text{mm}$
for
$\unicode[STIX]{x1D706}\ll 15.5~\text{mm}$
for
![]() $\text{CO}_{2}$
bubbles in water. Our case fulfils this condition, since the wavelength we measure is smaller than 0.2 mm. We can thus neglect the gravity term in (3.10). Besides, for a spherical bubble, the angular wave vector has to be a natural number because of the periodic geometry. As shown in Lamb (Reference Lamb1895, pp. 468–469), the dispersion relation for the
$\text{CO}_{2}$
bubbles in water. Our case fulfils this condition, since the wavelength we measure is smaller than 0.2 mm. We can thus neglect the gravity term in (3.10). Besides, for a spherical bubble, the angular wave vector has to be a natural number because of the periodic geometry. As shown in Lamb (Reference Lamb1895, pp. 468–469), the dispersion relation for the
![]() $n$
mode of an air bubble in a liquid follows
$n$
mode of an air bubble in a liquid follows
with capillary time
![]() $\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
, and the angular phase velocity
$\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
, and the angular phase velocity
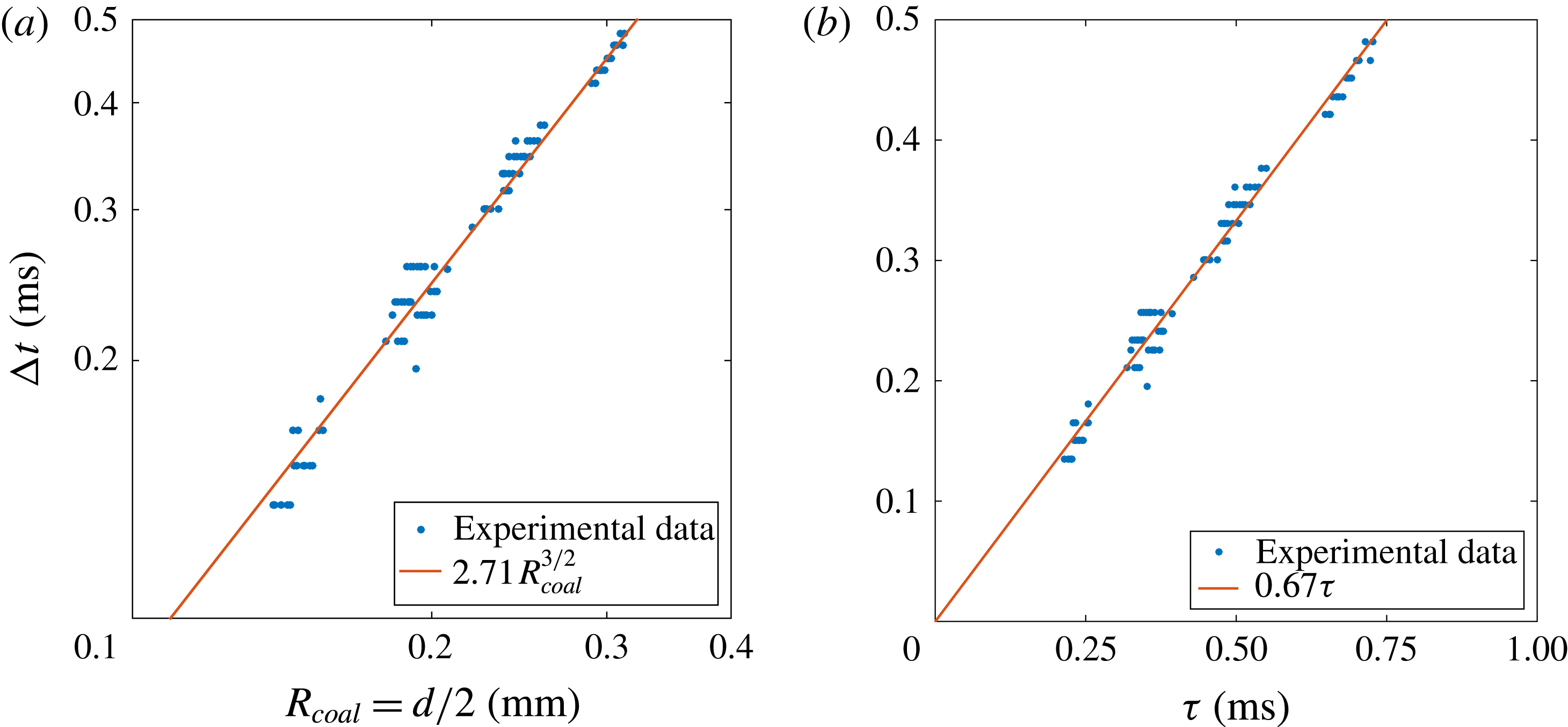
Figure 8. Time difference
![]() $\unicode[STIX]{x0394}t$
between the beginning of the coalescence and the convergence of the upper and lower waves at the opposite side of the coalescing bubbles (a) as a function of the bubble radius at coalescence (
$\unicode[STIX]{x0394}t$
between the beginning of the coalescence and the convergence of the upper and lower waves at the opposite side of the coalescing bubbles (a) as a function of the bubble radius at coalescence (
![]() $R_{coal}=d/2$
) on a logarithmic scale and (b) as a function of the capillary time
$R_{coal}=d/2$
) on a logarithmic scale and (b) as a function of the capillary time
![]() $\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
. The panels contain many different coalescence events. The red lines correspond to the best fit following (a) a power law and (b) a linear law.
$\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D70C}(d/2)^{3}/\unicode[STIX]{x1D70E}}$
. The panels contain many different coalescence events. The red lines correspond to the best fit following (a) a power law and (b) a linear law.
The propagation of the surface deformation is a wave packet composed of many angular frequencies moving with different velocities, since the phase velocity increases with
![]() $n$
. To account for the wave packet main velocity, we measure the time
$n$
. To account for the wave packet main velocity, we measure the time
![]() $\unicode[STIX]{x0394}t$
between the beginning of the coalescence and the moment in which the upper and lower waves meet each other at the sides of the bubble. Figure 8(a) shows the influence of the bubble radius at detachment
$\unicode[STIX]{x0394}t$
between the beginning of the coalescence and the moment in which the upper and lower waves meet each other at the sides of the bubble. Figure 8(a) shows the influence of the bubble radius at detachment
![]() $R_{coal}$
on this time
$R_{coal}$
on this time
![]() $\unicode[STIX]{x0394}t$
for many different coalescence events. It is observed that the time the waves need to travel along the bubble surface and meet each other at the opposite apex from the coalescence point follows the power law
$\unicode[STIX]{x0394}t$
for many different coalescence events. It is observed that the time the waves need to travel along the bubble surface and meet each other at the opposite apex from the coalescence point follows the power law
![]() $\unicode[STIX]{x0394}t\propto R_{coal}^{3/2}$
. Therefore, it is straightforward to plot the measured time
$\unicode[STIX]{x0394}t\propto R_{coal}^{3/2}$
. Therefore, it is straightforward to plot the measured time
![]() $\unicode[STIX]{x0394}t$
against the capillary time
$\unicode[STIX]{x0394}t$
against the capillary time
![]() $\unicode[STIX]{x1D70F}$
. Clearly the plot in figure 8(b) reveals a linear dependency with a slope that corresponds to
$\unicode[STIX]{x1D70F}$
. Clearly the plot in figure 8(b) reveals a linear dependency with a slope that corresponds to
![]() $\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
. Defining
$\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
. Defining
![]() $c_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x0394}\unicode[STIX]{x1D703}/\unicode[STIX]{x0394}t$
, with
$c_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x0394}\unicode[STIX]{x1D703}/\unicode[STIX]{x0394}t$
, with
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
being the angle
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
being the angle
![]() $\unicode[STIX]{x1D703}$
(graphically defined in figure 9
a) travelled by the wave packet during
$\unicode[STIX]{x1D703}$
(graphically defined in figure 9
a) travelled by the wave packet during
![]() $\unicode[STIX]{x0394}t$
, we can calculate a theoretical expression for the wave travelling time:
$\unicode[STIX]{x0394}t$
, we can calculate a theoretical expression for the wave travelling time:
The wave travels an angle
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
when it reaches the opposite apex of the bubble from the coalescence point. Thus, assuming only one single mode
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
when it reaches the opposite apex of the bubble from the coalescence point. Thus, assuming only one single mode
![]() $n$
and knowing that
$n$
and knowing that
![]() $\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
, we find that the average mode
$\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
, we find that the average mode
![]() $n=20$
governs the wave propagation.
$n=20$
governs the wave propagation.
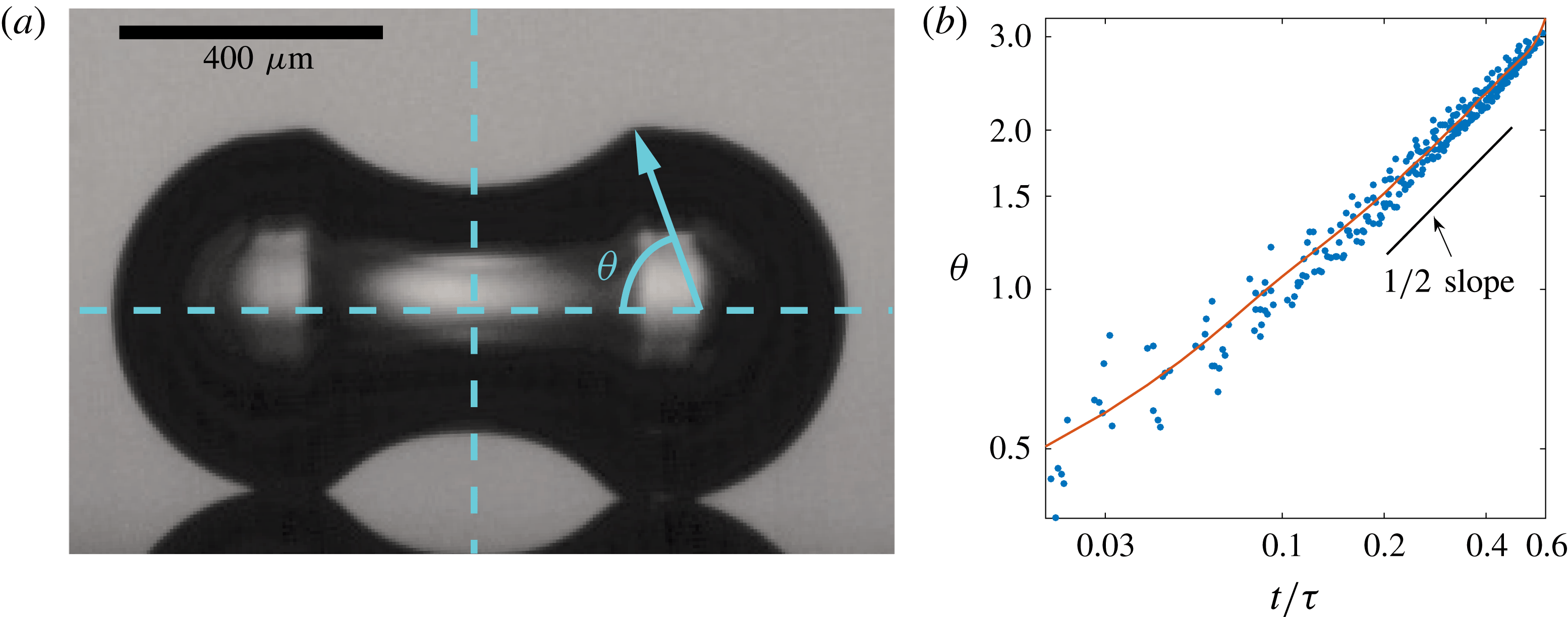
Figure 9. (a) Definition of the angular position
![]() $\unicode[STIX]{x1D703}$
as calculated from experiments. (b) Angular position
$\unicode[STIX]{x1D703}$
as calculated from experiments. (b) Angular position
![]() $\unicode[STIX]{x1D703}$
of the travelling deformation as a function of the dimensionless time. It has been measured for 15 coalescing bubbles of different radii. The plot is on double logarithmic scale, showing convergence to a power law with exponent
$\unicode[STIX]{x1D703}$
of the travelling deformation as a function of the dimensionless time. It has been measured for 15 coalescing bubbles of different radii. The plot is on double logarithmic scale, showing convergence to a power law with exponent
![]() $1/2$
. The red line corresponds to the results given by the (axisymmetric) BI code, showing the very precise agreement between the experiments and the simulation.
$1/2$
. The red line corresponds to the results given by the (axisymmetric) BI code, showing the very precise agreement between the experiments and the simulation.
After having corroborated that the capillary time is the proper time scale, it is interesting to study the time evolution of the wave packet while it propagates along the bubble surface. More specifically, we analyse the evolution of the angular position of the deformation from the very beginning of the coalescence until the upper and lower waves reach the sides of the coalescing bubbles. After that, the coalescing bubble starts to fold inward (figure 2 h), and the measurement of the angular position using the centre of the initial bubbles no longer applies.
For a better understanding of the evolution of the wave packet as it moves along the coalescing bubble surface, we define an equivalent single wave with mode
![]() $n$
at the angular position
$n$
at the angular position
![]() $\unicode[STIX]{x1D703}$
that will excite the same dominant mode of the wave packet at that same position. This dominant mode is obtained equalling the expression (3.12) to the corresponding definition of angular wave velocity
$\unicode[STIX]{x1D703}$
that will excite the same dominant mode of the wave packet at that same position. This dominant mode is obtained equalling the expression (3.12) to the corresponding definition of angular wave velocity
![]() $c_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D703}/t$
. Thus, assuming
$c_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D703}/t$
. Thus, assuming
![]() $n\gg 1$
, we conclude that
$n\gg 1$
, we conclude that
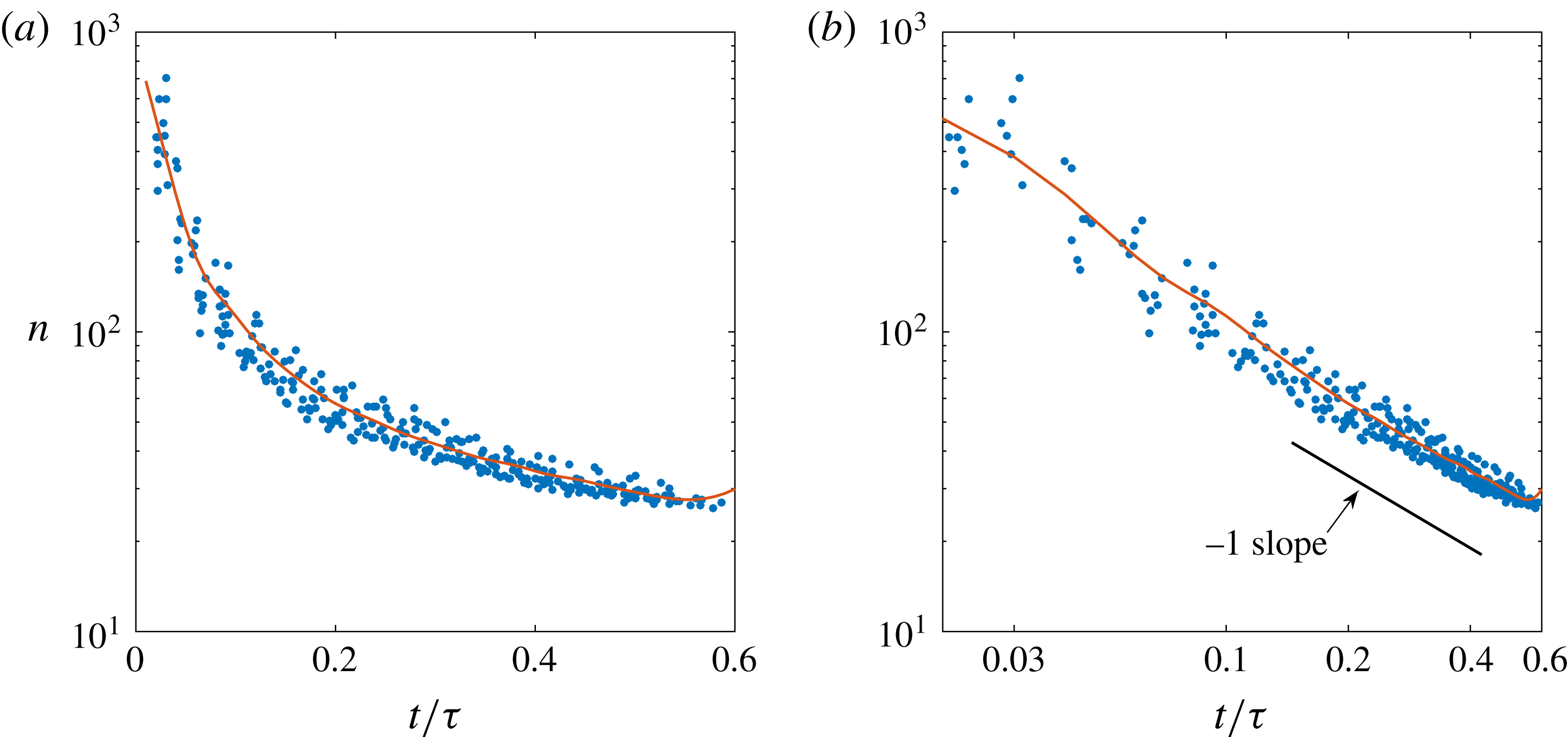
Figure 10. (a) Time evolution of the dominant mode of the wave packet during its propagation along the bubble surface, corresponding to the same experimental angular positions
![]() $\unicode[STIX]{x1D703}$
from figure 9;
$\unicode[STIX]{x1D703}$
from figure 9;
![]() $n$
is calculated for an equivalent single wave which would excite the same dominant mode as the wave packet, equation (3.14). (b) Logarithmic representation of the dominant mode, which suggests that its evolution follows a power law with an approximate exponent of
$n$
is calculated for an equivalent single wave which would excite the same dominant mode as the wave packet, equation (3.14). (b) Logarithmic representation of the dominant mode, which suggests that its evolution follows a power law with an approximate exponent of
![]() $-1$
. For both panels (a) and (b), the red curve stands for the BI code results, which again accurately match the experiments. A small deviation can be detected when the waves propagating along the upper and lower half-surface of the coalescing bubbles start approaching the opposite apex from the coalescence point. Even though the simulation results are within the spread of the experimental data, this deviation presumably originates from the simplifications employed in the BI code, i.e. the simulations neither account for viscous damping of the vibration modes (which becomes more relevant for the higher modes) nor for the presence of the pits which impede the free propagation of the lower wave. The small discrepancy can be better appreciated in figure 11.
$-1$
. For both panels (a) and (b), the red curve stands for the BI code results, which again accurately match the experiments. A small deviation can be detected when the waves propagating along the upper and lower half-surface of the coalescing bubbles start approaching the opposite apex from the coalescence point. Even though the simulation results are within the spread of the experimental data, this deviation presumably originates from the simplifications employed in the BI code, i.e. the simulations neither account for viscous damping of the vibration modes (which becomes more relevant for the higher modes) nor for the presence of the pits which impede the free propagation of the lower wave. The small discrepancy can be better appreciated in figure 11.
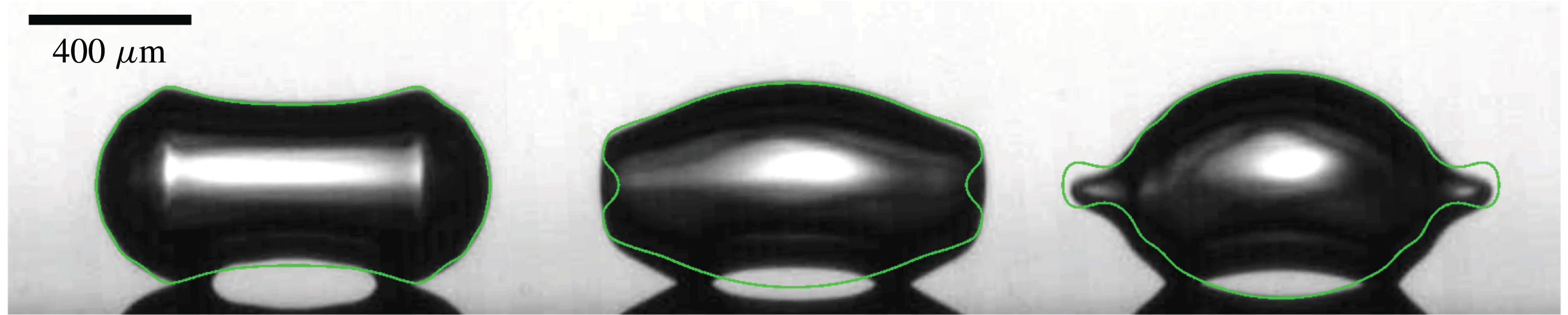
Figure 11. Comparison between the experiments and the (axisymmetric) BI simulation (green line) for
![]() $300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles. We notice the influence of the pits on the free propagation of the lower half-wave, thus the code only provides accurate results for the upper half-wave, which indeed freely propagates. Thus the final moments at which the two waves meet at the bubble sides cannot be simulated with the desired precision. Besides, the wave packet contains more oscillation modes in the simulation, since viscosity damps the higher modes in experiments, which is not accounted for in the simulation.
$300~\unicode[STIX]{x03BC}\text{m}$
radius bubbles. We notice the influence of the pits on the free propagation of the lower half-wave, thus the code only provides accurate results for the upper half-wave, which indeed freely propagates. Thus the final moments at which the two waves meet at the bubble sides cannot be simulated with the desired precision. Besides, the wave packet contains more oscillation modes in the simulation, since viscosity damps the higher modes in experiments, which is not accounted for in the simulation.
An equivalent relation can be found for the case of partial coalescence (Gilet et al.
Reference Gilet, Mulleners, Lecomte, Vandewalle and Dorbolo2007). Results are shown in figures 9(b) and 10, in which the results from different experiments with different
![]() $R$
and
$R$
and
![]() $d$
collapse when scaled with the capillary time (Zhang et al.
Reference Zhang, Thoraval, Thoroddsen and Taborek2015). We observe that the angular position does not change linearly with time because of the velocity dependence on
$d$
collapse when scaled with the capillary time (Zhang et al.
Reference Zhang, Thoraval, Thoroddsen and Taborek2015). We observe that the angular position does not change linearly with time because of the velocity dependence on
![]() $n$
. The dominant mode is extremely high at the beginning of the coalescence, decreasing afterwards very rapidly to a value
$n$
. The dominant mode is extremely high at the beginning of the coalescence, decreasing afterwards very rapidly to a value
![]() $n\approx 20$
, as also appreciated by Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008) and our results from (3.13). The logarithmic plots in figures 9(b) and 10(b) suggest that the time evolution of the angular position and dominant mode follow a power law with an exponent of approximately
$n\approx 20$
, as also appreciated by Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008) and our results from (3.13). The logarithmic plots in figures 9(b) and 10(b) suggest that the time evolution of the angular position and dominant mode follow a power law with an exponent of approximately
![]() $1/2$
and
$1/2$
and
![]() $-1$
, respectively, which is consistent with equation (3.14). The BI simulation precisely matches the experimental data except for the final points, where the deforming waves reach the bubble sides: see figure 11. Besides, although viscosity can be neglected in the neck dynamics, it affects the highest vibration modes, damping the high frequencies in the wave packet. Indeed, the viscous time for an
$-1$
, respectively, which is consistent with equation (3.14). The BI simulation precisely matches the experimental data except for the final points, where the deforming waves reach the bubble sides: see figure 11. Besides, although viscosity can be neglected in the neck dynamics, it affects the highest vibration modes, damping the high frequencies in the wave packet. Indeed, the viscous time for an
![]() $n$
mode is defined as
$n$
mode is defined as
where
![]() $\unicode[STIX]{x1D708}$
is the water kinematic viscosity. If we compare the capillary time
$\unicode[STIX]{x1D708}$
is the water kinematic viscosity. If we compare the capillary time
![]() $\unicode[STIX]{x1D70F}$
with the viscous time
$\unicode[STIX]{x1D70F}$
with the viscous time
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}$
for
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}$
for
![]() $R_{coal}=300~\unicode[STIX]{x03BC}\text{m}$
and
$R_{coal}=300~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D708}=9.64\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
(Frank et al.
Reference Frank, Kuipers and van Swaaij1996), we obtain
$\unicode[STIX]{x1D708}=9.64\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
(Frank et al.
Reference Frank, Kuipers and van Swaaij1996), we obtain
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=500)=0.02\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=500)=0.02\unicode[STIX]{x1D70F}$
,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=100)=0.54\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=100)=0.54\unicode[STIX]{x1D70F}$
,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=50)=2.2\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=50)=2.2\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=20)=13.5\unicode[STIX]{x1D70F}$
. Figure 8(b) shows that the average time scale of the propagation is
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D708}}(n=20)=13.5\unicode[STIX]{x1D70F}$
. Figure 8(b) shows that the average time scale of the propagation is
![]() $\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
, therefore the higher modes are quickly damped during the propagation. This further explains the differences with the BI simulations, which do not take viscosity into account.
$\unicode[STIX]{x0394}t/\unicode[STIX]{x1D70F}=0.67$
, therefore the higher modes are quickly damped during the propagation. This further explains the differences with the BI simulations, which do not take viscosity into account.

Figure 12. Snapshots of the coalescing bubble (a) before the convergence of the upper and lower wave and (b) after. The red arrows point to the position of the peaks whose distance in between corresponds to the wavelength.

Figure 13. (a) Distance between the two peaks on the bubble surface for different bubble radii after the convergence of the upper and lower wave. We use the radius of the new bubble
![]() $R_{b}$
, which is equal to
$R_{b}$
, which is equal to
![]() $\sqrt[3]{2}(d/2)$
by conservation of volume. The dominant mode is thus directly proportional to the radius of the final coalesced bubble, as plotted in red. (b) Wave angular velocity after the top and bottom waves have met at the bubble side. The red curve corresponds to the theoretical phase velocity calculated using (3.12) and the fit in (a) for the distance between the experimental peaks, defined as the wavelength.
$\sqrt[3]{2}(d/2)$
by conservation of volume. The dominant mode is thus directly proportional to the radius of the final coalesced bubble, as plotted in red. (b) Wave angular velocity after the top and bottom waves have met at the bubble side. The red curve corresponds to the theoretical phase velocity calculated using (3.12) and the fit in (a) for the distance between the experimental peaks, defined as the wavelength.
After the convergence of the waves at both bubble sides, we clearly see two peaks on the bubble surface instead of a single one: see figure 12. We measure the velocity of those peaks and the distance between them, concluding that they remain quasi-constant with time. This suggests that the distance between the two peaks corresponds to the wavelength of the capillary wave, and therefore, it has now been reduced to a packet with a clearly dominant mode. Figure 13(a,b) shows the influence of the bubble radius after the coalescence,
![]() $R_{b}=\sqrt[3]{2}(d/2)$
, on this wavelength and phase velocity. As expected, the wavelength seems to be proportional to the final coalesced bubble radius
$R_{b}=\sqrt[3]{2}(d/2)$
, on this wavelength and phase velocity. As expected, the wavelength seems to be proportional to the final coalesced bubble radius
![]() $R_{b}$
with a coefficient
$R_{b}$
with a coefficient
![]() $a=0.48$
: see figure 13(a). Since the wavelength is equal to
$a=0.48$
: see figure 13(a). Since the wavelength is equal to
![]() $2\unicode[STIX]{x03C0}R_{b}/n$
, we find the value
$2\unicode[STIX]{x03C0}R_{b}/n$
, we find the value
![]() $n=13$
for the dominant mode, which is smaller than the mode
$n=13$
for the dominant mode, which is smaller than the mode
![]() $n=20$
governing the early propagation of the upper and lower wave towards the bubble sides. We surmise that viscosity continues to play a role, damping the higher vibration modes of the bubble more and more, as also occurred in Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008). Partial coalescence, as shown by Gilet et al. (Reference Gilet, Mulleners, Lecomte, Vandewalle and Dorbolo2007), seems to follow the same mechanics regarding wave propagation.
$n=20$
governing the early propagation of the upper and lower wave towards the bubble sides. We surmise that viscosity continues to play a role, damping the higher vibration modes of the bubble more and more, as also occurred in Zhang & Thoroddsen (Reference Zhang and Thoroddsen2008). Partial coalescence, as shown by Gilet et al. (Reference Gilet, Mulleners, Lecomte, Vandewalle and Dorbolo2007), seems to follow the same mechanics regarding wave propagation.
Figure 14. Rising position of the bubble after detachment versus time. It can be appreciated that the actual rising of the bubble lies between the curves corresponding to the energy jump by the liberation of surface energy and the trajectory obtained by the equilibrium of forces on the bubble, equation (3.18). This implies that the coalesced bubble suffers from a small jump due to a partial energy liberation (which is much smaller than the calculated one) and is afterwards accelerated upwards by buoyancy.
3.4 Bubble detachment and rising
When the deforming wave passes again on its way back through the location of the pinning pits, the coalesced bubble typically detaches. Similarly to the case of droplets (Wisdom et al.
Reference Wisdom, Watson, Qu, Liu, Watson and Chen2013; Liu et al.
Reference Liu, Ghigliotti, Feng and Chen2014), once the two bubbles coalesce, there is a liberation of surface energy
![]() $\unicode[STIX]{x0394}E_{\unicode[STIX]{x1D70E}}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}(d/2)^{2}-\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}(d/\sqrt[3]{4})^{2}$
which is transformed into potential energy
$\unicode[STIX]{x0394}E_{\unicode[STIX]{x1D70E}}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}(d/2)^{2}-\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}(d/\sqrt[3]{4})^{2}$
which is transformed into potential energy
![]() $\unicode[STIX]{x0394}P=\unicode[STIX]{x1D70C}g\unicode[STIX]{x03C0}d^{3}h/6$
, where
$\unicode[STIX]{x0394}P=\unicode[STIX]{x1D70C}g\unicode[STIX]{x03C0}d^{3}h/6$
, where
![]() $h$
is the height reached during the vertical jump that occurs as a result of this energy liberation. Energy conservation results in a jump of height
$h$
is the height reached during the vertical jump that occurs as a result of this energy liberation. Energy conservation results in a jump of height
![]() $h=6(1/2-1/\sqrt[3]{16})\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}gd$
. Afterwards, the bubble rises due to the effect of buoyancy. The equilibrium of forces on the bubble surface (Lohse & Prosperetti Reference Lohse and Prosperetti2003) can be expressed as follows:
$h=6(1/2-1/\sqrt[3]{16})\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}gd$
. Afterwards, the bubble rises due to the effect of buoyancy. The equilibrium of forces on the bubble surface (Lohse & Prosperetti Reference Lohse and Prosperetti2003) can be expressed as follows:
where
![]() $V_{b}=\unicode[STIX]{x03C0}d^{3}/3$
is the bubble volume after coalescence,
$V_{b}=\unicode[STIX]{x03C0}d^{3}/3$
is the bubble volume after coalescence,
![]() $m_{b}=\unicode[STIX]{x1D70C}_{g}V_{b}$
and
$m_{b}=\unicode[STIX]{x1D70C}_{g}V_{b}$
and
![]() $m_{add}=\unicode[STIX]{x1D70C}V_{b}/2$
are the bubble and added masses and
$m_{add}=\unicode[STIX]{x1D70C}V_{b}/2$
are the bubble and added masses and
![]() $F_{d}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(d/\sqrt[3]{4}){\dot{h}}$
is the drag force, which corresponds to the well-known Stokes’ law on a clean bubble. This equation can be simplified considering that
$F_{d}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(d/\sqrt[3]{4}){\dot{h}}$
is the drag force, which corresponds to the well-known Stokes’ law on a clean bubble. This equation can be simplified considering that
![]() $\unicode[STIX]{x1D70C}_{g}\ll \unicode[STIX]{x1D70C}$
, resulting in the following ODE:
$\unicode[STIX]{x1D70C}_{g}\ll \unicode[STIX]{x1D70C}$
, resulting in the following ODE:
This equation with
![]() $\unicode[STIX]{x1D6FC}=24\unicode[STIX]{x1D707}/\sqrt[3]{4}\unicode[STIX]{x1D70C}d^{2}$
can be readily solved with initial conditions
$\unicode[STIX]{x1D6FC}=24\unicode[STIX]{x1D707}/\sqrt[3]{4}\unicode[STIX]{x1D70C}d^{2}$
can be readily solved with initial conditions
![]() $h(0)=0$
and
$h(0)=0$
and
![]() ${\dot{h}}(0)=0$
to obtain
${\dot{h}}(0)=0$
to obtain
The jump height and the buoyancy-driven rising position of the bubble are plotted in figure 14 in comparison to the experimental data. It can be noticed that the energy jump is barely influential in this case, due to the high drag which the environmental liquid causes on the bubble and the energy loss due to the depinning from the substrate. However, experiments show that the actual bubble trajectory lies in between the region delimited by the energy conservation jump and the trajectory obtained by equilibrium of forces on the bubble. This fact implies that the bubble at detachment jumps instantaneously to a certain height by liberation of energy, being afterwards accelerated upwards by buoyancy with the corresponding resistance caused by the Stokes’ law term. Note again that Stokes’ law is defined for a clean bubble, i.e. the slightest contamination will increase
![]() $F_{d}$
and thus
$F_{d}$
and thus
![]() $\unicode[STIX]{x1D6FC}$
. We have varied the value of
$\unicode[STIX]{x1D6FC}$
. We have varied the value of
![]() $F_{d}$
up to a maximum of
$F_{d}$
up to a maximum of
![]() $F_{d}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(d/\sqrt[3]{4}){\dot{h}}$
corresponding to a small sphere, verifying that the theoretical curve (3.18) in figure 14 barely changes. This fact implies that the drag force caused by the liquid viscosity does not play a major role in the equilibrium of forces after bubble detachment, i.e. the upward rising is mainly dominated by buoyancy. Consequently, after the initial jump, the tendencies of both the experimental data and the theoretical curve (3.18) run quasi-parallel at all times.
$F_{d}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}(d/\sqrt[3]{4}){\dot{h}}$
corresponding to a small sphere, verifying that the theoretical curve (3.18) in figure 14 barely changes. This fact implies that the drag force caused by the liquid viscosity does not play a major role in the equilibrium of forces after bubble detachment, i.e. the upward rising is mainly dominated by buoyancy. Consequently, after the initial jump, the tendencies of both the experimental data and the theoretical curve (3.18) run quasi-parallel at all times.
After detachment, the new bubble surface oscillates, flattening first vertically and then horizontally (figure 2
p–y). This surface waving can be perfectly appreciated in the experimental data plotted in figure 14. The travelling waves are still deforming the surface even after detachment. The oscillation continues and is progressively damped while the bubble is rising, leaving its place for the next couple of bubbles to grow. In Lamb (Reference Lamb1895) and Versluis et al. (Reference Versluis, Goertz, Palanchon, Heitman, van der Meer, Dollet, de Jong and Lohse2010), it is shown that for a single oscillating bubble, the natural period of a given
![]() $n$
mode can be written as
$n$
mode can be written as
This expression is directly associated with the well-known Minnaert frequency (Minnaert Reference Minnaert1933). Figure 15 shows the radial position of different points on the bubble surface during the oscillation after detachment. We notice that the oscillation amplitude is maximal at the angles
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
, and minimal at the angles
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
, and minimal at the angles
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/2$
(by symmetry). Figure 16 shows the radial position of the point
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/2$
(by symmetry). Figure 16 shows the radial position of the point
![]() $\unicode[STIX]{x1D703}=0$
for different bubble radii. We directly conclude that the oscillation period is proportional to
$\unicode[STIX]{x1D703}=0$
for different bubble radii. We directly conclude that the oscillation period is proportional to
![]() $\unicode[STIX]{x1D70F}_{b}=\sqrt{\unicode[STIX]{x1D70C}_{l}R_{b}^{3}/\unicode[STIX]{x1D70E}}$
, experimentally obtaining
$\unicode[STIX]{x1D70F}_{b}=\sqrt{\unicode[STIX]{x1D70C}_{l}R_{b}^{3}/\unicode[STIX]{x1D70E}}$
, experimentally obtaining
![]() $T_{exp}/\unicode[STIX]{x1D70F}_{b}=1.88\pm 0.25$
, which corresponds to the mode
$T_{exp}/\unicode[STIX]{x1D70F}_{b}=1.88\pm 0.25$
, which corresponds to the mode
![]() $n=2$
according to (3.19). Again, we see the effect of the energy loss at detachment and the viscosity in the damping of the higher modes of vibration.
$n=2$
according to (3.19). Again, we see the effect of the energy loss at detachment and the viscosity in the damping of the higher modes of vibration.

Figure 15. (a) Time evolution of the radial position of different points on the surface of the coalesced bubble after detachment. (b) Definition of the angles used for the curves in (a).
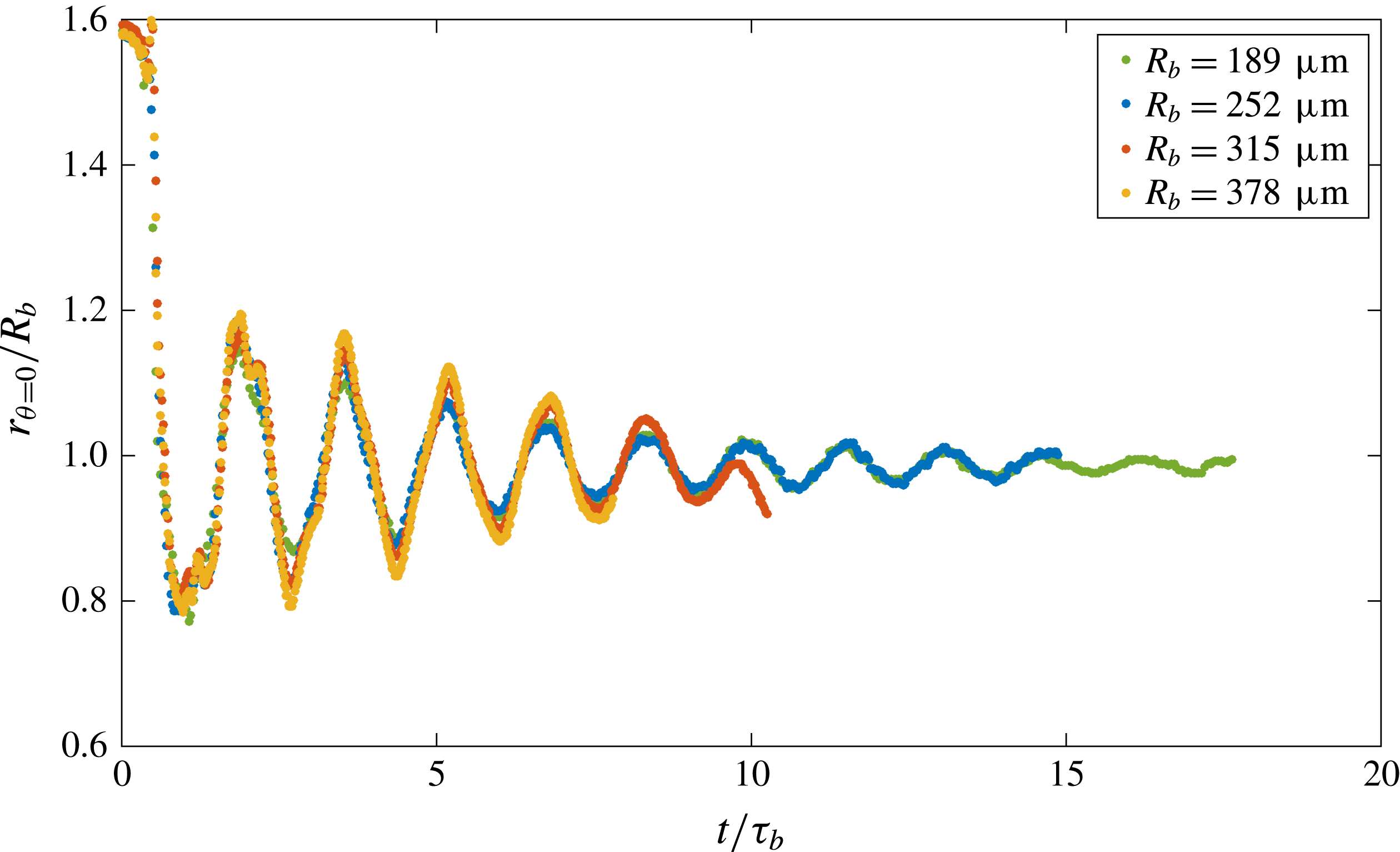
Figure 16. Evolution of the dimensionless radial length
![]() $r_{\unicode[STIX]{x1D703}=0}/R_{b}$
with the dimensionless time
$r_{\unicode[STIX]{x1D703}=0}/R_{b}$
with the dimensionless time
![]() $t/\unicode[STIX]{x1D70F}_{b}$
after bubble detachment, where
$t/\unicode[STIX]{x1D70F}_{b}$
after bubble detachment, where
![]() $\unicode[STIX]{x1D70F}_{b}$
is the capillary time using the reference radius
$\unicode[STIX]{x1D70F}_{b}$
is the capillary time using the reference radius
![]() $R_{b}$
.
$R_{b}$
.
4 Conclusions
Quasi-static, slow diffusive growth of two bubbles pinned to nearby pre-designed sites results in a well-controlled bubble coalescence without any instabilities caused by refreshing flows around the bubbles, spurious velocities, impact vibrations, chemical reactions or gas-feeding needles. Moreover, and contrary to drops, gravity and viscosity have no influence on the cause of the coalescence process in our current configuration, i.e. bubbles do not deform, reaching a perfect spherical shape, and coalescence is granted thanks to the low viscosity of the gas compared to that of the liquid and the presence of the pinning points on the substrate. The whole coalescence is only driven by capillary–inertia, with viscosity only playing a role in the damping of the vibration modes in the coalescing wave packet later in time. The capillary–inertial model (3.6) with the corrected term accounting for half of the horizontal spacing between bubbles accurately describes the evolution of the neck that bounds the two bubbles in the early coalescence. This evolution has been found to be universal, no matter which method triggers the coalescence, i.e. bubbles growing by diffusion have the same neck evolution while coalescing as bubbles in flows, bubbles coalescing by impact or bubbles generated by chemical reactions. On the other hand, the neck radius of curvature is hard to express in a theoretical way since it is very dependent on the deformation caused by the surface wave originated at the beginning of the coalescence. This deformation has been proved to be due to a pure capillary wave. The wave packet which propagates along the bubble surface can be approximately modelled by a single mode wave as the rest of the deformation spectrum (i.e. the vibration modes) is progressively damped, and therefore the propagating wave reaches a constant velocity in the end. The damping of the wave packet may be determinant for the potential detachment event to occur. Comparing the experimental data with the results of a BI code, we find an extremely similar coalescence evolution, except for the moment in which the capillary waves approach the opposite apex of the bubbles from the coalescence point, since the code does not account either for the presence of the two pinning spots or the role of viscosity in the damping of high modes in the wave packet. The deviations could be perfectly appreciated in figure 11. However, we proved that BI code and experiments can be compared one-to-one in the modelling of the upper half-bubble coalescence process, since this surface is not affected by the presence of the pits and can thus evolve freely. After detachment, the jump generated by surface energy liberation is barely influential compared to the buoyancy effect, equation (3.18), which makes the bubble rise rapidly. The fact that we achieved bubble detachment before the bubbles reach their theoretical detachment radius (
![]() ${\approx}450~\unicode[STIX]{x03BC}\text{s}$
for a
${\approx}450~\unicode[STIX]{x03BC}\text{s}$
for a
![]() $R_{p}=10~\unicode[STIX]{x03BC}\text{s}$
and
$R_{p}=10~\unicode[STIX]{x03BC}\text{s}$
and
![]() ${\approx}750~\unicode[STIX]{x03BC}\text{s}$
for a
${\approx}750~\unicode[STIX]{x03BC}\text{s}$
for a
![]() $R_{p}=50~\unicode[STIX]{x03BC}\text{s}$
) provides a good starting point for many applications which need to enhance bubble detachment for transporting gas away from a surface. While rising, the bubble keeps oscillating with a viscous-caused lower wave mode according to its Minnaert frequency. All the coalescence events occur in an extremely reproducible way, with no apparent influence of gas depletion caused by bubble detachment.
$R_{p}=50~\unicode[STIX]{x03BC}\text{s}$
) provides a good starting point for many applications which need to enhance bubble detachment for transporting gas away from a surface. While rising, the bubble keeps oscillating with a viscous-caused lower wave mode according to its Minnaert frequency. All the coalescence events occur in an extremely reproducible way, with no apparent influence of gas depletion caused by bubble detachment.

Figure 17. Snapshots of a coalescence event in which the final bubble does not detach from the sample, with pit radius of
![]() $50~\unicode[STIX]{x03BC}\text{m}$
and pit separation of
$50~\unicode[STIX]{x03BC}\text{m}$
and pit separation of
![]() $d=150~\unicode[STIX]{x03BC}\text{m}$
. The first eight images are separated by
$d=150~\unicode[STIX]{x03BC}\text{m}$
. The first eight images are separated by
![]() $75~\unicode[STIX]{x03BC}\text{s}$
(including the interval between snapshots (8) and (9)), whereas the last eight images are spaced by
$75~\unicode[STIX]{x03BC}\text{s}$
(including the interval between snapshots (8) and (9)), whereas the last eight images are spaced by
![]() $600~\unicode[STIX]{x03BC}\text{s}$
. Note that the resulting bubble will continue growing diffusively on a much larger time scale until it reaches its detachment radius or coalesces with a new growing bubble from the other pit.
$600~\unicode[STIX]{x03BC}\text{s}$
. Note that the resulting bubble will continue growing diffusively on a much larger time scale until it reaches its detachment radius or coalesces with a new growing bubble from the other pit.

Figure 18. Snapshots of two different coalescence events when one bubble is much bigger than the other one. The images in the same row are separated by
![]() $75~\unicode[STIX]{x03BC}\text{s}$
. This configuration is obtained by letting bubbles grow and coalesce without detaching. The bubble that remains pinned to the pit keeps growing while a new one grows from the other pit. After several coalescences have occurred, the difference in the radii of the bubble pair is more than noticeable.
$75~\unicode[STIX]{x03BC}\text{s}$
. This configuration is obtained by letting bubbles grow and coalesce without detaching. The bubble that remains pinned to the pit keeps growing while a new one grows from the other pit. After several coalescences have occurred, the difference in the radii of the bubble pair is more than noticeable.
Acknowledgements
We want to thank S. Schlautmann for helping with the preparation of the substrates to perform the experiments. This work was supported by the Netherlands Centre for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the government of the Netherlands.
Supplementary movie
A supplementary movie is available at https://doi.org/10.1017/jfm.2018.277.
Appendix. Bubble coalescence without detachment
In one of our experimental designs, the distance
![]() $d$
between the pits where the bubbles attach during their growth is chosen in such a way that the final bubble after coalescence does not reach the maximum volume which surface tension can exert (see e.g. Fritz Reference Fritz1935; Og̃uz & Prosperetti Reference Og̃uz and Prosperetti1993; Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017). If the pit radii are
$d$
between the pits where the bubbles attach during their growth is chosen in such a way that the final bubble after coalescence does not reach the maximum volume which surface tension can exert (see e.g. Fritz Reference Fritz1935; Og̃uz & Prosperetti Reference Og̃uz and Prosperetti1993; Moreno Soto et al.
Reference Moreno Soto, Prosperetti, van der Meer and Lohse2017). If the pit radii are
![]() $50~\unicode[STIX]{x03BC}\text{m}$
and the distance between them is
$50~\unicode[STIX]{x03BC}\text{m}$
and the distance between them is
![]() $150~\unicode[STIX]{x03BC}\text{m}$
, we observe that the coalesced bubble does not detach from the sample. Snapshots of this case are shown in figure 17. The early coalescence is similar to that in figure 2. However, in this case, since the touching bubbles do not have exactly the same radius, there is no symmetry in the wave propagation on the different bubbles. Whereas the smaller bubble detaches from the pit and merges into the bigger one due to its higher Laplace pressure, the bigger bubble stays on the substrate since the capillary force is strong enough to keep the coalesced bubble pinned to the surface. This event is followed by new bubble growth from the pit where the now absorbed bubble was before, while the absorbing bubble keeps growing on the other pit until it reaches its detachment radius or coalesces with the much smaller new growing bubble. If the bubbles touched one more time, they would also collapse, but their radii would be significantly different, as shown in figure 18. The perturbation wave which is produced would also be considerably smaller than for the first coalescence, barely perturbing the absorbing bubble.
$150~\unicode[STIX]{x03BC}\text{m}$
, we observe that the coalesced bubble does not detach from the sample. Snapshots of this case are shown in figure 17. The early coalescence is similar to that in figure 2. However, in this case, since the touching bubbles do not have exactly the same radius, there is no symmetry in the wave propagation on the different bubbles. Whereas the smaller bubble detaches from the pit and merges into the bigger one due to its higher Laplace pressure, the bigger bubble stays on the substrate since the capillary force is strong enough to keep the coalesced bubble pinned to the surface. This event is followed by new bubble growth from the pit where the now absorbed bubble was before, while the absorbing bubble keeps growing on the other pit until it reaches its detachment radius or coalesces with the much smaller new growing bubble. If the bubbles touched one more time, they would also collapse, but their radii would be significantly different, as shown in figure 18. The perturbation wave which is produced would also be considerably smaller than for the first coalescence, barely perturbing the absorbing bubble.