Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-19T20:55:39.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible Rayleigh–Taylor turbulent mixing layer between Newtonian miscible fluids

Published online by Cambridge University Press:  29 September 2017

Serge Gauthier Open the ORCID record for Serge Gauthier [Opens in a new window]
Serge Gauthier*
Affiliation:
CEA, DAM, DIF, 91297 Arpajon, France
*
†Email address for correspondence: Serge.Gauthier@orange.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Rayleigh–Taylor instability induced turbulence between two compressible miscible Newtonian fluids is studied in a strongly stratified configuration at a moderate Atwood number. A direct numerical simulation has been carried out with an auto-adaptive multidomain Chebyshev–Fourier–Fourier numerical method. The spatial resolution is increased up to 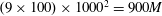$(9\times 100)\times 1000^{2}=900M$ collocation points. These numerical data are compared with those obtained from a simulation carried out at a lower Reynolds number and at the same Atwood number, and those obtained from a simulation carried out within the Boussinesq approximation at the same Reynolds number. A comprehensive data analysis is reported. Physical-variable mean profiles – density, concentration, temperature, entropy, velocity, vorticity, helicity and palinstrophy – are provided. Anisotropy is studied in the spectral space. The intermediate-scale isotropy and the small-scale anisotropy are exhibited for the scalars, i.e. concentration and temperature. Velocity is anisotropic at all scales but this anisotropy is more marked at small scales. The data are also analysed with the Favre-averaged equations. Sources of the turbulent kinetic energy, mass flux, root-mean-square density and energy equations are analysed. Compressibility effects are discussed in particular with the Kovàsznay-mode decomposition. A statistical study is reported where skewnesses, flatnesses and probability density functions (PDFs) are displayed and commented. A flow visualization is also given. Finally, the temperature field appears to be the slave of the mixing. This conclusion is drawn from the comparison of power spectra, anisotropy spectra, skewnesses, flatnesses, PDFs and correlation coefficients. There is however a significant time lag between the density and temperature evolution.

JFM classification

Compressible Flows: Compressible Flows Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 211 - 256
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: (Retired) ChebyPhys, 2 rue des Capucines, 91630 Marolles en Hurepoix, France.

References

Anisimov, S., Drake, R., Gauthier, S., Meshkov, E. & Abarzhi, S. 2013 What is certain and what is not so certain in our knowledge of Rayleigh–Taylor mixing? Phil. Trans. R. Soc. Lond. A 371, 20130266–16.Google Scholar
Ash, R. 2017 Comment on ‘roles of bulk viscosity on Rayleigh–Taylor instability: non-equilibrium thermodynamics due to spatio-temporal pressure fronts’ [Phys. Fluids 28, 094102, 2016]. Phys. Fluids 29, 019101.Google Scholar
Ashurst, W., Kerstein, A., Kerr, R. & Gibson, C. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.Google Scholar
Atzeni, S. & Meyer-Ter-Vhen, J. 2004 The Physics of Inertial Fusion. Oxford University Press.Google Scholar
Baker, L. 1983 Compressible Rayleigh–Taylor instability. Phys. Fluids 26 (4), 950–952.Google Scholar
Bataille, F., Bertoglio, J.-P. & Marion, J.-D. 1992 Étude spectrale d’une turbulence isotrope faiblement compressible: résultats, deuxième partie. C. R. Acad. Sci. Paris II 315, 1459–1465.Google Scholar
Batchelor, G. 1971 Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G., Howells, I. & Townsend, A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.CrossRefGoogle Scholar
Bayliss, A. & Matkowsky, B. 1987 Fronts, relaxation oscillations and period doubling in solid fuel combustion. J. Comput. Phys. 71, 147–168.Google Scholar
Blake, G. M. 1972 Fluid dynamic stability of double radio sources. Mon. Not. R. Astron. Soc. 156, 67.Google Scholar
Boudesocque-Dubois, C., Clarisse, J.-M. & Gauthier, S. 2003 A spectral Chebyshev method for linear stability analysis of one-dimensional exact solutions of gas dynamics. J. Comput. Phys. 184, 592–618.CrossRefGoogle Scholar
Boyd, J. 2000 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Cabot, W. & Cook, A. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type-Ia supernovae. Nat. Phys. 2, 5621.Google Scholar
Cabot, W. & Zhou, Y. 2013 Statistical measurements of scaling and anisotropy of turbulent flows induced by Rayleigh–Taylor instability. Phys. Fluids 25, 015107.Google Scholar
Canuto, C., Hussaini, M., Quarteroni, A. & Zang, T. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Cao, N., Chen, S. & Doolen, D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.Google Scholar
Chassaing, P., Antonia, R., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence, Fluid Mechanics and its Applications, vol. 69. Kluwer.Google Scholar
Chu, B.-T. & Kovásznay, L. S. G. 1958 Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3, 494–514.Google Scholar
Chung, D. & Pullin, D. 2010 Direct numerical simulation and large-eddy simulation of stationary buoyancy-driven turbulence. J. Fluid Mech. 643, 279–308.Google Scholar
Cook, A. 2009 Enthalpy diffusion in multicomponent flows. Phys. Fluids 21, 055109.Google Scholar
Cook, A., Cabot, W. & Miller, P. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 026312.Google Scholar
Cook, A. & Dimotakis, P. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.Google Scholar
Cox, J. P. 1980 Theory of Stellar Pulsation. Princeton University Press.Google Scholar
Dalziel, S., Linden, P. & Youngs, D. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
EFLUIDS 2017 http://www.efluids.com/.Google Scholar
Gauthier, S. 1991 A semi-implicit collocation method: application to thermal convection in 2D compressible fluids. Intl J. Numer. Meth. Fluids 12, 985–1002.Google Scholar
Gauthier, S. 2013 Compressibility effects in Rayleigh–Taylor flows: influence of the stratification. Phys. Scr. T 155, 014012.Google Scholar
Gauthier, S., Le Creurer, B., Abéguilé, F., Boudesocque-Dubois, C. & Clarisse, J.-M. 2005 A self-adaptative domain decomposition method with Chebyshev method. Intl J. Pure Appl. Maths 24 (4), 553–577.Google Scholar
Gauthier, S. & Schneider, N. 2017 Low- and zero-Mach-number models for Rayleigh–Taylor flows. Comput. Fluids 151, 85–90.CrossRefGoogle Scholar
George, E. & Glimm, J. 2005 Self-similarity of Rayleigh–Taylor mixing rates. Phys. Fluids 17, 054101.Google Scholar
Grégoire, O., Souffland, D. & Gauthier, S. 2005 A second-order turbulence model for gaseous mixtures induced by Richtmyer–Meshkov instability. J. Turbul. 6 (29), 1–20.Google Scholar
Guillard, H., Malé, J.-M. & Peyret, R. 1992 Adaptive spectral methods with application to mixing layer computations. J. Comput. Phys. 102, 114–127.CrossRefGoogle Scholar
Guillard, H. & Peyret, R. 1988 On the use of spectral methods for the numerical solution of stiff problems. Comput. Meth. Appl. Mech. Engng 66, 17–43.Google Scholar
Hirschfelder, J., Curtiss, C. & Bird, R. 1954 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
Jin, H., Liu, X. F., Lu, T., Cheng, B., Glimm, J. & Sharp, D. H. 2005 Rayleigh–Taylor mixing rates for compressible flows. Phys. Fluids 17, 024104.Google Scholar
Kalelkar, C. 2006 Statistics of pressure fluctuations in decaying isotropic turbulence. Phys. Rev. E 73, 046301.Google Scholar
Kitamura, T., Nagata, K., Sakai, Y., Sasoh, A., Terashima, O., Saito, H. & Harasaki, T. 2014 On invariants in grid turbulence at moderate Reynolds numbers. J. Fluid Mech. 738, 378–406.Google Scholar
Lafay, M.-A.2008 Stabilité et simulation numérique de l’écoulement de Rayleigh–Taylor pour des fluides miscibles compressibles. PhD thesis, CEA-Université Paris-Sud, France.Google Scholar
Lafay, M.-A., Le Creurer, B. & Gauthier, S. 2007 Compressibility effects on the Rayleigh–Taylor instability growth between miscible fluids. Europhys. Lett. 79, 64002.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Course of Theoretical Physics VI, Fluid Mechanics. Pergamon.Google Scholar
Le Creurer, B.2005 Simulations numériques pseudo-spectrales de l’instabilité de Rayleigh–Taylor pour des fluides compressibles. PhD thesis, Université de Marne-la-Vallée.Google Scholar
Le Creurer, B. & Gauthier, S. 2008 A return toward equilibrium in a two-dimensional Rayleigh–Taylor flows instability for compressible miscible fluids. Theor. Comput. Fluid Dyn. 22, 125–144.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids. Kluwer Academic.CrossRefGoogle Scholar
Leslie, D. 1973 Developments in the Theory of Turbulence. Clarendon Press, Oxford University Press.Google Scholar
Linden, P., Redondo, J. & Youngs, D. 1994 Molecular mixing in Rayleigh–Taylor instability. J. Fluid Mech. 265, 97–124.Google Scholar
Livescu, D. 2004 Compressibility effects on the Rayleigh–Taylor instability growth between immiscible fluids. Phys. Fluids 16, 118–127.Google Scholar
Livescu, D. 2013 Numerical simulations of two-fluid turbulent mixing at large density ratios and applications to the Rayleigh–Taylor instability. Phil. Trans. R. Soc. Lond. A 371 (2003), 20120185.Google Scholar
Livescu, D. & Ristorcelli, J. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.Google Scholar
Livescu, D. & Ristorcelli, J. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.CrossRefGoogle Scholar
Livescu, D., Ristorcelli, J., Gore, R., Dean, S., Cabot, W. & Cook, A. 2009 High-Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10 (N13), 029103.Google Scholar
Livescu, D., Ristorcelli, J., Petersen, M. & Gore, R. 2010 New phenomena in variable-density Rayleigh–Taylor turbulence. Phys. Scr. T 142, 014015.Google Scholar
Mathews, W. G. & Blumenthal, G. R. 1977 Rayleigh–Taylor stability of compressible and incompressible radiation-supported surfaces and slabs: application to QSO clouds. Ap. J. 214, 10–20.CrossRefGoogle Scholar
Mellado, J. P., Sarkar, S. & Zhou, Y. 2005 Large-eddy simulation of Rayleigh–Taylor with compressible miscible fluids. Phys. Fluids 17, 076101.Google Scholar
Moffatt, H. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.Google Scholar
Monin, A. S. & Yaglom, A. M. 1962 Statistical Fluid Mechanics: Mechanics of Turbulence. MIT Press.Google Scholar
Oster, L. & Ulmschneider, P. 1973 Line profiles and turbulence generated by acoustic waves in the solar chronosphere I. Absorption profiles and height variation of velocity amplitudes. Astron. Astrophys. 29, 1–6.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Fluids. Springer.Google Scholar
Plesset, M. S. & Hsieh, D.-Y. 1964 General analysis of the stability of superposed fluids. Phys. Fluids 7, 1099–1108.Google Scholar
Poujade, O. & Peybernes, M. 2010 Growth rate of Rayleigh–Taylor turbulent mixing layers with the foliation approach. Phys. Rev. E 81, 016316.Google Scholar
Pulicani, J.-P. 1988 A spectral multi-domain method for the solution of 1D-Helmholtz and Stokes-type equations. Comput. Fluids 16, 207–215.Google Scholar
Pumir, A. 1994a A numerical study of pressure fluctuations in three-dimensional, incompressible, homogeneous, isotropic turbulence. Phys. Fluids 6 (6), 2071–2083.CrossRefGoogle Scholar
Pumir, A. 1994b A numerical study of the mixing of a passive scalar in three dimensions in the presence of a mean gradient. Phys. Fluids 6 (6), 2118–2132.Google Scholar
Ramaprabhu, P. & Andrews, M. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.Google Scholar
Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Reckinger, S., Livescu, D. & Vasilyev, O. 2012 Simulations of compressible Rayleigh–Taylor instability using the adaptive wavelet collocation method. In Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, Hawaii.Google Scholar
Reckinger, S., Livescu, D. & Vasilyev, O. 2016 Comprehensive numerical methodology for direct numerical simulations of compressible Rayleigh–Taylor instability. J. Comput. Phys. 313, 181–208.Google Scholar
Renaud, F.1996 Méthode spectrale de décomposition dynamique de domaines: application aux écoulements compressibles de Rayleigh–Bénard et de Kelvin–Helmholtz. PhD thesis, Université de Nice-Sophia Antipolis.Google Scholar
Renaud, F. & Gauthier, S. 1997 A dynamical pseudo-spectral domain decomposition technique: application to viscous compressible flows. J. Comput. Phys. 131, 89–108.Google Scholar
Ristorcelli, J. 2006 Passive scalar mixing: analytic study of time scale ratio, variance, and mix rate. Phys. Fluids 18, 075101.Google Scholar
Sandoval, D.1995 The dynamics of variable-density turbulence. PhD thesis, University of Washington.Google Scholar
Schneider, N.2015 Vorticité et mélange dans les écoulements de Rayleigh–Taylor turbulents, en approximation anélastique et de Boussinesq. PhD thesis, Université Pierre et Marie Curie, Paris.Google Scholar
Schneider, N. & Gauthier, S. 2015 Asymptotic analysis of Rayleigh–Taylor flow for Newtonian miscible fluids. J. Engng Maths 92 (1), 55–71.Google Scholar
Schneider, N. & Gauthier, S. 2016a Anelastic Rayleigh–Taylor mixing layers. Phys. Scr. 91, 074004.Google Scholar
Schneider, N. & Gauthier, S. 2016b Visualization of Rayleigh–Taylor flows from Boussinesq approximation to fully compressible Navier–Stokes model. Fluid Dyn. Res. 48, 015504.Google Scholar
Schneider, N. & Gauthier, S. 2016c Vorticity and mixing in Rayleigh–Taylor Boussinesq turbulence. J. Fluid Mech. 802, 395–436.Google Scholar
Schneider, N., Hammouch, Z., Labrosse, G. & Gauthier, S. 2015 A spectral anelastic Navier–Stokes solver for a stratified two-miscible-layer system in infinite horizontal channel. J. Comput. Phys. 299, 374–403.Google Scholar
Sengupta, T., Sengupta, A., Sharma, N., Sengupta, S., Bhole, A. & Shruti, K. 2016 Roles of bulk viscosity on Rayleigh–Taylor instability: non-equilibrium thermodynamics due to spatio-temporal pressure fronts. Phys. Fluids 28, 094102.CrossRefGoogle Scholar
She, Z.-S., Jackson, E. & Orszag, S. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.Google Scholar
Shipton, J.2009 Balance, gravity waves and jets in turbulent shallow water flows. PhD thesis, University of St. Andrews.Google Scholar
Siggia, E. 1981 Numerical study of small scale intermittency in three dimensional turbulence. J. Fluid Mech. 107, 375.Google Scholar
Strikwerda, J. 1977 Initial boundary value problems for incompletely parabolic systems. Commun. Pure Appl. Maths XXX, 797–822.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. 201, 192–196.Google Scholar
Thompson, K. 1990 Time dependent boundary conditions for hyperbolic systems, II. J. Comput. Phys. 89, 439–461.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.Google Scholar
Wang, Y.-M. & Robertson, J. 1985 Late stages of the Rayleigh–Taylor instability: a numerical study in the context of accreting neutron stars. Ap. J. 299, 85–108.CrossRefGoogle Scholar
Youngs, D. 1989 Modelling turbulent mixing by Rayleigh–Taylor instability. Physica D 37, 270–287.Google Scholar
Zhou, Y. 2017 Rayleigh–Taylor instability. Phys. Rep. Google Scholar
Zingale, M., Woosley, S. E., Rendleman, C. A., Day, M. S. & Bell, J. B. 2005 Three-dimensional numerical simulations of Rayleigh–Taylor unstable flames in Type Ia supernovae. Astrophys. J. 632, 1021–1034.Google Scholar