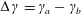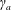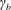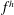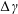1 Introduction
According to Lauga & Davis (Reference Lauga and Davis2012), Marangoni propulsion (Bush & Hu Reference Bush and Hu2006; Masoud & Stone Reference Masoud and Stone2014) refers to ‘the situation where a body, located at the surface of a fluid, generates an asymmetric distribution of surface active materials, thereby prompting a surface tension imbalance and a Marangoni flow, both of which lead to locomotion’. Examples of such bodies, which are sometimes called Marangoni surfers (Würger Reference Würger2014; Vandadi, Kang & Masoud Reference Vandadi, Kang and Masoud2017), include camphor scrapings (Van der Mensbrugghe Reference Van der Mensbrugghe1870; Nakata et al. Reference Nakata, Iguchi, Ose, Kuboyama, Ishii and Yoshikawa1997), organic solvent droplets (Oshima et al. Reference Oshima, Nomoto, Toyota and Fujinami2014; Janssens, Koizumi & Fried Reference Janssens, Koizumi and Fried2017) and water walking insects (Linsenmair & Jander Reference Linsenmair and Jander1963).

Figure 1. (a) Photograph of an acrylic glass water bath (
![]() $10\times 10\times 3~\text{cm}^{3}$
), resting on a light box, to which a partly submerged polytetrafluoroethylene (PTFE) cylinder with diameter 4.2 mm and length 10 cm is attached. (b) Side view photograph, taken with a drop shape analyser (DSA 100 Krüss) of the cylinder in (a). The gradient, the angles and the curves that represent the interface are superimposed on the original photograph for clarity. The lowermost curves are formed by the interaction of the water and the cylinder, and the uppermost curves result from the wetting of the bath wall. On both sides of the cylinder, the surface tensions are approximately
$10\times 10\times 3~\text{cm}^{3}$
), resting on a light box, to which a partly submerged polytetrafluoroethylene (PTFE) cylinder with diameter 4.2 mm and length 10 cm is attached. (b) Side view photograph, taken with a drop shape analyser (DSA 100 Krüss) of the cylinder in (a). The gradient, the angles and the curves that represent the interface are superimposed on the original photograph for clarity. The lowermost curves are formed by the interaction of the water and the cylinder, and the uppermost curves result from the wetting of the bath wall. On both sides of the cylinder, the surface tensions are approximately
![]() $72~\text{mN}~\text{m}^{-1}$
, the value for a water–air interface. The contact angles
$72~\text{mN}~\text{m}^{-1}$
, the value for a water–air interface. The contact angles
![]() $\unicode[STIX]{x1D703}_{a}$
and
$\unicode[STIX]{x1D703}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
are essentially equal and greater than
$\unicode[STIX]{x1D703}_{b}$
are essentially equal and greater than
![]() $\unicode[STIX]{x03C0}/2$
(
$\unicode[STIX]{x03C0}/2$
(
![]() $\unicode[STIX]{x1D703}_{a}\cong \unicode[STIX]{x1D703}_{b}>\unicode[STIX]{x03C0}/2$
), which is consistent with the hydrophobic character of PTFE. (c) Side view photograph, again taken with a drop shape analyser (DSA 100 Krüss) of the cylinder as in (a); however, the surface tension
$\unicode[STIX]{x1D703}_{a}\cong \unicode[STIX]{x1D703}_{b}>\unicode[STIX]{x03C0}/2$
), which is consistent with the hydrophobic character of PTFE. (c) Side view photograph, again taken with a drop shape analyser (DSA 100 Krüss) of the cylinder as in (a); however, the surface tension
![]() $\unicode[STIX]{x1D6FE}_{b}$
on the left-hand side of the cylinder is lowered relative to that,
$\unicode[STIX]{x1D6FE}_{b}$
on the left-hand side of the cylinder is lowered relative to that,
![]() $\unicode[STIX]{x1D6FE}_{a}$
, on the right-hand side of the cylinder by drop casting a practically water insoluble surfactant (oleic acid). The contact angles on either side of the cylinder obey
$\unicode[STIX]{x1D6FE}_{a}$
, on the right-hand side of the cylinder by drop casting a practically water insoluble surfactant (oleic acid). The contact angles on either side of the cylinder obey
![]() $\unicode[STIX]{x1D703}_{b}<\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D703}_{a}$
and the profile of the interface is no longer symmetric.
$\unicode[STIX]{x1D703}_{b}<\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D703}_{a}$
and the profile of the interface is no longer symmetric.
In this work, we explore how interfacial curvature influences Marangoni propulsion, a concern recently raised by Vandadi et al. (Reference Vandadi, Kang and Masoud2017) and Janssens et al. (Reference Janssens, Koizumi and Fried2017). To focus on curvature, we consider a situation where a surface tension imbalance is present but a Marangoni flow is absent. Experimentally, this situation is realized by the Langmuir film balance (Langmuir Reference Langmuir1917), in which a barrier separates surfactant-laden and surfactant-free portions of a liquid–gas interface. These respective interfaces have uniform surface tensions
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
that generate a surface tension imbalance
$\unicode[STIX]{x1D6FE}_{b}$
that generate a surface tension imbalance
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{a}-\unicode[STIX]{x1D6FE}_{b}$
. Therefore, we consider a class of problems inspired by the set-up present in such a balance. The horizontal component
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{a}-\unicode[STIX]{x1D6FE}_{b}$
. Therefore, we consider a class of problems inspired by the set-up present in such a balance. The horizontal component
![]() $f^{h}$
of the force that acts on a barrier, due to
$f^{h}$
of the force that acts on a barrier, due to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
, is measured with the balance. If the liquid–gas interface is assumed to be flat, which is the strategy originally used by Langmuir (Reference Langmuir1917), then
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
, is measured with the balance. If the liquid–gas interface is assumed to be flat, which is the strategy originally used by Langmuir (Reference Langmuir1917), then
![]() $f^{h}$
is equal in magnitude to
$f^{h}$
is equal in magnitude to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
when measured per unit length of the barrier. In actuality, however, the interface is curved (figure 1) and this appears, at first glance, to complicate the calculation of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
when measured per unit length of the barrier. In actuality, however, the interface is curved (figure 1) and this appears, at first glance, to complicate the calculation of
![]() $f^{h}$
. In § 2, we therefore perform a static force and torque analysis of a circular cylinder that acts as a surfactant barrier. This analysis, which generalizes studies of cylinders floating on liquids with uniform surface tension performed by Princen (Reference Princen and Matijević1969), Rapacchietta, Neumann & Omenyi (Reference Rapacchietta, Neumann and Omenyi1977), Bhatnagar & Finn (Reference Bhatnagar and Finn2006), Vella, Lee & Kim (Reference Vella, Lee and Kim2006) and Liu, Feng & Wang (Reference Liu, Feng and Wang2007), has never (at least to our knowledge) previously appeared in the literature.
$f^{h}$
. In § 2, we therefore perform a static force and torque analysis of a circular cylinder that acts as a surfactant barrier. This analysis, which generalizes studies of cylinders floating on liquids with uniform surface tension performed by Princen (Reference Princen and Matijević1969), Rapacchietta, Neumann & Omenyi (Reference Rapacchietta, Neumann and Omenyi1977), Bhatnagar & Finn (Reference Bhatnagar and Finn2006), Vella, Lee & Kim (Reference Vella, Lee and Kim2006) and Liu, Feng & Wang (Reference Liu, Feng and Wang2007), has never (at least to our knowledge) previously appeared in the literature.
One important consequence of our analysis is that lowering the surface tension on one side of a floating cylinder can alter the load-bearing capacity of that cylinder. In § 3.1.1, we therefore conduct a vertical force analysis on a hydrophobic cylinder. For more information on how objects at a liquid–gas interface with uniform surface tension float, we refer the reader to work by McCuan & Treinen (Reference McCuan and Treinen2013) and to a review by Vella (Reference Vella2015). In § 3.1.2, we perform a horizontal force analysis from which we infer that the magnitude of
![]() $f^{h}$
is equal to
$f^{h}$
is equal to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. In § 3.2, we extend the force analysis to the problem of a floating amphiphilic Janus cylinder and compare our results with the work on Janus beads by Casagrande et al. (Reference Casagrande, Fabre, Raphaël and Veyssié1989). In § 4 we use an energetic argument to prove that the magnitude of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. In § 3.2, we extend the force analysis to the problem of a floating amphiphilic Janus cylinder and compare our results with the work on Janus beads by Casagrande et al. (Reference Casagrande, Fabre, Raphaël and Veyssié1989). In § 4 we use an energetic argument to prove that the magnitude of
![]() $f^{h}$
is equal to
$f^{h}$
is equal to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
and show that this relation is applicable to a rod-like barrier with cross-sections of variable shape. Lastly, in § 5, we place our findings into context and discuss practical implications of the analysis for Marangoni propulsion and surface pressure measurements.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
and show that this relation is applicable to a rod-like barrier with cross-sections of variable shape. Lastly, in § 5, we place our findings into context and discuss practical implications of the analysis for Marangoni propulsion and surface pressure measurements.
2 Static analysis
2.1 Set-up of the problem
Figure 2 shows a schematic of a circular cylinder of radius
![]() $r$
acting as a surfactant barrier and illustrates the problem we address in this work. The surfactant-free and surfactant-laden portions of the interface have uniform surface tensions
$r$
acting as a surfactant barrier and illustrates the problem we address in this work. The surfactant-free and surfactant-laden portions of the interface have uniform surface tensions
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
. Edge effects can be ignored if the cylinder is much longer than the capillary length
$\unicode[STIX]{x1D6FE}_{b}$
. Edge effects can be ignored if the cylinder is much longer than the capillary length
where
![]() $\unicode[STIX]{x1D70C}_{l}$
and
$\unicode[STIX]{x1D70C}_{l}$
and
![]() $g$
denote the mass density of the liquid and the gravitational acceleration on Earth. For our purposes, it suffices to take the cylinder to be of infinite length.
$g$
denote the mass density of the liquid and the gravitational acceleration on Earth. For our purposes, it suffices to take the cylinder to be of infinite length.
The orthonormal basis vectors
![]() $\boldsymbol{\imath }$
,
$\boldsymbol{\imath }$
,
![]() $\boldsymbol{\jmath }$
and
$\boldsymbol{\jmath }$
and
![]() $\boldsymbol{k}$
are chosen so that
$\boldsymbol{k}$
are chosen so that
![]() $\boldsymbol{k}$
is parallel to the direction along which gravity acts,
$\boldsymbol{k}$
is parallel to the direction along which gravity acts,
![]() $\boldsymbol{\imath }$
is directed from the surfactant-laden portion of the liquid–gas interface to the surfactant-free portion of that interface and
$\boldsymbol{\imath }$
is directed from the surfactant-laden portion of the liquid–gas interface to the surfactant-free portion of that interface and
![]() $\boldsymbol{\jmath }$
is parallel to the cylinder axis. The Cartesian coordinates
$\boldsymbol{\jmath }$
is parallel to the cylinder axis. The Cartesian coordinates
![]() $x$
and
$x$
and
![]() $z$
increase in the directions of
$z$
increase in the directions of
![]() $\boldsymbol{\imath }$
and
$\boldsymbol{\imath }$
and
![]() $\boldsymbol{k}$
, respectively. Far from the cylinder, both portions of the liquid–gas interface have the same horizontal elevation and the origin
$\boldsymbol{k}$
, respectively. Far from the cylinder, both portions of the liquid–gas interface have the same horizontal elevation and the origin
![]() $o$
is positioned at that elevation. The axis of the cylinder is located at point
$o$
is positioned at that elevation. The axis of the cylinder is located at point
![]() $c$
with coordinates
$c$
with coordinates
![]() $x=0$
and
$x=0$
and
![]() $z=h_{c}$
. The lines along which the surfactant-free and surfactant-laden portions of the liquid–gas interface meet the cylinder are denoted by points
$z=h_{c}$
. The lines along which the surfactant-free and surfactant-laden portions of the liquid–gas interface meet the cylinder are denoted by points
![]() $a$
and
$a$
and
![]() $b$
, respectively, which are at respective angles
$b$
, respectively, which are at respective angles
![]() $\unicode[STIX]{x1D713}_{a}$
and
$\unicode[STIX]{x1D713}_{a}$
and
![]() $\unicode[STIX]{x1D713}_{b}$
. These angles are measured clockwise, with reference to figure 2, starting from ray
$\unicode[STIX]{x1D713}_{b}$
. These angles are measured clockwise, with reference to figure 2, starting from ray
![]() $cd$
and satisfy
$cd$
and satisfy
![]() $\unicode[STIX]{x1D713}_{a}<\unicode[STIX]{x1D713}_{b}$
. Thus, if
$\unicode[STIX]{x1D713}_{a}<\unicode[STIX]{x1D713}_{b}$
. Thus, if
![]() $a$
is located above
$a$
is located above
![]() $cd$
, which corresponds to the situation depicted in figure 2,
$cd$
, which corresponds to the situation depicted in figure 2,
![]() $\unicode[STIX]{x1D713}_{a}<0$
. However, if
$\unicode[STIX]{x1D713}_{a}<0$
. However, if
![]() $a$
is located below
$a$
is located below
![]() $cd$
,
$cd$
,
![]() $\unicode[STIX]{x1D713}_{a}>0$
. The wetted portion of the cylinder surface is found by following the surface of the cylinder clockwise from
$\unicode[STIX]{x1D713}_{a}>0$
. The wetted portion of the cylinder surface is found by following the surface of the cylinder clockwise from
![]() $a$
to
$a$
to
![]() $b$
. We express the respective
$b$
. We express the respective
![]() $x$
-coordinates
$x$
-coordinates
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
of
$x_{b}$
of
![]() $a$
and
$a$
and
![]() $b$
as
$b$
as
and the respective
![]() $z$
-coordinates
$z$
-coordinates
![]() $h_{a}$
and
$h_{a}$
and
![]() $h_{b}$
of
$h_{b}$
of
![]() $a$
and
$a$
and
![]() $b$
as
$b$
as
The contact angles
![]() $\unicode[STIX]{x1D703}_{a}$
and
$\unicode[STIX]{x1D703}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
are measured in the liquid and are always positive. The unit tangent vectors
$\unicode[STIX]{x1D703}_{b}$
are measured in the liquid and are always positive. The unit tangent vectors
![]() $\boldsymbol{t}_{a}$
and
$\boldsymbol{t}_{a}$
and
![]() $\boldsymbol{t}_{b}$
of the liquid–gas interface at
$\boldsymbol{t}_{b}$
of the liquid–gas interface at
![]() $a$
and
$a$
and
![]() $b$
are at respective angles
$b$
are at respective angles
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
relative to the horizon. These angles are positive for the situation depicted in figure 2. For reference, the various angles are connected by the geometrical relations
$\unicode[STIX]{x1D719}_{b}$
relative to the horizon. These angles are positive for the situation depicted in figure 2. For reference, the various angles are connected by the geometrical relations
The surfactant-laden and surfactant-free portions of the liquid–gas interface are represented by
respectively. Finally, the unit normal to the cylinder surface, directed outward into liquid and gas, is denoted by
![]() $\boldsymbol{n}$
.
$\boldsymbol{n}$
.
In contrast to the set-up in figure 1, we allow for vertical translation and the possibility of a uniform line load
![]() $\boldsymbol{f}_{L}$
on the apex of the cylinder. Horizontal translation of the cylinder is prevented by a reactive horizontal force
$\boldsymbol{f}_{L}$
on the apex of the cylinder. Horizontal translation of the cylinder is prevented by a reactive horizontal force
![]() $\boldsymbol{f}_{R}$
. We represent
$\boldsymbol{f}_{R}$
. We represent
![]() $\boldsymbol{f}_{R}$
by a traction that includes components that act horizontally and normal to the surface of the cylinder. The net force
$\boldsymbol{f}_{R}$
by a traction that includes components that act horizontally and normal to the surface of the cylinder. The net force
![]() $\boldsymbol{f}_{N}$
acting on the cylinder is zero in magnitude and, in addition to
$\boldsymbol{f}_{N}$
acting on the cylinder is zero in magnitude and, in addition to
![]() $\boldsymbol{f}_{L}$
and
$\boldsymbol{f}_{L}$
and
![]() $\boldsymbol{f}_{R}$
, accounts for the weight
$\boldsymbol{f}_{R}$
, accounts for the weight
![]() $\boldsymbol{f}_{G}$
of the cylinder, the force
$\boldsymbol{f}_{G}$
of the cylinder, the force
![]() $\boldsymbol{f}_{P}$
due to the hydrostatic pressure, and the force
$\boldsymbol{f}_{P}$
due to the hydrostatic pressure, and the force
![]() $\boldsymbol{f}_{T}$
due to surface tension. Rotation of the cylinder about its axis is prevented by a reactive torque
$\boldsymbol{f}_{T}$
due to surface tension. Rotation of the cylinder about its axis is prevented by a reactive torque
![]() $\unicode[STIX]{x1D749}_{R}$
induced by a pair of horizontal forces that are equal in magnitude but opposite in direction and act at the apex and the base of the cylinder surface. All forces, torques and areas considered in this work are measured per unit length of the cylinder.
$\unicode[STIX]{x1D749}_{R}$
induced by a pair of horizontal forces that are equal in magnitude but opposite in direction and act at the apex and the base of the cylinder surface. All forces, torques and areas considered in this work are measured per unit length of the cylinder.
Figure 2. Schematic of a circular cylinder of radius
![]() $r$
laying at a liquid–gas interface. The cylinder acts as a barrier between surfactant-free and surfactant-laden portions of that interface. The respective interfaces have uniform surface tensions
$r$
laying at a liquid–gas interface. The cylinder acts as a barrier between surfactant-free and surfactant-laden portions of that interface. The respective interfaces have uniform surface tensions
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
. Far from the cylinder, both interfaces are flat and have the same horizontal elevation. The orthonormal basis vectors
$\unicode[STIX]{x1D6FE}_{b}$
. Far from the cylinder, both interfaces are flat and have the same horizontal elevation. The orthonormal basis vectors
![]() $\boldsymbol{\imath }$
,
$\boldsymbol{\imath }$
,
![]() $\boldsymbol{\jmath }$
and
$\boldsymbol{\jmath }$
and
![]() $\boldsymbol{k}$
correspond to a rectangular Cartesian coordinate system with origin
$\boldsymbol{k}$
correspond to a rectangular Cartesian coordinate system with origin
![]() $o$
. The centre of the cylinder is horizontally aligned with
$o$
. The centre of the cylinder is horizontally aligned with
![]() $o$
and is located at point
$o$
and is located at point
![]() $c$
with coordinates
$c$
with coordinates
![]() $x=0$
and
$x=0$
and
![]() $z=h_{c}$
. The undisturbed portions of the liquid–gas interface are at the same height as
$z=h_{c}$
. The undisturbed portions of the liquid–gas interface are at the same height as
![]() $o$
. The angles
$o$
. The angles
![]() $\unicode[STIX]{x1D713}_{a}$
and
$\unicode[STIX]{x1D713}_{a}$
and
![]() $\unicode[STIX]{x1D713}_{b}$
define a circular arc and are measured clockwise, with reference to the figure, starting from ray
$\unicode[STIX]{x1D713}_{b}$
define a circular arc and are measured clockwise, with reference to the figure, starting from ray
![]() $cd$
and satisfy
$cd$
and satisfy
![]() $\unicode[STIX]{x1D713}_{a}<\unicode[STIX]{x1D713}_{b}$
. Therefore,
$\unicode[STIX]{x1D713}_{a}<\unicode[STIX]{x1D713}_{b}$
. Therefore,
![]() $\unicode[STIX]{x1D713}_{a}$
is negative for the situation depicted in the figure. The end points of that arc are located at solid–liquid–gas contact lines
$\unicode[STIX]{x1D713}_{a}$
is negative for the situation depicted in the figure. The end points of that arc are located at solid–liquid–gas contact lines
![]() $a$
and
$a$
and
![]() $b$
. Point
$b$
. Point
![]() $a$
has coordinates
$a$
has coordinates
![]() $x=x_{a}$
and
$x=x_{a}$
and
![]() $z=h_{a}$
, and point
$z=h_{a}$
, and point
![]() $b$
has coordinates
$b$
has coordinates
![]() $x=x_{b}$
and
$x=x_{b}$
and
![]() $z=h_{b}$
. The contact angles
$z=h_{b}$
. The contact angles
![]() $\unicode[STIX]{x1D703}_{a}$
and
$\unicode[STIX]{x1D703}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
are measured in the liquid phase and are always positive. The unit tangent vectors
$\unicode[STIX]{x1D703}_{b}$
are measured in the liquid phase and are always positive. The unit tangent vectors
![]() $\boldsymbol{t}_{a}$
and
$\boldsymbol{t}_{a}$
and
![]() $\boldsymbol{t}_{b}$
, of the liquid–gas interface at
$\boldsymbol{t}_{b}$
, of the liquid–gas interface at
![]() $a$
and
$a$
and
![]() $b$
, respectively, are at respective angles
$b$
, respectively, are at respective angles
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
relative to the horizon. For the situation depicted in the figure,
$\unicode[STIX]{x1D719}_{b}$
relative to the horizon. For the situation depicted in the figure,
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
are positive. The unit normal vector
$\unicode[STIX]{x1D719}_{b}$
are positive. The unit normal vector
![]() $\boldsymbol{n}$
points from the surface of the cylinder into the liquid and gas.
$\boldsymbol{n}$
points from the surface of the cylinder into the liquid and gas.
2.2 Weight and hydrostatic pressure
2.2.1 Weight
Consistent with the convention that
![]() $z$
increases in the direction
$z$
increases in the direction
![]() $\boldsymbol{k}$
along which gravity acts, we write
$\boldsymbol{k}$
along which gravity acts, we write
where
![]() $\unicode[STIX]{x1D70C}_{c}$
and
$\unicode[STIX]{x1D70C}_{c}$
and
![]() $r$
denote the mass density and the radius of the cylinder, respectively. It is convenient to let
$r$
denote the mass density and the radius of the cylinder, respectively. It is convenient to let
![]() $\unicode[STIX]{x1D70C}_{c}^{\ast }$
denote the maximum allowed mass density for which the cylinder floats at the liquid–gas interface in the absence of a line load
$\unicode[STIX]{x1D70C}_{c}^{\ast }$
denote the maximum allowed mass density for which the cylinder floats at the liquid–gas interface in the absence of a line load
![]() $\boldsymbol{f}_{L}$
.
$\boldsymbol{f}_{L}$
.
2.2.2 Hydrostatic pressure
The force
![]() $\boldsymbol{f}_{P}$
due to hydrostatic pressure
$\boldsymbol{f}_{P}$
due to hydrostatic pressure
![]() $p$
is obtained by integrating
$p$
is obtained by integrating
![]() $-p\boldsymbol{n}$
over the part
$-p\boldsymbol{n}$
over the part
![]() ${\mathcal{A}}$
of the cylinder surface that is in contact with the liquid. This operation gives
${\mathcal{A}}$
of the cylinder surface that is in contact with the liquid. This operation gives
where
![]() $\boldsymbol{n}$
is the unit normal to the surface of the cylinder, directed into the liquid, and
$\boldsymbol{n}$
is the unit normal to the surface of the cylinder, directed into the liquid, and
![]() $\text{d}s$
is the surface element. We assume that the pressure in the gas is uniform and take
$\text{d}s$
is the surface element. We assume that the pressure in the gas is uniform and take
![]() $p$
equal to zero at the horizontal level of the liquid–gas interface in the far field on either side of the cylinder.
$p$
equal to zero at the horizontal level of the liquid–gas interface in the far field on either side of the cylinder.
The generalized Archimedes principle (Mansfield, Sepangi & Eastwood Reference Mansfield, Sepangi and Eastwood1997; Keller Reference Keller1998) can be applied to obtain a more specific relation for the vertical component
![]() $f_{P}^{v}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{k}$
of
$f_{P}^{v}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{k}$
of
![]() $\boldsymbol{f}_{P}$
. The surface tension difference
$\boldsymbol{f}_{P}$
. The surface tension difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry which is confirmed by the experiment shown in figure 1(c), so that the
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry which is confirmed by the experiment shown in figure 1(c), so that the
![]() $z$
-coordinates
$z$
-coordinates
![]() $h_{a}$
and
$h_{a}$
and
![]() $h_{b}$
of the respective solid–liquid–gas contact lines at
$h_{b}$
of the respective solid–liquid–gas contact lines at
![]() $a$
and
$a$
and
![]() $b$
are not equal. The horizontal component
$b$
are not equal. The horizontal component
![]() $f_{P}^{h}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{\imath }$
of
$f_{P}^{h}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{\imath }$
of
![]() $\boldsymbol{f}_{P}$
is therefore generated by an average pressure
$\boldsymbol{f}_{P}$
is therefore generated by an average pressure
![]() $\bar{p}$
that acts over a projected (signed) area
$\bar{p}$
that acts over a projected (signed) area
![]() $\unicode[STIX]{x0394}h=h_{a}-h_{b}$
, giving
$\unicode[STIX]{x0394}h=h_{a}-h_{b}$
, giving
Introducing
![]() $\bar{p}=\unicode[STIX]{x1D70C}_{l}gh_{m}$
, with
$\bar{p}=\unicode[STIX]{x1D70C}_{l}gh_{m}$
, with
![]() $h_{m}=(h_{a}+h_{b})/2$
, we rewrite relation (2.8) as
$h_{m}=(h_{a}+h_{b})/2$
, we rewrite relation (2.8) as
Following Keller (Reference Keller1998), we obtain (2.9) by parametrizing
![]() ${\mathcal{A}}$
with respect to arclength
${\mathcal{A}}$
with respect to arclength
![]() $t$
, from
$t$
, from
![]() $b$
to
$b$
to
![]() $a$
, so that
$a$
, so that
![]() $\text{d}s=\text{d}t$
,
$\text{d}s=\text{d}t$
,
![]() $t_{b}=0$
and
$t_{b}=0$
and
![]() $t_{a}={\mathcal{A}}$
. Using a superposed hat to indicate parametrization with respect to
$t_{a}={\mathcal{A}}$
. Using a superposed hat to indicate parametrization with respect to
![]() $t$
and denoting the derivative with respect to
$t$
and denoting the derivative with respect to
![]() $t$
with a subscript, we then express
$t$
with a subscript, we then express
![]() $p$
and
$p$
and
![]() $\boldsymbol{n}$
respectively as
$\boldsymbol{n}$
respectively as
Writing
![]() $f_{P}^{h}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{\imath }$
, and using (2.7) and (2.10), we thus obtain
$f_{P}^{h}=\boldsymbol{f}_{P}\boldsymbol{\cdot }\boldsymbol{\imath }$
, and using (2.7) and (2.10), we thus obtain
 $$\begin{eqnarray}\displaystyle f_{P}^{h} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}g\int _{t_{b}}^{t_{a}}\hat{z}(-\hat{z}_{t}\boldsymbol{\imath }+\hat{x}_{t}\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{\imath }\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{l}g\int _{h_{b}}^{h_{a}}z\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{l}g}{2}(h_{a}^{2}-h_{b}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{P}^{h} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}g\int _{t_{b}}^{t_{a}}\hat{z}(-\hat{z}_{t}\boldsymbol{\imath }+\hat{x}_{t}\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{\imath }\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{l}g\int _{h_{b}}^{h_{a}}z\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{l}g}{2}(h_{a}^{2}-h_{b}^{2}).\end{eqnarray}$$
It is noteworthy that relation (2.9) is valid for cylinders of non-circular cross-section.
For a cylinder with circular cross-section, we can also write
![]() $\text{d}s=r\,\text{d}\unicode[STIX]{x1D713}$
, and using (2.7), obtain
$\text{d}s=r\,\text{d}\unicode[STIX]{x1D713}$
, and using (2.7), obtain
where
![]() $\unicode[STIX]{x1D713}_{a}$
and
$\unicode[STIX]{x1D713}_{a}$
and
![]() $\unicode[STIX]{x1D713}_{b}$
are the angles defining a circular arc with end points located at the contact lines
$\unicode[STIX]{x1D713}_{b}$
are the angles defining a circular arc with end points located at the contact lines
![]() $a$
and
$a$
and
![]() $b$
. For a point on the cylinder surface at elevation
$b$
. For a point on the cylinder surface at elevation
![]() $r\sin \unicode[STIX]{x1D713}+h_{c}$
, where
$r\sin \unicode[STIX]{x1D713}+h_{c}$
, where
![]() $h_{c}$
is the
$h_{c}$
is the
![]() $z$
-coordinate of the centre
$z$
-coordinate of the centre
![]() $c$
of the cylinder, we may express
$c$
of the cylinder, we may express
![]() $p$
as
$p$
as
Writing
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{k}=\sin \unicode[STIX]{x1D713}$
and
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{k}=\sin \unicode[STIX]{x1D713}$
and
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{\imath }=\cos \unicode[STIX]{x1D713}$
, we thus find that the respective vertical and horizontal components
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{\imath }=\cos \unicode[STIX]{x1D713}$
, we thus find that the respective vertical and horizontal components
![]() $f_{P}^{v}$
and
$f_{P}^{v}$
and
![]() $f_{P}^{h}$
of
$f_{P}^{h}$
of
![]() $\boldsymbol{f}_{P}$
are given by
$\boldsymbol{f}_{P}$
are given by
 $$\begin{eqnarray}\displaystyle f_{P}^{v} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}gr\int _{\unicode[STIX]{x1D713}_{a}}^{\unicode[STIX]{x1D713}_{b}}(r\sin \unicode[STIX]{x1D713}+h_{c})\sin \unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D713}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\unicode[STIX]{x1D70C}_{l}gr^{2}}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{P}^{v} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}gr\int _{\unicode[STIX]{x1D713}_{a}}^{\unicode[STIX]{x1D713}_{b}}(r\sin \unicode[STIX]{x1D713}+h_{c})\sin \unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D713}\nonumber\\ \displaystyle & = & \displaystyle -\frac{\unicode[STIX]{x1D70C}_{l}gr^{2}}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right),\qquad\end{eqnarray}$$
with
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{b}-\unicode[STIX]{x1D713}_{a}$
, and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{b}-\unicode[STIX]{x1D713}_{a}$
, and
 $$\begin{eqnarray}\displaystyle f_{P}^{h} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}gr\int _{\unicode[STIX]{x1D713}_{a}}^{\unicode[STIX]{x1D713}_{b}}(r\sin \unicode[STIX]{x1D713}+h_{c})\cos \unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D713}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{l}gr^{2}(\sin \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b})}{2}\left(\sin \unicode[STIX]{x1D713}_{a}+\sin \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{P}^{h} & = & \displaystyle -\unicode[STIX]{x1D70C}_{l}gr\int _{\unicode[STIX]{x1D713}_{a}}^{\unicode[STIX]{x1D713}_{b}}(r\sin \unicode[STIX]{x1D713}+h_{c})\cos \unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D713}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{l}gr^{2}(\sin \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b})}{2}\left(\sin \unicode[STIX]{x1D713}_{a}+\sin \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}\right).\end{eqnarray}$$
The relations (2.14) and (2.15) can also be obtained as respective consequences of (2.9) and the generalized Archimedes principle (Mansfield et al. Reference Mansfield, Sepangi and Eastwood1997; Keller Reference Keller1998).
2.3 Surface tension
The unit tangent vectors
![]() $\boldsymbol{t}_{a}$
and
$\boldsymbol{t}_{a}$
and
![]() $\boldsymbol{t}_{b}$
, of the liquid–gas interface at the contact lines
$\boldsymbol{t}_{b}$
, of the liquid–gas interface at the contact lines
![]() $a$
and
$a$
and
![]() $b$
, are at respective angles
$b$
, are at respective angles
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
relative to the horizon. The force
$\unicode[STIX]{x1D719}_{b}$
relative to the horizon. The force
![]() $\boldsymbol{f}_{T}$
due to the surface tension is the sum of
$\boldsymbol{f}_{T}$
due to the surface tension is the sum of
![]() $\unicode[STIX]{x1D6FE}_{a}\boldsymbol{t}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}\boldsymbol{t}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}\boldsymbol{t}_{b}$
. The vertical and horizontal components
$\unicode[STIX]{x1D6FE}_{b}\boldsymbol{t}_{b}$
. The vertical and horizontal components
![]() $f_{T}^{v}=\boldsymbol{f}_{T}\boldsymbol{\cdot }\boldsymbol{k}$
and
$f_{T}^{v}=\boldsymbol{f}_{T}\boldsymbol{\cdot }\boldsymbol{k}$
and
![]() $f_{T}^{h}=\boldsymbol{f}_{T}\boldsymbol{\cdot }\boldsymbol{\imath }$
of
$f_{T}^{h}=\boldsymbol{f}_{T}\boldsymbol{\cdot }\boldsymbol{\imath }$
of
![]() $\boldsymbol{f}_{T}$
are given by
$\boldsymbol{f}_{T}$
are given by
2.4 Torque
The torque
![]() $\unicode[STIX]{x1D749}$
about the axis of the cylinder is the sum of
$\unicode[STIX]{x1D749}$
about the axis of the cylinder is the sum of
![]() $\unicode[STIX]{x1D749}_{a}=r\boldsymbol{n}\times \unicode[STIX]{x1D6FE}_{a}\boldsymbol{t}_{a}$
and
$\unicode[STIX]{x1D749}_{a}=r\boldsymbol{n}\times \unicode[STIX]{x1D6FE}_{a}\boldsymbol{t}_{a}$
and
![]() $\unicode[STIX]{x1D749}_{b}=r\boldsymbol{n}\times \unicode[STIX]{x1D6FE}_{b}\boldsymbol{t}_{a}$
. The only non-vanishing component of
$\unicode[STIX]{x1D749}_{b}=r\boldsymbol{n}\times \unicode[STIX]{x1D6FE}_{b}\boldsymbol{t}_{a}$
. The only non-vanishing component of
![]() $\unicode[STIX]{x1D749}$
, namely
$\unicode[STIX]{x1D749}$
, namely
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{\jmath }$
, is given by
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{\jmath }$
, is given by
where
![]() $\unicode[STIX]{x1D703}_{a}$
and
$\unicode[STIX]{x1D703}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
are the respective contact angles at the contact lines
$\unicode[STIX]{x1D703}_{b}$
are the respective contact angles at the contact lines
![]() $a$
and
$a$
and
![]() $b$
, measured in the liquid phase. Because
$b$
, measured in the liquid phase. Because
![]() $\boldsymbol{f}_{P}$
and
$\boldsymbol{f}_{P}$
and
![]() $\boldsymbol{f}_{G}$
act radially, they do not exert any torque on the cylinder about its axis. As a result, the net torque
$\boldsymbol{f}_{G}$
act radially, they do not exert any torque on the cylinder about its axis. As a result, the net torque
![]() $\unicode[STIX]{x1D749}_{N}$
is
$\unicode[STIX]{x1D749}_{N}$
is
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{\jmath }$
. This quantity is balanced by
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{\jmath }$
. This quantity is balanced by
![]() $\unicode[STIX]{x1D749}_{R}$
, which prevents rotation of the cylinder about its axis. Writing
$\unicode[STIX]{x1D749}_{R}$
, which prevents rotation of the cylinder about its axis. Writing
![]() $\unicode[STIX]{x1D70F}_{R}=\unicode[STIX]{x1D749}_{R}\boldsymbol{\cdot }\boldsymbol{\jmath }$
, we express this balance as
$\unicode[STIX]{x1D70F}_{R}=\unicode[STIX]{x1D749}_{R}\boldsymbol{\cdot }\boldsymbol{\jmath }$
, we express this balance as
![]() $-\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{R}$
. Singh & Hesla (Reference Singh and Hesla2004) showed that the torque vanishes if the contact angles and the surface tensions are the same. By specializing (2.17) appropriately, we recover this result.
$-\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{R}$
. Singh & Hesla (Reference Singh and Hesla2004) showed that the torque vanishes if the contact angles and the surface tensions are the same. By specializing (2.17) appropriately, we recover this result.
2.5 Net force on cylinder
Let
![]() $\boldsymbol{f}$
be the sum of
$\boldsymbol{f}$
be the sum of
![]() $\boldsymbol{f}_{P}$
,
$\boldsymbol{f}_{P}$
,
![]() $\boldsymbol{f}_{T}$
and
$\boldsymbol{f}_{T}$
and
![]() $\boldsymbol{f}_{G}$
, with respective vertical and horizontal components
$\boldsymbol{f}_{G}$
, with respective vertical and horizontal components
where, with reference to (2.6), (2.14) and (2.16a
),
![]() $f^{v}$
is given by
$f^{v}$
is given by
 $$\begin{eqnarray}\displaystyle f^{v} & = & \displaystyle -\frac{\unicode[STIX]{x1D70C}_{l}gr^{2}}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FE}_{a}\sin \unicode[STIX]{x1D719}_{a}-\unicode[STIX]{x1D6FE}_{b}\sin \unicode[STIX]{x1D719}_{b}+\unicode[STIX]{x1D70C}_{c}g\unicode[STIX]{x03C0}r^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f^{v} & = & \displaystyle -\frac{\unicode[STIX]{x1D70C}_{l}gr^{2}}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2h_{c}}{r}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FE}_{a}\sin \unicode[STIX]{x1D719}_{a}-\unicode[STIX]{x1D6FE}_{b}\sin \unicode[STIX]{x1D719}_{b}+\unicode[STIX]{x1D70C}_{c}g\unicode[STIX]{x03C0}r^{2},\end{eqnarray}$$
and, with reference to (2.15) and (2.16b
),
![]() $f^{h}$
is given by
$f^{h}$
is given by
Then, writing
![]() $f_{L}=\boldsymbol{f}_{L}\boldsymbol{\cdot }k$
and
$f_{L}=\boldsymbol{f}_{L}\boldsymbol{\cdot }k$
and
![]() $f_{R}=\boldsymbol{f}_{R}\boldsymbol{\cdot }\boldsymbol{\imath }$
, we see that the vertical and horizontal components
$f_{R}=\boldsymbol{f}_{R}\boldsymbol{\cdot }\boldsymbol{\imath }$
, we see that the vertical and horizontal components
![]() $f_{N}^{v}=\boldsymbol{f}_{N}\boldsymbol{\cdot }k$
and
$f_{N}^{v}=\boldsymbol{f}_{N}\boldsymbol{\cdot }k$
and
![]() $f_{N}^{h}=\boldsymbol{f}_{N}\boldsymbol{\cdot }\boldsymbol{\imath }$
of the net force
$f_{N}^{h}=\boldsymbol{f}_{N}\boldsymbol{\cdot }\boldsymbol{\imath }$
of the net force
![]() $\boldsymbol{f}_{N}$
take the form
$\boldsymbol{f}_{N}$
take the form
In equilibrium, the condition of force balance yields
![]() $f^{v}=-f_{L}$
and
$f^{v}=-f_{L}$
and
![]() $f^{h}=-f_{R}$
.
$f^{h}=-f_{R}$
.
2.6 Contact angle versus surface tension
The surface of a solid is hydrophobic if the static contact angle
![]() $\unicode[STIX]{x1D703}$
, formed at a surfactant-free solid–water–air contact line located at the surface of that solid, is greater than
$\unicode[STIX]{x1D703}$
, formed at a surfactant-free solid–water–air contact line located at the surface of that solid, is greater than
![]() $\unicode[STIX]{x03C0}/2$
when measured in the water phase. Moreover, a solid is hydrophilic if
$\unicode[STIX]{x03C0}/2$
when measured in the water phase. Moreover, a solid is hydrophilic if
![]() $\unicode[STIX]{x1D703}$
is less than
$\unicode[STIX]{x1D703}$
is less than
![]() $\unicode[STIX]{x03C0}/2$
. Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973) reported on the contact angles that water droplets loaded with soluble surfactants make with hydrophobic substrates. Their measurements show that
$\unicode[STIX]{x03C0}/2$
. Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973) reported on the contact angles that water droplets loaded with soluble surfactants make with hydrophobic substrates. Their measurements show that
![]() $\unicode[STIX]{x1D6FE}_{b}\cos \unicode[STIX]{x1D703}_{b}$
decreases with increasing
$\unicode[STIX]{x1D6FE}_{b}\cos \unicode[STIX]{x1D703}_{b}$
decreases with increasing
![]() $\unicode[STIX]{x1D6FE}_{b}$
according to the relation
$\unicode[STIX]{x1D6FE}_{b}$
according to the relation
where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are obtained by linear regression. It is noteworthy that
$\unicode[STIX]{x1D6FD}$
are obtained by linear regression. It is noteworthy that
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
remain constant as the surfactant concentration increases from zero up to the critical micelle concentration. From works of Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973), Szymczyk & Jańczuk (Reference Szymczyk and Jańczuk2007) and Chaudhuri, Sunayana & Paria (Reference Chaudhuri, Sunayana and Paria2012), it is evident that
$\unicode[STIX]{x1D6FD}$
remain constant as the surfactant concentration increases from zero up to the critical micelle concentration. From works of Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973), Szymczyk & Jańczuk (Reference Szymczyk and Jańczuk2007) and Chaudhuri, Sunayana & Paria (Reference Chaudhuri, Sunayana and Paria2012), it is evident that
![]() $\unicode[STIX]{x1D6FC}$
ranges from
$\unicode[STIX]{x1D6FC}$
ranges from
![]() $0.6$
to
$0.6$
to
![]() $1.0$
and that
$1.0$
and that
![]() $\unicode[STIX]{x1D6FD}$
ranges from 0 to
$\unicode[STIX]{x1D6FD}$
ranges from 0 to
![]() $50~\text{mN}~\text{m}^{-1}$
, depending on which surfactants and solids are involved. Lucassen-Reynders (Reference Lucassen-Reynders1963) showed that
$50~\text{mN}~\text{m}^{-1}$
, depending on which surfactants and solids are involved. Lucassen-Reynders (Reference Lucassen-Reynders1963) showed that
![]() $\unicode[STIX]{x1D6FC}$
can be represented by
$\unicode[STIX]{x1D6FC}$
can be represented by
where
![]() $I_{SG}$
,
$I_{SG}$
,
![]() $I_{SL}$
and
$I_{SL}$
and
![]() $I_{LG}$
denote the excess concentrations of surfactant molecules on the solid–gas, solid–liquid and liquid–gas interfaces, respectively. This relation was established by invoking the equation of state (Gibbs Reference Gibbs1878, p. 398)
$I_{LG}$
denote the excess concentrations of surfactant molecules on the solid–gas, solid–liquid and liquid–gas interfaces, respectively. This relation was established by invoking the equation of state (Gibbs Reference Gibbs1878, p. 398)
where
![]() $i$
stands for
$i$
stands for
![]() $SL$
,
$SL$
,
![]() $SG$
or
$SG$
or
![]() $LG$
,
$LG$
,
![]() $\unicode[STIX]{x1D701}$
is the activity of a surfactant,
$\unicode[STIX]{x1D701}$
is the activity of a surfactant,
![]() ${\mathcal{R}}$
is the ideal gas constant and
${\mathcal{R}}$
is the ideal gas constant and
![]() $T_{A}$
is the absolute temperature. Using the integrated form of (2.23) along with Young’s (Reference Young1805) equation,
$T_{A}$
is the absolute temperature. Using the integrated form of (2.23) along with Young’s (Reference Young1805) equation,
results in (2.22). For
![]() $\unicode[STIX]{x1D6FC}$
equal to unity, Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973) explained how, on the basis of Fowkes’ (Reference Fowkes1964) hypothesis, to find the constant of integration
$\unicode[STIX]{x1D6FC}$
equal to unity, Bargeman & Van Voorst Vader (Reference Bargeman and Van Voorst Vader1973) explained how, on the basis of Fowkes’ (Reference Fowkes1964) hypothesis, to find the constant of integration
![]() $\unicode[STIX]{x1D6FD}$
from independent experiments. With
$\unicode[STIX]{x1D6FD}$
from independent experiments. With
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
constant, and with
$\unicode[STIX]{x1D6FD}$
constant, and with
![]() $\unicode[STIX]{x1D6FE}_{b}$
decreasing as a function of
$\unicode[STIX]{x1D6FE}_{b}$
decreasing as a function of
![]() $I_{LG}$
, we see from (2.22) that
$I_{LG}$
, we see from (2.22) that
![]() $\unicode[STIX]{x1D703}_{b}$
decreases with surfactant concentration.
$\unicode[STIX]{x1D703}_{b}$
decreases with surfactant concentration.
Although our concern is with insoluble surfactants, we use (2.22) as a first approximation. This is supported by the experiment shown in figure 1(c), from which we find that
![]() $\unicode[STIX]{x1D703}_{b}$
decreases with increasing surfactant concentration. From the same experiment, we also see that
$\unicode[STIX]{x1D703}_{b}$
decreases with increasing surfactant concentration. From the same experiment, we also see that
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{a}$
are not affected by changing
$\unicode[STIX]{x1D703}_{a}$
are not affected by changing
![]() $\unicode[STIX]{x1D6FE}_{b}$
and, thus,
$\unicode[STIX]{x1D6FE}_{b}$
and, thus,
![]() $\unicode[STIX]{x1D703}_{b}$
. A hydrophobic cylinder can therefore act as a surfactant barrier.
$\unicode[STIX]{x1D703}_{b}$
. A hydrophobic cylinder can therefore act as a surfactant barrier.
2.7 Young–Laplace equation
At the surfactant-free and surfactant-laden portions of the interface, force balance takes the form of the respective one-dimensional hydrostatic Young–Laplace equations (Laplace Reference Laplace1805; Young Reference Young1805)
where a subscripted
![]() $x$
denotes differentiation with respect to
$x$
denotes differentiation with respect to
![]() $x$
and
$x$
and
![]() $\operatorname{sgn}$
denotes the signum function, so that the right-hand side of each equation represents the signed curvature of the appropriate portion of the liquid–gas interface. The relations in (2.26) can be derived from the three-dimensional version
$\operatorname{sgn}$
denotes the signum function, so that the right-hand side of each equation represents the signed curvature of the appropriate portion of the liquid–gas interface. The relations in (2.26) can be derived from the three-dimensional version
![]() $\unicode[STIX]{x0394}p=2\unicode[STIX]{x1D6FE}{\mathcal{H}}$
of the Young–Laplace equation, where
$\unicode[STIX]{x0394}p=2\unicode[STIX]{x1D6FE}{\mathcal{H}}$
of the Young–Laplace equation, where
![]() $\unicode[STIX]{x1D6FE}$
denotes the surface tension and
$\unicode[STIX]{x1D6FE}$
denotes the surface tension and
![]() ${\mathcal{H}}$
is the mean curvature of the surface.
${\mathcal{H}}$
is the mean curvature of the surface.
2.8 Scaling
We adopt a scaling in which lengths are measured relative to
![]() $l_{c}$
, mass densities are measured relative to
$l_{c}$
, mass densities are measured relative to
![]() $\unicode[STIX]{x1D70C}_{l}$
, forces are measured relative to
$\unicode[STIX]{x1D70C}_{l}$
, forces are measured relative to
![]() $\unicode[STIX]{x1D6FE}_{a}$
and torques are measured relative to
$\unicode[STIX]{x1D6FE}_{a}$
and torques are measured relative to
![]() $l_{c}\unicode[STIX]{x1D6FE}_{a}$
. In addition to the Bond number
$l_{c}\unicode[STIX]{x1D6FE}_{a}$
. In addition to the Bond number
this leads to dimensionless measures
of surface tension, the parameter
![]() $\unicode[STIX]{x1D6FD}$
entering the relation (2.22) between
$\unicode[STIX]{x1D6FD}$
entering the relation (2.22) between
![]() $\unicode[STIX]{x1D6FE}_{b}$
and
$\unicode[STIX]{x1D6FE}_{b}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
, mass density and the maximum allowed mass density for which the cylinder floats. In addition, we introduce the dimensionless lengths
$\unicode[STIX]{x1D703}_{b}$
, mass density and the maximum allowed mass density for which the cylinder floats. In addition, we introduce the dimensionless lengths
dimensionless force components
and dimensionless torque components
As a particular consequence of (2.27) and (2.29), we see that
![]() $Bo=R^{2}$
.
$Bo=R^{2}$
.
For the relations in (2.2) determining the
![]() $x$
-coordinates
$x$
-coordinates
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
of
$x_{b}$
of
![]() $a$
and
$a$
and
![]() $b$
, we obtain dimensionless counterparts
$b$
, we obtain dimensionless counterparts
and for the relations in (2.3) determining the
![]() $z$
-coordinates
$z$
-coordinates
![]() $h_{a}$
and
$h_{a}$
and
![]() $h_{b}$
of
$h_{b}$
of
![]() $a$
and
$a$
and
![]() $b$
, we obtain
$b$
, we obtain
Furthermore, for the relations (2.9), (2.16b
), (2.19) and (2.20) determining the force components
![]() $f_{P}^{h}$
,
$f_{P}^{h}$
,
![]() $f_{T}^{h}$
,
$f_{T}^{h}$
,
![]() $f^{v}$
and
$f^{v}$
and
![]() $f^{h}$
, we obtain
$f^{h}$
, we obtain
 $$\begin{eqnarray}\displaystyle & \displaystyle F^{v}=-\frac{Bo}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2H_{c}}{R}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle -\,(\sin \unicode[STIX]{x1D719}_{a}+\unicode[STIX]{x1D6E4}\sin \unicode[STIX]{x1D719}_{b})+D\unicode[STIX]{x03C0}Bo, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F^{v}=-\frac{Bo}{2}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}_{a}\cos \unicode[STIX]{x1D713}_{a}-\sin \unicode[STIX]{x1D713}_{b}\cos \unicode[STIX]{x1D713}_{b}+\frac{2H_{c}}{R}(\cos \unicode[STIX]{x1D713}_{a}-\cos \unicode[STIX]{x1D713}_{b})\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle -\,(\sin \unicode[STIX]{x1D719}_{a}+\unicode[STIX]{x1D6E4}\sin \unicode[STIX]{x1D719}_{b})+D\unicode[STIX]{x03C0}Bo, & \displaystyle\end{eqnarray}$$
and
while for the relation (2.17) determining
![]() $\unicode[STIX]{x1D70F}$
, we obtain
$\unicode[STIX]{x1D70F}$
, we obtain
Additionally, the relation (2.22) connecting
![]() $\unicode[STIX]{x1D6FE}_{b}$
and
$\unicode[STIX]{x1D6FE}_{b}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
can be expressed in the form
$\unicode[STIX]{x1D703}_{b}$
can be expressed in the form
while the equilibrium conditions (2.26) yield
In § 3.1.1, we evaluate the effect of
![]() $\unicode[STIX]{x1D6E4}$
on the load-bearing capacity of a floating cylinder. We do this with the dimensionless quantity
$\unicode[STIX]{x1D6E4}$
on the load-bearing capacity of a floating cylinder. We do this with the dimensionless quantity
which is the ratio of
![]() $D^{\ast }$
in the presence of a surface tension imbalance to
$D^{\ast }$
in the presence of a surface tension imbalance to
![]() $D^{\ast }$
in the absence of a surface tension imbalance.
$D^{\ast }$
in the absence of a surface tension imbalance.
2.9 Surface profiles
Mansfield et al. (Reference Mansfield, Sepangi and Eastwood1997) observed that the results of integrating equations that are mathematically identical to those in (2.40), with the same boundary conditions as in the present work, were expounded by Thompson & Tait (Reference Thompson and Tait1867, pp. 454–457). We integrate (2.40a ) and (2.40b ) subject to the respective far-field conditions
After the first integration we obtain
If
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
are positive, as shown in figure 2, then
$\unicode[STIX]{x1D719}_{b}$
are positive, as shown in figure 2, then
![]() $H_{a}$
and
$H_{a}$
and
![]() $H_{b}$
should be positive. Alternatively, if
$H_{b}$
should be positive. Alternatively, if
![]() $\unicode[STIX]{x1D719}_{a}$
and
$\unicode[STIX]{x1D719}_{a}$
and
![]() $\unicode[STIX]{x1D719}_{b}$
are negative, then
$\unicode[STIX]{x1D719}_{b}$
are negative, then
![]() $H_{a}$
and
$H_{a}$
and
![]() $H_{b}$
should be negative. The presence of signum functions in (2.43) assures this. After the second integration, we find that the surfactant-laden and surfactant-free profiles of the liquid–gas interface are given by
$H_{b}$
should be negative. The presence of signum functions in (2.43) assures this. After the second integration, we find that the surfactant-laden and surfactant-free profiles of the liquid–gas interface are given by
and
respectively, where
![]() $C_{a}$
and
$C_{a}$
and
![]() $C_{b}$
denote constants that we determine from the respective near-field conditions (2.32).
$C_{b}$
denote constants that we determine from the respective near-field conditions (2.32).
2.10 Specialization
If
![]() $\unicode[STIX]{x1D6FE}_{b}=\unicode[STIX]{x1D6FE}_{a}$
, so that there is no surface tension imbalance and, thus,
$\unicode[STIX]{x1D6FE}_{b}=\unicode[STIX]{x1D6FE}_{a}$
, so that there is no surface tension imbalance and, thus,
![]() $\unicode[STIX]{x1D6E4}=1$
, we write
$\unicode[STIX]{x1D6E4}=1$
, we write
![]() $\unicode[STIX]{x1D703}_{a}=\unicode[STIX]{x1D703}_{b}=\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D703}_{a}=\unicode[STIX]{x1D703}_{b}=\unicode[STIX]{x1D703}$
,
![]() $\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{b}=\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}_{b}=\unicode[STIX]{x03C0}-\unicode[STIX]{x1D713}_{a}$
. By (2.36) and (2.33a
), we are thus led to a relation,
$\unicode[STIX]{x1D713}_{b}=\unicode[STIX]{x03C0}-\unicode[STIX]{x1D713}_{a}$
. By (2.36) and (2.33a
), we are thus led to a relation,
reminiscent of an earlier result due to Princen (Reference Princen and Matijević1969). If, moreover, we completely neglect surface tension, then the liquid–gas interface must be flat. In this case, we write
![]() $H_{a}=0$
and
$H_{a}=0$
and
![]() $\unicode[STIX]{x1D719}=0$
, so that, on setting
$\unicode[STIX]{x1D719}=0$
, so that, on setting
![]() $F^{v}=0$
in (2.46), we arrive at a substantially simpler relation,
$F^{v}=0$
in (2.46), we arrive at a substantially simpler relation,
which can also be obtained as a direct consequence of Archimedes’ principle.
3 Implications of the force analysis
3.1 Hydrophobic cylinder
To explore some implications of the general force analysis, we consider values of
![]() $Bo$
between
$Bo$
between
![]() $10^{-3}$
and
$10^{-3}$
and
![]() $10^{2}$
and values of
$10^{2}$
and values of
![]() $\unicode[STIX]{x1D6E4}$
between
$\unicode[STIX]{x1D6E4}$
between
![]() $3/7$
and
$3/7$
and
![]() $1$
. The particular value
$1$
. The particular value
![]() $\unicode[STIX]{x1D6E4}=3/7$
of
$\unicode[STIX]{x1D6E4}=3/7$
of
![]() $\unicode[STIX]{x1D6E4}$
is the ratio of the surface tension of surfactant-laden water–air interface (
$\unicode[STIX]{x1D6E4}$
is the ratio of the surface tension of surfactant-laden water–air interface (
![]() $\unicode[STIX]{x1D6FE}_{b}\approx 30~\text{mN}~\text{m}^{-1}$
) to that of surfactant-free water–air interface (
$\unicode[STIX]{x1D6FE}_{b}\approx 30~\text{mN}~\text{m}^{-1}$
) to that of surfactant-free water–air interface (
![]() $\unicode[STIX]{x1D6FE}_{a}\approx 70~\text{mN}~\text{m}^{-1}$
), both being measured at room temperature. We use
$\unicode[STIX]{x1D6FE}_{a}\approx 70~\text{mN}~\text{m}^{-1}$
), both being measured at room temperature. We use
![]() $\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FC}=1$
and
![]() $\unicode[STIX]{x1D6E4}_{0}=4/7$
in the dimensionless counterpart (2.39) of (2.22), so that
$\unicode[STIX]{x1D6E4}_{0}=4/7$
in the dimensionless counterpart (2.39) of (2.22), so that
![]() $\unicode[STIX]{x1D703}_{b}$
must lie between
$\unicode[STIX]{x1D703}_{b}$
must lie between
![]() $70.5^{\circ }$
and
$70.5^{\circ }$
and
![]() $115.4^{\circ }$
. Additionally, we fix
$115.4^{\circ }$
. Additionally, we fix
![]() $\unicode[STIX]{x1D703}_{a}$
at
$\unicode[STIX]{x1D703}_{a}$
at
![]() $115.4^{\circ }$
and we use parentheses to indicate the particular values of
$115.4^{\circ }$
and we use parentheses to indicate the particular values of
![]() $D^{\ast }$
and
$D^{\ast }$
and
![]() $Q$
corresponding to different choices of
$Q$
corresponding to different choices of
![]() $\unicode[STIX]{x1D6E4}$
. With
$\unicode[STIX]{x1D6E4}$
. With
![]() $D$
known, we obtain the load
$D$
known, we obtain the load
![]() $F_{L}$
required to maintain the centre of the cylinder at dimensionless vertical position
$F_{L}$
required to maintain the centre of the cylinder at dimensionless vertical position
![]() $H_{c}$
by solving (2.33), (2.36) and (2.43) numerically. However, in most cases we take
$H_{c}$
by solving (2.33), (2.36) and (2.43) numerically. However, in most cases we take
![]() $F_{L}=-F^{v}=0$
and compute
$F_{L}=-F^{v}=0$
and compute
![]() $H_{c}$
. Using these results, we calculate the horizontal force components. Since we perform a static analysis, the value of the net force on the cylinder always vanishes.
$H_{c}$
. Using these results, we calculate the horizontal force components. Since we perform a static analysis, the value of the net force on the cylinder always vanishes.
3.1.1 Implications of the vertical force analysis
Figure 3(a,b) shows cross-sections of two identical cylinders (
![]() $D=1.63,R=1$
) at a water–air interface for respective values
$D=1.63,R=1$
) at a water–air interface for respective values
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=3/7$
. The loads on both cylinders vanish, so that
$\unicode[STIX]{x1D6E4}=3/7$
. The loads on both cylinders vanish, so that
![]() $F_{L}=-F^{v}=0$
. Since
$F_{L}=-F^{v}=0$
. Since
![]() $F_{T}^{v}$
is larger for
$F_{T}^{v}$
is larger for
![]() $\unicode[STIX]{x1D6E4}=1$
than for
$\unicode[STIX]{x1D6E4}=1$
than for
![]() $\unicode[STIX]{x1D6E4}=3/7$
, the vertical position of the cylinder in figure 3(a) is higher than that in figure 3(b). Although the water–air interface profiles depicted in figure 3(a) are mirror images, the symmetry is broken in figure 3(b). Figure 3(c,d) shows
$\unicode[STIX]{x1D6E4}=3/7$
, the vertical position of the cylinder in figure 3(a) is higher than that in figure 3(b). Although the water–air interface profiles depicted in figure 3(a) are mirror images, the symmetry is broken in figure 3(b). Figure 3(c,d) shows
![]() $F^{v}$
as a function of
$F^{v}$
as a function of
![]() $H_{c}$
for the cylinders depicted in figures 3(a) and 3(b), respectively. Movie 1 (see supplementary movie https://doi.org/10.1017/jfm.2017.537) provides the corresponding cross-sections. The point where the two dashed curves in figure 3(c) intersect the solid curve corresponds to the situation that is depicted in figure 3(a). At that point,
$H_{c}$
for the cylinders depicted in figures 3(a) and 3(b), respectively. Movie 1 (see supplementary movie https://doi.org/10.1017/jfm.2017.537) provides the corresponding cross-sections. The point where the two dashed curves in figure 3(c) intersect the solid curve corresponds to the situation that is depicted in figure 3(a). At that point,
![]() $\text{d}F^{v}/\text{d}H_{c}<0$
, which shows that the cylinder is in a stable configuration. However, when
$\text{d}F^{v}/\text{d}H_{c}<0$
, which shows that the cylinder is in a stable configuration. However, when
![]() $\text{d}F^{v}/\text{d}H_{c}>0$
, the cylinder is in an unstable configuration. The point where the two dashed curves intersect the solid curve in figure 3(d) corresponds to the situation that is depicted in figure 3(b). At that point,
$\text{d}F^{v}/\text{d}H_{c}>0$
, the cylinder is in an unstable configuration. The point where the two dashed curves intersect the solid curve in figure 3(d) corresponds to the situation that is depicted in figure 3(b). At that point,
![]() $\text{d}F^{v}/\text{d}H_{c}=0$
, which implies that the cylinder in figure 3(a) has the maximum allowed mass density
$\text{d}F^{v}/\text{d}H_{c}=0$
, which implies that the cylinder in figure 3(a) has the maximum allowed mass density
![]() $D^{\ast }$
for floating.
$D^{\ast }$
for floating.
Figure 3. Cross-sections of two identical circular cylinders (
![]() $D=1.63,R=1$
) at an water–air interface for respective values (a)
$D=1.63,R=1$
) at an water–air interface for respective values (a)
![]() $\unicode[STIX]{x1D6E4}=1$
and (b)
$\unicode[STIX]{x1D6E4}=1$
and (b)
![]() $\unicode[STIX]{x1D6E4}=3/7$
. The loads on both cylinders vanish (
$\unicode[STIX]{x1D6E4}=3/7$
. The loads on both cylinders vanish (
![]() $F_{L}=-F^{v}=0$
). For
$F_{L}=-F^{v}=0$
). For
![]() $\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FC}=1$
and
![]() $\unicode[STIX]{x1D6E4}_{0}=4/7$
, the contact angle
$\unicode[STIX]{x1D6E4}_{0}=4/7$
, the contact angle
![]() $\unicode[STIX]{x1D703}_{b}$
, which is located at contact line
$\unicode[STIX]{x1D703}_{b}$
, which is located at contact line
![]() $b$
, is
$b$
, is
![]() $70.5^{\circ }$
for
$70.5^{\circ }$
for
![]() $\unicode[STIX]{x1D6E4}=3/7$
and
$\unicode[STIX]{x1D6E4}=3/7$
and
![]() $115.4^{\circ }$
for
$115.4^{\circ }$
for
![]() $\unicode[STIX]{x1D6E4}=1$
. The contact angle
$\unicode[STIX]{x1D6E4}=1$
. The contact angle
![]() $\unicode[STIX]{x1D703}_{a}$
, which is located at contact line
$\unicode[STIX]{x1D703}_{a}$
, which is located at contact line
![]() $a$
, is fixed and set equal to
$a$
, is fixed and set equal to
![]() $115.4^{\circ }$
. In (a) the cylinder is positioned higher than in (b) since
$115.4^{\circ }$
. In (a) the cylinder is positioned higher than in (b) since
![]() $F_{T}^{v}$
is larger for
$F_{T}^{v}$
is larger for
![]() $\unicode[STIX]{x1D6E4}=1$
than for
$\unicode[STIX]{x1D6E4}=1$
than for
![]() $\unicode[STIX]{x1D6E4}=3/7$
. Although the water–air interface profiles depicted in (a) are mirror images, the symmetry is broken in (b). In (c) and (d),
$\unicode[STIX]{x1D6E4}=3/7$
. Although the water–air interface profiles depicted in (a) are mirror images, the symmetry is broken in (b). In (c) and (d),
![]() $F^{v}$
is plotted as a function of
$F^{v}$
is plotted as a function of
![]() $H_{c}$
for the respective cylinders depicted in (a) and (b). Movie 1 provides the corresponding cross-sections of (c) and (d). The point where the two dashed lines in (c) intersect the curve corresponds to the situation depicted in (a). At that point,
$H_{c}$
for the respective cylinders depicted in (a) and (b). Movie 1 provides the corresponding cross-sections of (c) and (d). The point where the two dashed lines in (c) intersect the curve corresponds to the situation depicted in (a). At that point,
![]() $\text{d}F^{v}/\text{d}H_{c}<0$
, which shows that the cylinder is in a stable configuration. The point where the two dashed lines intersect the curve in (d) corresponds to the situation that is depicted in (b). At that point,
$\text{d}F^{v}/\text{d}H_{c}<0$
, which shows that the cylinder is in a stable configuration. The point where the two dashed lines intersect the curve in (d) corresponds to the situation that is depicted in (b). At that point,
![]() $\text{d}F^{v}/\text{d}H_{c}=0$
, which implies that the cylinder in (a) has the maximum allowed mass density
$\text{d}F^{v}/\text{d}H_{c}=0$
, which implies that the cylinder in (a) has the maximum allowed mass density
![]() $D^{\ast }$
for floating.
$D^{\ast }$
for floating.
Figure 4(a) shows how
![]() $D^{\ast }(1)$
,
$D^{\ast }(1)$
,
![]() $D^{\ast }(3/7)$
and
$D^{\ast }(3/7)$
and
![]() $Q(3/7)$
vary with
$Q(3/7)$
vary with
![]() $Bo$
. We observe that
$Bo$
. We observe that
![]() $D^{\ast }(1)$
is always larger than
$D^{\ast }(1)$
is always larger than
![]() $D^{\ast }(3/7)$
and that
$D^{\ast }(3/7)$
and that
![]() $Q$
reaches a minimum at
$Q$
reaches a minimum at
![]() $Bo\approx 2.5\times 10^{-2}$
. By fixing
$Bo\approx 2.5\times 10^{-2}$
. By fixing
![]() $\unicode[STIX]{x1D703}_{b}$
to
$\unicode[STIX]{x1D703}_{b}$
to
![]() $115.4^{\circ }$
, we find that (2.39) creates this minimum. The slope of
$115.4^{\circ }$
, we find that (2.39) creates this minimum. The slope of
![]() $Q$
is positive from
$Q$
is positive from
![]() $Bo\approx 2.5\times 10^{-2}$
since surface tension effects vanish for large values of
$Bo\approx 2.5\times 10^{-2}$
since surface tension effects vanish for large values of
![]() $Bo$
. Figure 4(b) provides a contour plot of how
$Bo$
. Figure 4(b) provides a contour plot of how
![]() $Q$
varies with
$Q$
varies with
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $Bo$
. In view of the values of
$Bo$
. In view of the values of
![]() $Q$
in figure 4(a), the maximum value of
$Q$
in figure 4(a), the maximum value of
![]() $\unicode[STIX]{x1D6E4}$
for each contour line is expected at
$\unicode[STIX]{x1D6E4}$
for each contour line is expected at
![]() $Bo\approx 2.5\times 10^{-2}$
. Figure 4(b) shows that
$Bo\approx 2.5\times 10^{-2}$
. Figure 4(b) shows that
![]() $Q>0.6$
for all combinations of
$Q>0.6$
for all combinations of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $Bo$
.
$Bo$
.
Figure 4. (a)
![]() $D^{\ast }(1)$
,
$D^{\ast }(1)$
,
![]() $D^{\ast }(3/7)$
and
$D^{\ast }(3/7)$
and
![]() $Q(3/7)$
as a function of Bond number
$Q(3/7)$
as a function of Bond number
![]() $Bo$
. (b) Contour plot of
$Bo$
. (b) Contour plot of
![]() $Q$
as a function of
$Q$
as a function of
![]() $Bo$
and
$Bo$
and
![]() $\unicode[STIX]{x1D6E4}$
. In (a) and (b), the load is zero (
$\unicode[STIX]{x1D6E4}$
. In (a) and (b), the load is zero (
![]() $F_{L}=-F^{v}=0$
),
$F_{L}=-F^{v}=0$
),
![]() $\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FC}=1$
and
![]() $\unicode[STIX]{x1D6E4}_{0}=4/7$
. Moreover,
$\unicode[STIX]{x1D6E4}_{0}=4/7$
. Moreover,
![]() $Q>0.6$
for all combinations of
$Q>0.6$
for all combinations of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $Bo$
.
$Bo$
.
3.1.2 Implications of the horizontal force analysis
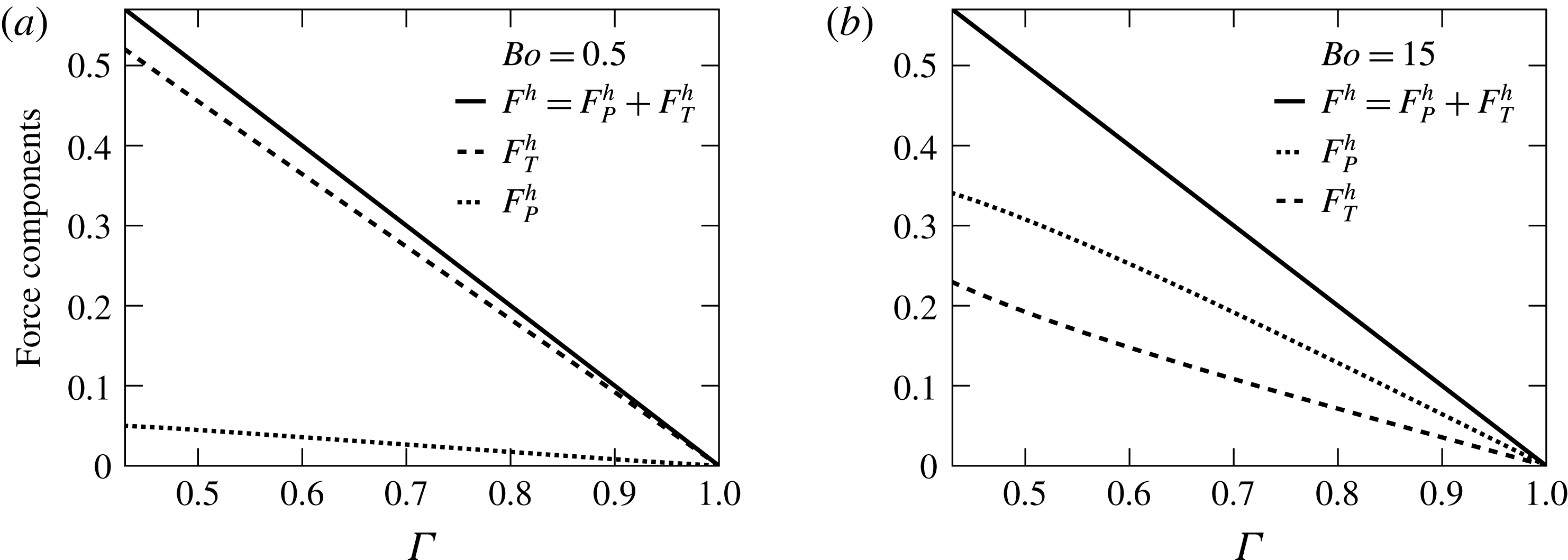
Figure 5. The horizontal force components
![]() $F_{T}^{h}$
,
$F_{T}^{h}$
,
![]() $F_{P}^{h}$
and
$F_{P}^{h}$
and
![]() $F^{h}$
as functions of
$F^{h}$
as functions of
![]() $\unicode[STIX]{x1D6E4}$
for
$\unicode[STIX]{x1D6E4}$
for
![]() $F^{v}=0$
,
$F^{v}=0$
,
![]() $D=0.9$
,
$D=0.9$
,
![]() $\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FC}=1$
and
![]() $\unicode[STIX]{x1D6E4}_{0}=4/7$
. In (a)
$\unicode[STIX]{x1D6E4}_{0}=4/7$
. In (a)
![]() $Bo=0.5$
and in (b)
$Bo=0.5$
and in (b)
![]() $Bo=15$
. Additionally, the contribution of
$Bo=15$
. Additionally, the contribution of
![]() $F_{P}^{h}$
and
$F_{P}^{h}$
and
![]() $F_{T}^{h}$
to
$F_{T}^{h}$
to
![]() $F^{h}$
depends on
$F^{h}$
depends on
![]() $Bo$
and
$Bo$
and
![]() $F^{h}=1-\unicode[STIX]{x1D6E4}$
.
$F^{h}=1-\unicode[STIX]{x1D6E4}$
.
We now investigate how
![]() $F^{h},F_{P}^{h}$
and
$F^{h},F_{P}^{h}$
and
![]() $F_{T}^{h}$
vary with
$F_{T}^{h}$
vary with
![]() $\unicode[STIX]{x1D6E4}$
for
$\unicode[STIX]{x1D6E4}$
for
![]() $F^{v}=0$
, considering two choices,
$F^{v}=0$
, considering two choices,
![]() $Bo=0.5$
and
$Bo=0.5$
and
![]() $Bo=0.15$
, of
$Bo=0.15$
, of
![]() $Bo$
and, taking
$Bo$
and, taking
![]() $D=0.9$
to ensure floating. Figure 5 shows that the contribution of
$D=0.9$
to ensure floating. Figure 5 shows that the contribution of
![]() $F_{P}^{h}$
and
$F_{P}^{h}$
and
![]() $F_{T}^{h}$
to
$F_{T}^{h}$
to
![]() $F^{h}$
depends on
$F^{h}$
depends on
![]() $Bo$
. We also observe that
$Bo$
. We also observe that
![]() $F^{h}$
follows the simple relation
$F^{h}$
follows the simple relation
We now demonstrate that the pivotal relation (3.1) holds for a cylinder of arbitrary cross-sectional shape. First, using (2.34) and (2.35) results in
Substituting (2.43a
) and (2.43b
) in (3.2), we next arrive at (3.1), the dimensional counterpart of which shows that horizontal force
![]() $f^{h}$
induced by
$f^{h}$
induced by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is given by
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is given by
The relations (3.2) and (3.3) show that the surface tension difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry that in addition to the horizontal force due to surface tension creates a horizontal force due to hydrostatic pressure. The sum of these forces, when measured per unit length of the cylinder, is exactly equal to
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry that in addition to the horizontal force due to surface tension creates a horizontal force due to hydrostatic pressure. The sum of these forces, when measured per unit length of the cylinder, is exactly equal to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
and is independent of the vertically applied load. In § 4 we use an energetic argument to show that (3.3) is also valid for a rod-like barrier with cross-sections of variable shape.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
and is independent of the vertically applied load. In § 4 we use an energetic argument to show that (3.3) is also valid for a rod-like barrier with cross-sections of variable shape.
3.2 Amphiphilic Janus cylinder
The surface of a solid is amphiphilic if it consists of two subsurfaces, one hydrophilic and the other hydrophobic. If parts
![]() ${\mathcal{A}}_{1}$
and
${\mathcal{A}}_{1}$
and
![]() ${\mathcal{A}}_{2}$
of the surface of a cylinder of dimensionless radius
${\mathcal{A}}_{2}$
of the surface of a cylinder of dimensionless radius
![]() $R$
, described by respective coordinates
$R$
, described by respective coordinates
![]() $\unicode[STIX]{x1D713}\in [\unicode[STIX]{x1D713}_{c}-\unicode[STIX]{x03C0},\unicode[STIX]{x1D713}_{c}]$
and
$\unicode[STIX]{x1D713}\in [\unicode[STIX]{x1D713}_{c}-\unicode[STIX]{x03C0},\unicode[STIX]{x1D713}_{c}]$
and
![]() $\unicode[STIX]{x1D713}\in [\unicode[STIX]{x1D713}_{c},\unicode[STIX]{x1D713}_{c}+\unicode[STIX]{x03C0}]$
, have different properties, then the cylinder is a symmetric ‘Janus cylinder’. Here, the angle
$\unicode[STIX]{x1D713}\in [\unicode[STIX]{x1D713}_{c},\unicode[STIX]{x1D713}_{c}+\unicode[STIX]{x03C0}]$
, have different properties, then the cylinder is a symmetric ‘Janus cylinder’. Here, the angle
![]() $\unicode[STIX]{x1D713}_{c}$
describes the orientation of the cylinder.
$\unicode[STIX]{x1D713}_{c}$
describes the orientation of the cylinder.
To apply our force analysis to an amphiphilic Janus cylinder, we choose
![]() $\unicode[STIX]{x1D713}_{c}=\unicode[STIX]{x03C0}/2$
,
$\unicode[STIX]{x1D713}_{c}=\unicode[STIX]{x03C0}/2$
,
![]() $Bo=1$
,
$Bo=1$
,
![]() $D=0.5$
,
$D=0.5$
,
![]() $\unicode[STIX]{x1D6E4}=1$
and contact angles
$\unicode[STIX]{x1D6E4}=1$
and contact angles
![]() $\unicode[STIX]{x1D703}_{1}=2\unicode[STIX]{x03C0}/3$
and
$\unicode[STIX]{x1D703}_{1}=2\unicode[STIX]{x03C0}/3$
and
![]() $\unicode[STIX]{x1D703}_{2}=\unicode[STIX]{x03C0}/6$
for the respective subsurfaces
$\unicode[STIX]{x1D703}_{2}=\unicode[STIX]{x03C0}/6$
for the respective subsurfaces
![]() ${\mathcal{A}}_{1}$
and
${\mathcal{A}}_{1}$
and
![]() ${\mathcal{A}}_{2}$
. Figure 6(a) shows the cross-section of the Janus cylinder at a water–air interface for
${\mathcal{A}}_{2}$
. Figure 6(a) shows the cross-section of the Janus cylinder at a water–air interface for
![]() $F_{L}=-F^{v}=0$
. To obtain this result, we proceed as in § 3.1. Using (2.38) and (3.1), we also obtain that a torque of dimensionless magnitude
$F_{L}=-F^{v}=0$
. To obtain this result, we proceed as in § 3.1. Using (2.38) and (3.1), we also obtain that a torque of dimensionless magnitude
![]() $T=1.37$
is generated despite the absence of a horizontal force component (
$T=1.37$
is generated despite the absence of a horizontal force component (
![]() $F^{h}=0$
).
$F^{h}=0$
).

Figure 6. Cross-sections of two identical amphiphilic Janus cylinders (
![]() $D=0.5,R=1$
) at a water–air interface for (a)
$D=0.5,R=1$
) at a water–air interface for (a)
![]() $\unicode[STIX]{x1D6E4}=1$
and (b)
$\unicode[STIX]{x1D6E4}=1$
and (b)
![]() $F_{L}=-F^{v}=0$
. The respective contact angles
$F_{L}=-F^{v}=0$
. The respective contact angles
![]() $\unicode[STIX]{x1D703}_{a}$
and
$\unicode[STIX]{x1D703}_{a}$
and
![]() $\unicode[STIX]{x1D703}_{b}$
are located at the contact lines
$\unicode[STIX]{x1D703}_{b}$
are located at the contact lines
![]() $a$
and
$a$
and
![]() $b$
, and the respective orientations of the cylinder in (a) and (b) are
$b$
, and the respective orientations of the cylinder in (a) and (b) are
![]() $\unicode[STIX]{x1D713}_{c}=\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x1D713}_{c}=\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x1D713}_{c}=0$
. The subsurfaces
$\unicode[STIX]{x1D713}_{c}=0$
. The subsurfaces
![]() ${\mathcal{A}}_{1}$
and
${\mathcal{A}}_{1}$
and
![]() ${\mathcal{A}}_{2}$
on the dark and on the light sides of the cylinders have low (
${\mathcal{A}}_{2}$
on the dark and on the light sides of the cylinders have low (
![]() $\unicode[STIX]{x1D703}_{1}=2\unicode[STIX]{x03C0}/3$
) and high (
$\unicode[STIX]{x1D703}_{1}=2\unicode[STIX]{x03C0}/3$
) and high (
![]() $\unicode[STIX]{x1D703}_{2}=\unicode[STIX]{x03C0}/6$
) degrees of wettability, respectively. Therefore, in (a)
$\unicode[STIX]{x1D703}_{2}=\unicode[STIX]{x03C0}/6$
) degrees of wettability, respectively. Therefore, in (a)
![]() $\unicode[STIX]{x1D703}_{a}=2\unicode[STIX]{x03C0}/3$
and
$\unicode[STIX]{x1D703}_{a}=2\unicode[STIX]{x03C0}/3$
and
![]() $\unicode[STIX]{x1D703}_{b}=\unicode[STIX]{x03C0}/6$
. While the dimensionless torque
$\unicode[STIX]{x1D703}_{b}=\unicode[STIX]{x03C0}/6$
. While the dimensionless torque
![]() $T$
is equal to
$T$
is equal to
![]() $1.37$
in (a) it vanishes in (b). Also,
$1.37$
in (a) it vanishes in (b). Also,
![]() $\unicode[STIX]{x1D703}_{a}=\unicode[STIX]{x03C0}/2=\unicode[STIX]{x1D703}_{b}$
in (b), so that the water–air interface is flat on both sides of the cylinder.
$\unicode[STIX]{x1D703}_{a}=\unicode[STIX]{x03C0}/2=\unicode[STIX]{x1D703}_{b}$
in (b), so that the water–air interface is flat on both sides of the cylinder.
In the process of reducing the magnitude of
![]() $T_{R}$
to zero, the Janus cylinder rotates to ensure that a larger portion of
$T_{R}$
to zero, the Janus cylinder rotates to ensure that a larger portion of
![]() ${\mathcal{A}}_{2}$
contacts the liquid. For
${\mathcal{A}}_{2}$
contacts the liquid. For
![]() $T=0$
and
$T=0$
and
![]() $\unicode[STIX]{x1D713}_{c}=0$
, we use relation (2.46) and find three regimes for which solutions can be found. These regimes correspond to the following alternatives:
$\unicode[STIX]{x1D713}_{c}=0$
, we use relation (2.46) and find three regimes for which solutions can be found. These regimes correspond to the following alternatives:
-
(i)
 $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/6$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/6$
and
 $\unicode[STIX]{x1D713}_{a}\geqslant 0$
,
$\unicode[STIX]{x1D713}_{a}\geqslant 0$
, -
(ii)
 $\unicode[STIX]{x03C0}/6\leqslant \unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}/3$
and
$\unicode[STIX]{x03C0}/6\leqslant \unicode[STIX]{x1D703}\leqslant 2\unicode[STIX]{x03C0}/3$
and
 $\unicode[STIX]{x1D713}_{a}=0$
,
$\unicode[STIX]{x1D713}_{a}=0$
, -
(iii)
 $\unicode[STIX]{x1D703}=2\unicode[STIX]{x03C0}/3$
and
$\unicode[STIX]{x1D703}=2\unicode[STIX]{x03C0}/3$
and
 $\unicode[STIX]{x1D713}_{a}\leqslant 0$
.
$\unicode[STIX]{x1D713}_{a}\leqslant 0$
.
For
![]() $F_{L}=-F^{v}=0$
, we numerically find the solution in the second regime with
$F_{L}=-F^{v}=0$
, we numerically find the solution in the second regime with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, meaning that the water–air interface is flat on both sides of the cylinder, as shown in figure 6(b). Using (2.46) and (2.4), we prove that
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, meaning that the water–air interface is flat on both sides of the cylinder, as shown in figure 6(b). Using (2.46) and (2.4), we prove that
![]() $D=0.5$
for any amphiphilic circular Janus cylinder with
$D=0.5$
for any amphiphilic circular Janus cylinder with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
. Moreover, for a circular cylinder with uniform wetting properties and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
. Moreover, for a circular cylinder with uniform wetting properties and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, the liquid–gas interface is also flat if
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, the liquid–gas interface is also flat if
![]() $D=0.5$
.
$D=0.5$
.
Casagrande et al. (Reference Casagrande, Fabre, Raphaël and Veyssié1989) used an energetic argument to show that
![]() $\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
for amphiphilic Janus beads, with
$\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
for amphiphilic Janus beads, with
![]() $Bo\ll 1$
,
$Bo\ll 1$
,
![]() $\unicode[STIX]{x1D713}_{c}=0$
and
$\unicode[STIX]{x1D713}_{c}=0$
and
![]() $F^{v}=0$
. For an amphiphilic Janus cylinder with
$F^{v}=0$
. For an amphiphilic Janus cylinder with
![]() $Bo\ll 1$
,
$Bo\ll 1$
,
![]() $\unicode[STIX]{x1D713}_{c}=0$
and
$\unicode[STIX]{x1D713}_{c}=0$
and
![]() $F^{v}=0$
, (2.46) reduces to
$F^{v}=0$
, (2.46) reduces to
![]() $\unicode[STIX]{x1D719}\approx 0$
. With (2.4) and
$\unicode[STIX]{x1D719}\approx 0$
. With (2.4) and
![]() $\unicode[STIX]{x1D719}\approx 0$
, we find that
$\unicode[STIX]{x1D719}\approx 0$
, we find that
![]() $\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
, which shows that the result for amphiphilic Janus beads (namely
$\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
, which shows that the result for amphiphilic Janus beads (namely
![]() $\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
) also holds for amphiphilic Janus cylinders.
$\unicode[STIX]{x1D703}\approx \unicode[STIX]{x03C0}/2$
) also holds for amphiphilic Janus cylinders.
4 Energetic argument
Here, we obtain (3.3) with an alternative energetic argument. A single cross-section of a rod with cross-sections of variable shape is depicted in figure 7(a). The rod acts as a barrier between surfactant-free and surfactant-laden interfaces with respective surface tensions
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
. In figure 7(b), the rod is displaced horizontally by an amount
$\unicode[STIX]{x1D6FE}_{b}$
. In figure 7(b), the rod is displaced horizontally by an amount
![]() $\unicode[STIX]{x0394}x$
relative to its position in figure 7(a). Let
$\unicode[STIX]{x0394}x$
relative to its position in figure 7(a). Let
![]() $E_{13}^{(a)}$
and
$E_{13}^{(a)}$
and
![]() $E_{02}^{(b)}$
denote the surface energies, both measured per unit length of the cylinder, of the system in the configurations depicted in figure 7(a) and figure 7(b), respectively. Before and after displacement, the shapes of the liquid–gas interfaces around the rod are identical and the wetting of the rod is the same. Therefore, the surface energy
$E_{02}^{(b)}$
denote the surface energies, both measured per unit length of the cylinder, of the system in the configurations depicted in figure 7(a) and figure 7(b), respectively. Before and after displacement, the shapes of the liquid–gas interfaces around the rod are identical and the wetting of the rod is the same. Therefore, the surface energy
![]() $E_{12}^{(a)}$
measured between 1 and 2 in figure 7(a) is equal to the surface energy
$E_{12}^{(a)}$
measured between 1 and 2 in figure 7(a) is equal to the surface energy
![]() $E_{12}^{(b)}$
measured between 1 and 2 in figure 7(b). The displacement implies that far from the rod, where the both portions of the liquid–gas interface are assumed to be flat, a surfactant-laden interface is created over width
$E_{12}^{(b)}$
measured between 1 and 2 in figure 7(b). The displacement implies that far from the rod, where the both portions of the liquid–gas interface are assumed to be flat, a surfactant-laden interface is created over width
![]() $\unicode[STIX]{x0394}x$
and a surfactant-free interface is consumed over width
$\unicode[STIX]{x0394}x$
and a surfactant-free interface is consumed over width
![]() $\unicode[STIX]{x0394}x$
. The respective energies of these liquid–gas interfaces are
$\unicode[STIX]{x0394}x$
. The respective energies of these liquid–gas interfaces are
![]() $E_{01}^{(b)}$
and
$E_{01}^{(b)}$
and
![]() $E_{23}^{(a)}$
. With
$E_{23}^{(a)}$
. With
![]() $E_{13}^{(a)}=E_{12}^{(a)}+E_{23}^{(a)}$
and
$E_{13}^{(a)}=E_{12}^{(a)}+E_{23}^{(a)}$
and
![]() $E_{02}^{(b)}=E_{01}^{(b)}+E_{12}^{(b)}$
, we express the energy difference
$E_{02}^{(b)}=E_{01}^{(b)}+E_{12}^{(b)}$
, we express the energy difference
![]() $\unicode[STIX]{x0394}E$
between the interfaces depicted in figures 7(a) and 7(b) as
$\unicode[STIX]{x0394}E$
between the interfaces depicted in figures 7(a) and 7(b) as
Furthermore, with
![]() $E_{12}^{(b)}=E_{12}^{(a)}$
,
$E_{12}^{(b)}=E_{12}^{(a)}$
,
![]() $E_{01}^{(b)}=\unicode[STIX]{x1D6FE}_{b}\unicode[STIX]{x0394}x$
and
$E_{01}^{(b)}=\unicode[STIX]{x1D6FE}_{b}\unicode[STIX]{x0394}x$
and
![]() $E_{23}^{(a)}=\unicode[STIX]{x1D6FE}_{a}\unicode[STIX]{x0394}x$
, we see that (4.1) becomes
$E_{23}^{(a)}=\unicode[STIX]{x1D6FE}_{a}\unicode[STIX]{x0394}x$
, we see that (4.1) becomes
from which we conclude that
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces a horizontal force per unit length given by
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces a horizontal force per unit length given by
Relation (4.3) proves that in general, equation (3.3) is valid for a rod-like barrier with cross-sections of variable shape.
Figure 7. (a) Schematic cross-section of a rod-like barrier with cross-sections of variable shape, which lies at a liquid–gas interface and acts as a barrier between a surfactant-free and a surfactant-laden interface. The respective surfaces have surface tensions
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
. (b) The rod displaced over width
$\unicode[STIX]{x1D6FE}_{b}$
. (b) The rod displaced over width
![]() $\unicode[STIX]{x0394}x$
. At points 0, 1, 2 and 3, far away from the rod, the liquid–gas interfaces are flat and located at the same height.
$\unicode[STIX]{x0394}x$
. At points 0, 1, 2 and 3, far away from the rod, the liquid–gas interfaces are flat and located at the same height.
5 Practical implications
5.1 Rove beetle
Certain water walking creatures that are capable of releasing surfactant from their abdominal glands, such as the rove beetle (Stenus comma), exhibit surfactant-driven locomotion at water–air interfaces. The rove beetle supports its entire body on leg parts called tarsi. Each of the six legs has a single tarsus. By modelling the tarsi of such a beetle by a cylinder with a length that is equal to the combined length
![]() $l_{l}$
of the tarsi and by calculating the mass density of the cylinder from the weight
$l_{l}$
of the tarsi and by calculating the mass density of the cylinder from the weight
![]() $w_{b}$
of the beetle, we can use our findings to estimate the load-bearing capacity of the beetle in the absence of hydrodynamic and edge effects. From Betz (Reference Betz2002) we know that typical values for the weight of the beetle and the total length of its tarsi are
$w_{b}$
of the beetle, we can use our findings to estimate the load-bearing capacity of the beetle in the absence of hydrodynamic and edge effects. From Betz (Reference Betz2002) we know that typical values for the weight of the beetle and the total length of its tarsi are
![]() $w_{b}=26~\unicode[STIX]{x03BC}\text{N}$
and
$w_{b}=26~\unicode[STIX]{x03BC}\text{N}$
and
![]() $l_{l}=4.7~\text{mm}$
, and moreover, that
$l_{l}=4.7~\text{mm}$
, and moreover, that
![]() $\unicode[STIX]{x1D703}_{a}=139^{\circ }$
at
$\unicode[STIX]{x1D703}_{a}=139^{\circ }$
at
![]() $\unicode[STIX]{x1D6FE}_{a}=69~\text{mN}~\text{m}^{-1}$
and
$\unicode[STIX]{x1D6FE}_{a}=69~\text{mN}~\text{m}^{-1}$
and
![]() $r=24~\unicode[STIX]{x03BC}\text{m}$
. We assume that the beetle produces a strong surfactant (
$r=24~\unicode[STIX]{x03BC}\text{m}$
. We assume that the beetle produces a strong surfactant (
![]() $\unicode[STIX]{x1D6FE}_{b}\approx 30~\text{mN}~\text{m}^{-1}$
) and that its legs remain hydrophobic (
$\unicode[STIX]{x1D6FE}_{b}\approx 30~\text{mN}~\text{m}^{-1}$
) and that its legs remain hydrophobic (
![]() $\unicode[STIX]{x1D703}_{b}=90^{\circ }$
at
$\unicode[STIX]{x1D703}_{b}=90^{\circ }$
at
![]() $\unicode[STIX]{x1D6FE}_{b}=30~\text{mN}~\text{m}^{-1}$
). It then follows that the load-bearing capacity is
$\unicode[STIX]{x1D6FE}_{b}=30~\text{mN}~\text{m}^{-1}$
). It then follows that the load-bearing capacity is
![]() $25w_{b}$
for a surfactant-free water surface,
$25w_{b}$
for a surfactant-free water surface,
![]() $16w_{b}$
for the tarsi acting as a surfactant barrier between a surfactant-laden interface and surfactant-free interface and
$16w_{b}$
for the tarsi acting as a surfactant barrier between a surfactant-laden interface and surfactant-free interface and
![]() $10w_{b}$
for a surfactant-laden interface. When the beetle walks, only three of its six tarsi might touch the water surface so that the load-bearing capacity is reduced by a factor of two. Since the abdominal glands of the beetle are located at the rear edge of its body, it is reasonable to assume that immediately after surfactant release the surface tension imbalance only acts on the two hind tarsi. With reference to (4.3) we then predict that the acceleration of the beetle is
$10w_{b}$
for a surfactant-laden interface. When the beetle walks, only three of its six tarsi might touch the water surface so that the load-bearing capacity is reduced by a factor of two. Since the abdominal glands of the beetle are located at the rear edge of its body, it is reasonable to assume that immediately after surfactant release the surface tension imbalance only acts on the two hind tarsi. With reference to (4.3) we then predict that the acceleration of the beetle is
![]() $2g$
from rest. Experimental studies that extend the work of Linsenmair & Jander (Reference Linsenmair and Jander1963) would be necessary to confirm our predictions. We anticipate that a deviation may arise from a Marangoni flow as well as from the beetle moving its tarsi immediately subsequent to the release of surfactant.
$2g$
from rest. Experimental studies that extend the work of Linsenmair & Jander (Reference Linsenmair and Jander1963) would be necessary to confirm our predictions. We anticipate that a deviation may arise from a Marangoni flow as well as from the beetle moving its tarsi immediately subsequent to the release of surfactant.
5.2 Acetone droplet in a Leidenfrost state on warm water
To explain self-propulsion of an acetone droplet on warm water, Janssens et al. (Reference Janssens, Koizumi and Fried2017) modelled an acetone droplet as a perfectly non-wetting partly submerged rigid cylinder. By ignoring hydrostatic pressure, they obtained the relation
![]() $f^{h}\approx \unicode[STIX]{x1D6FE}_{a}\cos \unicode[STIX]{x1D719}_{a}-\unicode[STIX]{x1D6FE}_{b}\cos \unicode[STIX]{x1D719}_{b}$
. With the result
$f^{h}\approx \unicode[STIX]{x1D6FE}_{a}\cos \unicode[STIX]{x1D719}_{a}-\unicode[STIX]{x1D6FE}_{b}\cos \unicode[STIX]{x1D719}_{b}$
. With the result
![]() $f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
of our present findings, that relation can both be extended to account for hydrostatic pressure and simplified.
$f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
of our present findings, that relation can both be extended to account for hydrostatic pressure and simplified.
5.3 Surface pressure measurements
From the work of Petty & Barlow (Reference Petty, Barlow and Roberts1990) and the references they cite, the Langmuir balance and the Wilhelmy plate are the two devices which are most often used for measuring a surface tension imbalance. Each of these devices has its own advantages.
A Langmuir balance can be made by detaching the cylinder in figure 1 from the walls of the water bath and connecting it to a force sensor. An accepted strategy for preventing surfactant from leaking through the gap between the walls of the bath and the edges of the cylinder involves connecting thin polytetrafluoroethylene strips to the edges of the cylinder and the bath walls (Albrecht Reference Albrecht1983). The attachment to a force sensor assures that the cylinder is essentially static and makes it possible to measure
![]() $f^{h}l$
, where
$f^{h}l$
, where
![]() $l$
is the length of the cylinder. If the water–air interfaces are assumed to be flat, it is then evident that
$l$
is the length of the cylinder. If the water–air interfaces are assumed to be flat, it is then evident that
![]() $f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. Using this relation, the surface tension difference
$f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. Using this relation, the surface tension difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is obtained with a Langmuir balance. The same expression, namely
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is obtained with a Langmuir balance. The same expression, namely
![]() $f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
, arises from § 3.1.2, while allowing both portions of the liquid–gas interface to be curved. This lends credence to the accuracy of measurements made with Langmuir balances, provided that the length and the width of the liquid bath are much greater than the capillary length determined by the liquid with the highest surface tension.
$f^{h}=\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
, arises from § 3.1.2, while allowing both portions of the liquid–gas interface to be curved. This lends credence to the accuracy of measurements made with Langmuir balances, provided that the length and the width of the liquid bath are much greater than the capillary length determined by the liquid with the highest surface tension.
6 Conclusions
This work focuses on the force and torque analysis of a partly submerged circular cylinder under influence of the surface tension imbalance
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. For a hydrophobic cylinder, the vertical force analysis shows that the load-bearing capacity at a water–air interface is reduced by less than 40 % after introducing a strong surfactant (resulting in a surface tension difference of the order of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. For a hydrophobic cylinder, the vertical force analysis shows that the load-bearing capacity at a water–air interface is reduced by less than 40 % after introducing a strong surfactant (resulting in a surface tension difference of the order of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=40~\text{mN}~\text{m}^{-1}$
) on one side of the cylinder. From the horizontal force analysis, we learn that
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=40~\text{mN}~\text{m}^{-1}$
) on one side of the cylinder. From the horizontal force analysis, we learn that
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry that in addition to the horizontal force due to surface tension creates a horizontal force due to hydrostatic pressure. When measured per unit length cylinder, the sum
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
induces an asymmetry that in addition to the horizontal force due to surface tension creates a horizontal force due to hydrostatic pressure. When measured per unit length cylinder, the sum
![]() $f^{h}$
of these forces is of magnitude
$f^{h}$
of these forces is of magnitude
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. We derive this relation analytically for a cylinder of arbitrary cross-sectional shape by combining the Young–Laplace equation and a relation obtained by Keller (Reference Keller1998). We also consider the force analysis on an amphiphilic Janus cylinder and recover a relation obtained by Princen (Reference Princen and Matijević1969) for the vertical force on a circular cylinder due to surface tension, buoyancy and gravity, in the special case where the surface tension imbalance vanishes, namely for
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
. We derive this relation analytically for a cylinder of arbitrary cross-sectional shape by combining the Young–Laplace equation and a relation obtained by Keller (Reference Keller1998). We also consider the force analysis on an amphiphilic Janus cylinder and recover a relation obtained by Princen (Reference Princen and Matijević1969) for the vertical force on a circular cylinder due to surface tension, buoyancy and gravity, in the special case where the surface tension imbalance vanishes, namely for
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=0$
. In addition to our force and torque analysis, we use an energetic argument to show that the magnitude of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=0$
. In addition to our force and torque analysis, we use an energetic argument to show that the magnitude of
![]() $f^{h}$
is equal to
$f^{h}$
is equal to
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
for a rod-like barrier with cross-sections of variable shape. Finally, we discuss practical implications of the analysis for Marangoni propulsion and surface pressure measurements.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
for a rod-like barrier with cross-sections of variable shape. Finally, we discuss practical implications of the analysis for Marangoni propulsion and surface pressure measurements.
Acknowledgements
We thank D. Vázquez-Cortés and K. Toda-Peters for their help with the fabrication of the acrylic glass water bath and we acknowledge the constructive comments and the helpful suggestions of the anonymous referees. We also gratefully acknowledge support from the Okinawa Institute of Science and Technology Graduate University with subsidy funding from the Cabinet Office, Government of Japan.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2017.537.