Article contents
Flow around an inclined circular disk
Published online by Cambridge University Press: 31 July 2018
Abstract
Direct numerical simulations are performed for the uniform flow around an inclined circular disk. The diameter–thickness aspect ratio (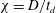 $\unicode[STIX]{x1D712}=D/t_{d}$) of the disk is 50 and the inclination angle (
$\unicode[STIX]{x1D712}=D/t_{d}$) of the disk is 50 and the inclination angle ( $\unicode[STIX]{x1D6FC}$) is considered over the range of
$\unicode[STIX]{x1D6FC}$) is considered over the range of 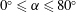 $0^{\circ }\leqslant \unicode[STIX]{x1D6FC}\leqslant 80^{\circ }$, where
$0^{\circ }\leqslant \unicode[STIX]{x1D6FC}\leqslant 80^{\circ }$, where 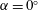 $\unicode[STIX]{x1D6FC}=0^{\circ }$ refers to the condition where the flow is normal to the disk. The Reynolds number (
$\unicode[STIX]{x1D6FC}=0^{\circ }$ refers to the condition where the flow is normal to the disk. The Reynolds number (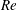 $\mathit{Re}$), based on the short axis of projection in the streamwise direction, is defined as
$\mathit{Re}$), based on the short axis of projection in the streamwise direction, is defined as 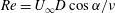 $\mathit{Re}=U_{\infty }D\cos \unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D708}$, where
$\mathit{Re}=U_{\infty }D\cos \unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D708}$, where 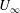 $U_{\infty }$ is the velocity of the flow and
$U_{\infty }$ is the velocity of the flow and  $\unicode[STIX]{x1D708}$ is the kinematic viscosity.
$\unicode[STIX]{x1D708}$ is the kinematic viscosity. 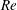 $\mathit{Re}$ is investigated over the range of 50
$\mathit{Re}$ is investigated over the range of 50 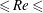 ${\leqslant}\mathit{Re}\leqslant$ 300. In the considered
${\leqslant}\mathit{Re}\leqslant$ 300. In the considered 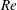 $\mathit{Re}$–
$\mathit{Re}$– $\unicode[STIX]{x1D6FC}$ parametric space, five states are observed and denoted as: (I) steady state (SS); (II) periodic state (PS); (III) periodic state with a low frequency modulation (PSL); (IV) quasi-periodic state (QP) and (V) chaotic state (CS). Both
$\unicode[STIX]{x1D6FC}$ parametric space, five states are observed and denoted as: (I) steady state (SS); (II) periodic state (PS); (III) periodic state with a low frequency modulation (PSL); (IV) quasi-periodic state (QP) and (V) chaotic state (CS). Both 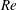 $\mathit{Re}$ and
$\mathit{Re}$ and  $\unicode[STIX]{x1D6FC}$ affect the bifurcation mechanism. The bifurcating sequence occurring at
$\unicode[STIX]{x1D6FC}$ affect the bifurcation mechanism. The bifurcating sequence occurring at 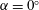 $\unicode[STIX]{x1D6FC}=0^{\circ }$ is generally observed over the whole
$\unicode[STIX]{x1D6FC}=0^{\circ }$ is generally observed over the whole 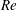 $\mathit{Re}$–
$\mathit{Re}$– $\unicode[STIX]{x1D6FC}$ space, although it is advanced at small
$\unicode[STIX]{x1D6FC}$ space, although it is advanced at small  $\unicode[STIX]{x1D6FC}$ and delayed at large
$\unicode[STIX]{x1D6FC}$ and delayed at large  $\unicode[STIX]{x1D6FC}$. The advancement of thresholds for different states is due to the effects introduced by inclination, which tend to select the plane of symmetry for the wake in order to regulate the wake and intensify some flow features. Nevertheless, the bifurcations are still in the dominant position when leading a state without stable symmetry, i.e. the planar symmetry could not be recovered by small
$\unicode[STIX]{x1D6FC}$. The advancement of thresholds for different states is due to the effects introduced by inclination, which tend to select the plane of symmetry for the wake in order to regulate the wake and intensify some flow features. Nevertheless, the bifurcations are still in the dominant position when leading a state without stable symmetry, i.e. the planar symmetry could not be recovered by small  $\unicode[STIX]{x1D6FC}$. These phenomena are further discussed with respect to the vortex shedding patterns behind the disk. Furthermore, for any fixed disk, the wake behaviour is only associated with that found in the steady vertical state of a freely falling disk. The fully coupled fluid–body system is fundamentally different from the fixed cases.
$\unicode[STIX]{x1D6FC}$. These phenomena are further discussed with respect to the vortex shedding patterns behind the disk. Furthermore, for any fixed disk, the wake behaviour is only associated with that found in the steady vertical state of a freely falling disk. The fully coupled fluid–body system is fundamentally different from the fixed cases.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
These authors contributed equally to this work.
References
- 34
- Cited by


