Thermodynamic fluctuations of pressure, density, temperature or entropy 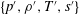 $\{p^{\prime },\unicode[STIX]{x1D70C}^{\prime },T^{\prime },s^{\prime }\}$ in compressible aerodynamic turbulence, although generated by the flow, are fundamentally related to one another by the thermodynamic equation of state. Ratios between non-dimensional root-mean-square (r.m.s.) levels (
$\{p^{\prime },\unicode[STIX]{x1D70C}^{\prime },T^{\prime },s^{\prime }\}$ in compressible aerodynamic turbulence, although generated by the flow, are fundamentally related to one another by the thermodynamic equation of state. Ratios between non-dimensional root-mean-square (r.m.s.) levels (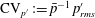 $\text{CV}_{p^{\prime }}:=\bar{p}^{-1}\,p_{rms}^{\prime }$,
$\text{CV}_{p^{\prime }}:=\bar{p}^{-1}\,p_{rms}^{\prime }$, 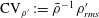 $\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}:=\bar{\unicode[STIX]{x1D70C}}^{-1}\,\unicode[STIX]{x1D70C}_{rms}^{\prime }$,
$\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}:=\bar{\unicode[STIX]{x1D70C}}^{-1}\,\unicode[STIX]{x1D70C}_{rms}^{\prime }$, 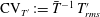 $\text{CV}_{T^{\prime }}:=\bar{T}^{-1}\,T_{rms}^{\prime }$), along with all possible 2-moment correlation coefficients
$\text{CV}_{T^{\prime }}:=\bar{T}^{-1}\,T_{rms}^{\prime }$), along with all possible 2-moment correlation coefficients 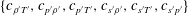 $\{c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }},c_{p^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{p^{\prime }T^{\prime }},c_{s^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{s^{\prime }T^{\prime }},c_{s^{\prime }p^{\prime }}\}$, represent, in the sense of Bradshaw (Annu. Rev. Fluid Mech., vol. 9, 1977, pp. 33–54), the thermodynamic turbulence structure of the flow. We use direct numerical simulation (DNS) data, both for plane channel flow and for sustained homogeneous isotropic turbulence, to determine the range of validity of the leading-order, formally
$\{c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }},c_{p^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{p^{\prime }T^{\prime }},c_{s^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{s^{\prime }T^{\prime }},c_{s^{\prime }p^{\prime }}\}$, represent, in the sense of Bradshaw (Annu. Rev. Fluid Mech., vol. 9, 1977, pp. 33–54), the thermodynamic turbulence structure of the flow. We use direct numerical simulation (DNS) data, both for plane channel flow and for sustained homogeneous isotropic turbulence, to determine the range of validity of the leading-order, formally 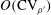 $O(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }})$, approximations of the exact relations between thermodynamic turbulence structure parameters. Available DNS data are mapped on the
$O(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }})$, approximations of the exact relations between thermodynamic turbulence structure parameters. Available DNS data are mapped on the 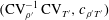 $(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}^{-1}\,\text{CV}_{T^{\prime }},c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }})$-plane and their loci, identified using the leading-order approximations, highlight specific behaviour for different flows or flow regions. For the particular case of sustained compressible homogeneous isotropic turbulence, it is shown that the DNS data collapse onto a single curve corresponding to
$(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}^{-1}\,\text{CV}_{T^{\prime }},c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }})$-plane and their loci, identified using the leading-order approximations, highlight specific behaviour for different flows or flow regions. For the particular case of sustained compressible homogeneous isotropic turbulence, it is shown that the DNS data collapse onto a single curve corresponding to 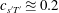 $c_{s^{\prime }T^{\prime }}\approxeq 0.2$ (for air flow), while the approximation
$c_{s^{\prime }T^{\prime }}\approxeq 0.2$ (for air flow), while the approximation 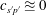 $c_{s^{\prime }p^{\prime }}\approxeq 0$ fits reasonably well wall turbulence DNS data, providing building blocks towards the construction of simple phenomenological models.
$c_{s^{\prime }p^{\prime }}\approxeq 0$ fits reasonably well wall turbulence DNS data, providing building blocks towards the construction of simple phenomenological models.
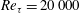 $Re_{\unicode[STIX]{x1D70F}}=20\,000$
$Re_{\unicode[STIX]{x1D70F}}=20\,000$