Article contents
Flow-induced vibration of D-section cylinders: an afterbody is not essential for vortex-induced vibration
Published online by Cambridge University Press: 20 July 2018
Abstract
While it has been known that an afterbody (i.e. the structural part of a bluff body downstream of the flow separation points) plays an important role affecting the wake characteristics and even may change the nature of the flow-induced vibration (FIV) of a structure, the question of whether an afterbody is essential for the occurrence of one particular common form of FIV, namely vortex-induced vibration (VIV), still remains. This has motivated the present study to experimentally investigate the FIV of an elastically mounted forward- or backward-facing D-section (closed semicircular) cylinder over the reduced velocity range 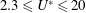 $2.3\leqslant U^{\ast }\leqslant 20$, where
$2.3\leqslant U^{\ast }\leqslant 20$, where 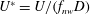 $U^{\ast }=U/(f_{nw}D)$. Here,
$U^{\ast }=U/(f_{nw}D)$. Here, 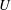 $U$ is the free-stream velocity,
$U$ is the free-stream velocity, 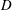 $D$ the cylinder diameter and
$D$ the cylinder diameter and 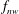 $f_{nw}$ the natural frequency of the system in quiescent fluid (water). The normal orientation with the body’s flat surface facing upstream is known to be subject to another common form of FIV, galloping, while the reverse D-section with the body’s curved surface facing upstream, due to the lack of an afterbody, has previously been reported to be immune to VIV. The fluid–structure system was modelled on a low-friction air-bearing system in conjunction with a recirculating water channel facility to achieve a low mass ratio (defined as the ratio of the total oscillating mass to that of the displaced fluid mass). Interestingly, through a careful overall examination of the dynamic responses, including the vibration amplitude and frequency, fluid forces and phases, our new findings showed that the D-section exhibits a VIV-dominated response for
$f_{nw}$ the natural frequency of the system in quiescent fluid (water). The normal orientation with the body’s flat surface facing upstream is known to be subject to another common form of FIV, galloping, while the reverse D-section with the body’s curved surface facing upstream, due to the lack of an afterbody, has previously been reported to be immune to VIV. The fluid–structure system was modelled on a low-friction air-bearing system in conjunction with a recirculating water channel facility to achieve a low mass ratio (defined as the ratio of the total oscillating mass to that of the displaced fluid mass). Interestingly, through a careful overall examination of the dynamic responses, including the vibration amplitude and frequency, fluid forces and phases, our new findings showed that the D-section exhibits a VIV-dominated response for 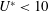 $U^{\ast }<10$, galloping-dominated response for
$U^{\ast }<10$, galloping-dominated response for 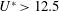 $U^{\ast }>12.5$, and a transition regime with a VIV–galloping interaction in between. Also observed for the first time were interesting wake modes associated with these response regimes. However, in contrast to previous studies at high Reynolds number (defined by
$U^{\ast }>12.5$, and a transition regime with a VIV–galloping interaction in between. Also observed for the first time were interesting wake modes associated with these response regimes. However, in contrast to previous studies at high Reynolds number (defined by 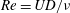 $Re=UD/\unicode[STIX]{x1D708}$, with
$Re=UD/\unicode[STIX]{x1D708}$, with  $\unicode[STIX]{x1D708}$ the kinematic viscosity), which have showed that the D-section was subject to ‘hard’ galloping that required a substantial initial amplitude to trigger, it was observed in the present study that the D-section can gallop softly from rest. Surprisingly, on the other hand, it was found that the reverse D-section exhibits pure VIV features. Remarkable similarities were observed in a direct comparison with a circular cylinder of the same mass ratio, in terms of the onset
$\unicode[STIX]{x1D708}$ the kinematic viscosity), which have showed that the D-section was subject to ‘hard’ galloping that required a substantial initial amplitude to trigger, it was observed in the present study that the D-section can gallop softly from rest. Surprisingly, on the other hand, it was found that the reverse D-section exhibits pure VIV features. Remarkable similarities were observed in a direct comparison with a circular cylinder of the same mass ratio, in terms of the onset 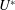 $U^{\ast }$ of significant vibration, the peak amplitude (only approximately 6 % less than that of the circular cylinder), and also the fluid forces and phases. Of most significance, this study shows that an afterbody is not essential for VIV at low mass and damping ratios.
$U^{\ast }$ of significant vibration, the peak amplitude (only approximately 6 % less than that of the circular cylinder), and also the fluid forces and phases. Of most significance, this study shows that an afterbody is not essential for VIV at low mass and damping ratios.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Zhao et al. supplementary movie 1
Phase-averaged vorticity contours showing 2S mode at U*=3.4 for the case of α=0°.
Zhao et al. supplementary movie 2
Phase-averaged vorticity contours showing 2S mode at U*=4.0 for the case of α=0°.
Zhao et al. supplementary movie 3
Phase-averaged vorticity contours showing 2Po mode at U*=5.0 for the case of α=0°.
Zhao et al. supplementary movie 4
Phase-averaged vorticity contours showing 2To mode at U*=6.0 for the case of α=0°.
Zhao et al. supplementary movie 5
Phase-averaged vorticity contours showing 2To mode at U*=6.3 for the case of α=0°.
Zhao et al. supplementary movie 6
Phase-averaged vorticity contours showing 2To mode at U*=8.0 for the case of α=0°.
Zhao et al. supplementary movie 7
Phase-averaged vorticity contours showing 2T mode at U*=12.0 for the case of α=0°.
Zhao et al. supplementary movie 8
Phase-averaged vorticity contours showing 2T-C mode at U*=6.0 for the case of α=0°.
Zhao et al. supplementary movie 9
Phase-averaged vorticity contours showing 2S mode at U*=4.0 for the case of α=180°.
- 84
- Cited by


