Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-17T16:48:24.926Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of the seam in the swing of a cricket ball

Published online by Cambridge University Press:  19 July 2018

Rahul Deshpande Open the ORCID record for Rahul Deshpande [Opens in a new window] ,
Ravi Shakya  and
Sanjay Mittal Open the ORCID record for Sanjay Mittal [Opens in a new window]
Rahul Deshpande
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP, India 208016 National Wind Tunnel Facility, Indian Institute of Technology Kanpur, UP, India 208016
Ravi Shakya
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP, India 208016 National Wind Tunnel Facility, Indian Institute of Technology Kanpur, UP, India 208016
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP, India 208016 National Wind Tunnel Facility, Indian Institute of Technology Kanpur, UP, India 208016
*
†Email address for correspondence: smittal@iitk.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The role of the seam in the ‘swing’ of a cricket ball is investigated via unsteady force and surface-pressure measurements and oil-flow visualization in a low-turbulence wind tunnel. Various seam angles of the ball and flow speeds are considered. Static tests are carried out on a new ‘SG Test’ cricket ball as well as its idealized models: a smooth sphere with one and five trips. To study the effect of surface roughness of the ball as the game progresses, force measurements are also carried out on a cricket ball that is manually roughened, on one-half and completely, to model a ball that has been in play for approximately 40 overs (240 deliveries/balls). The Reynolds number (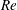$Re$) is based on the free-stream speed and diameter of the respective model. A new cricket ball experiences three flow states with increase in 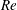$Re$: no swing (NS), conventional swing (CS) and reverse swing (RS). At relatively low 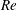$Re$, in the NS regime, the seam does not have any significant effect on the flow. The separation of the laminar boundary layer, with no subsequent reattachment, is almost axisymmetric with respect to the free-stream flow. Therefore, the ball does not experience any significant lateral force. Beyond a certain 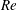$Re$, the boundary layer on the seam side of the ball undergoes transition. The boundary layer on the non-seam side, however, continues to undergo a laminar separation with no reattachment, thereby creating a lateral force in the direction of the seam, leading to CS. The onset of the CS regime is marked by intermittent formation of a laminar separation bubble (LSB) on the surface of the ball in the region between the laminar separation of the boundary layer and its reattachment at a downstream location. Owing to the varying azimuthal location of the seam, with respect to the front stagnation point on the ball, the transition via LSB formation is localized to a specific region over the seam side. In other regions, the boundary layer either transitions directly without the formation of an LSB, or separates on encountering the seam with no further reattachment. The spatial extent of the region where the flow directly transitions to a turbulent state increases with increase in 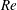$Re$, while that of the LSB decreases. Interestingly, the flow dynamics is such that the magnitude of the swing force coefficient stays relatively constant with increase in 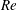$Re$. With further increase in 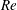$Re$, the boundary layer on the non-seam side undergoes a transition via formation of an LSB. This, along with an upstream shift of the separation point on the seam side, leads to a switch in the direction of the lateral force. It now acts away from the seam, and leads to RS. The transition from CS to RS occurs over a very narrow range of 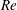$Re$ wherein the flow intermittently switches between the two flow states. It is observed that the transition of the boundary layer on the seam side leads to an upstream shift of the separation point on the non-seam side at the onset of CS. A complementary effect is observed at the onset of RS. Experiments on a ball that is manually roughened bring out the relative effect of the seam and roughness on the transition of the boundary layer. Compared to a new ball, the magnitude of the maximum swing force coefficient for a rough ball is smaller during the CS regime, and larger during the RS regime. Unlike other models, the ball with roughened non-seam side and smooth seam side, for certain seam orientations, exhibits RS at relatively lower speeds and CS at higher speeds. The forces measured on the cricket ball are utilized to estimate the trajectory of the ball bowled at various initial speeds and seam angles. The lateral movement of the ball depends very significantly on the seam angle, surface roughness and speed of the ball at its delivery. The maximum lateral deviation of a new ball during RS is found to be less than half of that observed in CS. On the other hand, the lateral movement of a roughened ball during RS may significantly exceed its movement during CS. The range of the speed of the ball, for various seam orientations and surface roughnesses, are estimated wherein it undergoes CS, RS or one followed by the other. Optimal conditions are estimated for the desired lateral movement of the ball.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer separation Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 50 - 82
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1972 Experiments on the flow past spheres at very high Reynolds numbers. J. Fluid Mech. 54 (03), 565–575.Google Scholar
Achenbach, E. 1974 The effects of surface roughness and tunnel blockage on the flow past spheres. J. Fluid Mech. 65 (01), 113–125.Google Scholar
Anderson, J. D. 1991 Fundamentals of Aerodynamics. McGraw-Hill.Google Scholar
Baker, C. J. 2010 A calculation of cricket ball trajectories. Proc. Inst. Mech. Engrs C 224 (9), 1947–1958.Google Scholar
Barton, N. G. 1982 On the swing of a cricket ball in flight. Proc. R. Soc. London A 379, 109–131.Google Scholar
Bentley, K., Varty, P., Proudlove, M. & Mehta, R. D.1982 An experimental study of cricket ball swing. Aero Tech. Note, Imperial College, pp. 82–106.Google Scholar
Cadot, O., Desai, A., Mittal, S., Saxena, S. & Chandra, B. 2015 Statistics and dynamics of the boundary layer reattachments during the drag crisis transitions of a circular cylinder. Phys. Fluids 27 (1), 014101.Google Scholar
Deshpande, R., Kanti, V., Desai, A. & Mittal, S. 2017 Intermittency of laminar separation bubble on a sphere during drag crisis. J. Fluid Mech. 812, 815–840.Google Scholar
Igarashi, T. 1986 Effect of tripping wires on the flow around a circular cylinder normal to an airstream. Bull. JSME 29 (255), 2917–2924.Google Scholar
Imbrosciano, A.1981 The swing of a cricket ball. Proj. Rep. 810714, Newcastle College of Advanced Education.Google Scholar
Kim, J., Choi, H., Park, H. & Yoo, J. Y. 2014 Inverse Magnus effect on a rotating sphere: when and why. J. Fluid Mech. 754, R2.Google Scholar
Maxworthy, T. 1969 Experiments on the flow around a sphere at high Reynolds numbers. Trans. ASME J. Appl. Mech. 36 (3), 598–607.Google Scholar
Mehta, R. D. 1985 Aerodynamics of sports balls. Annu. Rev. Fluid Mech. 17 (1), 151–189.Google Scholar
Mehta, R. D. 2005 An overview of cricket ball swing. Sports Engng 8 (4), 181–192.Google Scholar
Mehta, R. D. 2014 Fluid Mechanics of Cricket Ball Swing. In 19th Australasian Fluid Mechanics Conference.Google Scholar
Mehta, R. D., Bentley, K., Proudlove, M. & Varty, P. 1983 Factors affecting cricket ball swing. Nature 303, 787–788.Google Scholar
Norman, A. K., Kerrigan, E. C. & McKeon, B. J. 2011 The effect of small-amplitude time-dependent changes to the surface morphology of a sphere. J. Fluid Mech. 675, 268–296.Google Scholar
Norman, A. K. & McKeon, B. J. 2008 Effect of sting size on the wake of a sphere at subcritical Reynolds numbers. In AIAA 8th Fluid Dyn. Conf. and Exhibit. AIAA 2008-4237.Google Scholar
Norman, A. K. & McKeon, B. J. 2011 Unsteady force measurements in sphere flow from subcritical to supercritical Reynolds numbers. Exp. Fluids 51 (5), 1439–1453.Google Scholar
Scobie, J. A., Pickering, S. G., Almond, D. P. & Lock, G. D. 2012 Fluid dynamics of cricket ball swing. Proc. Inst. Mech. Engrs P 227 (3), 196–208.Google Scholar
Sherwin, K. & Sproston, J. L. 1982 Aerodynamics of a cricket ball. Int. J. Mech. Educ 10 (7), 1–79.Google Scholar
Singh, S. P. & Mittal, S. 2005 Flow past a cylinder: shear layer instability and drag crisis. Intl J. Numer. Meth. Fluids 47 (1), 75–98.Google Scholar
Son, K., Choi, J., Jeon, W.-P. & Choi, H. 2010 Effect of free-stream turbulence on the flow over a sphere. Phys. Fluids 22 (4), 045101.Google Scholar
Son, K., Choi, J., Jeon, W.-P. & Choi, H. 2011 Mechanism of drag reduction by a surface trip wire on a sphere. J. Fluid Mech. 672, 411–427.Google Scholar
Suryanarayana, G. K., Pauer, H. & Meier, G. E. A. 1993 Bluff-body drag reduction by passive ventilation. Exp. Fluids 16 (2), 73–81.Google Scholar
Suryanarayana, G. K. & Prabhu, A. 2000 Effect of natural ventilation on the boundary layer separation and near-wake vortex shedding characteristics of a sphere. Exp. Fluids 29 (6), 582–591.Google Scholar
Taneda, S. 1978 Visual observations of the flow past a sphere at Reynolds numbers between 104 and 106 . J. Fluid Mech. 85 (01), 187–192.Google Scholar
Wieselsberger, C. 1914 Der luftwiderstand von kugeln. Z. Flugtechnik Motorluftschiffahrt 5, 140–145.Google Scholar
Wieselsberger, C. 1922 Neuere feststellungen über die gesetze des flüssigkeits- und luftwiderstandes. Phys. Z. 22 (11), 321–328.Google Scholar