Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Citro, V.
Tchoufag, J.
Fabre, D.
Giannetti, F.
and
Luchini, P.
2016.
Linear stability and weakly nonlinear analysis of the flow past rotating spheres.
Journal of Fluid Mechanics,
Vol. 807,
Issue. ,
p.
62.
Rajamuni, Methma M.
Thompson, Mark C.
and
Hourigan, Kerry
2018.
Vortex-induced vibration of a transversely rotating sphere.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
786.
Nagata, T.
Nonomura, T.
Takahashi, S.
Mizuno, Y.
and
Fukuda, K.
2018.
Direct numerical simulation of flow past a transversely rotating sphere up to a Reynolds number of 300 in compressible flow.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
878.
Auguste, Franck
and
Magnaudet, Jacques
2018.
Path oscillations and enhanced drag of light rising spheres.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
228.
Sareen, A.
Zhao, J.
Lo Jacono, D.
Sheridan, J.
Hourigan, K.
and
Thompson, M. C.
2018.
Vortex-induced vibration of a rotating sphere.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
p.
258.
Neeraj, M.P.
and
Tiwari, Shaligram
2018.
Wake characteristics of a sphere performing streamwise rotary oscillations.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
485.
Rajamuni, Methma M.
Thompson, Mark C.
and
Hourigan, Kerry
2019.
Vortex-induced vibration of elastically-mounted spheres: A comparison of the response of three degrees of freedom and one degree of freedom systems.
Journal of Fluids and Structures,
Vol. 89,
Issue. ,
p.
142.
Manelil, Neeraj P.
and
Tiwari, Shaligram
2019.
Wake characteristics of a sphere performing transverse rotary oscillations.
European Journal of Mechanics - B/Fluids,
Vol. 77,
Issue. ,
p.
148.
Shi, Pengyu
and
Rzehak, Roland
2019.
Lift forces on solid spherical particles in unbounded flows.
Chemical Engineering Science,
Vol. 208,
Issue. ,
p.
115145.
Lorite-Díez, M.
and
Jiménez-González, J. I.
2020.
Description of the transitional wake behind a strongly streamwise rotating sphere.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Rajamuni, Methma M.
Thompson, Mark C.
and
Hourigan, Kerry
2020.
Vortex dynamics and vibration modes of a tethered sphere.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Rajamuni, Methma M.
Thompson, Mark C.
and
Hourigan, Kerry
2020.
Efficient FSI solvers for multiple-degrees-of-freedom flow-induced vibration of a rigid body.
Computers & Fluids,
Vol. 196,
Issue. ,
p.
104340.
Hu, Ruifeng
and
Tang, Hui
2020.
An elliptic foil rotating in uniform low-Reynolds-number flows.
Fluid Dynamics Research,
Vol. 52,
Issue. 5,
p.
055509.
Rastello, Marie
and
Marié, Jean-Louis
2020.
Wake behind contaminated bubbles in a solid-body rotating flow.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Yang, Xianyu
Cai, Jihua
Jiang, Guosheng
Xie, Jingyu
Shi, Yanping
Chen, Shuya
Yue, Ye
Yu, Lang
He, Yichao
and
Xie, Kunzhi
2020.
Nanoparticle plugging prediction of shale pores: A numerical and experimental study.
Energy,
Vol. 208,
Issue. ,
p.
118337.
Yin, Guang
and
Ong, Muk Chen
2020.
On the wake flow behind a sphere in a pipe flow at low Reynolds numbers.
Physics of Fluids,
Vol. 32,
Issue. 10,
Chandel, A.
and
Das, S. P.
2021.
Wake of transversely rotating and translating sphere in quiescent water at low Reynolds number.
Acta Mechanica,
Vol. 232,
Issue. 3,
p.
949.
Thompson, Mark C.
Leweke, Thomas
and
Hourigan, Kerry
2021.
Bluff Bodies and Wake–Wall Interactions.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
347.
Pantokratoras, Asterios
2021.
Lift, drag and torque on a rotating sphere in a stream of non-Newtonian power-law fluid.
Rheologica Acta,
Vol. 60,
Issue. 4,
p.
175.
Sahoo, Bapuji
Sarkar, Subharthi
Sivakumar, R.
and
Sekhar, T.V.S.
2021.
On the numerical capture of Taylor column phenomena in rotating viscous fluid.
European Journal of Mechanics - B/Fluids,
Vol. 89,
Issue. ,
p.
126.
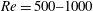 $\mathit{Re}=500{-}1000$ is directly simulated using an unstructured finite volume collocated code. The effect of rotation rate on the flow is studied by increasing the dimensionless rotation rate,
$\mathit{Re}=500{-}1000$ is directly simulated using an unstructured finite volume collocated code. The effect of rotation rate on the flow is studied by increasing the dimensionless rotation rate, 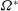 ${\it\Omega}^{\ast }$ , from 0 to 1.20, where
${\it\Omega}^{\ast }$ , from 0 to 1.20, where 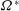 ${\it\Omega}^{\ast }$ is the maximum sphere surface velocity normalised by the free stream velocity. This study investigates the marked unsteadiness of the flow structures at
${\it\Omega}^{\ast }$ is the maximum sphere surface velocity normalised by the free stream velocity. This study investigates the marked unsteadiness of the flow structures at 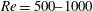 $\mathit{Re}=500{-}1000$ . Comparison with previous numerical data (Giacobello et al., J. Fluid Mech., vol. 621, 2009, pp. 103–130; Kim, J. Mech. Sci. Technol., vol. 23, 2009, pp. 578–589) reveals a new flow regime, namely a ‘shear layer–stable foci’ regime, besides the widely reported ‘vortex shedding’ and ‘shear layer instability’ regimes. The ‘shear layer–stable foci’ regime is observed at
$\mathit{Re}=500{-}1000$ . Comparison with previous numerical data (Giacobello et al., J. Fluid Mech., vol. 621, 2009, pp. 103–130; Kim, J. Mech. Sci. Technol., vol. 23, 2009, pp. 578–589) reveals a new flow regime, namely a ‘shear layer–stable foci’ regime, besides the widely reported ‘vortex shedding’ and ‘shear layer instability’ regimes. The ‘shear layer–stable foci’ regime is observed at 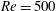 $\mathit{Re}=500$ and
$\mathit{Re}=500$ and 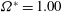 ${\it\Omega}^{\ast }=1.00$ ;
${\it\Omega}^{\ast }=1.00$ ; 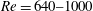 $\mathit{Re}=640{-}1000$ and
$\mathit{Re}=640{-}1000$ and 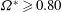 ${\it\Omega}^{\ast }\geqslant 0.80$ . In this flow regime, the shear layer on the advancing side of the sphere (where the sphere surface velocity vector opposes the free stream velocity) shortens significantly while fluid from the retreating side (opposite to the advancing side) is drawn towards the mid-plane normal to the peripheral velocity. This results in the formation of a stable focus near the onset of the shear layer instability. This stable focus becomes more pronounced with increasing
${\it\Omega}^{\ast }\geqslant 0.80$ . In this flow regime, the shear layer on the advancing side of the sphere (where the sphere surface velocity vector opposes the free stream velocity) shortens significantly while fluid from the retreating side (opposite to the advancing side) is drawn towards the mid-plane normal to the peripheral velocity. This results in the formation of a stable focus near the onset of the shear layer instability. This stable focus becomes more pronounced with increasing 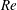 $\mathit{Re}$ and
$\mathit{Re}$ and 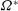 ${\it\Omega}^{\ast }$ . It increases the oscillation magnitude and decreases the oscillation frequency of the hydrodynamic forces.
${\it\Omega}^{\ast }$ . It increases the oscillation magnitude and decreases the oscillation frequency of the hydrodynamic forces.

