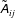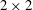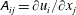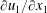1. Introduction
The fine scales of turbulence are primarily characterised by the velocity gradient tensor (VGT), which can be split into a symmetric and skew-symmetric tensor as follows:
with the scalar analogues to strain rate (
![]() $\unicode[STIX]{x1D61A}_{ij}$
) and rotation (
$\unicode[STIX]{x1D61A}_{ij}$
) and rotation (
![]() ${\it\Omega}_{ij}$
) being dissipation (
${\it\Omega}_{ij}$
) being dissipation (
![]() ${\it\epsilon}$
) and enstrophy (
${\it\epsilon}$
) and enstrophy (
![]() ${\it\omega}^{2}$
) respectively. In the Richardson–Kolmogorov phenomenology the dissipative (Kolmogorov) length scale is defined from the mean rate of dissipation within a flow and thus the VGT can be considered to provide one of the few rigid definitions of ‘scales’ within the energy cascade (Tsinober Reference Tsinober2009). The fluctuation of enstrophy is a characterising feature of turbulent flows (Tennekes & Lumley Reference Tennekes and Lumley1972) and it is used, for example, as a threshold quantity to distinguish between turbulent and non-turbulent fluid in free shear flows, e.g. Bisset, Hunt & Rogers (Reference Bisset, Hunt and Rogers2002) and da Silva & Pereira (Reference da Silva and Pereira2008). For further details an excellent review of the phenomena of the VGT can be found in Meneveau (Reference Meneveau2011).
${\it\omega}^{2}$
) respectively. In the Richardson–Kolmogorov phenomenology the dissipative (Kolmogorov) length scale is defined from the mean rate of dissipation within a flow and thus the VGT can be considered to provide one of the few rigid definitions of ‘scales’ within the energy cascade (Tsinober Reference Tsinober2009). The fluctuation of enstrophy is a characterising feature of turbulent flows (Tennekes & Lumley Reference Tennekes and Lumley1972) and it is used, for example, as a threshold quantity to distinguish between turbulent and non-turbulent fluid in free shear flows, e.g. Bisset, Hunt & Rogers (Reference Bisset, Hunt and Rogers2002) and da Silva & Pereira (Reference da Silva and Pereira2008). For further details an excellent review of the phenomena of the VGT can be found in Meneveau (Reference Meneveau2011).
The Navier–Stokes equations can be re-formulated to reveal the dynamics of the strain-rate tensor and the rotation tensor as follows:
where
![]() $s_{i}$
are the (three) eigenvalues of
$s_{i}$
are the (three) eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
with corresponding eigenvectors
$\unicode[STIX]{x1D61A}_{ij}$
with corresponding eigenvectors
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
,
$\boldsymbol{e}_{\boldsymbol{i}}$
,
![]() $\hat{\cdot }$
implies a unit vector and repetition of the subscript
$\hat{\cdot }$
implies a unit vector and repetition of the subscript
![]() $i$
implies summation.
$i$
implies summation.
The strain-rate eigenvalues
![]() $s_{i}$
can be ordered such that
$s_{i}$
can be ordered such that
![]() $s_{1}\geqslant s_{2}\geqslant s_{3}$
with
$s_{1}\geqslant s_{2}\geqslant s_{3}$
with
![]() $s_{1}\geqslant 0$
(extensive) and
$s_{1}\geqslant 0$
(extensive) and
![]() $s_{3}\leqslant 0$
(compressive). Continuity for an incompressible fluid requires that
$s_{3}\leqslant 0$
(compressive). Continuity for an incompressible fluid requires that
![]() $s_{1}+s_{2}+s_{3}=0$
and thus the intermediate eigenvalue,
$s_{1}+s_{2}+s_{3}=0$
and thus the intermediate eigenvalue,
![]() $s_{2}$
, is either mildly extensive or compressive but bounded by the magnitudes of
$s_{2}$
, is either mildly extensive or compressive but bounded by the magnitudes of
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{3}$
. In this way Betchov (Reference Betchov1956) explains that the topological evolution of a fluid element is determined by the sign of
$s_{3}$
. In this way Betchov (Reference Betchov1956) explains that the topological evolution of a fluid element is determined by the sign of
![]() $s_{2}$
, with
$s_{2}$
, with
![]() $s_{2}>0$
implying two orthogonal extensive strain rates and a further orthogonal compressive strain rate leading to the formation of ‘sheet-like structures’ and
$s_{2}>0$
implying two orthogonal extensive strain rates and a further orthogonal compressive strain rate leading to the formation of ‘sheet-like structures’ and
![]() $s_{2}<0$
implying two orthogonal compressive strain rates in conjunction with a further orthogonal extensive strain rate leading to the formation of ‘tube-like’ structures. It has since been observed that the interaction between strain rate and rotation is characterised by a surprising (considering that
$s_{2}<0$
implying two orthogonal compressive strain rates in conjunction with a further orthogonal extensive strain rate leading to the formation of ‘tube-like’ structures. It has since been observed that the interaction between strain rate and rotation is characterised by a surprising (considering that
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle >0$
) preferential parallel alignment between the vorticity vector and the intermediate strain-rate eigenvector, i.e.
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle >0$
) preferential parallel alignment between the vorticity vector and the intermediate strain-rate eigenvector, i.e.
![]() $(\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{{\bf\omega}})^{2}\approx 1$
in (1.4) (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Tanahashi, Iwase & Miyauchi Reference Tanahashi, Iwase and Miyauchi2001; Mullin & Dahm Reference Mullin and Dahm2006), although it has subsequently been shown that the
$(\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{{\bf\omega}})^{2}\approx 1$
in (1.4) (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Tanahashi, Iwase & Miyauchi Reference Tanahashi, Iwase and Miyauchi2001; Mullin & Dahm Reference Mullin and Dahm2006), although it has subsequently been shown that the
![]() $(\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{{\bf\omega}})^{2}$
alignment is more significant in determining the sign of
$(\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{{\bf\omega}})^{2}$
alignment is more significant in determining the sign of
![]() ${\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}$
(Buxton & Ganapathisubramani Reference Buxton and Ganapathisubramani2010).
${\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}$
(Buxton & Ganapathisubramani Reference Buxton and Ganapathisubramani2010).
A full topological classification of the flow, defined in terms of the strain rate and rotation and their inviscid source/sink terms, can be achieved by examination of the invariants of the characteristic equation for the VGT (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990):
The first invariant is equal to the negative of the trace of the VGT (
![]() $P=-\unicode[STIX]{x1D608}_{ii}$
) which is equivalent to the divergence of the flow field and is thus zero for an incompressible flow. The state of fluid elements within a turbulent flow is thus described by the second invariant
$P=-\unicode[STIX]{x1D608}_{ii}$
) which is equivalent to the divergence of the flow field and is thus zero for an incompressible flow. The state of fluid elements within a turbulent flow is thus described by the second invariant
![]() $Q=(\Vert {\it\Omega}_{ij}\Vert ^{2}-\Vert \unicode[STIX]{x1D61A}_{ij}\Vert ^{2})/2$
, which represents the local excess of rotation over strain rate, and the third invariant
$Q=(\Vert {\it\Omega}_{ij}\Vert ^{2}-\Vert \unicode[STIX]{x1D61A}_{ij}\Vert ^{2})/2$
, which represents the local excess of rotation over strain rate, and the third invariant
![]() $R$
, which is defined as the negative of the determinant of
$R$
, which is defined as the negative of the determinant of
![]() $\unicode[STIX]{x1D608}_{ij}$
, thus
$\unicode[STIX]{x1D608}_{ij}$
, thus
![]() $R=(-\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki}-(3/4){\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j})/3$
is the local excess of self-amplification of strain rate over amplification of enstrophy. In
$R=(-\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki}-(3/4){\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j})/3$
is the local excess of self-amplification of strain rate over amplification of enstrophy. In
![]() $P$
–
$P$
–
![]() $Q$
–
$Q$
–
![]() $R$
space the discriminant surface that separates purely real roots to (1.5) from one real root and a complex-conjugate pair of roots is
$R$
space the discriminant surface that separates purely real roots to (1.5) from one real root and a complex-conjugate pair of roots is
and thus for incompressible flows
![]() $(P=0)$
the discriminant can be given by
$(P=0)$
the discriminant can be given by
![]() ${\it\Delta}=Q^{3}+(27/4)R^{2}$
. When
${\it\Delta}=Q^{3}+(27/4)R^{2}$
. When
![]() ${\it\Delta}<0$
only real eigenvalues exist and the flow is purely straining whereas when
${\it\Delta}<0$
only real eigenvalues exist and the flow is purely straining whereas when
![]() ${\it\Delta}>0$
the fluid is swirling (Perry & Chong Reference Perry and Chong1994). The joint probability density function (p.d.f.) of the second and third invariants produces a distinct, characteristic ‘tear drop’ shape which is considered to be ‘universal’ for fully developed turbulent flows (Elsinga & Marusic Reference Elsinga and Marusic2010). The line for
${\it\Delta}>0$
the fluid is swirling (Perry & Chong Reference Perry and Chong1994). The joint probability density function (p.d.f.) of the second and third invariants produces a distinct, characteristic ‘tear drop’ shape which is considered to be ‘universal’ for fully developed turbulent flows (Elsinga & Marusic Reference Elsinga and Marusic2010). The line for
![]() ${\it\Delta}=0$
acts as an attractor, giving the ‘Vieillefosse tail’ (Vieillefosse Reference Vieillefosse1982) which can be seen in the bottom right quadrant of figure 1.
${\it\Delta}=0$
acts as an attractor, giving the ‘Vieillefosse tail’ (Vieillefosse Reference Vieillefosse1982) which can be seen in the bottom right quadrant of figure 1.

Figure 1. Joint probability density function (p.d.f.) between
![]() $Q$
and
$Q$
and
![]() $R$
for the mixing layer data of the present study. Contours scale logarithmically. The ‘teardrop’ shape is considered to be a ‘universal’ property for all fully developed turbulent flows.
$R$
for the mixing layer data of the present study. Contours scale logarithmically. The ‘teardrop’ shape is considered to be a ‘universal’ property for all fully developed turbulent flows.
Invariants can also be computed for the strain-rate and rotation tensors individually. For an incompressible flow both tensors have zero trace (the rotation tensor is skew symmetric and thus has no trace by definition), hence
![]() $P_{S}=-\unicode[STIX]{x1D61A}_{ii}=-\unicode[STIX]{x1D608}_{ii}=0$
and
$P_{S}=-\unicode[STIX]{x1D61A}_{ii}=-\unicode[STIX]{x1D608}_{ii}=0$
and
![]() $P_{{\it\Omega}}=-{\it\Omega}_{ii}=0$
and the determinant of the rotation tensor is zero meaning that
$P_{{\it\Omega}}=-{\it\Omega}_{ii}=0$
and the determinant of the rotation tensor is zero meaning that
![]() $R_{{\it\Omega}}=0$
. The remaining invariants are given by
$R_{{\it\Omega}}=0$
. The remaining invariants are given by
![]() $Q_{S}=-(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij})/2$
,
$Q_{S}=-(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij})/2$
,
![]() $R_{S}=-(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki})/3$
and
$R_{S}=-(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki})/3$
and
![]() $Q_{{\it\Omega}}=({\it\Omega}_{ij}{\it\Omega}_{ij})/2$
(the strain or rotation parts of the invariants of the VGT). The second strain-rate and rotation matrix invariants are given physical meaning in the following equations:
$Q_{{\it\Omega}}=({\it\Omega}_{ij}{\it\Omega}_{ij})/2$
(the strain or rotation parts of the invariants of the VGT). The second strain-rate and rotation matrix invariants are given physical meaning in the following equations:
Despite the wealth of information that can be extracted from the VGT in a developed turbulent flow it is only relatively recently that experimental techniques, such as holographic particle image velocimetry (PIV) (Zhang, Tao & Katz Reference Zhang, Tao and Katz1997) or tomographic PIV (Elsinga et al.
Reference Elsinga, Scarano, Wieneke and van Oudheusden2006) have developed the capability to produce the three-dimensional, three-component (3D3C) data that are required. However, limitations in the spatial resolution and signal to noise ratio for these techniques are still a significant hindrance to studying the kinematics of the VGT. Additionally, it is not possible to acquire 3D3C data in real time with present technology levels (either experimentally or numerically). Thus to formulate a model of the VGT, that can act as the observed state in a closed-loop feedback controller to ‘control’ velocity gradient phenomena (such as dissipation, for example) it is necessary to place bounds upon such phenomena from 2D2C data which can be acquired in real time. An example of an experiment capable of acquiring such data would be two offset ‘X-wire’ CTA (constant temperature anemometry) probes used in conjunction with Taylor’s frozen flow field hypothesis (Taylor Reference Taylor1938b
). For these reasons Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) explored the invariants of the reduced VGT,
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
, which is defined as a
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
, which is defined as a
![]() $2\times 2$
matrix extracted from the full VGT, and is thus comprised of 2D2C data that are readily obtainable in a laboratory experiment. For convenience Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) consider the upper left
$2\times 2$
matrix extracted from the full VGT, and is thus comprised of 2D2C data that are readily obtainable in a laboratory experiment. For convenience Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) consider the upper left
![]() $2\times 2$
block of the full VGT (velocity components
$2\times 2$
block of the full VGT (velocity components
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
in the
$u_{2}$
in the
![]() $x_{1}{-}x_{2}$
plane).
$x_{1}{-}x_{2}$
plane).
Using an approach in which 2D2C data were used to describe three-dimensional topological features of high-Reynolds-number, fine-scale turbulence, the recently published study of Fiscaletti, Westerweel & Elsinga (Reference Fiscaletti, Westerweel and Elsinga2014) made use of the reduced VGT to demonstrate the topology of intense dissipation and enstrophy in a high-Reynolds-number (
![]() $\mathit{Re}_{{\it\lambda}}=349$
) axisymmetric jet with excellent spatial resolution. They made use of microscopic, planar PIV experiments (purely two-dimensional data) to show the tendency for regions of high dissipation to be distributed as sheet-like structures surrounding the perimeter of high-enstrophy tubes at a characteristic offset that scales with the Kolmogorov length scale. These results are in agreement with the scalings derived in much lower Reynolds number 3D3C simulations/experiments (e.g. Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993 and Mullin & Dahm Reference Mullin and Dahm2006) and thus demonstrate the capability to infer fully three-dimensional topological velocity gradient information from the reduced VGT.
$\mathit{Re}_{{\it\lambda}}=349$
) axisymmetric jet with excellent spatial resolution. They made use of microscopic, planar PIV experiments (purely two-dimensional data) to show the tendency for regions of high dissipation to be distributed as sheet-like structures surrounding the perimeter of high-enstrophy tubes at a characteristic offset that scales with the Kolmogorov length scale. These results are in agreement with the scalings derived in much lower Reynolds number 3D3C simulations/experiments (e.g. Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993 and Mullin & Dahm Reference Mullin and Dahm2006) and thus demonstrate the capability to infer fully three-dimensional topological velocity gradient information from the reduced VGT.
The characteristic equation for the reduced VGT is given as
where
![]() $p$
and
$p$
and
![]() $q$
are the first and second invariants respectively. Unlike its 3D counterpart, the first invariant of the reduced VGT,
$q$
are the first and second invariants respectively. Unlike its 3D counterpart, the first invariant of the reduced VGT,
![]() $p=-\text{tr}(\tilde{\unicode[STIX]{x1D63C}})$
, is usually non-zero in an incompressible flow (if
$p=-\text{tr}(\tilde{\unicode[STIX]{x1D63C}})$
, is usually non-zero in an incompressible flow (if
![]() $\text{tr}(\unicode[STIX]{x1D608}_{ij})=0$
,
$\text{tr}(\unicode[STIX]{x1D608}_{ij})=0$
,
![]() $\text{tr}(\tilde{\unicode[STIX]{x1D608}_{ij}})=0$
only when
$\text{tr}(\tilde{\unicode[STIX]{x1D608}_{ij}})=0$
only when
![]() $\unicode[STIX]{x1D608}_{33}=0$
) and so the 2D projection of an incompressible 3D flow appears compressible. The invariant
$\unicode[STIX]{x1D608}_{33}=0$
) and so the 2D projection of an incompressible 3D flow appears compressible. The invariant
![]() $p$
determines the stability of the flow locally, with regions for which
$p$
determines the stability of the flow locally, with regions for which
![]() $p<0$
being unstable when perturbed (Perry & Chong Reference Perry and Chong1987). The second invariant is computed as
$p<0$
being unstable when perturbed (Perry & Chong Reference Perry and Chong1987). The second invariant is computed as
![]() $q=\text{det}(\tilde{\unicode[STIX]{x1D63C}})$
. Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) showed that the joint p.d.f. of the invariants of the reduced VGT has been found to also produce a characteristic ‘teapot’ shape for a number of turbulent flows, with the discriminant
$q=\text{det}(\tilde{\unicode[STIX]{x1D63C}})$
. Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) showed that the joint p.d.f. of the invariants of the reduced VGT has been found to also produce a characteristic ‘teapot’ shape for a number of turbulent flows, with the discriminant
![]() $\tilde{{\it\Delta}}=(p^{2}-q)/4=0$
also acting as an attractor, as in the 3D case. When
$\tilde{{\it\Delta}}=(p^{2}-q)/4=0$
also acting as an attractor, as in the 3D case. When
![]() $\tilde{{\it\Delta}}>0$
the reduced system has two real, distinct eigenvalues and critical points in the flow will produce nodes or saddles; whilst when
$\tilde{{\it\Delta}}>0$
the reduced system has two real, distinct eigenvalues and critical points in the flow will produce nodes or saddles; whilst when
![]() $\tilde{{\it\Delta}}<0$
they will form foci (Perry & Chong Reference Perry and Chong1987).
$\tilde{{\it\Delta}}<0$
they will form foci (Perry & Chong Reference Perry and Chong1987).
Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) were able to derive a number of important statistical results by using the assumption of local homogeneity, namely they showed that
![]() $\langle p\rangle =0$
and
$\langle p\rangle =0$
and
![]() $\langle q\rangle =0$
. Further, they are able to show that
$\langle q\rangle =0$
. Further, they are able to show that
![]() $\langle pq\rangle <0$
which is shown to follow mathematically from the observation that
$\langle pq\rangle <0$
which is shown to follow mathematically from the observation that
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle >0$
since under the further assumption of local isotropy
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle >0$
since under the further assumption of local isotropy
![]() $\langle pq\rangle =-\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle /15$
. Finally, by consideration of the eigenvalues of the reduced strain-rate tensor (
$\langle pq\rangle =-\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle /15$
. Finally, by consideration of the eigenvalues of the reduced strain-rate tensor (
![]() $\tilde{s}_{i}$
) they are able to show that for a limited number of points within the flow, namely
$\tilde{s}_{i}$
) they are able to show that for a limited number of points within the flow, namely
![]() $\tilde{s}_{1}>\tilde{s}_{2}>0$
and
$\tilde{s}_{1}>\tilde{s}_{2}>0$
and
![]() $\tilde{s}_{2}<\tilde{s}_{1}<0$
then the sign of the intermediate strain-rate eigenvalue (
$\tilde{s}_{2}<\tilde{s}_{1}<0$
then the sign of the intermediate strain-rate eigenvalue (
![]() $s_{2}$
) can be inferred and thus whether the fluid is undergoing ‘sheet-forming’ or ‘tube-forming’ topological evolution. This manuscript makes further progress by seeking more rigid bounds on 3D VGT quantities, such as
$s_{2}$
) can be inferred and thus whether the fluid is undergoing ‘sheet-forming’ or ‘tube-forming’ topological evolution. This manuscript makes further progress by seeking more rigid bounds on 3D VGT quantities, such as
![]() $s_{2}$
, from their counterparts in the reduced VGT. Additionally the instantaneous variation of these VGT quantities with their 3D VGT counterparts will be considered as this is a vital step in the formulation of a model of the VGT to close the feedback loop in which the reduced VGT plays the role of the observed state.
$s_{2}$
, from their counterparts in the reduced VGT. Additionally the instantaneous variation of these VGT quantities with their 3D VGT counterparts will be considered as this is a vital step in the formulation of a model of the VGT to close the feedback loop in which the reduced VGT plays the role of the observed state.
2. Invariants of the full and reduced VGT
By using the assumptions of homogeneity and local isotropy Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) were able to derive the following relations:
We follow the convention of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) and choose to define the reduced VGT as the upper left-hand
![]() $2\times 2$
block of the VGT, i.e. gradients of
$2\times 2$
block of the VGT, i.e. gradients of
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
in the
$u_{2}$
in the
![]() $x_{1}{-}x_{2}$
plane. This choice is arbitrary and we subsequently discuss the choice of the interrogation plane for the formation of the VGT in § 7. The invariants of the reduced VGT can thus be expressed as
$x_{1}{-}x_{2}$
plane. This choice is arbitrary and we subsequently discuss the choice of the interrogation plane for the formation of the VGT in § 7. The invariants of the reduced VGT can thus be expressed as
![]() $p=-\text{tr}(\tilde{\unicode[STIX]{x1D608}}_{ij})=-(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})$
and
$p=-\text{tr}(\tilde{\unicode[STIX]{x1D608}}_{ij})=-(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})$
and
![]() $q=\text{det}(\tilde{\unicode[STIX]{x1D608}}_{ij})=\unicode[STIX]{x1D608}_{11}\unicode[STIX]{x1D608}_{22}-\unicode[STIX]{x1D608}_{12}\unicode[STIX]{x1D608}_{21}$
. Rewriting the second and third invariants of the full VGT,
$q=\text{det}(\tilde{\unicode[STIX]{x1D608}}_{ij})=\unicode[STIX]{x1D608}_{11}\unicode[STIX]{x1D608}_{22}-\unicode[STIX]{x1D608}_{12}\unicode[STIX]{x1D608}_{21}$
. Rewriting the second and third invariants of the full VGT,
![]() $Q$
and
$Q$
and
![]() $R$
respectively, we thus obtain
$R$
respectively, we thus obtain
![]() $R$
, on the other hand, is a sum of triple velocity gradient products and reveals the local excess of inviscid strain-rate amplification over enstrophy amplification. These terms are not present in the dynamics of two-dimensional turbulence, with the only mechanism by which enstrophy changes in time being via the direct action of viscosity (Batchelor Reference Batchelor1969). This is reflected in (2.4) in which no decoupling of the terms of the reduced VGT and those not captured in the reduced VGT is possible with the exception of the first term,
$R$
, on the other hand, is a sum of triple velocity gradient products and reveals the local excess of inviscid strain-rate amplification over enstrophy amplification. These terms are not present in the dynamics of two-dimensional turbulence, with the only mechanism by which enstrophy changes in time being via the direct action of viscosity (Batchelor Reference Batchelor1969). This is reflected in (2.4) in which no decoupling of the terms of the reduced VGT and those not captured in the reduced VGT is possible with the exception of the first term,
![]() $-pq$
, the mean of which is shown to predict
$-pq$
, the mean of which is shown to predict
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
under the assumption of isotropy in (2.2).
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
under the assumption of isotropy in (2.2).
3. Relationship between the full and reduced strain-rate tensors
We now re-write the strain-rate tensor,
![]() $\unicode[STIX]{x1D61A}_{ij}$
, as
$\unicode[STIX]{x1D61A}_{ij}$
, as
 $$\begin{eqnarray}\unicode[STIX]{x1D61A}_{ij}:=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D608}_{11} & \unicode[STIX]{x1D60B}_{12} & \unicode[STIX]{x1D60B}_{13}\\ \unicode[STIX]{x1D60B}_{12} & \unicode[STIX]{x1D608}_{22} & \unicode[STIX]{x1D60B}_{23}\\ \unicode[STIX]{x1D60B}_{13} & \unicode[STIX]{x1D60B}_{23} & -(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D61A}_{ij}:=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D608}_{11} & \unicode[STIX]{x1D60B}_{12} & \unicode[STIX]{x1D60B}_{13}\\ \unicode[STIX]{x1D60B}_{12} & \unicode[STIX]{x1D608}_{22} & \unicode[STIX]{x1D60B}_{23}\\ \unicode[STIX]{x1D60B}_{13} & \unicode[STIX]{x1D60B}_{23} & -(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})\end{array}\right)\end{eqnarray}$$
and, following Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013), the reduced strain-rate tensor
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is taken to be the upper-left
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is taken to be the upper-left
![]() $2\times 2$
block of
$2\times 2$
block of
![]() $\unicode[STIX]{x1D61A}_{ij}$
, that is,
$\unicode[STIX]{x1D61A}_{ij}$
, that is,
Recall that the eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
are denoted
$\unicode[STIX]{x1D61A}_{ij}$
are denoted
![]() $s_{i}$
(with corresponding eigenvectors
$s_{i}$
(with corresponding eigenvectors
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
) and are assumed to be ordered
$\boldsymbol{e}_{\boldsymbol{i}}$
) and are assumed to be ordered
![]() $s_{1}\geqslant s_{2}\geqslant s_{3}$
, while the eigenvalues
$s_{1}\geqslant s_{2}\geqslant s_{3}$
, while the eigenvalues
![]() $\tilde{s}_{i}$
(and corresponding eigenvectors
$\tilde{s}_{i}$
(and corresponding eigenvectors
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
) of the reduced strain-rate tensor
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
) of the reduced strain-rate tensor
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
are assumed to satisfy
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
are assumed to satisfy
![]() $\tilde{s}_{1}\geqslant \tilde{s}_{2}$
, although no strict sign condition may be placed upon them. The purpose of this section is to discuss to what extent information on the eigenvalues/eigenvectors of
$\tilde{s}_{1}\geqslant \tilde{s}_{2}$
, although no strict sign condition may be placed upon them. The purpose of this section is to discuss to what extent information on the eigenvalues/eigenvectors of
![]() $\unicode[STIX]{x1D61A}_{ij}$
can be determined, given that
$\unicode[STIX]{x1D61A}_{ij}$
can be determined, given that
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is known.
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is known.
3.1. Eigenvalue bounds
Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) showed that the sign of the intermediate eigenvalue
![]() $s_{2}$
can be determined when the two reduced eigenvalues have the same sign: if
$s_{2}$
can be determined when the two reduced eigenvalues have the same sign: if
![]() $0<\tilde{s}_{2}\leqslant \tilde{s}_{1}$
, then
$0<\tilde{s}_{2}\leqslant \tilde{s}_{1}$
, then
![]() $s_{2}>0$
; while if
$s_{2}>0$
; while if
![]() $\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
it follows that
$\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
it follows that
![]() $s_{2}<0$
. Whilst interesting from the point of view that the sign of
$s_{2}<0$
. Whilst interesting from the point of view that the sign of
![]() $s_{2}$
determines whether the flow is locally ‘sheet-forming’ or ‘tube-forming’, such a result does not place any bounds upon the magnitude of
$s_{2}$
determines whether the flow is locally ‘sheet-forming’ or ‘tube-forming’, such a result does not place any bounds upon the magnitude of
![]() $s_{2}$
, nor give any information regarding the remaining eigenvalues
$s_{2}$
, nor give any information regarding the remaining eigenvalues
![]() $s_{1},s_{3}$
.
$s_{1},s_{3}$
.
To provide such information, observe that since
![]() $\unicode[STIX]{x1D61A}_{ij}$
is symmetric it follows from Horn & Johnson (Reference Horn and Johnson2013, Theorem 4.3.17), that the eigenvalues of the two matrices are ‘interlaced’, namely,
$\unicode[STIX]{x1D61A}_{ij}$
is symmetric it follows from Horn & Johnson (Reference Horn and Johnson2013, Theorem 4.3.17), that the eigenvalues of the two matrices are ‘interlaced’, namely,
It is immediate that the result of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) follows from the central pair of inequalities
![]() $\tilde{s}_{2}\leqslant s_{2}\leqslant \tilde{s}_{1}$
. Interestingly, (3.3) requires only the fact that
$\tilde{s}_{2}\leqslant s_{2}\leqslant \tilde{s}_{1}$
. Interestingly, (3.3) requires only the fact that
![]() $\unicode[STIX]{x1D61A}_{ij}$
is symmetric, whereas the proof presented in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) requires the assumption of incompressibility. Furthermore, in addition to determining the sign of
$\unicode[STIX]{x1D61A}_{ij}$
is symmetric, whereas the proof presented in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) requires the assumption of incompressibility. Furthermore, in addition to determining the sign of
![]() $s_{2}$
, (3.3) now enables bounds to be placed upon the remaining eigenvalues of
$s_{2}$
, (3.3) now enables bounds to be placed upon the remaining eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
.
$\unicode[STIX]{x1D61A}_{ij}$
.
If we additionally assume that the flow is incompressible we can show that
where
![]() $\boldsymbol{k}$
is a unit vector in the
$\boldsymbol{k}$
is a unit vector in the
![]() $x_{3}$
direction. Now, the Rayleigh–Ritz theorem (Horn & Johnson Reference Horn and Johnson2013) states that the maximum and minimum eigenvalues of
$x_{3}$
direction. Now, the Rayleigh–Ritz theorem (Horn & Johnson Reference Horn and Johnson2013) states that the maximum and minimum eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
provide upper and lower bounds for the quantity
$\unicode[STIX]{x1D61A}_{ij}$
provide upper and lower bounds for the quantity
![]() $\sup \{v_{i}\unicode[STIX]{x1D61A}_{ij}v_{j}:v^{2}=1\}$
. Consequently,
$\sup \{v_{i}\unicode[STIX]{x1D61A}_{ij}v_{j}:v^{2}=1\}$
. Consequently,
Combining (3.3) and (3.5), we can infer the following information regarding the eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
from the reduced strain-rate tensor
$\unicode[STIX]{x1D61A}_{ij}$
from the reduced strain-rate tensor
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
:
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
:
Hence, incompressibility provides an improved bound on
![]() $s_{3}$
when
$s_{3}$
when
![]() $2\tilde{s}_{2}+\tilde{s}_{1}>0$
, and an improved bound upon
$2\tilde{s}_{2}+\tilde{s}_{1}>0$
, and an improved bound upon
![]() $s_{1}$
when
$s_{1}$
when
![]() $2\tilde{s}_{1}+\tilde{s}_{2}<0$
. We now derive asymmetric bounds such that, for example, if
$2\tilde{s}_{1}+\tilde{s}_{2}<0$
. We now derive asymmetric bounds such that, for example, if
![]() $\tilde{s}_{1}<0$
then, by (3.6),
$\tilde{s}_{1}<0$
then, by (3.6),
![]() $s_{1}\geqslant -(\tilde{s}_{1}+\tilde{s}_{2})\geqslant -2\tilde{s}_{1}$
. These bounds, which are specific examples of the more general (3.6), are summarised as follows:
$s_{1}\geqslant -(\tilde{s}_{1}+\tilde{s}_{2})\geqslant -2\tilde{s}_{1}$
. These bounds, which are specific examples of the more general (3.6), are summarised as follows:
It is important to emphasise that the bounds on the eigenvalues shown in (3.6) were proven using only the facts that
![]() $\unicode[STIX]{x1D61A}_{ij}$
is symmetric and trace-free, that is, that the velocities were sampled from an incompressible flow. It is only the particular form of the distributions within these bounds which captures the intricacies of the flow physics.
$\unicode[STIX]{x1D61A}_{ij}$
is symmetric and trace-free, that is, that the velocities were sampled from an incompressible flow. It is only the particular form of the distributions within these bounds which captures the intricacies of the flow physics.
3.2. Invariants of the full and reduced strain-rate tensor
As discussed in § 1, the invariants
![]() $Q=(\Vert {\it\Omega}_{ij}\Vert -\Vert \unicode[STIX]{x1D61A}_{ij}\Vert )/2$
and
$Q=(\Vert {\it\Omega}_{ij}\Vert -\Vert \unicode[STIX]{x1D61A}_{ij}\Vert )/2$
and
![]() $R=(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki}-(3/4){\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j})/3$
of the VGT are convenient tools with which to describe the instantaneous flow topology. Since the invariants of the strain-rate tensor are given by
$R=(\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{jk}\unicode[STIX]{x1D61A}_{ki}-(3/4){\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j})/3$
of the VGT are convenient tools with which to describe the instantaneous flow topology. Since the invariants of the strain-rate tensor are given by
it is clear that evaluating these invariants has direct implications for the behaviour of the full VGT. Furthermore, the first reduced strain-rate invariant determines the dissipation of kinetic energy due to viscous friction as illustrated in (1.7).
It is therefore of interest to discuss the extent to which
![]() $Q_{S}$
and
$Q_{S}$
and
![]() $R_{S}$
can be estimated, given that the reduced strain-rate tensor
$R_{S}$
can be estimated, given that the reduced strain-rate tensor
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is known. Analogously to the VGT, the reduced invariants of
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
is known. Analogously to the VGT, the reduced invariants of
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
are defined to be the coefficients of its characteristic polynomial
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
are defined to be the coefficients of its characteristic polynomial
Since the full invariants can be expressed in terms of the eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
as
$\unicode[STIX]{x1D61A}_{ij}$
as
it appears that
![]() $Q_{S}$
and
$Q_{S}$
and
![]() $q_{S}$
are likely to be most closely related. Indeed, the bounds identified in (3.6) allow
$q_{S}$
are likely to be most closely related. Indeed, the bounds identified in (3.6) allow
![]() $Q_{S}$
to be estimated in terms of
$Q_{S}$
to be estimated in terms of
![]() $q_{S}$
.
$q_{S}$
.
To this end, suppose first that
![]() $q_{S}\leqslant 0$
. Then, by (3.6),
$q_{S}\leqslant 0$
. Then, by (3.6),
![]() $s_{3}\leqslant \tilde{s}_{2}\leqslant 0\leqslant \tilde{s}_{1}\leqslant s_{1}$
and it follows that
$s_{3}\leqslant \tilde{s}_{2}\leqslant 0\leqslant \tilde{s}_{1}\leqslant s_{1}$
and it follows that
![]() $s_{1}s_{3}\leqslant \tilde{s}_{1}\tilde{s}_{2}$
. Assuming incompressibility,
$s_{1}s_{3}\leqslant \tilde{s}_{1}\tilde{s}_{2}$
. Assuming incompressibility,
Next, suppose that
![]() $q_{S}>0$
. This occurs if either
$q_{S}>0$
. This occurs if either
![]() $\tilde{s}_{1}\geqslant \tilde{s}_{2}>0$
or
$\tilde{s}_{1}\geqslant \tilde{s}_{2}>0$
or
![]() $\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
. In the former case,
$\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
. In the former case,
![]() $s_{3}=-(s_{1}+s_{2})$
can substituted into (3.10) to show that
$s_{3}=-(s_{1}+s_{2})$
can substituted into (3.10) to show that
where the final inequality follows from (3.6). In the latter, a similar argument provides that same bound:
In summary,
3.3. Statistics of the reduced strain-rate tensor
In §§ 3.1 and 3.2 it has been shown that, as a consequence of incompressibility, bounds can be placed upon the invariants and eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
based only upon knowledge of
$\unicode[STIX]{x1D61A}_{ij}$
based only upon knowledge of
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
. However, to determine how often these bounds can provide useful information, it is of interest to understand the statistics of the reduced eigenvalues.
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
. However, to determine how often these bounds can provide useful information, it is of interest to understand the statistics of the reduced eigenvalues.
For example, to infer from (3.6) that the flow is either ‘tube-forming’ or ‘sheet-forming’ requires
![]() $\tilde{s}_{1}<0$
or
$\tilde{s}_{1}<0$
or
![]() $\tilde{s}_{2}>0$
, respectively, and it was noted in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that such situations occur in approximately 14.2 % of the studied data ensemble. However, currently, the only known statistical information is that
$\tilde{s}_{2}>0$
, respectively, and it was noted in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that such situations occur in approximately 14.2 % of the studied data ensemble. However, currently, the only known statistical information is that
![]() $\langle \tilde{s}_{1}\rangle =-\langle \tilde{s}_{2}\rangle$
and that
$\langle \tilde{s}_{1}\rangle =-\langle \tilde{s}_{2}\rangle$
and that
![]() $\langle \tilde{s}_{1}\tilde{s}_{2}\rangle =-(5/4)\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
. Under the assumptions of homogeneous and isotropic turbulence, we now extend these results.
$\langle \tilde{s}_{1}\tilde{s}_{2}\rangle =-(5/4)\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
. Under the assumptions of homogeneous and isotropic turbulence, we now extend these results.
3.3.1. Expectation of
 $\tilde{s}_{1},\tilde{s}_{2}$
$\tilde{s}_{1},\tilde{s}_{2}$
A direct computation gives
and since
![]() $\langle p_{S}\rangle =\langle p\rangle =0$
, it follows that
$\langle p_{S}\rangle =\langle p\rangle =0$
, it follows that
Here, we have defined the positive variable
![]() $X=(\unicode[STIX]{x1D608}_{11}-\unicode[STIX]{x1D608}_{22})^{2}+4\unicode[STIX]{x1D60B}_{12}^{2}=p_{S}^{2}-4q_{S}$
.
$X=(\unicode[STIX]{x1D608}_{11}-\unicode[STIX]{x1D608}_{22})^{2}+4\unicode[STIX]{x1D60B}_{12}^{2}=p_{S}^{2}-4q_{S}$
.
Evaluating the expected value of the square root of
![]() $X$
directly is difficult. However,
$X$
directly is difficult. However,
![]() $X$
depends only upon terms in the symmetric strain-rate tensor. Therefore, under the assumption of isotropy and homogeneity, its moments can be expressed in terms of the moments of
$X$
depends only upon terms in the symmetric strain-rate tensor. Therefore, under the assumption of isotropy and homogeneity, its moments can be expressed in terms of the moments of
![]() $\partial u_{1}/\partial x_{1}$
(Hierro & Dopazo Reference Hierro and Dopazo2003). Indeed, we obtain
$\partial u_{1}/\partial x_{1}$
(Hierro & Dopazo Reference Hierro and Dopazo2003). Indeed, we obtain
This information can be used to estimate
![]() $\langle X^{1/2}\rangle$
.
$\langle X^{1/2}\rangle$
.
First, the Cauchy–Schwarz inequality implies that
![]() $\langle X^{1/2}\rangle \leqslant \langle X\rangle ^{1/2}$
. Next, suppose that constants
$\langle X^{1/2}\rangle \leqslant \langle X\rangle ^{1/2}$
. Next, suppose that constants
![]() $a,b>0$
are chosen such that
$a,b>0$
are chosen such that
![]() $x^{1/2}\geqslant -ax^{2}+bx$
, for all
$x^{1/2}\geqslant -ax^{2}+bx$
, for all
![]() $x\geqslant 0$
. Then it is shown in appendix A that
$x\geqslant 0$
. Then it is shown in appendix A that
Hence, using (3.16) and (3.17),
where
![]() ${\it\kappa}:=\langle (\partial u_{1}/\partial x_{1})^{4}\rangle /\langle (\partial u_{1}/\partial x_{1})^{2}\rangle ^{2}$
is the kurtosis of
${\it\kappa}:=\langle (\partial u_{1}/\partial x_{1})^{4}\rangle /\langle (\partial u_{1}/\partial x_{1})^{2}\rangle ^{2}$
is the kurtosis of
![]() $\partial u_{1}/\partial x_{1}$
.
$\partial u_{1}/\partial x_{1}$
.
It is clear that the lower bound in (3.19) is only meaningful if
![]() $c(a,b):=b-2a{\it\kappa}/3>0$
, and that a larger value of this constant provides a tighter estimate of
$c(a,b):=b-2a{\it\kappa}/3>0$
, and that a larger value of this constant provides a tighter estimate of
![]() $\langle \tilde{s}_{1}\rangle$
. Consequently, we should aim to maximize
$\langle \tilde{s}_{1}\rangle$
. Consequently, we should aim to maximize
![]() $c(a,b)$
subject to the constraint
$c(a,b)$
subject to the constraint
![]() $x^{1/2}\geqslant -ax^{2}+bx$
, for all
$x^{1/2}\geqslant -ax^{2}+bx$
, for all
![]() $x\geqslant 0$
. It is shown in appendix A that the solution to this constrained optimisation problem is
$x\geqslant 0$
. It is shown in appendix A that the solution to this constrained optimisation problem is
![]() $c_{max}=\sqrt{3/2{\it\kappa}}$
. Hence,
$c_{max}=\sqrt{3/2{\it\kappa}}$
. Hence,
 $$\begin{eqnarray}\sqrt{\frac{3}{2{\it\kappa}}}\leqslant \frac{\langle \tilde{s}_{1}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant 1\end{eqnarray}$$
$$\begin{eqnarray}\sqrt{\frac{3}{2{\it\kappa}}}\leqslant \frac{\langle \tilde{s}_{1}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant 1\end{eqnarray}$$
and since
![]() $\langle \tilde{s}_{2}\rangle =-\langle \tilde{s}_{1}\rangle$
,
$\langle \tilde{s}_{2}\rangle =-\langle \tilde{s}_{1}\rangle$
,
 $$\begin{eqnarray}-1\leqslant \frac{\langle \tilde{s}_{2}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant -\sqrt{\frac{3}{2{\it\kappa}}}.\end{eqnarray}$$
$$\begin{eqnarray}-1\leqslant \frac{\langle \tilde{s}_{2}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant -\sqrt{\frac{3}{2{\it\kappa}}}.\end{eqnarray}$$
The estimates (3.20) and (3.21) agree with and extend the previously proven (Cardesa et al.
Reference Cardesa, Mistry, Gan and Dawson2013) result that, assuming isotropy and homogeneity,
![]() $\langle \tilde{s}_{2}\rangle =-\langle \tilde{s}_{1}\rangle \leqslant 0\leqslant \langle \tilde{s}_{1}\rangle$
.
$\langle \tilde{s}_{2}\rangle =-\langle \tilde{s}_{1}\rangle \leqslant 0\leqslant \langle \tilde{s}_{1}\rangle$
.
Figure 2 shows the kurtosis (
![]() ${\it\kappa}$
) profile of
${\it\kappa}$
) profile of
![]() $\unicode[STIX]{x1D608}_{11}$
throughout the mixing layer data we introduce in § 4. The study of Van Atta & Antonia (Reference Van Atta and Antonia1980) compiles the experimental variation of
$\unicode[STIX]{x1D608}_{11}$
throughout the mixing layer data we introduce in § 4. The study of Van Atta & Antonia (Reference Van Atta and Antonia1980) compiles the experimental variation of
![]() ${\it\kappa}$
for a variety of different turbulent flows over a range of turbulent Reynolds numbers,
${\it\kappa}$
for a variety of different turbulent flows over a range of turbulent Reynolds numbers,
![]() $\mathit{Re}_{{\it\lambda}}$
. They show that in the range
$\mathit{Re}_{{\it\lambda}}$
. They show that in the range
![]() $10^{2}<\mathit{Re}_{{\it\lambda}}<10^{3}~{\it\kappa}$
varies as
$10^{2}<\mathit{Re}_{{\it\lambda}}<10^{3}~{\it\kappa}$
varies as
![]() ${\it\kappa}\sim \mathit{Re}_{{\it\lambda}}^{m}$
, where
${\it\kappa}\sim \mathit{Re}_{{\it\lambda}}^{m}$
, where
![]() $m$
is roughly bounded by
$m$
is roughly bounded by
![]() $0.32\lesssim m\lesssim 0.41$
. For a nominally two-dimensional free shear flow, such as the mixing layer data,
$0.32\lesssim m\lesssim 0.41$
. For a nominally two-dimensional free shear flow, such as the mixing layer data,
![]() $\mathit{Re}_{{\it\lambda}}$
is evidently a function of
$\mathit{Re}_{{\it\lambda}}$
is evidently a function of
![]() $x_{2}$
requiring
$x_{2}$
requiring
![]() ${\it\kappa}$
to be a function of
${\it\kappa}$
to be a function of
![]() $x_{2}$
as illustrated in the figure. The value of
$x_{2}$
as illustrated in the figure. The value of
![]() ${\it\kappa}$
at
${\it\kappa}$
at
![]() $x_{2}=0$
of 6.3 compares favourably to that for the mixing layer of Wyngaard & Tennekes (Reference Wyngaard and Tennekes1970) (
$x_{2}=0$
of 6.3 compares favourably to that for the mixing layer of Wyngaard & Tennekes (Reference Wyngaard and Tennekes1970) (
![]() $6.0\pm 0.2$
) at a comparable
$6.0\pm 0.2$
) at a comparable
![]() $\mathit{Re}_{{\it\lambda}}\approx 300$
for the data introduced in § 4. It should be noted that since
$\mathit{Re}_{{\it\lambda}}\approx 300$
for the data introduced in § 4. It should be noted that since
![]() ${\it\kappa}$
is minimised at the centreline of the mixing layer (excluding the free stream) the bounding of
${\it\kappa}$
is minimised at the centreline of the mixing layer (excluding the free stream) the bounding of
![]() $\langle \tilde{s}_{i}\rangle$
is at its narrowest on the centreline and increases towards the peripheries of the mixing layer.
$\langle \tilde{s}_{i}\rangle$
is at its narrowest on the centreline and increases towards the peripheries of the mixing layer.

Figure 2. Profile of
![]() ${\it\kappa}(x_{2})$
.
${\it\kappa}(x_{2})$
.
3.3.2. Variance of
 $\tilde{s}_{1},\tilde{s}_{2}$
$\tilde{s}_{1},\tilde{s}_{2}$
To estimate the variance of the reduced eigenvalues, we first consider their second moments, again assuming isotropy and homogeneity. Using (3.15),
Now
![]() $\langle p_{S}^{2}\rangle =\langle \unicode[STIX]{x1D608}_{11}^{2}+\unicode[STIX]{x1D608}_{22}^{2}+2\unicode[STIX]{x1D608}_{11}\unicode[STIX]{x1D608}_{22}\rangle$
and using the result for double products of velocity derivatives under the assumption of homogeneous isotropic turbulence
$\langle p_{S}^{2}\rangle =\langle \unicode[STIX]{x1D608}_{11}^{2}+\unicode[STIX]{x1D608}_{22}^{2}+2\unicode[STIX]{x1D608}_{11}\unicode[STIX]{x1D608}_{22}\rangle$
and using the result for double products of velocity derivatives under the assumption of homogeneous isotropic turbulence
we obtain
![]() $\langle p_{S}^{2}\rangle =\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
. Hence, using (3.17),
$\langle p_{S}^{2}\rangle =\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
. Hence, using (3.17),
and since
![]() $\langle \tilde{s}_{1}\rangle =-\langle \tilde{s}_{2}\rangle$
, the variances of the reduced eigenvalues are related by
$\langle \tilde{s}_{1}\rangle =-\langle \tilde{s}_{2}\rangle$
, the variances of the reduced eigenvalues are related by
Therefore, the sign of
![]() $\langle p_{S}\sqrt{X}\rangle$
determines which of the reduced eigenvalues has the greater variance. Furthermore, the bounds of (3.20), (3.21) and (3.24) can be used to show that the variances are upper bounded by
$\langle p_{S}\sqrt{X}\rangle$
determines which of the reduced eigenvalues has the greater variance. Furthermore, the bounds of (3.20), (3.21) and (3.24) can be used to show that the variances are upper bounded by
 $$\begin{eqnarray}\frac{{\it\sigma}_{\tilde{s}_{1,2}}^{2}}{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }\leqslant \frac{1}{4}\left(7-\frac{9}{{\it\kappa}}\mp 2\langle p_{S}\sqrt{X}\rangle \bigg/\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle \right).\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\sigma}_{\tilde{s}_{1,2}}^{2}}{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }\leqslant \frac{1}{4}\left(7-\frac{9}{{\it\kappa}}\mp 2\langle p_{S}\sqrt{X}\rangle \bigg/\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle \right).\end{eqnarray}$$
Unfortunately, at present, we are unable to analytically determine the sign of
![]() $\langle p_{S}\sqrt{X}\rangle$
. However, since
$\langle p_{S}\sqrt{X}\rangle$
. However, since
![]() $\sqrt{X}$
is positive and
$\sqrt{X}$
is positive and
![]() $p_{S}$
is zero-mean and negatively skewed, we conjecture that
$p_{S}$
is zero-mean and negatively skewed, we conjecture that
![]() $\langle p_{S}\sqrt{X}\rangle >0$
and, more specifically, that
$\langle p_{S}\sqrt{X}\rangle >0$
and, more specifically, that
 $$\begin{eqnarray}\frac{\langle p_{S}\sqrt{X}\rangle }{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }=\frac{1}{2},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\langle p_{S}\sqrt{X}\rangle }{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }=\frac{1}{2},\end{eqnarray}$$
which is supported by its numerical value of 0.50 in the mixing layer data of § 4.
Finally, since
![]() $\langle \tilde{s}_{1}\tilde{s}_{2}\rangle =-(5/4)\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
, the bound of (3.20) can be used to estimate the covariance
$\langle \tilde{s}_{1}\tilde{s}_{2}\rangle =-(5/4)\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
, the bound of (3.20) can be used to estimate the covariance
![]() ${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})=\langle \tilde{s}_{1}\tilde{s}_{2}\rangle -\langle \tilde{s}_{1}\rangle \langle \tilde{s}_{2}\rangle$
of the reduced eigenvalues:
${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})=\langle \tilde{s}_{1}\tilde{s}_{2}\rangle -\langle \tilde{s}_{1}\rangle \langle \tilde{s}_{2}\rangle$
of the reduced eigenvalues:
 $$\begin{eqnarray}\frac{1}{4}\left(\frac{9}{{\it\kappa}}-5\right)\leqslant \frac{{\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})}{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }\leqslant \frac{1}{4}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{4}\left(\frac{9}{{\it\kappa}}-5\right)\leqslant \frac{{\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})}{\displaystyle \left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle }\leqslant \frac{1}{4}.\end{eqnarray}$$
The fact that the above bound is asymmetric about zero is suggestive of the fact that for the majority of data points,
![]() $\tilde{s}_{2}<0<\tilde{s}_{1}$
. This condition is indeed met for 85.8 % of the ensemble of the data of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) and 85.2 % of the ensemble of the data presented in § 4.
$\tilde{s}_{2}<0<\tilde{s}_{1}$
. This condition is indeed met for 85.8 % of the ensemble of the data of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) and 85.2 % of the ensemble of the data presented in § 4.
4. Data
In order to observe the dependences discussed in § 2 and validate the bounds that we derive in § 3 we must choose a suitable test case flow with access to the full VGT. In order for our assumptions of incompressibility, homogeneity and isotropy to be largely fulfilled we require data from a region of fully developed turbulence, which in the Richardson–Kolmogorov phenomenology should exhibit statistical isotropy and homogeneity at the small scales (but in practice of course will only closely approximate this). George & Hussein (Reference George and Hussein1991) illustrate that at finite Reynolds numbers there is no such thing as a perfectly isotropic flow and thus quantify the degree of (an)isotropy by using their parameters
![]() $K_{1},K_{2},K_{3}$
and
$K_{1},K_{2},K_{3}$
and
![]() $K_{4}$
. Taylor (Reference Taylor1935) derives the value for all four of these parameters to be unity for homogeneous isotropic turbulence (HIT). Further, George & Hussein (Reference George and Hussein1991) produce an exhaustive list of the values of these parameters in a wealth of different flow configurations and experiments (their tables 1 and 2). Departure from unity for these parameters can thus be used to assess the degree of (an)isotropy of the small scales of a flow and this departure can easily be compared to that for other flows.
$K_{4}$
. Taylor (Reference Taylor1935) derives the value for all four of these parameters to be unity for homogeneous isotropic turbulence (HIT). Further, George & Hussein (Reference George and Hussein1991) produce an exhaustive list of the values of these parameters in a wealth of different flow configurations and experiments (their tables 1 and 2). Departure from unity for these parameters can thus be used to assess the degree of (an)isotropy of the small scales of a flow and this departure can easily be compared to that for other flows.
In the event of small-scale anisotropy (to whatever extent) the choice of source plane for the reduced VGT, i.e. which
![]() $2\times 2$
block of the VGT, is no longer an arbitrary choice but must be carefully considered. This is further discussed in § 7. Whilst many numerical studies with excellent HIT data exist this will not allow us to examine the effect of large-scale anisotropy on the choice of source plane for the reduced VGT. In order to do this we must instead consider a shear flow. We thus choose to use a mixing layer, which can be considered the most canonical of all the free shear flows. Winant & Browand (Reference Winant and Browand1974) state, ‘the region between two parallel streams moving at different speeds is the simplest free shear flow which can be considered’ and is thus the ideal flow against which to test our analyses.
$2\times 2$
block of the VGT, is no longer an arbitrary choice but must be carefully considered. This is further discussed in § 7. Whilst many numerical studies with excellent HIT data exist this will not allow us to examine the effect of large-scale anisotropy on the choice of source plane for the reduced VGT. In order to do this we must instead consider a shear flow. We thus choose to use a mixing layer, which can be considered the most canonical of all the free shear flows. Winant & Browand (Reference Winant and Browand1974) state, ‘the region between two parallel streams moving at different speeds is the simplest free shear flow which can be considered’ and is thus the ideal flow against which to test our analyses.
The data that we choose are identical to those used by Buxton, Laizet & Ganapathisubramani (Reference Buxton, Laizet and Ganapathisubramani2011b
) of a nominally two-dimensional, planar mixing layer produced by means of a direct numerical simulation (DNS) of two flows of different free-stream velocities (
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
, in the ratio
$U_{2}$
, in the ratio
![]() $U_{1}/U_{2}=2$
) either side of a splitter plate of thickness
$U_{1}/U_{2}=2$
) either side of a splitter plate of thickness
![]() $h$
, similar to the study of Laizet, Lardeau & Lamballais (Reference Laizet, Lardeau and Lamballais2010). The computational domain
$h$
, similar to the study of Laizet, Lardeau & Lamballais (Reference Laizet, Lardeau and Lamballais2010). The computational domain
![]() $(L_{x_{1}}\times L_{x_{2}}\times L_{x_{3}})=(230.4h\times 48h\times 28.8h)$
is discretised on a Cartesian mesh that is stretched in the cross-stream (
$(L_{x_{1}}\times L_{x_{2}}\times L_{x_{3}})=(230.4h\times 48h\times 28.8h)$
is discretised on a Cartesian mesh that is stretched in the cross-stream (
![]() $x_{2}$
) direction of
$x_{2}$
) direction of
![]() $(2049\times 513\times 256)$
mesh nodes. The stretching of the mesh in the cross-stream direction leads to a minimal mesh size of
$(2049\times 513\times 256)$
mesh nodes. The stretching of the mesh in the cross-stream direction leads to a minimal mesh size of
![]() ${\rm\Delta}x_{2}\approx 0.03h$
. The time step,
${\rm\Delta}x_{2}\approx 0.03h$
. The time step,
![]() ${\rm\Delta}t=0.05h/U_{c}$
, where
${\rm\Delta}t=0.05h/U_{c}$
, where
![]() $U_{c}=(U_{1}+U_{2})/2$
is the mean convection velocity, is low enough to satisfy the Courant–Friedrichs–Lewy condition, ensuring temporal stability of the solution.
$U_{c}=(U_{1}+U_{2})/2$
is the mean convection velocity, is low enough to satisfy the Courant–Friedrichs–Lewy condition, ensuring temporal stability of the solution.
A sub-domain that consisted of the final 301 (
![]() $\times \,513\times 256$
) mesh nodes in the streamwise (
$\times \,513\times 256$
) mesh nodes in the streamwise (
![]() $x_{1}$
) direction was isolated and three time steps that were sufficiently well spaced in time to ensure statistical independence were saved. This sub-domain is in the far field of the mixing layer in which the turbulence is fully developed with self-similar mean velocity profiles throughout, with all subsequent data and analysis presented in this manuscript coming from this sub-domain. The Reynolds number based on
$x_{1}$
) direction was isolated and three time steps that were sufficiently well spaced in time to ensure statistical independence were saved. This sub-domain is in the far field of the mixing layer in which the turbulence is fully developed with self-similar mean velocity profiles throughout, with all subsequent data and analysis presented in this manuscript coming from this sub-domain. The Reynolds number based on
![]() $U_{c}$
and
$U_{c}$
and
![]() $h$
(
$h$
(
![]() $\mathit{Re}_{W}$
) is 1000 and the Reynolds number based on the Taylor microscale, computed assuming isotropic turbulence (Taylor Reference Taylor1935), is
$\mathit{Re}_{W}$
) is 1000 and the Reynolds number based on the Taylor microscale, computed assuming isotropic turbulence (Taylor Reference Taylor1935), is
![]() $\mathit{Re}_{{\it\lambda}}\approx 270$
along the centreline.
$\mathit{Re}_{{\it\lambda}}\approx 270$
along the centreline.
The code ‘incompact3d’ (Laizet & Lamballais Reference Laizet and Lamballais2009), based on sixth-order compact schemes for spatial discretisation and second-order Adams–Bashforth schemes for time advancement, is used to solve the incompressible non-dimensionalised Navier–Stokes equations. To treat the incompressibility condition a projection method is used requiring the solution of a Poisson equation for the pressure. This equation is fully solved in spectral space via the use of the relevant three-dimensional fast Fourier transforms (FFT). The boundary conditions are inflow/outflow in the streamwise direction (velocity boundary conditions of the Dirichlet type), free slip in the cross-stream direction at
![]() $x_{2}=\pm L_{x_{2}}/2$
and periodic in the spanwise direction at
$x_{2}=\pm L_{x_{2}}/2$
and periodic in the spanwise direction at
![]() $x_{3}=\pm L_{x_{3}}/2$
. The pressure mesh is staggered from the velocity mesh to avoid spurious pressure oscillations. Using the concept of modified wavenumber, the divergence-free condition is ensured up to the machine accuracy. More details on the simulation, including the generation of the inlet/initial conditions (including the boundary layers on both sides of the splitter plate), can be found in Laizet et al. (Reference Laizet, Lardeau and Lamballais2010) and more details about the code, its validation and the original treatment of the pressure in spectral space can be found in Laizet & Lamballais (Reference Laizet and Lamballais2009).
$x_{3}=\pm L_{x_{3}}/2$
. The pressure mesh is staggered from the velocity mesh to avoid spurious pressure oscillations. Using the concept of modified wavenumber, the divergence-free condition is ensured up to the machine accuracy. More details on the simulation, including the generation of the inlet/initial conditions (including the boundary layers on both sides of the splitter plate), can be found in Laizet et al. (Reference Laizet, Lardeau and Lamballais2010) and more details about the code, its validation and the original treatment of the pressure in spectral space can be found in Laizet & Lamballais (Reference Laizet and Lamballais2009).
In order to ensure that only data in the turbulent region of the flow are considered a criterion based on the enstrophy was devised. Thresholds based on enstrophy have been found to be the most suitable for the identification of turbulent/non-turbulent fluid in free shear flows (Bisset et al.
Reference Bisset, Hunt and Rogers2002). Thus a threshold based on the mean enstrophy for each time step,
![]() ${\it\omega}_{thres.}^{2}=0.025\langle {\it\omega}^{2}\rangle$
, was chosen based on figure 3 to ensure that data from the potential flow region were discarded. Data points with enstrophies below 2.5 % of the means were removed, accounting for some 30 % of the original data.
${\it\omega}_{thres.}^{2}=0.025\langle {\it\omega}^{2}\rangle$
, was chosen based on figure 3 to ensure that data from the potential flow region were discarded. Data points with enstrophies below 2.5 % of the means were removed, accounting for some 30 % of the original data.

Figure 3. Instantaneous contours of enstrophy for a plane of constant
![]() $x_{3}$
.
$x_{3}$
.
4.1. Isotropy validation
The assumption of local isotropy requires that there is no statistically preferential direction at a given point within the flow. Consequently the mean square of each of the off-diagonal terms of the VGT ought to be equal to each other and equal to twice the mean square of each of the diagonal terms (George & Hussein Reference George and Hussein1991). A sixth-order Lagrange interpolating polynomial numerical scheme was used to compute the velocity gradients. For grid flow, values of the isotropic parameters of George & Hussein (Reference George and Hussein1991)
![]() $K_{1}\in [1.04,1.09]$
and
$K_{1}\in [1.04,1.09]$
and
![]() $K_{3}\in [0.72,0.8]$
are deemed reasonable approximations of isotropy (Valente & Vassilicos Reference Valente and Vassilicos2014). Thus it can be seen that the turbulence in the far field of the mixing layer can be reasonably approximated as being locally isotropic (better in fact than these recent grid flows):
$K_{3}\in [0.72,0.8]$
are deemed reasonable approximations of isotropy (Valente & Vassilicos Reference Valente and Vassilicos2014). Thus it can be seen that the turbulence in the far field of the mixing layer can be reasonably approximated as being locally isotropic (better in fact than these recent grid flows):
Under the assumption of local isotropy, the dissipation rate can be expressed as
 $$\begin{eqnarray}{\it\epsilon}=\left\{\begin{array}{@{}ll@{}}\displaystyle 15{\it\nu}\left\langle \frac{\partial u_{i}}{\partial x_{j}}\right\rangle \quad & \text{if}\;i=j,\\ \displaystyle 7.5{\it\nu}\left\langle \frac{\partial u_{i}}{\partial x_{j}}\right\rangle \quad & \text{if}\;i\neq j.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\epsilon}=\left\{\begin{array}{@{}ll@{}}\displaystyle 15{\it\nu}\left\langle \frac{\partial u_{i}}{\partial x_{j}}\right\rangle \quad & \text{if}\;i=j,\\ \displaystyle 7.5{\it\nu}\left\langle \frac{\partial u_{i}}{\partial x_{j}}\right\rangle \quad & \text{if}\;i\neq j.\end{array}\right.\end{eqnarray}$$
For the current data the approximations ranged from
![]() $0.897\langle {\it\epsilon}\rangle$
to
$0.897\langle {\it\epsilon}\rangle$
to
![]() $1.086\langle {\it\epsilon}\rangle$
, where
$1.086\langle {\it\epsilon}\rangle$
, where
![]() $\langle {\it\epsilon}\rangle$
is the mean rate of dissipation computed without assumption as
$\langle {\it\epsilon}\rangle$
is the mean rate of dissipation computed without assumption as
![]() $\langle {\it\epsilon}\rangle =2{\it\nu}\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle$
. The closest dissipation estimate assuming local isotropy was obtained using the
$\langle {\it\epsilon}\rangle =2{\it\nu}\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle$
. The closest dissipation estimate assuming local isotropy was obtained using the
![]() $\partial u_{2}/\partial x_{2}$
component, giving a value of
$\partial u_{2}/\partial x_{2}$
component, giving a value of
![]() $1.011\langle {\it\epsilon}\rangle$
. Conventionally, the first diagonal term is used which gives an estimate of
$1.011\langle {\it\epsilon}\rangle$
. Conventionally, the first diagonal term is used which gives an estimate of
![]() $0.949\langle {\it\epsilon}\rangle$
.
$0.949\langle {\it\epsilon}\rangle$
.
Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) derived the relationships in (2.1) and (2.2), relating the invariants of the reduced VGT to the mean enstrophy amplification rate
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
using the assumptions of homogeneity and local isotropy. A further consideration of the validity of the assumption of local isotropy for the mixing layer data, in the context of the reduced VGT, is presented in table 1. It can thus be seen that the flow is, again, on the whole close to meeting the conditions for local isotropy.
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
using the assumptions of homogeneity and local isotropy. A further consideration of the validity of the assumption of local isotropy for the mixing layer data, in the context of the reduced VGT, is presented in table 1. It can thus be seen that the flow is, again, on the whole close to meeting the conditions for local isotropy.
5. Validation of our bounds against the mixing layer data
5.1. Invariants of the reduced VGT
Figure 4 shows the joint p.d.f. between
![]() $p$
and
$p$
and
![]() $q$
which again shows the characteristic ‘teapot’ shape reported in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) and Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014) for a variety of turbulent flows. These new data add further credence to the notion that the shape of the
$q$
which again shows the characteristic ‘teapot’ shape reported in Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) and Fiscaletti et al. (Reference Fiscaletti, Westerweel and Elsinga2014) for a variety of turbulent flows. These new data add further credence to the notion that the shape of the
![]() $p{-}q$
joint p.d.f. is also a ‘universal’ feature of turbulent flows, similarly to that for the full invariants
$p{-}q$
joint p.d.f. is also a ‘universal’ feature of turbulent flows, similarly to that for the full invariants
![]() $Q$
and
$Q$
and
![]() $R$
(Elsinga & Marusic Reference Elsinga and Marusic2010).
$R$
(Elsinga & Marusic Reference Elsinga and Marusic2010).

Figure 4. Joint p.d.f. of reduced VGT invariants
![]() $p$
and
$p$
and
![]() $q$
. Contours scale logarithmically.
$q$
. Contours scale logarithmically.
The joint p.d.f.s between the invariants of the VGT and those for the reduced VGT are presented in figure 5 which shows the joint p.d.f.s between
![]() $Q$
and
$Q$
and
![]() $(-p^{2}+q)$
(a) and
$(-p^{2}+q)$
(a) and
![]() $R$
and
$R$
and
![]() $-pq$
(b). There is a clear trend for
$-pq$
(b). There is a clear trend for
![]() $Q$
to be distributed along the line
$Q$
to be distributed along the line
![]() $Q=(-p^{2}+q)$
, derived in (2.3), in figure 5(a), with a stretching of the contours of the joint p.d.f. along this line meaning localised peaks (modes) in the conditional p.d.f.s of
$Q=(-p^{2}+q)$
, derived in (2.3), in figure 5(a), with a stretching of the contours of the joint p.d.f. along this line meaning localised peaks (modes) in the conditional p.d.f.s of
![]() $Q$
against
$Q$
against
![]() $(-p^{2}+q)$
. The contours are also observed to be stretched along
$(-p^{2}+q)$
. The contours are also observed to be stretched along
![]() $(-p^{2}+q)=0$
, but this is subsequently shown to be a generic property of a trace-free
$(-p^{2}+q)=0$
, but this is subsequently shown to be a generic property of a trace-free
![]() $3\times 3$
matrix. It can be seen that there is a much greater spread of the data for
$3\times 3$
matrix. It can be seen that there is a much greater spread of the data for
![]() $Q>(-p^{2}+q)$
than for
$Q>(-p^{2}+q)$
than for
![]() $Q<(-p^{2}+q)$
indicating that as the excess of rotation (swirling) over strain rate for the fluid element becomes greater, then less information regarding the VGT is carried in the invariants of the reduced VGT. Figure 5(b) on the other hand shows very little structure whatsoever to the contour levels of the joint p.d.f. between
$Q<(-p^{2}+q)$
indicating that as the excess of rotation (swirling) over strain rate for the fluid element becomes greater, then less information regarding the VGT is carried in the invariants of the reduced VGT. Figure 5(b) on the other hand shows very little structure whatsoever to the contour levels of the joint p.d.f. between
![]() $R$
and
$R$
and
![]() $-pq$
, derived in (2.4). This emphasises the difficulty in gleaning information on the third invariant
$-pq$
, derived in (2.4). This emphasises the difficulty in gleaning information on the third invariant
![]() $R$
, which is a property of three-dimensional turbulence that is not present in two-dimensional turbulence, from the reduced VGT, which is of course a two-dimensional projection of the full VGT.
$R$
, which is a property of three-dimensional turbulence that is not present in two-dimensional turbulence, from the reduced VGT, which is of course a two-dimensional projection of the full VGT.

Figure 5. Joint p.d.f.s of
![]() $Q$
(a) and
$Q$
(a) and
![]() $R$
(b) against their constituent terms from the reduced VGT. Contours scale logarithmically.
$R$
(b) against their constituent terms from the reduced VGT. Contours scale logarithmically.
The dependence of
![]() $Q$
on the individual invariants,
$Q$
on the individual invariants,
![]() $p$
(a) and
$p$
(a) and
![]() $q$
(b), of the reduced VGT is illustrated in figure 6 with
$q$
(b), of the reduced VGT is illustrated in figure 6 with
![]() $Q=-p^{2}$
and
$Q=-p^{2}$
and
![]() $Q=q$
shown as the dashed lines respectively. The first reduced invariant,
$Q=q$
shown as the dashed lines respectively. The first reduced invariant,
![]() $p$
, is an indication of the compressibility of the flow when projected onto a 2D plane. Buxton, Laizet & Ganapathisubramani (Reference Buxton, Laizet and Ganapathisubramani2011a
) show that artificial compressibility introduced by experimental noise increases and indeed alters the distribution of the
$p$
, is an indication of the compressibility of the flow when projected onto a 2D plane. Buxton, Laizet & Ganapathisubramani (Reference Buxton, Laizet and Ganapathisubramani2011a
) show that artificial compressibility introduced by experimental noise increases and indeed alters the distribution of the
![]() $Q$
–
$Q$
–
![]() $R$
joint p.d.f. No distribution around
$R$
joint p.d.f. No distribution around
![]() $Q=-p^{2}$
whatsoever is observed for the estimation of
$Q=-p^{2}$
whatsoever is observed for the estimation of
![]() $Q$
from the ‘compressibility’ invariant,
$Q$
from the ‘compressibility’ invariant,
![]() $p$
in the joint p.d.f. of figure 6(a). In contrast it can be seen from the joint p.d.f. in figure 6(b) that the distribution of the contours about
$p$
in the joint p.d.f. of figure 6(a). In contrast it can be seen from the joint p.d.f. in figure 6(b) that the distribution of the contours about
![]() $Q=q$
is similar to that for
$Q=q$
is similar to that for
![]() $Q=-p^{2}+q$
in figure 5(a) with strong peaks in probability observed for
$Q=-p^{2}+q$
in figure 5(a) with strong peaks in probability observed for
![]() $Q=q$
. It is observed that the sign of
$Q=q$
. It is observed that the sign of
![]() $q$
is an excellent predictor of the sign of
$q$
is an excellent predictor of the sign of
![]() $Q$
for
$Q$
for
![]() $Q<0$
(local excess of strain rate over rotation): 85.3 % of the data for which
$Q<0$
(local excess of strain rate over rotation): 85.3 % of the data for which
![]() $q<0$
exhibits concurrent
$q<0$
exhibits concurrent
![]() $Q<0$
(the bottom left-hand quadrant of figure 6
b). However,
$Q<0$
(the bottom left-hand quadrant of figure 6
b). However,
![]() $q$
being positive is a significantly inferior predictor of the sign of
$q$
being positive is a significantly inferior predictor of the sign of
![]() $Q$
, with only 54.1 % of data having a positive value of
$Q$
, with only 54.1 % of data having a positive value of
![]() $Q$
(local excess of rotation over strain rate) for
$Q$
(local excess of rotation over strain rate) for
![]() $q>0$
. By inspection of the joint p.d.f. contours it can also be seen that the variance of the distribution of the joint p.d.f. when
$q>0$
. By inspection of the joint p.d.f. contours it can also be seen that the variance of the distribution of the joint p.d.f. when
![]() $Q>0$
and
$Q>0$
and
![]() $q>0$
is significantly greater than that for when
$q>0$
is significantly greater than that for when
![]() $Q<0$
and
$Q<0$
and
![]() $q<0$
, further reducing the quality of predictions for
$q<0$
, further reducing the quality of predictions for
![]() $Q$
from
$Q$
from
![]() $q$
. It is thus argued that the two-dimensional projection of local straining is a far more accurate guide to the underlying three-dimensional physics than the projection of rotation.
$q$
. It is thus argued that the two-dimensional projection of local straining is a far more accurate guide to the underlying three-dimensional physics than the projection of rotation.

Figure 6. Joint p.d.f.s of
![]() $Q$
against the invariants of the reduced VGT
$Q$
against the invariants of the reduced VGT
![]() $p$
(a) and
$p$
(a) and
![]() $q$
(b). Contours scale logarithmically.
$q$
(b). Contours scale logarithmically.
In order to show that the strong dependence between
![]() $Q$
and
$Q$
and
![]() $q$
is a property of Navier–Stokes turbulence and not a generic property of trace-free
$q$
is a property of Navier–Stokes turbulence and not a generic property of trace-free
![]() $3\times 3$
matrices a synthetic divergence-free velocity field was produced for comparison. A
$3\times 3$
matrices a synthetic divergence-free velocity field was produced for comparison. A
![]() $100\times 100\times 100$
domain of velocities modelled as Gaussian distributed uncorrelated noise with the same extrema as the velocity components of the DNS data was generated. Incompressibility was enforced by assigning
$100\times 100\times 100$
domain of velocities modelled as Gaussian distributed uncorrelated noise with the same extrema as the velocity components of the DNS data was generated. Incompressibility was enforced by assigning
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{2}$
and
$u_{2}$
and
![]() $\unicode[STIX]{x1D608}_{33}=-(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})$
and thereby computing
$\unicode[STIX]{x1D608}_{33}=-(\unicode[STIX]{x1D608}_{11}+\unicode[STIX]{x1D608}_{22})$
and thereby computing
![]() $u_{3}$
. The resulting joint p.d.f.s of
$u_{3}$
. The resulting joint p.d.f.s of
![]() $Q$
against
$Q$
against
![]() $p$
and
$p$
and
![]() $q$
(equivalent to those in figure 6) are presented in figure 7. It can be seen that the shapes and peaks of the joint p.d.f.s in figure 6 are distinct from those of figure 7, particularly that of the joint p.d.f. between
$q$
(equivalent to those in figure 6) are presented in figure 7. It can be seen that the shapes and peaks of the joint p.d.f.s in figure 6 are distinct from those of figure 7, particularly that of the joint p.d.f. between
![]() $q$
and
$q$
and
![]() $Q$
, and can therefore be assumed to result from the turbulent flow being examined and thus the Navier–Stokes equations. The observed stretching of the joint p.d.f. contours along
$Q$
, and can therefore be assumed to result from the turbulent flow being examined and thus the Navier–Stokes equations. The observed stretching of the joint p.d.f. contours along
![]() $q=0$
in figure 6(b) is additionally observed in figure 7(b), showing that this is a property of a trace-free
$q=0$
in figure 6(b) is additionally observed in figure 7(b), showing that this is a property of a trace-free
![]() $3\times 3$
matrix as opposed to representing the underlying physics of the Navier–Stokes equations.
$3\times 3$
matrix as opposed to representing the underlying physics of the Navier–Stokes equations.

Figure 7. Joint p.d.f.s of
![]() $Q$
against
$Q$
against
![]() $p$
(a) and
$p$
(a) and
![]() $q$
(b) for a synthetic velocity field of Gaussian noise. Contours scale logarithmically.
$q$
(b) for a synthetic velocity field of Gaussian noise. Contours scale logarithmically.
5.2. The reduced strain-rate tensor
Figures 8 and 9 show joint p.d.f.s of the reduced and full strain-rate eigenvalues for the mixing layer data. Note that the interlacing bounds of (3.3) all hold and are sharp in the sense that the joint densities are non-zero arbitrarily close to each bound. The bounds derived in (3.7) are also observed to hold and are also sharp. The fact that these bounds are derived merely from incompressibility and are not representative of any physics themselves is illustrated in figure 10. This shows a similar series of joint p.d.f.s between
![]() $s_{i}$
and
$s_{i}$
and
![]() $\tilde{s}_{2}$
formed from the synthetic, divergence-free, velocity field consisting of Gaussian distributed noise. The physics of Navier–Stokes turbulence are encapsulated in the statistical distributions of the joint p.d.f.s of figures 8 and 9 within these bounds.
$\tilde{s}_{2}$
formed from the synthetic, divergence-free, velocity field consisting of Gaussian distributed noise. The physics of Navier–Stokes turbulence are encapsulated in the statistical distributions of the joint p.d.f.s of figures 8 and 9 within these bounds.

Figure 8. The joint p.d.f.s of
![]() $\tilde{s}_{1}$
against
$\tilde{s}_{1}$
against
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
and
$s_{2}$
and
![]() $s_{3}$
, (a)–(c) respectively. Contours scale logarithmically.
$s_{3}$
, (a)–(c) respectively. Contours scale logarithmically.

Figure 9. The joint p.d.f.s of
![]() $\tilde{s}_{2}$
against
$\tilde{s}_{2}$
against
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
and
$s_{2}$
and
![]() $s_{3}$
, (a)–(c) respectively. Contours scale logarithmically.
$s_{3}$
, (a)–(c) respectively. Contours scale logarithmically.

Figure 10. Joint p.d.f.s of
![]() $\tilde{s}_{2}$
against
$\tilde{s}_{2}$
against
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
and
$s_{2}$
and
![]() $s_{3}$
, (a)–(c) respectively, for a synthetic velocity field consisting of Gaussian distributed noise. Contours scale logarithmically.
$s_{3}$
, (a)–(c) respectively, for a synthetic velocity field consisting of Gaussian distributed noise. Contours scale logarithmically.
It can be seen from figure 8 that the joint p.d.f.s are more skewed towards the bound given by
![]() $s_{1}=-2\tilde{s}_{1}$
than that given by
$s_{1}=-2\tilde{s}_{1}$
than that given by
![]() $s_{1}=\tilde{s}_{1}$
, and towards
$s_{1}=\tilde{s}_{1}$
, and towards
![]() $s_{3}=-\tilde{s}_{1}/2$
rather than
$s_{3}=-\tilde{s}_{1}/2$
rather than
![]() $s_{3}=\tilde{s}_{1}$
. Similarly, figure 9 shows that the joint densities for
$s_{3}=\tilde{s}_{1}$
. Similarly, figure 9 shows that the joint densities for
![]() $\tilde{s}_{2}$
are skewed towards
$\tilde{s}_{2}$
are skewed towards
![]() $s_{1}=-\tilde{s}_{2}/2$
as opposed to
$s_{1}=-\tilde{s}_{2}/2$
as opposed to
![]() $s_{1}=\tilde{s}_{2}$
, and towards
$s_{1}=\tilde{s}_{2}$
, and towards
![]() $s_{3}=-2\tilde{s}_{2}$
rather than
$s_{3}=-2\tilde{s}_{2}$
rather than
![]() $s_{3}=\tilde{s}_{2}$
.
$s_{3}=\tilde{s}_{2}$
.
The modal values of the intermediate eigenvalue are seen to approximately follow
![]() $s_{2}=\tilde{s}_{1}/4$
and
$s_{2}=\tilde{s}_{1}/4$
and
![]() $s_{2}=-\tilde{s}_{2}/3$
. The exact equations for the modal values of the full eigenvalues for each of the given reduced eigenvalues are
$s_{2}=-\tilde{s}_{2}/3$
. The exact equations for the modal values of the full eigenvalues for each of the given reduced eigenvalues are
Figure 11 shows the first three standardised moments of the full eigenvalues
![]() $s_{i}$
, conditioned upon the respective reduced eigenvalues
$s_{i}$
, conditioned upon the respective reduced eigenvalues
![]() $\tilde{s}_{1},\tilde{s}_{2}$
. The nomenclature
$\tilde{s}_{1},\tilde{s}_{2}$
. The nomenclature
![]() $M(s_{i}|\tilde{s}_{i})$
denotes the statistical moment of
$M(s_{i}|\tilde{s}_{i})$
denotes the statistical moment of
![]() $s_{i}$
given
$s_{i}$
given
![]() $\tilde{s}_{i}$
, where
$\tilde{s}_{i}$
, where
![]() $M$
is either
$M$
is either
![]() ${\it\mu}$
(mean,
${\it\mu}$
(mean,
![]() $\langle s_{i}\rangle$
),
$\langle s_{i}\rangle$
),
![]() ${\it\sigma}^{2}$
(variance,
${\it\sigma}^{2}$
(variance,
![]() $\langle {s_{i}}^{2}\rangle -\langle s_{i}\rangle ^{2}$
) or
$\langle {s_{i}}^{2}\rangle -\langle s_{i}\rangle ^{2}$
) or
![]() ${\it\gamma}$
(skewness,
${\it\gamma}$
(skewness,
![]() $\langle {s_{i}}^{3}\rangle /\langle {s_{i}}^{2}\rangle ^{3/2}$
).
$\langle {s_{i}}^{3}\rangle /\langle {s_{i}}^{2}\rangle ^{3/2}$
).

Figure 11. Statistical moments of the strain-rate eigenvalues conditioned on
![]() $\tilde{s}_{i}$
. (a) Mean
$\tilde{s}_{i}$
. (a) Mean
![]() ${\it\mu}(s_{i}|\tilde{s}_{1})$
, (b)
${\it\mu}(s_{i}|\tilde{s}_{1})$
, (b)
![]() ${\it\mu}(s_{i}|\tilde{s}_{2})$
, (c) variance
${\it\mu}(s_{i}|\tilde{s}_{2})$
, (c) variance
![]() ${\it\sigma}^{2}(s_{i}|\tilde{s}_{1})$
, (d)
${\it\sigma}^{2}(s_{i}|\tilde{s}_{1})$
, (d)
![]() ${\it\sigma}^{2}(s_{i}|\tilde{s}_{2})$
(e) skewness
${\it\sigma}^{2}(s_{i}|\tilde{s}_{2})$
(e) skewness
![]() ${\it\gamma}(s_{i}|\tilde{s}_{1})$
and (f)
${\it\gamma}(s_{i}|\tilde{s}_{1})$
and (f)
![]() ${\it\gamma}(s_{i}|\tilde{s}_{2})$
.
${\it\gamma}(s_{i}|\tilde{s}_{2})$
.
For the most commonly occurring case of
![]() $\tilde{s}_{1}>0$
and
$\tilde{s}_{1}>0$
and
![]() $\tilde{s}_{2}<0$
it can be seen that
$\tilde{s}_{2}<0$
it can be seen that
![]() ${\it\mu}(s_{2}|\tilde{s}_{i})>0$
. For
${\it\mu}(s_{2}|\tilde{s}_{i})>0$
. For
![]() $0<\tilde{s}_{1}/\langle \tilde{\unicode[STIX]{x1D61A}}_{ij}\tilde{\unicode[STIX]{x1D61A}}_{ij}\rangle ^{1/2}<1$
and
$0<\tilde{s}_{1}/\langle \tilde{\unicode[STIX]{x1D61A}}_{ij}\tilde{\unicode[STIX]{x1D61A}}_{ij}\rangle ^{1/2}<1$
and
![]() $-1<\tilde{s}_{2}/\langle \tilde{\unicode[STIX]{x1D61A}}_{ij}\tilde{\unicode[STIX]{x1D61A}}_{ij}\rangle ^{1/2}<0$
it is observed that the ratio
$-1<\tilde{s}_{2}/\langle \tilde{\unicode[STIX]{x1D61A}}_{ij}\tilde{\unicode[STIX]{x1D61A}}_{ij}\rangle ^{1/2}<0$
it is observed that the ratio
![]() ${\it\mu}(s_{3}|\tilde{s}_{i}):{\it\mu}(s_{2}|\tilde{s}_{i}):{\it\mu}(s_{1}|\tilde{s}_{i})$
is approximately
${\it\mu}(s_{3}|\tilde{s}_{i}):{\it\mu}(s_{2}|\tilde{s}_{i}):{\it\mu}(s_{1}|\tilde{s}_{i})$
is approximately
![]() $-4.8$
:1:3.8, which is slightly higher than the reported modal ratios of roughly
$-4.8$
:1:3.8, which is slightly higher than the reported modal ratios of roughly
![]() $-4$
:1:3 (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992) in other turbulent flows (for completeness the modal ratio for the entirety of the turbulent region of the mixing layer data is
$-4$
:1:3 (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992) in other turbulent flows (for completeness the modal ratio for the entirety of the turbulent region of the mixing layer data is
![]() $-3.6$
:1:2.6). Whilst the ratio
$-3.6$
:1:2.6). Whilst the ratio
![]() ${\it\mu}(s_{3}|\tilde{s}_{i}):{\it\mu}(s_{2}|\tilde{s}_{i}):{\it\mu}(s_{1}|\tilde{s}_{i})$
is observed to remain largely constant as
${\it\mu}(s_{3}|\tilde{s}_{i}):{\it\mu}(s_{2}|\tilde{s}_{i}):{\it\mu}(s_{1}|\tilde{s}_{i})$
is observed to remain largely constant as
![]() $\tilde{s}_{1}$
is increased it is observed to decrease to approximately
$\tilde{s}_{1}$
is increased it is observed to decrease to approximately
![]() $-3.5$
:1:2.5 for large magnitudes of (negative)
$-3.5$
:1:2.5 for large magnitudes of (negative)
![]() $\tilde{s}_{2}$
. This is indicative of a relatively stronger extensive intermediate strain rate and hence more aggressive ‘sheet-forming’ topological evolution when
$\tilde{s}_{2}$
. This is indicative of a relatively stronger extensive intermediate strain rate and hence more aggressive ‘sheet-forming’ topological evolution when
![]() $\tilde{s}_{2}$
is a higher magnitude negative value. Thus knowledge of the reduced strain-rate tensor eigenvalues gives us an indication of the intensity of the topological evolution of the fluid element in three dimensions.
$\tilde{s}_{2}$
is a higher magnitude negative value. Thus knowledge of the reduced strain-rate tensor eigenvalues gives us an indication of the intensity of the topological evolution of the fluid element in three dimensions.
The conditional means
![]() ${\it\mu}(s_{1}|\tilde{s}_{1})$
and
${\it\mu}(s_{1}|\tilde{s}_{1})$
and
![]() ${\it\mu}(s_{3}|\tilde{s}_{1})$
behave similarly to the bounds of (3.6), in that their gradients change by a factor of around
${\it\mu}(s_{3}|\tilde{s}_{1})$
behave similarly to the bounds of (3.6), in that their gradients change by a factor of around
![]() $-1/2$
as
$-1/2$
as
![]() $\tilde{s}_{1}$
passes zero. The reduction in gradient of
$\tilde{s}_{1}$
passes zero. The reduction in gradient of
![]() ${\it\mu}(s_{2}|\tilde{s}_{1})$
as
${\it\mu}(s_{2}|\tilde{s}_{1})$
as
![]() $\tilde{s}_{1}$
passes zero does not appear to be related to the bounds considered in the previous section. The means of the full eigenvalues
$\tilde{s}_{1}$
passes zero does not appear to be related to the bounds considered in the previous section. The means of the full eigenvalues
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{3}$
conditioned upon
$s_{3}$
conditioned upon
![]() $\tilde{s}_{2}$
, shown in figure 11(b), behave similarly. However, when conditioned upon
$\tilde{s}_{2}$
, shown in figure 11(b), behave similarly. However, when conditioned upon
![]() $\tilde{s}_{2}$
it is observed that the gradient of
$\tilde{s}_{2}$
it is observed that the gradient of
![]() ${\it\mu}(s_{2}|\tilde{s}_{2})$
not only changes its magnitude as it passes
${\it\mu}(s_{2}|\tilde{s}_{2})$
not only changes its magnitude as it passes
![]() $\tilde{s}_{2}=0$
but also its sign, meaning that
$\tilde{s}_{2}=0$
but also its sign, meaning that
![]() $\langle s_{2}\rangle$
remains positive for all
$\langle s_{2}\rangle$
remains positive for all
![]() $\tilde{s}_{2}$
and hence ‘sheet-forming’ is favoured over ‘tube-forming’. Thus
$\tilde{s}_{2}$
and hence ‘sheet-forming’ is favoured over ‘tube-forming’. Thus
![]() ${\it\mu}(s_{2}|\tilde{s}_{1})$
more closely follows
${\it\mu}(s_{2}|\tilde{s}_{1})$
more closely follows
![]() ${\it\mu}(s_{3}|\tilde{s}_{1})$
, whereas
${\it\mu}(s_{3}|\tilde{s}_{1})$
, whereas
![]() ${\it\mu}(s_{2}|\tilde{s}_{2})$
varies as
${\it\mu}(s_{2}|\tilde{s}_{2})$
varies as
![]() ${\it\mu}(s_{1}|\tilde{s}_{2})$
, resulting in preferential ‘tube-forming’ topological evolution when
${\it\mu}(s_{1}|\tilde{s}_{2})$
, resulting in preferential ‘tube-forming’ topological evolution when
![]() $\tilde{s}_{1}<0$
, in agreement with Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013).
$\tilde{s}_{1}<0$
, in agreement with Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013).
Such dependence upon the sign of the reduced eigenvalues is also prominent in the case of skewness. In particular,
![]() ${\it\gamma}(s_{2}|\tilde{s}_{1})$
abruptly changes from positive to negative as
${\it\gamma}(s_{2}|\tilde{s}_{1})$
abruptly changes from positive to negative as
![]() $\tilde{s}_{1}$
passes zero. An explanation for this behaviour is suggested by the structure of the joint p.d.f. presented in figure 8(b). In particular, for
$\tilde{s}_{1}$
passes zero. An explanation for this behaviour is suggested by the structure of the joint p.d.f. presented in figure 8(b). In particular, for
![]() $\tilde{s}_{1}<0$
the conditional density of
$\tilde{s}_{1}<0$
the conditional density of
![]() $s_{2}$
is monotonic until the upper bound
$s_{2}$
is monotonic until the upper bound
![]() $s_{2}=\tilde{s}_{1}$
. However, for
$s_{2}=\tilde{s}_{1}$
. However, for
![]() $\tilde{s}_{1}>0$
, the conditional density has a maximum value strictly before the upper bound is met. Again, this behaviour is not indicated by the eigenvalue bounds of (3.6). Opposite behaviour to this is observed for
$\tilde{s}_{1}>0$
, the conditional density has a maximum value strictly before the upper bound is met. Again, this behaviour is not indicated by the eigenvalue bounds of (3.6). Opposite behaviour to this is observed for
![]() ${\it\gamma}(s_{3}|\tilde{s}_{1})$
with a decrease (and negative skewness) observed up until
${\it\gamma}(s_{3}|\tilde{s}_{1})$
with a decrease (and negative skewness) observed up until
![]() $\tilde{s}_{1}/\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle ^{1/2}\approx 1$
before subsequently increasing as the unimodal behaviour of the joint p.d.f. of figure 8(c) becomes more significant. The skewness for all of the turbulent strain rates is subsequently observed to be uniform for large values of
$\tilde{s}_{1}/\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle ^{1/2}\approx 1$
before subsequently increasing as the unimodal behaviour of the joint p.d.f. of figure 8(c) becomes more significant. The skewness for all of the turbulent strain rates is subsequently observed to be uniform for large values of
![]() $\tilde{s}_{1}$
.
$\tilde{s}_{1}$
.
A similar change in
![]() ${\it\gamma}(s_{3}|\tilde{s}_{2})$
can be observed in figure 11(f). Again, it can be seen from figure 9(c) that the conditional density changes from monotonic to unimodal as
${\it\gamma}(s_{3}|\tilde{s}_{2})$
can be observed in figure 11(f). Again, it can be seen from figure 9(c) that the conditional density changes from monotonic to unimodal as
![]() $\tilde{s}_{2}$
changes sign. This time, however, the change can be attributed to the bound
$\tilde{s}_{2}$
changes sign. This time, however, the change can be attributed to the bound
![]() $s_{3}\leqslant \min \{\tilde{s}_{2},-(\tilde{s}_{1}+\tilde{s}_{2})\}$
. In particular, the second bound
$s_{3}\leqslant \min \{\tilde{s}_{2},-(\tilde{s}_{1}+\tilde{s}_{2})\}$
. In particular, the second bound
![]() $s_{3}\leqslant -(\tilde{s}_{1}+\tilde{s}_{2})$
is active when
$s_{3}\leqslant -(\tilde{s}_{1}+\tilde{s}_{2})$
is active when
![]() $2\tilde{s}_{2}+\tilde{s}_{1}\geqslant 0$
, and this is most likely to be the case when
$2\tilde{s}_{2}+\tilde{s}_{1}\geqslant 0$
, and this is most likely to be the case when
![]() $\tilde{s}_{2}$
is positive. Hence, in this range, the behaviour of
$\tilde{s}_{2}$
is positive. Hence, in this range, the behaviour of
![]() $s_{3}$
is influenced by both reduced eigenvalues, serving to push the peak of the conditional p.d.f. away from the conservative bound
$s_{3}$
is influenced by both reduced eigenvalues, serving to push the peak of the conditional p.d.f. away from the conservative bound
![]() $s_{3}\leqslant -2\tilde{s}_{2}$
indicated in figure 9. It is observed that
$s_{3}\leqslant -2\tilde{s}_{2}$
indicated in figure 9. It is observed that
![]() ${\it\gamma}(s_{1}|\tilde{s}_{2})$
and
${\it\gamma}(s_{1}|\tilde{s}_{2})$
and
![]() ${\it\gamma}(s_{2}|\tilde{s}_{2})$
follow a contrasting pattern to that for
${\it\gamma}(s_{2}|\tilde{s}_{2})$
follow a contrasting pattern to that for
![]() ${\it\gamma}(s_{3}|\tilde{s}_{1})$
, with constant skewness seen for lower magnitudes of
${\it\gamma}(s_{3}|\tilde{s}_{1})$
, with constant skewness seen for lower magnitudes of
![]() $\tilde{s}_{2}$
and negative skewness seen at larger (negative) magnitudes.
$\tilde{s}_{2}$
and negative skewness seen at larger (negative) magnitudes.
The conditional variances represent the quality of information that each of the reduced eigenvalues
![]() $\tilde{s}_{1},\tilde{s}_{2}$
contains about the full eigenvalues
$\tilde{s}_{1},\tilde{s}_{2}$
contains about the full eigenvalues
![]() $s_{i}$
. For example, figure 11(c) shows asymmetry of
$s_{i}$
. For example, figure 11(c) shows asymmetry of
![]() ${\it\sigma}^{2}(s_{1}|\tilde{s}_{1})$
, with higher conditional variance for
${\it\sigma}^{2}(s_{1}|\tilde{s}_{1})$
, with higher conditional variance for
![]() $\tilde{s}_{1}<0$
. Again, this is explained by the nature of the bound of (3.6): in the range
$\tilde{s}_{1}<0$
. Again, this is explained by the nature of the bound of (3.6): in the range
![]() $\tilde{s}_{1}<0$
the active bound on
$\tilde{s}_{1}<0$
the active bound on
![]() $s_{1}$
from (3.6) is
$s_{1}$
from (3.6) is
![]() $s_{1}\geqslant -(\tilde{s}_{1}+\tilde{s}_{2})$
; while in the range
$s_{1}\geqslant -(\tilde{s}_{1}+\tilde{s}_{2})$
; while in the range
![]() $\tilde{s}_{1}>0$
the bound
$\tilde{s}_{1}>0$
the bound
![]() $s_{1}\geqslant \tilde{s}_{1}$
is most likely active. Hence, it is not unexpected that for a given
$s_{1}\geqslant \tilde{s}_{1}$
is most likely active. Hence, it is not unexpected that for a given
![]() ${\it\alpha}>0$
, we have
${\it\alpha}>0$
, we have
![]() ${\it\sigma}^{2}(s_{1}|\tilde{s_{1}}=-{\it\alpha})>{\it\sigma}^{2}(s_{1}|\tilde{s}_{1}={\it\alpha})$
. The variances for all
${\it\sigma}^{2}(s_{1}|\tilde{s_{1}}=-{\it\alpha})>{\it\sigma}^{2}(s_{1}|\tilde{s}_{1}={\it\alpha})$
. The variances for all
![]() $s_{i}$
are observed to drop dramatically at
$s_{i}$
are observed to drop dramatically at
![]() $\tilde{s}_{i}=0$
(although this is accentuated for
$\tilde{s}_{i}=0$
(although this is accentuated for
![]() $s_{1}$
due to the ‘peakiness’ of the distributions). This can be explained by the fact that for
$s_{1}$
due to the ‘peakiness’ of the distributions). This can be explained by the fact that for
![]() $\tilde{s}_{i}=0$
the bounds observed in figures 8 and 9 force the modal values of the p.d.f.s of
$\tilde{s}_{i}=0$
the bounds observed in figures 8 and 9 force the modal values of the p.d.f.s of
![]() $s_{i}$
to be located at zero, with monotonic, logarithmically decreasing tails, whereas the modal value moves away from the origin for all other
$s_{i}$
to be located at zero, with monotonic, logarithmically decreasing tails, whereas the modal value moves away from the origin for all other
![]() $\tilde{s}_{i}$
, thereby increasing the variance.
$\tilde{s}_{i}$
, thereby increasing the variance.
Figure 12 shows the joint p.d.f. between
![]() $Q_{S}$
and
$Q_{S}$
and
![]() $q_{S}$
. The asymmetric sector bounds derived in (3.14), dependent upon the sign of
$q_{S}$
. The asymmetric sector bounds derived in (3.14), dependent upon the sign of
![]() $q_{S}$
, are again observed to be sharp. It can be seen that the distribution is slightly skewed towards the bound of
$q_{S}$
, are again observed to be sharp. It can be seen that the distribution is slightly skewed towards the bound of
![]() $Q_{S}\leqslant q_{S}$
for
$Q_{S}\leqslant q_{S}$
for
![]() $q_{S}\leqslant 0$
.
$q_{S}\leqslant 0$
.

Figure 12. Joint p.d.f. of
![]() $Q_{S}$
against
$Q_{S}$
against
![]() $q_{S}$
. Contours scale logarithmically.
$q_{S}$
. Contours scale logarithmically.
We show in (3.20) and (3.21) that the bounds on the mean values of the reduced strain-rate eigenvalues,
![]() $\langle \tilde{s}_{i}\rangle$
, are a function of the kurtosis of
$\langle \tilde{s}_{i}\rangle$
, are a function of the kurtosis of
![]() $\unicode[STIX]{x1D608}_{11}~({\it\kappa})$
. Further, figure 2, illustrates that
$\unicode[STIX]{x1D608}_{11}~({\it\kappa})$
. Further, figure 2, illustrates that
![]() ${\it\kappa}$
is itself a function of the cross-stream direction
${\it\kappa}$
is itself a function of the cross-stream direction
![]() $x_{2}$
. Incorporating the entire turbulent region of the mixing layer as defined by the region in which the enstrophy exceeded the enstrophy threshold (see § 4) the mean kurtosis is computed to be
$x_{2}$
. Incorporating the entire turbulent region of the mixing layer as defined by the region in which the enstrophy exceeded the enstrophy threshold (see § 4) the mean kurtosis is computed to be
![]() ${\it\kappa}=9.4$
leading to the bounds
${\it\kappa}=9.4$
leading to the bounds
 $$\begin{eqnarray}0.40\leqslant \frac{\langle \tilde{s}_{1}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant 1,\quad -1\leqslant \frac{\langle \tilde{s}_{2}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant -0.40,\end{eqnarray}$$
$$\begin{eqnarray}0.40\leqslant \frac{\langle \tilde{s}_{1}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant 1,\quad -1\leqslant \frac{\langle \tilde{s}_{2}\rangle }{\displaystyle \sqrt{\frac{3}{2}}\left\langle \left(\frac{\partial u_{1}}{\partial x_{1}}\right)^{2}\right\rangle ^{1/2}}\leqslant -0.40,\end{eqnarray}$$
which are indicated by vertical lines on the inset of figure 13 showing the p.d.f.s of
![]() $\tilde{s}_{i}$
. Equations (3.20) and (3.21) and figure 2, however, illustrate that tighter bounds on
$\tilde{s}_{i}$
. Equations (3.20) and (3.21) and figure 2, however, illustrate that tighter bounds on
![]() $\langle \tilde{s}_{i}\rangle$
can be found closer to the centreline of the mixing layer than the periphery. The appropriately normalised expected values are 0.58 and
$\langle \tilde{s}_{i}\rangle$
can be found closer to the centreline of the mixing layer than the periphery. The appropriately normalised expected values are 0.58 and
![]() $-0.66$
, respectively, which can be seen to lie within the expected ranges. We observe, however, that
$-0.66$
, respectively, which can be seen to lie within the expected ranges. We observe, however, that
![]() $-\langle \tilde{s}_{1}\rangle /\langle \tilde{s}_{2}\rangle =0.88$
instead of taking the value 1, which would be the case if the flow were truly isotropic.
$-\langle \tilde{s}_{1}\rangle /\langle \tilde{s}_{2}\rangle =0.88$
instead of taking the value 1, which would be the case if the flow were truly isotropic.
Further, assuming that (3.27) holds and using
![]() ${\it\kappa}=9.4$
, the upper bounds of
${\it\kappa}=9.4$
, the upper bounds of
![]() ${\it\sigma}_{\tilde{s}_{1,2}}^{2}$
from (3.26) are 1.26 and 1.76, respectively. These compare to their respective numerical values of 0.980 and 1.388. We note that the conjecture
${\it\sigma}_{\tilde{s}_{1,2}}^{2}$
from (3.26) are 1.26 and 1.76, respectively. These compare to their respective numerical values of 0.980 and 1.388. We note that the conjecture
![]() $\langle p_{S}\sqrt{X}\rangle >0$
is supported by the distributions of the reduced eigenvalues shown in figure 13, where it can be seen that
$\langle p_{S}\sqrt{X}\rangle >0$
is supported by the distributions of the reduced eigenvalues shown in figure 13, where it can be seen that
![]() $\tilde{s}_{2}$
takes a wider range of values than
$\tilde{s}_{2}$
takes a wider range of values than
![]() $\tilde{s}_{1}$
. This supports the observation of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that the tails of the p.d.f. of
$\tilde{s}_{1}$
. This supports the observation of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that the tails of the p.d.f. of
![]() $\tilde{s}_{2}$
are more extensive than those of
$\tilde{s}_{2}$
are more extensive than those of
![]() $\tilde{s}_{1}$
.
$\tilde{s}_{1}$
.
Equation (3.3) shows that knowledge of the magnitude of the reduced strain-rate eigenvalues allows us to place bounds on
![]() $s_{i}$
. By making use of the properties of the expectation operator we may additionally write
$s_{i}$
. By making use of the properties of the expectation operator we may additionally write
and thus we can see that we may bound the mean values of the strain-rate eigenvalues themselves from (3.20) and (3.21). Figure 13 shows that these bounds are actually reasonably tight for a typical free shear flow. Furthermore, knowledge of higher-order moments of
![]() $\tilde{s}_{1}$
and
$\tilde{s}_{1}$
and
![]() $\tilde{s}_{2}$
(such as
$\tilde{s}_{2}$
(such as
![]() ${\it\sigma}_{\tilde{s}_{1,2}}^{2}$
), will give us a better indication of the strength of these bounds that we may place on
${\it\sigma}_{\tilde{s}_{1,2}}^{2}$
), will give us a better indication of the strength of these bounds that we may place on
![]() $s_{i}$
.
$s_{i}$
.

Figure 14. P.d.f.s of the alignment cosines between the three-dimensional embedding of the eigenvectors of
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
and the eigenvectors of
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
and the eigenvectors of
![]() $\unicode[STIX]{x1D61A}_{ij}$
.
$\unicode[STIX]{x1D61A}_{ij}$
.
6. Eigenvectors of
 $\unicode[STIX]{x1D61A}_{ij}$
and
$\unicode[STIX]{x1D61A}_{ij}$
and
 $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
Further to the discussion presented in § 1, (1.4) shows that the interaction between strain rate and rotation, and the enstrophy amplification term
![]() ${\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}$
is strongly dependent upon the alignment cosines between the vorticity vector and the strain-rate eigenvectors. The mean value of the enstrophy amplification term can be shown to relate to the skewness of one of the components of the VGT under the assumption of local isotropy (Betchov Reference Betchov1956):
${\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}$
is strongly dependent upon the alignment cosines between the vorticity vector and the strain-rate eigenvectors. The mean value of the enstrophy amplification term can be shown to relate to the skewness of one of the components of the VGT under the assumption of local isotropy (Betchov Reference Betchov1956):
However, this does not reveal anything of the directionality of the two-dimensional projection of the three strain-rate eigenvectors instantaneously, or indeed whether this is reflected in the eigenvectors (eigenframe) of the reduced strain-rate tensor. These are defined in a similar convention to those of the full strain-rate tensor, with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
corresponding to the first reduced eigenvalue,
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
corresponding to the first reduced eigenvalue,
![]() $\tilde{s}_{1}$
, and
$\tilde{s}_{1}$
, and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
corresponding to
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
corresponding to
![]() $\tilde{s}_{2}$
.
$\tilde{s}_{2}$
.
P.d.f.s of the alignment cosines between the three-dimensional embedding of
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
, defined as
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
, defined as
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}^{3D}=[\tilde{e}_{ix_{1}},\tilde{e}_{ix_{2}},0]^{\text{T}}$
, and
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}^{3D}=[\tilde{e}_{ix_{1}},\tilde{e}_{ix_{2}},0]^{\text{T}}$
, and
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
are presented in figure 14. This three-dimensional embedding of the reduced strain-rate eigenvectors was used such that the out of plane component of
$\boldsymbol{e}_{\boldsymbol{i}}$
are presented in figure 14. This three-dimensional embedding of the reduced strain-rate eigenvectors was used such that the out of plane component of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
,
$\boldsymbol{e}_{\boldsymbol{i}}$
,
![]() $e_{ix_{3}}$
, was included in the norm of
$e_{ix_{3}}$
, was included in the norm of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
when computing the alignment cosines
$\boldsymbol{e}_{\boldsymbol{i}}$
when computing the alignment cosines
in which
![]() $\hat{a}$
denotes a (normalised) unit vector. This is an important consideration for the case in which the eigenvectors of the strain-rate tensor are predominantly oriented perpendicularly to the source plane of the reduced VGT. In this case the alignment between the two-dimensional projection of
$\hat{a}$
denotes a (normalised) unit vector. This is an important consideration for the case in which the eigenvectors of the strain-rate tensor are predominantly oriented perpendicularly to the source plane of the reduced VGT. In this case the alignment between the two-dimensional projection of
![]() $\boldsymbol{e}_{\boldsymbol{i}}\;(=[e_{ix_{1}},e_{ix_{2}}]^{\text{T}})$
and
$\boldsymbol{e}_{\boldsymbol{i}}\;(=[e_{ix_{1}},e_{ix_{2}}]^{\text{T}})$
and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
is heavily distorted by the artificially small norm of the two-dimensional projection of vector
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
is heavily distorted by the artificially small norm of the two-dimensional projection of vector
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
.
$\boldsymbol{e}_{\boldsymbol{i}}$
.
Figure 14 shows that there is a very strong preferential alignment between
![]() $\boldsymbol{e}_{\mathbf{1}}$
and the three-dimensional embedding of
$\boldsymbol{e}_{\mathbf{1}}$
and the three-dimensional embedding of
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
. Whilst there is a progressively increasing probability of the cosine of the angle between the two vectors for increasing
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
. Whilst there is a progressively increasing probability of the cosine of the angle between the two vectors for increasing
![]() $|\!\cos {\it\theta}|$
there is an extremely sharp spike at
$|\!\cos {\it\theta}|$
there is an extremely sharp spike at
![]() $|\!\cos {\it\theta}|=1$
. Qualitatively similar behaviour is also observed for the alignment cosine between
$|\!\cos {\it\theta}|=1$
. Qualitatively similar behaviour is also observed for the alignment cosine between
![]() $\boldsymbol{e}_{\mathbf{3}}$
and the three-dimensional embedding of
$\boldsymbol{e}_{\mathbf{3}}$
and the three-dimensional embedding of
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
, the most compressive of the reduced strain-rate eigenvectors. This evidences the fact that as long as the norm of
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
, the most compressive of the reduced strain-rate eigenvectors. This evidences the fact that as long as the norm of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
factors in the out of plane component (with respect to the reduced VGT source plane) then the eigenvectors of the reduced strain-rate tensor are an excellent predictor of the two-dimensional projection of the full, three-dimensional strain-rate eigenvectors. Evidently the two-dimensional projection of the strain-rate eigenvectors can be described by a vector sum of the unit eigenvectors of
$\boldsymbol{e}_{\boldsymbol{i}}$
factors in the out of plane component (with respect to the reduced VGT source plane) then the eigenvectors of the reduced strain-rate tensor are an excellent predictor of the two-dimensional projection of the full, three-dimensional strain-rate eigenvectors. Evidently the two-dimensional projection of the strain-rate eigenvectors can be described by a vector sum of the unit eigenvectors of
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
. This requires that in cases in which the two-dimensional projection of
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
. This requires that in cases in which the two-dimensional projection of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
is instantaneously aligned in parallel with
$\boldsymbol{e}_{\boldsymbol{i}}$
is instantaneously aligned in parallel with
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
it must be aligned perpendicularly to
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
it must be aligned perpendicularly to
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
and so forth. This is also reflected in the figure with large modal peaks at
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
and so forth. This is also reflected in the figure with large modal peaks at
![]() $|\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}^{3D}|\approx 0$
and
$|\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}^{3D}|\approx 0$
and
![]() $|\hat{\boldsymbol{e}}_{\mathbf{3}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{1}}^{3D}|\approx 0$
. The loci of the alignment cosines between the two-dimensional projections of
$|\hat{\boldsymbol{e}}_{\mathbf{3}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{1}}^{3D}|\approx 0$
. The loci of the alignment cosines between the two-dimensional projections of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
and
$\boldsymbol{e}_{\boldsymbol{i}}$
and
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
are thus circles centred upon the origin with unity radius.
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
are thus circles centred upon the origin with unity radius.
In contrast figure 14 also shows that the alignment between
![]() $\boldsymbol{e}_{\mathbf{2}}$
and the three-dimensional embedding of the reduced strain-rate eigenvectors is bimodal. There are peaks corresponding to parallel and perpendicular alignment with both
$\boldsymbol{e}_{\mathbf{2}}$
and the three-dimensional embedding of the reduced strain-rate eigenvectors is bimodal. There are peaks corresponding to parallel and perpendicular alignment with both
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}^{3D}$
and
$\tilde{\boldsymbol{e}}_{\mathbf{1}}^{3D}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}^{3D}$
, although parallel alignment is more likely for both. It can therefore be seen that there is a minimum preferential alignment at approximately
$\tilde{\boldsymbol{e}}_{\mathbf{2}}^{3D}$
, although parallel alignment is more likely for both. It can therefore be seen that there is a minimum preferential alignment at approximately
![]() $|\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{1}}^{3D}|=0.64$
, which corresponds to an angle
$|\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{1}}^{3D}|=0.64$
, which corresponds to an angle
![]() ${\it\theta}_{\hat{\boldsymbol{e}}_{\mathbf{1}},\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}}\approx 0.9$
between the two vectors and a corresponding minimum preferential alignment at approximately
${\it\theta}_{\hat{\boldsymbol{e}}_{\mathbf{1}},\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}}\approx 0.9$
between the two vectors and a corresponding minimum preferential alignment at approximately
![]() $|\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}^{3D}|=0.73$
corresponding to
$|\hat{\boldsymbol{e}}_{\mathbf{2}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}^{3D}|=0.73$
corresponding to
![]() ${\it\theta}_{\hat{\boldsymbol{e}}_{\mathbf{1}},\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}}\approx 0.7$
.
${\it\theta}_{\hat{\boldsymbol{e}}_{\mathbf{1}},\hat{\tilde{\boldsymbol{e}}}_{\mathbf{2}}}\approx 0.7$
.
Whilst
![]() $\tilde{s}_{2}\leqslant \tilde{s}_{1}$
, by definition, both
$\tilde{s}_{2}\leqslant \tilde{s}_{1}$
, by definition, both
![]() $\tilde{s}_{1}\leqslant 0$
and
$\tilde{s}_{1}\leqslant 0$
and
![]() $\tilde{s}_{2}\geqslant 0$
are possible meaning that the ‘most extensive’ reduced eigenvalue can in fact be compressive and the ‘most compressive’ reduced eigenvalue can be extensive. Figure 15 shows the alignment cosines between
$\tilde{s}_{2}\geqslant 0$
are possible meaning that the ‘most extensive’ reduced eigenvalue can in fact be compressive and the ‘most compressive’ reduced eigenvalue can be extensive. Figure 15 shows the alignment cosines between
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
and the three-dimensional embedding of
$\boldsymbol{e}_{\boldsymbol{i}}$
and the three-dimensional embedding of
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
, similar to figure 14, conditioned on the special cases of
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
, similar to figure 14, conditioned on the special cases of
![]() $\tilde{s}_{1}<0$
(a–c) and
$\tilde{s}_{1}<0$
(a–c) and
![]() $\tilde{s}_{2}>0$
(d–f). Both of these special cases are shown to have higher-order statistical moments of greater magnitude for the strain-rate eigenvalues conditioned on
$\tilde{s}_{2}>0$
(d–f). Both of these special cases are shown to have higher-order statistical moments of greater magnitude for the strain-rate eigenvalues conditioned on
![]() $\tilde{s}_{i}$
than for the more common occurrences of
$\tilde{s}_{i}$
than for the more common occurrences of
![]() $\tilde{s}_{1}>0$
and
$\tilde{s}_{1}>0$
and
![]() $\tilde{s}_{2}<0$
in figure 11, in addition to larger gradients of these statistical moments with respect to
$\tilde{s}_{2}<0$
in figure 11, in addition to larger gradients of these statistical moments with respect to
![]() $\tilde{s}_{i}$
.
$\tilde{s}_{i}$
.

Figure 15. Conditional p.d.f.s of the alignment cosines between the three-dimensional embedding of the eigenvectors of
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
and the strain-rate eigenvectors, similar to figure 14. (a–c) Conditioned on
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
and the strain-rate eigenvectors, similar to figure 14. (a–c) Conditioned on
![]() $\tilde{s}_{1}<0$
, (d–f) conditioned on
$\tilde{s}_{1}<0$
, (d–f) conditioned on
![]() $\tilde{s}_{2}>0$
.
$\tilde{s}_{2}>0$
.
We observe the same trend for a dominant parallel alignment tendency between the most compressive reduced strain-rate eigenvector (
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
) and the compressive strain-rate eigenvector (
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
) and the compressive strain-rate eigenvector (
![]() $\boldsymbol{e}_{\mathbf{3}}$
) in the case of two compressive reduced strain rates,
$\boldsymbol{e}_{\mathbf{3}}$
) in the case of two compressive reduced strain rates,
![]() $\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
(figure 15
c). Similarly, there is a preferential parallel alignment between the most extensive reduced strain-rate eigenvector (
$\tilde{s}_{2}\leqslant \tilde{s}_{1}<0$
(figure 15
c). Similarly, there is a preferential parallel alignment between the most extensive reduced strain-rate eigenvector (
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
) and the extensive strain-rate eigenvector in the case of two extensive reduced strain rates,
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
) and the extensive strain-rate eigenvector in the case of two extensive reduced strain rates,
![]() $0<\tilde{s}_{2}\leqslant \tilde{s}_{1}$
(figure 15
d). The alignment of the intermediate strain-rate eigenvector with
$0<\tilde{s}_{2}\leqslant \tilde{s}_{1}$
(figure 15
d). The alignment of the intermediate strain-rate eigenvector with
![]() $\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
is now no longer bimodal. It can be seen that there is now a preferential alignment with the three-dimensional embedding of the most extensive reduced strain-rate eigenvector (
$\tilde{\boldsymbol{e}}_{\boldsymbol{i}}$
is now no longer bimodal. It can be seen that there is now a preferential alignment with the three-dimensional embedding of the most extensive reduced strain-rate eigenvector (
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
) for the case of two compressive reduced strain rates (figure 15
b) and with the most compressive reduced strain-rate eigenvector (
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
) for the case of two compressive reduced strain rates (figure 15
b) and with the most compressive reduced strain-rate eigenvector (
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
) for the case of two extensive reduced strain rates (figure 15
e). It is thus observed that the intermediate strain-rate eigenvector, whose corresponding eigenvalue magnitude is bounded by the extensive and compressive strain rates, preferentially aligns in parallel with the eigenvector of the lower magnitude reduced strain-rate eigenvalue in these special cases. The alignment tendencies of
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
) for the case of two extensive reduced strain rates (figure 15
e). It is thus observed that the intermediate strain-rate eigenvector, whose corresponding eigenvalue magnitude is bounded by the extensive and compressive strain rates, preferentially aligns in parallel with the eigenvector of the lower magnitude reduced strain-rate eigenvalue in these special cases. The alignment tendencies of
![]() $|\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\boldsymbol{i}}^{3D}|$
in figure 15(a) and
$|\hat{\boldsymbol{e}}_{\mathbf{1}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\boldsymbol{i}}^{3D}|$
in figure 15(a) and
![]() $|\hat{\boldsymbol{e}}_{\mathbf{3}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\boldsymbol{i}}^{3D}|$
in figure 15(f) shows that there is zero probability of parallel alignment between the three-dimensional embedding of the reduced strain-rate eigenvectors and the extensive strain-rate eigenvector for the case of two compressive reduced strain rates (figure 15
a) and the compressive strain-rate eigenvector for the case of two extensive reduced strain rates (figure 15
f). This is indicative of the fact that for these special cases, for which Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) were directly able to infer the sign of
$|\hat{\boldsymbol{e}}_{\mathbf{3}}\boldsymbol{\cdot }\hat{\tilde{\boldsymbol{e}}}_{\boldsymbol{i}}^{3D}|$
in figure 15(f) shows that there is zero probability of parallel alignment between the three-dimensional embedding of the reduced strain-rate eigenvectors and the extensive strain-rate eigenvector for the case of two compressive reduced strain rates (figure 15
a) and the compressive strain-rate eigenvector for the case of two extensive reduced strain rates (figure 15
f). This is indicative of the fact that for these special cases, for which Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) were directly able to infer the sign of
![]() $s_{2}$
from the reduced VGT data, the corresponding strain-rate eigenvectors are oriented out of plane with respect to the source plane for the reduced VGT.
$s_{2}$
from the reduced VGT data, the corresponding strain-rate eigenvectors are oriented out of plane with respect to the source plane for the reduced VGT.
7. Reduced VGT interrogation plane
The assumption of local isotropy for turbulence is a restrictive one that is often only closely approximated by real turbulent flows (George & Hussein Reference George and Hussein1991), requiring statistical invariance to any direction within the flow. Indeed it can be seen in § 4.1 that although the assumption is considered to be reasonable for the present data it is not fulfilled precisely. This led to the development of the less restrictive assumption of local axisymmetry (Batchelor Reference Batchelor1946; Chandrasekhar Reference Chandrasekhar1950) in which there is a rotational symmetry about a given axis for the statistics of the VGT. (NB for both isotropic and axisymmetric turbulence the assumption of homogeneity, that is a statistical independence from location within the flow field, is additionally required.) The assumption of local axisymmetry is thus particularly relevant to flows that have an obvious preferential direction with regards to the VGT. In the present study the boundary conditions in the
![]() $x_{3}$
direction are periodic, and the growth rate of the mixing layer (and hence mean shear in the streamwise direction) is considered small in the far field, whereas there is a significant shear in the cross-stream (
$x_{3}$
direction are periodic, and the growth rate of the mixing layer (and hence mean shear in the streamwise direction) is considered small in the far field, whereas there is a significant shear in the cross-stream (
![]() $x_{2}$
) direction.
$x_{2}$
) direction.
George & Hussein (Reference George and Hussein1991) derived seven velocity gradient relations that are satisfied by locally axisymmetric turbulence, given in table 2, in which
![]() $x_{x}$
is defined as the preferred flow direction which is assumed to be in the
$x_{x}$
is defined as the preferred flow direction which is assumed to be in the
![]() $x_{2}$
direction of the present mixing layer. The two axes that define the symmetry plane, assumed to be the
$x_{2}$
direction of the present mixing layer. The two axes that define the symmetry plane, assumed to be the
![]() $x_{1}{-}x_{3}$
plane for the present mixing layer, are denoted
$x_{1}{-}x_{3}$
plane for the present mixing layer, are denoted
![]() $x_{r{\it\theta}_{1}}$
and
$x_{r{\it\theta}_{1}}$
and
![]() $x_{r{\it\theta}_{2}}$
. It can be seen that the data largely satisfy the conditions for axisymmetric turbulence with the exception of the first condition which compares the square of the VGT components of the
$x_{r{\it\theta}_{2}}$
. It can be seen that the data largely satisfy the conditions for axisymmetric turbulence with the exception of the first condition which compares the square of the VGT components of the
![]() $u_{2}$
velocity in the
$u_{2}$
velocity in the
![]() $x_{1}$
direction, in which the mixing layer is spreading, and the
$x_{1}$
direction, in which the mixing layer is spreading, and the
![]() $u_{2}$
velocity in the
$u_{2}$
velocity in the
![]() $x_{3}$
direction in which the boundary conditions are periodic. Some of the discrepancies may also be due to the ‘incorrect’ choice of preferred direction, which is likely to have components in both the
$x_{3}$
direction in which the boundary conditions are periodic. Some of the discrepancies may also be due to the ‘incorrect’ choice of preferred direction, which is likely to have components in both the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{1}$
directions.
$x_{1}$
directions.
Table 2. Conditions on velocity gradients for locally axisymmetric turbulence (from George & Hussein Reference George and Hussein1991).

Approximations for the dissipation rate under the assumption of local axisymmetry were derived by George & Hussein (Reference George and Hussein1991), with values compared to those computed with no assumptions:
 $$\begin{eqnarray}\displaystyle {\it\epsilon} & = & \displaystyle {\it\nu}\left[\frac{5}{3}\left\langle \left(\frac{\partial u_{x}}{\partial x_{x}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{x}}{\partial x_{r{\it\theta}_{2}}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{x}}\right)^{2}\right\rangle +\frac{8}{3}\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{r{\it\theta}_{2}}}\right)^{2}\right\rangle \right]\nonumber\\ \displaystyle & = & \displaystyle 1.042\langle {\it\epsilon}\rangle \nonumber\\ \displaystyle & = & \displaystyle {\it\nu}\left[-\left\langle \left(\frac{\partial u_{x}}{\partial x_{x}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{x}}{\partial x_{r{\it\theta}_{1}}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{x}}\right)^{2}\right\rangle +8\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{r{\it\theta}_{1}}}\right)^{2}\right\rangle \right]\nonumber\\ \displaystyle & = & \displaystyle 0.968\langle {\it\epsilon}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\epsilon} & = & \displaystyle {\it\nu}\left[\frac{5}{3}\left\langle \left(\frac{\partial u_{x}}{\partial x_{x}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{x}}{\partial x_{r{\it\theta}_{2}}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{x}}\right)^{2}\right\rangle +\frac{8}{3}\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{r{\it\theta}_{2}}}\right)^{2}\right\rangle \right]\nonumber\\ \displaystyle & = & \displaystyle 1.042\langle {\it\epsilon}\rangle \nonumber\\ \displaystyle & = & \displaystyle {\it\nu}\left[-\left\langle \left(\frac{\partial u_{x}}{\partial x_{x}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{x}}{\partial x_{r{\it\theta}_{1}}}\right)^{2}\right\rangle +2\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{x}}\right)^{2}\right\rangle +8\left\langle \left(\frac{\partial u_{r{\it\theta}_{1}}}{\partial x_{r{\it\theta}_{1}}}\right)^{2}\right\rangle \right]\nonumber\\ \displaystyle & = & \displaystyle 0.968\langle {\it\epsilon}\rangle ,\end{eqnarray}$$
The range in dissipation estimates is lower than those computed under the assumption of local isotropy and the errors of 4.2 % and
![]() $-3.2\,\%$
are small. The difference in the two values indicates that the flow is not truly locally axisymmetric; however, it can be seen that the two estimates are close to and encompass the true value.
$-3.2\,\%$
are small. The difference in the two values indicates that the flow is not truly locally axisymmetric; however, it can be seen that the two estimates are close to and encompass the true value.
For convenience Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) chose the reduced VGT to consist of the upper left-hand quadrant of the VGT, encompassing all gradients in the streamwise and cross-stream directions. To some extent, however, this is an arbitrary choice as a reduced VGT can be formed from any plane within the flow for which data are available. A priori information on a flow field such as the planar mixing layer of this study would make it obvious that for an ‘infinite’ region of the flow (simulated here with periodic boundary conditions in the
![]() $x_{3}$
direction) the preferred plane to choose would indeed be the
$x_{3}$
direction) the preferred plane to choose would indeed be the
![]() $x_{1}{-}x_{2}$
plane. On the other hand if the flow is assumed to be well approximated by local axisymmetry, as is suggested by the results of (7.1), then the kinematics of the reduced VGT would not be expected to be identical if formed from the
$x_{1}{-}x_{2}$
plane. On the other hand if the flow is assumed to be well approximated by local axisymmetry, as is suggested by the results of (7.1), then the kinematics of the reduced VGT would not be expected to be identical if formed from the
![]() $x_{1}{-}x_{3}$
plane (which is assumed to be the rotationally symmetric plane) as opposed to the
$x_{1}{-}x_{3}$
plane (which is assumed to be the rotationally symmetric plane) as opposed to the
![]() $x_{1}{-}x_{2}$
plane.
$x_{1}{-}x_{2}$
plane.
Figure 16 shows the joint p.d.f.s between
![]() $Q$
and the invariants
$Q$
and the invariants
![]() $p$
(a) and
$p$
(a) and
![]() $q$
(b) of the reduced VGT formed from data in the
$q$
(b) of the reduced VGT formed from data in the
![]() $x_{1}{-}x_{3}$
plane, similar to figure 6 which uses the reduced VGT formed in the
$x_{1}{-}x_{3}$
plane, similar to figure 6 which uses the reduced VGT formed in the
![]() $x_{1}{-}x_{2}$
plane. It can be seen that both sets of figures look virtually identical. Furthermore the prediction of the sign of
$x_{1}{-}x_{2}$
plane. It can be seen that both sets of figures look virtually identical. Furthermore the prediction of the sign of
![]() $Q$
from the sign of
$Q$
from the sign of
![]() $q$
is also extremely similar to the data produced from the
$q$
is also extremely similar to the data produced from the
![]() $x_{1}{-}x_{2}$
plane with negative
$x_{1}{-}x_{2}$
plane with negative
![]() $Q$
concurrent to negative
$Q$
concurrent to negative
![]() $q$
85.6 % of the time (cf. 85.3 %) and positive
$q$
85.6 % of the time (cf. 85.3 %) and positive
![]() $Q$
concurrent to positive
$Q$
concurrent to positive
![]() $q$
52.1 % of the time (cf. 54.1 %). Joint p.d.f.s of the eigenvalues of the strain-rate tensor against those from the reduced strain-rate tensor formed in the
$q$
52.1 % of the time (cf. 54.1 %). Joint p.d.f.s of the eigenvalues of the strain-rate tensor against those from the reduced strain-rate tensor formed in the
![]() $x_{1}{-}x_{3}$
plane were also found to be almost identical to figures 8 and 9 but are not shown for brevity.
$x_{1}{-}x_{3}$
plane were also found to be almost identical to figures 8 and 9 but are not shown for brevity.

Figure 16. Joint p.d.f.s of full invariant
![]() $Q$
against invariants
$Q$
against invariants
![]() $p$
(a) and
$p$
(a) and
![]() $q$
(b) of the reduced VGT formed from data in the
$q$
(b) of the reduced VGT formed from data in the
![]() $x_{1}{-}x_{3}$
plane. Contours scale logarithmically.
$x_{1}{-}x_{3}$
plane. Contours scale logarithmically.
![]() $Q$
and
$Q$
and
![]() $s_{i}$
, however, are scalars whereas in § 6 it is shown that the reduced VGT can also act as a predictor for the projection of the strain-rate eigenvectors onto the plane defining the reduced VGT. Figure 17 shows the p.d.f.s of the alignment cosines between the three-dimensional embedding of the eigenvectors of the reduced strain-rate tensor formed from data in the
$s_{i}$
, however, are scalars whereas in § 6 it is shown that the reduced VGT can also act as a predictor for the projection of the strain-rate eigenvectors onto the plane defining the reduced VGT. Figure 17 shows the p.d.f.s of the alignment cosines between the three-dimensional embedding of the eigenvectors of the reduced strain-rate tensor formed from data in the
![]() $x_{1}{-}x_{3}$
plane and the strain-rate eigenvectors, similar to figure 14 for
$x_{1}{-}x_{3}$
plane and the strain-rate eigenvectors, similar to figure 14 for
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
from the
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
from the
![]() $x_{1}{-}x_{2}$
plane. It is observed that the quantitative trends for the alignment tendencies of
$x_{1}{-}x_{2}$
plane. It is observed that the quantitative trends for the alignment tendencies of
![]() $\boldsymbol{e}_{\boldsymbol{i}}$
with the reduced strain-rate eigenvectors in figures 14 and 17 are almost identical. It can thus be concluded that the reduced VGT is a good predictor of the behaviour of the fully three-dimensional strain-rate tensor in a shear flow, both in terms of vector and scalar quantities, without a priori knowledge as to the orientation of the mean strain. This provides evidence that the fine scales of the strain-rate tensor, at least, behave in a more locally isotropic manner than in a locally axisymmetric manner, reinforced by the near unity values of the isotropy parameters in § 4.1. This observation further validates the approach that is taken in this manuscript of bounding
$\boldsymbol{e}_{\boldsymbol{i}}$
with the reduced strain-rate eigenvectors in figures 14 and 17 are almost identical. It can thus be concluded that the reduced VGT is a good predictor of the behaviour of the fully three-dimensional strain-rate tensor in a shear flow, both in terms of vector and scalar quantities, without a priori knowledge as to the orientation of the mean strain. This provides evidence that the fine scales of the strain-rate tensor, at least, behave in a more locally isotropic manner than in a locally axisymmetric manner, reinforced by the near unity values of the isotropy parameters in § 4.1. This observation further validates the approach that is taken in this manuscript of bounding
![]() $\unicode[STIX]{x1D61A}_{ij}$
from
$\unicode[STIX]{x1D61A}_{ij}$
from
![]() $\tilde{\unicode[STIX]{x1D61A}}_{ij}$
under the assumption of local isotropy and thus increases the confidence with which one may use the reduced VGT as an observable state of the full, three-dimensional VGT.
$\tilde{\unicode[STIX]{x1D61A}}_{ij}$
under the assumption of local isotropy and thus increases the confidence with which one may use the reduced VGT as an observable state of the full, three-dimensional VGT.

Figure 17. P.d.f.s of the alignment of the reduced strain-rate eigenvectors
![]() $\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and
$\tilde{\boldsymbol{e}}_{\mathbf{1}}$
and
![]() $\tilde{\boldsymbol{e}}_{\mathbf{2}}$
in the
$\tilde{\boldsymbol{e}}_{\mathbf{2}}$
in the
![]() $x_{1}{-}x_{3}$
plane with the full strain-rate eigenvectors
$x_{1}{-}x_{3}$
plane with the full strain-rate eigenvectors
![]() $\boldsymbol{e}_{\mathbf{1}}$
,
$\boldsymbol{e}_{\mathbf{1}}$
,
![]() $\boldsymbol{e}_{\mathbf{2}}$
and
$\boldsymbol{e}_{\mathbf{2}}$
and
![]() $\boldsymbol{e}_{\mathbf{3}}$
.
$\boldsymbol{e}_{\mathbf{3}}$
.
8. Conclusions
The reduced VGT (
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
) is defined as a
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
) is defined as a
![]() $2\times 2$
block, from a single interrogation plane, of the full VGT. It has subsequently been shown in the study of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that the joint p.d.f. of the invariants,
$2\times 2$
block, from a single interrogation plane, of the full VGT. It has subsequently been shown in the study of Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) that the joint p.d.f. of the invariants,
![]() $p$
and
$p$
and
![]() $q$
, for the characteristic equation for
$q$
, for the characteristic equation for
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
displays a characteristic ‘teapot’ shape for a number of turbulent flows. This distribution is confirmed in this study, lending credence to the notion that this shape is also a ‘universal’ feature of turbulent flows similar to the ‘teardrop’ shape for the joint p.d.f. between the second and third invariants of the full VGT.
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
displays a characteristic ‘teapot’ shape for a number of turbulent flows. This distribution is confirmed in this study, lending credence to the notion that this shape is also a ‘universal’ feature of turbulent flows similar to the ‘teardrop’ shape for the joint p.d.f. between the second and third invariants of the full VGT.
The third invariant,
![]() $R$
, of the VGT is comprised of the inviscid source/sink terms in the dynamics of strain rate (symmetric part of VGT) and rotation (skew-symmetric part of VGT), as emphasised in (1.2) and (1.3) respectively, and thus consists of sums of triple velocity gradient products. These terms are not present in two-dimensional turbulence and thus it is observed that the invariants of the reduced VGT are poor predictors of the kinematics of
$R$
, of the VGT is comprised of the inviscid source/sink terms in the dynamics of strain rate (symmetric part of VGT) and rotation (skew-symmetric part of VGT), as emphasised in (1.2) and (1.3) respectively, and thus consists of sums of triple velocity gradient products. These terms are not present in two-dimensional turbulence and thus it is observed that the invariants of the reduced VGT are poor predictors of the kinematics of
![]() $R$
, despite the fact that the ensemble average
$R$
, despite the fact that the ensemble average
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
can be related to
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
can be related to
![]() $\langle pq\rangle$
by (2.2). Contrastingly the second invariant
$\langle pq\rangle$
by (2.2). Contrastingly the second invariant
![]() $Q$
reveals the local excess of rotation over strain rate, something that is described by two-dimensional turbulent phenomena. It is subsequently found that whilst the first invariant of
$Q$
reveals the local excess of rotation over strain rate, something that is described by two-dimensional turbulent phenomena. It is subsequently found that whilst the first invariant of
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
,
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
,
![]() $p$
, which effectively reveals the ‘compressibility’ of the reduced VGT is a poor predictor of
$p$
, which effectively reveals the ‘compressibility’ of the reduced VGT is a poor predictor of
![]() $Q$
, the second invariant,
$Q$
, the second invariant,
![]() $q$
, carries significant information on
$q$
, carries significant information on
![]() $Q$
.
$Q$
.
Further, it was observed that the ability to make predictions about the three-dimensional VGT from
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
was significantly increased for straining regions of the flow (
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
was significantly increased for straining regions of the flow (
![]() $Q<0$
) as opposed to swirling regions of the flow (
$Q<0$
) as opposed to swirling regions of the flow (
![]() $Q>0$
). This is evidenced by the greater variance of the joint p.d.f. between
$Q>0$
). This is evidenced by the greater variance of the joint p.d.f. between
![]() $Q$
and
$Q$
and
![]() $q$
of figure 6 for
$q$
of figure 6 for
![]() $Q>0$
and subsequent ability to predict the sign of
$Q>0$
and subsequent ability to predict the sign of
![]() $Q$
based on
$Q$
based on
![]() $q$
. This observation can be rationalised as follows:
$q$
. This observation can be rationalised as follows:
![]() $Q>0$
requires a dominance of rotation (skew-symmetric tensor) over strain rate (symmetric tensor). In three dimensions swirling is defined by a real and complex-conjugate pair of roots to the characteristic equation for
$Q>0$
requires a dominance of rotation (skew-symmetric tensor) over strain rate (symmetric tensor). In three dimensions swirling is defined by a real and complex-conjugate pair of roots to the characteristic equation for
![]() $\unicode[STIX]{x1D608}_{ij}$
, with the real eigenvector normal to the complex plane and defining the normal vector to the local swirling (Zhou et al.
Reference Zhou, Adrian, Balachandar and Kendall1999). In two dimensions this real eigenvector cannot exist with only real or a complex-conjugate pair of roots being permissible for the characteristic equation for
$\unicode[STIX]{x1D608}_{ij}$
, with the real eigenvector normal to the complex plane and defining the normal vector to the local swirling (Zhou et al.
Reference Zhou, Adrian, Balachandar and Kendall1999). In two dimensions this real eigenvector cannot exist with only real or a complex-conjugate pair of roots being permissible for the characteristic equation for
![]() $\tilde{\unicode[STIX]{x1D608}}_{ij}$
. To successfully describe swirling via the reduced VGT it is thus necessary to project this swirling eigenvector onto the two-dimensional plane from which the reduced VGT is formed. Whilst it is shown that the interrogation plane, that from which the reduced VGT is formed, is unimportant in the ability to predict the kinematics of both scalar quantities and vectors in three dimensions, the eigenframe of the strain-rate tensor will always have at least two vectors with a significant component in the interrogation plane. This is not necessarily the case for a single swirling eigenvector. Figure 15 shows that the special cases of
$\tilde{\unicode[STIX]{x1D608}}_{ij}$
. To successfully describe swirling via the reduced VGT it is thus necessary to project this swirling eigenvector onto the two-dimensional plane from which the reduced VGT is formed. Whilst it is shown that the interrogation plane, that from which the reduced VGT is formed, is unimportant in the ability to predict the kinematics of both scalar quantities and vectors in three dimensions, the eigenframe of the strain-rate tensor will always have at least two vectors with a significant component in the interrogation plane. This is not necessarily the case for a single swirling eigenvector. Figure 15 shows that the special cases of
![]() $\tilde{s}_{1}$
and
$\tilde{s}_{1}$
and
![]() $\tilde{s}_{2}$
both having the same sign arise when there is a negligibly small component of
$\tilde{s}_{2}$
both having the same sign arise when there is a negligibly small component of
![]() $\boldsymbol{e}_{\mathbf{1}}$
or
$\boldsymbol{e}_{\mathbf{1}}$
or
![]() $\boldsymbol{e}_{\mathbf{3}}$
within the interrogation plane. There is evidently a higher likelihood of a single vector having a small component in the interrogation plane than an eigenframe of three vectors, hence the reduced ability of the reduced VGT to predict the full VGT in rotationally dominated regions of the flow.
$\boldsymbol{e}_{\mathbf{3}}$
within the interrogation plane. There is evidently a higher likelihood of a single vector having a small component in the interrogation plane than an eigenframe of three vectors, hence the reduced ability of the reduced VGT to predict the full VGT in rotationally dominated regions of the flow.
Compared to the case of the full VGT, significantly more information can be derived about the strain-rate tensor
![]() $\unicode[STIX]{x1D61A}_{ij}$
from its reduced counterpart. A simple consequence of the fact that
$\unicode[STIX]{x1D61A}_{ij}$
from its reduced counterpart. A simple consequence of the fact that
![]() $\unicode[STIX]{x1D61A}_{ij}$
is symmetric implies that the full and reduced eigenvalues are ‘interlaced’ according to (3.3), meaning that knowledge of the reduced eigenvalues
$\unicode[STIX]{x1D61A}_{ij}$
is symmetric implies that the full and reduced eigenvalues are ‘interlaced’ according to (3.3), meaning that knowledge of the reduced eigenvalues
![]() $\tilde{s}_{i}$
restricts the location of the full eigenvalues
$\tilde{s}_{i}$
restricts the location of the full eigenvalues
![]() $s_{i}$
to certain intervals of the real line. If incompressibility is assumed, then stronger bounds can be placed upon the most extensive and compressive eigenvalues of
$s_{i}$
to certain intervals of the real line. If incompressibility is assumed, then stronger bounds can be placed upon the most extensive and compressive eigenvalues of
![]() $\unicode[STIX]{x1D61A}_{ij}$
, with these bounds implying that
$\unicode[STIX]{x1D61A}_{ij}$
, with these bounds implying that
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{3}$
lie in triangular cones in
$s_{3}$
lie in triangular cones in
![]() $(\tilde{s}_{1},\tilde{s}_{2},s_{1})$
-space and
$(\tilde{s}_{1},\tilde{s}_{2},s_{1})$
-space and
![]() $(\tilde{s}_{1},\tilde{s}_{2},s_{3})$
-space, respectively. Furthermore, whilst it has been shown that
$(\tilde{s}_{1},\tilde{s}_{2},s_{3})$
-space, respectively. Furthermore, whilst it has been shown that
![]() $\langle s_{2}\rangle >0$
for turbulent flows (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Lund & Rogers Reference Lund and Rogers1994), suggesting a mean tendency towards ‘sheet-forming’ topological evolution,
$\langle s_{2}\rangle >0$
for turbulent flows (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Tsinober et al.
Reference Tsinober, Kit and Dracos1992; Lund & Rogers Reference Lund and Rogers1994), suggesting a mean tendency towards ‘sheet-forming’ topological evolution,
![]() $\langle s_{2}\rangle <0$
and hence preferential ‘tube-forming’ is observed for regions of the flow in which
$\langle s_{2}\rangle <0$
and hence preferential ‘tube-forming’ is observed for regions of the flow in which
![]() $\tilde{s}_{1}<0$
.
$\tilde{s}_{1}<0$
.
Since the characteristic ‘teardrop’ shape of the p.d.f.s of
![]() $Q$
and
$Q$
and
![]() $R$
is thought to be ‘universal’ for turbulent flows, it is not unreasonable to expect that simpler quantities such as the p.d.f.s of the reduced eigenvalues
$R$
is thought to be ‘universal’ for turbulent flows, it is not unreasonable to expect that simpler quantities such as the p.d.f.s of the reduced eigenvalues
![]() $\tilde{s}_{i}$
enjoy a similar property. To begin to address this question, bounds have been derived upon the first two statistical moments of
$\tilde{s}_{i}$
enjoy a similar property. To begin to address this question, bounds have been derived upon the first two statistical moments of
![]() $\tilde{s}_{i}$
, under the assumptions of isotropy and homogeneity. For example, the expected value
$\tilde{s}_{i}$
, under the assumptions of isotropy and homogeneity. For example, the expected value
![]() $\langle \tilde{s}_{1}\rangle$
must lie in a strictly positive interval, the lower end of which depends upon the kurtosis
$\langle \tilde{s}_{1}\rangle$
must lie in a strictly positive interval, the lower end of which depends upon the kurtosis
![]() ${\it\kappa}$
of
${\it\kappa}$
of
![]() $\partial u_{1}/\partial x_{1}$
, and tighter bounds are obtained for smaller values of
$\partial u_{1}/\partial x_{1}$
, and tighter bounds are obtained for smaller values of
![]() ${\it\kappa}$
. Whether this suggests that
${\it\kappa}$
. Whether this suggests that
![]() $\langle \tilde{s}_{1}\rangle$
is itself dependent upon
$\langle \tilde{s}_{1}\rangle$
is itself dependent upon
![]() ${\it\kappa}$
, or simply that the proven bound varies with
${\it\kappa}$
, or simply that the proven bound varies with
![]() ${\it\kappa}$
, is an open question. Interestingly, the numerical data suggest that the
${\it\kappa}$
, is an open question. Interestingly, the numerical data suggest that the
![]() ${\it\kappa}$
-independent bound on the upper end of the interval, proven by an application of the Cauchy–Schwarz inequality, is actually the most conservative.
${\it\kappa}$
-independent bound on the upper end of the interval, proven by an application of the Cauchy–Schwarz inequality, is actually the most conservative.
Using the proven bounds for the expected values of
![]() $\tilde{s}_{i}$
, bounds are also placed upon the variances and the covariance of the two eigenvalues. The covariance
$\tilde{s}_{i}$
, bounds are also placed upon the variances and the covariance of the two eigenvalues. The covariance
![]() ${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})$
is shown to lie in the interval
${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})$
is shown to lie in the interval
![]() $[1/4((9/{\it\kappa})-5),1/4]$
which appears conservative, since it is expected that
$[1/4((9/{\it\kappa})-5),1/4]$
which appears conservative, since it is expected that
![]() ${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})<0$
by virtue of the fact that
${\it\sigma}(\tilde{s}_{1},\tilde{s}_{2})<0$
by virtue of the fact that
![]() $\tilde{s}_{2}<0<\tilde{s}_{1}$
for over 85.2 % of spatial locations. However, the upper bound of
$\tilde{s}_{2}<0<\tilde{s}_{1}$
for over 85.2 % of spatial locations. However, the upper bound of
![]() $1/4$
may be lowered if a better upper bound can be found for
$1/4$
may be lowered if a better upper bound can be found for
![]() $\langle \tilde{s}_{1}\rangle$
, again suggesting that attention should be focused upon improving this bound. Finally, we note that figure 13 suggests that
$\langle \tilde{s}_{1}\rangle$
, again suggesting that attention should be focused upon improving this bound. Finally, we note that figure 13 suggests that
![]() $\tilde{s}_{1}$
is positively skewed, while
$\tilde{s}_{1}$
is positively skewed, while
![]() $\tilde{s}_{2}$
is negatively skewed. Whether these properties can be inferred for isotropy and homogeneity presents an interesting question for future research.
$\tilde{s}_{2}$
is negatively skewed. Whether these properties can be inferred for isotropy and homogeneity presents an interesting question for future research.
Acknowledgement
The authors would like to acknowledge Dr S. Laizet for his role in the simulation of the dataset.
Appendix A
Suppose that
![]() $a,b>0$
are constants such that
$a,b>0$
are constants such that
Since
![]() $\langle X\rangle >0$
, it follows from substituting
$\langle X\rangle >0$
, it follows from substituting
![]() $y=x/\langle X\rangle$
into (A 1) that
$y=x/\langle X\rangle$
into (A 1) that
Now, let
![]() $f_{X}$
be the p.d.f. of the fluctuating variable
$f_{X}$
be the p.d.f. of the fluctuating variable
![]() $X$
, which is assumed to be continuous. Then,
$X$
, which is assumed to be continuous. Then,
 $$\begin{eqnarray}\displaystyle \langle X^{1/2}\rangle & = & \displaystyle \int _{0}^{\infty }y^{1/2}f_{X}(y)\text{d}y\geqslant \left(-\frac{a}{\langle X\rangle ^{2}}\int _{0}^{\infty }y^{2}f_{X}(y)\text{d}y+\frac{b}{\langle X\rangle }\int _{0}^{\infty }yf_{X}(y)\text{d}y\right)\langle X\rangle ^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \left(-a\frac{\langle X^{2}\rangle }{\langle X\rangle ^{2}}+b\right)\langle X\rangle ^{1/2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle X^{1/2}\rangle & = & \displaystyle \int _{0}^{\infty }y^{1/2}f_{X}(y)\text{d}y\geqslant \left(-\frac{a}{\langle X\rangle ^{2}}\int _{0}^{\infty }y^{2}f_{X}(y)\text{d}y+\frac{b}{\langle X\rangle }\int _{0}^{\infty }yf_{X}(y)\text{d}y\right)\langle X\rangle ^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \left(-a\frac{\langle X^{2}\rangle }{\langle X\rangle ^{2}}+b\right)\langle X\rangle ^{1/2}\end{eqnarray}$$
To maximize
![]() $(b-2a{\it\kappa}/3)$
subject to the constaint (A 1), note first that (A 1) holds if and only if
$(b-2a{\it\kappa}/3)$
subject to the constaint (A 1), note first that (A 1) holds if and only if
![]() $ay^{3}-by+1\geqslant 0$
, for all
$ay^{3}-by+1\geqslant 0$
, for all
![]() $y\geqslant 0$
. Elementary calculus can be used to show that this inequality holds if and only if
$y\geqslant 0$
. Elementary calculus can be used to show that this inequality holds if and only if
Since the objective
![]() $b-2a{\it\kappa}/3$
is increasing in
$b-2a{\it\kappa}/3$
is increasing in
![]() $b$
, the optimal value is obtained when
$b$
, the optimal value is obtained when
![]() $b=(4a/27)^{1/3}$
. Hence, the solution is given by the maximization problem
$b=(4a/27)^{1/3}$
. Hence, the solution is given by the maximization problem