Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mitrano, Peter P.
Garzó, Vicente
and
Hrenya, Christine M.
2014.
Instabilities in granular binary mixtures at moderate densities.
Physical Review E,
Vol. 89,
Issue. 2,
Khalil, Nagi
and
Garzó, Vicente
2014.
Homogeneous states in driven granular mixtures: Enskog kinetic theory versus molecular dynamics simulations.
The Journal of Chemical Physics,
Vol. 140,
Issue. 16,
Louge, M. Y.
2014.
The surprising relevance of a continuum description to granular clusters.
Journal of Fluid Mechanics,
Vol. 742,
Issue. ,
p.
1.
Vega Reyes, Francisco
and
Santos, Andrés
2015.
Steady state in a gas of inelastic rough spheres heated by a uniform stochastic force.
Physics of Fluids,
Vol. 27,
Issue. 11,
Yang, Shiliang
Cahyadi, Andy
Wang, Jingwei
and
Chew, Jia Wei
2016.
DEM study of granular flow characteristics in the active and passive regions of a three‐dimensional rotating drum.
AIChE Journal,
Vol. 62,
Issue. 11,
p.
3874.
Chen, Xizhong
Wang, Junwu
and
Li, Jinghai
2016.
Multiscale modeling of rapid granular flow with a hybrid discrete-continuum method.
Powder Technology,
Vol. 304,
Issue. ,
p.
177.
Abrahamsson, P.J.
Sasic, S.
and
Rasmuson, A.
2016.
On continuum modelling of dense inelastic granular flows of relevance for high shear granulation.
Powder Technology,
Vol. 294,
Issue. ,
p.
323.
Fullmer, William D.
and
Hrenya, Christine M.
2016.
Quantitative assessment of fine‐grid kinetic‐theory‐based predictions of mean‐slip in unbounded fluidization.
AIChE Journal,
Vol. 62,
Issue. 1,
p.
11.
Fullmer, William D.
and
Hrenya, Christine M.
2017.
The Homogeneous Cooling State as a Verification Test for Kinetic Theory-Based Continuum Models of Gas–Solid Flows.
Journal of Verification, Validation and Uncertainty Quantification,
Vol. 2,
Issue. 4,
Fullmer, William D.
and
Hrenya, Christine M.
2017.
The Clustering Instability in Rapid Granular and Gas-Solid Flows.
Annual Review of Fluid Mechanics,
Vol. 49,
Issue. 1,
p.
485.
Fullmer, William D.
Liu, Guodong
Yin, Xiaolong
and
Hrenya, Christine M.
2017.
Clustering instabilities in sedimenting fluid–solid systems: critical assessment of kinetic-theory-based predictions using direct numerical simulation data.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
433.
Fullmer, William D.
and
Hrenya, Christine M.
2017.
Are continuum predictions of clustering chaotic?.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 27,
Issue. 3,
Zhao, Bidan
Wang, Jing
and
Wang, Junwu
2017.
An entropy criterion for the validity of Navier-Stokes order continuum theory for gas-solid flow: Kinetic theory analysis.
Chemical Engineering Science,
Vol. 172,
Issue. ,
p.
297.
Fullmer, William D.
and
Hrenya, Christine M.
2018.
Continuum prediction of scale-dependent, anisotropic fluctuating kinetic energy in gas-solid flows.
Chemical Engineering Science,
Vol. 186,
Issue. ,
p.
84.
Chen, Xizhong
and
Wang, Junwu
2018.
Mesoscale-structure-based dynamic multiscale method for gas-solid flow.
Chemical Engineering Science,
Vol. 192,
Issue. ,
p.
864.
Guo, Lei
and
Capecelatro, Jesse
2019.
The role of clusters on heat transfer in sedimenting gas-solid flows.
International Journal of Heat and Mass Transfer,
Vol. 132,
Issue. ,
p.
1217.
Ge, Wei
Chang, Qi
Li, Chengxiang
and
Wang, Junwu
2019.
Multiscale structures in particle–fluid systems: Characterization, modeling, and simulation.
Chemical Engineering Science,
Vol. 198,
Issue. ,
p.
198.
Wang, Jing
Chen, Xizhong
Bian, Wei
Zhao, Bidan
and
Wang, Junwu
2019.
Quantifying the non-equilibrium characteristics of heterogeneous gas–solid flow of smooth, inelastic spheres using a computational fluid dynamics–discrete element method.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
776.
Garzó, Vicente
2019.
Granular Gaseous Flows.
p.
141.
Wang, Junwu
2020.
Continuum theory for dense gas-solid flow: A state-of-the-art review.
Chemical Engineering Science,
Vol. 215,
Issue. ,
p.
115428.
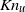 $K{n}_{u} $ ) at the time of cluster detection reveals
$K{n}_{u} $ ) at the time of cluster detection reveals 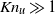 $K{n}_{u} \gg 1$ due to the presence of large velocity gradients associated with vortices. Although kinetic-theory-based continuum models are based on a small-
$K{n}_{u} \gg 1$ due to the presence of large velocity gradients associated with vortices. Although kinetic-theory-based continuum models are based on a small- 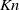 $Kn$ (i.e. small-gradient) assumption, our findings suggest that, similar to molecular gases, Navier–Stokes-order (small-
$Kn$ (i.e. small-gradient) assumption, our findings suggest that, similar to molecular gases, Navier–Stokes-order (small- 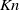 $Kn$ ) theories are surprisingly accurate outside their expected range of validity.
$Kn$ ) theories are surprisingly accurate outside their expected range of validity.
