Article contents
A numerical study of a variable-density low-speed turbulent mixing layer
Published online by Cambridge University Press: 02 October 2017
Abstract
Direct numerical simulations of a temporally developing, low-speed, variable-density, turbulent, plane mixing layer are performed. The Navier–Stokes equations in the low-Mach-number approximation are solved using a novel algorithm based on an extended version of the velocity–vorticity formulation used by Kim et al. (J. Fluid Mech., vol 177, 1987, 133–166) for incompressible flows. Four cases with density ratios 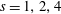 $s=1,2,4$ and 8 are considered. The simulations are run with a Prandtl number of 0.7, and achieve a
$s=1,2,4$ and 8 are considered. The simulations are run with a Prandtl number of 0.7, and achieve a 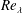 $Re_{\unicode[STIX]{x1D706}}$ up to 150 during the self-similar evolution of the mixing layer. It is found that the growth rate of the mixing layer decreases with increasing density ratio, in agreement with theoretical models of this phenomenon. Comparison with high-speed data shows that the reduction of the growth rates with increasing density ratio has a weak dependence with the Mach number. In addition, the shifting of the mixing layer to the low-density stream has been characterized by analysing one-point statistics within the self-similar interval. This shifting has been quantified, and related to the growth rate of the mixing layer under the assumption that the shape of the mean velocity and density profiles do not change with the density ratio. This leads to a predictive model for the reduction of the growth rate of the momentum thickness, which agrees reasonably well with the available data. Finally, the effect of the density ratio on the turbulent structure has been analysed using flow visualizations and spectra. It is found that with increasing density ratio the longest scales in the high-density side are gradually inhibited. A gradual reduction of the energy in small scales with increasing density ratio is also observed.
$Re_{\unicode[STIX]{x1D706}}$ up to 150 during the self-similar evolution of the mixing layer. It is found that the growth rate of the mixing layer decreases with increasing density ratio, in agreement with theoretical models of this phenomenon. Comparison with high-speed data shows that the reduction of the growth rates with increasing density ratio has a weak dependence with the Mach number. In addition, the shifting of the mixing layer to the low-density stream has been characterized by analysing one-point statistics within the self-similar interval. This shifting has been quantified, and related to the growth rate of the mixing layer under the assumption that the shape of the mean velocity and density profiles do not change with the density ratio. This leads to a predictive model for the reduction of the growth rate of the momentum thickness, which agrees reasonably well with the available data. Finally, the effect of the density ratio on the turbulent structure has been analysed using flow visualizations and spectra. It is found that with increasing density ratio the longest scales in the high-density side are gradually inhibited. A gradual reduction of the energy in small scales with increasing density ratio is also observed.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 35
- Cited by


