Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dastvareh, B.
Azaiez, J.
and
Tsai, P. A.
2019.
Nanocatalytic chemohydrodynamic instability: Deposition effects.
Physical Review E,
Vol. 100,
Issue. 5,
Tsuzuki, Reiko
Li, Qian
Nagatsu, Yuichiro
and
Chen, Ching-Yao
2019.
Numerical study of immiscible viscous fingering in chemically reactive Hele-Shaw flows: Production of surfactants.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Sharma, Vandita
Nand, Sada
Pramanik, Satyajit
Chen, Ching-Yao
and
Mishra, Manoranjan
2020.
Control of radial miscible viscous fingering.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Shukla, Priyanka
and
De Wit, A.
2020.
Influence of the Péclet number on reactive viscous fingering.
Physical Review Fluids,
Vol. 5,
Issue. 1,
De Wit, A.
2020.
Chemo-Hydrodynamic Patterns and Instabilities.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
531.
Omori, Keiichiro
and
Nagatsu, Yuichiro
2020.
Numerical simulations of miscible viscous fingering involving viscosity changes of the displacing fluid by A + B → C chemical reactions.
AIP Advances,
Vol. 10,
Issue. 9,
Maharana, Surya Narayan
and
Mishra, Manoranjan
2021.
Reaction induced interfacial instability of miscible fluids in a channel.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Vienne, Lucien
and
Marié, Simon
2021.
Lattice Boltzmann study of miscible viscous fingering for binary and ternary mixtures.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Kim, Min Chan
Pramanik, Satyajit
Sharma, Vandita
and
Mishra, Manoranjan
2021.
Unstable miscible displacements in radial flow with chemical reactions.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Lei, Timan
and
Luo, Kai H.
2021.
Pore-scale simulation of miscible viscous fingering with dissolution reaction in porous media.
Physics of Fluids,
Vol. 33,
Issue. 3,
Sharma, Vandita
Othman, Hamirul Bin
Nagatsu, Yuichiro
and
Mishra, Manoranjan
2021.
Viscous fingering of miscible annular ring.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Hirano, Sae
Nagatsu, Yuichiro
and
Suzuki, Ryuta X.
2022.
Reversal of effects from gel production in a reacting flow dependent on gel strength.
Physical Review Fluids,
Vol. 7,
Issue. 2,
Maharana, Surya Narayan
and
Mishra, Manoranjan
2022.
Effects of low and high viscous product on Kelvin–Helmholtz instability triggered by A+B→C type reaction.
Physics of Fluids,
Vol. 34,
Issue. 1,
Kim, Min Chan
and
Song, Kwang Ho
2022.
Colloidal nanoparticle-assisted double diffusive gravitational fingering in a vertical Hele-Shaw cell: Theoretical and numerical studies.
Colloid and Interface Science Communications,
Vol. 50,
Issue. ,
p.
100660.
Verma, Priya
Sharma, Vandita
and
Mishra, Manoranjan
2022.
Radial viscous fingering induced by an infinitely fast chemical reaction.
Journal of Fluid Mechanics,
Vol. 945,
Issue. ,
Zahid, Syed
Halkarni, Surfarazhussain S.
and
Tapan Kumar Hota
2023.
Effect of sinusoidal injection velocity on miscible viscous fingering of a finite sample: Nonlinear simulation.
Heliyon,
Vol. 9,
Issue. 3,
p.
e14480.
Sharma, Vandita
Chen, Ching-Yao
and
Mishra, Manoranjan
2023.
A linear stability analysis of instabilities with reactive flows in porous medium.
Physics of Fluids,
Vol. 35,
Issue. 6,
Maharana, Surya Narayan
Sahu, Kirti Chandra
and
Mishra, Manoranjan
2023.
Stability of a layered reactive channel flow.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 479,
Issue. 2271,
Chou, Chi-Chian
Huang, Wei-Cheng
and
Chen, Ching-Yao
2023.
Pattern rupture and channeling effect by alternating radial displacement.
International Journal of Heat and Mass Transfer,
Vol. 207,
Issue. ,
p.
123983.
Kim, Min Chan
and
Pramanik, Satyajit
2023.
Miscible viscous fingering in a packed cylindrical column: Theory and numerics.
Physical Review Fluids,
Vol. 8,
Issue. 1,
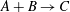 $A+B\rightarrow C$ fronts is analysed numerically in a radial geometry. We are interested to understand miscible fingering instabilities when the simple chemical reaction changes the viscosity of the fluid locally and a non-monotonic viscosity profile with a global maximum or minimum is formed. We consider viscosity-matched reactants
$A+B\rightarrow C$ fronts is analysed numerically in a radial geometry. We are interested to understand miscible fingering instabilities when the simple chemical reaction changes the viscosity of the fluid locally and a non-monotonic viscosity profile with a global maximum or minimum is formed. We consider viscosity-matched reactants 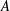 $A$ and
$A$ and 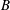 $B$ generating a product
$B$ generating a product 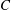 $C$ having different viscosity than the reactants. Depending on the effect of
$C$ having different viscosity than the reactants. Depending on the effect of 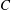 $C$ on the viscosity relative to the reactants, different viscous fingering (VF) patterns are captured which are in good qualitative agreement with the existing radial experiments. We have found that, for a given chemical reaction rate, an unfavourable viscosity contrast is not always sufficient to trigger the instability. For every fixed Péclet number (
$C$ on the viscosity relative to the reactants, different viscous fingering (VF) patterns are captured which are in good qualitative agreement with the existing radial experiments. We have found that, for a given chemical reaction rate, an unfavourable viscosity contrast is not always sufficient to trigger the instability. For every fixed Péclet number (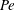 $Pe$), these effects of chemical reaction on VF are summarized in the Damköhler number (
$Pe$), these effects of chemical reaction on VF are summarized in the Damköhler number (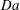 $Da$)
$Da$)  $-$ the log-mobility ratio (
$-$ the log-mobility ratio (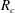 $R_{c}$) parameter space that exhibits a stable region separating two unstable regions corresponding to the cases of more and less viscous product. Fixing
$R_{c}$) parameter space that exhibits a stable region separating two unstable regions corresponding to the cases of more and less viscous product. Fixing 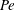 $Pe$, we determine
$Pe$, we determine 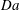 $Da$-dependent critical log-mobility ratios
$Da$-dependent critical log-mobility ratios 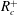 $R_{c}^{+}$ and
$R_{c}^{+}$ and 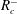 $R_{c}^{-}$ such that no VF is observable whenever
$R_{c}^{-}$ such that no VF is observable whenever 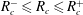 $R_{c}^{-}\leqslant R_{c}\leqslant R_{c}^{+}$. The effect of geometry is observable on the onset of instability, where we obtain significant differences from existing results in the rectilinear geometry.
$R_{c}^{-}\leqslant R_{c}\leqslant R_{c}^{+}$. The effect of geometry is observable on the onset of instability, where we obtain significant differences from existing results in the rectilinear geometry.
