1 Introduction
Path selection of a deformable capsule suspended in an external fluid flowing through a branched microchannel is an important problem that is relevant to understand blood-related flows in the microcirculation (Popel & Johnson Reference Popel and Johnson2005; Secomb Reference Secomb2017), aerosol particle deposition in respiratory airways (Kleinstreuer & Zhang Reference Kleinstreuer and Zhang2010) or to develop microfluidic technologies to separate or enrich suspensions (Gossett et al. Reference Gossett, Weaver, Mach, Hur, Tse, Lee, Amini and Di Carlo2010; Tripathi et al. Reference Tripathi, Kumar, Prabhakar, Joshi and Agrawal2015). The aim of such studies is usually to determine the path selection of the suspended particles at a bifurcation, depending on their position in the feed channel, the flow rate split between the two branches and the bifurcation geometry. This is a complex problem that involves the interactions of a particle with the channel wall or other particles, as well as the effect of the flow field.
In this paper, we eliminate particle–particle interactions and consider a single capsule centred on the feed channel axis far from the bifurcation. Our objective is to understand the fundamental fluid dynamic processes that lead a small capsule to flow into one branch rather than the other, depending on the bifurcation geometry and flow conditions. Another objective is to identify an optimal microfluidic geometry for capsule suspension enrichment.
Different bifurcation configurations have been considered to study the path selection of single fluid-suspended cells or elastic capsules (figure 1): they are defined by the angles between the feed channel and the two daughter branches
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
, and also by the respective cross-sections of the different branches. Typical cases include the symmetric Y-bifurcation where
$\unicode[STIX]{x1D6FD}$
, and also by the respective cross-sections of the different branches. Typical cases include the symmetric Y-bifurcation where
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
, the symmetric T-bifurcation where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
, the symmetric T-bifurcation where
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x03C0}/2$
and the lateral bifurcation (a straight channel with an orthogonal side branch) where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=\unicode[STIX]{x03C0}/2$
and the lateral bifurcation (a straight channel with an orthogonal side branch) where
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x1D6FD}=0$
.
$\unicode[STIX]{x1D6FD}=0$
.
The path selection of a red blood cell (RBC) at a bifurcation has been considered by Fung and co-workers (Fung Reference Fung1973; Yen & Fung Reference Yen and Fung1978), who have proposed a simple qualitative model (Fung’s model) that tries to predict which branch an RBC will take. To this effect, they have considered a single RBC centred at the entrance of a symmetrical Y-bifurcation with branches of equal section (figure 1 a), and estimated the pressure and viscous shear forces acting on it. They find that the resultant force is pointing towards the fast channel, and that consequently, the RBC will flow into the branch with the highest flow rate, or equivalently, the highest velocity. Over the years, Fung’s model has been quoted using velocity or flow rate indifferently as the criterion for branch selection. Although the notions of flow rate or velocity are equivalent when the branches are equal, this is, however, not the case when the branch sections are different. So the question that arises is: when the branches of a bifurcation have different sections, does a particle (deformable or not) flow into the branch which has the highest flow rate or the highest velocity? The answer to this question is important if one wishes to predict the path selection of particles in a network. Surprisingly enough, there are few studies of the path selection of a particle in an asymmetric bifurcation.
Recent careful microfluidic experiments on the flow of a hard sphere in a T-bifurcation (figure 1 b) have shown that when the particle is close to the flow separation line, it has a tendency to enter the low flow rate branch rather than the high flow rate one (Doyeux et al. Reference Doyeux, Podgorski, Peponas, Ismail and Coupier2011). The effect is more pronounced for particles with a radius comparable to the channel cross-section, than for very small particles, which tend to follow the flow streamlines. This phenomenon can also be inferred from the results of two-dimensional numerical models of particle flow in Y- or lateral bifurcations (Barber et al. Reference Barber, Alberding, Restrepo and Secomb2008; Doyeux et al. Reference Doyeux, Podgorski, Peponas, Ismail and Coupier2011; Ye, Huang & Lu Reference Ye, Huang and Lu2015) – see the recent review of Secomb (Reference Secomb2017). But these studies were mainly concerned by the flow of off-centred particles in order to investigate the Zweifach–Fung effect (Svanes & Zweifach Reference Svanes and Zweifach1968; Fung Reference Fung1973; Pries et al. Reference Pries, Ley, Claassen and Gaehtgens1989), which deals with RBC suspensions flowing through a bifurcation. This is a more complex problem than that considered in Fung’s model.
In the specific case of a centred capsule, Woolfenden & Blyth (Reference Woolfenden and Blyth2011) designed a low Reynolds number two-dimensional numerical model of the flow of a RBC-like capsule in an asymmetric Y-bifurcation with
![]() $\unicode[STIX]{x1D6FD}=0$
and different values of
$\unicode[STIX]{x1D6FD}=0$
and different values of
![]() $\unicode[STIX]{x1D6FC}$
. They find that the capsule takes the branch with the highest flow rate, when the two branches have the same cross-section (as predicted by Fung’s model). For branches with unequal cross-sections but equal flow rates, they find that the capsule goes into the branch with the highest velocity. However, this does not answer the question of path selection criterion (velocity or flow rate), since only one value of flow rate split was considered. Note that two-dimensional models reduce the effect of bifurcation geometry to a channel size ratio and branching angle
$\unicode[STIX]{x1D6FC}$
. They find that the capsule takes the branch with the highest flow rate, when the two branches have the same cross-section (as predicted by Fung’s model). For branches with unequal cross-sections but equal flow rates, they find that the capsule goes into the branch with the highest velocity. However, this does not answer the question of path selection criterion (velocity or flow rate), since only one value of flow rate split was considered. Note that two-dimensional models reduce the effect of bifurcation geometry to a channel size ratio and branching angle
![]() $\unicode[STIX]{x1D6FC}$
values, and in addition may introduce a bias to flow situations, which are inherently three-dimensional.
$\unicode[STIX]{x1D6FC}$
values, and in addition may introduce a bias to flow situations, which are inherently three-dimensional.
Recently, Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016) designed a three-dimensional model of the flow of a finite-sized deformable capsule in a lateral bifurcation made of cylindrical tubes having the same diameter and consisting of a straight channel with an orthogonal side branch (figure 1
c) with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
. They found that at low Reynolds number
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
. They found that at low Reynolds number
![]() $Re$
, a capsule favours the branch which receives the most flow, provided it is not too deformable. However, at equal flow split between the two downstream branches, inertia may affect the path selection of a capsule, which tends to flow straight as
$Re$
, a capsule favours the branch which receives the most flow, provided it is not too deformable. However, at equal flow split between the two downstream branches, inertia may affect the path selection of a capsule, which tends to flow straight as
![]() $Re$
is increased. Thus, under small inertial effects, the capsule can flow into the straight downstream tube even when it receives less flow than the side branch. This indicates the fact that the qualitative model of Fung and co-workers has its limitations and that phenomena such as inertia can modify the relative position of deformable particles with respect to the fluid separation line. Although this previous study opened a new viewpoint on Fung’s model, it provided little information on how to control the particle’s trajectory: an open question being the possibility to optimise the vessel geometry to lead deformable particles into a preferred branch.
$Re$
is increased. Thus, under small inertial effects, the capsule can flow into the straight downstream tube even when it receives less flow than the side branch. This indicates the fact that the qualitative model of Fung and co-workers has its limitations and that phenomena such as inertia can modify the relative position of deformable particles with respect to the fluid separation line. Although this previous study opened a new viewpoint on Fung’s model, it provided little information on how to control the particle’s trajectory: an open question being the possibility to optimise the vessel geometry to lead deformable particles into a preferred branch.

Figure 1. Typical configurations of branched channels: (a) Y-bifurcation; (b) T-bifurcation; (c) lateral bifurcation (straight channel with an orthogonal side branch).
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
represent the angles between the feed channel and the two daughter branches as shown in (a).
$\unicode[STIX]{x1D6FD}$
represent the angles between the feed channel and the two daughter branches as shown in (a).
Numerically, it is possible to calculate the flow of capsules in bifurcations with any cross-section geometry (cylindrical, prismatic, etc.). Experimentally, it is, however, difficult and expensive to fabricate bifurcated cylindrical microchannels. Fortunately, with the recent development of microfluidic techniques, one can nowadays fabricate bifurcated microchannels with various size ratios and geometries at relatively low cost. The drawback of the soft lithography techniques, which are classically used, is that the microfluidic channel section is usually square or rectangular. For the same cross-sectional area of a side branch, there can be many different possible bifurcation geometries.
We thus consider the case of a capsule flowing in a microfluidic asymmetric bifurcation consisting of a straight channel with a narrowed lateral bifurcation (figure 1 b) and numerically model its path selection under different conditions. The capsule has dimensions comparable to the side branch cross-section and is centred along the feeding channel axis by hydrodynamic forces or by some flow-focusing devices. This situation is pertinent for the design of particle/cell enrichment devices (Yang, Ündar & Zahn Reference Yang, Ündar and Zahn2006; Gossett et al. Reference Gossett, Weaver, Mach, Hur, Tse, Lee, Amini and Di Carlo2010; Kersaudy-Kerhoas et al. Reference Kersaudy-Kerhoas, Dhariwal, Desmulliez and Jouvet2010; Shields IV, Reyes & López Reference Shields IV, Reyes and López2015), for which it is essential that the branch collecting the particles receives as little suspending fluid as possible. Many questions still remain regarding the magnitude of the velocity difference that allows separation and the effect of the flow pattern in the bifurcation, since microfluidic technology allows for different bifurcation designs. The objective of this study is to analyse the effect of the side branch geometry on flow patterns in the channel and on path selection of a single capsule flowing through an asymmetric lateral bifurcation. This should help not only advance the fundamental understanding of capsule trajectory at complicated bifurcations, but also identify an optimal geometry for capsule suspension enrichment.
The fluid–capsule interaction problem is solved by means of immersed boundaries coupled to a three-dimensional lattice-Boltzmann method. This is detailed in § 2 along with the main parameters and numerical method. In the result sections, we present the flow patterns and pressure drops as a function of the bifurcation geometries and determine the path selection of initially spherical capsules as a function of the capsule properties, bifurcation geometry and flow Reynolds number. This leads to phase diagrams that allow selection of efficient enrichment devices. We first present the results for three main distinctive geometries in § 3 and discuss the effect of side branch geometry on the background flow and on the capsule path selection. In § 4, we discuss the efficiency of other bifurcation geometries and show how the present results obtained for constant flow rate conditions can be extended to pressure-controlled systems. We then conclude the paper in § 5.
2 Problem statement and numerical method
2.1 Problem statement
We consider an initially spherical capsule with radius
![]() $a$
, flowing through a straight channel with an orthogonal side branch. The parent channel and the downstream straight daughter channel have a constant square cross-section
$a$
, flowing through a straight channel with an orthogonal side branch. The parent channel and the downstream straight daughter channel have a constant square cross-section
![]() $4l^{2}$
with a side length
$4l^{2}$
with a side length
![]() $2l$
. Different bifurcation geometries have been studied, as shown in figure 2. A three-dimensional Cartesian coordinate system is used with
$2l$
. Different bifurcation geometries have been studied, as shown in figure 2. A three-dimensional Cartesian coordinate system is used with
![]() $x$
-axis along the axis of the main channel,
$x$
-axis along the axis of the main channel,
![]() $z$
-axis along the side branch axis and
$z$
-axis along the side branch axis and
![]() $x=y=z=0$
at the bifurcation centre. As the reference case, we consider a side branch channel (channel A, figure 2
a,b), with the same square cross-section area
$x=y=z=0$
at the bifurcation centre. As the reference case, we consider a side branch channel (channel A, figure 2
a,b), with the same square cross-section area
![]() $4l^{2}$
as the main channel. Then we consider a narrow side branch with cross-section
$4l^{2}$
as the main channel. Then we consider a narrow side branch with cross-section
![]() $w\times d=2l^{2}$
, where
$w\times d=2l^{2}$
, where
![]() $w$
and
$w$
and
![]() $d$
are measured along the
$d$
are measured along the
![]() $x$
- and
$x$
- and
![]() $y$
-directions respectively. The cross-section area is thus half that of the straight channel but still allows the passage of the capsule. With this later restriction in mind, the side branch has been narrowed in two different ways: along the
$y$
-directions respectively. The cross-section area is thus half that of the straight channel but still allows the passage of the capsule. With this later restriction in mind, the side branch has been narrowed in two different ways: along the
![]() $x$
-direction (channel B, figure 2
b) or along the
$x$
-direction (channel B, figure 2
b) or along the
![]() $y$
-direction (channel C, figure 2
b). The side branches and main channels for the above geometries are centre-connected. From a microfabrication point of view, channels A and B are easier to make than channel C. In all cases, the length of the parent channel is
$y$
-direction (channel C, figure 2
b). The side branches and main channels for the above geometries are centre-connected. From a microfabrication point of view, channels A and B are easier to make than channel C. In all cases, the length of the parent channel is
![]() $12l$
, and the length of the two daughter channels is
$12l$
, and the length of the two daughter channels is
![]() $10l$
.
$10l$
.
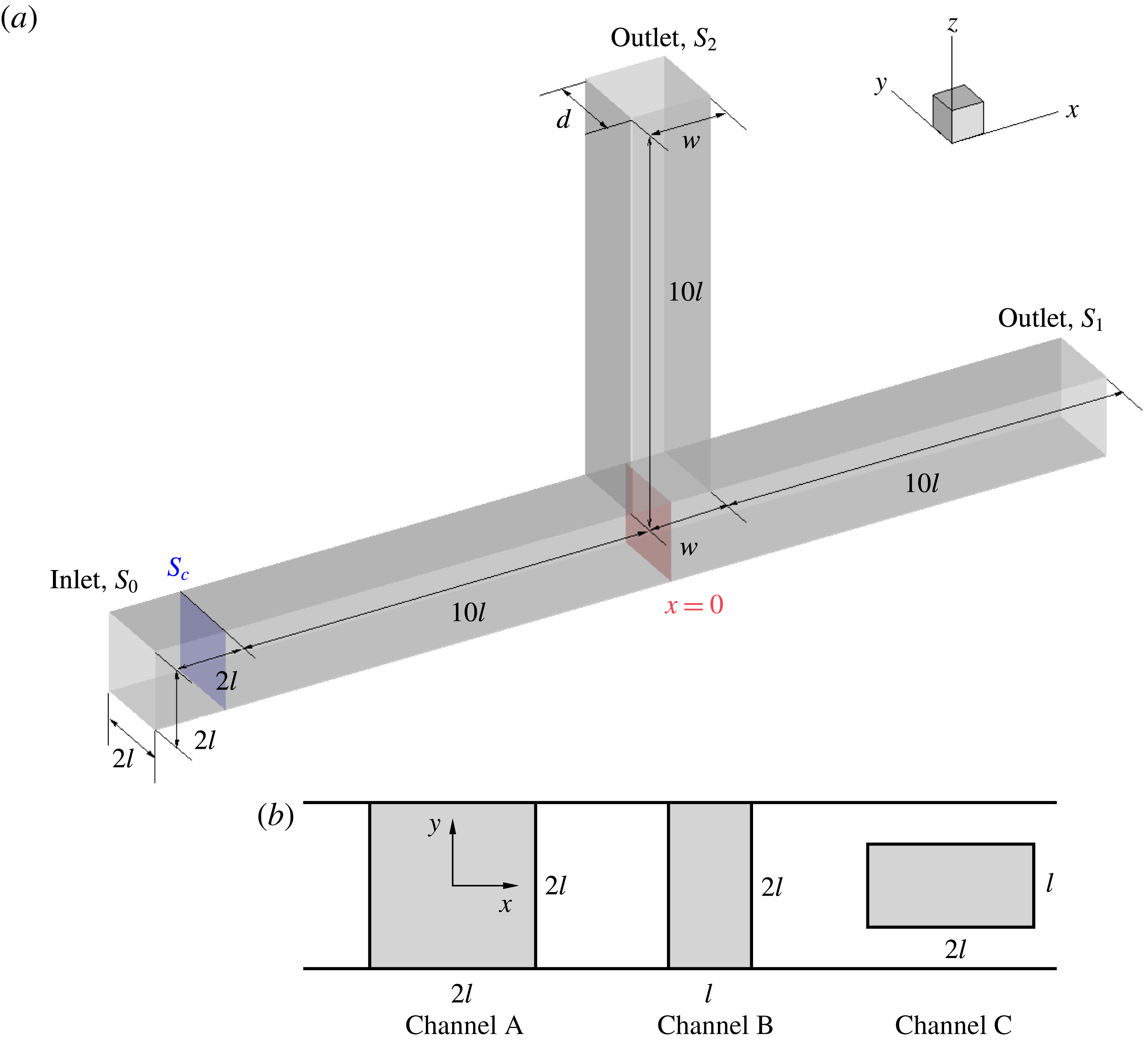
Figure 2. (a) Three-dimensional geometry of a branched channel. The width and depth of the side branch are
![]() $w$
and
$w$
and
![]() $d$
, respectively. (b) Top view of the side branches for channel A (
$d$
, respectively. (b) Top view of the side branches for channel A (
![]() $w=d=2l$
), channel B (
$w=d=2l$
), channel B (
![]() $w=l,d=2l$
) and channel C (
$w=l,d=2l$
) and channel C (
![]() $w=2l,d=l$
). All side branches are centre-connected to the main channel.
$w=2l,d=l$
). All side branches are centre-connected to the main channel.
The fluid motion is governed by the Navier–Stokes equations, with a no-slip condition imposed at the channel wall. We operate under imposed flow rates in the different branches of the bifurcation. We checked that the inlet
![]() $S_{0}$
and outlet sections
$S_{0}$
and outlet sections
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
were far enough for the disturbance due to the bifurcation to be negligible. The flows at
$S_{2}$
were far enough for the disturbance due to the bifurcation to be negligible. The flows at
![]() $S_{0}$
,
$S_{0}$
,
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
are thus fully developed laminar channel flows, with constant imposed flow rates
$S_{2}$
are thus fully developed laminar channel flows, with constant imposed flow rates
![]() $Q_{0}$
,
$Q_{0}$
,
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
respectively, such that
$Q_{2}$
respectively, such that
![]() $Q_{0}=Q_{1}+Q_{2}$
. The velocity profiles corresponding to the respective flow rate and section geometry are well known (e.g. White Reference White1991). The mean inlet velocity in
$Q_{0}=Q_{1}+Q_{2}$
. The velocity profiles corresponding to the respective flow rate and section geometry are well known (e.g. White Reference White1991). The mean inlet velocity in
![]() $S_{0}$
is denoted by
$S_{0}$
is denoted by
![]() $V$
and serves as a reference velocity throughout. Note that the pressures
$V$
and serves as a reference velocity throughout. Note that the pressures
![]() $P_{0}(t)$
,
$P_{0}(t)$
,
![]() $P_{1}(t)$
and
$P_{1}(t)$
and
![]() $P_{2}(t)$
in sections
$P_{2}(t)$
in sections
![]() $S_{0}$
,
$S_{0}$
,
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
, respectively, vary with time
$S_{2}$
, respectively, vary with time
![]() $t$
when a capsule flows in the bifurcated system. It is also possible to operate the system under constant pressure conditions, where the pressures
$t$
when a capsule flows in the bifurcated system. It is also possible to operate the system under constant pressure conditions, where the pressures
![]() $P_{0}$
,
$P_{0}$
,
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
are kept constant. In this case, the flow rates
$P_{2}$
are kept constant. In this case, the flow rates
![]() $Q_{0}(t)$
,
$Q_{0}(t)$
,
![]() $Q_{1}(t)$
and
$Q_{1}(t)$
and
![]() $Q_{2}(t)$
will depend on time. The constant pressure drop operation of the system is further discussed in § 4.2.
$Q_{2}(t)$
will depend on time. The constant pressure drop operation of the system is further discussed in § 4.2.
The capsule is enclosed by a hyperelastic membrane with a small bending stiffness. The fluids inside and outside the capsule are incompressible Newtonian liquids with identical viscosity
![]() $\unicode[STIX]{x1D707}$
and density
$\unicode[STIX]{x1D707}$
and density
![]() $\unicode[STIX]{x1D70C}$
. We initially place the undeformed capsule on the centreline of the parent channel, with its mass centre in the cross-section
$\unicode[STIX]{x1D70C}$
. We initially place the undeformed capsule on the centreline of the parent channel, with its mass centre in the cross-section
![]() $S_{c}$
at a distance
$S_{c}$
at a distance
![]() $2l$
from the entrance
$2l$
from the entrance
![]() $S_{0}$
(see figure 2). We find that the capsule reaches its steady-state shape once its centre of mass has travelled a distance of approximately
$S_{0}$
(see figure 2). We find that the capsule reaches its steady-state shape once its centre of mass has travelled a distance of approximately
![]() $5l$
.
$5l$
.
The shear deformation and area dilatation of the capsule membrane are modelled using the strain-hardening Skalak’s (SK) law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973),
where
![]() $W$
is the strain energy density per unit undeformed surface area,
$W$
is the strain energy density per unit undeformed surface area,
![]() $G_{s}$
is the surface shear elasticity modulus,
$G_{s}$
is the surface shear elasticity modulus,
![]() $I_{1}={\unicode[STIX]{x1D706}_{1}}^{2}+{\unicode[STIX]{x1D706}_{2}}^{2}-2$
and
$I_{1}={\unicode[STIX]{x1D706}_{1}}^{2}+{\unicode[STIX]{x1D706}_{2}}^{2}-2$
and
![]() $I_{2}=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}-1$
are the first and second strain invariants of the surface deformation, and
$I_{2}=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}-1$
are the first and second strain invariants of the surface deformation, and
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{2}$
are the principal extension ratios in the plane of the membrane. The membrane area dilatation modulus in SK law is
$\unicode[STIX]{x1D706}_{2}$
are the principal extension ratios in the plane of the membrane. The membrane area dilatation modulus in SK law is
![]() $K_{s}=(1+2C)G_{s}$
. We take
$K_{s}=(1+2C)G_{s}$
. We take
![]() $C=1$
in the present study.
$C=1$
in the present study.
The bending resistance of the membrane is modelled following Helfrich’s formulation for bending energy (Zhong-Can & Helfrich Reference Zhong-Can and Helfrich1989):
Here
![]() $k_{c}$
is the bending modulus,
$k_{c}$
is the bending modulus,
![]() $H$
is the mean curvature,
$H$
is the mean curvature,
![]() $c_{0}$
is the spontaneous curvature and
$c_{0}$
is the spontaneous curvature and
![]() $A$
is the surface area. A small bending stiffness (
$A$
is the surface area. A small bending stiffness (
![]() $k_{c}=0.0008G_{s}l^{2}$
) is used to prevent the formation of wrinkles on the capsule membrane, like in our previous study (Wang et al.
Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016).
$k_{c}=0.0008G_{s}l^{2}$
) is used to prevent the formation of wrinkles on the capsule membrane, like in our previous study (Wang et al.
Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016).
The non-dimensional parameters of the problem are as follows.
(i) The branch flow ratio
 $q$
, which is the flow rate in the side branch normalised by the flow rate in the parent channel, (2.3)
$q$
, which is the flow rate in the side branch normalised by the flow rate in the parent channel, (2.3) $$\begin{eqnarray}q=\frac{Q_{2}}{Q_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}q=\frac{Q_{2}}{Q_{0}}.\end{eqnarray}$$
(ii) The flow Reynolds number
 $Re$
in the parent channel, (2.4)
$Re$
in the parent channel, (2.4) $$\begin{eqnarray}Re=\frac{2\unicode[STIX]{x1D70C}Vl}{\unicode[STIX]{x1D707}}.\end{eqnarray}$$
$$\begin{eqnarray}Re=\frac{2\unicode[STIX]{x1D70C}Vl}{\unicode[STIX]{x1D707}}.\end{eqnarray}$$
(iii) The size ratio
 $a/l$
between the capsule characteristic size (radius of the initially spherical capsule) and the half-cross-sectional dimension of the parent channel. Note that in a narrowed side branch, the local size ratio is doubled, which puts limits on the magnitude of
$a/l$
between the capsule characteristic size (radius of the initially spherical capsule) and the half-cross-sectional dimension of the parent channel. Note that in a narrowed side branch, the local size ratio is doubled, which puts limits on the magnitude of
 $a/l$
.
$a/l$
.(iv) The capillary number
 $Ca$
, which compares the viscous fluid force acting on the capsule to the membrane elastic force, (2.5)
$Ca$
, which compares the viscous fluid force acting on the capsule to the membrane elastic force, (2.5) $$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}V}{G_{s}}.\end{eqnarray}$$
$$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}V}{G_{s}}.\end{eqnarray}$$
It is clear from equations (2.4) and (2.5) that both the capillary number and the Reynolds number increase with
![]() $V$
and are related by
$V$
and are related by
The ratio depends only on the physical properties of the channel flow and of the capsule.
2.2 Numerical method and validation
The numerical method is similar to the one used for capsules flowing through a circular branched channel (Wang et al.
Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016) and will only be outlined briefly here. The fluid flow in the whole domain is computed by means of a lattice-Boltzmann method (LBM) with a standard grid size
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.04l$
. A second-order bounce-back scheme based on interpolations (Bouzidi, Firdaouss & Lallemand Reference Bouzidi, Firdaouss and Lallemand2001) has been employed to apply the no-slip boundary condition to the solid walls of the branched channel. At the inlet and outlets of the channel, velocity boundary conditions have been implemented using a second-order non-equilibrium extrapolation method (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002). A finite-element membrane model is employed to obtain the forces acting at the discrete nodes of the membrane (detailed in Sui et al. (Reference Sui, Chew, Roy and Low2008)). The typical membrane mesh size is chosen to be of the same order as the LBM mesh. It thus depends on the capsule size. Correspondingly, for
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.04l$
. A second-order bounce-back scheme based on interpolations (Bouzidi, Firdaouss & Lallemand Reference Bouzidi, Firdaouss and Lallemand2001) has been employed to apply the no-slip boundary condition to the solid walls of the branched channel. At the inlet and outlets of the channel, velocity boundary conditions have been implemented using a second-order non-equilibrium extrapolation method (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002). A finite-element membrane model is employed to obtain the forces acting at the discrete nodes of the membrane (detailed in Sui et al. (Reference Sui, Chew, Roy and Low2008)). The typical membrane mesh size is chosen to be of the same order as the LBM mesh. It thus depends on the capsule size. Correspondingly, for
![]() $a/l=0.2$
, the three-dimensional capsule membrane is discretised into 2048 flat triangular elements connecting 1026 nodes, leading to a maximum element edge length
$a/l=0.2$
, the three-dimensional capsule membrane is discretised into 2048 flat triangular elements connecting 1026 nodes, leading to a maximum element edge length
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.03l$
and a ratio
$\unicode[STIX]{x0394}L_{c}\sim 0.03l$
and a ratio
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.75$
. For a capsule with
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.75$
. For a capsule with
![]() $a/l=0.3$
, a membrane mesh of 8192 elements connecting 4098 nodes is used, leading to
$a/l=0.3$
, a membrane mesh of 8192 elements connecting 4098 nodes is used, leading to
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.023l$
and
$\unicode[STIX]{x0394}L_{c}\sim 0.023l$
and
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.58$
. At time
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.58$
. At time
![]() $t=0$
, the capsule centre of mass is positioned at the centre of section
$t=0$
, the capsule centre of mass is positioned at the centre of section
![]() $Sc$
. The computation is stopped when the capsule centre is at a distance of
$Sc$
. The computation is stopped when the capsule centre is at a distance of
![]() $2l$
from the exit section: we have verified that the corresponding exit velocity was not significantly perturbed then.
$2l$
from the exit section: we have verified that the corresponding exit velocity was not significantly perturbed then.
The immersed-boundary method (IBM) of Peskin (Reference Peskin1977) has been used to solve the fluid–capsule interaction. The membrane force is transmitted to the fluid by means of a three-dimensional Dirac function which is spread over approximately two fluid elements (
![]() $2\unicode[STIX]{x0394}x$
) on both sides of the membrane. As a result, the method cannot resolve the film flow when the minimum distance between the capsule and channel wall is comparable to
$2\unicode[STIX]{x0394}x$
) on both sides of the membrane. As a result, the method cannot resolve the film flow when the minimum distance between the capsule and channel wall is comparable to
![]() $2\unicode[STIX]{x0394}x$
. This has limited the study to small capsules with
$2\unicode[STIX]{x0394}x$
. This has limited the study to small capsules with
![]() $a/l\leqslant 0.3$
, this ratio being doubled in the narrowed side branch. A larger capsule is otherwise likely to get closer than
$a/l\leqslant 0.3$
, this ratio being doubled in the narrowed side branch. A larger capsule is otherwise likely to get closer than
![]() $2\unicode[STIX]{x0394}x$
, to the wall. This is a significant limitation of the method.
$2\unicode[STIX]{x0394}x$
, to the wall. This is a significant limitation of the method.
In order to evaluate the effect of the LBM mesh size, we analyse the trajectory of a capsule with
![]() $a/l=0.3$
flowing in channel C at
$a/l=0.3$
flowing in channel C at
![]() $Re=1,Ca=0.005,q=0.44$
. The capsule membrane is discretised with 8192 elements (
$Re=1,Ca=0.005,q=0.44$
. The capsule membrane is discretised with 8192 elements (
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.023l$
), but we consider three LBM meshes with
$\unicode[STIX]{x0394}L_{c}\sim 0.023l$
), but we consider three LBM meshes with
![]() $\unicode[STIX]{x0394}x=0.063l,0.04l,0.031l$
. As shown in figure 3, the capsule trajectories are almost superimposed for the two fine meshes
$\unicode[STIX]{x0394}x=0.063l,0.04l,0.031l$
. As shown in figure 3, the capsule trajectories are almost superimposed for the two fine meshes
![]() $\unicode[STIX]{x0394}x=0.04l$
or
$\unicode[STIX]{x0394}x=0.04l$
or
![]() $0.031l$
. For the coarse mesh
$0.031l$
. For the coarse mesh
![]() $\unicode[STIX]{x0394}x=0.063l$
, the trajectory deviates by at most
$\unicode[STIX]{x0394}x=0.063l$
, the trajectory deviates by at most
![]() $0.05l$
near the exit of the channel. This justifies the use of an LBM mesh size of
$0.05l$
near the exit of the channel. This justifies the use of an LBM mesh size of
![]() $0.04l$
throughout the study. Furthermore, we have verified that increasing the channel lengths leads to negligible changes in the capsule trajectory near the bifurcation.
$0.04l$
throughout the study. Furthermore, we have verified that increasing the channel lengths leads to negligible changes in the capsule trajectory near the bifurcation.

Figure 3. Trajectories of a capsule flowing in channel C for
![]() $a/l=0.3,Re=1,Ca=0.005,q=0.44$
. Different grid resolutions are used:
$a/l=0.3,Re=1,Ca=0.005,q=0.44$
. Different grid resolutions are used:
![]() $\unicode[STIX]{x0394}x=0.063R$
(dash-dotted line, green online),
$\unicode[STIX]{x0394}x=0.063R$
(dash-dotted line, green online),
![]() $\unicode[STIX]{x0394}x=0.04R$
(solid line, red online),
$\unicode[STIX]{x0394}x=0.04R$
(solid line, red online),
![]() $\unicode[STIX]{x0394}x=0.031R$
(dashed line, blue online). The maximum membrane element edge length is
$\unicode[STIX]{x0394}x=0.031R$
(dashed line, blue online). The maximum membrane element edge length is
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.023l$
in all cases.
$\unicode[STIX]{x0394}L_{c}\sim 0.023l$
in all cases.

Figure 4. Steady profiles of an initially spherical capsule with an SK membrane (
![]() $C=1$
) flowing in a square section channel for
$C=1$
) flowing in a square section channel for
![]() $a/l=0.85,Re=0.25,Ca=0.1$
. The bending stiffness of the membrane is, in this case, set to zero to be consistent with Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013). Dotted line (blue online), profile
$a/l=0.85,Re=0.25,Ca=0.1$
. The bending stiffness of the membrane is, in this case, set to zero to be consistent with Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013). Dotted line (blue online), profile
![]() $C_{1}$
, obtained with 32 768 flat triangular elements; solid line (red online), profile
$C_{1}$
, obtained with 32 768 flat triangular elements; solid line (red online), profile
![]() $C_{2}$
obtained with 8192 elements; dashed line (black online), profile obtained by Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013) for
$C_{2}$
obtained with 8192 elements; dashed line (black online), profile obtained by Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013) for
![]() $Re=0$
, using a boundary element method.
$Re=0$
, using a boundary element method.
In order to validate the membrane discretisation, we compute the equilibrium deformed profiles of a spherical capsule with
![]() $a/l=0.85$
enclosed by an SK membrane (
$a/l=0.85$
enclosed by an SK membrane (
![]() $C=1$
) without bending stiffness, when it flows in a
$C=1$
) without bending stiffness, when it flows in a
![]() $20l$
-long straight square channel with
$20l$
-long straight square channel with
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $B=0$
. The LBM mesh size is
$B=0$
. The LBM mesh size is
![]() $\unicode[STIX]{x0394}x=0.04l$
. The membrane is discretised into either 32 768 elements (
$\unicode[STIX]{x0394}x=0.04l$
. The membrane is discretised into either 32 768 elements (
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x\leqslant 0.82$
, profile
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x\leqslant 0.82$
, profile
![]() $C_{1}$
) or 8192 elements (
$C_{1}$
) or 8192 elements (
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x\leqslant 1.63$
, profile
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x\leqslant 1.63$
, profile
![]() $C_{2}$
). As shown in figure 4, the two profiles
$C_{2}$
). As shown in figure 4, the two profiles
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are almost superimposed, which indicates that 8192 elements are sufficient to model the capsule membrane with good accuracy. The equilibrium profile
$C_{2}$
are almost superimposed, which indicates that 8192 elements are sufficient to model the capsule membrane with good accuracy. The equilibrium profile
![]() $C_{1}$
is also compared to the deformed profile
$C_{1}$
is also compared to the deformed profile
![]() $C_{3}$
obtained by Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013) for
$C_{3}$
obtained by Hu et al. (Reference Hu, Sévénié, Salsac, Leclerc and Barthès-Biesel2013) for
![]() $Re=0$
, using a boundary element method. The distance between
$Re=0$
, using a boundary element method. The distance between
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{3}$
is measured by means of the Hausdorff distance (Dubuisson & Jain Reference Dubuisson and Jain1994). Correspondingly, we consider a set of
$C_{3}$
is measured by means of the Hausdorff distance (Dubuisson & Jain Reference Dubuisson and Jain1994). Correspondingly, we consider a set of
![]() $m$
points,
$m$
points,
![]() $R=\{r_{1},r_{2},r_{3},\ldots ,r_{m}\}$
from
$R=\{r_{1},r_{2},r_{3},\ldots ,r_{m}\}$
from
![]() $C_{3}$
, and another set of
$C_{3}$
, and another set of
![]() $n$
points,
$n$
points,
![]() $T=\{t_{1},t_{2},t_{3},\ldots ,t_{n}\}$
from
$T=\{t_{1},t_{2},t_{3},\ldots ,t_{n}\}$
from
![]() $C_{1}$
. Assuming that the two sets of points have the same barycentre, we define the maximum
$C_{1}$
. Assuming that the two sets of points have the same barycentre, we define the maximum
![]() $h(R,T)$
and mean
$h(R,T)$
and mean
![]() $\overline{h}(R,T)$
Hausdorff distances as
$\overline{h}(R,T)$
Hausdorff distances as
where
![]() $d(r,t)$
is the distance from any point in
$d(r,t)$
is the distance from any point in
![]() $R$
to any point in
$R$
to any point in
![]() $T$
. We find that the Hausdorff distances between
$T$
. We find that the Hausdorff distances between
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{3}$
are
$C_{3}$
are
![]() $h(R,T)=0.032l$
and
$h(R,T)=0.032l$
and
![]() $\overline{h}(R,T)=0.011l$
. Note that the maximum Hausdorff distance corresponds to one grid mesh, as could be expected in view of the fundamental difference between the two methods. The fact that our results are obtained for
$\overline{h}(R,T)=0.011l$
. Note that the maximum Hausdorff distance corresponds to one grid mesh, as could be expected in view of the fundamental difference between the two methods. The fact that our results are obtained for
![]() $Re=0.25$
, while those of Hu et al. are for zero Reynolds number, may also be the cause of differences between the equilibrium profiles. With the lattice-Boltzmann method, the computational time significantly increases as the
$Re=0.25$
, while those of Hu et al. are for zero Reynolds number, may also be the cause of differences between the equilibrium profiles. With the lattice-Boltzmann method, the computational time significantly increases as the
![]() $Re$
value decreases, which makes it computationally unaffordable to consider cases where
$Re$
value decreases, which makes it computationally unaffordable to consider cases where
![]() $Re\ll 0.25$
.
$Re\ll 0.25$
.
Altogether, the above study on the influence of LBM mesh size and membrane discretisation shows that the numerical parameters we have selected (
![]() $\unicode[STIX]{x0394}x=0.04l$
and 8192 elements on the largest capsule considered) are enough to ensure that the average numerical errors on the capsule shape or trajectory will be of the order of 1 % or less. The capsule trajectory results, which are presented henceforward, take approximately 72 h on the High-Performance Computing facility at Queen Mary, University of London, using 12 threads in parallel computing.
$\unicode[STIX]{x0394}x=0.04l$
and 8192 elements on the largest capsule considered) are enough to ensure that the average numerical errors on the capsule shape or trajectory will be of the order of 1 % or less. The capsule trajectory results, which are presented henceforward, take approximately 72 h on the High-Performance Computing facility at Queen Mary, University of London, using 12 threads in parallel computing.
3 Capsule flowing in channels A, B and C
Channel A corresponds to the simple situation where all of the channels have the same cross-section, whereas channels B and C correspond to two narrowed side branches with different orientations. Note that for equal flow split (
![]() $q=0.5$
) in channels B and C, the mean velocity in the side branch is twice the mean velocity in the straight daughter branch. We first determine the background flow in each channel when no capsule is present. We then study the path selection of a capsule for different values of the problem parameters
$q=0.5$
) in channels B and C, the mean velocity in the side branch is twice the mean velocity in the straight daughter branch. We first determine the background flow in each channel when no capsule is present. We then study the path selection of a capsule for different values of the problem parameters
![]() $a/l,Ca,Re$
.
$a/l,Ca,Re$
.
3.1 Fluid separation line in the absence of a capsule

Figure 5. Background flow separation lines calculated in cross-section
![]() $S_{c}$
for different side branch geometries at different Reynolds numbers with
$S_{c}$
for different side branch geometries at different Reynolds numbers with
![]() $q=0.5$
. The cross-section
$q=0.5$
. The cross-section
![]() $S_{c}$
is
$S_{c}$
is
![]() $2l$
from the entrance, where the flow is already fully developed, and the side branch is going upwards. In the cross-section, the fluid elements above the separation line enter the side branch and those below remain in the main channel. (a)
$2l$
from the entrance, where the flow is already fully developed, and the side branch is going upwards. In the cross-section, the fluid elements above the separation line enter the side branch and those below remain in the main channel. (a)
![]() $Re=0.25$
; (b)
$Re=0.25$
; (b)
![]() $Re=10$
; (c)
$Re=10$
; (c)
![]() $Re=40$
.
$Re=40$
.
At any cross-section of the parent channel perpendicular to the channel axis, one can define a separation line which divides the fluid elements that flow into the side branch from those flowing into the downstream main channel. The flow separation line is computed in cross-section
![]() $S_{c}$
by means of the approach of Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016). We concentrate on the influence of side branch geometry and Reynolds number on the position of the flow separation line for
$S_{c}$
by means of the approach of Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016). We concentrate on the influence of side branch geometry and Reynolds number on the position of the flow separation line for
![]() $q=0.5$
.
$q=0.5$
.
As shown in figure 5, we first note that channels A and B exhibit very similar flow patterns irrespective of the value of
![]() $Re$
: the separation line bends towards the side branch, which indicates a tendency for the fluid particles in the centre of the cross-section to flow straight rather than take the branch when
$Re$
: the separation line bends towards the side branch, which indicates a tendency for the fluid particles in the centre of the cross-section to flow straight rather than take the branch when
![]() $Re$
increases. As pointed out by Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016), this pattern is in agreement with experiments and numerical simulations, albeit for cylindrical channels (Rong & Carr Reference Rong and Carr1990; Enden & Popel Reference Enden and Popel1992; Carr & Kotha Reference Carr and Kotha1995). However, the situation is different for channel C: for
$Re$
increases. As pointed out by Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016), this pattern is in agreement with experiments and numerical simulations, albeit for cylindrical channels (Rong & Carr Reference Rong and Carr1990; Enden & Popel Reference Enden and Popel1992; Carr & Kotha Reference Carr and Kotha1995). However, the situation is different for channel C: for
![]() $Re\leqslant 10$
, the fluid particles near the left and right walls (i.e.
$Re\leqslant 10$
, the fluid particles near the left and right walls (i.e.
![]() $y=\pm l$
) flow straight because they are located in corners where the bifurcation has no influence; conversely, the fluid particles located near the centre tend to take the branch. It is only for
$y=\pm l$
) flow straight because they are located in corners where the bifurcation has no influence; conversely, the fluid particles located near the centre tend to take the branch. It is only for
![]() $Re\geqslant 20$
that the influence of the bifurcation extends to particles near the wall as well as centred ones (figure 5
c): this leads to a tendency for centred particles to flow straight.
$Re\geqslant 20$
that the influence of the bifurcation extends to particles near the wall as well as centred ones (figure 5
c): this leads to a tendency for centred particles to flow straight.
To complement the study of the separation line, we compare the bifurcation velocity fields in the
![]() $x=0$
plane for channels B and C in figures 6 and 7 for
$x=0$
plane for channels B and C in figures 6 and 7 for
![]() $Re=0.25$
and
$Re=0.25$
and
![]() $Re=20$
, respectively. Recall that
$Re=20$
, respectively. Recall that
![]() $x=y=z=0$
is defined as the channel bifurcation centre. The flow into channel C from the straight channel is hindered by the two corners of the main channel (figures 6
b and 7
b). Thus in order to keep the same flow rate (as compared to channel B) in the side branch, more fluid from the central region of the main channel has to be to fed into the side branch of channel C. This explains why the fluid separation line at the centre of
$x=y=z=0$
is defined as the channel bifurcation centre. The flow into channel C from the straight channel is hindered by the two corners of the main channel (figures 6
b and 7
b). Thus in order to keep the same flow rate (as compared to channel B) in the side branch, more fluid from the central region of the main channel has to be to fed into the side branch of channel C. This explains why the fluid separation line at the centre of
![]() $S_{c}$
is lower for channel C than for channels A and B at any value of
$S_{c}$
is lower for channel C than for channels A and B at any value of
![]() $Re$
. It can thus be expected that a side branch similar to channel C will be more efficient at capturing fluid elements flowing in the central region of the parent channel than geometries like A and B. Furthermore, the flow velocity maps of figures 6 and 7 show clearly that the bifurcation perturbation has disappeared for
$Re$
. It can thus be expected that a side branch similar to channel C will be more efficient at capturing fluid elements flowing in the central region of the parent channel than geometries like A and B. Furthermore, the flow velocity maps of figures 6 and 7 show clearly that the bifurcation perturbation has disappeared for
![]() $x>2l$
in the straight branch and
$x>2l$
in the straight branch and
![]() $z>2l$
in the side branch for low
$z>2l$
in the side branch for low
![]() $Re$
. When inertial effects are not negligible (e.g.
$Re$
. When inertial effects are not negligible (e.g.
![]() $Re=20$
) the bifurcation perturbation extends to longer distances in the side branch and dies out for
$Re=20$
) the bifurcation perturbation extends to longer distances in the side branch and dies out for
![]() $z>3l$
. This study thus shows that for the same level of inertia effects, as measured by
$z>3l$
. This study thus shows that for the same level of inertia effects, as measured by
![]() $Re$
, geometry plays a significant role in the flow pattern determination near the bifurcation.
$Re$
, geometry plays a significant role in the flow pattern determination near the bifurcation.

Figure 6. Unperturbed velocity field (non-dimensionalised by
![]() $V$
) in the vicinity of the bifurcation for channels B and C. The contours represent the fluid velocity in the
$V$
) in the vicinity of the bifurcation for channels B and C. The contours represent the fluid velocity in the
![]() $z$
-direction.
$z$
-direction.
![]() $Re=0.25$
and
$Re=0.25$
and
![]() $q=0.5$
. (a)
$q=0.5$
. (a)
![]() $y=0$
-plane; (b)
$y=0$
-plane; (b)
![]() $x=0$
-plane.
$x=0$
-plane.

Figure 7. The same legend as in figure 6 but for
![]() $Re=20$
and
$Re=20$
and
![]() $q=0.5$
.
$q=0.5$
.
A simple model may help understand the effect of the channel geometry on the relative position of the fluid separation lines in
![]() $S_{c}$
(figure 5). If one considers a massless diffusiveless particle, initially positioned on the parent channel centreline and passing through the bifurcation, its deflection
$S_{c}$
(figure 5). If one considers a massless diffusiveless particle, initially positioned on the parent channel centreline and passing through the bifurcation, its deflection
![]() $d_{z}$
in the
$d_{z}$
in the
![]() $z$
-direction will be of the order of
$z$
-direction will be of the order of
![]() $V_{mz}T$
, where the residence time
$V_{mz}T$
, where the residence time
![]() $T$
can be estimated to be
$T$
can be estimated to be
![]() $T=w/V_{mx}$
, and where
$T=w/V_{mx}$
, and where
![]() $V_{mx}$
and
$V_{mx}$
and
![]() $V_{mz}$
are the averages of the mean flow velocities at the entrance and exit of the bifurcation along the
$V_{mz}$
are the averages of the mean flow velocities at the entrance and exit of the bifurcation along the
![]() $x$
- and
$x$
- and
![]() $z$
-directions, respectively. The larger the value of
$z$
-directions, respectively. The larger the value of
![]() $d_{z}$
, the lower the separation line is in
$d_{z}$
, the lower the separation line is in
![]() $S_{c}$
. For
$S_{c}$
. For
![]() $q=0.5$
, the values of
$q=0.5$
, the values of
![]() $w$
,
$w$
,
![]() $V_{mx}$
,
$V_{mx}$
,
![]() $V_{mz}$
,
$V_{mz}$
,
![]() $T$
and
$T$
and
![]() $d_{z}$
can be easily calculated for channels A, B and C (listed in table 1). We note that
$d_{z}$
can be easily calculated for channels A, B and C (listed in table 1). We note that
![]() $d_{z}$
is systematically larger for channel C than for channels A and B, which explains the relative positions of the separation lines in figure 5.
$d_{z}$
is systematically larger for channel C than for channels A and B, which explains the relative positions of the separation lines in figure 5.
Table 1. Estimations of the distance
![]() $d_{z}$
that a particle travels along the
$d_{z}$
that a particle travels along the
![]() $z$
-direction in the bifurcation of different channels for
$z$
-direction in the bifurcation of different channels for
![]() $q=0.5$
. Note that channel E is introduced in § 4.1.
$q=0.5$
. Note that channel E is introduced in § 4.1.

3.2 Phase diagram
The critical branch flow ratio
![]() $q_{c}$
is the flow rate above which a centred capsule enters the side branch. The lower
$q_{c}$
is the flow rate above which a centred capsule enters the side branch. The lower
![]() $q_{c}$
is, the larger the range of branch flow ratios
$q_{c}$
is, the larger the range of branch flow ratios
![]() $q_{c}<q<1$
is for which the capsule will flow to the side branch. In order to determine
$q_{c}<q<1$
is for which the capsule will flow to the side branch. In order to determine
![]() $q_{c}$
for a given
$q_{c}$
for a given
![]() $Re$
, we vary
$Re$
, we vary
![]() $q$
by steps of
$q$
by steps of
![]() $0.02$
near the transition region of path selection. The value of
$0.02$
near the transition region of path selection. The value of
![]() $q_{c}$
is the average value of the two successive branch flow ratios wherein the capsule enters the side branch at the larger value but remains in the main channel at the smaller one. Thus
$q_{c}$
is the average value of the two successive branch flow ratios wherein the capsule enters the side branch at the larger value but remains in the main channel at the smaller one. Thus
![]() $q_{c}$
is determined within
$q_{c}$
is determined within
![]() $\pm 0.01$
.
$\pm 0.01$
.

Figure 8. Phase diagram: critical branch flow ratio as a function of the channel Reynolds number for capsules with different sizes and membrane shear elasticity (
![]() $Ca=0.005Re$
) flowing in branched channels with different geometries. For
$Ca=0.005Re$
) flowing in branched channels with different geometries. For
![]() $q>q_{c}$
, the capsule flows into the side branch. (a) Comparison of the results for
$q>q_{c}$
, the capsule flows into the side branch. (a) Comparison of the results for
![]() $a/l=0.2$
versus a point particle (
$a/l=0.2$
versus a point particle (
![]() $a/l=0$
); (b)
$a/l=0$
); (b)
![]() $a/l=0.3$
.
$a/l=0.3$
.
The values of
![]() $q_{c}$
as a function of
$q_{c}$
as a function of
![]() $Re$
are shown for small capsules with
$Re$
are shown for small capsules with
![]() $a/l=0.2$
in figure 8(a) and for larger capsules
$a/l=0.2$
in figure 8(a) and for larger capsules
![]() $a/l=0.3$
in figure 8(b). Figure 8(a) also compares the results to the ones obtained in the case of a point particle to see when the capsule follows the flow streamlines similarly to particle with negligible size and deformation. The results are surprising in two respects. Firstly, the values of
$a/l=0.3$
in figure 8(b). Figure 8(a) also compares the results to the ones obtained in the case of a point particle to see when the capsule follows the flow streamlines similarly to particle with negligible size and deformation. The results are surprising in two respects. Firstly, the values of
![]() $q_{c}$
for channels A and B are very similar. This means that narrowing the side branch (as done for channel B) and thus increasing the flow speed does not help the capsule enter this branch. In fact, it slightly hinders it for
$q_{c}$
for channels A and B are very similar. This means that narrowing the side branch (as done for channel B) and thus increasing the flow speed does not help the capsule enter this branch. In fact, it slightly hinders it for
![]() $Re\leqslant 10$
, since
$Re\leqslant 10$
, since
![]() $q_{cB}>q_{cA}$
. Secondly, for each Reynolds number, the value of
$q_{cB}>q_{cA}$
. Secondly, for each Reynolds number, the value of
![]() $q_{c}$
for channel C is significantly lower than those obtained for channels A or B. In order to analyse the effect of capsule deformability, we have also considered the case
$q_{c}$
for channel C is significantly lower than those obtained for channels A or B. In order to analyse the effect of capsule deformability, we have also considered the case
![]() $Ca=0.02Re$
, which corresponds to values of
$Ca=0.02Re$
, which corresponds to values of
![]() $Ca$
four times higher than those of the case
$Ca$
four times higher than those of the case
![]() $Ca=0.005Re$
, for the same
$Ca=0.005Re$
, for the same
![]() $Re$
. For channels A, B or C, this leads to a decrease of
$Re$
. For channels A, B or C, this leads to a decrease of
![]() $q_{c}$
of order 0.01 only if
$q_{c}$
of order 0.01 only if
![]() $Re\geqslant 20$
(not shown).
$Re\geqslant 20$
(not shown).
As an illustration in figure 9, we show the trajectories of a capsule with
![]() $a/l=0.3$
in the bifurcations B and C for flow conditions where the difference between the two channel configurations appears clearly. When inertia effects are small (
$a/l=0.3$
in the bifurcations B and C for flow conditions where the difference between the two channel configurations appears clearly. When inertia effects are small (
![]() $Re=1$
,
$Re=1$
,
![]() $Ca=0.005$
,
$Ca=0.005$
,
![]() $q=0.46$
), the capsule is only slightly deformed (due to the low flow strength, as measured by
$q=0.46$
), the capsule is only slightly deformed (due to the low flow strength, as measured by
![]() $Ca$
) and follows the centre streamline that originates from the centre of
$Ca$
) and follows the centre streamline that originates from the centre of
![]() $S_{c}$
. In channel B, the centre streamline is below the separating streamline and the capsule flows into the downstream straight branch (figure 9
a); however in channel C, the centre streamline is above the separating streamline and the capsule enters the side branch (figure 9
b). Since inertial effects are negligible in this case, the difference in capsule trajectories is only due to the bifurcation geometry and to the residence time in the bifurcation, which depends on the orientation of the side branch. The case of a quite deformable capsule (
$S_{c}$
. In channel B, the centre streamline is below the separating streamline and the capsule flows into the downstream straight branch (figure 9
a); however in channel C, the centre streamline is above the separating streamline and the capsule enters the side branch (figure 9
b). Since inertial effects are negligible in this case, the difference in capsule trajectories is only due to the bifurcation geometry and to the residence time in the bifurcation, which depends on the orientation of the side branch. The case of a quite deformable capsule (
![]() $Re=20,Ca=0.1,q=0.54$
) flowing through channels B and C is shown in figure 9(c,d). In both instances, the deformability of the capsule leads to a deviation of its trajectory from the centre streamline. In all four cases shown in figure 9, the perturbation created by the bifurcation leads to a significant offset of the capsule from the axis of the branch it takes. It is thus to be expected that the capsule motion and deformation will be strongly influenced by the walls of the daughter channel in which it flows.
$Re=20,Ca=0.1,q=0.54$
) flowing through channels B and C is shown in figure 9(c,d). In both instances, the deformability of the capsule leads to a deviation of its trajectory from the centre streamline. In all four cases shown in figure 9, the perturbation created by the bifurcation leads to a significant offset of the capsule from the axis of the branch it takes. It is thus to be expected that the capsule motion and deformation will be strongly influenced by the walls of the daughter channel in which it flows.

Figure 9. Effect of narrowing the side branch on the capsule trajectory in the symmetric
![]() $xz$
-plane for
$xz$
-plane for
![]() $a/l=0.3$
. The thick solid line (blue online) represents the trajectory of the capsule centre. The dark line with arrows (red online) represents the unperturbed streamline starting from the centre of
$a/l=0.3$
. The thick solid line (blue online) represents the trajectory of the capsule centre. The dark line with arrows (red online) represents the unperturbed streamline starting from the centre of
![]() $S_{c}$
in the absence of a capsule, while the grey line with arrows (green online) represents the separating streamlines that divide the fluid elements entering the side branch from those entering the downstream straight channel. (a,b)
$S_{c}$
in the absence of a capsule, while the grey line with arrows (green online) represents the separating streamlines that divide the fluid elements entering the side branch from those entering the downstream straight channel. (a,b)
![]() $Re=1$
,
$Re=1$
,
![]() $Ca=0.005$
,
$Ca=0.005$
,
![]() $q=0.46$
; (c,d)
$q=0.46$
; (c,d)
![]() $Re=20$
,
$Re=20$
,
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $q=0.54$
; (a,c) channel B; (b,d) channel C.
$q=0.54$
; (a,c) channel B; (b,d) channel C.

Figure 10. Effect of the side branch geometry and confinement on the capsule motion and deformation in channels A, B and C for
![]() $Re=20$
,
$Re=20$
,
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $q=0.7$
. The cross-sections of the deformed capsules are shown in two orthogonal planes, using Cartesian coordinate systems centred on the capsule mass centre, with directions
$q=0.7$
. The cross-sections of the deformed capsules are shown in two orthogonal planes, using Cartesian coordinate systems centred on the capsule mass centre, with directions
![]() $x^{\prime }$
,
$x^{\prime }$
,
![]() $y^{\prime }$
,
$y^{\prime }$
,
![]() $z^{\prime }$
parallel to the respective directions
$z^{\prime }$
parallel to the respective directions
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
of figure 2. The solid straight lines represent the walls of the side branch.
$z$
of figure 2. The solid straight lines represent the walls of the side branch.
Indeed, the effect of the bifurcation geometry and confinement on the capsule deformation is illustrated in figure 10, for
![]() $a/l=0.3,Re=20,Ca=0.1$
and
$a/l=0.3,Re=20,Ca=0.1$
and
![]() $q=0.7$
, corresponding to flow conditions for which the capsule takes the side branch in all three bifurcations. We can immediately note that the deformed profiles of the capsule depend significantly on the geometry of the bifurcation: this illustrates clearly that the phenomena are three-dimensional and cannot be well represented by a two-dimensional model. In channels A and B, the deformation occurs mostly in the
$q=0.7$
, corresponding to flow conditions for which the capsule takes the side branch in all three bifurcations. We can immediately note that the deformed profiles of the capsule depend significantly on the geometry of the bifurcation: this illustrates clearly that the phenomena are three-dimensional and cannot be well represented by a two-dimensional model. In channels A and B, the deformation occurs mostly in the
![]() $xz$
-plane and is due essentially to the drag created by the proximity of the wall (with little influence of the added effect of the confinement in channel B). The
$xz$
-plane and is due essentially to the drag created by the proximity of the wall (with little influence of the added effect of the confinement in channel B). The
![]() $yz$
-plane profile is barely deformed because there is no confinement in this direction. In channel C, the capsule is deformed in the two directions, because of wall drag in the
$yz$
-plane profile is barely deformed because there is no confinement in this direction. In channel C, the capsule is deformed in the two directions, because of wall drag in the
![]() $xz$
-plane and because of confinement in the
$xz$
-plane and because of confinement in the
![]() $yz$
-plane.
$yz$
-plane.
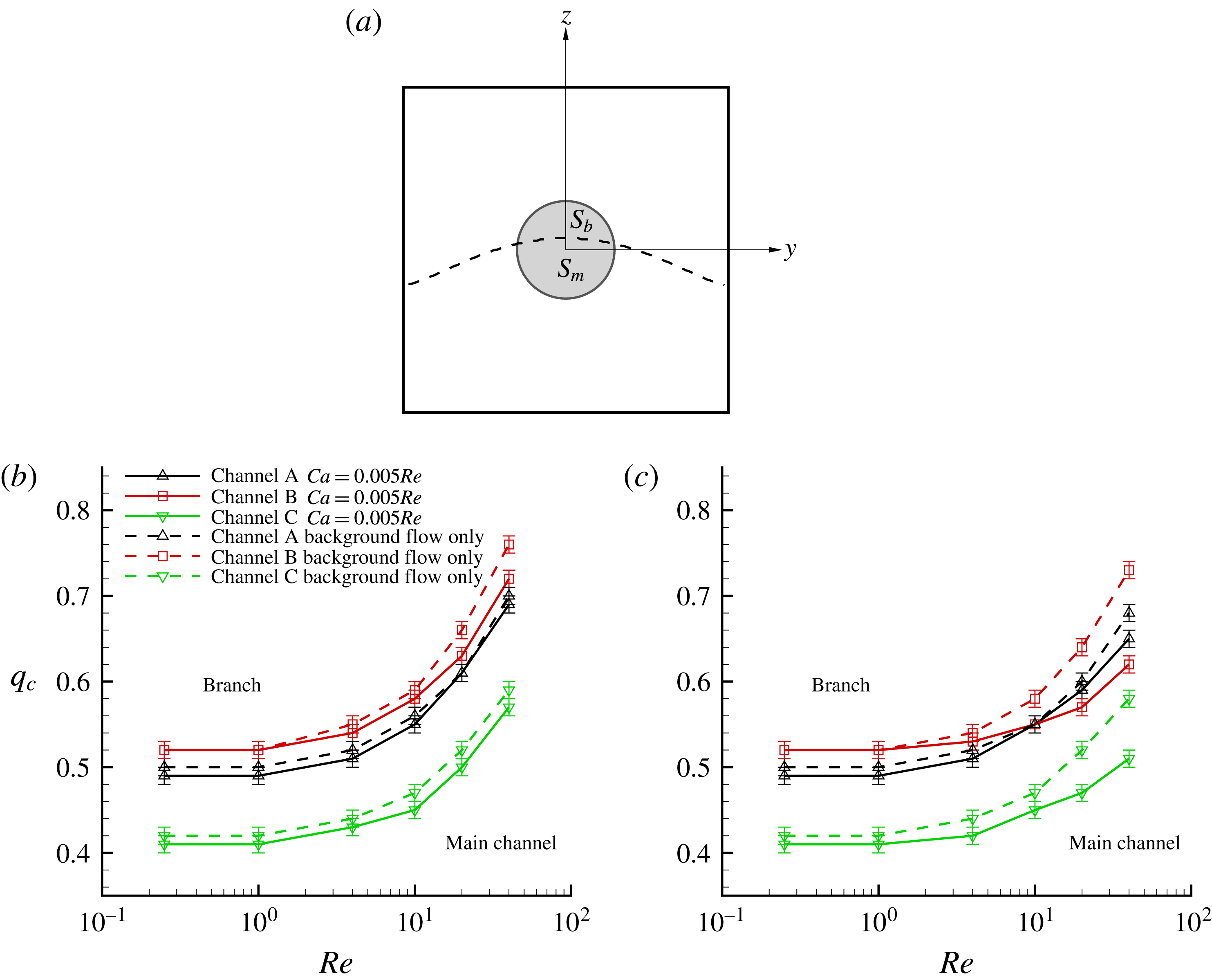
Figure 11. (a) Illustration of the definition of the momentum ratio. The dashed line is a fluid separation line (for
![]() $q=0.5$
,
$q=0.5$
,
![]() $Re=10$
in channel A), which divides the cross-sectional area of the capsule (shaded circle) into two regions,
$Re=10$
in channel A), which divides the cross-sectional area of the capsule (shaded circle) into two regions,
![]() $S_{b}$
and
$S_{b}$
and
![]() $S_{m}$
, the fluid elements of which finally enter the side branch and the downstream main channel, respectively. (b) Phase diagram: critical branch flow ratio as a function of the channel Reynolds number for a capsule with
$S_{m}$
, the fluid elements of which finally enter the side branch and the downstream main channel, respectively. (b) Phase diagram: critical branch flow ratio as a function of the channel Reynolds number for a capsule with
![]() $a/l=0.2$
flowing in branched channels with different geometries. Solid lines, full fluid–structure simulations with a capsule (see figure 8); dashed lines,
$a/l=0.2$
flowing in branched channels with different geometries. Solid lines, full fluid–structure simulations with a capsule (see figure 8); dashed lines,
![]() $q_{cm}$
from the background flow only. (c) The same as (b), with
$q_{cm}$
from the background flow only. (c) The same as (b), with
![]() $a/l=0.3$
.
$a/l=0.3$
.
We now investigate the importance of the background flow on the path selection of the capsule. An approximate way of doing this is to use the simplified model of Wang et al. (Reference Wang, Sui, Salsac, Barthès-Biesel and Wang2016), which is based on the momentum split in section
![]() $S_{c}$
. Specifically, the cross-sectional area of the undeformed capsule in
$S_{c}$
. Specifically, the cross-sectional area of the undeformed capsule in
![]() $S_{c}$
is divided by the fluid separation line into two regions
$S_{c}$
is divided by the fluid separation line into two regions
![]() $S_{b}$
and
$S_{b}$
and
![]() $S_{m}$
, corresponding to fluid elements that later flow into the branch or the downstream channel, respectively (figure 11
a). The background fluid momentum ratio
$S_{m}$
, corresponding to fluid elements that later flow into the branch or the downstream channel, respectively (figure 11
a). The background fluid momentum ratio
![]() $M$
is defined as
$M$
is defined as
 $$\begin{eqnarray}M=\frac{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}}{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}+\int _{S_{m}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{m}},\end{eqnarray}$$
$$\begin{eqnarray}M=\frac{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}}{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}+\int _{S_{m}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{m}},\end{eqnarray}$$
where
![]() $u(y,z)$
is the undisturbed fluid velocity along the
$u(y,z)$
is the undisturbed fluid velocity along the
![]() $x$
-direction in
$x$
-direction in
![]() $S_{c}$
. We then assume that the background flow carries a capsule into the lateral branch if
$S_{c}$
. We then assume that the background flow carries a capsule into the lateral branch if
![]() $M>0.5$
and we compute the corresponding value
$M>0.5$
and we compute the corresponding value
![]() $q_{cm}$
of
$q_{cm}$
of
![]() $q$
for which
$q$
for which
![]() $M=0.5$
. The determination of
$M=0.5$
. The determination of
![]() $q_{cm}$
is similar to that of
$q_{cm}$
is similar to that of
![]() $q_{c}$
, so that
$q_{c}$
, so that
![]() $q_{cm}$
is also determined within
$q_{cm}$
is also determined within
![]() $\pm 0.01$
. The values of
$\pm 0.01$
. The values of
![]() $q_{cm}$
are compared with the values
$q_{cm}$
are compared with the values
![]() $q_{c}$
obtained from the full fluid–structure interaction simulations in figure 11(b,c). Several interesting observations can be made. Firstly, the order of
$q_{c}$
obtained from the full fluid–structure interaction simulations in figure 11(b,c). Several interesting observations can be made. Firstly, the order of
![]() $q_{cm}$
always follows
$q_{cm}$
always follows
![]() $q_{cmC}<q_{cmA}<q_{cmB}$
for capsules with different sizes at different Reynolds numbers. Secondly, there is only a small difference between
$q_{cmC}<q_{cmA}<q_{cmB}$
for capsules with different sizes at different Reynolds numbers. Secondly, there is only a small difference between
![]() $q_{c}$
and
$q_{c}$
and
![]() $q_{cm}$
for small capsules (figure 11
b): this is not surprising as a small capsule creates a small perturbation and thus essentially follows the undisturbed centre flow streamline. Thirdly, for all three channel geometries, the values of
$q_{cm}$
for small capsules (figure 11
b): this is not surprising as a small capsule creates a small perturbation and thus essentially follows the undisturbed centre flow streamline. Thirdly, for all three channel geometries, the values of
![]() $q_{cm}$
and
$q_{cm}$
and
![]() $q_{c}$
are close for low Reynolds numbers (i.e.
$q_{c}$
are close for low Reynolds numbers (i.e.
![]() $Re\leqslant 4$
for
$Re\leqslant 4$
for
![]() $a/l=0.3$
and
$a/l=0.3$
and
![]() $Re\leqslant 10$
for
$Re\leqslant 10$
for
![]() $a/l=0.2$
) when the capsule deformation is negligible. Finally, at higher Reynolds numbers, the deviation of
$a/l=0.2$
) when the capsule deformation is negligible. Finally, at higher Reynolds numbers, the deviation of
![]() $q_{cm}$
from
$q_{cm}$
from
![]() $q_{c}$
becomes significant, in particular for channels with a narrowed side branch. This phenomenon is due to the fact that we consider a capsule with fixed intrinsic properties at constant
$q_{c}$
becomes significant, in particular for channels with a narrowed side branch. This phenomenon is due to the fact that we consider a capsule with fixed intrinsic properties at constant
![]() $Ca/Re$
ratio: thus when we increase
$Ca/Re$
ratio: thus when we increase
![]() $Re$
, it follows that
$Re$
, it follows that
![]() $Ca$
and the capsule deformation increase accordingly, a phenomenon that tends to lower
$Ca$
and the capsule deformation increase accordingly, a phenomenon that tends to lower
![]() $q_{c}$
. We can thus surmise from figure 11(c) that there are instances where the simple model based on the background flow and the full numerical model lead to different predictions. Specifically, in figure 11(c) this occurs for flow conditions corresponding to the parameter domain between the dashed and solid line curves of a given channel. As an illustration, we show the case of a capsule in channel C for
$q_{c}$
. We can thus surmise from figure 11(c) that there are instances where the simple model based on the background flow and the full numerical model lead to different predictions. Specifically, in figure 11(c) this occurs for flow conditions corresponding to the parameter domain between the dashed and solid line curves of a given channel. As an illustration, we show the case of a capsule in channel C for
![]() $a/l=0.3,Re=20,Ca=0.1,q=0.5$
(figure 12). In the feed branch, the capsule centre is slightly below the flow separation streamline. The centre streamline continues into the straight daughter branch, but the capsule trajectory crosses the separation streamline to flow into the side branch. The main conclusion of this study is that the flow path selection of a capsule is not completely determined by the background flow, especially when the capsule has a non-negligible size and when its deformation is significant.
$a/l=0.3,Re=20,Ca=0.1,q=0.5$
(figure 12). In the feed branch, the capsule centre is slightly below the flow separation streamline. The centre streamline continues into the straight daughter branch, but the capsule trajectory crosses the separation streamline to flow into the side branch. The main conclusion of this study is that the flow path selection of a capsule is not completely determined by the background flow, especially when the capsule has a non-negligible size and when its deformation is significant.
Finally, we note that after the capsule has passed the bifurcation, it is no longer centred on the channel axis but has been deported near one channel wall. This means that we can expect the capsule to eventually migrate back towards the channel axis (Helmy & Barthès-Biesel Reference Helmy and Barthès-Biesel1982; Secomb, Styp-Rekowska & Pries Reference Secomb, Styp-Rekowska and Pries2007; Doddi & Bagchi Reference Doddi and Bagchi2008). However, this process is slow and cannot be captured by the present simulation because the daughter branches of the channel are not long enough.

Figure 12. Capsule crossing the background flow separation streamline in channel C for
![]() $a/l=0.3,Re=20,Ca=0.1,q=0.5$
.
$a/l=0.3,Re=20,Ca=0.1,q=0.5$
.
3.3 Additional pressure drop due to the capsule
Under constant flow rates, the capsule creates time-dependent additional pressure drops
![]() $\unicode[STIX]{x0394}P_{1}^{cap}$
and
$\unicode[STIX]{x0394}P_{1}^{cap}$
and
![]() $\unicode[STIX]{x0394}P_{2}^{cap}$
for the straight channel and side branch, respectively. These are defined as
$\unicode[STIX]{x0394}P_{2}^{cap}$
for the straight channel and side branch, respectively. These are defined as
where
![]() $P_{0}(0)-P_{1}(0)$
and
$P_{0}(0)-P_{1}(0)$
and
![]() $P_{0}(0)-P_{2}(0)$
are the pressure drops from the inlet to the outlets of the straight downstream channel and of the side branch, respectively, when the capsule is absent. As an example, we consider channel C with
$P_{0}(0)-P_{2}(0)$
are the pressure drops from the inlet to the outlets of the straight downstream channel and of the side branch, respectively, when the capsule is absent. As an example, we consider channel C with
![]() $a/l=0.3$
,
$a/l=0.3$
,
![]() $Re=20$
,
$Re=20$
,
![]() $Ca=0.1$
, for which
$Ca=0.1$
, for which
![]() $q_{c}=0.47$
. We then show the time evolution of the additional pressure drops in the straight channel and in the side branch (figure 13) as the capsule flows across the bifurcation for two different values of
$q_{c}=0.47$
. We then show the time evolution of the additional pressure drops in the straight channel and in the side branch (figure 13) as the capsule flows across the bifurcation for two different values of
![]() $q$
below and above
$q$
below and above
![]() $q_{c}$
. For
$q_{c}$
. For
![]() $q=0.46$
, the capsule goes straight, whereas it flows into the side branch for
$q=0.46$
, the capsule goes straight, whereas it flows into the side branch for
![]() $q=0.48$
. In all cases, the crossing of the bifurcation itself creates a significant pressure perturbation across the two branches because the capsule hinders the flow temporarily. After the capsule has passed the bifurcation,
$q=0.48$
. In all cases, the crossing of the bifurcation itself creates a significant pressure perturbation across the two branches because the capsule hinders the flow temporarily. After the capsule has passed the bifurcation,
![]() $\unicode[STIX]{x0394}P_{1}^{cap}(t)$
goes to zero when the capsule takes the lateral branch. When the capsule flows straight,
$\unicode[STIX]{x0394}P_{1}^{cap}(t)$
goes to zero when the capsule takes the lateral branch. When the capsule flows straight,
![]() $\unicode[STIX]{x0394}P_{1}^{cap}(t)\rightarrow \unicode[STIX]{x0394}P_{1\infty }^{cap}$
, a value that corresponds to the perturbation that the capsule would create in an infinite channel where the straight channel flow conditions prevail. It is clear from figure 13 that
$\unicode[STIX]{x0394}P_{1}^{cap}(t)\rightarrow \unicode[STIX]{x0394}P_{1\infty }^{cap}$
, a value that corresponds to the perturbation that the capsule would create in an infinite channel where the straight channel flow conditions prevail. It is clear from figure 13 that
![]() $\unicode[STIX]{x0394}P_{1\infty }^{cap}$
is quite small because the capsule is small compared to the straight branch cross-dimensions. However, when the capsule flows into the side branch, the reduced branch section leads to significant interactions between the wall and the capsule, so that
$\unicode[STIX]{x0394}P_{1\infty }^{cap}$
is quite small because the capsule is small compared to the straight branch cross-dimensions. However, when the capsule flows into the side branch, the reduced branch section leads to significant interactions between the wall and the capsule, so that
![]() $\unicode[STIX]{x0394}P_{2}^{cap}(t)$
tends towards a much larger value
$\unicode[STIX]{x0394}P_{2}^{cap}(t)$
tends towards a much larger value
![]() $\unicode[STIX]{x0394}P_{2\infty }^{cap}$
. The latter corresponds to the additional pressure drop created by this capsule in a rectangular channel, when it has reached an equilibrium state under the flow conditions specified above.
$\unicode[STIX]{x0394}P_{2\infty }^{cap}$
. The latter corresponds to the additional pressure drop created by this capsule in a rectangular channel, when it has reached an equilibrium state under the flow conditions specified above.

Figure 13. Time evolution of the capsule additional pressure drop in channel C under constant flow rate conditions (
![]() $a/l=0.3,Re=20,Ca=0.1,q_{c}=0.47$
). The positions of the capsule mass centre in the respective branches are shown by the arrows.
$a/l=0.3,Re=20,Ca=0.1,q_{c}=0.47$
). The positions of the capsule mass centre in the respective branches are shown by the arrows.

Figure 14. Additional capsule pressure drop in a rectangular side branch (section
![]() $2l\times l$
) as a function of the flow split ratio for
$2l\times l$
) as a function of the flow split ratio for
![]() $a/l=0.3,Ca=0.005Re$
. Note that
$a/l=0.3,Ca=0.005Re$
. Note that
![]() $Re$
is defined in the parent channel.
$Re$
is defined in the parent channel.
Since there are no published data on the additional pressure drop created by a capsule in a rectangular channel, we have systematically determined the relation between
![]() $\unicode[STIX]{x0394}P_{2\infty }^{cap}$
and the flow split ratio
$\unicode[STIX]{x0394}P_{2\infty }^{cap}$
and the flow split ratio
![]() $q$
for a capsule flowing in a straight rectangular channel (
$q$
for a capsule flowing in a straight rectangular channel (
![]() $2l\times l$
) for
$2l\times l$
) for
![]() $a/l=0.3$
and
$a/l=0.3$
and
![]() $Ca=0.005Re$
at two values of
$Ca=0.005Re$
at two values of
![]() $Re$
. The results are shown in figure 14. The additional pressure drop increases, as is expected, with
$Re$
. The results are shown in figure 14. The additional pressure drop increases, as is expected, with
![]() $q$
(i.e. with the mean flow velocity in the channel). The fact that it decreases when
$q$
(i.e. with the mean flow velocity in the channel). The fact that it decreases when
![]() $Re$
increases is mainly because the local increase of the Reynolds number has led to larger deformation of the capsule. We have also computed the corresponding values of
$Re$
increases is mainly because the local increase of the Reynolds number has led to larger deformation of the capsule. We have also computed the corresponding values of
![]() $\unicode[STIX]{x0394}P_{1\infty }^{cap}$
and found that, although they increase with
$\unicode[STIX]{x0394}P_{1\infty }^{cap}$
and found that, although they increase with
![]() $q$
, they are all lower than 0.08. As mentioned earlier, this is due to the small size ratio between the capsule and the channel.
$q$
, they are all lower than 0.08. As mentioned earlier, this is due to the small size ratio between the capsule and the channel.
3.4 Comparison with Fung’s model
Recall that the simple qualitative Fung’s model, developed for a symmetric Y-shaped bifurcation, predicts that an RBC enters the branch where the flow rate or velocity is highest. In the case of channel A, where the all branches have the same cross-section, Fung’s theory leads to
![]() $q_{c}^{F}=0.5$
, which is in good agreement with the numerical model predictions for moderate Reynolds number (
$q_{c}^{F}=0.5$
, which is in good agreement with the numerical model predictions for moderate Reynolds number (
![]() $Re<5$
), even though the bifurcation geometry is not Y-shaped (figure 8
a). In the case of channels B and C and low inertia (
$Re<5$
), even though the bifurcation geometry is not Y-shaped (figure 8
a). In the case of channels B and C and low inertia (
![]() $Re\leqslant 1$
), it is clear that Fung’s criterion on flow rate does not apply:
$Re\leqslant 1$
), it is clear that Fung’s criterion on flow rate does not apply:
![]() $q$
must be larger than 0.52 for the capsule to flow into the side branch of channel B. For channel C,
$q$
must be larger than 0.52 for the capsule to flow into the side branch of channel B. For channel C,
![]() $q_{c}$
is about 20 % lower than the equal flow split criterion of Fung’s model, which means that for
$q_{c}$
is about 20 % lower than the equal flow split criterion of Fung’s model, which means that for
![]() $0.4<q<0.5$
, the capsule flows into the side branch even though the flow rate there is lower than in the straight branch. Trying to apply Fung’s criterion based on velocities rather that flow rate would lead to
$0.4<q<0.5$
, the capsule flows into the side branch even though the flow rate there is lower than in the straight branch. Trying to apply Fung’s criterion based on velocities rather that flow rate would lead to
![]() $q_{c}^{F}=1/3$
for channels B and C, which is much lower than what is calculated (figure 8). As inertial effects increase,
$q_{c}^{F}=1/3$
for channels B and C, which is much lower than what is calculated (figure 8). As inertial effects increase,
![]() $q_{c}$
increases too, which means that for
$q_{c}$
increases too, which means that for
![]() $0.5\leqslant q<q_{c}$
, the capsule tends to go straight even if the flow rate is higher in the side branch than in the straight one.
$0.5\leqslant q<q_{c}$
, the capsule tends to go straight even if the flow rate is higher in the side branch than in the straight one.
We conclude that Fung’s model does not apply to bifurcations with equal branch cross-sections, if inertia effects are significant. It does not apply either to bifurcations where the branch sections are different, even when inertia effects are small. The results show clearly that, for a given bifurcation geometry, the flow rate is better than the velocity as the main criterion for path selection, but that the three-dimensional phenomena that occur at the bifurcation are too complex to be amenable to a simple phenomenological, one-dimensional theory.
4 Suspension enrichment with a right-angled bifurcation device
4.1 Effect of bifurcation geometry

Figure 15. (a) Top view of the side branch geometries for channels C, D, E and F. Channels C and E are centre-connected to the main channel. (b) Fluid separation lines for channels C, D, E and F. From left to right:
![]() $Re=0.25$
;
$Re=0.25$
;
![]() $Re=10$
;
$Re=10$
;
![]() $Re=40$
.
$Re=40$
.
The present simulation results can be useful in guiding the design of microfluidic devices, which use a side branch to enrich capsules in suspending fluid (Gossett et al.
Reference Gossett, Weaver, Mach, Hur, Tse, Lee, Amini and Di Carlo2010; Shields IV et al.
Reference Shields IV, Reyes and López2015; Tripathi et al.
Reference Tripathi, Kumar, Prabhakar, Joshi and Agrawal2015). Obviously, this purpose is best achieved for
![]() $q_{c}<0.5$
, as the smaller
$q_{c}<0.5$
, as the smaller
![]() $q_{c}$
, the more efficient the device. Our results (figure 8) indicate that channel C is the most efficient design to achieve suspension enrichment as
$q_{c}$
, the more efficient the device. Our results (figure 8) indicate that channel C is the most efficient design to achieve suspension enrichment as
![]() $q_{c}$
is just over 0.4 up to
$q_{c}$
is just over 0.4 up to
![]() $Re=5$
and remains lower than 0.5 up to
$Re=5$
and remains lower than 0.5 up to
![]() $Re=20$
for the larger particle confinement ratio (
$Re=20$
for the larger particle confinement ratio (
![]() $a/l=0.3$
). Of course, as the particle becomes small (
$a/l=0.3$
). Of course, as the particle becomes small (
![]() $a/l\leqslant 0.2$
), it tends to follow the streamlines and thus
$a/l\leqslant 0.2$
), it tends to follow the streamlines and thus
![]() $q_{c}$
increases with
$q_{c}$
increases with
![]() $Re$
. However, it should be noted that channel C presents some drawbacks: firstly, it is not very easy to fabricate with soft lithography methods; secondly, its narrow width puts a limit on the confinement ratios that can be used. It is then worthwhile to test whether other branch geometries may lead to better suspension enrichment. We have thus considered three other bifurcations (channels D, E and F, as shown in figure 15
a) with the same branch angle and the same area ratio between the cross-sections of the side branch and of the straight channel. Channel D has the same orientation and cross-section as channel C, but is not centre-connected to the main branch. Channel E and F have square sections with side
$Re$
. However, it should be noted that channel C presents some drawbacks: firstly, it is not very easy to fabricate with soft lithography methods; secondly, its narrow width puts a limit on the confinement ratios that can be used. It is then worthwhile to test whether other branch geometries may lead to better suspension enrichment. We have thus considered three other bifurcations (channels D, E and F, as shown in figure 15
a) with the same branch angle and the same area ratio between the cross-sections of the side branch and of the straight channel. Channel D has the same orientation and cross-section as channel C, but is not centre-connected to the main branch. Channel E and F have square sections with side
![]() $\sqrt{2}l$
and are respectively centre-connected or not. The advantage of channels E and F is that the minimum cross-section dimension is approximately 40 % larger than that of channel C and thus allows larger capsules to flow. The advantage of off-centred channels D and F is that they have one side wall aligned with that of the main channel: they are thus easier to fabricate with soft lithography methods than channels C and E.
$\sqrt{2}l$
and are respectively centre-connected or not. The advantage of channels E and F is that the minimum cross-section dimension is approximately 40 % larger than that of channel C and thus allows larger capsules to flow. The advantage of off-centred channels D and F is that they have one side wall aligned with that of the main channel: they are thus easier to fabricate with soft lithography methods than channels C and E.
The separation lines for channels C, D, E and F are shown in figure 15(b). For centred channels (C and E), the flow patterns are similar to those discussed in § 3.1. Note that at the centre of
![]() $S_{c}$
, the separation line for channel E is between those of channels B and C, as predicted by the simple residence time model where
$S_{c}$
, the separation line for channel E is between those of channels B and C, as predicted by the simple residence time model where
![]() $d_{z}=2\sqrt{2}l/3$
for channel E. For the two off-centred channels D and F, the separation line is warped, indicating that fluid particles located at
$d_{z}=2\sqrt{2}l/3$
for channel E. For the two off-centred channels D and F, the separation line is warped, indicating that fluid particles located at
![]() $y>0.5l$
or
$y>0.5l$
or
![]() $y>0.7l$
for channel D or F, respectively tend to flow straight for small values of
$y>0.7l$
for channel D or F, respectively tend to flow straight for small values of
![]() $Re$
. As inertia effects increase, the side branch influence extends to a larger area in the section.
$Re$
. As inertia effects increase, the side branch influence extends to a larger area in the section.
We have determined the critical branch flow ratios for capsules with
![]() $a/l=0,0.2$
and
$a/l=0,0.2$
and
![]() $0.3$
in channels C, D, E and F. We find that, as regards
$0.3$
in channels C, D, E and F. We find that, as regards
![]() $q_{c}$
, there is little difference between channels C and D, and between channels E and F (not shown). This is due to the fact that we consider centred, fairly small capsules only, and that the flow separation patterns are not very different near the centre of the channel (figure 15
b). In conclusion the critical branch flow ratios for all of the channels are shown in figure 16. Channels C or D correspond to the most efficient capsule enrichment geometry, followed by the square section channels E and F. The choice between the two types of geometries may be guided by the average size of the suspended capsules.
$q_{c}$
, there is little difference between channels C and D, and between channels E and F (not shown). This is due to the fact that we consider centred, fairly small capsules only, and that the flow separation patterns are not very different near the centre of the channel (figure 15
b). In conclusion the critical branch flow ratios for all of the channels are shown in figure 16. Channels C or D correspond to the most efficient capsule enrichment geometry, followed by the square section channels E and F. The choice between the two types of geometries may be guided by the average size of the suspended capsules.
4.2 Case of pressure-control systems
The above study corresponds to systems where the flow rates at the inlet and outlets are controlled and kept constant, independently of the capsule presence. However, there are other microfluidic systems where the flow is driven by constant pressure differences between the entrance and exit sections. It is therefore meaningful to investigate how the present results can apply to pressure-control systems. In order to do so, we first have to find the relation between the imposed pressure differences and the resulting flow split. Then the influence of a capsule on the flow has to be determined.
4.2.1 Pressure drops across the bifurcation

Figure 16. Phase diagram: critical branch flow ratio as a function of the channel Reynolds number for capsules in branched channels A, B, C and E. The values of
![]() $q_{c}$
in channels D and F are very close to those in channels C and E, respectively, and are therefore not shown.
$q_{c}$
in channels D and F are very close to those in channels C and E, respectively, and are therefore not shown.
![]() $Ca=0.005Re$
. (a)
$Ca=0.005Re$
. (a)
![]() $a/l=0.2$
; (b)
$a/l=0.2$
; (b)
![]() $a/l=0.3$
.
$a/l=0.3$
.
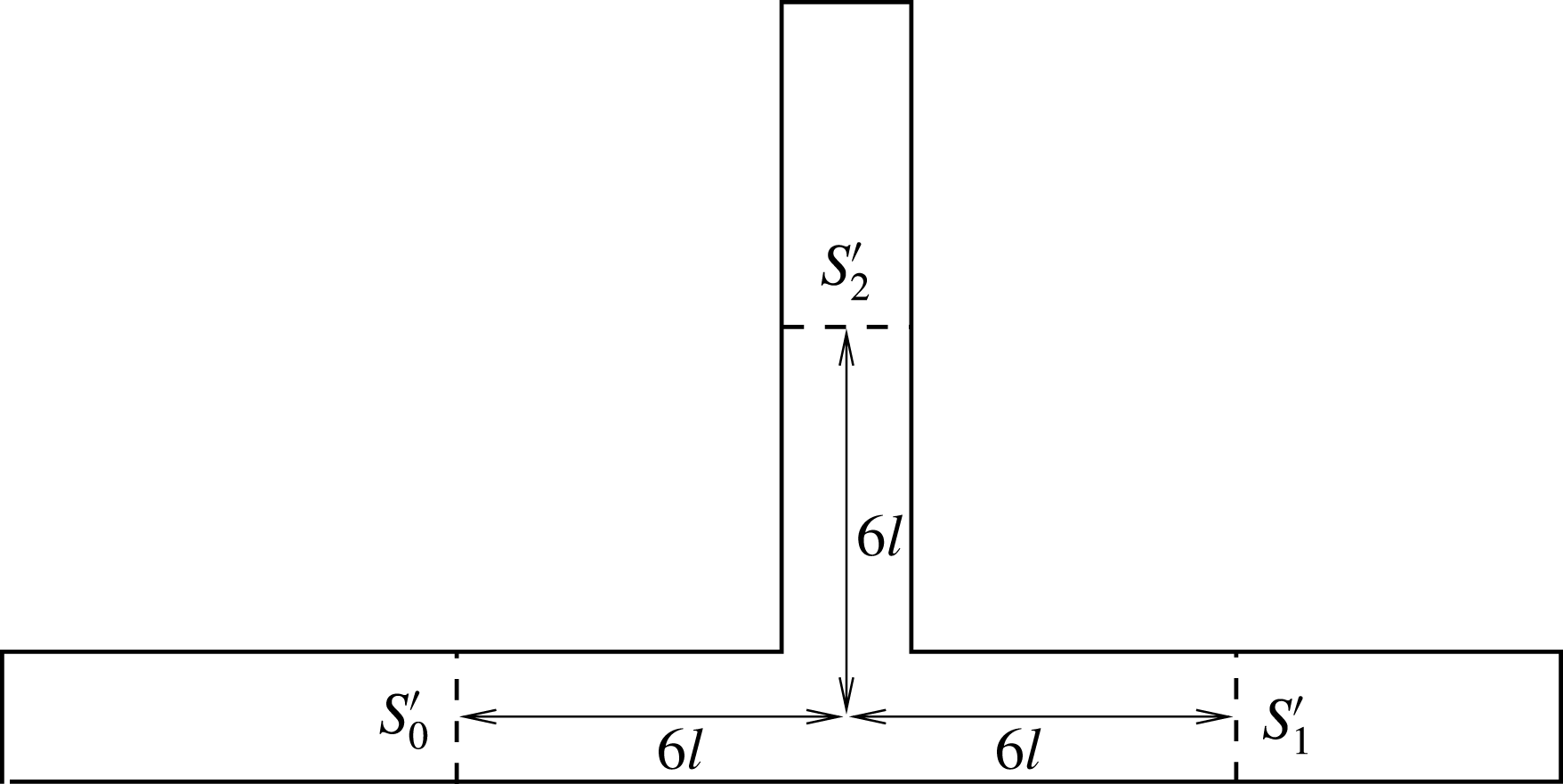
Figure 17. Definition of the cross-sections where the pressure is evaluated to determine the pressure drop in the bifurcation.

Figure 18. The additional pressure drop
![]() $\unicode[STIX]{x0394}P_{1}^{\prime }$
and
$\unicode[STIX]{x0394}P_{1}^{\prime }$
and
![]() $\unicode[STIX]{x0394}P_{2}^{\prime }$
(non-dimensionalised by
$\unicode[STIX]{x0394}P_{2}^{\prime }$
(non-dimensionalised by
![]() $\unicode[STIX]{x1D707}V/l$
) due to the bifurcation as a function of the branch flow ratio
$\unicode[STIX]{x1D707}V/l$
) due to the bifurcation as a function of the branch flow ratio
![]() $q$
in branched channel flows without the capsule. (a)
$q$
in branched channel flows without the capsule. (a)
![]() $Re=0.25$
; (b)
$Re=0.25$
; (b)
![]() $Re=20$
.
$Re=20$
.
It is of interest to compute systematically the pressure drop across the bifurcation, as it is information that is not available in the literature. In order to eliminate the influence of the channel lengths, we consider three cross-sections located at a distance
![]() $6l$
from the bifurcation centre:
$6l$
from the bifurcation centre:
![]() $S_{0}^{\prime }$
in the parent channel and
$S_{0}^{\prime }$
in the parent channel and
![]() $S_{1}^{\prime },S_{2}^{\prime }$
in the two downstream channels (figure 17). As shown in figures 6 and 7 and discussed in § 3.1, the flows in those sections are fully developed with pressures denoted by
$S_{1}^{\prime },S_{2}^{\prime }$
in the two downstream channels (figure 17). As shown in figures 6 and 7 and discussed in § 3.1, the flows in those sections are fully developed with pressures denoted by
![]() $P_{0}^{\prime },P_{1}^{\prime }$
and
$P_{0}^{\prime },P_{1}^{\prime }$
and
![]() $P_{2}^{\prime }$
, respectively. In order to highlight the bifurcation effect, we define a measure of the singular pressure drop as
$P_{2}^{\prime }$
, respectively. In order to highlight the bifurcation effect, we define a measure of the singular pressure drop as
Here
![]() $\unicode[STIX]{x0394}P_{0}(6l)$
,
$\unicode[STIX]{x0394}P_{0}(6l)$
,
![]() $\unicode[STIX]{x0394}P_{1}(6l)$
and
$\unicode[STIX]{x0394}P_{1}(6l)$
and
![]() $\unicode[STIX]{x0394}P_{2}(6l)$
are the pressure drops for fully developed flows over the distance of
$\unicode[STIX]{x0394}P_{2}(6l)$
are the pressure drops for fully developed flows over the distance of
![]() $6l$
in the parent channel, the downstream straight channel and the side branch, respectively. They are easily computed analytically (e.g. White Reference White1991).
$6l$
in the parent channel, the downstream straight channel and the side branch, respectively. They are easily computed analytically (e.g. White Reference White1991).
The additional pressure drops due to the bifurcation as a function of the branch flow ratio
![]() $q$
are shown in figure 18 for all of the channel geometries considered in the present study at
$q$
are shown in figure 18 for all of the channel geometries considered in the present study at
![]() $Re=0.25$
and 20. The additional pressure drop
$Re=0.25$
and 20. The additional pressure drop
![]() $\unicode[STIX]{x0394}P_{1}^{\prime }$
is always negative. This is because the flow in the straight channel is relatively regular and the effective wall area of the control volume with length
$\unicode[STIX]{x0394}P_{1}^{\prime }$
is always negative. This is because the flow in the straight channel is relatively regular and the effective wall area of the control volume with length
![]() $12l$
is diminished by an amount equal to the area of the side branch entrance. This is also the reason why
$12l$
is diminished by an amount equal to the area of the side branch entrance. This is also the reason why
![]() $\unicode[STIX]{x0394}P_{2}^{\prime }$
is negative at
$\unicode[STIX]{x0394}P_{2}^{\prime }$
is negative at
![]() $Re=0.25$
and at very low branch flow ratios at
$Re=0.25$
and at very low branch flow ratios at
![]() $Re=20$
. However, for high branch flow ratios at
$Re=20$
. However, for high branch flow ratios at
![]() $Re=20$
,
$Re=20$
,
![]() $\unicode[STIX]{x0394}P_{2}^{\prime }$
becomes positive due to the increasing inertial flow perturbation, as shown in figure 7. The differences between the different bifurcation geometries with the same side branch cross-sectional area are slight, and result from differences in flow patterns at the bifurcation.
$\unicode[STIX]{x0394}P_{2}^{\prime }$
becomes positive due to the increasing inertial flow perturbation, as shown in figure 7. The differences between the different bifurcation geometries with the same side branch cross-sectional area are slight, and result from differences in flow patterns at the bifurcation.
The total pressure drops across the channel branches are then obtained by adding the contribution from those channel lengths between section
![]() $S_{0}$
and each exit
$S_{0}$
and each exit
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
using analytical solutions:
$S_{2}$
using analytical solutions:
where
![]() $L_{0},L_{1},L_{2}$
are the lengths of the system branches.
$L_{0},L_{1},L_{2}$
are the lengths of the system branches.
4.2.2 Example: dynamic flow split for a capsule in channel C
As an example, we have carried out constant pressure simulations for a capsule in channel C with
![]() $a/l=0.3$
at
$a/l=0.3$
at
![]() $Re=20$
and
$Re=20$
and
![]() $Ca=0.1$
. Using the results of § 4.2.1, we first compute the constant pressure differences
$Ca=0.1$
. Using the results of § 4.2.1, we first compute the constant pressure differences
![]() $P_{0}-P_{1}$
and
$P_{0}-P_{1}$
and
![]() $P_{0}-P_{2}$
that must be applied to obtain two initial values of the flow split
$P_{0}-P_{2}$
that must be applied to obtain two initial values of the flow split
![]() $q_{1}(0)=0.46$
and
$q_{1}(0)=0.46$
and
![]() $q_{2}(0)=0.48$
, which are just below and above the critical value
$q_{2}(0)=0.48$
, which are just below and above the critical value
![]() $q_{c}=0.47$
. Of course, the presence of the capsule changes the flow rates in each channel and the branch flow ratio varies with time, as shown in figure 19. In both cases, the maximum variation of
$q_{c}=0.47$
. Of course, the presence of the capsule changes the flow rates in each channel and the branch flow ratio varies with time, as shown in figure 19. In both cases, the maximum variation of
![]() $q$
with time is less than
$q$
with time is less than
![]() $0.01$
and therefore the instantaneous flow split remains above or below the critical branch flow ratio: the path selection of the capsule is thus unchanged. This is due to the fact that we have considered a single capsule, which is small compared with the channel. We have found similar unchanged capsule path selection in other tests with different channel geometries and flow Reynolds numbers.
$0.01$
and therefore the instantaneous flow split remains above or below the critical branch flow ratio: the path selection of the capsule is thus unchanged. This is due to the fact that we have considered a single capsule, which is small compared with the channel. We have found similar unchanged capsule path selection in other tests with different channel geometries and flow Reynolds numbers.

Figure 19. Time evolution of the branch flow ratio
![]() $q$
in channel C when using constant pressure boundary conditions for
$q$
in channel C when using constant pressure boundary conditions for
![]() $a/l=0.3,Re=20,Ca=0.1,q_{c}=0.47$
. The positions of the capsule mass centre in the respective branches are shown by the arrows.
$a/l=0.3,Re=20,Ca=0.1,q_{c}=0.47$
. The positions of the capsule mass centre in the respective branches are shown by the arrows.
5 Discussion and conclusion
This extensive three-dimensional study of the flow in different bifurcation geometries is the first of its kind, whether it be for the background flow in a rectangular cross-section bifurcation or for the path selection of a deformable capsule. It is important to note that small but finite inertia effects have also been taken into account. We have thus been able to provide new extensive data on the flow pattern and pressure drop across microfluidic bifurcations with a right-angled lateral branch with different cross-section shapes and different positions with respect to the parent channel axis. The study puts into evidence the crucial importance of accounting for three-dimensional effects in the simulation. Indeed, a two-dimensional model is unable to distinguish between the different bifurcation geometries that have been studied here. This is a significant drawback of such models as we have shown that the specific bifurcation geometry plays an important role in the path selection of the capsule. Furthermore, the deformation of the capsule is itself a three-dimensional mechanical process as it appears in figure 10. The application of two-dimensional numerical models to actual three-dimensional situations would potentially have led to erroneous conclusions.
Although the bifurcation flow pattern is quite complex, we have shown that it is possible to use simplified models to guide the choice of a geometry. For example, the residence time evaluation can be correlated with the capture efficiency of a side branch: the longer a capsule stays in the bifurcation the more likely it is to take the side branch. For more refined predictions of the capsule path selection, it is necessary to compute the background flow (a task which is much easier than the solution of the full fluid–structure interaction problem). We show that a simplified model based on the background flow predicts well the trajectory of small or low-inertia capsules and even provides decent estimates for higher-inertia flows. Another important conclusion of this study is that the commonly accepted Fung’s model only applies to bifurcations with equal cross-sections when inertia effects are negligible. When inertia starts to play a role and/or when the branches’ cross-sections are not equal, Fung’s model does not apply.
The main results of the study are summarised in phase diagrams, which can help choose an efficient design for a capsule enrichment device, taking into account the ease of fabrication with the present soft lithography techniques. For suspension enrichment, the efficiency of a system depends on the values of
![]() $q_{c}$
, which should be as small as possible. For example, we can expect
$q_{c}$
, which should be as small as possible. For example, we can expect
![]() $q_{c}>0.5$
for a symmetric Y- or T-bifurcation (figure 1
a,b). With lateral bifurcations such as the ones considered here, we find values of
$q_{c}>0.5$
for a symmetric Y- or T-bifurcation (figure 1
a,b). With lateral bifurcations such as the ones considered here, we find values of
![]() $q_{c}$
which can be significantly lower than 0.5, depending on the configuration. Specifically, a narrowed side branch with a cross-section which is half that of the main branch is shown to be an efficient geometry, provided it is correctly oriented like channels C or D. The smallest values of
$q_{c}$
which can be significantly lower than 0.5, depending on the configuration. Specifically, a narrowed side branch with a cross-section which is half that of the main branch is shown to be an efficient geometry, provided it is correctly oriented like channels C or D. The smallest values of
![]() $q_{c}$
are obtained for low Reynolds numbers. Inertia effects (
$q_{c}$
are obtained for low Reynolds numbers. Inertia effects (
![]() $Re>1$
) lead to an increase of
$Re>1$
) lead to an increase of
![]() $q_{c}$
, which is more pronounced for small particles than for larger more deformable ones. This may well be due to the specific lateral bifurcation geometry we have studied here, where elevated inertia forces lead to a tendency for the capsule to flow into the straight branch rather than take the turn into the side branch. We have also shown that for small particles (
$q_{c}$
, which is more pronounced for small particles than for larger more deformable ones. This may well be due to the specific lateral bifurcation geometry we have studied here, where elevated inertia forces lead to a tendency for the capsule to flow into the straight branch rather than take the turn into the side branch. We have also shown that for small particles (
![]() $a/l\leqslant 0.2$
), the path selection of the capsule can be fairly well evaluated from the background flow, but that is not quite the case for moderate confinement ratios (
$a/l\leqslant 0.2$
), the path selection of the capsule can be fairly well evaluated from the background flow, but that is not quite the case for moderate confinement ratios (
![]() $a/l\leqslant 0.3$
) when inertia effects are becoming important (
$a/l\leqslant 0.3$
) when inertia effects are becoming important (
![]() $Re\geqslant 5$
). In this situation, there is a small range of flow parameters where the capsule path deviates from the background flow.
$Re\geqslant 5$
). In this situation, there is a small range of flow parameters where the capsule path deviates from the background flow.
We have systematically computed the additional pressure drops created in the bifurcation itself and by the friction between the capsule and the channel wall in the narrow branch. As a consequence, although the main results have been obtained under constant flow rate conditions, they can also be used to monitor the same device operating under constant pressure conditions at the entrance and exit sections.
It is of interest to consider now how a train of non-interacting capsules would be separated from the ambient fluid. This question is pertinent for practical applications of the device. A particle separation of one diameter is enough to avoid hydrodynamic interactions between the capsules (Wang & Skalak Reference Wang and Skalak1969; Quéguiner & Barthès-Biesel Reference Quéguiner and Barthès-Biesel1997). When the system operates under constant flow rate, the capsule path has no reason to change even if there are many capsules in the side branch: this is because the energy input into the flow system is unlimited. However, when the system operates under constant pressure (or constant energy), the additional pressure drop created by the presence of the capsules leads to a decrease of
![]() $q(t)$
. This effect appears clearly in figure 19: when one capsule enters the side branch (
$q(t)$
. This effect appears clearly in figure 19: when one capsule enters the side branch (
![]() $q(0)=0.48$
), there is a significant decrease of
$q(0)=0.48$
), there is a significant decrease of
![]() $q(t)$
which eventually tends to
$q(t)$
which eventually tends to
![]() $q(0)-0.002$
. Of course this decrease depends on the global hydraulic resistance between
$q(0)-0.002$
. Of course this decrease depends on the global hydraulic resistance between
![]() $S_{0}$
and
$S_{0}$
and
![]() $S_{2}$
, which is a function of the specific configuration of the bifurcation and of the length and section geometry of the parent and branch channels. For
$S_{2}$
, which is a function of the specific configuration of the bifurcation and of the length and section geometry of the parent and branch channels. For
![]() $n$
capsules in the branch, it is quite possible that
$n$
capsules in the branch, it is quite possible that
![]() $q(t)$
may decrease below
$q(t)$
may decrease below
![]() $q_{c}$
, which would change the path of the capsules. The system may then undergo oscillation where the capsules enter alternatively the branch or the straight daughter channel. This indicates that it is easier to control a separation system by using constant flow rate conditions.
$q_{c}$
, which would change the path of the capsules. The system may then undergo oscillation where the capsules enter alternatively the branch or the straight daughter channel. This indicates that it is easier to control a separation system by using constant flow rate conditions.
This study can also be applied to predict the separation in a dilute suspension of particles flowing through a bifurcation when the confinement is small. Under those conditions, assuming a homogeneous particle distribution and ignoring interactions, all the particles, which are above the flow separation line in the feed channel, should flow into the side branch. At low Reynolds number, in the channel A, where
![]() $q_{c}\sim 0.5$
, we thus predict that the particle concentration is highest in the branch where the flow rate (or velocity) is highest. This prediction is in agreement with the Zweifach–Fung effect, which showed that the flow of RBC suspensions in a microcapillary network is mainly determined by two factors: the particle relative position with respect to the fluid separation line, and the hydrodynamic interactions between the particles, fluid flow and bifurcation wall (Svanes & Zweifach Reference Svanes and Zweifach1968; Fung Reference Fung1973; Pries et al.
Reference Pries, Ley, Claassen and Gaehtgens1989). In vivo, this effect has been found not to depend on the specific geometry of the bifurcation (Pries et al.
Reference Pries, Ley, Claassen and Gaehtgens1989; Pries, Secomb & Gaehtgens Reference Pries, Secomb and Gaehtgens1996). Roman et al. (Reference Roman, Merlo, Duru, Risso and Lorthois2016) have reached the same conclusion for RBCs flowing in symmetric T-bifurcations (figure 1
b) at low hematocrit. However, recently, Shen et al. (Reference Shen, Coupier, Kaoui, Polack, Harting, Misbah and Podgorski2016) observed an inversion of the Zweifach–Fung effect, when considering RBC suspensions flowing through a microfluidic T-bifurcation. They attributed this phenomenon to RBC organisation in the feeding channel as a consequence of cell volume fraction, deformability and interactions with the channel walls. The phase diagram presently obtained for centred capsules in channels B and C (figure 8) invalidates Fung’s model and therefore the Zweifach–Fung effect for almost all the Reynolds number values considered. The underlying mechanism is, however, different from that of Shen et al. (Reference Shen, Coupier, Kaoui, Polack, Harting, Misbah and Podgorski2016), as we do not change the positions of the capsules in the feed channel, but control the 3-D geometry of the fluid separation line by varying the side branch geometry. The present study, therefore, provides a new mechanism to control the path selection of capsules at a bifurcation.
$q_{c}\sim 0.5$
, we thus predict that the particle concentration is highest in the branch where the flow rate (or velocity) is highest. This prediction is in agreement with the Zweifach–Fung effect, which showed that the flow of RBC suspensions in a microcapillary network is mainly determined by two factors: the particle relative position with respect to the fluid separation line, and the hydrodynamic interactions between the particles, fluid flow and bifurcation wall (Svanes & Zweifach Reference Svanes and Zweifach1968; Fung Reference Fung1973; Pries et al.
Reference Pries, Ley, Claassen and Gaehtgens1989). In vivo, this effect has been found not to depend on the specific geometry of the bifurcation (Pries et al.
Reference Pries, Ley, Claassen and Gaehtgens1989; Pries, Secomb & Gaehtgens Reference Pries, Secomb and Gaehtgens1996). Roman et al. (Reference Roman, Merlo, Duru, Risso and Lorthois2016) have reached the same conclusion for RBCs flowing in symmetric T-bifurcations (figure 1
b) at low hematocrit. However, recently, Shen et al. (Reference Shen, Coupier, Kaoui, Polack, Harting, Misbah and Podgorski2016) observed an inversion of the Zweifach–Fung effect, when considering RBC suspensions flowing through a microfluidic T-bifurcation. They attributed this phenomenon to RBC organisation in the feeding channel as a consequence of cell volume fraction, deformability and interactions with the channel walls. The phase diagram presently obtained for centred capsules in channels B and C (figure 8) invalidates Fung’s model and therefore the Zweifach–Fung effect for almost all the Reynolds number values considered. The underlying mechanism is, however, different from that of Shen et al. (Reference Shen, Coupier, Kaoui, Polack, Harting, Misbah and Podgorski2016), as we do not change the positions of the capsules in the feed channel, but control the 3-D geometry of the fluid separation line by varying the side branch geometry. The present study, therefore, provides a new mechanism to control the path selection of capsules at a bifurcation.
This indicates that further studies are necessary to elucidate the complex interactions between the capsules (or cells) themselves, the background flow and the capsules to elucidate the flow behaviour of a suspension of deformable particles near a bifurcation, or more interesting maybe, in a series of successive bifurcations.
Acknowledgements
Z.W. acknowledges the PhD studentship from Queen Mary University of London (QMUL). All of the authors thank the Royal Society Research Grant under the International Exchange Programme (reference no. IE140496). The simulations were performed using the high-performance computer clusters provided by QMUL (funded by the UK EPSRC grant EP/K000128/1). This research was conducted under the framework of the Labex MS2T (ANR-11-IDEX-0004-02) funded by the French Agence Nationale de la Recherche.