Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mistry, Aashutosh
and
Mukherjee, Partha P.
2019.
Deconstructing electrode pore network to learn transport distortion.
Physics of Fluids,
Vol. 31,
Issue. 12,
Ray, Nadja
Oberlander, Jens
and
Frolkovic, Peter
2019.
Numerical investigation of a fully coupled micro-macro model for mineral dissolution and precipitation.
Computational Geosciences,
Vol. 23,
Issue. 5,
p.
1173.
Soulaine, Cyprien
Creux, Patrice
and
Tchelepi, Hamdi A.
2019.
Micro-continuum Framework for Pore-Scale Multiphase Fluid Transport in Shale Formations.
Transport in Porous Media,
Vol. 127,
Issue. 1,
p.
85.
Nissan, Alon
and
Berkowitz, Brian
2019.
Reactive Transport in Heterogeneous Porous Media Under Different Péclet Numbers.
Water Resources Research,
Vol. 55,
Issue. 12,
p.
10119.
Tournassat, Christophe
and
Steefel, Carl I.
2019.
Reactive Transport Modeling of Coupled Processes in Nanoporous Media.
Reviews in Mineralogy and Geochemistry,
Vol. 85,
Issue. 1,
p.
75.
Poonoosamy, Jenna
Westerwalbesloh, Christoph
Deissmann, Guido
Mahrous, Mohamed
Curti, Enzo
Churakov, Sergey V.
Klinkenberg, Martina
Kohlheyer, Dietrich
von Lieres, Eric
Bosbach, Dirk
and
Prasianakis, Nikolaos I.
2019.
A microfluidic experiment and pore scale modelling diagnostics for assessing mineral precipitation and dissolution in confined spaces.
Chemical Geology,
Vol. 528,
Issue. ,
p.
119264.
Lou, Qin
Huang, Yi-Fan
and
Li, Ling
2019.
Lattice Boltzmann model of gas-liquid two-phase flow of incomprssible power-law fluid and its application in the displacement problem of porous media.
Acta Physica Sinica,
Vol. 68,
Issue. 21,
p.
214702.
Carrillo, Francisco J.
and
Bourg, Ian C.
2019.
A Darcy‐Brinkman‐Biot Approach to Modeling the Hydrology and Mechanics of Porous Media Containing Macropores and Deformable Microporous Regions.
Water Resources Research,
Vol. 55,
Issue. 10,
p.
8096.
Snippe, Jeroen
Berg, Steffen
Ganga, Keschma
Brussee, Niels
and
Gdanski, Rick
2020.
Experimental and numerical investigation of wormholing during CO2 storage and water alternating gas injection.
International Journal of Greenhouse Gas Control,
Vol. 94,
Issue. ,
p.
102901.
Jiménez‐Martínez, Joaquín
Hyman, Jeffrey D.
Chen, Yu
Carey, J. William
Porter, Mark L.
Kang, Qinjun
Guthrie, George
and
Viswanathan, Hari S.
2020.
Homogenization of Dissolution and Enhanced Precipitation Induced by Bubbles in Multiphase Flow Systems.
Geophysical Research Letters,
Vol. 47,
Issue. 7,
Yang, Yong
Su, Xin
Fan, Zongliang
Wang, Dongliang
and
Li, Jiyan
2020.
Numerical investigation of naphthalene deposition dynamics during CO2 leakage.
International Journal of Greenhouse Gas Control,
Vol. 92,
Issue. ,
p.
102860.
Anjikar, Ishan S.
Wales, Shelby
and
Beckingham, Lauren E.
2020.
Fused Filament Fabrication 3‐D Printing of Reactive Porous Media.
Geophysical Research Letters,
Vol. 47,
Issue. 9,
You, Jiahui
and
Lee, Kyung Jae
2020.
Analyzing the Dynamics of Mineral Dissolution During Acid Fracturing by Pore–Scale Modeling of Acid–Rock Interaction.
Prasianakis, Nikolaos I.
Haller, Robin
Mahrous, Mohamed
Poonoosamy, Jenna
Pfingsten, Wilfried
and
Churakov, Sergey V.
2020.
Neural network based process coupling and parameter upscaling in reactive transport simulations.
Geochimica et Cosmochimica Acta,
Vol. 291,
Issue. ,
p.
126.
Gärttner, Stephan
Frolkovič, Peter
Knabner, Peter
and
Ray, Nadja
2020.
Efficiency and Accuracy of Micro‐Macro Models for Mineral Dissolution.
Water Resources Research,
Vol. 56,
Issue. 8,
Morais, Sandy
Cario, Anaïs
Liu, Na
Bernard, Dominique
Lecoutre, Carole
Garrabos, Yves
Ranchou-Peyruse, Anthony
Dupraz, Sébastien
Azaroual, Mohamed
Hartman, Ryan L.
and
Marre, Samuel
2020.
Studying key processes related to CO2 underground storage at the pore scale using high pressure micromodels.
Reaction Chemistry & Engineering,
Vol. 5,
Issue. 7,
p.
1156.
Carrillo, Francisco J.
Bourg, Ian C.
and
Soulaine, Cyprien
2020.
Multiphase flow modeling in multiscale porous media: An open-source micro-continuum approach.
Journal of Computational Physics: X,
Vol. 8,
Issue. ,
p.
100073.
Maes, Julien
and
Soulaine, Cyprien
2020.
A unified single-field Volume-of-Fluid-based formulation for multi-component interfacial transfer with local volume changes.
Journal of Computational Physics,
Vol. 402,
Issue. ,
p.
109024.
Rasoulzadeh, Mojdeh
Al Hubail, Mustafa Makki H.
Deng, Hang
and
Kuchuk, Fikri J.
2020.
Hydrodynamic driven dissolution in porous media with embedded cavities.
Physics of Fluids,
Vol. 32,
Issue. 7,
Jayasekara, D.W.
Ranjith, P.G.
Wanniarachchi, W.A.M.
and
Rathnaweera, T.D.
2020.
Understanding the chemico-mineralogical changes of caprock sealing in deep saline CO2 sequestration environments: A review study.
The Journal of Supercritical Fluids,
Vol. 161,
Issue. ,
p.
104819.
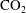 $\text{CO}_{2}$
$\text{CO}_{2}$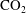 $\text{CO}_{2}$ bubbles in the domain. The dissolution of the calcite crystal and the production of gas during the acidizing process are analysed. We then show that the production of
$\text{CO}_{2}$ bubbles in the domain. The dissolution of the calcite crystal and the production of gas during the acidizing process are analysed. We then show that the production of 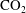 $\text{CO}_{2}$ bubbles during the injection of acid in a carbonate formation may limit the overall dissolution rate and prevent the emergence of wormholes.
$\text{CO}_{2}$ bubbles during the injection of acid in a carbonate formation may limit the overall dissolution rate and prevent the emergence of wormholes.

