1 Introduction
Besides wind-driven upwelling in the Southern Ocean, interior mixing has been identified as a major contributor to maintaining the global ocean circulation (e.g. Munk & Wunsch Reference Munk and Wunsch1998; Talley Reference Talley2013, and references therein). Much of the mixing energy is contained in the internal wave field, and up to half of the internal wave energy is estimated to stem from tidal flow over abyssal topography (Egbert & Ray Reference Egbert and Ray2001; Wunsch & Ferrari Reference Wunsch and Ferrari2004). This tidal forcing is anisotropic, because the energy conversion from the tides to the internal waves depends on the shape of the topography and the orientation of the tidal ellipse. The theoretical framework typically employed to describe the internal tide field is that of vertical eigenmodes. Especially the low-mode internal tides, which have a higher energy content and larger scales than the higher modes, are important for large-scale ocean dynamics. They can propagate over thousands of kilometres away from their generation sites before their energy dissipates and contributes to turbulent mixing (Olbers Reference Olbers1983).
Existing (semi-)analytical models of internal tide generation typically do not resolve the directional dependence of the generated energy flux (e.g. Bell Reference Bell1975b ; Nycander Reference Nycander2005; Falahat et al. Reference Falahat, Nycander, Roquet and Zarroug2014b ) and if they do, they describe the modal structure of the internal tide field only in approximate form (Vic et al. Reference Vic, Naveira Garabato, Green, Spingys, Forryan, Zhao and Sharples2018). To close this gap and to help improve mixing parametrisations based on internal wave dynamics, we here present a new semi-analytical method to calculate both the horizontal direction and the magnitude of the energy flux from the barotropic tide into the different vertical modes, taking the full vertical structure of the stratification into account.
Tidal energy conversion can also be simulated with three-dimensional ocean models (e.g. Niwa & Hibiya Reference Niwa and Hibiya2004; Zilberman et al.
Reference Zilberman, Becker, Merrifield and Carter2009; Arbic, Wallcraft & Metzger Reference Arbic, Wallcraft and Metzger2010; Müller et al.
Reference Müller, Cherniawsky, Foreman and von Storch2012). However, it is not straightforward to diagnose the generation of internal waves, and even less so its angular distribution, from such simulations. For example, computing the energy flux through a vertical test surface gives the net flux, but does not differentiate between the fluxes passing through the surface from different directions. Further drawbacks are the high computational cost required for global simulations with high-resolution topography, so that in practice only the first few modes can be resolved, and the need to parametrise where and how baroclinic tidal energy dissipates, which happens on spatial scales too small to be resolved in global ocean models. This motivates the semi-analytical treatment of the internal tide generation problem. One of the first to follow this approach was Bell (Reference Bell1975a
,Reference Bell
b
), who computed the energy conversion into linear internal waves radiating away from the seafloor in a manner consistent with the Wentzel–Kramers–Brillouin (WKB) approximation, i.e. for waves that vary on smaller vertical scales than the scales of variation of the background stratification. The underlying assumptions which render the problem analytically tractable are that the topographic heights are small compared to the vertical wavelength of the waves and that the topographic slopes are much smaller than the slope of the tidal beam. By decomposing the wave field into vertical normal modes, Llewellyn Smith & Young (Reference Llewellyn Smith and Young2002, hereafter LSY02) extended this method to arbitrary stratification. They found that the main effect of finite compared to infinite depth is that conversion rates are suppressed for horizontal topographic scales larger than the horizontal wavelength of the first internal wave mode. Using the WKB approximation, they moreover showed that the properties of the stratification relevant for the energy conversion are the buoyancy frequency’s vertical average,
![]() $\overline{N}$
, and its value at the bottom,
$\overline{N}$
, and its value at the bottom,
![]() $N_{B}$
. For
$N_{B}$
. For
![]() $\text{d}N/\text{d}z=0$
, these WKB solutions for the eigenfunctions, wavenumbers and conversion rates are exact for all modes (LSY02); for the weak variations of
$\text{d}N/\text{d}z=0$
, these WKB solutions for the eigenfunctions, wavenumbers and conversion rates are exact for all modes (LSY02); for the weak variations of
![]() $N(z)$
observed in the ocean interior, they provide a reasonable description of the conversion field except for the lowest modes (Zarroug, Nycander & Döös Reference Zarroug, Nycander and Döös2010).
$N(z)$
observed in the ocean interior, they provide a reasonable description of the conversion field except for the lowest modes (Zarroug, Nycander & Döös Reference Zarroug, Nycander and Döös2010).
Calculations of the energy conversion rate in the global ocean building on these results were performed for example by Egbert, Ray & Bills (Reference Egbert, Ray and Bills2004), Nycander (Reference Nycander2005) and Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). Egbert et al. (Reference Egbert, Ray and Bills2004) implemented a computationally less expensive, approximate version of the convolution integral derived by LSY02 in a hydrostatic shallow-water model, showing that the modelled tidal elevations could reproduce those estimated from altimetry data with a root-mean-square (r.m.s.) error of 5 cm. Nycander (Reference Nycander2005) introduced a filter to the expression of Bell (Reference Bell1975a
,Reference Bell
b
), thereby suppressing internal tide radiation from long topographic scales in line with the findings by LSY02. The total conversion rates were in good agreement with the numbers found by Egbert & Ray (Reference Egbert and Ray2001) from satellite altimetry data; the more detailed evaluation performed by Green & Nycander (Reference Green and Nycander2013), testing different wave drag parametrisations in a barotropic tidal model, confirmed the positive assessment of the method. Further support of the semi-analytical approach was given by the reasonable correlation between microstructure measurements of turbulent kinetic energy dissipation rates and energy conversion rates calculated using a variation of Nycander’s formalism (Falahat et al.
Reference Falahat, Nycander, Roquet, Thurnherr and Hibiya2014a
). Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
), on the other hand, based their global calculations on the approach by LSY02 and solved the vertical eigenvalue problem for the first 10 internal tide modes. They compared their results to those of Nycander (Reference Nycander2005) and found that the two methods diverged most strongly in the upper ocean, with the global integrals of the energy conversion rate differing by 16 %. In idealised test cases, taking the full vertical structure of the stratification into account led to more accurate results than the WKB-based method of Nycander (Reference Nycander2005), which considers
![]() $N_{B}$
rather than
$N_{B}$
rather than
![]() $N(z)$
.
$N(z)$
.
Our objective is to describe the directional dependence of the tidal energy conversion. Recently, Vic et al. (Reference Vic, Naveira Garabato, Green, Spingys, Forryan, Zhao and Sharples2018) calculated the direction of the energy conversion over the northern Mid-Atlantic Ridge based on the formulation of St Laurent & Garrett (Reference St Laurent and Garrett2002), which is an approximation of the expression of Bell (Reference Bell1975b ) in the limit of small tidal excursion and involves a first-order correction for the finite ocean depth based on the assumption of an exponential buoyancy frequency profile. Here, we instead take the full vertical structure into account by following the vertical-mode treatment of LSY02. We calculate the energy conversion as an integral over the energy flux instead of, as done by Nycander (Reference Nycander2005) and Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b ), an integral over the energy sources. Apart from providing information on the direction, another, practical, advantage of the new method is that the energy flux is positive definite, whereas integrating over the energy sources can produce negative conversion rates (e.g. Falahat et al. Reference Falahat, Nycander, Roquet and Zarroug2014b ) and hence requires further treatment before it can be used, for example, as source term in internal wave models.
Our new method is based on the assumptions of a bounded source region and a horizontally constant tidal velocity. These assumptions are not valid for an entire ocean basin, and we thus propose to subdivide the seafloor into overlapping circular patches. By multiplying the topography within each patch by a Gaussian, the effect of the remote topography on the conversion rates is neglected and the far-field expression, which is proportional to the Fourier-transformed topography within the patch, is locally valid. Considering each patch in turn, the energy conversion for the entire ocean floor can be calculated.
The derivation of the relevant equations is described in § 2. In § 3, we explain the numerical implementation of the method for large-scale calculations. In § 4, we discuss the evaluation of the method based on idealised test cases, which allows the identification of suitable parameter settings, such as the overlap of neighbouring patches. The energy conversion for a region of realistic topography is presented in § 5 before offering a summary and conclusions in § 6. The focus of this paper is on the introduction of the new method and its evaluation; global calculations of the angular energy flux into vertical modes using realistic topography, tidal velocities and stratification will be presented in a follow-up publication.
2 Derivation of the energy flux
LSY02 derive the expression for the energy conversion into vertical normal modes for an ocean of non-uniform finite depth with the ocean bottom at depth
![]() $z_{B}=-H+h(x,y)$
, where
$z_{B}=-H+h(x,y)$
, where
![]() $H$
is a constant. They make the following approximations. First, the topography is assumed to be weak, so that the bottom boundary condition can be applied at the flat bottom
$H$
is a constant. They make the following approximations. First, the topography is assumed to be weak, so that the bottom boundary condition can be applied at the flat bottom
![]() $z=-H$
, which requires that topographic slopes
$z=-H$
, which requires that topographic slopes
![]() $\unicode[STIX]{x1D735}h$
are much less than the slope of the tidal beam (‘subcritical topography’) and that the height of the topography is smaller than the vertical wavelength of the internal waves. Second, the tidal excursion is assumed to be small compared to the horizontal scale of the topography,
$\unicode[STIX]{x1D735}h$
are much less than the slope of the tidal beam (‘subcritical topography’) and that the height of the topography is smaller than the vertical wavelength of the internal waves. Second, the tidal excursion is assumed to be small compared to the horizontal scale of the topography,
![]() $L$
, i.e.
$L$
, i.e.
![]() $U_{0}/(\unicode[STIX]{x1D714}L)\ll 1$
, so that advective effects of the barotropic tide can be neglected. Here,
$U_{0}/(\unicode[STIX]{x1D714}L)\ll 1$
, so that advective effects of the barotropic tide can be neglected. Here,
![]() $U_{0}$
is the amplitude of the tidal velocity and
$U_{0}$
is the amplitude of the tidal velocity and
![]() $\unicode[STIX]{x1D714}$
the fundamental tidal frequency. Third, they use the hydrostatic approximation, which is justified as long as
$\unicode[STIX]{x1D714}$
the fundamental tidal frequency. Third, they use the hydrostatic approximation, which is justified as long as
![]() $\unicode[STIX]{x1D714}/N\ll 1$
.
$\unicode[STIX]{x1D714}/N\ll 1$
.
Internal wave disturbances induced by tidal flow over rough bottom topography can be described by the linearised hydrostatic Boussinesq equations, which LSY02 projected onto vertical normal modes defined by the following eigenvalue problem:
Here,
![]() $c_{m}$
is the mode-
$c_{m}$
is the mode-
![]() $m$
internal tide phase speed, which is related to the horizontal wavenumber
$m$
internal tide phase speed, which is related to the horizontal wavenumber
![]() $\unicode[STIX]{x1D705}_{m}$
, the Coriolis frequency
$\unicode[STIX]{x1D705}_{m}$
, the Coriolis frequency
![]() $f$
and the tidal frequency
$f$
and the tidal frequency
![]() $\unicode[STIX]{x1D714}$
as
$\unicode[STIX]{x1D714}$
as
The eigenfunctions satisfy the following orthogonality condition:
where
![]() $\unicode[STIX]{x1D709}_{m}$
is a non-dimensional normalisation constant which we set to unity without loss of generality. The eigenfunctions
$\unicode[STIX]{x1D709}_{m}$
is a non-dimensional normalisation constant which we set to unity without loss of generality. The eigenfunctions
![]() $a_{m}(z)$
link the horizontal modal fields to their corresponding three-dimensional counterparts, e.g. for the perturbation pressure
$a_{m}(z)$
link the horizontal modal fields to their corresponding three-dimensional counterparts, e.g. for the perturbation pressure
![]() $p$
(see LSY02, equations 22 and 23):
$p$
(see LSY02, equations 22 and 23):
where
![]() $a_{m}^{\prime }=\text{d}a_{m}/\text{d}z$
. In this paper bold-face variables represent two-dimensional horizontal vectors and tensors, e.g. the coordinate vector
$a_{m}^{\prime }=\text{d}a_{m}/\text{d}z$
. In this paper bold-face variables represent two-dimensional horizontal vectors and tensors, e.g. the coordinate vector
![]() $\boldsymbol{r}=(x,y)$
, whose modulus is denoted by
$\boldsymbol{r}=(x,y)$
, whose modulus is denoted by
![]() $r=|\boldsymbol{r}|$
, and the corresponding unit vector in the radial direction,
$r=|\boldsymbol{r}|$
, and the corresponding unit vector in the radial direction,
![]() $\hat{\boldsymbol{r}}=\hat{\boldsymbol{x}}\cos \unicode[STIX]{x1D719}+\hat{\boldsymbol{y}}\sin \unicode[STIX]{x1D719}$
, involving the eastward and northward unit vectors
$\hat{\boldsymbol{r}}=\hat{\boldsymbol{x}}\cos \unicode[STIX]{x1D719}+\hat{\boldsymbol{y}}\sin \unicode[STIX]{x1D719}$
, involving the eastward and northward unit vectors
![]() $\hat{\boldsymbol{x}}$
and
$\hat{\boldsymbol{x}}$
and
![]() $\hat{\boldsymbol{y}}$
, respectively. The modal pressure
$\hat{\boldsymbol{y}}$
, respectively. The modal pressure
![]() $p_{m}(\boldsymbol{r},t)$
and the tidal velocity
$p_{m}(\boldsymbol{r},t)$
and the tidal velocity
![]() $\boldsymbol{u}(t)$
are assumed to have a sinusoidal time dependence with complex amplitudes
$\boldsymbol{u}(t)$
are assumed to have a sinusoidal time dependence with complex amplitudes
![]() $P_{m}$
and
$P_{m}$
and
![]() $\boldsymbol{U}$
, respectively:
$\boldsymbol{U}$
, respectively:
where
![]() $\text{Re}$
denotes the real part. For the normal-mode decomposition described above, the modal conversion rate was identified by LSY02 (see their equation 28) as
$\text{Re}$
denotes the real part. For the normal-mode decomposition described above, the modal conversion rate was identified by LSY02 (see their equation 28) as
where the angle brackets denote the time average over a period,
![]() $A$
the area including the topographic sources,
$A$
the area including the topographic sources,
![]() $\text{d}x\,\text{d}y$
the area element and
$\text{d}x\,\text{d}y$
the area element and
![]() $\unicode[STIX]{x1D735}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$
. The variable
$\unicode[STIX]{x1D735}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$
. The variable
![]() $\unicode[STIX]{x1D701}_{m}$
is a dimensionless quantity related to the vertical derivative of the eigenfunctions as
$\unicode[STIX]{x1D701}_{m}$
is a dimensionless quantity related to the vertical derivative of the eigenfunctions as
Note that, for constant stratification, (2.1) can be solved analytically and
LSY02 derived the following inhomogeneous Helmholtz equation for the modal pressure amplitude
![]() $P_{m}$
(see their equation 33):
$P_{m}$
(see their equation 33):
with the source function
where
![]() $\unicode[STIX]{x1D70E}_{m,0}$
is real. Equation (2.10) is the starting point for our derivation of a new method to resolve the direction of the energy flux into the different internal tide modes. Note that this equation arises in many physical situations, e.g. atmospheric lee-wave generation or Lighthill radiation, so that our novel approach to solving (2.10) is in fact not limited to the phenomenon of oceanic internal tides.
$\unicode[STIX]{x1D70E}_{m,0}$
is real. Equation (2.10) is the starting point for our derivation of a new method to resolve the direction of the energy flux into the different internal tide modes. Note that this equation arises in many physical situations, e.g. atmospheric lee-wave generation or Lighthill radiation, so that our novel approach to solving (2.10) is in fact not limited to the phenomenon of oceanic internal tides.
We first derive an energy equation from (2.10) by multiplication with
![]() $P^{\ast }$
, the complex conjugate of
$P^{\ast }$
, the complex conjugate of
![]() $P$
:
$P$
:
where we have dropped the subscript ‘
![]() $m$
’ for the sake of brevity. Taking the imaginary part
$m$
’ for the sake of brevity. Taking the imaginary part
![]() $\text{Im}$
, this reduces to
$\text{Im}$
, this reduces to
This step is motivated by the comparison of (2.10) and (2.12) to the time-dependent form of the standard two-dimensional forced wave equation and the resultant energy conservation equation (see appendix A). The left-hand side of (2.13) can then be identified as the divergence of the energy flux, but only up to a real multiplicative coefficient
![]() $B$
given below, which relates the modal pressure amplitude
$B$
given below, which relates the modal pressure amplitude
![]() $P$
to wave energy.
$P$
to wave energy.
In consequence, the energy source density
![]() $s$
is given by
$s$
is given by
and the energy flux
![]() $\boldsymbol{F}$
is related to the pressure according to
$\boldsymbol{F}$
is related to the pressure according to
The energy conversion can then be computed either as the integral over the source density,
or as the integral of the energy flux across a closed curve
![]() $\unicode[STIX]{x1D6FE}$
around the source region
$\unicode[STIX]{x1D6FE}$
around the source region
![]() $A$
,
$A$
,
where
![]() $\hat{\boldsymbol{n}}$
denotes the unit vector pointing outwards at the boundary. Note that
$\hat{\boldsymbol{n}}$
denotes the unit vector pointing outwards at the boundary. Note that
![]() $\boldsymbol{F}$
and
$\boldsymbol{F}$
and
![]() $C$
here denote the average over a time period, i.e. we have for simplicity omitted the angular brackets used in appendix A. The coefficient
$C$
here denote the average over a time period, i.e. we have for simplicity omitted the angular brackets used in appendix A. The coefficient
![]() $B$
can be determined from (2.16) by comparison to the expression obtained by substituting (2.11) into (2.7):
$B$
can be determined from (2.16) by comparison to the expression obtained by substituting (2.11) into (2.7):
 $$\begin{eqnarray}\displaystyle B=\frac{\unicode[STIX]{x1D70C}_{0}}{2\unicode[STIX]{x1D705}f\sqrt{1-\displaystyle \frac{f^{2}}{\unicode[STIX]{x1D714}^{2}}}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B=\frac{\unicode[STIX]{x1D70C}_{0}}{2\unicode[STIX]{x1D705}f\sqrt{1-\displaystyle \frac{f^{2}}{\unicode[STIX]{x1D714}^{2}}}}. & & \displaystyle\end{eqnarray}$$
Previous studies (e.g. Falahat et al. Reference Falahat, Nycander, Roquet and Zarroug2014b ) invoked (2.16) to calculate the energy conversion. In order to resolve the horizontal direction of the energy flux we instead have to rely on (2.17). Both methods require solving (2.10) for the pressure, which can be accomplished following a standard Green’s function approach:
The Green’s function
![]() $G$
describes the radiation from a point source and is given by
$G$
describes the radiation from a point source and is given by
where
![]() $H_{0}^{1}$
denotes the Hankel function of the first kind of order zero, and
$H_{0}^{1}$
denotes the Hankel function of the first kind of order zero, and
![]() $\text{J}$
and
$\text{J}$
and
![]() $\text{Y}$
are Bessel functions of the first and second kind, respectively. The Green’s function has the property
$\text{Y}$
are Bessel functions of the first and second kind, respectively. The Green’s function has the property
where the
![]() $\unicode[STIX]{x1D6FF}$
-function originates from the term
$\unicode[STIX]{x1D6FF}$
-function originates from the term
![]() $\text{Y}_{0}$
in (2.20), and the term
$\text{Y}_{0}$
in (2.20), and the term
![]() $\text{J}_{0}$
in (2.20) ensures that the energy flux is directed away from the origin, as can be verified by inserting
$\text{J}_{0}$
in (2.20) ensures that the energy flux is directed away from the origin, as can be verified by inserting
![]() $G(\unicode[STIX]{x1D705}|\boldsymbol{r}|)$
into (2.15).
$G(\unicode[STIX]{x1D705}|\boldsymbol{r}|)$
into (2.15).
When the pressure field is evaluated at a point far away from all sources, the asymptotic expansion of the Hankel transform
can be used in (2.19). As a result, the pressure field can be approximated as
where the tilde denotes the Fourier transform
and
![]() $\boldsymbol{k}$
is the two-dimensional wavenumber vector (see appendix B for details of the derivation). Inserting (2.23) into (2.15) leads to the following expression for the far-field energy flux:
$\boldsymbol{k}$
is the two-dimensional wavenumber vector (see appendix B for details of the derivation). Inserting (2.23) into (2.15) leads to the following expression for the far-field energy flux:
whose magnitude is the same on opposite sides of the sources because of
![]() $\tilde{\unicode[STIX]{x1D70E}}_{0}^{\ast }(\boldsymbol{k})=\tilde{\unicode[STIX]{x1D70E}}_{0}(-\boldsymbol{k})$
. Expressing the radial unit vector in terms of the Cartesian counterparts,
$\tilde{\unicode[STIX]{x1D70E}}_{0}^{\ast }(\boldsymbol{k})=\tilde{\unicode[STIX]{x1D70E}}_{0}(-\boldsymbol{k})$
. Expressing the radial unit vector in terms of the Cartesian counterparts,
![]() $\hat{\boldsymbol{r}}=\hat{\boldsymbol{x}}\cos \unicode[STIX]{x1D719}+\hat{\boldsymbol{y}}\sin \unicode[STIX]{x1D719}$
, underlines that this expression is indeed the directional energy flux in terms of the horizontal angle
$\hat{\boldsymbol{r}}=\hat{\boldsymbol{x}}\cos \unicode[STIX]{x1D719}+\hat{\boldsymbol{y}}\sin \unicode[STIX]{x1D719}$
, underlines that this expression is indeed the directional energy flux in terms of the horizontal angle
![]() $\unicode[STIX]{x1D719}$
. Following (2.17), the total energy conversion becomes
$\unicode[STIX]{x1D719}$
. Following (2.17), the total energy conversion becomes
The same expression can also be obtained by using (2.19) and (2.20) in (2.16) and exploiting symmetry:
This equation was used by Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) to compute the global energy conversion. It can be rewritten by means of the following known expression for the Fourier transform of the Bessel function
![]() $\text{J}_{0}$
:
$\text{J}_{0}$
:
which leads indeed to the same expression as (2.26). The difference is that the first derivation based on the approximate Hankel function is more explicit in requiring that the expression be evaluated far away from the source region (note that both approaches make use of the radiation condition; see also appendix B).
3 Implementation
The numerical implementation is based on (2.25). The flux magnitude
![]() $F=|\boldsymbol{F}|$
can be written as
$F=|\boldsymbol{F}|$
can be written as
with the symmetric tensor
The advantage of writing the energy flux as in (3.1) is that the tidal velocity is treated separately, so that, for example, the spring–neap tidal cycle can be taken into account by letting the tidal amplitude
![]() $U$
vary slowly in time. Tensor
$U$
vary slowly in time. Tensor
![]() $\unicode[STIX]{x1D64D}$
can be thought of as a drag tensor (Green & Nycander Reference Green and Nycander2013), which can be transformed into Cartesian coordinates using
$\unicode[STIX]{x1D64D}$
can be thought of as a drag tensor (Green & Nycander Reference Green and Nycander2013), which can be transformed into Cartesian coordinates using
Equation (3.2) shows that the directional energy flux depends on the Fourier transform of the topography in polar coordinates. An apparently straightforward approach would be to first calculate the Fourier transform of the topography in Cartesian coordinates and then interpolate it onto a polar grid in spectral space. Simple tests comparing (2.17) and (2.16) for idealised topography such as top-hat or Gaussian seamounts, however, demonstrate that the interpolation of the Fourier-transformed topography requires a very high spatial resolution. A more practicable alternative, in terms of both accuracy and computational speed, is to calculate the Fourier transform in polar coordinates. Baddour (Reference Baddour2009) showed that taking the two-dimensional Fourier transform of a function in polar coordinates is, after appropriate scaling, equivalent to first determining its Fourier series expansion in the angular direction and then calculating the
![]() $n$
th-order Hankel transform of the radial variable. This implies that the transform needs to be calculated for one specific wavenumber only instead of all of them, which additionally reduces the computational expense. In consequence, the implementation involves the following steps.
$n$
th-order Hankel transform of the radial variable. This implies that the transform needs to be calculated for one specific wavenumber only instead of all of them, which additionally reduces the computational expense. In consequence, the implementation involves the following steps.
(i) Interpolation to a polar grid. The topography
 $h(x,y)$
is on the Cartesian grid represented by a bivariate spline, which is then evaluated at the polar grid points. This gives
$h(x,y)$
is on the Cartesian grid represented by a bivariate spline, which is then evaluated at the polar grid points. This gives
 $h(r,\unicode[STIX]{x1D719})$
.
$h(r,\unicode[STIX]{x1D719})$
.(ii) Calculation of angular modes. A Fourier expansion (fast Fourier transform, FFT) of
 $h(r,\unicode[STIX]{x1D719})$
in the
$h(r,\unicode[STIX]{x1D719})$
in the
 $\unicode[STIX]{x1D719}$
-direction is performed to compute the angular modes
$\unicode[STIX]{x1D719}$
-direction is performed to compute the angular modes
 $h_{n}(r)$
, where
$h_{n}(r)$
, where
 $n$
is the angular mode number: (3.4)
$n$
is the angular mode number: (3.4) $$\begin{eqnarray}\displaystyle h(r,\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{n=\infty }h_{n}(r)\text{e}^{\text{i}n\unicode[STIX]{x1D719}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(r,\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{n=\infty }h_{n}(r)\text{e}^{\text{i}n\unicode[STIX]{x1D719}}. & & \displaystyle\end{eqnarray}$$
(iii) Hankel transform. We are interested in the Fourier-transformed angular modes
 $\tilde{h}_{n}(k)$
. As shown by Baddour (Reference Baddour2009), these are related to the angular modes calculated in step (ii),
$\tilde{h}_{n}(k)$
. As shown by Baddour (Reference Baddour2009), these are related to the angular modes calculated in step (ii),
 $h_{n}(r)$
, through the Hankel transform: (3.5)This integral is solved using numerical quadrature (Simpson’s rule) for the specific wavenumber
$h_{n}(r)$
, through the Hankel transform: (3.5)This integral is solved using numerical quadrature (Simpson’s rule) for the specific wavenumber $$\begin{eqnarray}\displaystyle \tilde{h}_{n}(k)=\frac{2\unicode[STIX]{x03C0}}{i^{n}}\int _{0}^{\infty }h_{n}(r)\text{J}_{n}(kr)r\,\text{d}r. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{h}_{n}(k)=\frac{2\unicode[STIX]{x03C0}}{i^{n}}\int _{0}^{\infty }h_{n}(r)\text{J}_{n}(kr)r\,\text{d}r. & & \displaystyle\end{eqnarray}$$
 $k=\unicode[STIX]{x1D705}$
.
$k=\unicode[STIX]{x1D705}$
.(iv) Calculation of the Fourier-transformed topography as a function of angle. An inverse FFT relates the modes
 $\tilde{h}_{n}(\unicode[STIX]{x1D705})$
to the Fourier transform of the topography,
$\tilde{h}_{n}(\unicode[STIX]{x1D705})$
to the Fourier transform of the topography,
 $\tilde{h}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FD})$
: (3.6)This can be evaluated at
$\tilde{h}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FD})$
: (3.6)This can be evaluated at $$\begin{eqnarray}\displaystyle \tilde{h}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FD})=\mathop{\sum }_{n=-\infty }^{n=\infty }\tilde{h}_{n}(\unicode[STIX]{x1D705})\text{e}^{\text{i}n\unicode[STIX]{x1D6FD}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{h}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FD})=\mathop{\sum }_{n=-\infty }^{n=\infty }\tilde{h}_{n}(\unicode[STIX]{x1D705})\text{e}^{\text{i}n\unicode[STIX]{x1D6FD}}. & & \displaystyle\end{eqnarray}$$
 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D719}$
.
In the real ocean, the sources are not confined to small, bounded regions, nor are the tidal velocity amplitude
![]() $\boldsymbol{U}$
or the horizontal wavenumber
$\boldsymbol{U}$
or the horizontal wavenumber
![]() $\unicode[STIX]{x1D705}$
constant in space (or time), as assumed in the derivation of (2.10). Therefore, the far-field expression derived in the previous section cannot be applied directly. The same problem arises when computing the energy conversion as the integral over the source density using (2.27), as was done by Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). They dealt with this issue by truncating the Bessel function in the integral after a certain number of zero crossings, effectively neglecting the influence of topography far away from the point at which the conversion is calculated. In the same spirit, we only consider the topography in a certain area around the point of interest to be relevant for the energy conversion. To that end, we subdivide the topography into overlapping circular patches of radius
$\unicode[STIX]{x1D705}$
constant in space (or time), as assumed in the derivation of (2.10). Therefore, the far-field expression derived in the previous section cannot be applied directly. The same problem arises when computing the energy conversion as the integral over the source density using (2.27), as was done by Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). They dealt with this issue by truncating the Bessel function in the integral after a certain number of zero crossings, effectively neglecting the influence of topography far away from the point at which the conversion is calculated. In the same spirit, we only consider the topography in a certain area around the point of interest to be relevant for the energy conversion. To that end, we subdivide the topography into overlapping circular patches of radius
![]() $r_{p}$
. In each of these circles, identified by indices
$r_{p}$
. In each of these circles, identified by indices
![]() $i,j$
and centred at
$i,j$
and centred at
![]() $\boldsymbol{r}_{i,j}$
, the topography is multiplied by a Gaussian and interpolated onto a polar grid, which is also centred at
$\boldsymbol{r}_{i,j}$
, the topography is multiplied by a Gaussian and interpolated onto a polar grid, which is also centred at
![]() $\boldsymbol{r}_{i,j}$
:
$\boldsymbol{r}_{i,j}$
:
This ‘screened’ topography
![]() $h_{i,j}(\boldsymbol{r})$
is hence confined to a region of length scale
$h_{i,j}(\boldsymbol{r})$
is hence confined to a region of length scale
![]() $r_{G}$
and we can therefore, if
$r_{G}$
and we can therefore, if
![]() $r_{G}$
is small enough, apply the far-field expression for each patch individually, choosing different values for
$r_{G}$
is small enough, apply the far-field expression for each patch individually, choosing different values for
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\boldsymbol{U}$
in the different patches. In other words, for each patch, we follow steps (i)–(iv) and calculate the angular energy flux
$\boldsymbol{U}$
in the different patches. In other words, for each patch, we follow steps (i)–(iv) and calculate the angular energy flux
![]() $rF_{i,j}$
based on (3.1) and (3.2), thereby covering the entire ocean floor. Note that multiplying the topography by a Gaussian is a tapering to avoid sharp cutoffs at the patch boundary, not a smoothing that removes small topographic scales.
$rF_{i,j}$
based on (3.1) and (3.2), thereby covering the entire ocean floor. Note that multiplying the topography by a Gaussian is a tapering to avoid sharp cutoffs at the patch boundary, not a smoothing that removes small topographic scales.
The mean angular flux density per unit area at the patch centre,
is obtained by normalising the energy flux by the effective patch area
![]() $a_{i,j}$
,
$a_{i,j}$
,
where the square in the integral accounts for the quadratic dependence of the energy conversion on the screened topography. The procedure is illustrated in figure 1.
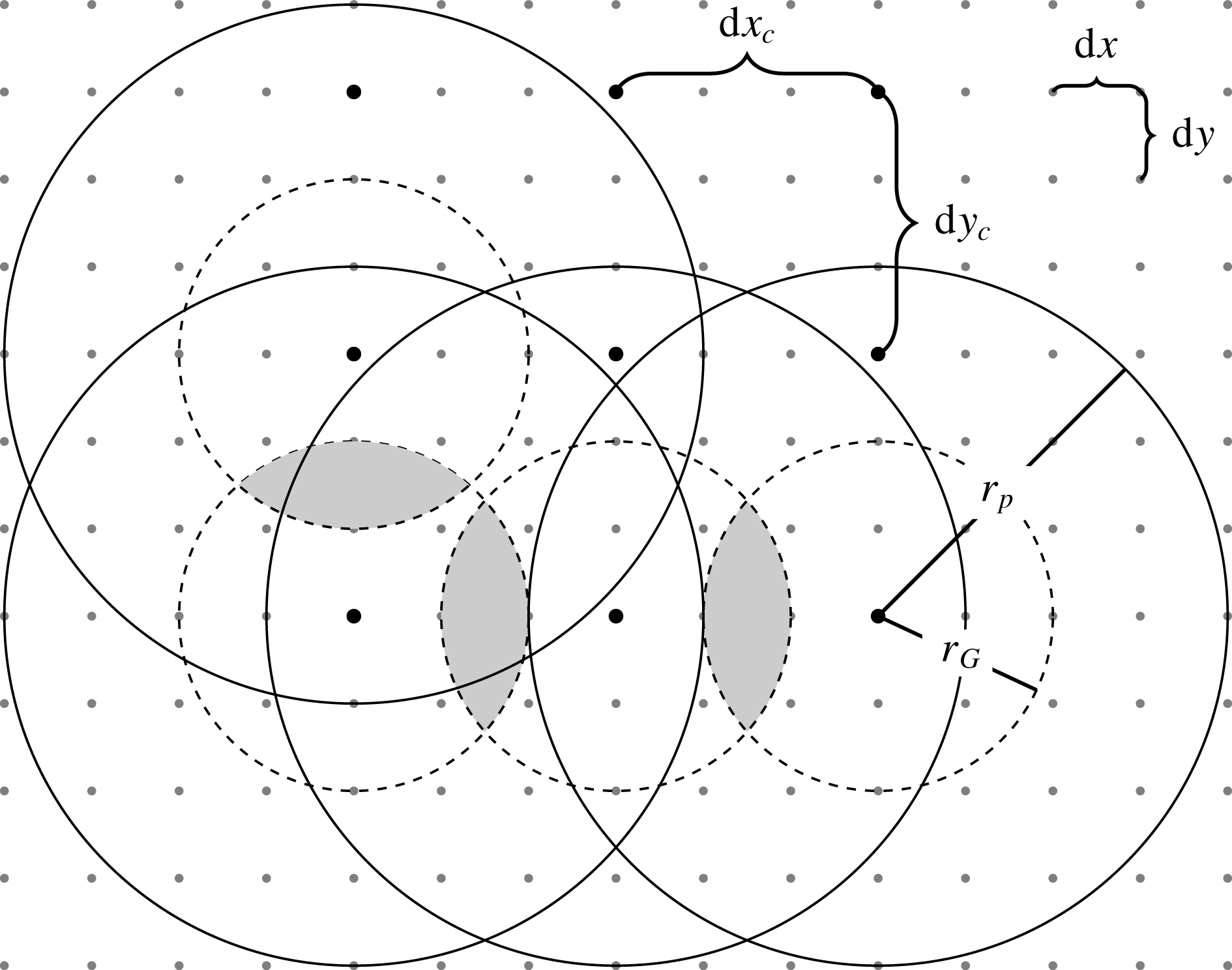
Figure 1. Illustration of the method. The topography is given on a Cartesian grid with spacing
![]() $\text{d}x$
and
$\text{d}x$
and
![]() $\text{d}y$
(small points). The total domain is subdivided into circular patches of radius
$\text{d}y$
(small points). The total domain is subdivided into circular patches of radius
![]() $r_{p}$
, whose centres are spaced at a distance of
$r_{p}$
, whose centres are spaced at a distance of
![]() $\text{d}x_{c}$
and
$\text{d}x_{c}$
and
![]() $\text{d}y_{c}$
(larger points). In each patch, the topography is interpolated onto a polar grid and multiplied by a Gaussian, whose width (standard deviation) is given by
$\text{d}y_{c}$
(larger points). In each patch, the topography is interpolated onto a polar grid and multiplied by a Gaussian, whose width (standard deviation) is given by
![]() $r_{G}$
. The numerical parameters which have to be set are: (1) the patch size relative to that of the Gaussian, controlled by the parameter
$r_{G}$
. The numerical parameters which have to be set are: (1) the patch size relative to that of the Gaussian, controlled by the parameter
![]() $f_{l}=r_{p}/r_{G}$
; (2) the size of the Gaussian relative to the wavenumber for which the conversion is calculated, controlled by the parameter
$f_{l}=r_{p}/r_{G}$
; (2) the size of the Gaussian relative to the wavenumber for which the conversion is calculated, controlled by the parameter
![]() $f_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D705}r_{G}$
; (3) the grid spacing
$f_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D705}r_{G}$
; (3) the grid spacing
![]() $\text{d}x_{c}$
and
$\text{d}x_{c}$
and
![]() $\text{d}y_{c}$
relative to the Gaussian width, i.e. to what extent the effective patch area
$\text{d}y_{c}$
relative to the Gaussian width, i.e. to what extent the effective patch area
![]() $\unicode[STIX]{x03C0}r_{G}^{2}$
overlaps (shaded areas), controlled by the parameter
$\unicode[STIX]{x03C0}r_{G}^{2}$
overlaps (shaded areas), controlled by the parameter
![]() $f_{p}=r_{G}/\text{d}x_{c}$
; and (4) the resolution of the polar grid within each patch,
$f_{p}=r_{G}/\text{d}x_{c}$
; and (4) the resolution of the polar grid within each patch,
![]() $\text{d}r=r_{p}/n_{r}$
and
$\text{d}r=r_{p}/n_{r}$
and
![]() $\text{d}\unicode[STIX]{x1D719}=2\unicode[STIX]{x03C0}/n_{\unicode[STIX]{x1D719}}$
, where
$\text{d}\unicode[STIX]{x1D719}=2\unicode[STIX]{x03C0}/n_{\unicode[STIX]{x1D719}}$
, where
![]() $n_{r}$
and
$n_{r}$
and
![]() $n_{\unicode[STIX]{x1D719}}$
denote the number of grid points in the radial and angular directions.
$n_{\unicode[STIX]{x1D719}}$
denote the number of grid points in the radial and angular directions.
For the numerical implementation, the following parameters have to be set:
(i)
 $f_{l}=r_{p}/r_{G}$
, the size of the patch relative to that of the Gaussian;
$f_{l}=r_{p}/r_{G}$
, the size of the patch relative to that of the Gaussian;(ii)
 $f_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D705}r_{G}$
, the size of the Gaussian itself relative to the wavenumber for which the conversion is calculated;
$f_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D705}r_{G}$
, the size of the Gaussian itself relative to the wavenumber for which the conversion is calculated;(iii)
 $f_{p}=r_{G}/\text{d}x_{c}$
, the extent to which neighbouring patches overlap, relating the Gaussian width
$f_{p}=r_{G}/\text{d}x_{c}$
, the extent to which neighbouring patches overlap, relating the Gaussian width
 $r_{G}$
to the patch centre spacing
$r_{G}$
to the patch centre spacing
 $\text{d}x_{c}$
; and
$\text{d}x_{c}$
; and(iv) the resolution of the polar grid in each patch,
 $\text{d}r=r_{p}/n_{r}$
and
$\text{d}r=r_{p}/n_{r}$
and
 $\text{d}\unicode[STIX]{x1D719}=2\unicode[STIX]{x03C0}/n_{\unicode[STIX]{x1D719}}$
, where
$\text{d}\unicode[STIX]{x1D719}=2\unicode[STIX]{x03C0}/n_{\unicode[STIX]{x1D719}}$
, where
 $n_{r}$
is the number of points in the radial direction and
$n_{r}$
is the number of points in the radial direction and
 $n_{\unicode[STIX]{x1D719}}$
is the number of points in the angular direction – the parameter
$n_{\unicode[STIX]{x1D719}}$
is the number of points in the angular direction – the parameter
 $n_{\unicode[STIX]{x1D719}}$
thus determines the resolution of the angular energy flux
$n_{\unicode[STIX]{x1D719}}$
thus determines the resolution of the angular energy flux
 $\boldsymbol{F}$
.
$\boldsymbol{F}$
.
Suitable parameter settings are determined in convergence tests using idealised topography, which are presented in the following section.
4 Tests with idealised topography
The basic evaluation of the method achieved through the comparison of (2.17), describing the conversion as the integrated energy flux, and (2.16), defining the conversion in terms of the integrated source density, showed that for top-hat and stretched Gaussian topographies, the two solutions for the conversion rate agree well. For a more detailed evaluation and in order to determine the numerical parameters introduced in the previous section, we focus on the so-called ‘witch of Agnesi’ profile, for which it is possible to calculate the conversion rate analytically. This idealised topography is described as
 $$\begin{eqnarray}\displaystyle h(x)=\frac{h_{0}}{1+\displaystyle \frac{x^{2}}{\unicode[STIX]{x1D6EC}^{2}}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(x)=\frac{h_{0}}{1+\displaystyle \frac{x^{2}}{\unicode[STIX]{x1D6EC}^{2}}}, & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6EC}$
denotes the topographic length scale (half-width of the ridge) and
$\unicode[STIX]{x1D6EC}$
denotes the topographic length scale (half-width of the ridge) and
![]() $h_{0}$
the maximum ridge height. Tidal currents flowing across this idealised topography will generate parallel wavetrains propagating away from the ridge in the
$h_{0}$
the maximum ridge height. Tidal currents flowing across this idealised topography will generate parallel wavetrains propagating away from the ridge in the
![]() $x$
-direction – buoyancy oscillations and propagating internal gravity waves can only originate from flow across, not along, the topographic obstacle. Thus, the orientation of the tidal ellipse strongly affects the magnitude of the energy conversion for approximately one-dimensional topography, and in this case, the conversion per unit length in the
$x$
-direction – buoyancy oscillations and propagating internal gravity waves can only originate from flow across, not along, the topographic obstacle. Thus, the orientation of the tidal ellipse strongly affects the magnitude of the energy conversion for approximately one-dimensional topography, and in this case, the conversion per unit length in the
![]() $y$
-direction (
$y$
-direction (
![]() $\text{W}~\text{m}^{-1}$
) is a function of the zonal velocity component only (see e.g. Falahat et al.
Reference Falahat, Nycander, Roquet and Zarroug2014b
):
$\text{W}~\text{m}^{-1}$
) is a function of the zonal velocity component only (see e.g. Falahat et al.
Reference Falahat, Nycander, Roquet and Zarroug2014b
):
with the Fourier transform of the topography,
We follow Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) and set
![]() $h_{0}=100~\text{m}$
,
$h_{0}=100~\text{m}$
,
![]() $H=4~\text{km}$
,
$H=4~\text{km}$
,
![]() $f=8\times 10^{-5}~\text{s}^{-1}$
, the mean seawater density to
$f=8\times 10^{-5}~\text{s}^{-1}$
, the mean seawater density to
![]() $\unicode[STIX]{x1D70C}_{0}=1040~\text{kg}~\text{m}^{-3}$
, the tidal frequency corresponding to that of the
$\unicode[STIX]{x1D70C}_{0}=1040~\text{kg}~\text{m}^{-3}$
, the tidal frequency corresponding to that of the
![]() $M_{2}$
-tide,
$M_{2}$
-tide,
![]() $\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
, and the tidal amplitude to
$\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
, and the tidal amplitude to
![]() $U_{0}=4~\text{cm}~\text{s}^{-1}$
. The ridge is located at the centre of a domain which extends 4000 km in each direction with a grid spacing of
$U_{0}=4~\text{cm}~\text{s}^{-1}$
. The ridge is located at the centre of a domain which extends 4000 km in each direction with a grid spacing of
![]() $\text{d}x=\text{d}y=1~\text{km}$
. For topographic scales
$\text{d}x=\text{d}y=1~\text{km}$
. For topographic scales
![]() $\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
, the underlying assumptions of weak topography and small tidal excursion are met.
$\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
, the underlying assumptions of weak topography and small tidal excursion are met.
The numerical solution
![]() $C_{num}$
comparable to the analytical solution of the energy conversion in (4.2),
$C_{num}$
comparable to the analytical solution of the energy conversion in (4.2),
![]() $C_{an}$
, is obtained by integrating
$C_{an}$
, is obtained by integrating
![]() $D_{i,j}$
over all angles and across the ridge, replacing the integrals by simple sums:
$D_{i,j}$
over all angles and across the ridge, replacing the integrals by simple sums:
which is the same for any choice of
![]() $j=1,\ldots ,ny_{c}$
for reasons of symmetry. In order to determine suitable choices of the numerical parameters, we compare
$j=1,\ldots ,ny_{c}$
for reasons of symmetry. In order to determine suitable choices of the numerical parameters, we compare
![]() $C_{num,ny_{c}/2}=C_{num}$
and
$C_{num,ny_{c}/2}=C_{num}$
and
![]() $C_{an}$
for the different topographic scales
$C_{an}$
for the different topographic scales
![]() $\unicode[STIX]{x1D6EC}$
and different horizontal wavenumbers
$\unicode[STIX]{x1D6EC}$
and different horizontal wavenumbers
![]() $\unicode[STIX]{x1D705}$
given above. We first consider the case of uniform stratification with
$\unicode[STIX]{x1D705}$
given above. We first consider the case of uniform stratification with
![]() $N=9.02\times 10^{-4}~\text{s}^{-1}$
, so that
$N=9.02\times 10^{-4}~\text{s}^{-1}$
, so that
![]() $\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
(see (2.9)). The resolution of the polar grid is set such that, at the outer patch boundary, the resolution is the same as that of the Cartesian grid, i.e.
$\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
(see (2.9)). The resolution of the polar grid is set such that, at the outer patch boundary, the resolution is the same as that of the Cartesian grid, i.e.
![]() $n_{r}=r_{p}/\text{d}x$
and
$n_{r}=r_{p}/\text{d}x$
and
![]() $n_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}n_{r}$
. For most test cases, this is a much higher resolution than necessary for reproducing the analytical solution within 1 %, but we keep it that high in order not to lose any information – as shown by Nycander (Reference Nycander2005), insufficient resolution of topography is the most important error source in real applications.
$n_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}n_{r}$
. For most test cases, this is a much higher resolution than necessary for reproducing the analytical solution within 1 %, but we keep it that high in order not to lose any information – as shown by Nycander (Reference Nycander2005), insufficient resolution of topography is the most important error source in real applications.
Figure 2 shows the convergence of the numerical solution towards the analytical one (see (4.2)) for a topographic scale of
![]() $\unicode[STIX]{x1D6EC}=5~\text{km}$
, using increasing values of the Gaussian width, the patch size relative to that of the Gaussian and the patch overlap. The latter is described as the ratio of Gaussian width
$\unicode[STIX]{x1D6EC}=5~\text{km}$
, using increasing values of the Gaussian width, the patch size relative to that of the Gaussian and the patch overlap. The latter is described as the ratio of Gaussian width
![]() $r_{G}$
to the patch centre spacing
$r_{G}$
to the patch centre spacing
![]() $\text{d}x_{c}$
, which is related to the area overlap relative to the effective patch area,
$\text{d}x_{c}$
, which is related to the area overlap relative to the effective patch area,
![]() $O_{p}$
, according to
$O_{p}$
, according to
For values of
![]() $\unicode[STIX]{x1D705}$
between
$\unicode[STIX]{x1D705}$
between
![]() $0.1~\text{km}^{-1}$
and
$0.1~\text{km}^{-1}$
and
![]() $0.5~\text{km}^{-1}$
, the numerical solution agrees very well with the analytical one for settings of
$0.5~\text{km}^{-1}$
, the numerical solution agrees very well with the analytical one for settings of
![]() $f_{\unicode[STIX]{x1D705}}\geqslant 20$
,
$f_{\unicode[STIX]{x1D705}}\geqslant 20$
,
![]() $f_{l}\geqslant 2.5$
and a patch centre distance comparable to the Gaussian width, that is,
$f_{l}\geqslant 2.5$
and a patch centre distance comparable to the Gaussian width, that is,
![]() $f_{p}\geqslant 0.8$
or
$f_{p}\geqslant 0.8$
or
![]() $O_{p}\geqslant 0.25$
. This requires
$O_{p}\geqslant 0.25$
. This requires
![]() $(17,33,49,65,80)$
patches in each direction, or, in other words, a patch centre spacing of
$(17,33,49,65,80)$
patches in each direction, or, in other words, a patch centre spacing of
![]() $\text{d}x_{c}=\text{d}y_{c}=(235.3,121.2,81.6,61.5,50.0)$
km. The deviation from the analytical solution is approximately 1 % for modes 3–5 and less for modes 1 and 2. These threshold values are hence chosen as the reference settings for the following simulations. Note that we do not explore the three-dimensional parameter space, but keep two parameters fixed at their reference value while varying the third.
$\text{d}x_{c}=\text{d}y_{c}=(235.3,121.2,81.6,61.5,50.0)$
km. The deviation from the analytical solution is approximately 1 % for modes 3–5 and less for modes 1 and 2. These threshold values are hence chosen as the reference settings for the following simulations. Note that we do not explore the three-dimensional parameter space, but keep two parameters fixed at their reference value while varying the third.
In the following step, these reference settings are evaluated for the different values of the ridge width
![]() $\unicode[STIX]{x1D6EC}$
given above (see figure 3
a). These test cases show that, for wider ridges, the proportion of energy flux into the first vertical mode increases – for
$\unicode[STIX]{x1D6EC}$
given above (see figure 3
a). These test cases show that, for wider ridges, the proportion of energy flux into the first vertical mode increases – for
![]() $\unicode[STIX]{x1D6EC}=20~\text{km}$
, the only mode carrying a significant amount of energy is the first one. Moreover, these tests demonstrate that the agreement with the analytical solution is very good except for scenarios with very low conversion rates. Setting
$\unicode[STIX]{x1D6EC}=20~\text{km}$
, the only mode carrying a significant amount of energy is the first one. Moreover, these tests demonstrate that the agreement with the analytical solution is very good except for scenarios with very low conversion rates. Setting
![]() $\unicode[STIX]{x1D6EC}=20~\text{km}$
, the analytical solutions decrease below
$\unicode[STIX]{x1D6EC}=20~\text{km}$
, the analytical solutions decrease below
![]() $0.002~\text{W}~\text{m}^{-1}$
as
$0.002~\text{W}~\text{m}^{-1}$
as
![]() $\unicode[STIX]{x1D705}\geqslant 0.3~\text{km}^{-1}$
and the corresponding numerical solutions deviate by more than 10 % from the analytical values. Very low energy conversion rates are hence typically overestimated by this method, but fortunately of minor importance for the energy budget of the internal tide field. Conversion rates above
$\unicode[STIX]{x1D705}\geqslant 0.3~\text{km}^{-1}$
and the corresponding numerical solutions deviate by more than 10 % from the analytical values. Very low energy conversion rates are hence typically overestimated by this method, but fortunately of minor importance for the energy budget of the internal tide field. Conversion rates above
![]() $0.002~\text{W}~\text{m}^{-1}$
, on the other hand, are reproduced within 10 %, and rates above
$0.002~\text{W}~\text{m}^{-1}$
, on the other hand, are reproduced within 10 %, and rates above
![]() $0.2~\text{W}~\text{m}^{-1}$
within 1 %, mostly better. As depicted in figure 3(a), the total energy conversion is considerably higher than
$0.2~\text{W}~\text{m}^{-1}$
within 1 %, mostly better. As depicted in figure 3(a), the total energy conversion is considerably higher than
![]() $0.2~\text{W}~\text{m}^{-1}$
for the four different ridge length scales. For relevant energy conversion rates, the proposed method with standard settings
$0.2~\text{W}~\text{m}^{-1}$
for the four different ridge length scales. For relevant energy conversion rates, the proposed method with standard settings
![]() $f_{\unicode[STIX]{x1D705}}=20$
,
$f_{\unicode[STIX]{x1D705}}=20$
,
![]() $f_{l}=2.5$
and
$f_{l}=2.5$
and
![]() $f_{p}=0.8$
is thus confirmed for this idealised topography with constant stratification and a ridge width
$f_{p}=0.8$
is thus confirmed for this idealised topography with constant stratification and a ridge width
![]() $\unicode[STIX]{x1D6EC}$
varying between 2.5 km and 20 km.
$\unicode[STIX]{x1D6EC}$
varying between 2.5 km and 20 km.
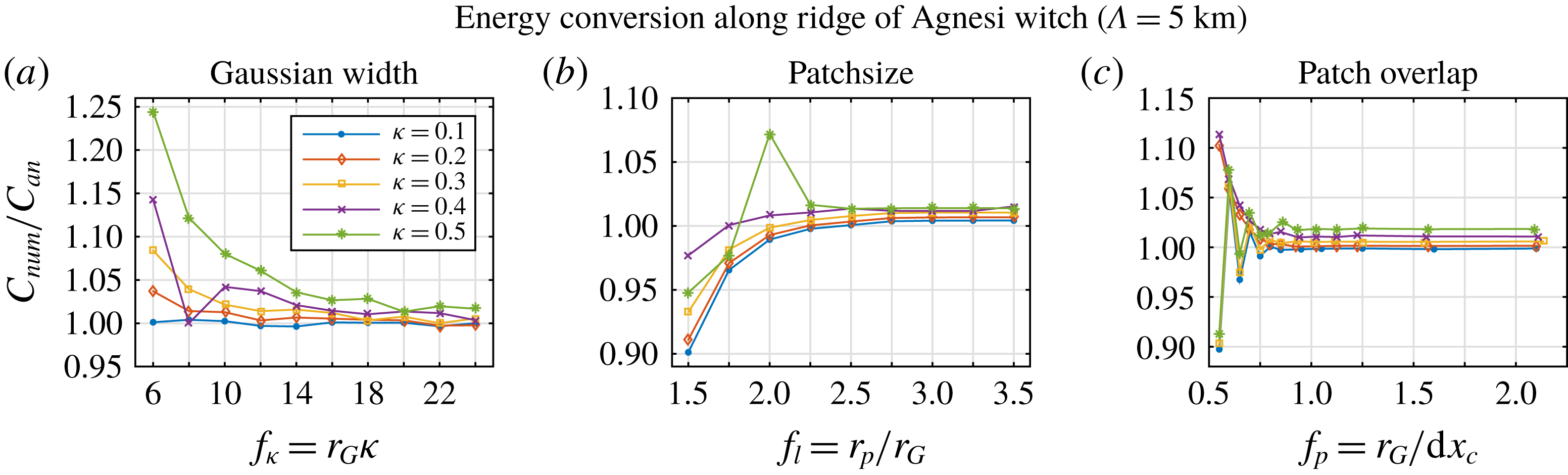
Figure 2. Ratio of numerical and analytical solutions,
![]() $C_{num}$
and
$C_{num}$
and
![]() $C_{an}$
, for the ‘witch of Agnesi’ profile with a topographic length scale of
$C_{an}$
, for the ‘witch of Agnesi’ profile with a topographic length scale of
![]() $\unicode[STIX]{x1D6EC}=5~\text{km}$
. Other settings are given in the main text. Note the different
$\unicode[STIX]{x1D6EC}=5~\text{km}$
. Other settings are given in the main text. Note the different
![]() $y$
-axis scalings. One parameter at a time is varied while keeping the other two at their reference values: in (a,b),
$y$
-axis scalings. One parameter at a time is varied while keeping the other two at their reference values: in (a,b),
![]() $f_{p}=0.8$
; in (a,c),
$f_{p}=0.8$
; in (a,c),
![]() $f_{l}=2.5$
; and in (b,c),
$f_{l}=2.5$
; and in (b,c),
![]() $f_{\unicode[STIX]{x1D705}}=20$
.
$f_{\unicode[STIX]{x1D705}}=20$
.
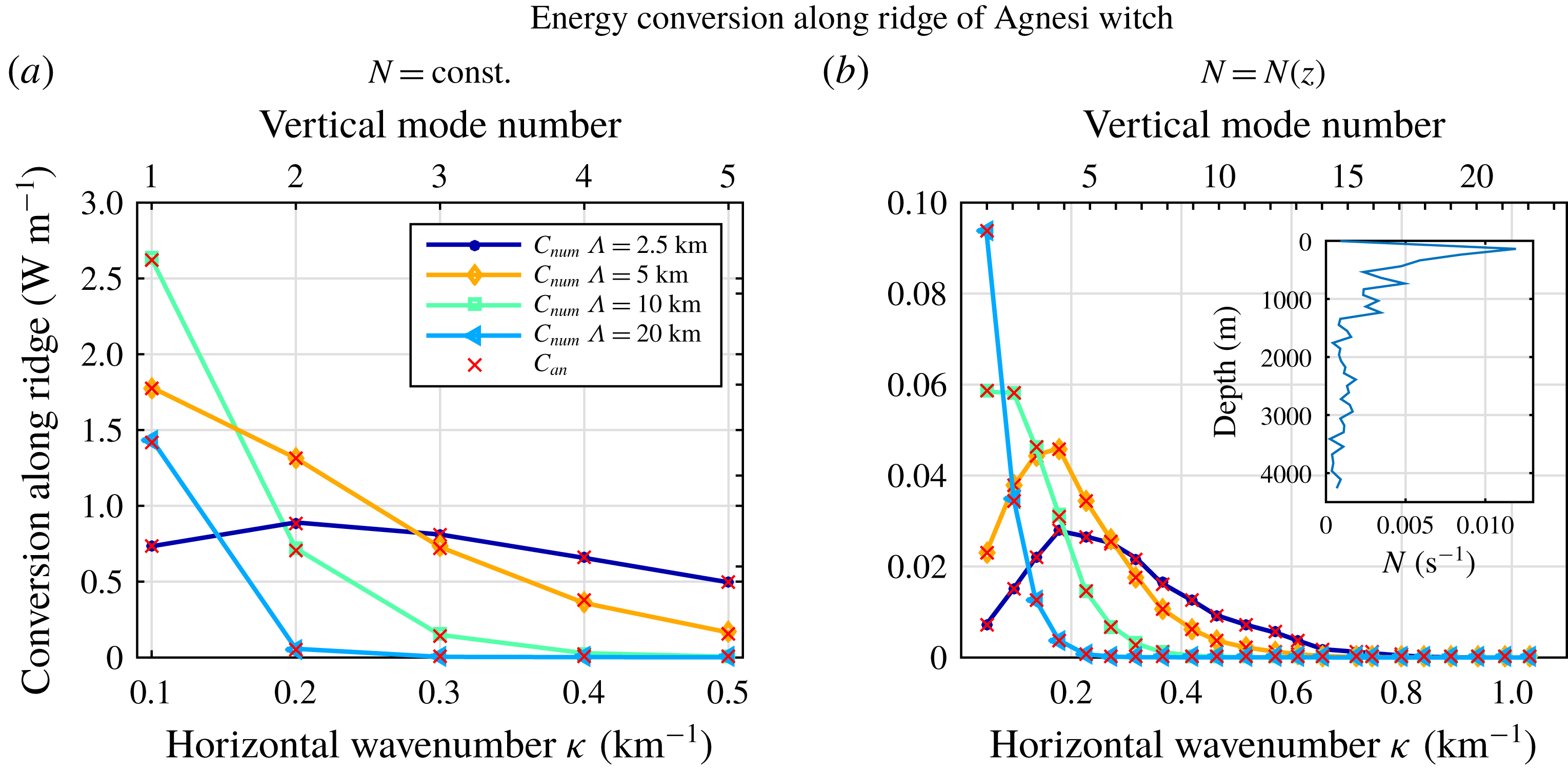
Figure 3. Energy conversion
![]() $C_{num}$
along a ‘witch of Agnesi’ ridge for four different topographic scales as a function of horizontal wavenumber for (a) constant and (b) variable stratification, with crosses showing the analytical solution given by (4.2). In the former case, the Coriolis frequency is
$C_{num}$
along a ‘witch of Agnesi’ ridge for four different topographic scales as a function of horizontal wavenumber for (a) constant and (b) variable stratification, with crosses showing the analytical solution given by (4.2). In the former case, the Coriolis frequency is
![]() $f=8\times 10^{-5}~\text{s}^{-1}$
; in the latter it is adjusted to the specific latitude of the
$f=8\times 10^{-5}~\text{s}^{-1}$
; in the latter it is adjusted to the specific latitude of the
![]() $N$
-profile, taken from the WOCE database from
$N$
-profile, taken from the WOCE database from
![]() $25^{\circ }\,\text{N}$
,
$25^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
and shown in a vertically smoothed version in the inset in panel (b), i.e.
$43^{\circ }\,\text{W}$
and shown in a vertically smoothed version in the inset in panel (b), i.e.
![]() $f=6\times 10^{-5}~\text{s}^{-1}$
. The other parameters are the same in both scenarios and given in the main text. The numerical parameters are
$f=6\times 10^{-5}~\text{s}^{-1}$
. The other parameters are the same in both scenarios and given in the main text. The numerical parameters are
![]() $f_{l}=2.5$
,
$f_{l}=2.5$
,
![]() $f_{\unicode[STIX]{x1D705}}=20$
and
$f_{\unicode[STIX]{x1D705}}=20$
and
![]() $f_{p}=0.8$
. In the test cases with variable stratification (b), deviations from the analytical solution by more than 10 % are observed for
$f_{p}=0.8$
. In the test cases with variable stratification (b), deviations from the analytical solution by more than 10 % are observed for
![]() $\unicode[STIX]{x1D705}\geqslant (0.75,0.80,0.46,0.23)~\text{km}^{-1}$
for
$\unicode[STIX]{x1D705}\geqslant (0.75,0.80,0.46,0.23)~\text{km}^{-1}$
for
![]() $\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
; conversion rates higher than
$\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
; conversion rates higher than
![]() $0.001~\text{W}~\text{m}^{-1}$
are very well reproduced. Assuming a constant stratification
$0.001~\text{W}~\text{m}^{-1}$
are very well reproduced. Assuming a constant stratification
![]() $N=9.02\times 10^{-4}~\text{s}^{-1}$
(a), such deviations only occur for
$N=9.02\times 10^{-4}~\text{s}^{-1}$
(a), such deviations only occur for
![]() $\unicode[STIX]{x1D705}\geqslant 0.5$
for
$\unicode[STIX]{x1D705}\geqslant 0.5$
for
![]() $\unicode[STIX]{x1D6EC}=10~\text{km}$
and for
$\unicode[STIX]{x1D6EC}=10~\text{km}$
and for
![]() $\unicode[STIX]{x1D705}\geqslant 0.3$
for
$\unicode[STIX]{x1D705}\geqslant 0.3$
for
![]() $\unicode[STIX]{x1D6EC}=20~\text{km}$
, when conversion rates are below
$\unicode[STIX]{x1D6EC}=20~\text{km}$
, when conversion rates are below
![]() $0.002~\text{W}~\text{m}^{-1}$
.
$0.002~\text{W}~\text{m}^{-1}$
.
This also holds true for vertically variable stratification (see figure 3
b). In this case, the full eigenvalue problem given in (2.1) has to be solved, which is done numerically following the method described by Chelton et al. (Reference Chelton, Deszoeke, Schlax, El Naggar and Siwertz1998). We use an
![]() $N$
-profile from the WOCE Global Climatology (Koltermann, Gouretski & Jancke Reference Koltermann, Gouretski and Jancke2011) – this profile was downloaded from the eWOCE website maintained by R. Schlitzer at the Alfred Wegener Institute for Polar and Marine Research, Bremerhaven, Germany – from
$N$
-profile from the WOCE Global Climatology (Koltermann, Gouretski & Jancke Reference Koltermann, Gouretski and Jancke2011) – this profile was downloaded from the eWOCE website maintained by R. Schlitzer at the Alfred Wegener Institute for Polar and Marine Research, Bremerhaven, Germany – from
![]() $25^{\circ }\,\text{N}$
,
$25^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
, which is characterised by a bottom value of
$43^{\circ }\,\text{W}$
, which is characterised by a bottom value of
![]() $N_{B}=3.77\times 10^{-4}~\text{s}^{-1}$
and shown in the inset of figure 3(b). We adjust the Coriolis parameter to a representative value of
$N_{B}=3.77\times 10^{-4}~\text{s}^{-1}$
and shown in the inset of figure 3(b). We adjust the Coriolis parameter to a representative value of
![]() $f=6\times 10^{-5}~\text{s}^{-1}$
and keep the other parameters at the values listed above. As already observed for the test cases with constant stratification, the energy flux into higher modes decreases for wider ridges. It is interesting to note that in this idealised case with one-dimensional topography, there is a clear relation between ridge width and wavelength
$f=6\times 10^{-5}~\text{s}^{-1}$
and keep the other parameters at the values listed above. As already observed for the test cases with constant stratification, the energy flux into higher modes decreases for wider ridges. It is interesting to note that in this idealised case with one-dimensional topography, there is a clear relation between ridge width and wavelength
![]() $\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D705}$
of maximum energy conversion:
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D705}$
of maximum energy conversion:
![]() $\unicode[STIX]{x1D706}(C_{max})=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6EC}$
. This explains why the maximum conversion is observed for lower modes when increasing
$\unicode[STIX]{x1D706}(C_{max})=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6EC}$
. This explains why the maximum conversion is observed for lower modes when increasing
![]() $\unicode[STIX]{x1D6EC}$
and is a useful relation to determine the Gaussian width for the ‘witch of Agnesi’ profile. It is less useful, however, for calculations with realistic topography, which is characterised by many different topographic length scales.
$\unicode[STIX]{x1D6EC}$
and is a useful relation to determine the Gaussian width for the ‘witch of Agnesi’ profile. It is less useful, however, for calculations with realistic topography, which is characterised by many different topographic length scales.
As illustrated in figure 3(b), the numerical solution reproduces the analytical one well as long as conversion rates are higher than
![]() $0.001~\text{W}~\text{m}^{-1}$
. Deviations from the analytical solution by more than 10 % are found for modes higher than
$0.001~\text{W}~\text{m}^{-1}$
. Deviations from the analytical solution by more than 10 % are found for modes higher than
![]() $(15,17,9,4)$
, i.e. the critical wavenumber is
$(15,17,9,4)$
, i.e. the critical wavenumber is
![]() $\unicode[STIX]{x1D705}_{crit}=(0.75,0.80,0.46,0.23)~\text{km}^{-1}$
for
$\unicode[STIX]{x1D705}_{crit}=(0.75,0.80,0.46,0.23)~\text{km}^{-1}$
for
![]() $\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
. The corresponding conversion rates amount to
$\unicode[STIX]{x1D6EC}=(2.5,5,10,20)~\text{km}$
. The corresponding conversion rates amount to
![]() $C_{an}=(0.001,1.34\times 10^{-5},1.45\times 10^{-4},6.32\times 10^{-4})~\text{W}~\text{m}^{-1}$
and are hence much lower than the total energy conversion into the lower modes with
$C_{an}=(0.001,1.34\times 10^{-5},1.45\times 10^{-4},6.32\times 10^{-4})~\text{W}~\text{m}^{-1}$
and are hence much lower than the total energy conversion into the lower modes with
![]() $\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}_{crit}$
. In conclusion, the new method based on circular patches and using the standard settings defined above accounts well for the bulk of the energy converted into baroclinic tides at a one-dimensional ridge.
$\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}_{crit}$
. In conclusion, the new method based on circular patches and using the standard settings defined above accounts well for the bulk of the energy converted into baroclinic tides at a one-dimensional ridge.
If there is more than one ridge, wave interference may significantly change the total conversion (e.g. Karimpour et al.
Reference Karimpour, Zareei, Tchoufag and Alam2017; Zhang et al.
Reference Zhang, Buijsman, Comino and Swinney2017). In order to illustrate how the new method can capture this and to shed light on the relevance of the parameter
![]() $r_{G}$
, we consider a double ridge system defined as
$r_{G}$
, we consider a double ridge system defined as
 $$\begin{eqnarray}\displaystyle h(x)=\frac{h_{0}}{1+\displaystyle \frac{(x+x_{0}/2)^{2}}{\unicode[STIX]{x1D6EC}^{2}}}+\frac{h_{0}}{1+\displaystyle \frac{(x-x_{0}/2)^{2}}{\unicode[STIX]{x1D6EC}^{2}}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(x)=\frac{h_{0}}{1+\displaystyle \frac{(x+x_{0}/2)^{2}}{\unicode[STIX]{x1D6EC}^{2}}}+\frac{h_{0}}{1+\displaystyle \frac{(x-x_{0}/2)^{2}}{\unicode[STIX]{x1D6EC}^{2}}}, & & \displaystyle\end{eqnarray}$$
that is, two ‘witch of Agnesi’ ridges with a peak separation distance
![]() $x_{0}$
. The analytical solution for the conversion rate is given by (4.2) with the Fourier-transformed topography adjusted to
$x_{0}$
. The analytical solution for the conversion rate is given by (4.2) with the Fourier-transformed topography adjusted to
Figure 4 shows the total conversion into the first five internal tide modes with
![]() $\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
. The internal tides interfere constructively or destructively, depending on peak separation distance, which leads to an oscillating behaviour. The agreement between the numerical and analytical solutions decreases as the distance between the ridge peaks is increased. For very large ridge distances, the numerical solution is equal to twice the conversion of one isolated ridge (i.e. (4.1) – note the factor of two difference between (4.1) and (4.6) for
$\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
. The internal tides interfere constructively or destructively, depending on peak separation distance, which leads to an oscillating behaviour. The agreement between the numerical and analytical solutions decreases as the distance between the ridge peaks is increased. For very large ridge distances, the numerical solution is equal to twice the conversion of one isolated ridge (i.e. (4.1) – note the factor of two difference between (4.1) and (4.6) for
![]() $x_{0}=0$
). Focusing on the conversion maxima obtained for
$x_{0}=0$
). Focusing on the conversion maxima obtained for
![]() $x_{0}=2n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D705}_{m}$
,
$x_{0}=2n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D705}_{m}$
,
![]() $n=0,1,2,3\ldots$
, the numerical solution reproduces the analytical one for the different individual modes within 10 % as long as
$n=0,1,2,3\ldots$
, the numerical solution reproduces the analytical one for the different individual modes within 10 % as long as
![]() $x_{0}<r_{G}$
(not shown). The parameter
$x_{0}<r_{G}$
(not shown). The parameter
![]() $r_{G}$
can thus be thought of as representing the correlation length scale of internal tides: only the interaction between waves generated by topographic features located within a distance
$r_{G}$
can thus be thought of as representing the correlation length scale of internal tides: only the interaction between waves generated by topographic features located within a distance
![]() $r_{G}$
from each other is taken into account. In consequence, calculations for more complex topography should use sufficiently large patch radii and a patch centre distance
$r_{G}$
from each other is taken into account. In consequence, calculations for more complex topography should use sufficiently large patch radii and a patch centre distance
![]() $\text{d}x_{c}$
and
$\text{d}x_{c}$
and
![]() $\text{d}y_{c}$
smaller than
$\text{d}y_{c}$
smaller than
![]() $r_{G}$
in order to correctly represent the effect of wave interference on conversion rate estimates.
$r_{G}$
in order to correctly represent the effect of wave interference on conversion rate estimates.
Figure 4. Analytical and numerical energy conversion per unit length in the
![]() $y$
-direction (see (4.2) and (4.4), respectively) into modes 1–5 for a double ridge system of two ‘witch of Agnesi’ peaks in the
$y$
-direction (see (4.2) and (4.4), respectively) into modes 1–5 for a double ridge system of two ‘witch of Agnesi’ peaks in the
![]() $x$
-direction as defined in (4.6). The stratification is assumed to be constant, using
$x$
-direction as defined in (4.6). The stratification is assumed to be constant, using
![]() $\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
,
$\unicode[STIX]{x1D705}_{m}=m\times 0.1~\text{km}^{-1}$
,
![]() $r_{G}=20/\unicode[STIX]{x1D705}_{m}$
and
$r_{G}=20/\unicode[STIX]{x1D705}_{m}$
and
![]() $\unicode[STIX]{x1D6EC}=5~\text{km}$
. The other parameter settings are the same as for the single ridge and constant stratification.
$\unicode[STIX]{x1D6EC}=5~\text{km}$
. The other parameter settings are the same as for the single ridge and constant stratification.
5 Energy conversion for a region of realistic topography
In order to determine suitable numerical parameter settings for realistic topography, we choose a region of interesting topography that involves no land points and is large enough to incorporate a reasonable number of circular patches for a variety of parameters: spanning
![]() $30.85{-}55.83^{\circ }\,\text{W}$
and
$30.85{-}55.83^{\circ }\,\text{W}$
and
![]() $10.83{-}35.83^{\circ }\,\text{N}$
, it covers an area of
$10.83{-}35.83^{\circ }\,\text{N}$
, it covers an area of
![]() $2.78\times 10^{3}~\text{km}$
in latitudinal and
$2.78\times 10^{3}~\text{km}$
in latitudinal and
![]() $2.55\times 10^{3}~\text{km}$
in longitudinal direction (at the centre at approximately
$2.55\times 10^{3}~\text{km}$
in longitudinal direction (at the centre at approximately
![]() $23^{\circ }\,\text{N}$
) over the Mid-Atlantic Ridge (MAR). In order to avoid boundary effects, the domain is on all sides extended by approximately 500 km, in which the bathymetric height is tapered by a
$23^{\circ }\,\text{N}$
) over the Mid-Atlantic Ridge (MAR). In order to avoid boundary effects, the domain is on all sides extended by approximately 500 km, in which the bathymetric height is tapered by a
![]() $\sin ^{2}$
function to the average value at the respective side, and another approximately 900 km of this constant average (refer to figure 8 for an illustration of the topography, where much of the surrounding taper was cropped). The topographic elevation was taken from Becker et al. (Reference Becker, Sandwell, Smith, Braud, Binder, Depner, Fabre, Factor, Ingalls, Kim, Ladner, Marks, Nelson, Pharaoh, Trimmer, Von Rosenberg, Wallace and Weatherall2009) with a resolution of 30 arcsec, which corresponds to 0.93 km at the equator. Within each patch, the topography is now tapered towards the average topography
$\sin ^{2}$
function to the average value at the respective side, and another approximately 900 km of this constant average (refer to figure 8 for an illustration of the topography, where much of the surrounding taper was cropped). The topographic elevation was taken from Becker et al. (Reference Becker, Sandwell, Smith, Braud, Binder, Depner, Fabre, Factor, Ingalls, Kim, Ladner, Marks, Nelson, Pharaoh, Trimmer, Von Rosenberg, Wallace and Weatherall2009) with a resolution of 30 arcsec, which corresponds to 0.93 km at the equator. Within each patch, the topography is now tapered towards the average topography
![]() $\overline{h_{i,j}}$
over the patch, instead of towards zero, by multiplication with a Gaussian. That is, (3.7) is replaced by
$\overline{h_{i,j}}$
over the patch, instead of towards zero, by multiplication with a Gaussian. That is, (3.7) is replaced by
We set
![]() $f=6\times 10^{-5}~\text{s}^{-1}$
and reduce
$f=6\times 10^{-5}~\text{s}^{-1}$
and reduce
![]() $n_{\unicode[STIX]{x1D719}}$
to
$n_{\unicode[STIX]{x1D719}}$
to
![]() $n_{\unicode[STIX]{x1D719}}=n_{r}$
to save computational time. This step is justified by the observation that, in various test cases, this reduced angular resolution leads to conversion rates within 0.01 % (0.001 %) for constant (variable) stratification from the results obtained for
$n_{\unicode[STIX]{x1D719}}=n_{r}$
to save computational time. This step is justified by the observation that, in various test cases, this reduced angular resolution leads to conversion rates within 0.01 % (0.001 %) for constant (variable) stratification from the results obtained for
![]() $n_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}n_{r}$
. All the other parameters are kept as before, i.e. the tidal velocity is
$n_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}n_{r}$
. All the other parameters are kept as before, i.e. the tidal velocity is
![]() $\boldsymbol{U}=(0.04,0)~\text{m}~\text{s}^{-1}$
, the mean seawater density is
$\boldsymbol{U}=(0.04,0)~\text{m}~\text{s}^{-1}$
, the mean seawater density is
![]() $\unicode[STIX]{x1D70C}_{0}=1040~\text{kg}~\text{m}^{-3}$
and the tidal frequency corresponds to that of the
$\unicode[STIX]{x1D70C}_{0}=1040~\text{kg}~\text{m}^{-3}$
and the tidal frequency corresponds to that of the
![]() $M_{2}$
-tide,
$M_{2}$
-tide,
![]() $\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
. Owing to the lack of an analytical reference solution, suitable numerical parameters are determined by successively increasing their values until the total energy conversion saturates. This form of convergence test is made possible by the tapering of the topography at the boundary of the region.
$\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
. Owing to the lack of an analytical reference solution, suitable numerical parameters are determined by successively increasing their values until the total energy conversion saturates. This form of convergence test is made possible by the tapering of the topography at the boundary of the region.
Figure 5 shows these sensitivity studies both for constant and for vertically variable stratification. Here, the total energy conversion into one vertical mode is considered, that is, we take the sum of (4.4) over all
![]() $j=1,\ldots ,ny_{c}$
and multiply by the corresponding
$j=1,\ldots ,ny_{c}$
and multiply by the corresponding
![]() $\text{d}y_{c}$
:
$\text{d}y_{c}$
:
Note that here
![]() $\text{d}x_{c}$
is a function of
$\text{d}x_{c}$
is a function of
![]() $j$
, as it varies with latitude. In the first case, we set
$j$
, as it varies with latitude. In the first case, we set
![]() $N=9.02\times 10^{-4}~\text{s}^{-1}$
with
$N=9.02\times 10^{-4}~\text{s}^{-1}$
with
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{1}=0.1~\text{km}^{-1}$
and the reference settings
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{1}=0.1~\text{km}^{-1}$
and the reference settings
![]() $f_{l}=2.75$
,
$f_{l}=2.75$
,
![]() $f_{\unicode[STIX]{x1D705}}=25$
and
$f_{\unicode[STIX]{x1D705}}=25$
and
![]() $f_{p}=1.25$
(that is,
$f_{p}=1.25$
(that is,
![]() $n_{xc}=n_{yc}=29$
or
$n_{xc}=n_{yc}=29$
or
![]() $O_{p}=0.5$
). In the second case, we use the
$O_{p}=0.5$
). In the second case, we use the
![]() $N$
-profile from
$N$
-profile from
![]() $25^{\circ }\,\text{N}$
,
$25^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
(see figure 3
b) and show the convergence of the numerical solution for
$43^{\circ }\,\text{W}$
(see figure 3
b) and show the convergence of the numerical solution for
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
with reference settings of
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
with reference settings of
![]() $f_{l}=2.75$
,
$f_{l}=2.75$
,
![]() $f_{\unicode[STIX]{x1D705}}=25$
and
$f_{\unicode[STIX]{x1D705}}=25$
and
![]() $f_{p}=1.25$
(that is,
$f_{p}=1.25$
(that is,
![]() $n_{xc}=n_{yc}=28$
or
$n_{xc}=n_{yc}=28$
or
![]() $O_{p}=0.5$
). The influence of variable stratification is evident, with lower total energy conversion rates observed in the scenario with
$O_{p}=0.5$
). The influence of variable stratification is evident, with lower total energy conversion rates observed in the scenario with
![]() $N=N(z)$
due to the differences mainly in
$N=N(z)$
due to the differences mainly in
![]() $\unicode[STIX]{x1D701}_{m}$
.
$\unicode[STIX]{x1D701}_{m}$
.
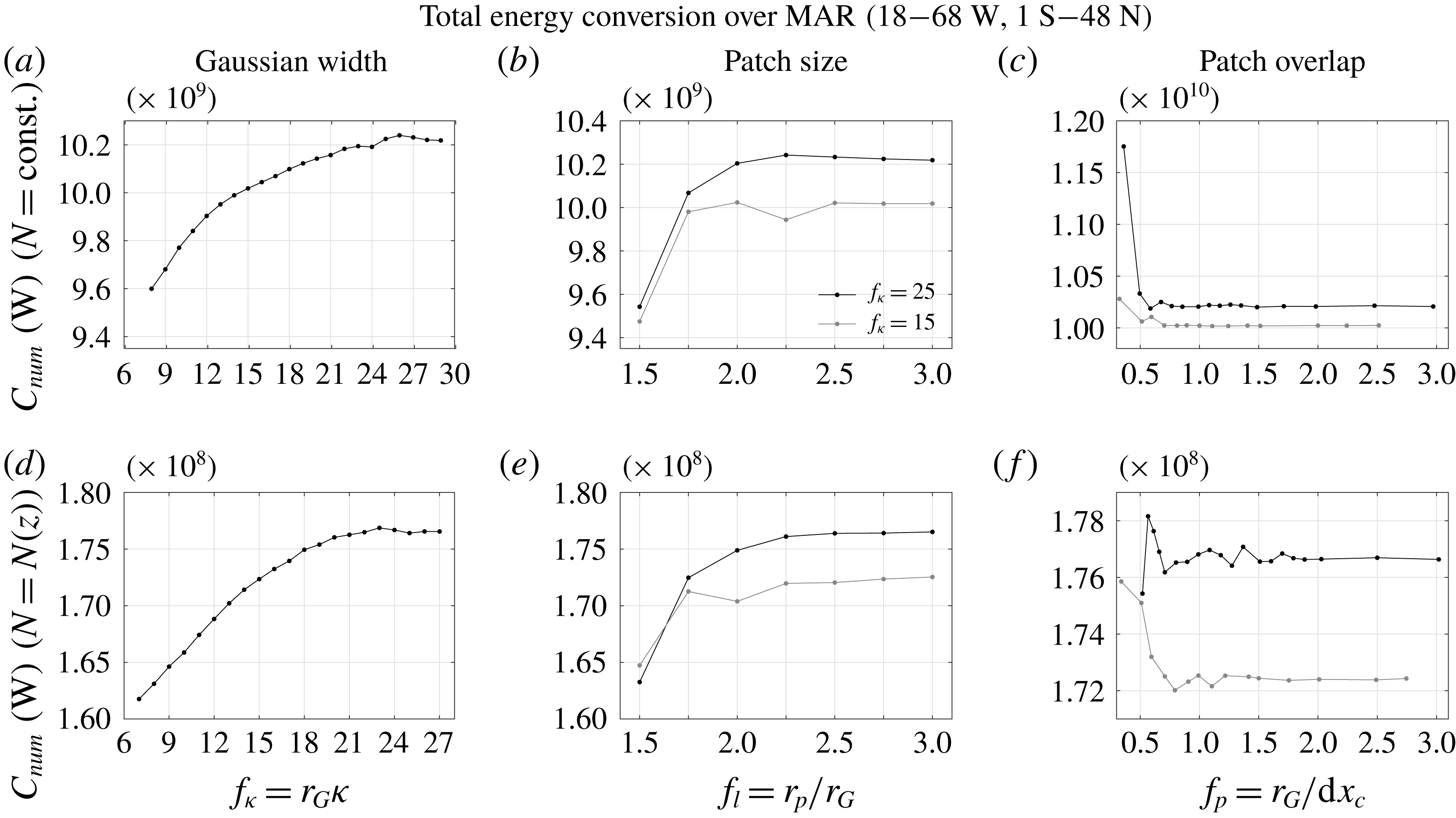
Figure 5. Sensitivity analysis of the total energy conversion (see (5.2)) over the MAR at
![]() $18^{\circ }$
–
$18^{\circ }$
–
![]() $68^{\circ }\,\text{W}$
and
$68^{\circ }\,\text{W}$
and
![]() $1^{\circ }\,\text{S}$
–
$1^{\circ }\,\text{S}$
–
![]() $48^{\circ }\,\text{N}$
for (top) constant stratification with
$48^{\circ }\,\text{N}$
for (top) constant stratification with
![]() $N=9.02\times 10^{-4}~\text{s}^{-1}$
and
$N=9.02\times 10^{-4}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{1}=0.1~\text{km}^{-1}$
and (bottom) variable stratification with the
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{1}=0.1~\text{km}^{-1}$
and (bottom) variable stratification with the
![]() $N$
-profile from
$N$
-profile from
![]() $25^{\circ }\,\text{N}$
,
$25^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
and
$43^{\circ }\,\text{W}$
and
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
. Refer to the main text for details. One parameter is varied at a time, while the other two are kept constant. The reference settings are
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
. Refer to the main text for details. One parameter is varied at a time, while the other two are kept constant. The reference settings are
![]() $f_{p}=1.25$
,
$f_{p}=1.25$
,
![]() $f_{l}=2.75$
and
$f_{l}=2.75$
and
![]() $f_{\unicode[STIX]{x1D705}}=25$
or
$f_{\unicode[STIX]{x1D705}}=25$
or
![]() $f_{\unicode[STIX]{x1D705}}=15$
. Note the different
$f_{\unicode[STIX]{x1D705}}=15$
. Note the different
![]() $y$
-axis scalings.
$y$
-axis scalings.
The smallest variations are seen when varying the patch overlap, which almost disappear for
![]() $f_{p}=r_{G}/\text{d}x_{c}$
higher than unity. For increasing
$f_{p}=r_{G}/\text{d}x_{c}$
higher than unity. For increasing
![]() $f_{l}$
and
$f_{l}$
and
![]() $f_{\unicode[STIX]{x1D705}}$
, the total conversion smoothly increases until it saturates for
$f_{\unicode[STIX]{x1D705}}$
, the total conversion smoothly increases until it saturates for
![]() $f_{l}\geqslant 2.5$
and
$f_{l}\geqslant 2.5$
and
![]() $f_{\unicode[STIX]{x1D705}}\geqslant 25$
. These threshold values are confirmed in simulations with
$f_{\unicode[STIX]{x1D705}}\geqslant 25$
. These threshold values are confirmed in simulations with
![]() $f_{\unicode[STIX]{x1D705}}=15$
as the reference value (figure 5
b,c). Setting
$f_{\unicode[STIX]{x1D705}}=15$
as the reference value (figure 5
b,c). Setting
![]() $f_{\unicode[STIX]{x1D705}}=15$
rather than
$f_{\unicode[STIX]{x1D705}}=15$
rather than
![]() $f_{\unicode[STIX]{x1D705}}=25$
reduces the patch radius from 724 km to 434 km (from 688 km to 413 km for constant stratification), but gives a total conversion already within 3 % of the asymptotic value shown in figure 5(a). While larger patches imply larger correlation length scales
$f_{\unicode[STIX]{x1D705}}=25$
reduces the patch radius from 724 km to 434 km (from 688 km to 413 km for constant stratification), but gives a total conversion already within 3 % of the asymptotic value shown in figure 5(a). While larger patches imply larger correlation length scales
![]() $r_{G}$
, they also render the assumption of constant tidal velocity and horizontal wavenumber within the patch less realistic. Moreover, the spatial structure of the energy flux is best resolved for smaller patch sizes, i.e. smaller values of
$r_{G}$
, they also render the assumption of constant tidal velocity and horizontal wavenumber within the patch less realistic. Moreover, the spatial structure of the energy flux is best resolved for smaller patch sizes, i.e. smaller values of
![]() $f_{\unicode[STIX]{x1D705}}$
. This is illustrated in figure 6, where the zonally integrated energy flux density is shown as a function of latitude, demonstrating that increasing the patch radius effectively smooths this field. Consequently, there is a trade-off between angular and spatial resolution of the energy flux. Choosing a larger value of
$f_{\unicode[STIX]{x1D705}}$
. This is illustrated in figure 6, where the zonally integrated energy flux density is shown as a function of latitude, demonstrating that increasing the patch radius effectively smooths this field. Consequently, there is a trade-off between angular and spatial resolution of the energy flux. Choosing a larger value of
![]() $f_{\unicode[STIX]{x1D705}}$
leads to a higher number of angular modes
$f_{\unicode[STIX]{x1D705}}$
leads to a higher number of angular modes
![]() $n_{\unicode[STIX]{x1D719}}$
and hence a better resolution of the direction of the energy flux at each individual patch centre. At the same time, this leads to a coarser spatial resolution of the energy flux. This trade-off and the fact that, in the real ocean, sources of different length scales abound, render it difficult to decide on a universal value for
$n_{\unicode[STIX]{x1D719}}$
and hence a better resolution of the direction of the energy flux at each individual patch centre. At the same time, this leads to a coarser spatial resolution of the energy flux. This trade-off and the fact that, in the real ocean, sources of different length scales abound, render it difficult to decide on a universal value for
![]() $f_{\unicode[STIX]{x1D705}}$
. Since the focus of this study is on the evaluation of our new method, we set
$f_{\unicode[STIX]{x1D705}}$
. Since the focus of this study is on the evaluation of our new method, we set
![]() $f_{\unicode[STIX]{x1D705}}$
= 25; for realistic applications, a smaller value appears more appropriate. It is reassuring to see that even for half of our standard value the total conversion is close to the saturation result (figure 5
a).
$f_{\unicode[STIX]{x1D705}}$
= 25; for realistic applications, a smaller value appears more appropriate. It is reassuring to see that even for half of our standard value the total conversion is close to the saturation result (figure 5
a).
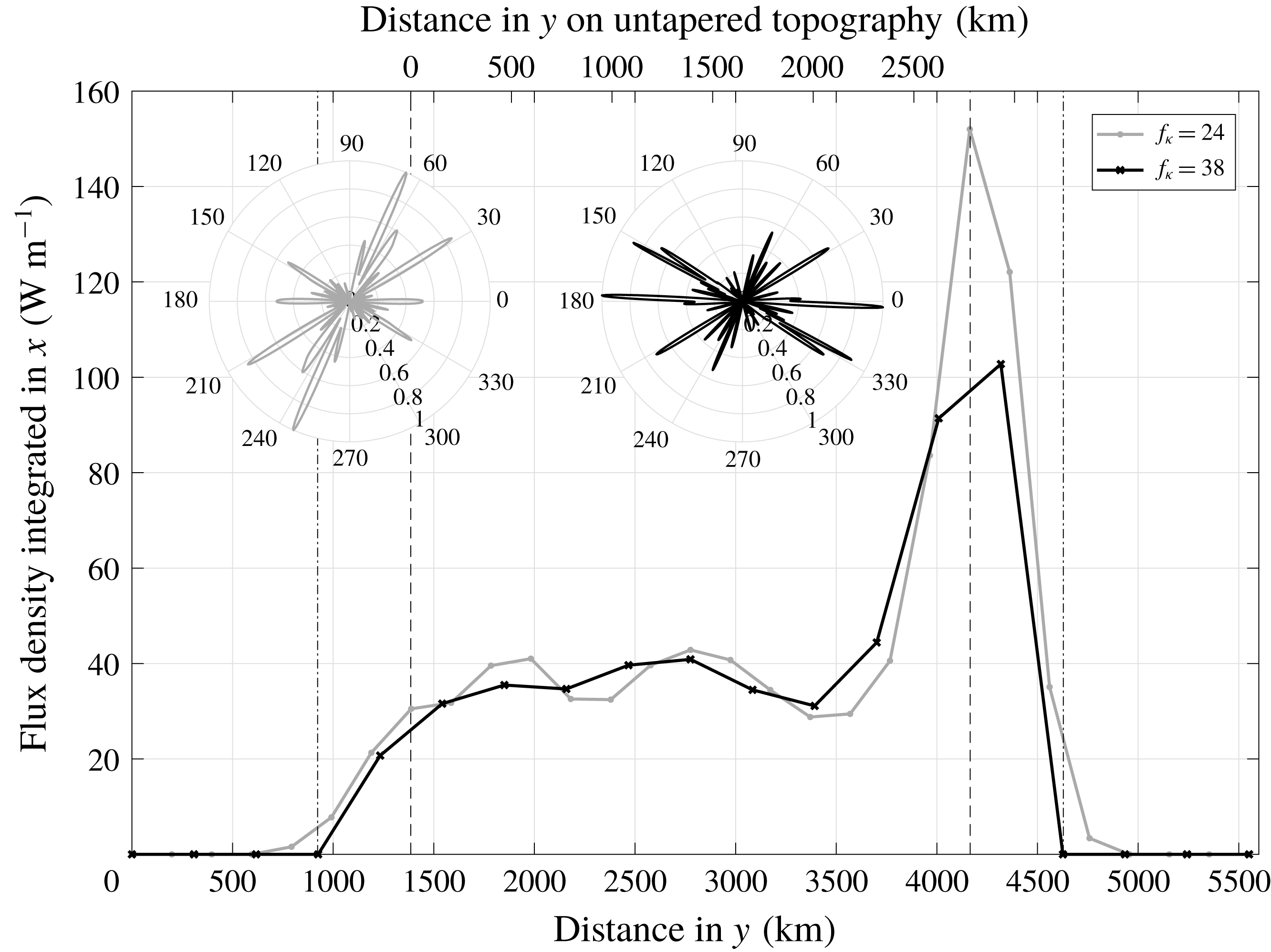
Figure 6. Zonally integrated flux density (see (4.4)) as a function of latitudinal distance across the domain of realistic topography shown (without much of the surrounding taper) in figure 8 for two different choices of
![]() $f_{\unicode[STIX]{x1D705}}$
. The dashed lines mark the region of untapered topography, and the dashed-dotted lines mark the border between constant and tapered topography. The results are shown for
$f_{\unicode[STIX]{x1D705}}$
. The dashed lines mark the region of untapered topography, and the dashed-dotted lines mark the border between constant and tapered topography. The results are shown for
![]() $\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
with the same settings as described in the caption of figure 5 for variable stratification. The insets show the energy flux
$\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
with the same settings as described in the caption of figure 5 for variable stratification. The insets show the energy flux
![]() $F$
at the patch centre circled in red in figure 8, scaled by its respective maximum in this specific patch, for these two cases, where colours correspond to those in the legend and zero degrees is eastward. Note that only the total conversion in the entire area is expected to converge for ever larger numerical parameters, while the directional variation of the energy flux in a specific patch is not.
$F$
at the patch centre circled in red in figure 8, scaled by its respective maximum in this specific patch, for these two cases, where colours correspond to those in the legend and zero degrees is eastward. Note that only the total conversion in the entire area is expected to converge for ever larger numerical parameters, while the directional variation of the energy flux in a specific patch is not.
The reference settings determined in this sensitivity analysis can be further evaluated in a comparison with the total conversion rate calculated by following the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). This is essentially a comparison between the right-hand side of (2.13), the basis of (2.27) which was used by Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
), and the left-hand side of (2.13), on which our direction resolving method is based. We exactly follow the method of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) and calculate the conversion rate at each topography grid point, i.e. at a resolution of
![]() $1/120^{\circ }$
. Two calculations are performed: first, the Bessel function in the integral is truncated after 13 zero crossings, then after 14. The conversion rate at the specific topography point is taken as the average of these two results. The sum of all conversion rates (positive and occasionally negative) in the entire MAR domain amounts to
$1/120^{\circ }$
. Two calculations are performed: first, the Bessel function in the integral is truncated after 13 zero crossings, then after 14. The conversion rate at the specific topography point is taken as the average of these two results. The sum of all conversion rates (positive and occasionally negative) in the entire MAR domain amounts to
![]() $C=1.1647\times 10^{10}~\text{W}$
for constant stratification and to
$C=1.1647\times 10^{10}~\text{W}$
for constant stratification and to
![]() $C=2.1883\times 10^{8}~\text{W}$
for variable stratification. The corresponding results using our method equal
$C=2.1883\times 10^{8}~\text{W}$
for variable stratification. The corresponding results using our method equal
![]() $C=1.0224\times 10^{10}~\text{W}$
and
$C=1.0224\times 10^{10}~\text{W}$
and
![]() $C=1.7641\times 10^{8}~\text{W}$
, respectively, i.e. 88 % and 81 % of the results following the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). Considering that both methods rely on setting a correlation length scale – in the form of
$C=1.7641\times 10^{8}~\text{W}$
, respectively, i.e. 88 % and 81 % of the results following the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
). Considering that both methods rely on setting a correlation length scale – in the form of
![]() $f_{\unicode[STIX]{x1D705}}$
for our approach and the number of zero crossings of the Bessel function for that of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) – and remain somewhat sensitive to that choice, an agreement within 10–20 % seems acceptable. A more detailed comparison is presented in figure 7, where the spatial distribution of the conversion is shown. Following the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) (figure 7
b), the conversion field has a much higher resolution than that based on the patch method (figure 7
a) and consequently reveals much more detail of the spatial variability. But it also features a large number of negative values, which is impracticable when the conversion field is to be used as a source function in internal wave models. One possibility to obtain a positive definite field is to average the conversion onto a coarser grid, e.g. the patch centre grid. The resultant conversion field (figure 7
c) is in reasonable agreement with that obtained using the patch method, but some negative values remain (marked white in the figure). Another possibility is to smooth the conversion field (not shown). Using
$f_{\unicode[STIX]{x1D705}}$
for our approach and the number of zero crossings of the Bessel function for that of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) – and remain somewhat sensitive to that choice, an agreement within 10–20 % seems acceptable. A more detailed comparison is presented in figure 7, where the spatial distribution of the conversion is shown. Following the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) (figure 7
b), the conversion field has a much higher resolution than that based on the patch method (figure 7
a) and consequently reveals much more detail of the spatial variability. But it also features a large number of negative values, which is impracticable when the conversion field is to be used as a source function in internal wave models. One possibility to obtain a positive definite field is to average the conversion onto a coarser grid, e.g. the patch centre grid. The resultant conversion field (figure 7
c) is in reasonable agreement with that obtained using the patch method, but some negative values remain (marked white in the figure). Another possibility is to smooth the conversion field (not shown). Using
![]() $r_{G}=262~\text{km}$
as a smoothing length scale, the agreement with figure 7(a) is very good but the conversion field still becomes negative occasionally, while using a smoothing scale of
$r_{G}=262~\text{km}$
as a smoothing length scale, the agreement with figure 7(a) is very good but the conversion field still becomes negative occasionally, while using a smoothing scale of
![]() $r_{p}=724~\text{km}$
results in a positive definite conversion field, but also in an overly smooth one, with very little spatial variation left. This emphasises an important advantage of the patch-based method: while previous approaches like that of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) require some a posteriori treatment of the conversion field before it can be used as an internal wave source function, involving some ad hoc choices of smoothing or averaging length scales, the patch method provides a ready-to-use positive definite conversion field because it includes this averaging in a systematic way, relating the corresponding length scale to the local internal tide wavenumber.
$r_{p}=724~\text{km}$
results in a positive definite conversion field, but also in an overly smooth one, with very little spatial variation left. This emphasises an important advantage of the patch-based method: while previous approaches like that of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) require some a posteriori treatment of the conversion field before it can be used as an internal wave source function, involving some ad hoc choices of smoothing or averaging length scales, the patch method provides a ready-to-use positive definite conversion field because it includes this averaging in a systematic way, relating the corresponding length scale to the local internal tide wavenumber.
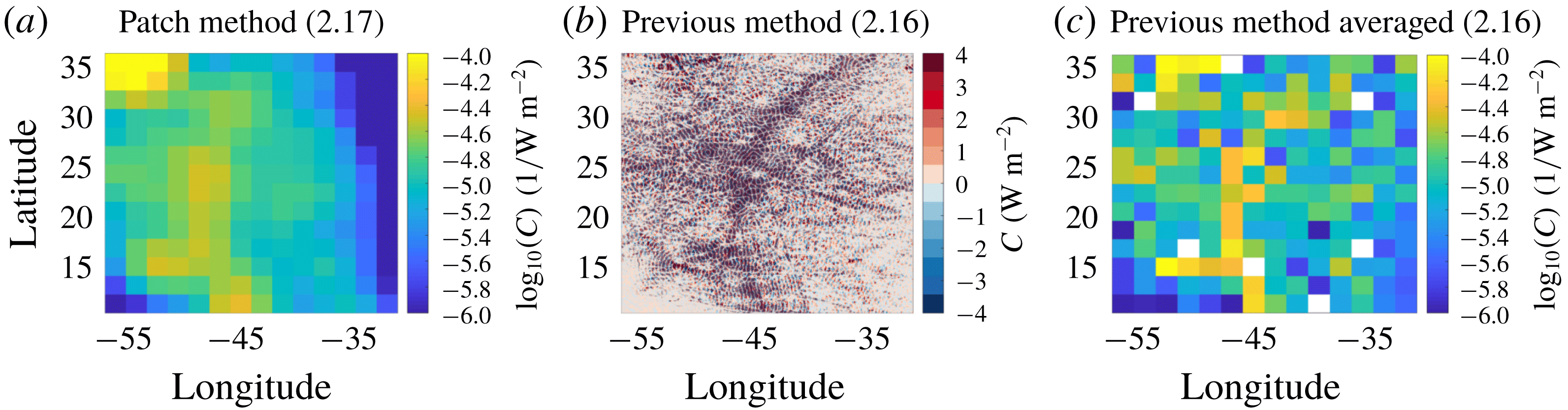
Figure 7. The conversion to the mode-2
![]() $M_{2}$
-tide in the region of untapered realistic topography (i.e. within the red lines in figure 8) calculated (a) using the new, patch-based method following (2.17), (b) using the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) following (2.16), and (c) as in (b) but averaged over the same horizontal grid as in (a), with white colours denoting negative values. The parameter settings are the same as in the previous figure for variable stratification, i.e.
$M_{2}$
-tide in the region of untapered realistic topography (i.e. within the red lines in figure 8) calculated (a) using the new, patch-based method following (2.17), (b) using the approach of Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) following (2.16), and (c) as in (b) but averaged over the same horizontal grid as in (a), with white colours denoting negative values. The parameter settings are the same as in the previous figure for variable stratification, i.e.
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
,
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{2}\approx 0.1~\text{km}^{-1}$
,
![]() $f_{\unicode[STIX]{x1D705}}=25$
,
$f_{\unicode[STIX]{x1D705}}=25$
,
![]() $f_{l}=2.75$
and
$f_{l}=2.75$
and
![]() $f_{p}=1.25$
. Further details on the set-up and parameter choices are given at the beginning of this section.
$f_{p}=1.25$
. Further details on the set-up and parameter choices are given at the beginning of this section.
The directional energy flux density for this realistic topography is presented in figure 8 for the mode-3 internal tide with
![]() $\unicode[STIX]{x1D705}_{3}=0.14~\text{km}^{-1}$
. The inset in the top right corner illustrates that, at each patch centre, the energy flux density is shown in a polar coordinate frame, in which both the direction (eastward corresponds to an angle of
$\unicode[STIX]{x1D705}_{3}=0.14~\text{km}^{-1}$
. The inset in the top right corner illustrates that, at each patch centre, the energy flux density is shown in a polar coordinate frame, in which both the direction (eastward corresponds to an angle of
![]() $\unicode[STIX]{x1D719}=0$
) and the magnitude (i.e. the distance along the radial axis) can be represented. If the energy flux density were the same in all directions, this manner of presentation would show a circle at the patch centre in question. Circles, however, are observed at no location; on the contrary, in many patches the energy flux occurs mainly in one direction. This underlines the necessity to explicitly model these variations of the energy flux direction in order to realistically implement the tidal forcing in internal gravity wave models. Based on the sensitivity study shown in figure 5, the numerical parameters are set to
$\unicode[STIX]{x1D719}=0$
) and the magnitude (i.e. the distance along the radial axis) can be represented. If the energy flux density were the same in all directions, this manner of presentation would show a circle at the patch centre in question. Circles, however, are observed at no location; on the contrary, in many patches the energy flux occurs mainly in one direction. This underlines the necessity to explicitly model these variations of the energy flux direction in order to realistically implement the tidal forcing in internal gravity wave models. Based on the sensitivity study shown in figure 5, the numerical parameters are set to
![]() $f_{p}=1.25$
,
$f_{p}=1.25$
,
![]() $f_{\unicode[STIX]{x1D705}}=25$
and
$f_{\unicode[STIX]{x1D705}}=25$
and
![]() $f_{l}=2.75$
. The Gaussian width hence amounts to 185 km and the total patch radius to 509 km. With a zonal tidal ellipse with
$f_{l}=2.75$
. The Gaussian width hence amounts to 185 km and the total patch radius to 509 km. With a zonal tidal ellipse with
![]() $\boldsymbol{U}=(4,0)~\text{cm}~\text{s}^{-1}$
, the energy flux is somewhat larger west of the MAR than east of it, especially near the southern and northern boundaries of the domain. In the northwestern corner of the domain, sharp topography gradients lead to very high conversion rates, but this is at least to some degree an artefact of the tapering.
$\boldsymbol{U}=(4,0)~\text{cm}~\text{s}^{-1}$
, the energy flux is somewhat larger west of the MAR than east of it, especially near the southern and northern boundaries of the domain. In the northwestern corner of the domain, sharp topography gradients lead to very high conversion rates, but this is at least to some degree an artefact of the tapering.
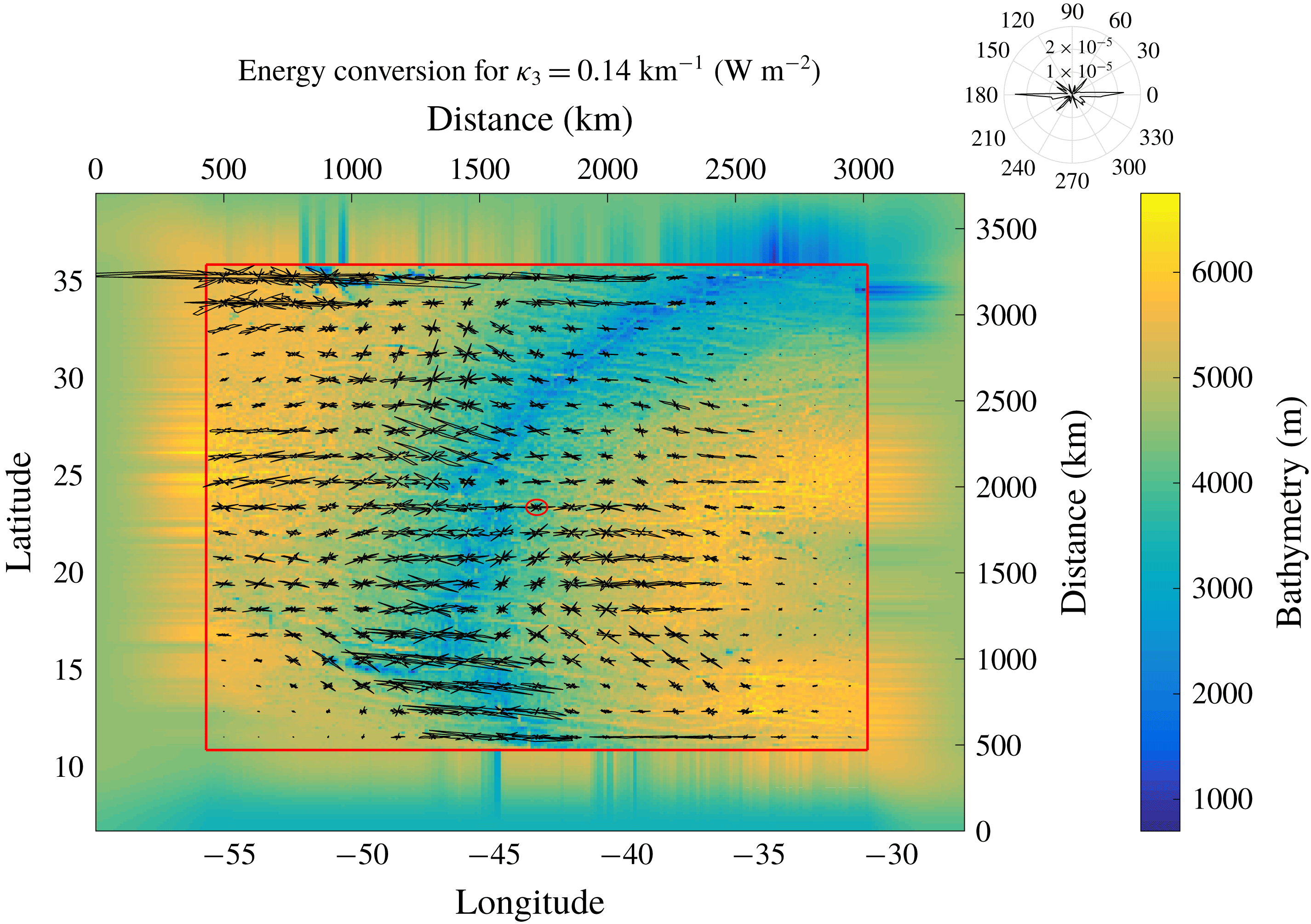
Figure 8. Energy conversion for variable stratification and realistic topography. At each patch centre, the energy flux density
![]() $D$
(see (3.8)), scaled by the maximum energy flux observed in the patch circled in red, is shown as a function of angle as illustrated in the polar coordinate plot inset in the top right corner. The magnitude of
$D$
(see (3.8)), scaled by the maximum energy flux observed in the patch circled in red, is shown as a function of angle as illustrated in the polar coordinate plot inset in the top right corner. The magnitude of
![]() $D$
is represented by the distance from the coordinate system’s centre along the radial axis, which produces a circle for patches in which the energy flux is the same in all directions. The underlying topography is represented in colour, with red lines delimiting the untapered topography at the centre of the domain (the resolution of the topography input used in the calculations is 15 times higher in each dimension than in this figure). Note that the 900 km of constant topography, which were added on each side of the tapered topography to ensure a smooth decrease of the conversion rates at the boundaries, was cropped here for clarity. The stratification is assumed to be horizontally constant, taking the same vertical profile from
$D$
is represented by the distance from the coordinate system’s centre along the radial axis, which produces a circle for patches in which the energy flux is the same in all directions. The underlying topography is represented in colour, with red lines delimiting the untapered topography at the centre of the domain (the resolution of the topography input used in the calculations is 15 times higher in each dimension than in this figure). Note that the 900 km of constant topography, which were added on each side of the tapered topography to ensure a smooth decrease of the conversion rates at the boundaries, was cropped here for clarity. The stratification is assumed to be horizontally constant, taking the same vertical profile from
![]() $25^{\circ }\,\text{N}$
,
$25^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
as used before, and we use
$43^{\circ }\,\text{W}$
as used before, and we use
![]() $\boldsymbol{U}=(4,0)~\text{cm}~\text{s}^{-1}$
,
$\boldsymbol{U}=(4,0)~\text{cm}~\text{s}^{-1}$
,
![]() $f=6\times 10^{-5}~\text{s}^{-1}$
and
$f=6\times 10^{-5}~\text{s}^{-1}$
and
![]() $n_{\unicode[STIX]{x1D719}}=551$
. The energy conversion is shown for the mode-3 internal wave with
$n_{\unicode[STIX]{x1D719}}=551$
. The energy conversion is shown for the mode-3 internal wave with
![]() $\unicode[STIX]{x1D705}_{3}=0.14~\text{km}^{-1}$
, setting
$\unicode[STIX]{x1D705}_{3}=0.14~\text{km}^{-1}$
, setting
![]() $f_{\unicode[STIX]{x1D705}}=25$
,
$f_{\unicode[STIX]{x1D705}}=25$
,
![]() $f_{l}=2.75$
and
$f_{l}=2.75$
and
![]() $f_{p}=1.25$
(
$f_{p}=1.25$
(
![]() $n_{xc}=n_{yc}=39$
or
$n_{xc}=n_{yc}=39$
or
![]() $O_{p}=0.5$
). The red circle at
$O_{p}=0.5$
). The red circle at
![]() $23^{\circ }\,\text{N}$
,
$23^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
identifies the patch whose energy flux is shown in the polar coordinate plot and which is analysed in more detail in figure 9.
$43^{\circ }\,\text{W}$
identifies the patch whose energy flux is shown in the polar coordinate plot and which is analysed in more detail in figure 9.
Figure 9 illustrates how these results are influenced by the direction of the barotropic tidal currents. At a given location over the MAR (
![]() $26^{\circ }\,\text{N}$
,
$26^{\circ }\,\text{N}$
,
![]() $45^{\circ }\,\text{W}$
; the corresponding patch centre is denoted by a red circle in figure 8), the direction of the energy flux in the first four baroclinic wave modes is shown for eastward, northward and northeastward orientations of the tidal ellipse. For modes 1, 3 and 4, the sensitivity study to the parameter
$45^{\circ }\,\text{W}$
; the corresponding patch centre is denoted by a red circle in figure 8), the direction of the energy flux in the first four baroclinic wave modes is shown for eastward, northward and northeastward orientations of the tidal ellipse. For modes 1, 3 and 4, the sensitivity study to the parameter
![]() $f_{\unicode[STIX]{x1D705}}$
was repeated, showing that, for mode 1,
$f_{\unicode[STIX]{x1D705}}$
was repeated, showing that, for mode 1,
![]() $f_{\unicode[STIX]{x1D705}}$
should be reduced to
$f_{\unicode[STIX]{x1D705}}$
should be reduced to
![]() $f_{\unicode[STIX]{x1D705}}=13$
, while for modes 3 and 4, the previous setting of
$f_{\unicode[STIX]{x1D705}}=13$
, while for modes 3 and 4, the previous setting of
![]() $f_{\unicode[STIX]{x1D705}}=25$
is suitable, too. For mode 5 (not shown) the corresponding threshold value was also determined as
$f_{\unicode[STIX]{x1D705}}=25$
is suitable, too. For mode 5 (not shown) the corresponding threshold value was also determined as
![]() $f_{\unicode[STIX]{x1D705}}=25$
, which suggests that this numerical parameter indeed converges towards a common value for all but the first mode.
$f_{\unicode[STIX]{x1D705}}=25$
, which suggests that this numerical parameter indeed converges towards a common value for all but the first mode.
The orientation of the tidal ellipse influences both the magnitude and the direction of the energy conversion density. The lowest conversion rates are observed for zonal and the highest for meridional orientation, respectively. This can be attributed to the orientation of the bottom topography in this patch: at locations where the topography is predominantly zonal (e.g. in the northwestern corner of the domain), the energy conversion is much higher for meridional than for zonal flow and peaks in the direction of the tidal flow (not shown). In the patch analysed in figure 9, there are strong signals also in directions other than that of the tidal flow, highlighting the complexity of the topography in that area. In any event, there is no energy flux in the direction orthogonal to that of the tidal flow.
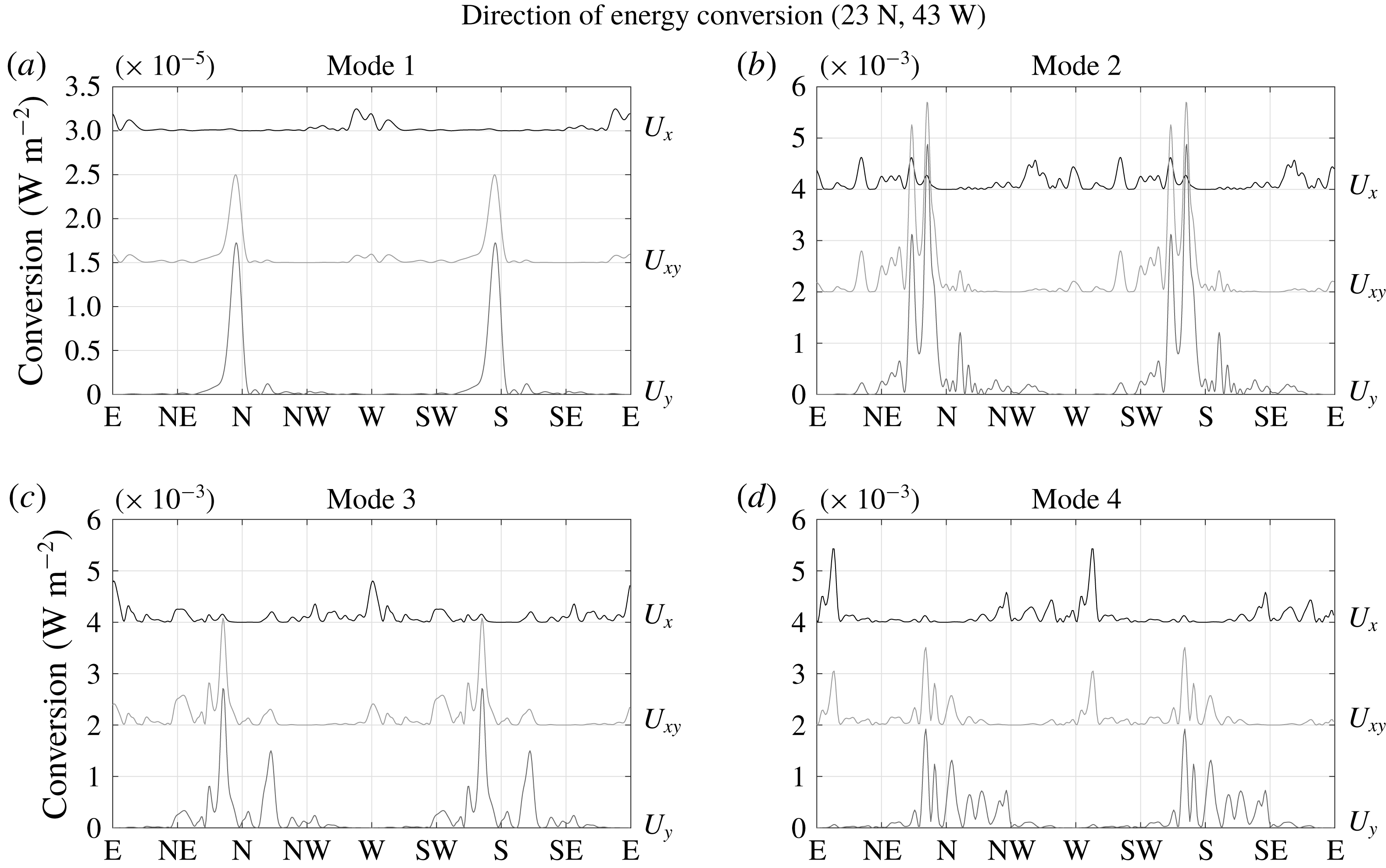
Figure 9. Effect of tidal velocity on energy conversion. The energy conversion density
![]() $D$
(see (3.8)) at a patch centred on the MAR (
$D$
(see (3.8)) at a patch centred on the MAR (
![]() $23^{\circ }\,\text{N}$
,
$23^{\circ }\,\text{N}$
,
![]() $43^{\circ }\,\text{W}$
, denoted by a red circle in figure 8) is shown as a function of direction for the first four modes. For each mode, the tidal velocity is varied between
$43^{\circ }\,\text{W}$
, denoted by a red circle in figure 8) is shown as a function of direction for the first four modes. For each mode, the tidal velocity is varied between
![]() $U_{x}=(u,0)$
,
$U_{x}=(u,0)$
,
![]() $U_{y}=(0,u)$
and
$U_{y}=(0,u)$
and
![]() $U_{xy}=(u/\sqrt{2},u/\sqrt{2})$
with
$U_{xy}=(u/\sqrt{2},u/\sqrt{2})$
with
![]() $u=4~\text{cm}~\text{s}^{-1}$
. To differentiate between these three velocity scenarios, a vertical offset of
$u=4~\text{cm}~\text{s}^{-1}$
. To differentiate between these three velocity scenarios, a vertical offset of
![]() $1.5\times 10^{-5}~\text{W}~\text{m}^{-2}$
(mode 1) or
$1.5\times 10^{-5}~\text{W}~\text{m}^{-2}$
(mode 1) or
![]() $2\times 10^{-3}~\text{W}~\text{m}^{-2}$
(modes 2–4) is introduced. Note also the different
$2\times 10^{-3}~\text{W}~\text{m}^{-2}$
(modes 2–4) is introduced. Note also the different
![]() $y$
-axis scaling for mode 1. The other parameter settings are as in the previous figure except for the Gaussian width, which was set to
$y$
-axis scaling for mode 1. The other parameter settings are as in the previous figure except for the Gaussian width, which was set to
![]() $f_{\unicode[STIX]{x1D705}}=(13,25,25,25)$
for modes 1 to 4, which are characterised by wavenumbers
$f_{\unicode[STIX]{x1D705}}=(13,25,25,25)$
for modes 1 to 4, which are characterised by wavenumbers
![]() $\unicode[STIX]{x1D705}=(0.046,0.095,0.135,0.178)~\text{km}^{-1}$
.
$\unicode[STIX]{x1D705}=(0.046,0.095,0.135,0.178)~\text{km}^{-1}$
.
6 Summary and conclusions
A new method to calculate both the magnitude and direction of tidally forced internal gravity waves is presented. The main difference from previously applied schemes is that the energy conversion is derived from the far-field energy flux instead of an integral over the sources. This offers the noteworthy advantage that the conversion rate is positive definite, in contrast to integrating over the energy sources, which can produce negative values (e.g. Zilberman et al. Reference Zilberman, Becker, Merrifield and Carter2009; Falahat et al. Reference Falahat, Nycander, Roquet and Zarroug2014b ). Negative conversion rates can be attributed to the influence of remote internal tides (e.g. Kurapov et al. Reference Kurapov, Egbert, Allen, Miller, Erofeeva and Kosro2003; Kelly & Nash Reference Kelly and Nash2010) and are thus not unrealistic, but nevertheless present a problem when using the conversion rate estimates as external source in internal wave models used, for example, to parametrise mixing – Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b ), for example, had to average their results over some area to obtain positive values (see also figure 7). The underlying assumptions of this semi-analytical method, based on the vertical-mode treatment of LSY02, involve, for example, that the source regions should be bounded (to allow the application of the radiation condition) and that the tidal velocity be constant, which do not hold for global calculations using realistic bathymetry. In consequence, the method is implemented by considering individual, overlapping circular patches, in which the topography is multiplied by a Gaussian centred at the circle’s centre in order to smoothly decrease the influence of the remote topography. The energy flux from each patch is then calculated by computing the Fourier spectrum of the topography within the patch.
This approach introduces some numerical parameters: the size of the patches, the size of the Gaussian and the extent to which neighbouring patches overlap. Convergence tests based on idealised and realistic topography permit the identification of suitable parameter settings, showing that the patch radius should be at least 2.5 times the Gaussian standard deviation
![]() $r_{G}$
, which itself should be slightly larger than the patch centre spacing
$r_{G}$
, which itself should be slightly larger than the patch centre spacing
![]() $\text{d}x_{c}$
. For mode numbers higher than one, the parameter
$\text{d}x_{c}$
. For mode numbers higher than one, the parameter
![]() $f_{\unicode[STIX]{x1D705}}$
(the product of
$f_{\unicode[STIX]{x1D705}}$
(the product of
![]() $r_{G}$
and the wavenumber
$r_{G}$
and the wavenumber
![]() $\unicode[STIX]{x1D705}$
) should be around 25.
$\unicode[STIX]{x1D705}$
) should be around 25.
The choice of the Gaussian width
![]() $r_{G}$
relative to the wavenumber is the most difficult one. The effect of multiplying the topography with a Gaussian is that coherent interaction such as wave interference is neglected on length scales larger than
$r_{G}$
relative to the wavenumber is the most difficult one. The effect of multiplying the topography with a Gaussian is that coherent interaction such as wave interference is neglected on length scales larger than
![]() $r_{G}$
. In the ocean, factors such as nonlinear effects or inhomogeneities caused by eddies impede coherent interaction over large distances (e.g. Olbers Reference Olbers1983), and, ideally, the size of the Gaussian
$r_{G}$
. In the ocean, factors such as nonlinear effects or inhomogeneities caused by eddies impede coherent interaction over large distances (e.g. Olbers Reference Olbers1983), and, ideally, the size of the Gaussian
![]() $r_{G}$
should reflect this correlation length scale. The natural correlation scale, which possibly varies in both space and time, is, however, too poorly understood to be of practical use for the numerical parameter choices. Instead, we performed test simulations with increasing
$r_{G}$
should reflect this correlation length scale. The natural correlation scale, which possibly varies in both space and time, is, however, too poorly understood to be of practical use for the numerical parameter choices. Instead, we performed test simulations with increasing
![]() $r_{G}$
until the total energy conversion saturated. There is however a trade-off between numerical convergence and the applicability of the assumption that wavenumber and tidal velocity can be considered constant within each patch. For realistic applications, a smaller value than the one chosen in this study, which focuses on the evaluation of the new method, might be more appropriate; it is therefore reassuring to see that already half of our standard setting of
$r_{G}$
until the total energy conversion saturated. There is however a trade-off between numerical convergence and the applicability of the assumption that wavenumber and tidal velocity can be considered constant within each patch. For realistic applications, a smaller value than the one chosen in this study, which focuses on the evaluation of the new method, might be more appropriate; it is therefore reassuring to see that already half of our standard setting of
![]() $f_{\unicode[STIX]{x1D705}}=25$
produces acceptable conversion rates. The sensitivity tests performed in this study serve as a rough guideline for the choice of this numerical parameter, but it seems that such tests would have to be repeated for different regions of the global ocean, depending on the details of the topography and the stratification.
$f_{\unicode[STIX]{x1D705}}=25$
produces acceptable conversion rates. The sensitivity tests performed in this study serve as a rough guideline for the choice of this numerical parameter, but it seems that such tests would have to be repeated for different regions of the global ocean, depending on the details of the topography and the stratification.
The effects of natural decorrelation could also be accounted for by including a linear damping in (2.10) instead of considering circular patches of limited size. This might be physically more appealing, but implies that the total flux decreases exponentially away from the sources, so that the far-field expression cannot be used and integration over the energy sources remains as the only possibility to calculate the conversion. In consequence, linear damping is no real alternative for the present purpose.
Another source of uncertainty stemming from the application of linear theory is the inherent assumption of subcritical topography. In the global ocean, however, some regions are characterised by supercritical slopes and the results obtained from linear theory are hence biased (see e.g. Holloway & Merrifield (Reference Holloway and Merrifield1999), Nycander (Reference Nycander2006), Pétrélis, Llewellyn Smith & Young (Reference Pétrélis, Llewellyn Smith and Young2006) and Garrett & Kunze (Reference Garrett and Kunze2007), and references therein, for descriptions of how the criticality of topographic slopes affects internal wave generation). The conversion rate in the subcritical domain is known to scale quadratically with the steepness parameter
where
![]() $\unicode[STIX]{x1D6FC}$
is the slope of the tidal beam and
$\unicode[STIX]{x1D6FC}$
is the slope of the tidal beam and
![]() $\unicode[STIX]{x1D716}<1$
characterises the subcritical regime (e.g. Khatiwala Reference Khatiwala2003). The dependence in the supercritical regime is not known, but numerical and analytical studies suggest that the conversion rate saturates for
$\unicode[STIX]{x1D716}<1$
characterises the subcritical regime (e.g. Khatiwala Reference Khatiwala2003). The dependence in the supercritical regime is not known, but numerical and analytical studies suggest that the conversion rate saturates for
![]() $\unicode[STIX]{x1D716}>1$
(Khatiwala Reference Khatiwala2003; Nycander Reference Nycander2006; Balmforth & Peacock Reference Balmforth and Peacock2009), so that the application of linear theory to supercritical topography possibly overestimates the conversion rates. In consequence, Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) proposed to correct for supercriticality by dividing the conversion rates by
$\unicode[STIX]{x1D716}>1$
(Khatiwala Reference Khatiwala2003; Nycander Reference Nycander2006; Balmforth & Peacock Reference Balmforth and Peacock2009), so that the application of linear theory to supercritical topography possibly overestimates the conversion rates. In consequence, Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) proposed to correct for supercriticality by dividing the conversion rates by
![]() $\unicode[STIX]{x1D716}^{2}$
wherever
$\unicode[STIX]{x1D716}^{2}$
wherever
![]() $\unicode[STIX]{x1D716}$
was larger than unity. Following this approach, we calculate the steepness parameter on the fine topographic grid (1/120
$\unicode[STIX]{x1D716}$
was larger than unity. Following this approach, we calculate the steepness parameter on the fine topographic grid (1/120
![]() $^{\circ }$
resolution), approximating the gradients by forward differences. If, in a
$^{\circ }$
resolution), approximating the gradients by forward differences. If, in a
![]() $1.75^{\circ }$
circle around each patch centre point (corresponding approximately to the Gaussian width for the scenario depicted in figure 8), at least 1 % (2 %) of the steepness parameter estimates exceed a value of unity, the correction proposed by Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) is applied. The correction factor is calculated as the squared average of all steepness parameter estimates in the
$1.75^{\circ }$
circle around each patch centre point (corresponding approximately to the Gaussian width for the scenario depicted in figure 8), at least 1 % (2 %) of the steepness parameter estimates exceed a value of unity, the correction proposed by Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) is applied. The correction factor is calculated as the squared average of all steepness parameter estimates in the
![]() $1.75^{\circ }$
circle in question that exceed unity. This correction is only implemented for untapered topography and affects 77 (17) out of the 319 patches depicted in figure 8. The total conversion rate in the entire domain is decreased by around 6 % (1 %). Since the majority of topography taken into account for the computation of the energy conversion shown in figure 8 is subcritical – less than 1 % of all the steepness parameter values are larger than unity – the uncertainty due to the application of linear theory to supercritical slopes is in this case, at least based on the simple approach by Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013), very small. In other areas of the global ocean or in a global integral, however, this uncertainty might be more prominent (both Nycander (Reference Nycander2005) and Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) find that approximately half of the energy conversion into internal tides stems from supercritical slopes).
$1.75^{\circ }$
circle in question that exceed unity. This correction is only implemented for untapered topography and affects 77 (17) out of the 319 patches depicted in figure 8. The total conversion rate in the entire domain is decreased by around 6 % (1 %). Since the majority of topography taken into account for the computation of the energy conversion shown in figure 8 is subcritical – less than 1 % of all the steepness parameter values are larger than unity – the uncertainty due to the application of linear theory to supercritical slopes is in this case, at least based on the simple approach by Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013), very small. In other areas of the global ocean or in a global integral, however, this uncertainty might be more prominent (both Nycander (Reference Nycander2005) and Falahat et al. (Reference Falahat, Nycander, Roquet and Zarroug2014b
) find that approximately half of the energy conversion into internal tides stems from supercritical slopes).
The applicability of linear theory also requires that the vertical topographic scales be small compared to the depth of the water column and that the tidal excursion
![]() $U_{0}/(\unicode[STIX]{x1D714}L)$
be small. Owing to the interplay of many different topographic scales (not all of which are necessarily resolved by the topography product used) on the real ocean floor, it is not straightforward to determine a single representative length scale. Since we use a fixed tidal velocity amplitude of
$U_{0}/(\unicode[STIX]{x1D714}L)$
be small. Owing to the interplay of many different topographic scales (not all of which are necessarily resolved by the topography product used) on the real ocean floor, it is not straightforward to determine a single representative length scale. Since we use a fixed tidal velocity amplitude of
![]() $0.04~\text{m}~\text{s}^{-1}$
and a tidal frequency of
$0.04~\text{m}~\text{s}^{-1}$
and a tidal frequency of
![]() $\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
, the smallness of the tidal excursion parameter requires that topographic length scales be larger than 285 m. Because topographic features of length scale
$\unicode[STIX]{x1D714}=1.4\times 10^{-4}~\text{s}^{-1}$
, the smallness of the tidal excursion parameter requires that topographic length scales be larger than 285 m. Because topographic features of length scale
![]() $\unicode[STIX]{x1D6EC}$
most efficiently force internal tides of comparable wavelength (LSY02), this criterion translates into requiring that wavenumbers be smaller than
$\unicode[STIX]{x1D6EC}$
most efficiently force internal tides of comparable wavelength (LSY02), this criterion translates into requiring that wavenumbers be smaller than
![]() $22~\text{km}^{-1}$
, which is fulfilled in the scenarios discussed here.
$22~\text{km}^{-1}$
, which is fulfilled in the scenarios discussed here.
Finally, it has to be noted that the resolution of the topography grid (SRTM30_PLUS; Becker et al. Reference Becker, Sandwell, Smith, Braud, Binder, Depner, Fabre, Factor, Ingalls, Kim, Ladner, Marks, Nelson, Pharaoh, Trimmer, Von Rosenberg, Wallace and Weatherall2009) is artificially high in many parts of the deep ocean, where only satellite data with an average resolution of 10 km are available and have been interpolated onto the much finer SRTM30_PLUS grid. In consequence, small-scale roughness, typically in the form of abyssal hills, is not resolved and the associated energy conversion is not accounted for (see e.g. Carter et al. (Reference Carter, Merrifield, Becker, Katsumata, Gregg, Luther, Levine, Boyd and Firing2008) and Zilberman et al. (Reference Zilberman, Becker, Merrifield and Carter2009) for how topographic smoothing decreases conversion rates). Blending the SRTM30_PLUS dataset with the abyssal hill spectral model proposed by Goff & Jordan (Reference Goff and Jordan1988), Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) estimated that, globally, the typically unresolved seafloor roughness leads to an additional 0.1 TW of energy conversion into the internal tide field. This amounts to roughly 10 % of the energy conversion due to the topography resolved in standard products such as SRTM30_PLUS; calculations based on the latter alone hence capture the bulk of the global energy conversion but underestimate it slightly. As Melet et al. (Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013) found this fraction to vary regionally, global calculations of internal tide generation as well as subsequent breaking and mixing might rely on including a spectral model like that of Goff & Jordan (Reference Goff and Jordan1988) for the small-scale roughness (e.g. Goff & Arbic Reference Goff and Arbic2010; Li & Mei Reference Li and Mei2014; Guo & Holmes-Cerfon Reference Guo and Holmes-Cerfon2016), noting, however, that such models involve further uncertainties themselves.
The proposed method with the standard settings identified in the scenarios tested here yields results in very good agreement with analytical solutions for idealised test cases. This motivates the application to realistic ocean bathymetry (recognising, however, the caveats discussed above). The results for the North Atlantic (see figure 8) underline that the magnitude of the energy flux varies substantially with direction. Klymak, Legg & Pinkel (Reference Klymak, Legg and Pinkel2010) observe that modes with eigenspeeds higher than that of the tidal velocity (modes 1–66 in the scenario in figure 8) radiate away from their generation site and contribute to the remote mixing in the ocean’s interior, whose vertical distribution significantly impacts the ocean’s state and dynamics (Samelson Reference Samelson1998; Zhang, Schmitt & Huang Reference Zhang, Schmitt and Huang1999; Melet et al. Reference Melet, Nikurashin, Muller, Falahat, Nycander, Timko, Arbic and Goff2013). It is therefore crucial for the consistency and reliability of ocean general circulation models to take the direction of the tidally generated internal gravity waves into account in internal wave-based mixing parametrisations. Naturally, the next step will be the application of the method presented here to global ocean bathymetry with realistic and horizontally variable tidal velocities and stratification to produce a database that can serve as an input for internal gravity wave models such as IWAM (Müller & Natarov Reference Müller and Natarov2003) or IDEMIX (Olbers & Eden Reference Olbers and Eden2013).
Acknowledgements
This work was begun while J.N. was a visiting scientist at the Geophysical Fluid Dynamics Laboratory (GFDL) and Princeton University. He is grateful for useful discussions with B. Hallberg, S. Legg and B. Mater. This paper is a contribution to the project S2 of the Collaborative Research Centre TRR 181 ‘Energy Transfer in Atmosphere and Ocean’ funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 274762653. F.P. also acknowledges support by the Cluster of Excellence 796 cliSAP (EXC177), also funded by the German Research Foundation. The authors gratefully acknowledge the constructive criticism offered by three anonymous referees.
Appendix A
This section illustrates the relation between the physical, time-dependent form of the forced wave equation and its formulation in complex notation, providing an interpretation of (2.13). The wave equation for a field variable
![]() $\unicode[STIX]{x1D703}(x,y,t)$
including a source
$\unicode[STIX]{x1D703}(x,y,t)$
including a source
![]() $\unicode[STIX]{x1D713}$
is given by
$\unicode[STIX]{x1D713}$
is given by
An energy conservation equation can be derived via multiplication by
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}t$
:
$\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}t$
:
From (A 2), the energy flux
![]() $\boldsymbol{F}$
and the total energy conversion
$\boldsymbol{F}$
and the total energy conversion
![]() $C$
can be identified:
$C$
can be identified:
In complex notation, assuming a fixed frequency, the field variables are written as
where
![]() $\unicode[STIX]{x1D6E9}$
and
$\unicode[STIX]{x1D6E9}$
and
![]() $\unicode[STIX]{x1D6F9}$
are complex amplitudes. Using these expressions in (A 3) and (A 4), the energy flux and conversion become
$\unicode[STIX]{x1D6F9}$
are complex amplitudes. Using these expressions in (A 3) and (A 4), the energy flux and conversion become
exploiting the relation
![]() $\langle ab\rangle =0.5\,\text{Re}\{AB^{\ast }\}$
for
$\langle ab\rangle =0.5\,\text{Re}\{AB^{\ast }\}$
for
![]() $a=\text{Re}\{A\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\}$
and
$a=\text{Re}\{A\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\}$
and
![]() $b=\text{Re}\{B\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\}$
, where angle brackets denote the average over a period and the star the complex conjugate.
$b=\text{Re}\{B\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}\}$
, where angle brackets denote the average over a period and the star the complex conjugate.
Inserting the complex expressions for the field variables, (A 5) and (A 6), into the forced wave equation, (A 1), yields
with
![]() $\unicode[STIX]{x1D705}^{2}=\unicode[STIX]{x1D714}^{2}/c^{2}$
. This shows that (A 9) is associated with an energy flux of the form (A 7) and an energy generation of the form (A 8). These energy expressions also contain a multiplicative coefficient that cannot be determined from the considerations above, and depends on the specific physical application. Equation (A 1) arises in many different physical situations.
$\unicode[STIX]{x1D705}^{2}=\unicode[STIX]{x1D714}^{2}/c^{2}$
. This shows that (A 9) is associated with an energy flux of the form (A 7) and an energy generation of the form (A 8). These energy expressions also contain a multiplicative coefficient that cannot be determined from the considerations above, and depends on the specific physical application. Equation (A 1) arises in many different physical situations.
Appendix B
Using the asymptotic expression for the Hankel transform in (2.19) gives
When the origin of the coordinate system is at the centre of the source distribution,
![]() $|\boldsymbol{r}^{\prime }|\ll |\boldsymbol{r}|$
and
$|\boldsymbol{r}^{\prime }|\ll |\boldsymbol{r}|$
and
Following (B 2), the factor
![]() $(\unicode[STIX]{x1D705}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1/2}$
is approximated as
$(\unicode[STIX]{x1D705}|\boldsymbol{r}-\boldsymbol{r}^{\prime }|)^{-1/2}$
is approximated as
![]() $(\unicode[STIX]{x1D705}r)^{-1/2}$
, while in the phase of the exponential, the terms
$(\unicode[STIX]{x1D705}r)^{-1/2}$
, while in the phase of the exponential, the terms
![]() $O(r^{\prime 2}/r)$
are neglected. For accuracy to order unity, this requires
$O(r^{\prime 2}/r)$
are neglected. For accuracy to order unity, this requires
![]() $\unicode[STIX]{x1D705}r^{\prime 2}/r\ll 1$
, i.e.
$\unicode[STIX]{x1D705}r^{\prime 2}/r\ll 1$
, i.e.
![]() $r/r^{\prime }\gg \unicode[STIX]{x1D705}r^{\prime }$
, so that for an increasing number of wavelengths across the source region, the energy flux must be evaluated further and further away from it for the far-field expression to be valid.
$r/r^{\prime }\gg \unicode[STIX]{x1D705}r^{\prime }$
, so that for an increasing number of wavelengths across the source region, the energy flux must be evaluated further and further away from it for the far-field expression to be valid.
Far away from the sources, (B 1) is hence approximated as
The integral in (B 3) can be identified as the Fourier transform of the source field
evaluated at wavenumber
![]() $\unicode[STIX]{x1D705}\hat{\boldsymbol{r}}$
. In consequence, using the far-field approximation of the Hankel transform allows us to express the pressure field in terms of the Fourier transform of the source field:
$\unicode[STIX]{x1D705}\hat{\boldsymbol{r}}$
. In consequence, using the far-field approximation of the Hankel transform allows us to express the pressure field in terms of the Fourier transform of the source field:











