Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vaz, R. H.
Boshier, F. A. T.
and
Mestel, A. J.
2018.
‘Unforced’ Navier–Stokes solutions derived from convection in a curved channel.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
676.
Alonso, Arantxa
Mercader, Isabel
and
Batiste, Oriol
2018.
Time-dependent patterns in quasivertical cylindrical binary convection.
Physical Review E,
Vol. 97,
Issue. 2,
Zier, Oliver
Zimmermann, Walter
and
Pesch, Werner
2019.
On low-Prandtl-number convection in an inclined layer of liquid mercury.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
76.
Falsaperla, Paolo
Giacobbe, Andrea
and
Mulone, Giuseppe
2019.
Inclined convection in a porous Brinkman layer: linear instability and nonlinear stability.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2223,
p.
20180614.
Mercader, Isabel
Batiste, Oriol
Alonso, Arantxa
and
Knobloch, Edgar
2019.
Effect of small inclination on binary convection in elongated rectangular cells.
Physical Review E,
Vol. 99,
Issue. 2,
Perez-Espejel, Diana
and
Avila, Ruben
2019.
Linear stability analysis of the natural convection in inclined rotating parallel plates.
Physics Letters A,
Vol. 383,
Issue. 9,
p.
859.
Reetz, Florian
Subramanian, Priya
and
Schneider, Tobias M.
2020.
Invariant states in inclined layer convection. Part 2. Bifurcations and connections between branches of invariant states.
Journal of Fluid Mechanics,
Vol. 898,
Issue. ,
Castellini, Stefano
Carpineti, Marina
Croccolo, Fabrizio
and
Vailati, Alberto
2020.
Inclined convection in a layer of liquid water with poorly conducting boundaries.
Physical Review Research,
Vol. 2,
Issue. 3,
Avila, Ruben
2020.
Linear instability analysis of the onset of thermal convection in an Ekman-Couette-flow.
International Journal of Heat and Mass Transfer,
Vol. 154,
Issue. ,
p.
119635.
Tuckerman, Laurette S.
2020.
Ricocheting inclined layer convection states.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Reetz, Florian
and
Schneider, Tobias M.
2020.
Invariant states in inclined layer convection. Part 1. Temporal transitions along dynamical connections between invariant states.
Journal of Fluid Mechanics,
Vol. 898,
Issue. ,
Madruga, Santiago
and
Curbelo, Jezabel
2021.
Effect of the inclination angle on the transient melting dynamics and heat transfer of a phase change material.
Physics of Fluids,
Vol. 33,
Issue. 5,
Zhang, Lu
Ding, Guang-Yu
and
Xia, Ke-Qing
2021.
On the effective horizontal buoyancy in turbulent thermal convection generated by cell tilting.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Ghadami, Amin
and
Epureanu, Bogdan I.
2022.
Deep learning for centre manifold reduction and stability analysis in nonlinear systems.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2229,
Alonso, Arantxa
Mercader, Isabel
Batiste, Oriol
and
Vega, José M.
2022.
Analyzing Slightly Inclined Cylindrical Binary Fluid Convection via Higher Order Dynamic Mode Decomposition.
SIAM Journal on Applied Dynamical Systems,
Vol. 21,
Issue. 3,
p.
2148.
Waris, Wasim
and
Lappa, Marcello
2022.
Patterning Behavior of Hybrid Buoyancy-Marangoni Convection in Inclined Layers Heated from Below.
Fluids,
Vol. 8,
Issue. 1,
p.
12.
Singh, Jitender
2023.
Longitudinal and transverse modes of temperature-modulated inclined layer convection.
Physical Review E,
Vol. 107,
Issue. 4,
Hernández, R.H.
and
Vial, M.
2023.
Heat transfer measurements in an inclined low aspect ratio Rayleigh–Bénard convection cell under feedback control.
International Journal of Thermal Sciences,
Vol. 194,
Issue. ,
p.
108518.
Zheng, Zheng
Tuckerman, Laurette S.
and
Schneider, Tobias M.
2024.
Natural convection in a vertical channel. Part 2. Oblique solutions and global bifurcations in a spanwise-extended domain.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Zhou, Na
Zheng, Lai-Yun
Zhang, Chao-Nan
and
Zhao, Bing-Xin
2024.
Effects of inclination angle and fluid parameters on binary fluid convection in a tilted rectangular cavity.
International Communications in Heat and Mass Transfer,
Vol. 156,
Issue. ,
p.
107699.
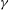 ${\it\gamma}$ and the Rayleigh number
${\it\gamma}$ and the Rayleigh number 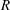 $R$ . The present numerical investigation of the inclined layer convection system is based on the standard Oberbeck–Boussinesq equations. The patterns are shown to originate from a complicated competition of buoyancy driven and shear-flow driven pattern forming mechanisms. The former are expressed as longitudinal convection rolls with their axes oriented parallel to the incline, the latter as perpendicular transverse rolls. Along with conventional methods to study roll patterns and their stability, we employ direct numerical simulations in large spatial domains, comparable with the experimental ones. As a result, we determine the phase diagram of the characteristic complex 3-D convection patterns above onset of convection in the
$R$ . The present numerical investigation of the inclined layer convection system is based on the standard Oberbeck–Boussinesq equations. The patterns are shown to originate from a complicated competition of buoyancy driven and shear-flow driven pattern forming mechanisms. The former are expressed as longitudinal convection rolls with their axes oriented parallel to the incline, the latter as perpendicular transverse rolls. Along with conventional methods to study roll patterns and their stability, we employ direct numerical simulations in large spatial domains, comparable with the experimental ones. As a result, we determine the phase diagram of the characteristic complex 3-D convection patterns above onset of convection in the 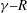 ${\it\gamma}{-}R$ plane, and find that it compares very well with the experiments. In particular we demonstrate that interactions of specific Fourier modes, characterized by a resonant interaction of their wavevectors in the layer plane, are key to understanding the pattern morphologies.
${\it\gamma}{-}R$ plane, and find that it compares very well with the experiments. In particular we demonstrate that interactions of specific Fourier modes, characterized by a resonant interaction of their wavevectors in the layer plane, are key to understanding the pattern morphologies.

