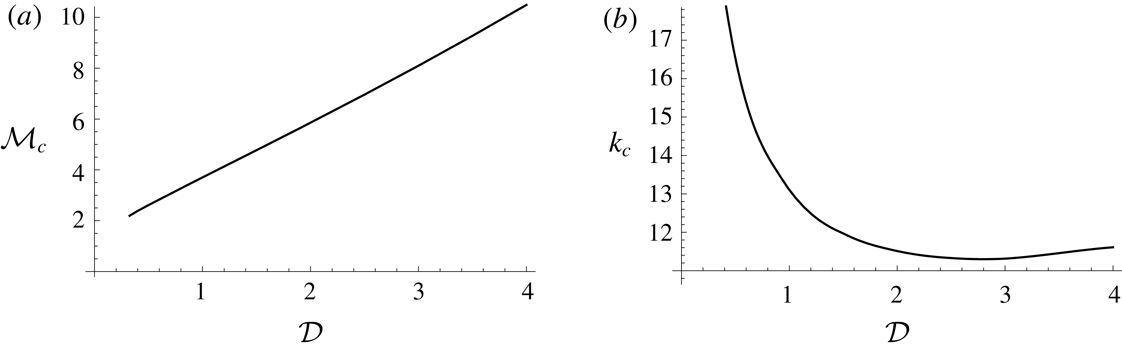1 Introduction
The phenomenon of viscous fingering usually occurs when a less viscous fluid penetrates a more viscous fluid in a small gap between two plates and the patterns that emerge have been investigated extensively since the seminal work of Saffman & Taylor (Reference Saffman and Taylor1958). Such instabilities occur in various settings in nature and in industrial applications (Taylor Reference Taylor1963; Mullins & Sekerka Reference Mullins and Sekerka1964; Orr & Taber Reference Orr and Taber1984; Reinelt Reference Reinelt1995; Cinar, Riaz & Tchelepi Reference Cinar, Riaz and Tchelepi2009). Complex fingering patterns can emerge (Saffman & Taylor Reference Saffman and Taylor1958; Paterson Reference Paterson1981; Homsy Reference Homsy1987; Chen Reference Chen1989; Thome et al. Reference Thome, Rabaud, Hakim and Couder1989; Manickam & Homsy Reference Manickam and Homsy1993) and depend on the injection rate (Li et al. Reference Li, Lowengrub, Fontana and Palffy-Muhoray2009; Dias & Miranda Reference Dias and Miranda2010; Dias et al. Reference Dias, Alvarez-Lacalle, Carvalho and Miranda2012), gradients in the flow passage (Nase, Derks & Lindner Reference Nase, Derks and Lindner2011; Al-Housseiny, Tsai & Stone Reference Al-Housseiny, Tsai and Stone2012; Juel Reference Juel2012; Dias & Miranda Reference Dias and Miranda2013), elasticity of the medium (Pihler-Puzovic et al. Reference Pihler-Puzovic, Illien, Heil and Juel2012, Reference Pihler-Puzovic, Perillat, Russell, Juel and Heil2013; Pihler-Puzovic, Juel & Heil Reference Pihler-Puzovic, Juel and Heil2014), anisotropy (Ben-Jacob et al. Reference Ben-Jacob, Godbey, Goldenfeld, Koplik, Levine, Mueller and Sander1985) and rheology (Kondic, Shelley & Palffy-Muhoray Reference Kondic, Shelley and Palffy-Muhoray1998; Fast et al. Reference Fast, Kondic, Shelley and Palffy-Muhoray2001; Kagei, Kanie & Kawaguchi Reference Kagei, Kanie and Kawaguchi2005).
It has been observed experimentally by Kowal & Worster (Reference Kowal and Worster2015) that viscous gravity currents lubricated from below by a less viscous fluid are prone to a novel viscous fingering instability and we have explored various physical mechanisms to explain the formation of the instability in the companion paper Kowal & Worster (Reference Kowal and Worster2019). We found that this is a frontal instability and that the mechanism of instability contrasts with that of classical Saffman–Taylor fingering (Saffman & Taylor Reference Saffman and Taylor1958; Homsy Reference Homsy1987) in porous media, in that it occurs as a result of changes in the hydrostatic rather than dynamic pressure gradients. The latter is stabilised by gradients in the flow passage (Al-Housseiny et al. Reference Al-Housseiny, Tsai and Stone2012), capillarity (Bretherton Reference Bretherton1961) and elastic effects (Pihler-Puzovic et al. Reference Pihler-Puzovic, Illien, Heil and Juel2012, Reference Pihler-Puzovic, Perillat, Russell, Juel and Heil2013, Reference Pihler-Puzovic, Juel and Heil2014), among others.
We devote the present paper to the analysis of another physical mechanism related to driving buoyancy forces associated with the lower layer near its nose. This takes place in the vicinity of the lubrication front – the location where the instability emerges – when there is a non-zero density difference between the two layers. Such an effect is akin to that relevant to the gravitational spreading of classical viscous gravity currents over a horizontal substrate driven by their own buoyancy, or the Barenblatt–Pattle self-similar solution for viscous gravity currents in the classical sense and in porous media. These were shown to be stable by Grundy & McLaughlin (Reference Grundy and McLaughlin1982) for symmetric disturbances and Mathunjwa & Hogg (Reference Mathunjwa and Hogg2006a ,Reference Mathunjwa and Hogg b ) for asymmetric disturbances. These driving buoyancy forces are stabilising and those associated with the lower layer near its nose act to suppress the frontal instability of lubricated viscous gravity currents. We wish to understand the competition between this stabilising mechanism and the destabilising mechanism of the fingering patters seen in the experiments.
In contrast to the analysis of the companion paper, the analysis presented in the present paper is non-local, perturbations are not assumed to grow faster than the basic state, that is, we do not use the frozen-time approximation, and the densities of the two layers are not assumed equal. The lubrication front can no longer be considered in terms of jump conditions as the basic state relevant to this problem is additionally singular at the front in the presence of these driving buoyancy forces. Another difference from the companion paper is that here the geometry of the basic state is axisymmetric, as in the experiments, rather than two-dimensional. We find that the onset conditions for equal-density layers are the same in these two geometries.
There are two difficulties associated with the analysis. The first is that the basic state is both time and space dependent in the experiments, which complicates a traditional linear, normal-mode stability analysis. To resolve this, we consider radially outward spreading currents, recast the problem in similarity coordinates and perform a stability analysis in a transformed time variable. This approach yields normal-mode solutions in the transformed coordinates.
The second difficulty is that the basic state is singular at the front of the lubricating fluid and at the front of the overlying fluid. There is also a weak, logarithmic singularity at the origin in the initially axisymmetric geometry of the experiments, which we adopt for the basic state. The singularity at the origin can be readily resolved for the basic state, but unfortunately becomes stronger with increasing wavenumbers for the equations governing the perturbations. A major problem stems from the fact that the two frontal singularities occur at moving, rather than fixed boundaries, and linearising about the unperturbed frontal positions leads to singular boundary conditions for the perturbations, in addition to singular terms in the governing equations.
Such problems arose previously in the study of the stability of the Barenblatt–Pattle similarity solution describing classical viscous gravity currents and various remedies have been introduced, including the method of strained coordinates (Grundy & McLaughlin Reference Grundy and McLaughlin1982) or transforming the dependent variable (Mathunjwa & Hogg Reference Mathunjwa and Hogg2006a ). The first of these methods regularises the problem at the frontal position, at which the solution has a singular first derivate, by formulating the problem in terms of an appropriate strained coordinate. The second of these methods involves reformulating the problem in terms of an appropriate function of the surface height, chosen so that its derivative remains finite at the front. We introduce a new approach that eliminates the need to linearise at the singular frontal positions, and use asymptotic matching conditions to couple the governing equations to asymptotic solutions that we derive near the singular fronts. Using this approach, we perform a linear stability analysis for this problem without employing any local spatial or frozen-time approximations.
We begin with a theoretical development in § 2 and an analysis of the problem, including asymptotic solutions and a new approach to formulating consistent perturbation equations in light of the frontal singularities in § 3. We present the linear stability analysis in § 4 and present a discussion on the stabilising and destabilising mechanisms in § 5. The paper closes with conclusions in § 6.
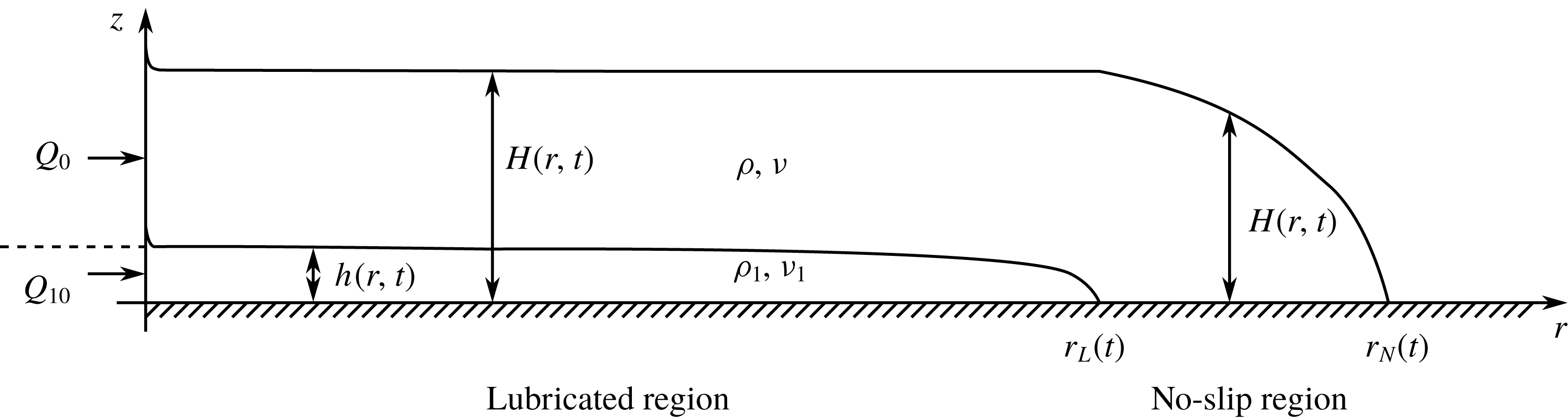
Figure 1. Schematic of two superposed thin films of viscous fluid spreading horizontally under gravity on a rigid horizontal surface. Reproduced and modified from Kowal & Worster (Reference Kowal and Worster2015).
2 Theoretical development
Consider the flow of two superposed, thin films of viscous fluid of dynamic viscosities
$\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}_{l}$
and densities
$\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}_{l}$
spreading radially outwards over a rigid, horizontal substrate and supplied at constant fluxes
$Q_{0}$
and
$Q_{l0}$
at the origin as shown in figure 2. The subscript
$_{l}$
denotes quantities relevant to the lower layer. We denote the surface heights of the upper and lower layers by
$z=H(r,\unicode[STIX]{x1D703},t)$
and
$z=h(r,\unicode[STIX]{x1D703},t)$
. We assume no surface tension between the layers and consider the limit in which vertical shear provides the dominant resistance to the flow of both layers. The following is based on the PhD thesis by Kowal (Reference Kowal2016).
We use the dimensional version of the equations derived in the companion paper in cylindrical coordinates. The fluxes of lower- and upper-layer fluids are
$$\begin{eqnarray}\displaystyle \boldsymbol{q}_{\boldsymbol{l}}=-\frac{\unicode[STIX]{x1D70C}g}{\unicode[STIX]{x1D707}}\left[\frac{{\mathcal{M}}}{3}h^{3}({\mathcal{D}}\unicode[STIX]{x1D735}h+\unicode[STIX]{x1D735}H)+\frac{{\mathcal{M}}}{2}h^{2}(H-h)\unicode[STIX]{x1D735}H\right]\quad (0\leqslant r\leqslant r_{L}), & & \displaystyle\end{eqnarray}$$
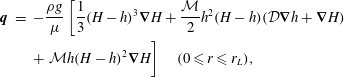$$\begin{eqnarray}\displaystyle \boldsymbol{q} & = & \displaystyle -\frac{\unicode[STIX]{x1D70C}g}{\unicode[STIX]{x1D707}}\left[\frac{1}{3}(H-h)^{3}\unicode[STIX]{x1D735}H+\frac{{\mathcal{M}}}{2}h^{2}(H-h)({\mathcal{D}}\unicode[STIX]{x1D735}h+\unicode[STIX]{x1D735}H)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\vphantom{\frac{1}{3}}{\mathcal{M}}h(H-h)^{2}\unicode[STIX]{x1D735}H\right]\quad (0\leqslant r\leqslant r_{L}),\end{eqnarray}$$
in the lubricated region and
$$\begin{eqnarray}\displaystyle \boldsymbol{q}=-\frac{\unicode[STIX]{x1D70C}g}{3\unicode[STIX]{x1D707}}H^{3}\unicode[STIX]{x1D735}H\quad (r_{L}\leqslant r\leqslant r_{N}), & & \displaystyle\end{eqnarray}$$
in the no-slip region. Here,
$$\begin{eqnarray}\displaystyle {\mathcal{M}}=\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x1D707}_{l}}\quad \text{and}\quad {\mathcal{D}}=\frac{\unicode[STIX]{x1D70C}_{l}-\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}}. & & \displaystyle\end{eqnarray}$$
The governing mass-conservation equations become, in components,
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}=-\frac{1}{r}\frac{\unicode[STIX]{x2202}(rq_{lr})}{\unicode[STIX]{x2202}r}-\frac{1}{r}\frac{\unicode[STIX]{x2202}q_{l\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (0\leqslant r\leqslant r_{L}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}(H-h)}{\unicode[STIX]{x2202}t}=-\frac{1}{r}\frac{\unicode[STIX]{x2202}(rq_{r})}{\unicode[STIX]{x2202}r}-\frac{1}{r}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (0\leqslant r\leqslant r_{L}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}t}=-\frac{1}{r}\frac{\unicode[STIX]{x2202}(rq_{r})}{\unicode[STIX]{x2202}r}-\frac{1}{r}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (r_{L}\leqslant r\leqslant r_{N}), & & \displaystyle\end{eqnarray}$$
for the no-slip region, where the subscript
$_{r}$
denotes the
$r$
component and the subscript
$_{\unicode[STIX]{x1D703}}$
denotes the
$\unicode[STIX]{x1D703}$
component of a vector. We apply a constant flux at the origin
$r=0$
$$\begin{eqnarray}\displaystyle \lim _{r\rightarrow 0}2\unicode[STIX]{x03C0}rq_{lr}=Q_{l0},\quad \lim _{r\rightarrow 0}2\unicode[STIX]{x03C0}rq_{r}=Q_{0}. & & \displaystyle\end{eqnarray}$$
For both
${\mathcal{D}}\equiv 0$
and
${\mathcal{D}}\neq 0$
, the height of the upper layer and the sum of the normal fluxes of both layers of fluid are continuous across the lubrication front. These conditions are summarised by
$$\begin{eqnarray}\displaystyle & \displaystyle [\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{n}_{\boldsymbol{L}}+\boldsymbol{q}_{\boldsymbol{l}}\boldsymbol{\cdot }\boldsymbol{n}_{\boldsymbol{L}}]^{-}=[\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{n}_{\boldsymbol{L}}]^{+}\quad (r=r_{L}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle [H]_{-}^{+}=0\quad (r=r_{L}). & \displaystyle\end{eqnarray}$$
In addition, the normal component of the upper-layer flux vanishes at the leading edge of the no-slip current,
$$\begin{eqnarray}\displaystyle \boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{n}_{\boldsymbol{N}}=0\quad (r=r_{N}), & & \displaystyle\end{eqnarray}$$
which is equivalent to
$$\begin{eqnarray}\displaystyle H=0\quad (r=r_{N}). & & \displaystyle\end{eqnarray}$$
Both fronts evolve kinematically
$$\begin{eqnarray}\displaystyle \boldsymbol{n}_{\boldsymbol{L}}\boldsymbol{\cdot }\dot{\boldsymbol{r}}_{\boldsymbol{L}}=\lim _{r\rightarrow r_{L}}\boldsymbol{n}_{\boldsymbol{L}}\boldsymbol{\cdot }\boldsymbol{q}_{\boldsymbol{l}}/h, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \boldsymbol{n}_{\boldsymbol{N}}\boldsymbol{\cdot }\dot{\boldsymbol{r}}_{\boldsymbol{N}}=\lim _{r\rightarrow r_{N}}\boldsymbol{n}_{\boldsymbol{N}}\boldsymbol{\cdot }\boldsymbol{q}/H, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{r}_{\boldsymbol{L}}=r_{L}\widehat{\boldsymbol{r}}$
and
$\boldsymbol{r}_{\boldsymbol{N}}=r_{N}\widehat{\boldsymbol{r}}$
are the position vectors of the two freely moving fronts. Explicitly,
$$\begin{eqnarray}\displaystyle {\dot{r}}_{L}=\lim _{r\rightarrow r_{L}}\left[q_{lr}-q_{l\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}r_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right]/h, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle {\dot{r}}_{N}=\lim _{r\rightarrow r_{N}}\left[q_{r}-q_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}r_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right]/H. & & \displaystyle\end{eqnarray}$$
These follow from conditions of zero normal component of flux and zero thickness at the front, which are also sufficient in determining the evolution of the frontal positions. However, the explicit kinematic evolution conditions stated above are of use in the numerical approach that we adopt and we will refer to these from now on.
When
${\mathcal{D}}\equiv 0$
, the nose of the lubricant does not spread under its own weight and ends abruptly with a non-zero thickness there (equivalently, non-zero frontal flux). However, if
${\mathcal{D}}\neq 0$
, the front of the lubricant spreads under its own weight and the flux of the lower-layer fluid vanishes at the lubrication front. Therefore, if
${\mathcal{D}}\neq 0$
, the following additional condition applies
$$\begin{eqnarray}\displaystyle \boldsymbol{q}_{\boldsymbol{l}}\boldsymbol{\cdot }\boldsymbol{n}_{\boldsymbol{L}}=0\quad (r=r_{L}). & & \displaystyle\end{eqnarray}$$
The order of the equations reduces by one when
${\mathcal{D}}\equiv 0$
and therefore no additional condition is necessary to fully specify the problem in this case.
3 Similarity variables
3.1 Governing equations
The description of the flow can be recast in terms of a similarity variable
$\unicode[STIX]{x1D709}$
, the azimuthal coordinate
$\unicode[STIX]{x1D703}$
and a transformed time variable
$\unicode[STIX]{x1D70F}$
, where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}=\log t,\quad \unicode[STIX]{x1D709}=r/(gQ_{0}^{3}\unicode[STIX]{x1D708}^{-1}t^{4})^{1/8}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [H(r,\unicode[STIX]{x1D703},t),h(r,\unicode[STIX]{x1D703},t)]=(\unicode[STIX]{x1D708}Q_{0}g^{-1})^{1/4}[F(\unicode[STIX]{x1D709},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F}),f(\unicode[STIX]{x1D709},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})]. & & \displaystyle\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}$
is the kinematic viscosity of the upper layer and
$g$
is the gravitational constant. In what follows,
$\unicode[STIX]{x1D735}$
denotes the gradient vector in the
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D703})$
cylindrical polar coordinate plane. The experiments of Kowal & Worster (Reference Kowal and Worster2015) tend towards self-similarity with time. The governing equations become
$$\begin{eqnarray}\displaystyle \boldsymbol{q}_{\boldsymbol{l}}=-\left[\frac{{\mathcal{M}}}{3}f^{3}({\mathcal{D}}\unicode[STIX]{x1D735}f+\unicode[STIX]{x1D735}F)+\frac{{\mathcal{M}}}{2}f^{2}(F-f)\unicode[STIX]{x1D735}F\right]\quad (0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}), & & \displaystyle\end{eqnarray}$$
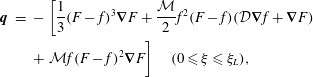$$\begin{eqnarray}\displaystyle \boldsymbol{q} & = & \displaystyle -\left[\frac{1}{3}(F-f)^{3}\unicode[STIX]{x1D735}F+\frac{{\mathcal{M}}}{2}f^{2}(F-f)({\mathcal{D}}\unicode[STIX]{x1D735}f+\unicode[STIX]{x1D735}F)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\mathcal{M}}f(F-f)^{2}\unicode[STIX]{x1D735}F\right]\quad (0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{q}=-{\textstyle \frac{1}{3}}F^{3}\unicode[STIX]{x1D735}F\quad (\unicode[STIX]{x1D709}_{L}\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{N}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-\frac{1}{2}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D709}q_{lr})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}q_{l\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}(F-f)}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-\frac{1}{2}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}(F-f)}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D709}q_{r})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}-\frac{1}{2}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D709}q_{r})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\frac{1}{\unicode[STIX]{x1D709}}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\quad (\unicode[STIX]{x1D709}_{L}\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{N}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D709}\rightarrow 0}2\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}q_{lr}={\mathcal{Q}},\quad \lim _{\unicode[STIX]{x1D709}\rightarrow 0}2\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}q_{r}=1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[(q_{r}+q_{lr})-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(q_{\unicode[STIX]{x1D703}}+q_{l\unicode[STIX]{x1D703}})\right]^{-}=\left[q_{r}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}q_{\unicode[STIX]{x1D703}}\right]^{+}\quad (\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}), & & \displaystyle\end{eqnarray}$$
along with
$$\begin{eqnarray}\displaystyle q_{lr}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}q_{l\unicode[STIX]{x1D703}}=0\quad (\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L})\quad \text{if }{\mathcal{D}}\neq 0, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle [F]_{-}^{+}=0\quad (\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}),\quad q_{r}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}q_{\unicode[STIX]{x1D703}}=0\quad (\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{N}). & & \displaystyle\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{N}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})$
are two free moving boundaries that depend on both
$\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D70F}$
and are determined by the kinematic conditions
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\frac{1}{2}\unicode[STIX]{x1D709}_{L}=\lim _{\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{L}}\left(q_{lr}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}q_{l\unicode[STIX]{x1D703}}\right)/f, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\frac{1}{2}\unicode[STIX]{x1D709}_{N}=\lim _{\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{N}}\left(q_{lr}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}q_{l\unicode[STIX]{x1D703}}\right)/F. & \displaystyle\end{eqnarray}$$
Taking
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\equiv 0$
and
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}\equiv 0$
gives governing equations and boundary conditions for the similarity solutions for the two layers (Kowal & Worster Reference Kowal and Worster2015).
3.2 Asymptotic solutions near the fronts
Near the leading edge
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{N}$
, the thickness of the current features a frontal singularity described by the leading-order asymptotic solution
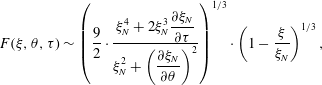$$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D709},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})\sim \left(\frac{9}{2}\cdot \frac{\displaystyle \unicode[STIX]{x1D709}_{N}^{4}+2\unicode[STIX]{x1D709}_{N}^{3}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}}{\displaystyle \unicode[STIX]{x1D709}_{N}^{2}+\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}}\right)^{1/3}\cdot \left(1-\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D709}_{N}}\right)^{1/3}, & & \displaystyle\end{eqnarray}$$
as
$\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{N}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})$
. Provided the density difference
${\mathcal{D}}$
between the two layers is non-zero, the lubrication front involves a singularity with a cube-root asymptotic spatial structure
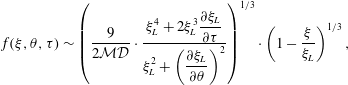$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D709},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})\sim \left(\frac{9}{2{\mathcal{M}}{\mathcal{D}}}\cdot \frac{\displaystyle \unicode[STIX]{x1D709}_{L}^{4}+2\unicode[STIX]{x1D709}_{L}^{3}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}}{\displaystyle \unicode[STIX]{x1D709}_{L}^{2}+\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)^{2}}\right)^{1/3}\cdot \left(1-\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D709}_{L}}\right)^{1/3}, & & \displaystyle\end{eqnarray}$$
as
$\unicode[STIX]{x1D709}\rightarrow \unicode[STIX]{x1D709}_{L}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})$
. The gradients of the lower-layer thickness near the lubrication front become steeper as the density difference decreases. In the limit of
${\mathcal{D}}\equiv 0$
, the frontal singularity turns into a frontal jump discontinuity that can be quantified in terms of the jump condition (3.10).
Both of these asymptotic solutions generalise the asymptotic results near the two fronts found by Kowal & Worster (Reference Kowal and Worster2015) for self-similar currents, to allow for non-self-similar variations in the time variable
$\unicode[STIX]{x1D70F}$
and across the azimuthal coordinate
$\unicode[STIX]{x1D703}$
, and are used as asymptotic matching conditions for our numerical solutions.
3.3 Mathematical formulation near the singular front
As the self-similar solutions involve gradients that become infinite at the lubrication front if
${\mathcal{D}}\neq 0$
and at the leading edge for general
${\mathcal{D}}$
, this leads to singular terms in the perturbation equations, preventing one from formulating consistent linearised boundary conditions at the front. To understand why, one may consider the no-flux boundary conditions at the two fronts, which reduce to vanishing frontal thickness conditions there. Consider such a condition at the lubrication front, for example. Linearising the frontal thickness a distance
$\unicode[STIX]{x1D6FF}\ll 1$
away from the lubrication front leads to
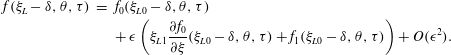$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D709}_{L}-\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F}) & = & \displaystyle f_{0}(\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D709}_{L1}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})+f_{1}(\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D703},\unicode[STIX]{x1D70F})\right)+O(\unicode[STIX]{x1D716}^{2}).\end{eqnarray}$$
The
$O(\unicode[STIX]{x1D716})$
terms involve contributions from the migration of the lubrication front as well as contributions from the layer thickness perturbations. As
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, the latter of these terms, appearing as the first term in the second group of terms on the right-hand side, involving the gradient in the basic state frontal thickness, diverges. To balance this at first order in
$\unicode[STIX]{x1D716}$
, the perturbed thickness necessarily diverges at the unperturbed lubrication front as well.
A similar problem appears while studying the stability of the Barenblatt–Pattle similarity solution. Grundy & McLaughlin (Reference Grundy and McLaughlin1982) introduced a remedy in this context by using the method of strained coordinates, while Mathunjwa & Hogg (Reference Mathunjwa and Hogg2006a ) scale out the singularities by transforming the dependent variable so that the gradient of the self-similar height at the front is finite.
For tractability and clarity of presentation, we introduce an approach that eliminates the need to linearise at the singular front by transforming the spatial domain. We make a change of variables
$$\begin{eqnarray}\displaystyle R=\unicode[STIX]{x1D709}/\unicode[STIX]{x1D709}_{L}\quad (0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}),\quad R=1+(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}_{L})/(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})\quad (\unicode[STIX]{x1D709}_{L}\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{N}), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle T=\unicode[STIX]{x1D70F},\quad \unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D703} & & \displaystyle\end{eqnarray}$$
so that the freely deforming lubricated region
$0\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{L}$
corresponds to the fixed interval
$0\leqslant R\leqslant 1$
and the unlubricated region
$\unicode[STIX]{x1D709}_{L}\leqslant \unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{N}$
corresponds to
$1\leqslant R\leqslant 2$
. The transformed equations become
$$\begin{eqnarray}\displaystyle \boldsymbol{q}_{\boldsymbol{l}}=-\frac{1}{\unicode[STIX]{x1D709}_{L}}\left[\frac{{\mathcal{M}}}{3}f^{3}({\mathcal{D}}\unicode[STIX]{x1D735}f+\unicode[STIX]{x1D735}F)+\frac{{\mathcal{M}}}{2}f^{2}(F-f)\unicode[STIX]{x1D735}F\right]\quad (0\leqslant R\leqslant 1), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q} & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D709}_{L}}\left[\frac{1}{3}(F-f)^{3}\unicode[STIX]{x1D735}F+\frac{{\mathcal{M}}}{2}f^{2}(F-f)({\mathcal{D}}\unicode[STIX]{x1D735}f+\unicode[STIX]{x1D735}F)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.{\mathcal{M}}f(F-f)^{2}\unicode[STIX]{x1D735}F\right]\quad (0\leqslant R\leqslant 1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{q}=-\frac{1}{3(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})}F^{3}\unicode[STIX]{x1D735}_{P\unicode[STIX]{x1D6E9}}F\quad (1\leqslant R\leqslant 2), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}T}-\frac{R}{\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}T}\frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}R}-\frac{1}{2}R\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}R}=-\frac{1}{\unicode[STIX]{x1D709}_{L}R}\frac{\unicode[STIX]{x2202}(Rq_{lr})}{\unicode[STIX]{x2202}R}+\frac{1}{\unicode[STIX]{x1D709}_{L}^{2}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\frac{\unicode[STIX]{x2202}q_{l\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}R}-\frac{1}{\unicode[STIX]{x1D709}_{L}R}\frac{\unicode[STIX]{x2202}q_{l\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\quad (0\leqslant R\leqslant 1), & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
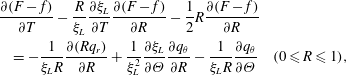$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}(F-f)}{\unicode[STIX]{x2202}T}-\frac{R}{\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}T}\frac{\unicode[STIX]{x2202}(F-f)}{\unicode[STIX]{x2202}R}-\frac{1}{2}R\frac{\unicode[STIX]{x2202}(F-f)}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{\unicode[STIX]{x1D709}_{L}R}\frac{\unicode[STIX]{x2202}(Rq_{r})}{\unicode[STIX]{x2202}R}+\frac{1}{\unicode[STIX]{x1D709}_{L}^{2}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}R}-\frac{1}{\unicode[STIX]{x1D709}_{L}R}\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\quad (0\leqslant R\leqslant 1),\end{eqnarray}$$
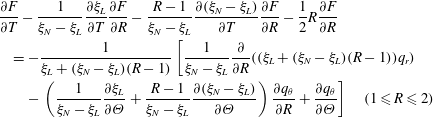$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}T}-\frac{1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}T}\frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}R}-\frac{R-1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})}{\unicode[STIX]{x2202}T}\frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}R}-\frac{1}{2}R\frac{\unicode[STIX]{x2202}F}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{\unicode[STIX]{x1D709}_{L}+(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})(R-1)}\left[\frac{1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}((\unicode[STIX]{x1D709}_{L}+(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})(R-1))q_{r})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.\left(\frac{1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+\frac{R-1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right)\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}q_{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right]\quad (1\leqslant R\leqslant 2)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{R\rightarrow 0}2\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}_{L}Rq_{lr}={\mathcal{Q}},\quad \lim _{R\rightarrow 0}2\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}_{L}Rq_{r}=1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[(q_{\unicode[STIX]{x1D709}}+q_{l\unicode[STIX]{x1D709}})-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}(q_{\unicode[STIX]{x1D703}}+q_{l\unicode[STIX]{x1D703}})\right]^{-}=\left[q_{\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}q_{\unicode[STIX]{x1D703}}\right]^{+}\quad (R=1), & & \displaystyle\end{eqnarray}$$
along with
$$\begin{eqnarray}\displaystyle q_{l\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}q_{l\unicode[STIX]{x1D703}}=0\quad (R=1)\quad \text{if }{\mathcal{D}}\neq 0, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle [F]_{-}^{+}=0\quad (R=1),\quad q_{\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}q_{\unicode[STIX]{x1D703}}=0\quad (R=1), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}T}+\frac{1}{2}\unicode[STIX]{x1D709}_{L}=\lim _{R\rightarrow 1}\left(q_{l\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}q_{l\unicode[STIX]{x1D703}}\right)/f, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}T}+\frac{1}{2}\unicode[STIX]{x1D709}_{N}=\lim _{R\rightarrow 2}\left(q_{l\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}q_{l\unicode[STIX]{x1D703}}\right)/F. & \displaystyle\end{eqnarray}$$
Here,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}=\frac{1}{\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\widehat{\unicode[STIX]{x1D743}}+\left(\frac{1}{R\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\frac{1}{\unicode[STIX]{x1D709}_{L}^{2}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right)\widehat{\unicode[STIX]{x1D73D}}, & & \displaystyle\end{eqnarray}$$
and
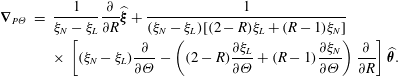$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}_{P\unicode[STIX]{x1D6E9}} & = & \displaystyle \frac{1}{\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\widehat{\unicode[STIX]{x1D743}}+\frac{1}{(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})[(2-R)\unicode[STIX]{x1D709}_{L}+(R-1)\unicode[STIX]{x1D709}_{N}]}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[(\unicode[STIX]{x1D709}_{N}-\unicode[STIX]{x1D709}_{L})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\left((2-R)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+(R-1)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R}\right]\widehat{\unicode[STIX]{x1D73D}}.\end{eqnarray}$$
4 Linear stability analysis
4.1 Perturbation equations
We look for a solution of the perturbed problem by expanding about the zeroth-order self-similar solution of Kowal & Worster (Reference Kowal and Worster2015). The self-similar solution can be obtained by taking
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}=0$
and
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
in the governing equations of § 3.1 and in the asymptotic solution of § 3.2. We write
$$\begin{eqnarray}\displaystyle X(R,\unicode[STIX]{x1D6E9},T)=X_{0}(R)+\unicode[STIX]{x1D716}X_{1}(R,\unicode[STIX]{x1D6E9},T)+\cdots & & \displaystyle\end{eqnarray}$$
for each of the variables
$X=f,F,\boldsymbol{q},\boldsymbol{q}_{\boldsymbol{l}}$
and
$$\begin{eqnarray}\displaystyle X(\unicode[STIX]{x1D6E9},T)=X_{0}+\unicode[STIX]{x1D716}X_{1}(\unicode[STIX]{x1D6E9},T)+\cdots & & \displaystyle\end{eqnarray}$$
for
$X=\unicode[STIX]{x1D709}_{L},\unicode[STIX]{x1D709}_{N}$
. The first-order perturbations to the
$r$
- and
$\unicode[STIX]{x1D703}$
-components of the lower-layer flux of the lubricated region are given by
$$\begin{eqnarray}\displaystyle & \displaystyle q_{l1r}=\unicode[STIX]{x1D6FC}_{l1R}\,f_{1}+\unicode[STIX]{x1D6FC}_{l2R}F_{1}+\unicode[STIX]{x1D6FC}_{l3R}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}R}+\unicode[STIX]{x1D6FC}_{l4R}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}R}+\unicode[STIX]{x1D6FC}_{l5R}\unicode[STIX]{x1D709}_{L1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle q_{l1\unicode[STIX]{x1D703}}=\frac{1}{R}\left[\unicode[STIX]{x1D6FC}_{l1\unicode[STIX]{x1D703}}f_{1}+\unicode[STIX]{x1D6FC}_{l2\unicode[STIX]{x1D703}}F_{1}+\unicode[STIX]{x1D6FC}_{l3\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+\unicode[STIX]{x1D6FC}_{l4\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+R\unicode[STIX]{x1D6FC}_{l5\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right], & \displaystyle\end{eqnarray}$$
and for the upper layer,
$$\begin{eqnarray}\displaystyle & \displaystyle q_{1r}=\unicode[STIX]{x1D6FC}_{1R}f_{1}+\unicode[STIX]{x1D6FC}_{2R}F_{1}+\unicode[STIX]{x1D6FC}_{3R}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}R}+\unicode[STIX]{x1D6FC}_{4R}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}R}+\unicode[STIX]{x1D6FC}_{5R}\unicode[STIX]{x1D709}_{L1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle q_{1\unicode[STIX]{x1D703}}=\frac{1}{R}\left[\unicode[STIX]{x1D6FC}_{1\unicode[STIX]{x1D703}}f_{1}+\unicode[STIX]{x1D6FC}_{2\unicode[STIX]{x1D703}}F_{1}+\unicode[STIX]{x1D6FC}_{3\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+\unicode[STIX]{x1D6FC}_{4\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+R\unicode[STIX]{x1D6FC}_{5\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right], & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}_{l1R},\ldots ,\unicode[STIX]{x1D6FC}_{l5R}$
,
$\unicode[STIX]{x1D6FC}_{l1\unicode[STIX]{x1D6E9}},\ldots ,\unicode[STIX]{x1D6FC}_{l5\unicode[STIX]{x1D6E9}}$
,
$\unicode[STIX]{x1D6FC}_{1R},\ldots ,\unicode[STIX]{x1D6FC}_{5R}$
and
$\unicode[STIX]{x1D6FC}_{1\unicode[STIX]{x1D6E9}},\ldots ,\unicode[STIX]{x1D6FC}_{5\unicode[STIX]{x1D6E9}}$
are functions of
$R$
and
$\unicode[STIX]{x1D6E9}$
that depend on the basic state, with
$\unicode[STIX]{x1D6FC}_{l1\unicode[STIX]{x1D703}},\unicode[STIX]{x1D6FC}_{l2\unicode[STIX]{x1D703}},\unicode[STIX]{x1D6FC}_{1\unicode[STIX]{x1D703}},\unicode[STIX]{x1D6FC}_{2\unicode[STIX]{x1D703}}=0$
since the basic state is independent of
$\unicode[STIX]{x1D6E9}$
, and the remaining functions are specified in appendix A.
The perturbations to the flux components in the unlubricated region are
$$\begin{eqnarray}\displaystyle & \displaystyle q_{1r}=\frac{F_{0}^{2}}{3(\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D709}_{N0})^{2}}\left((\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D709}_{N0})\left(F_{0}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}R}+3\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}F_{1}\right)-F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}(\unicode[STIX]{x1D709}_{L1}-\unicode[STIX]{x1D709}_{N1})\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle q_{1\unicode[STIX]{x1D703}}=\frac{F_{0}^{3}}{\unicode[STIX]{x1D6FE}}\left(\unicode[STIX]{x1D709}_{L0}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-R\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}-\unicode[STIX]{x1D709}_{N0}\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}+R\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right), & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}=3(\unicode[STIX]{x1D709}_{L0}-\unicode[STIX]{x1D709}_{N0})(-\unicode[STIX]{x1D709}_{L0}+R\unicode[STIX]{x1D709}_{L0}-R\unicode[STIX]{x1D709}_{N0}). & & \displaystyle\end{eqnarray}$$
At
$O(\unicode[STIX]{x1D716})$
, the governing equations in the lubricated region become
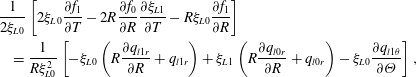$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D709}_{L0}}\left[2\unicode[STIX]{x1D709}_{L0}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}T}-2R\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}T}-R\unicode[STIX]{x1D709}_{L0}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}R}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{R\unicode[STIX]{x1D709}_{L0}^{2}}\left[-\unicode[STIX]{x1D709}_{L0}\left(R\frac{\unicode[STIX]{x2202}q_{l1r}}{\unicode[STIX]{x2202}R}+q_{l1r}\right)+\unicode[STIX]{x1D709}_{L1}\left(R\frac{\unicode[STIX]{x2202}q_{l0r}}{\unicode[STIX]{x2202}R}+q_{l0r}\right)-\unicode[STIX]{x1D709}_{L0}\frac{\unicode[STIX]{x2202}q_{l1\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right],\end{eqnarray}$$
for the lower layer and
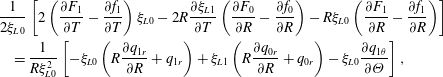$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D709}_{L0}}\left[2\left(\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}T}-\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}T}\right)\unicode[STIX]{x1D709}_{L0}-2R\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}T}\left(\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}-\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}\right)-R\unicode[STIX]{x1D709}_{L0}\left(\frac{\unicode[STIX]{x2202}F_{1}}{\unicode[STIX]{x2202}R}-\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}R}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{R\unicode[STIX]{x1D709}_{L0}^{2}}\left[-\unicode[STIX]{x1D709}_{L0}\left(R\frac{\unicode[STIX]{x2202}q_{1r}}{\unicode[STIX]{x2202}R}+q_{1r}\right)+\unicode[STIX]{x1D709}_{L1}\left(R\frac{\unicode[STIX]{x2202}q_{0r}}{\unicode[STIX]{x2202}R}+q_{0r}\right)-\unicode[STIX]{x1D709}_{L0}\frac{\unicode[STIX]{x2202}q_{1\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}\right],\end{eqnarray}$$
for the upper layer. The governing equations in the unlubricated region can be obtained similarly.
The condition of zero perturbation flux in the upper layer at the origin reduces to
$$\begin{eqnarray}\displaystyle \lim _{R\rightarrow 0}2\unicode[STIX]{x03C0}R(\unicode[STIX]{x1D709}_{L0}q_{1r}+\unicode[STIX]{x1D709}_{L1}q_{0r})=0, & & \displaystyle\end{eqnarray}$$
and for the lower layer,
$$\begin{eqnarray}\displaystyle \lim _{R\rightarrow 0}2\unicode[STIX]{x03C0}R(\unicode[STIX]{x1D709}_{L0}q_{l1r}+\unicode[STIX]{x1D709}_{L1}q_{l0r})=0. & & \displaystyle\end{eqnarray}$$
As the domains of both the lubricated and unlubricated regions are mapped to fixed intervals, the height continuity condition in the transformed coordinates does not involve contributions from the propagation of the perturbed lubrication front and reduces to
$$\begin{eqnarray}\displaystyle [F_{1}]_{-}^{+}=0\quad (R=1). & & \displaystyle\end{eqnarray}$$
As the basic state frontal flux vanishes for
${\mathcal{D}}\neq 0$
, the perturbed zero-flux condition at the lubrication front also does not involve contributions from the perturbed position of the lubrication front and reduces to
$$\begin{eqnarray}\displaystyle q_{lr}=0\quad (R=1^{-}), & & \displaystyle\end{eqnarray}$$
which reduces to
$$\begin{eqnarray}\displaystyle f_{1}=0\quad (R=1^{-}), & & \displaystyle\end{eqnarray}$$
by performing an asymptotic analysis close to the singular lubrication front for
${\mathcal{D}}\neq 0$
. By performing a similar asymptotic analysis near the leading edge
$\unicode[STIX]{x1D709}_{N}$
, we find that the zero-flux condition at
$\unicode[STIX]{x1D709}_{N}$
gives that the perturbed height of the current in the unlubricated region vanishes there
$$\begin{eqnarray}\displaystyle F_{1}=0\quad (R=2). & & \displaystyle\end{eqnarray}$$
Rather than featuring contributions from the perturbed position of the lubrication front explicitly, the condition of continuity of flux involves such contributions implicitly through the definitions of the perturbed fluxes and reduces to
$$\begin{eqnarray}\displaystyle [q_{1r}+q_{l1r}]^{-}=[q_{1r}]^{+}\quad (R=1). & & \displaystyle\end{eqnarray}$$
The first-order kinematic condition for the evolution of the perturbed lubrication front reduces to
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{L1}}{\unicode[STIX]{x2202}T}+\frac{1}{2}\unicode[STIX]{x1D709}_{L1}=\lim _{R\rightarrow 1}\left[\frac{q_{l1r}}{f_{0}}-\frac{q_{l0r}f_{1}}{f_{0}^{2}}\right]. & & \displaystyle\end{eqnarray}$$
Similarly, the perturbed leading edge
$\unicode[STIX]{x1D709}_{N}$
evolves according to
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{N1}}{\unicode[STIX]{x2202}T}+\frac{1}{2}\unicode[STIX]{x1D709}_{N1}=\lim _{R\rightarrow 2}\left[\frac{q_{1r}}{F_{0}}-\frac{q_{0r}F_{1}}{F_{0}^{2}}\right]. & & \displaystyle\end{eqnarray}$$
Searching for normal-mode solutions
$X_{1}(R,\unicode[STIX]{x1D6E9},T)=\widetilde{X}_{1}(R)\text{e}^{\unicode[STIX]{x1D70E}T+\text{i}k\unicode[STIX]{x1D6E9}},$
and dropping tildes gives the following governing mass-conservation equations for the lower layer of the lubricated region
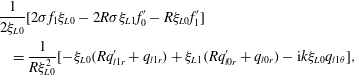$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D709}_{L0}}[2\unicode[STIX]{x1D70E}f_{1}\unicode[STIX]{x1D709}_{L0}-2R\unicode[STIX]{x1D70E}\unicode[STIX]{x1D709}_{L1}f_{0}^{\prime }-R\unicode[STIX]{x1D709}_{L0}f_{1}^{\prime }]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{R\unicode[STIX]{x1D709}_{L0}^{2}}[-\unicode[STIX]{x1D709}_{L0}(Rq_{l1r}^{\prime }+q_{l1r})+\unicode[STIX]{x1D709}_{L1}(Rq_{l0r}^{\prime }+q_{l0r})-\text{i}k\unicode[STIX]{x1D709}_{L0}q_{l1\unicode[STIX]{x1D703}}],\end{eqnarray}$$
and for the upper layer
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D709}_{L0}}[2\unicode[STIX]{x1D70E}(F_{1}-f_{1})\unicode[STIX]{x1D709}_{L0}-2R\unicode[STIX]{x1D70E}\unicode[STIX]{x1D709}_{L1}(F_{0}^{\prime }-f_{0}^{\prime })-R\unicode[STIX]{x1D709}_{L0}(F_{1}^{\prime }-f_{1}^{\prime })]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{R\unicode[STIX]{x1D709}_{L0}^{2}}[-\unicode[STIX]{x1D709}_{L0}(Rq_{1r}^{\prime }+q_{1r})+\unicode[STIX]{x1D709}_{L1}(Rq_{0r}^{\prime }+q_{0r})-\text{i}k\unicode[STIX]{x1D709}_{L0}q_{1\unicode[STIX]{x1D703}}].\end{eqnarray}$$
The governing equation in the unlubricated region reduces to
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{1r}+\unicode[STIX]{x1D6FD}_{2r})\unicode[STIX]{x1D709}_{L1}+(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{3r}+\unicode[STIX]{x1D6FD}_{4r})\unicode[STIX]{x1D709}_{N1}+\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{5r}F_{1}+\unicode[STIX]{x1D6FD}_{6r}F_{1}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FD}_{7r}q_{1r}+\unicode[STIX]{x1D6FD}_{8r}q_{1r}^{\prime }+\unicode[STIX]{x1D6FD}_{9r}\unicode[STIX]{x1D709}_{L1}+\unicode[STIX]{x1D6FD}_{10r}\unicode[STIX]{x1D709}_{N1}+\text{i}k\unicode[STIX]{x1D6FD}_{11r}q_{1\unicode[STIX]{x1D703}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}_{1r},\ldots ,\unicode[STIX]{x1D6FD}_{11r}$
are functions of
$P$
that depend on the basic state and are specified in appendix A. Here, the
$r$
-components of the linearised fluxes in the upper and lower layers of the two regions are given by real functions of
$R$
alone, while the
$\unicode[STIX]{x1D703}$
-components are proportional to
$\text{i}k$
.
The structure of the input flux conditions at the origin and the height and flux conditions at the lubrication front for the amplitudes of the normal-mode solutions to the perturbed problem remains as the same as (4.12)–(4.18), whereas the kinematic condition for the evolution of the perturbed lubrication front reduces to
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}\unicode[STIX]{x1D709}_{L1}+\frac{1}{2}\unicode[STIX]{x1D709}_{L1}=\lim _{R\rightarrow 1}\left[\frac{q_{l1r}}{f_{0}}-\frac{q_{l0r}f_{1}}{f_{0}^{2}}\right], & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}\unicode[STIX]{x1D709}_{N1}+\frac{1}{2}\unicode[STIX]{x1D709}_{N1}=\lim _{R\rightarrow 2}\left[\frac{q_{1r}}{F_{0}}-\frac{q_{0r}F_{1}}{F_{0}^{2}}\right] & & \displaystyle\end{eqnarray}$$
for the evolution of the perturbation to the leading edge
$\unicode[STIX]{x1D709}_{N}$
. The system of differential equations (4.21)–(4.23) along with the boundary conditions (4.12)–(4.18) and (4.24)–(4.25) are a complete formulation for the perturbed problem.
4.2 Asymptotic solutions for perturbations
By perturbing the asymptotic solution near the lubrication front (3.16), we find that at
$O(\unicode[STIX]{x1D716})$
, the lower-layer thickness has a cube-root singularity
$$\begin{eqnarray}\displaystyle f_{1}\sim \left(\frac{4}{3{\mathcal{M}}{\mathcal{D}}\unicode[STIX]{x1D709}_{L0}}\right)^{1/3}\unicode[STIX]{x1D709}_{L1}(\unicode[STIX]{x1D70E}+1)(1-R)^{1/3}\quad \text{as}~R\rightarrow 1, & & \displaystyle\end{eqnarray}$$
at the lubrication front, independently of the wavenumber
$k$
. The spatial structure of the singularity in the perturbation to the lower-layer thickness at the lubrication front remains the same as that of the basic state, differing by the prefactor.
Similarly, perturbing the asymptotic solution (3.15), we find that the perturbation to the thickness of the current near the leading edge
$\unicode[STIX]{x1D709}_{N}$
obeys
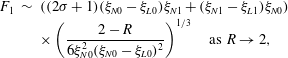$$\begin{eqnarray}\displaystyle F_{1} & {\sim} & \displaystyle ((2\unicode[STIX]{x1D70E}+1)(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})\unicode[STIX]{x1D709}_{N1}+(\unicode[STIX]{x1D709}_{N1}-\unicode[STIX]{x1D709}_{L1})\unicode[STIX]{x1D709}_{N0})\nonumber\\ \displaystyle & & \displaystyle \times \left(\frac{2-R}{6\unicode[STIX]{x1D709}_{N0}^{2}(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})^{2}}\right)^{1/3}\quad \text{as}~R\rightarrow 2,\end{eqnarray}$$
preserving the spatial structure, as before.
4.3 Numerical method
These asymptotic solutions are used as asymptotic matching conditions for our numerical solutions for the system of differential equations governing the perturbations. We solve the perturbation equations, which are singular at the two fronts and at the origin, numerically by shooting backwards for
$\unicode[STIX]{x1D709}_{L1}$
and
$\unicode[STIX]{x1D709}_{N1}$
from the front of the current of the unlubricated region at
$R=2$
. To initiate the computations, we use the asymptotic solution presented above at
$R=2-\unicode[STIX]{x1D6FF}_{1}$
, where
$\unicode[STIX]{x1D6FF}_{1}\ll 1$
, and integrate backwards towards the lubrication front, at which we use frontal matching conditions and the asymptotic solution at
$R=1-\unicode[STIX]{x1D6FF}_{1}$
to initiate computations for the lubricated region. We integrate the perturbation equations for the lubricated region numerically, backwards from
$R=1-\unicode[STIX]{x1D6FF}_{1}$
towards
$R=\unicode[STIX]{x1D6FF}_{2}\ll 1$
.
Although the singularity at the origin originates as a weak logarithmic singularity at zeroth order and when
$k=0$
, it unfortunately becomes stronger with increasing wavenumbers
$k$
. To aid in resolving this singularity at the origin for all wavenumbers, we reformulate the problem in terms of transformed functions
$g_{1,k}(R)$
and
$G_{1,k}(R)$
where
$$\begin{eqnarray}\displaystyle (f_{1},F_{1})=R^{-k}(1-\log R)^{-3/4}(g_{1,k}(R),G_{1,k}(R)) & & \displaystyle\end{eqnarray}$$
and solve the resulting perturbation equations numerically for
$g_{1,k}(R)$
and
$G_{1,k}(R)$
.
As the problem is
$2\unicode[STIX]{x03C0}$
-periodic, only integer multiples of
$k$
are admissible. When displaying the results, we interpolate for intermediate
$k$
.
The system of differential equations governing the perturbations admits non-zero solutions only for specific growth rates, or eigenvalues,
$\unicode[STIX]{x1D70E}$
. For a given wavenumber, we determine the growth rate
$\unicode[STIX]{x1D70E}$
and associated eigensolutions
$g_{1,k}(R)$
,
$G_{1,k}(R)$
,
$\unicode[STIX]{x1D709}_{L1}$
,
$\unicode[STIX]{x1D709}_{N1}$
iteratively by exploiting the linearity of the system of differential equations governing the perturbations. For each wavenumber and each choice of parameter values, we initiate the iterative process with an initial estimate for
$\unicode[STIX]{x1D70E}$
and at each iteration, we solve two perturbation problems numerically by shooting backwards as described above. Each iteration is solved using the standard Mathematica solver for nonlinear differential equations with default accuracy and precision.
These two perturbation problems are defined by the values of
$\unicode[STIX]{x1D709}_{L1}$
and
$\unicode[STIX]{x1D709}_{N1}$
. The first of these problems is defined by setting
$\unicode[STIX]{x1D709}_{L1}=1$
and
$\unicode[STIX]{x1D709}_{N1}=0$
, yielding a solution
$g_{1,k}^{a}(R)$
,
$G_{1,k}^{a}(R)$
,
$\unicode[STIX]{x1D709}_{L1}^{a}$
,
$\unicode[STIX]{x1D709}_{N1}^{a}$
, whereas the second is defined by setting
$\unicode[STIX]{x1D709}_{L1}=0$
and
$\unicode[STIX]{x1D709}_{N1}=1$
, yielding a solution
$g_{1,k}^{b}(R)$
,
$G_{1,k}^{b}(R)$
,
$\unicode[STIX]{x1D709}_{L1}^{b}$
,
$\unicode[STIX]{x1D709}_{N1}^{b}$
. These two problems yield non-zero, linearly independent solutions that satisfy the perturbation equations and all boundary conditions and matching conditions except for the source flux conditions. By linearity of the system of differential equations, any linear combination of these two solutions is another such solution. Any such linear combination does not, in general, satisfy the two source flux boundary conditions, for the lower and upper layers of the lubricated region, and carries with it a residual matrix
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64D}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}_{2}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D709}_{L0}q_{l1r}^{a}+\unicode[STIX]{x1D709}_{L1}q_{l0r}^{a} & \unicode[STIX]{x1D709}_{L0}q_{l1r}^{b}+\unicode[STIX]{x1D709}_{L1}q_{l0r}^{b}\\ \unicode[STIX]{x1D709}_{L0}q_{1r}^{a}+\unicode[STIX]{x1D709}_{L1}q_{0r}^{a} & \unicode[STIX]{x1D709}_{L0}q_{1r}^{b}+\unicode[STIX]{x1D709}_{L1}q_{0r}^{b}\end{array}\right). & & \displaystyle\end{eqnarray}$$
The columns of the residual matrix measure the departure from satisfied source flux conditions, per test solution.
The aim of the iteration is to find an appropriate linear combination of the two test solutions so that the determinant of the residual matrix is close to zero. The iteration terminates when there exists a linear combination of the two test solutions for which the two source flux boundary conditions are satisfied to within a specified tolerance. This occurs precisely when the residual matrix has zero determinant, to within a specified tolerance of
$10^{-5}$
. This is a one-dimensional root-finding problem for
$\unicode[STIX]{x1D70E}$
and Brent’s method, built into Mathematica, using the determinant of the residual matrix is used to update
$\unicode[STIX]{x1D70E}$
at each iteration. The process terminates when this occurs.
We are interested in the eigensolution for which the growth rate is largest. To select this eigensolution, we plot the residual (the determinant of the residual matrix) and pick out the root with the largest growth rate by constraining the search domain to one that contains only this root. This is done manually for a selection of test cases and parameter continuation is employed for intermediate values.
The spatial form of the resulting perturbations is shown in figure 4, where it is seen that there is a build up of the more viscous fluid ahead of the front.
5 Destabilising and stabilising mechanisms
The instability mechanism can be understood most clearly in the equal density limit
${\mathcal{D}}\equiv 0$
. The companion paper determines the mechanism of instability in terms of a jump in hydrostatic pressure gradient in the limit of
${\mathcal{D}}\equiv 0$
in a two-dimensional geometry. Here, we find a consistent criterion, despite the change to an axisymmetric geometry in a non-fixed frame of reference.
If
${\mathcal{D}}\equiv 0$
, then the frontal flux condition gives
$$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D709}_{L0}}[({\mathcal{M}}F_{0}^{3}-({\mathcal{M}}-1)(F_{0}-f_{0})^{3})F_{0}^{\prime }]^{-}=\frac{1}{\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0}}[F_{0}^{3}F_{0}^{\prime }]^{+}. & & \displaystyle\end{eqnarray}$$
Using the height continuity condition, we obtain
$$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D709}_{L0}}[({\mathcal{M}}-({\mathcal{M}}-1)(1-f_{0}/F_{0})^{3})F_{0}^{\prime }]^{-}=\frac{1}{\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0}}[F_{0}^{\prime }]^{+}. & & \displaystyle\end{eqnarray}$$
Hence
$$\begin{eqnarray}\displaystyle ({\mathcal{M}}-1)\left[\left(1-\left(1-\frac{f_{0}}{F_{0}}\right)^{3}\right)\frac{\text{d}F_{0}}{\text{d}\unicode[STIX]{x1D709}}\right]^{-}=\left[\frac{\text{d}F_{0}}{\text{d}\unicode[STIX]{x1D709}}\right]_{-}^{+}. & & \displaystyle\end{eqnarray}$$
Noting that
$$\begin{eqnarray}\displaystyle \left[\left(1-\left(1-\frac{f_{0}}{F_{0}}\right)^{3}\right)\frac{\text{d}F_{0}}{\text{d}\unicode[STIX]{x1D709}}\right]^{-}<0. & & \displaystyle\end{eqnarray}$$
We find that
$$\begin{eqnarray}\displaystyle \left[\frac{\text{d}F_{0}}{\text{d}\unicode[STIX]{x1D709}}\right]_{-}^{+}<0 & & \displaystyle\end{eqnarray}$$
if and only if
${\mathcal{M}}>1$
. We find that this is precisely when the flow is unstable as seen by the slope of the curves of figure 2 for various
${\mathcal{M}}$
, for example. This is consistent with and confirms one of the results of the local, frontal stability analysis of the companion paper, namely, that a lubricated viscous gravity current consisting of layers of equal density is prone to a viscous fingering instability in the local vicinity of the lubrication front precisely when the viscosity ratio satisfies
${\mathcal{M}}>1$
.
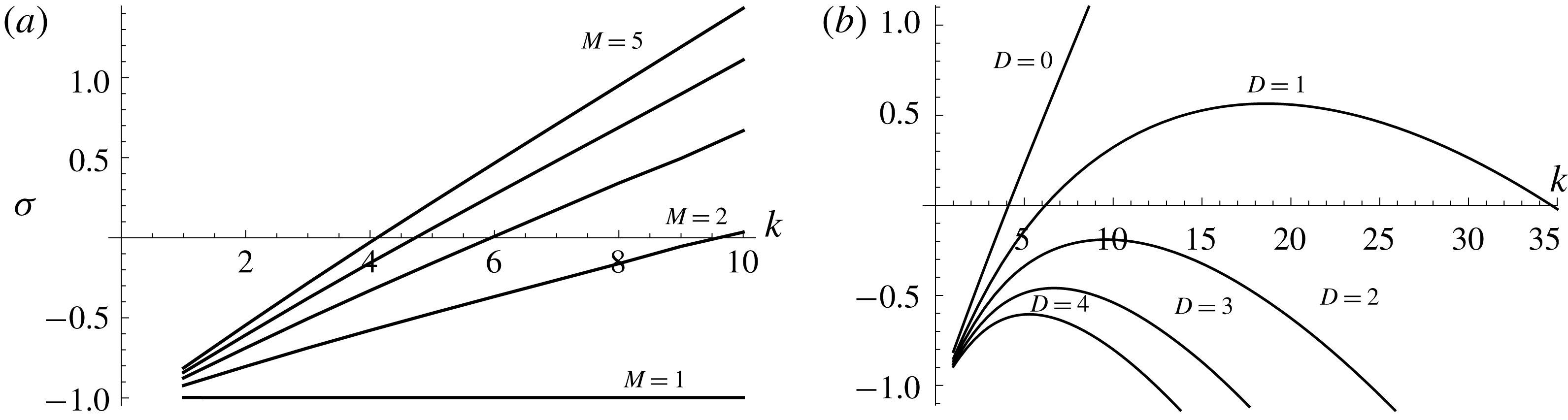
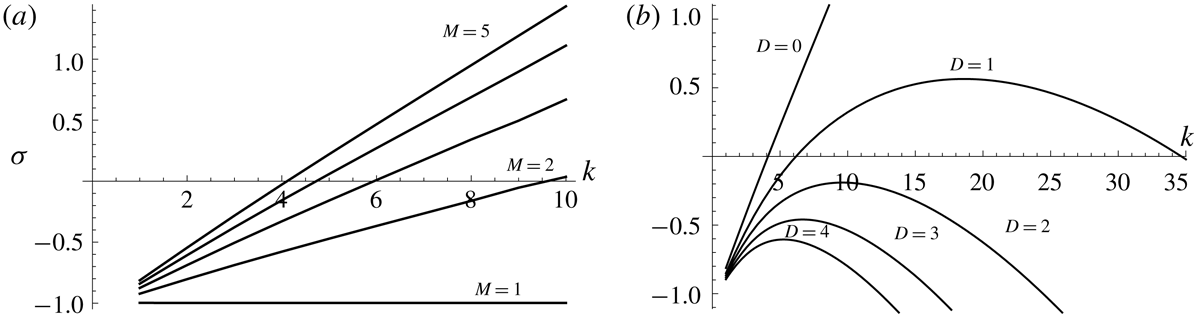
Figure 2. (a) Growth rates
$\unicode[STIX]{x1D70E}$
against wavenumber
$k$
for
${\mathcal{M}}=1,2,\ldots ,5$
(blue to red), and
${\mathcal{D}}=0,{\mathcal{Q}}=0.1$
. (b) Growth rates
$\unicode[STIX]{x1D70E}$
against wavenumber
$k$
for
${\mathcal{M}}=5$
,
${\mathcal{D}}=0,1,\ldots ,4$
(red to violet) and
${\mathcal{Q}}=0.1$
.
Figure 3. Growth rates
$\unicode[STIX]{x1D70E}$
against wavenumber
$k$
for
${\mathcal{M}}=2,4,\ldots ,20$
, and
${\mathcal{D}}=2$
,
${\mathcal{Q}}=0.1$
.
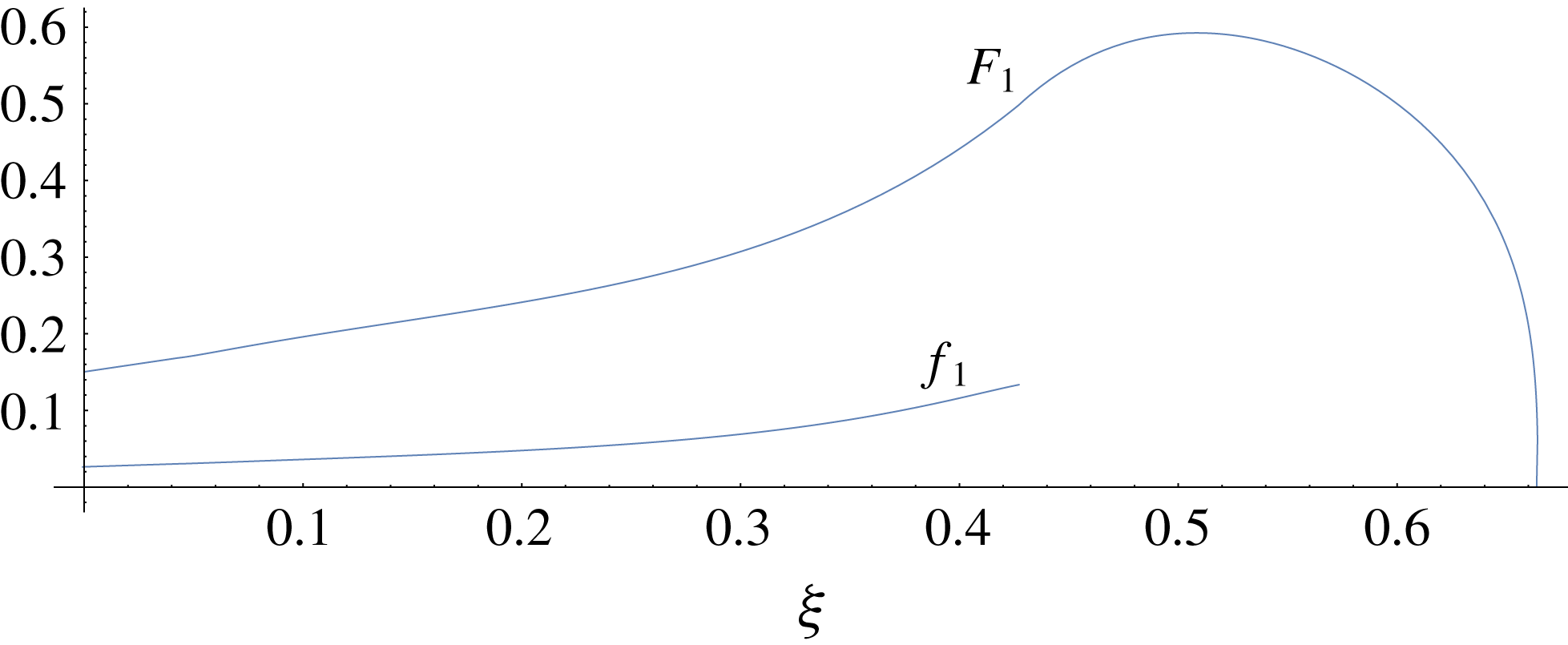
Figure 4. Spatial form of the perturbations for
${\mathcal{M}}=10,{\mathcal{D}}=0,{\mathcal{Q}}=0.1$
against the originally scaled similarity variable
$\unicode[STIX]{x1D709}$
.
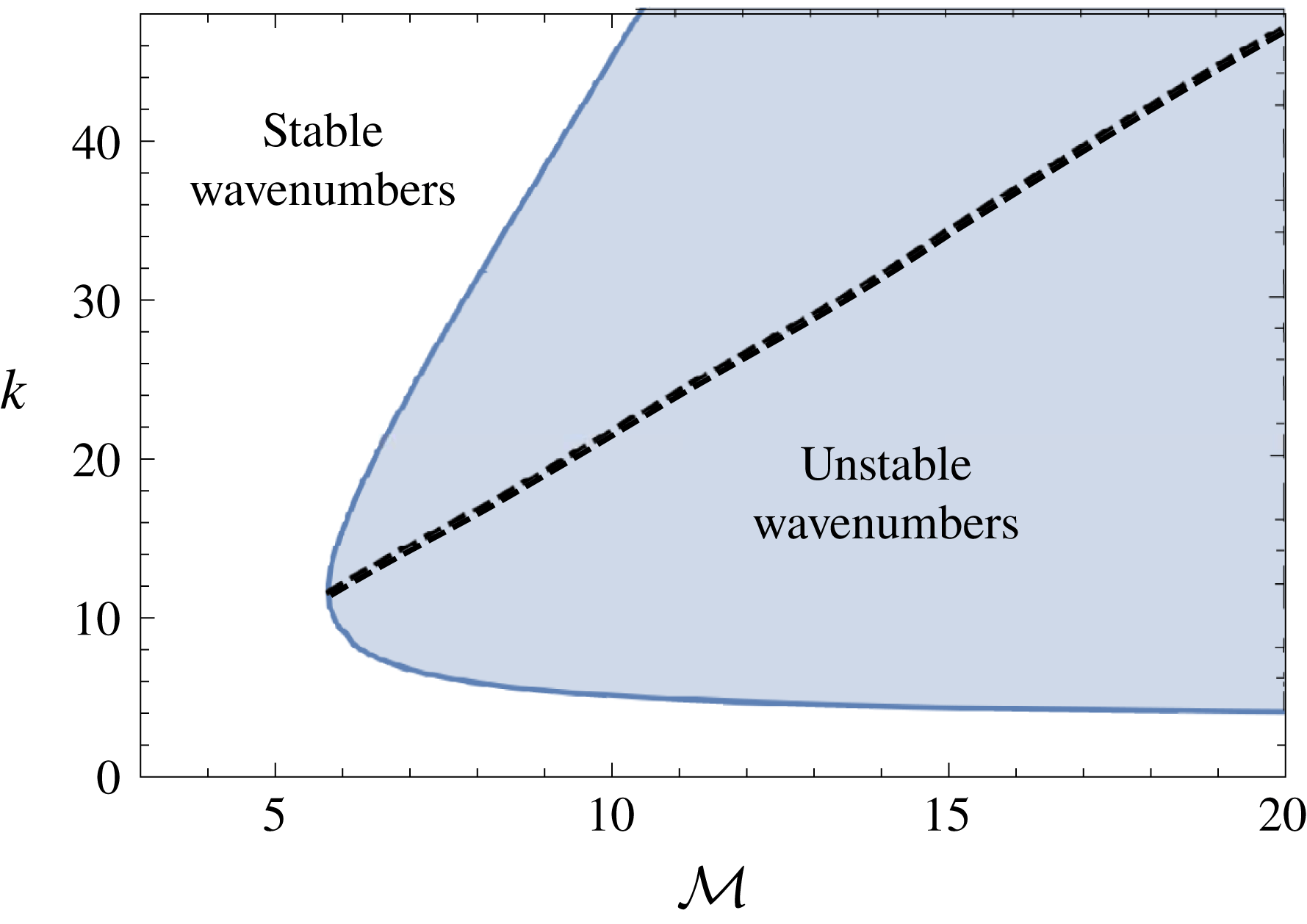
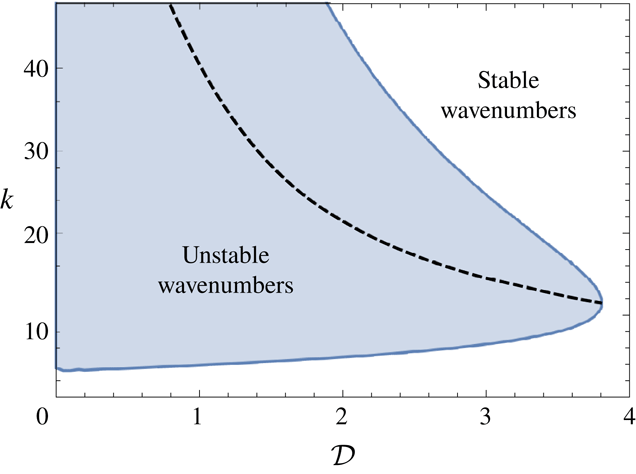
Figure 5. Stability region for
${\mathcal{D}}=2$
and
${\mathcal{Q}}=0.1$
. The wavenumber of the maximal growth rate is displayed as the dashed line.
Figure 2(a) shows the dispersion relations for illustrative parameter values in the equal-density limit, where positive slopes are observed precisely for
${\mathcal{M}}>1$
and a uniformly zero slope of the growth rate curve is observed when
${\mathcal{M}}=1$
. That is, for
${\mathcal{D}}\equiv 0$
, the flow becomes unstable (at large enough wavenumbers
$k$
) precisely when the jump in upper surface slope, or the jump in the hydrostatic pressure gradient, across the lubrication front is negative. This occurs when a less viscous fluid intrudes underneath a more viscous fluid of the same density into the unlubricated region as explained in the companion paper. In this case, the more viscous fluid spreads under a higher hydrostatic pressure gradient in the unlubricated region than in the lubricated region, and is characterised by higher surface gradients there. If the lubrication front is perturbed so that the less viscous fluid migrates into the unlubricated region, then it will become subject to higher hydrostatic pressure gradients. This will cause the less viscous fluid to advance forward, causing an instability.
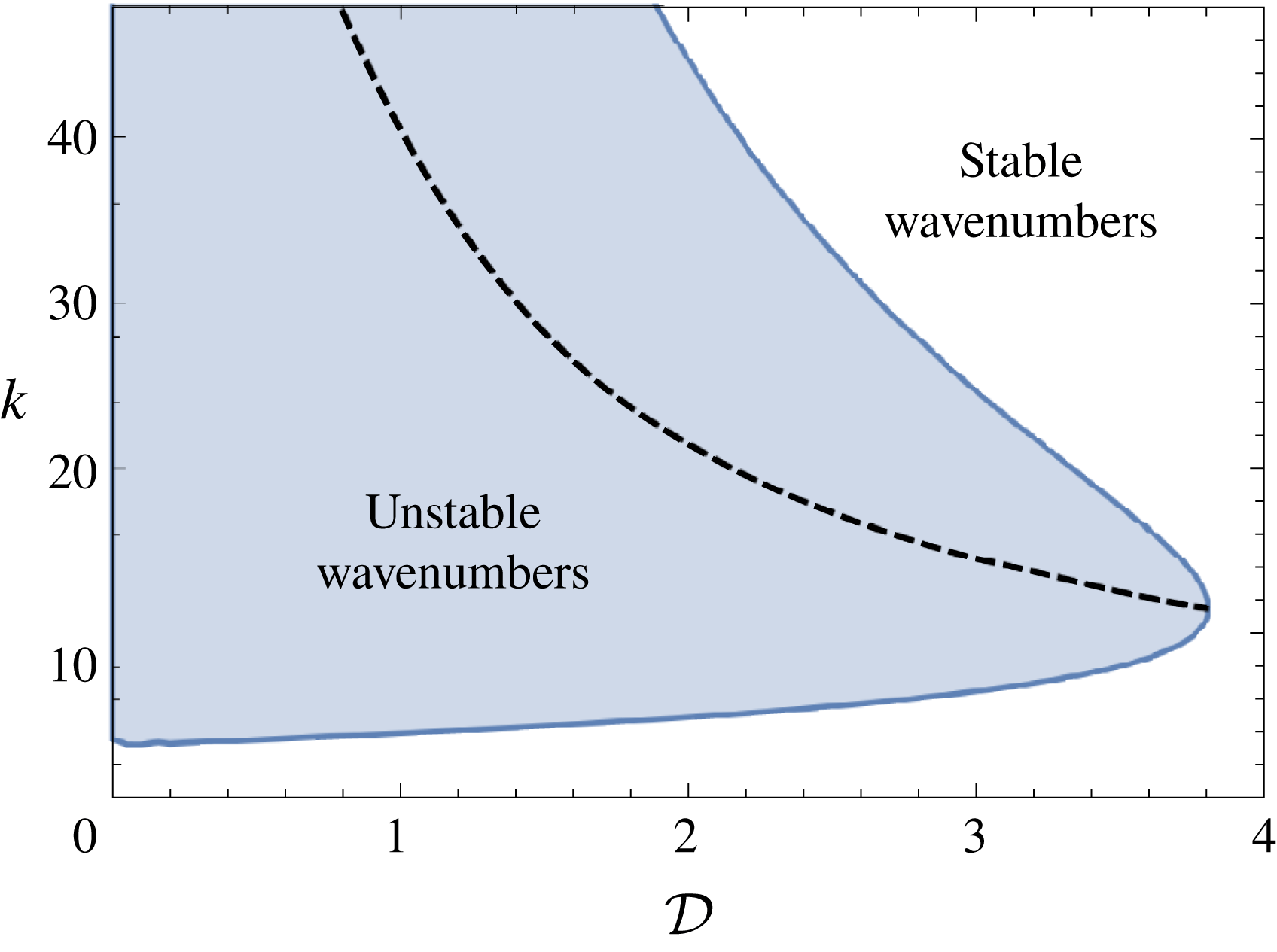
Figure 6. Stability region for
${\mathcal{M}}=10$
and
${\mathcal{Q}}=0.1$
. The wavenumber of the maximal growth rate is displayed as the dashed line.
This instability mechanism competes against a stabilising effect that takes place when
${\mathcal{D}}\neq 0$
. Figure 2(b) illustrates this effect for sample parameter values. Once the density difference between the two layers is non-zero, the growth rates no longer increase unboundedly as the wavenumber
$k$
increases, but instead decay at large wavenumbers leaving behind a band of most unstable wavenumbers, corresponding to either positive or negative growth rates depending on parameters. Illustrative dispersion relations for various values of the viscosity ratio
${\mathcal{M}}$
for which the interaction between the destabilising and stabilising mechanisms results in most unstable wavenumbers with positive growth rates are shown in figure 3. Large viscosity ratios
${\mathcal{M}}$
promote instability, and small density differences
${\mathcal{D}}$
give rise to weak stabilisation, promoting a large band of large, unstable wavenumbers. Larger values of
${\mathcal{D}}$
reduce this band of unstable wavenumbers.
Stability regions showing the stable and unstable wavenumbers as a function of the viscosity ratio
${\mathcal{M}}$
are shown in figure 5. It can be seen that the original instability criterion derived in the
${\mathcal{D}}=0$
limit changes once the lower-layer buoyancy forces become present in that larger viscosity ratios are now required for any instability to occur. In contrast to the
${\mathcal{D}}=0$
limit, in which the band of unstable wavenumbers is unbounded for large
$k$
, here the band of unstable wavenumbers is bounded to a finite interval for each viscosity ratio that is large enough for an instability to occur and this band becomes larger for increasing viscosity ratios.
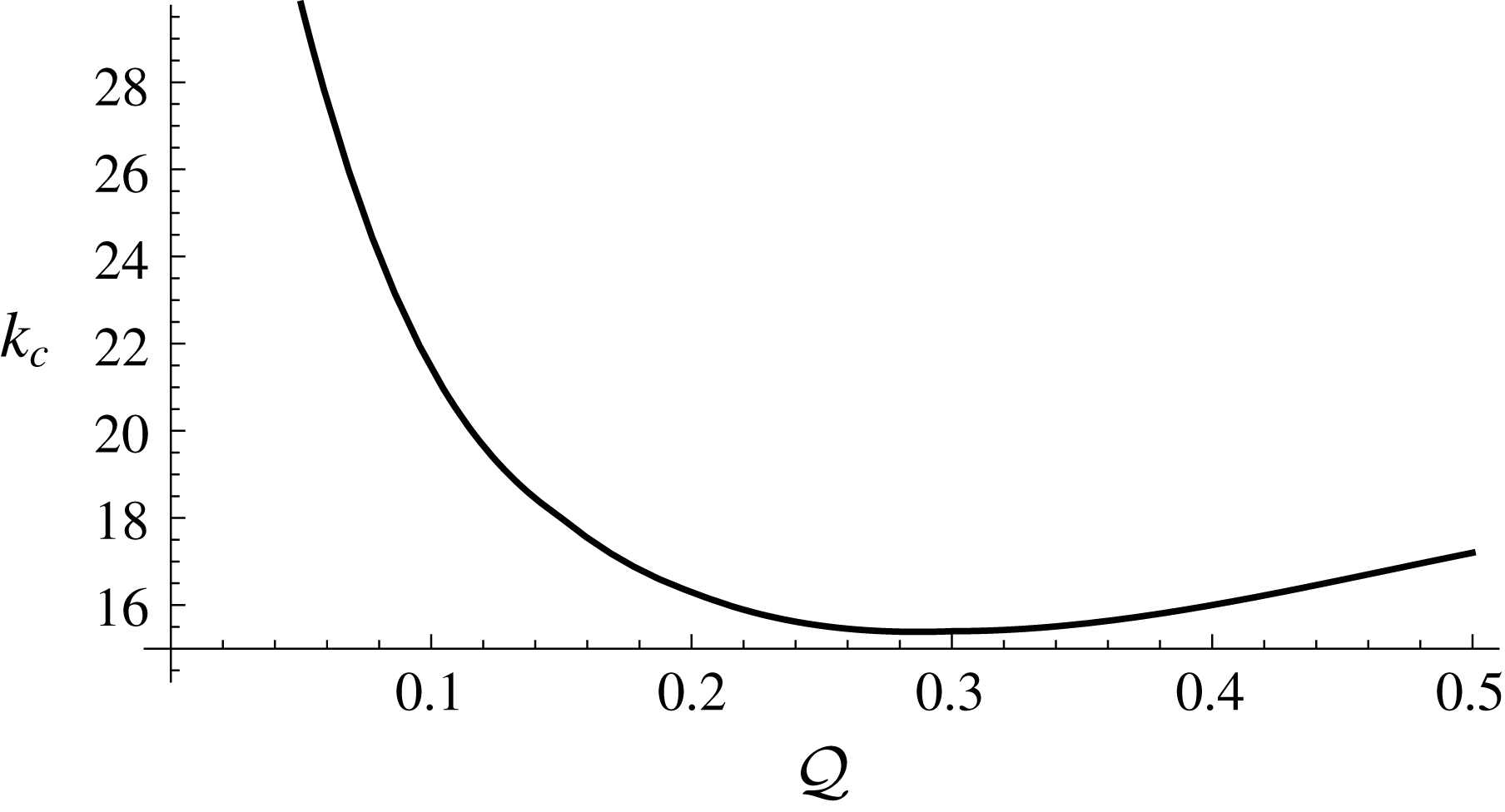
Figure 7. Wavenumber of the maximal growth rate as a function of the flux ratio
${\mathcal{Q}}$
for
${\mathcal{M}}=10$
and
${\mathcal{D}}=2$
.
Figure 6 shows stability regions as a function of the density difference
${\mathcal{D}}$
. The band of unstable wavenumbers is unbounded for
${\mathcal{D}}=0$
, becomes finite once
$D\neq 0$
and becomes smaller as the density difference increases. For large enough density differences, these driving buoyancy forces are large enough to suppress the instability completely, for all wavenumbers. The experiments of Kowal & Worster (Reference Kowal and Worster2015) correspond to the far right side of figure 5 and bottom left side of figure 6. In the experiments,
${\mathcal{M}}\sim 5000$
and
${\mathcal{D}}\sim 0.1$
. These results indicate a large range of unstable wavenumbers for parameters used in the experiments.
The wavenumber of the maximal growth rate is shown as a function of the flux ratio in figure 7. Large wavenumbers are preferred for thin underlying layers (small
${\mathcal{Q}}$
), which decrease towards a critical value up to a finite
${\mathcal{Q}}\approx 0.3$
. This is followed by a slight increase in the preferred wavenumber for larger
${\mathcal{Q}}$
, in line with increasing upper-layer slope reversals of the basic state upstream of the lubrication front.
Figure 8(a,b) shows the behaviour of the critical wavenumber
$k=k_{c}({\mathcal{D}})$
and associated minimal viscosity ratio
${\mathcal{M}}={\mathcal{M}}_{c}({\mathcal{D}})$
required for the onset of instability, as a function of
${\mathcal{D}}$
. As the wavenumbers of interest are increasingly large as
${\mathcal{D}}\rightarrow 0$
, the singularities inherent in the problem become increasingly strong in this region, prompting the need for a more careful numerical treatment in this region. We do not attempt to treat this large-wavenumber regime and display results bounded away from this region. It is expected for these results, which are calculated for an axisymmetric geometry, to be comparable to the results of the companion paper, specifically, that
${\mathcal{M}}_{c}=1$
for
${\mathcal{D}}=0$
, which are calculated for a two-dimensional geometry, in the limit
${\mathcal{D}}\rightarrow 0$
. Bounded away from this large-wavenumber regime, the critical wavenumber for the onset of instability decreases with the density difference, but increases again at large
${\mathcal{D}}$
. In contrast, the critical viscosity ratio
${\mathcal{M}}_{c}$
increases almost linearly with
${\mathcal{D}}$
, reducing the band of unstable wavenumbers as the density difference increases.
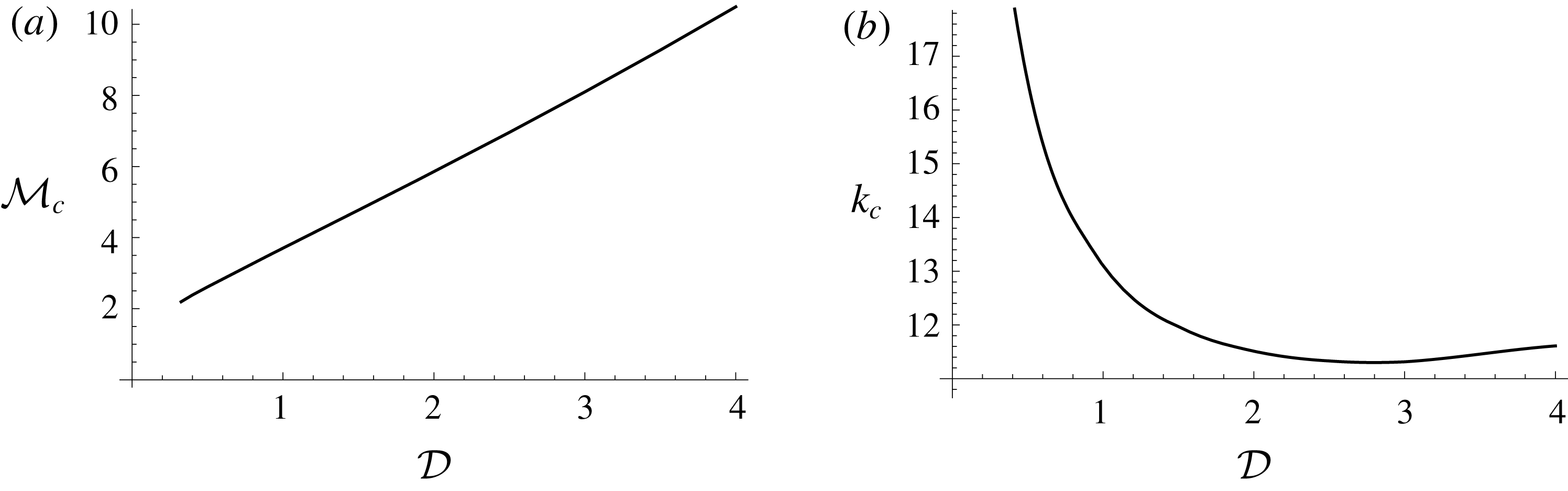
Figure 8. Critical (a) viscosity ratio
$M_{c}$
and (b) wavenumber
$k_{c}$
at the onset of instability as a function of the density difference
${\mathcal{D}}$
for
${\mathcal{Q}}=0.1$
.
6 Conclusions
This paper was devoted to the analysis of a stabilising physical mechanism related to driving buoyancy forces associated with the lower layer near its nose. This effect takes place in a neighbourhood of the lubrication front if there is a non-zero density difference between the two layers, which was absent in the local analysis of the companion paper, involving layers of equal density. Such gravitational spreading of a fluid under its weight alone has been found to be inherently stable in the context of classical, single-fluid viscous gravity currents described by the Barenblatt–Pattle similarity solution (Grundy & McLaughlin Reference Grundy and McLaughlin1982; Mathunjwa & Hogg Reference Mathunjwa and Hogg2006a ). Additionally, in contrast to the companion paper, the analysis of the present paper is non-local and does not employ the frozen-time approximation.
We have classified the behaviour depending on the density difference and the viscosity ratio between the two layers. We find that the geometry of the problem does not change the onset conditions for equal-density layers. When the two layers are of equal densities and the underlying layer spreads under the weight of the fluid above it, we found that the flow becomes unstable precisely when the jump in hydrostatic pressure gradient across the lubrication front is negative. This is consistent with the local frontal stability analysis of the companion paper, despite apparent differences in geometry and the use of local approximations and the frozen-time approximation in the companion paper. Further, we found that this occurs precisely when the viscosity of the underlying layer is smaller than that of the overlying layer of fluid, once again consistently with the results of the companion paper.
Once the density difference between the two layers is non-zero and the lower layer no longer ends abruptly with a non-zero thickness at its nose but instead spreads under its own weight and becomes singular as it approaches the lubrication front, we have shown that the driving buoyancy forces associated with the spreading nose of the underlying layer suppress the instability for large wavenumbers, giving wavelength selection. Therefore, unlike for the Saffman–Taylor instability, the hydrodynamic interactions in the lubricated system, notably the gravitational buoyancy forces, alone provide a mechanism for wavelength selection, without the influence of interfacial surface tension. As the density difference between the two layers increases, the driving buoyancy forces within the underlying layer in the vicinity of the lubrication front become larger and the band of unstable wavenumbers reduces, whereas the viscosity-based instability criterion changes in that the minimal viscosity ratio required for the onset of instability increases with the density difference.
The experiments in which this instability was discovered are in line with this instability criterion, though they exhibit a large range of unstable wavenumbers, which, on the whole, are lower (longer wavelength) than the most unstable wavenumber predicted by the analysis. Likely physical effects that may further stabilise the flow and reduce the most unstable wavenumber include the effects of horizontal shear, nonlinear saturation, diffusion across the interface between the two fluids and a secondary, internal de-wetting instability that occurs in the experiments away from the lubrication front. We have shown in the companion paper that the first two of these contribute to reducing the most unstable wavenumber in two-dimensional geometries.
Acknowledgements
K.N.K. acknowledges the support of a NERC PhD studentship. We are grateful to J. Lister and E. Brambley for helpful discussions on the analysis.
Appendix A. Perturbation equations
The
$r$
- and
$\unicode[STIX]{x1D703}$
-components of the perturbation fluxes of both upper- and lower-layer fluids are given in terms of the following functions of
$R$
and
$\unicode[STIX]{x1D6E9}$
that depend on the basic state,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{l1R}=\frac{{\mathcal{M}}}{2\unicode[STIX]{x1D709}_{L0}}\left[-2{\mathcal{D}}f_{0}^{2}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}+f_{0}^{2}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}-2f_{0}F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{l2R}=-\frac{{\mathcal{M}}}{2\unicode[STIX]{x1D709}_{L0}}\left[f_{0}^{2}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{l3R}=\unicode[STIX]{x1D6FC}_{l3\unicode[STIX]{x1D703}}=-\frac{{\mathcal{M}}D}{3\unicode[STIX]{x1D709}_{L0}}f_{0}^{3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{l4R}=\unicode[STIX]{x1D6FC}_{l4\unicode[STIX]{x1D703}}=\frac{{\mathcal{M}}}{6\unicode[STIX]{x1D709}_{L0}}[f_{0}^{2}(f_{0}-3F_{0})], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{l5R}=\unicode[STIX]{x1D6FC}_{l5\unicode[STIX]{x1D703}}=\frac{{\mathcal{M}}}{6\unicode[STIX]{x1D709}_{L0}^{2}}\left[2{\mathcal{D}}f_{0}^{3}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}-f_{0}^{3}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+3f_{0}^{2}F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right], & \displaystyle\end{eqnarray}$$
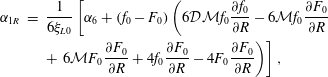$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{1R} & = & \displaystyle \frac{1}{6\unicode[STIX]{x1D709}_{L0}}\left[\unicode[STIX]{x1D6FC}_{6}+(f_{0}-F_{0})\left(6{\mathcal{D}}{\mathcal{M}}f_{0}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}-6{\mathcal{M}}f_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.6{\mathcal{M}}F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+4f_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}-4F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{2R}=\frac{1}{6\unicode[STIX]{x1D709}_{L0}}\left[-\unicode[STIX]{x1D6FC}_{6}+(f_{0}-F_{0})\left(6{\mathcal{M}}f_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}-4f_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+4F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\right)\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{3R}=\unicode[STIX]{x1D6FC}_{3\unicode[STIX]{x1D703}}=\frac{{\mathcal{M}}D}{2\unicode[STIX]{x1D709}_{L0}}(f_{0}-F_{0})f_{0}^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{4R}=\unicode[STIX]{x1D6FC}_{4\unicode[STIX]{x1D703}}=\frac{1}{6\unicode[STIX]{x1D709}_{L0}}(f_{0}-F_{0})(-3{\mathcal{M}}f_{0}^{2}+6{\mathcal{M}}f_{0}F_{0}+2(F_{0}-f_{0})^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{5R}=\unicode[STIX]{x1D6FC}_{5\unicode[STIX]{x1D703}}=\frac{1}{6\unicode[STIX]{x1D709}_{L0}^{2}}\unicode[STIX]{x1D6FC}_{6}(F_{0}-f_{0}), & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{6} & = & \displaystyle 3{\mathcal{D}}{\mathcal{M}}f_{0}^{2}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}R}-3{\mathcal{M}}f_{0}^{2}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+6{\mathcal{M}}f_{0}F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+2f_{0}^{2}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle -\,4f_{0}F_{0}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}+2F_{0}^{2}\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}R}.\end{eqnarray}$$
For convenience, define
$P=R-1$
so that the unlubricated region corresponds also to
$0\leqslant P\leqslant 1$
. The governing equation in the unlubricated region is specified in terms of functions of
$P$
that depend on the basic state and are given below,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{1r}=(P-1)(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})F_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{2r}=-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D709}_{N0}F_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{3r}=-P(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})F_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{4r}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D709}_{L0}F_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{5r}=(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{6r}={\textstyle \frac{1}{2}}[(2P-1)\unicode[STIX]{x1D709}_{L0}\unicode[STIX]{x1D709}_{N0}-P\unicode[STIX]{x1D709}_{L0}^{2}+\unicode[STIX]{x1D709}_{L0}^{2}-P\unicode[STIX]{x1D709}_{N0}^{2}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{7r}=\unicode[STIX]{x1D6FD}_{11r}=-\frac{1}{\unicode[STIX]{x1D6FD}_{r}}(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{8r}=-(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{9r}=\frac{1}{\unicode[STIX]{x1D6FD}_{r}^{2}}(-\unicode[STIX]{x1D6FD}_{r}^{2}q_{0r}^{\prime }+(1-P)(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})^{2}q_{0r}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{10r}=\frac{1}{\unicode[STIX]{x1D6FD}_{r}^{2}}(\unicode[STIX]{x1D6FD}_{r}^{2}q_{0r}^{\prime }+P(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})^{2}q_{0r}), & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}_{r}=P(\unicode[STIX]{x1D709}_{N0}-\unicode[STIX]{x1D709}_{L0})+\unicode[STIX]{x1D709}_{L0}. & & \displaystyle\end{eqnarray}$$
