Article contents
Three-dimensional mode selection of the flow past a rotating and inline oscillating cylinder
Published online by Cambridge University Press: 19 September 2018
Abstract
This paper studies the transition to three-dimensional flow in the wake of a cylinder immersed in a free stream, where the cylinder is externally forced to continuously rotate about its axis and to linearly oscillate in the streamwise direction. Floquet stability analysis is used to assess the stability of the nominal two-dimensional flows at a Reynolds number 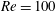 $Re=100$ and rotation rate
$Re=100$ and rotation rate 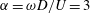 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D714}D/U=3$ to three-dimensional perturbations, as a function of the amplitude and frequency of the linear oscillations. Two modes of instability are found, distinguished by their spatial structure, temporal behaviour and apparent mechanism. The first mode has a shorter wavelength in the spanwise direction and appears to be linked to a centrifugal instability in the layer of fluid near the rotating body. The second mode has a longer wavelength and is linked to an instability of the vortex cores in the wake that is subharmonic, leading to a period doubling. Either mode can be stable while the other is unstable, depending primarily on the frequency of the oscillation of the cylinder. This indicates that either mode can control the transition to a three-dimensional flow. The results are compared to the fully three-dimensional simulation results of a rotating cylinder elastically mounted and free to oscillate in the streamwise direction from Bourguet & Lo Jacono (J. Fluid Mech., vol. 781, 2015, pp. 127–165), and appear to be able to explain the surprising switching of the observed spanwise wavelength in that flow as a change in the dominant mode, and therefore mechanism, of instability.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D714}D/U=3$ to three-dimensional perturbations, as a function of the amplitude and frequency of the linear oscillations. Two modes of instability are found, distinguished by their spatial structure, temporal behaviour and apparent mechanism. The first mode has a shorter wavelength in the spanwise direction and appears to be linked to a centrifugal instability in the layer of fluid near the rotating body. The second mode has a longer wavelength and is linked to an instability of the vortex cores in the wake that is subharmonic, leading to a period doubling. Either mode can be stable while the other is unstable, depending primarily on the frequency of the oscillation of the cylinder. This indicates that either mode can control the transition to a three-dimensional flow. The results are compared to the fully three-dimensional simulation results of a rotating cylinder elastically mounted and free to oscillate in the streamwise direction from Bourguet & Lo Jacono (J. Fluid Mech., vol. 781, 2015, pp. 127–165), and appear to be able to explain the surprising switching of the observed spanwise wavelength in that flow as a change in the dominant mode, and therefore mechanism, of instability.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 7
- Cited by


