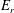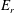1 Introduction
It is well known that the radial electric field,
![]() $E_{r}$
, plays an important role in tokamak turbulence (Itoh & Itoh Reference Itoh and Itoh1996; Burrell Reference Burrell1997; Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005; Watanabe, Sugama & Nunami Reference Watanabe, Sugama and Nunami2011). In particular, shear in
$E_{r}$
, plays an important role in tokamak turbulence (Itoh & Itoh Reference Itoh and Itoh1996; Burrell Reference Burrell1997; Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005; Watanabe, Sugama & Nunami Reference Watanabe, Sugama and Nunami2011). In particular, shear in
![]() $E_{r}$
can suppress turbulence through generation of zonal flows (Dorland et al.
Reference Dorland, Jenko, Kotschenreuther and Rogers2000; Rogers, Dorland & Kotschenreuther Reference Rogers, Dorland and Kotschenreuther2000; Terry Reference Terry2000). Tokamak zonal flows, and the related geodesic acoustic mode (GAM) oscillations, have been widely studied (Itoh et al.
Reference Itoh, Itoh, Diamond, Hahm, Fujisawa, Tynan, Yagi and Nagashima2006; Sugama & Watanabe Reference Sugama and Watanabe2006a
,Reference Sugama and Watanabe
b
, Reference Sugama and Watanabe2009). In particular, an initial radial electric field,
$E_{r}$
can suppress turbulence through generation of zonal flows (Dorland et al.
Reference Dorland, Jenko, Kotschenreuther and Rogers2000; Rogers, Dorland & Kotschenreuther Reference Rogers, Dorland and Kotschenreuther2000; Terry Reference Terry2000). Tokamak zonal flows, and the related geodesic acoustic mode (GAM) oscillations, have been widely studied (Itoh et al.
Reference Itoh, Itoh, Diamond, Hahm, Fujisawa, Tynan, Yagi and Nagashima2006; Sugama & Watanabe Reference Sugama and Watanabe2006a
,Reference Sugama and Watanabe
b
, Reference Sugama and Watanabe2009). In particular, an initial radial electric field,
![]() $E_{r}(0)$
, in an axisymmetric tokamak results in GAM oscillations. In a collisionless system, the GAMs Landau damp. It has been shown by Rosenbluth and Hinton (RH) (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) that, in the asymptotic steady state of this initial value problem, there persists a residual electric field,
$E_{r}(0)$
, in an axisymmetric tokamak results in GAM oscillations. In a collisionless system, the GAMs Landau damp. It has been shown by Rosenbluth and Hinton (RH) (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) that, in the asymptotic steady state of this initial value problem, there persists a residual electric field,
![]() $E_{r}(\infty )$
, and an associated parallel zonal flow. RH showed that the initial and final electric fields are related according to
$E_{r}(\infty )$
, and an associated parallel zonal flow. RH showed that the initial and final electric fields are related according to
![]() $E_{r}(0)=(1+{\mathcal{D}})E_{r}(\infty )$
, where
$E_{r}(0)=(1+{\mathcal{D}})E_{r}(\infty )$
, where
![]() ${\mathcal{D}}\sim 1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
in the large aspect ratio limit. Here,
${\mathcal{D}}\sim 1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
in the large aspect ratio limit. Here,
![]() $q$
is the tokamak safety factor and
$q$
is the tokamak safety factor and
![]() $\unicode[STIX]{x1D716}$
is the tokamak inverse aspect ratio. Since the initial
$\unicode[STIX]{x1D716}$
is the tokamak inverse aspect ratio. Since the initial
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow,
$\boldsymbol{E}\times \boldsymbol{B}$
flow,
![]() $U_{E}(0)$
, has a toroidal component and, thus, an initial toroidal angular momentum, and the final
$U_{E}(0)$
, has a toroidal component and, thus, an initial toroidal angular momentum, and the final
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow,
$\boldsymbol{E}\times \boldsymbol{B}$
flow,
![]() $U_{E}(\infty )\approx (\sqrt{\unicode[STIX]{x1D716}}/q^{2})U_{E}(0)$
is much smaller than the initial, a substantial parallel zonal flow must arise in order to preserve angular momentum (see figure 1). The size of the parallel zonal flow, as found by RH, can be deduced from the geometry of figure 1 to be of order
$U_{E}(\infty )\approx (\sqrt{\unicode[STIX]{x1D716}}/q^{2})U_{E}(0)$
is much smaller than the initial, a substantial parallel zonal flow must arise in order to preserve angular momentum (see figure 1). The size of the parallel zonal flow, as found by RH, can be deduced from the geometry of figure 1 to be of order
![]() $(\unicode[STIX]{x1D716}/q)U_{E}(0)$
.
$(\unicode[STIX]{x1D716}/q)U_{E}(0)$
.

Figure 1. Comparison of initial and final RH flows. The initial
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow
$\boldsymbol{E}\times \boldsymbol{B}$
flow
![]() $U_{E}(0)$
, shown in black, reduces to the final
$U_{E}(0)$
, shown in black, reduces to the final
![]() $U_{E}(\infty )$
, shown in red. To conserve angular momentum, an average parallel flow
$U_{E}(\infty )$
, shown in red. To conserve angular momentum, an average parallel flow
![]() $\langle U_{\Vert }\rangle$
must develop, as shown in purple. The field line makes an angle
$\langle U_{\Vert }\rangle$
must develop, as shown in purple. The field line makes an angle
![]() ${\approx}\unicode[STIX]{x1D716}/q$
with the toroidal (horizontal) direction.
${\approx}\unicode[STIX]{x1D716}/q$
with the toroidal (horizontal) direction.
A question arises when one considers the individual contributions to the angular momentum of the trapped particle (TP) and circulating particle (CP) populations of the plasma. It is well known that in the presence of a radial electric field, trapped particles precess toroidally. The speed of precession is of order
![]() $(q/\unicode[STIX]{x1D716})U_{E}$
and represents a rapid rate inasmuch as it is much larger than
$(q/\unicode[STIX]{x1D716})U_{E}$
and represents a rapid rate inasmuch as it is much larger than
![]() $U_{E}$
. In this paper, we note that the angular momentum in the TP population precessing in the final RH electric field is much larger than the total final RH angular momentum. The TP precession angular momentum is of order
$U_{E}$
. In this paper, we note that the angular momentum in the TP population precessing in the final RH electric field is much larger than the total final RH angular momentum. The TP precession angular momentum is of order
![]() $\sqrt{\unicode[STIX]{x1D716}}(q/\unicode[STIX]{x1D716})U_{E}(\infty )\approx (1/q)U_{E}(0)$
, while the RH calculated final angular momentum is of order
$\sqrt{\unicode[STIX]{x1D716}}(q/\unicode[STIX]{x1D716})U_{E}(\infty )\approx (1/q)U_{E}(0)$
, while the RH calculated final angular momentum is of order
![]() $(\unicode[STIX]{x1D716}/q)U_{E}(0)$
, as discussed above. Here we have accounted for the lower density of the trapped fraction, i.e.
$(\unicode[STIX]{x1D716}/q)U_{E}(0)$
, as discussed above. Here we have accounted for the lower density of the trapped fraction, i.e.
![]() $n^{\text{TP}}\sim O(\sqrt{\unicode[STIX]{x1D716}})$
. This represents an apparent paradox: the TP precession is larger than the total angular momentum by a factor of
$n^{\text{TP}}\sim O(\sqrt{\unicode[STIX]{x1D716}})$
. This represents an apparent paradox: the TP precession is larger than the total angular momentum by a factor of
![]() $(1/\unicode[STIX]{x1D716})$
.
$(1/\unicode[STIX]{x1D716})$
.

Figure 2. Bead-on-wire toy model. The rod models a field line inclined at angle
![]() $\unicode[STIX]{x1D6FC}$
to the toroidal axis. The rod moves rigidly under force
$\unicode[STIX]{x1D6FC}$
to the toroidal axis. The rod moves rigidly under force
![]() $F_{\bot }$
. Coordinates
$F_{\bot }$
. Coordinates
![]() $(r,s)$
measure distances parallel and perpendicular to
$(r,s)$
measure distances parallel and perpendicular to
![]() $\boldsymbol{B}$
. A deeply trapped particle (blue) is constrained to move only along the
$\boldsymbol{B}$
. A deeply trapped particle (blue) is constrained to move only along the
![]() $\unicode[STIX]{x1D701}$
axis. A freely circulating particle (red) moves freely along the rod.
$\unicode[STIX]{x1D701}$
axis. A freely circulating particle (red) moves freely along the rod.
This line of investigation raises further questions when one calculates separately the CP and TP flows associated with the residual RH zonal flows: as we will show, by direct calculation based on conventional drift-kinetic theory, the RH parallel flow for the TPs is found to be of
![]() $O(qU_{E}(\infty ))$
, smaller than the precession drift by
$O(qU_{E}(\infty ))$
, smaller than the precession drift by
![]() $1/\unicode[STIX]{x1D716}$
. In addition, a direct calculation of the net flux surface averaged poloidal flow of the TPs surprisingly gives a non-zero result, namely, a net poloidal flow of
$1/\unicode[STIX]{x1D716}$
. In addition, a direct calculation of the net flux surface averaged poloidal flow of the TPs surprisingly gives a non-zero result, namely, a net poloidal flow of
![]() $O(qU_{E}(\infty ))$
.
$O(qU_{E}(\infty ))$
.
As orientation, we note that the RH calculation was done using a gyrokinetic formulation, thus optimally allowing wavelengths of order the ion gyroradius, and allowing
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flows to be of order the magnetic drifts,
$\boldsymbol{E}\times \boldsymbol{B}$
flows to be of order the magnetic drifts,
![]() $\boldsymbol{v}_{\boldsymbol{D}}$
, i.e.
$\boldsymbol{v}_{\boldsymbol{D}}$
, i.e.
![]() $\boldsymbol{U}_{\boldsymbol{E}}\sim \boldsymbol{v}_{\boldsymbol{D}}$
. However, as will be shown in this paper, the key results of the RH paper can be checked to sustain even in the limit of long wavelengths, or if the super-diamagnetic limit,
$\boldsymbol{U}_{\boldsymbol{E}}\sim \boldsymbol{v}_{\boldsymbol{D}}$
. However, as will be shown in this paper, the key results of the RH paper can be checked to sustain even in the limit of long wavelengths, or if the super-diamagnetic limit,
![]() $\boldsymbol{U}_{\boldsymbol{E}}\gg \boldsymbol{v}_{\boldsymbol{D}}$
, were taken. Based on this observation, we restrict our calculation in the present paper, right from the start, to long wavelengths and super-diamagnetic flows. Accordingly, we use the drift-kinetic equation of Kulsrud as our starting point. This has the advantage of simplifying the calculations we present, as we will show. Particularly, in the super diamagnetic limit, zonal flows, GAMs and sound waves are decoupled from drift waves and a self-consistent nonlinear analysis of these modes can be carried out completely independent of the complications arising from the drift wave turbulence. Further, since the Kulsrud equations preserve the frozen-in theorem, the underlying physics is simpler to interpret. In particular, frozen-in allows a direct analogy to a bead-on-wire toy model (Cerfon & Freidberg Reference Cerfon and Freidberg2011), as we elaborate below.
$\boldsymbol{U}_{\boldsymbol{E}}\gg \boldsymbol{v}_{\boldsymbol{D}}$
, were taken. Based on this observation, we restrict our calculation in the present paper, right from the start, to long wavelengths and super-diamagnetic flows. Accordingly, we use the drift-kinetic equation of Kulsrud as our starting point. This has the advantage of simplifying the calculations we present, as we will show. Particularly, in the super diamagnetic limit, zonal flows, GAMs and sound waves are decoupled from drift waves and a self-consistent nonlinear analysis of these modes can be carried out completely independent of the complications arising from the drift wave turbulence. Further, since the Kulsrud equations preserve the frozen-in theorem, the underlying physics is simpler to interpret. In particular, frozen-in allows a direct analogy to a bead-on-wire toy model (Cerfon & Freidberg Reference Cerfon and Freidberg2011), as we elaborate below.
A toy model can be set-up as follows. We consider a massless rod and two beads of masses
![]() $m_{T},m_{C}$
that can slide freely, without interaction, along the rod; one of them (
$m_{T},m_{C}$
that can slide freely, without interaction, along the rod; one of them (
![]() $m_{T}$
) is further constrained in that it can only move horizontally, that is to say it stays trapped inside a linear horizontal one-dimensional channel. This system is depicted in figure 2. The rod represents a magnetic field line;
$m_{T}$
) is further constrained in that it can only move horizontally, that is to say it stays trapped inside a linear horizontal one-dimensional channel. This system is depicted in figure 2. The rod represents a magnetic field line;
![]() $m_{C}$
represents circulating particles, while
$m_{C}$
represents circulating particles, while
![]() $m_{T}$
represents deeply trapped particles. The rod is inclined at a small angle given by
$m_{T}$
represents deeply trapped particles. The rod is inclined at a small angle given by
![]() $\sin \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D716}/q\ll 1$
. Consider now an external perpendicular force,
$\sin \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D716}/q\ll 1$
. Consider now an external perpendicular force,
![]() $F_{\bot }$
, acting on the rod, as shown in the figure. We define the constrained Newton’s equation as
$F_{\bot }$
, acting on the rod, as shown in the figure. We define the constrained Newton’s equation as
![]() $M\ddot{s}=F_{\bot }$
, where
$M\ddot{s}=F_{\bot }$
, where
![]() $s$
is the distance measured along
$s$
is the distance measured along
![]() $F_{\bot }$
,
$F_{\bot }$
,
![]() $M$
is an effective mass and
$M$
is an effective mass and
![]() ${\dot{s}}$
is the speed of the rod in the laboratory frame. The Lagrangian for this system is
${\dot{s}}$
is the speed of the rod in the laboratory frame. The Lagrangian for this system is
leading to the equation of motion,
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \dot{\unicode[STIX]{x1D701}}=\frac{{\dot{s}}}{\sin \unicode[STIX]{x1D6FC}}=(q/\unicode[STIX]{x1D716}){\dot{s}},\quad \ddot{s}=\frac{F_{\bot }}{M},\\ \displaystyle \text{with}\quad M=m_{C}+\frac{m_{T}}{\sin ^{2}\unicode[STIX]{x1D6FC}}=m_{C}+m_{T}\frac{q^{2}}{\unicode[STIX]{x1D716}^{2}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \dot{\unicode[STIX]{x1D701}}=\frac{{\dot{s}}}{\sin \unicode[STIX]{x1D6FC}}=(q/\unicode[STIX]{x1D716}){\dot{s}},\quad \ddot{s}=\frac{F_{\bot }}{M},\\ \displaystyle \text{with}\quad M=m_{C}+\frac{m_{T}}{\sin ^{2}\unicode[STIX]{x1D6FC}}=m_{C}+m_{T}\frac{q^{2}}{\unicode[STIX]{x1D716}^{2}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
This toy model shows the relative rapid precession of the trapped mass, given by
![]() $\dot{\unicode[STIX]{x1D701}}$
. It also shows that the effective mass from the constrained mass,
$\dot{\unicode[STIX]{x1D701}}$
. It also shows that the effective mass from the constrained mass,
![]() $m_{T}$
, is
$m_{T}$
, is
![]() $m_{T}(q^{2}/\unicode[STIX]{x1D716}^{2})$
.
$m_{T}(q^{2}/\unicode[STIX]{x1D716}^{2})$
.
It follows from the toy model that, inasmuch as the trapped particle precession is rapid and the trapped particle population carries a significant angular momentum, we might expect a corresponding effective mass in the RH problem. When this hypothesis is tested, by adding a torque to the drift-kinetic equations (DKE), an effective mass is indeed identified, and found to be of order
![]() $m(1+{\mathcal{D}})$
. This, however, is much smaller than if the rapid TP momentum was included: this can be shown to give an effective mass of
$m(1+{\mathcal{D}})$
. This, however, is much smaller than if the rapid TP momentum was included: this can be shown to give an effective mass of
![]() ${\sim}1+O(n^{\text{TP}}q^{2}/\unicode[STIX]{x1D716}^{2})$
, much larger than the RH effective mass. This heuristic result adds to our original paradox.
${\sim}1+O(n^{\text{TP}}q^{2}/\unicode[STIX]{x1D716}^{2})$
, much larger than the RH effective mass. This heuristic result adds to our original paradox.
Our study in this paper is motivated by an attempt to understand the discrepancy in the individual TP and CP flows and angular momenta, as well as in the naively expected effective mass of the RH problem. The discussion below is organized as follows: In § 2, we present the basic system of equations, consisting of the drift-kinetic equation and the angular momentum conservation equation in axisymmetric toroidal geometry. We then solve the Rosenbluth–Hinton problem in the large flow and long wavelength limit in § 3 and point out the aforementioned discrepancies in the flows. We introduce the shifted coordinates in § 4 and revisit the RH problem in these new coordinates in § 5, to reconcile trapped particle toroidal precession in RH flows. In § 6, we illustrate the role of barely circulating particles in cancelling the large trapped particle precession and thereby explain the smaller overall RH effective mass. Finally, in § 7, we illustrate the role of the second adiabatic invariant in the sub-bounce dynamics of zonal flows. We summarize our results in § 8.
2 Kinetic equations
In this section we present the kinetic equations that are appropriate for studying the physics of the trapped particle precession. We shall only be considering flows that are large compared to the diamagnetic flow and, in principle, can be of the order of poloidal sonic flows. It is then appropriate to use the drift-kinetic equation (DKE) as formulated by Kulsrud (Reference Kulsrud1980). This DKE is derived in the ‘Magnetohydrodynamic (MHD) ordering’ and thus allows large, sonic level
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flows. In the literature it is also referred to as kinetic MHD (Cerfon & Freidberg Reference Cerfon and Freidberg2011; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015; Burby & Sengupta Reference Burby and Sengupta2017). Frieman and Hinton-Wong (Frieman, Davidson & Langdon Reference Frieman, Davidson and Langdon1966; Hinton & Wong Reference Hinton and Wong1985) have obtained equivalent DKEs. A consistent ordering also requires that the parallel electric field
$\boldsymbol{E}\times \boldsymbol{B}$
flows. In the literature it is also referred to as kinetic MHD (Cerfon & Freidberg Reference Cerfon and Freidberg2011; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015; Burby & Sengupta Reference Burby and Sengupta2017). Frieman and Hinton-Wong (Frieman, Davidson & Langdon Reference Frieman, Davidson and Langdon1966; Hinton & Wong Reference Hinton and Wong1985) have obtained equivalent DKEs. A consistent ordering also requires that the parallel electric field
![]() $E_{\Vert }$
be very small compared to
$E_{\Vert }$
be very small compared to
![]() $E_{\bot }$
. In the electrostatic limit (with frequencies much lower than the Alfvénic frequency) the collisionless DKE is given by
$E_{\bot }$
. In the electrostatic limit (with frequencies much lower than the Alfvénic frequency) the collisionless DKE is given by
where
is the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow and
$\boldsymbol{E}\times \boldsymbol{B}$
flow and
![]() $f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. The magnetic field
$f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. The magnetic field
![]() $\boldsymbol{B}$
, in axisymmetry, is given by
$\boldsymbol{B}$
, in axisymmetry, is given by
where,
![]() $R,\unicode[STIX]{x1D701}$
are the usual radial and toroidal angle in an axisymmetric toroidal geometry and
$R,\unicode[STIX]{x1D701}$
are the usual radial and toroidal angle in an axisymmetric toroidal geometry and
![]() $I$
represents the poloidal current through the flux surface
$I$
represents the poloidal current through the flux surface
![]() $\unicode[STIX]{x1D713}$
. Here, the
$\unicode[STIX]{x1D713}$
. Here, the
![]() $E_{\Vert }$
force term is of the same order as the other parallel force terms (the mirror force and inertial forces) in the equation. The above DKE applies for both ions and electrons, though we will assume small electron mass and thus the electron response will be taken to be adiabatic. The system in the electrostatic approximation consists of four variables, namely, the two distribution functions, the potential
$E_{\Vert }$
force term is of the same order as the other parallel force terms (the mirror force and inertial forces) in the equation. The above DKE applies for both ions and electrons, though we will assume small electron mass and thus the electron response will be taken to be adiabatic. The system in the electrostatic approximation consists of four variables, namely, the two distribution functions, the potential
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $E_{\Vert }$
. The potential
$E_{\Vert }$
. The potential
![]() $\unicode[STIX]{x1D711}$
satisfies the ‘MHD ordering’
$\unicode[STIX]{x1D711}$
satisfies the ‘MHD ordering’
![]() $e\unicode[STIX]{x1D711}/T\approx (1/\unicode[STIX]{x1D70C}_{\ast })$
, where
$e\unicode[STIX]{x1D711}/T\approx (1/\unicode[STIX]{x1D70C}_{\ast })$
, where
![]() $T$
is ion/electron temperature and
$T$
is ion/electron temperature and
![]() $\unicode[STIX]{x1D70C}_{\ast }$
is Larmor radius normalized to the system size. These four unknowns are governed by the two DKEs, the quasineutrality condition
$\unicode[STIX]{x1D70C}_{\ast }$
is Larmor radius normalized to the system size. These four unknowns are governed by the two DKEs, the quasineutrality condition
![]() $n_{e}=n_{i}$
, and the equation of conservation of angular momentum, namely (Hassam & Kleva Reference Hassam and Kleva2011)
$n_{e}=n_{i}$
, and the equation of conservation of angular momentum, namely (Hassam & Kleva Reference Hassam and Kleva2011)
where
![]() $\langle \cdot \rangle$
represents a flux surface average (Helander & Sigmar Reference Helander and Sigmar2005), and
$\langle \cdot \rangle$
represents a flux surface average (Helander & Sigmar Reference Helander and Sigmar2005), and
![]() $\unicode[STIX]{x1D70F}_{\bot }$
is a toroidal torque due to a perpendicular force
$\unicode[STIX]{x1D70F}_{\bot }$
is a toroidal torque due to a perpendicular force
![]() $F_{\bot }$
. The latter represents an external force, such as from a neutral beam, that could accelerate the
$F_{\bot }$
. The latter represents an external force, such as from a neutral beam, that could accelerate the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow. It can be shown that in axisymmetric geometry, the equation governing the angular momentum (2.4) is identical to the radial current quasineutrality condition. This equivalence is shown in appendix C. For the present purposes, we will find the former equation to be more convenient. It can also be shown that although the effects of curvature and grad B drifts do not appear in the DKE (2.1), they are fully retained in the current quasineutrality equation (and hence in (2.4)) through the divergence of the Chew–Goldberger–Low (CGL) pressure tensor. This allows us to capture the lowest-order banana width effects that are crucial for the neoclassical shielding effect discussed in RH’s original calculation.
$\boldsymbol{E}\times \boldsymbol{B}$
flow. It can be shown that in axisymmetric geometry, the equation governing the angular momentum (2.4) is identical to the radial current quasineutrality condition. This equivalence is shown in appendix C. For the present purposes, we will find the former equation to be more convenient. It can also be shown that although the effects of curvature and grad B drifts do not appear in the DKE (2.1), they are fully retained in the current quasineutrality equation (and hence in (2.4)) through the divergence of the Chew–Goldberger–Low (CGL) pressure tensor. This allows us to capture the lowest-order banana width effects that are crucial for the neoclassical shielding effect discussed in RH’s original calculation.
In this paper, we will only be concerned with time scales which are subsonic, i.e.
![]() $\text{d}/\text{d}t\ll c_{s}/qR$
. In this limit, as we will show more precisely later,
$\text{d}/\text{d}t\ll c_{s}/qR$
. In this limit, as we will show more precisely later,
![]() $E_{\Vert }$
is small and can be neglected. In that case, the system can be closed by simply using the DKE for ions, equation (2.1), and the angular momentum conservation equation (2.4). As a further simplification, we will order
$E_{\Vert }$
is small and can be neglected. In that case, the system can be closed by simply using the DKE for ions, equation (2.1), and the angular momentum conservation equation (2.4). As a further simplification, we will order
![]() $q\gg 1$
but
$q\gg 1$
but
![]() $U_{E}\sim v_{th}/q$
. In this ordering, the nonlinear in
$U_{E}\sim v_{th}/q$
. In this ordering, the nonlinear in
![]() $U_{E}$
terms in the DKE can be neglected compared with cross-terms in
$U_{E}$
terms in the DKE can be neglected compared with cross-terms in
![]() $v_{\Vert }$
and
$v_{\Vert }$
and
![]() $U_{E}$
, since
$U_{E}$
, since
![]() $|v_{\Vert }\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{b}\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}|\boldsymbol{ : }|\boldsymbol{b}\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}|\sim 1:1/q$
. Given these orderings, equation (2.1) can be recast as
$|v_{\Vert }\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{b}\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}|\boldsymbol{ : }|\boldsymbol{b}\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{ : }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}|\sim 1:1/q$
. Given these orderings, equation (2.1) can be recast as
We now use the form for
![]() $\boldsymbol{U}_{\boldsymbol{E}}$
, equation (2.2), to simplify (2.5). In particular,
$\boldsymbol{U}_{\boldsymbol{E}}$
, equation (2.2), to simplify (2.5). In particular,
![]() $\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D73F}=\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}B/B$
, in the low
$\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D73F}=\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}B/B$
, in the low
![]() $\unicode[STIX]{x1D6FD}$
limit. We also assume axisymmetry and thus
$\unicode[STIX]{x1D6FD}$
limit. We also assume axisymmetry and thus
![]() $\boldsymbol{B}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=IB\unicode[STIX]{x1D735}_{\Vert }$
, where
$\boldsymbol{B}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=IB\unicode[STIX]{x1D735}_{\Vert }$
, where
![]() $\unicode[STIX]{x1D735}_{\Vert }=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
. Given these, (2.5) can be recast to the form
$\unicode[STIX]{x1D735}_{\Vert }=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
. Given these, (2.5) can be recast to the form
where
![]() $f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. We will now use (2.6) and (2.4) as the closed set of equations for the two variables
$f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. We will now use (2.6) and (2.4) as the closed set of equations for the two variables
![]() $f$
and
$f$
and
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
As a closing remark, we reiterate that the large
![]() $q$
assumption has been made mainly to simplify the analysis, since it decouples the sound dynamics from the GAM dynamics. A calculation for
$q$
assumption has been made mainly to simplify the analysis, since it decouples the sound dynamics from the GAM dynamics. A calculation for
![]() $q\sim 1$
can be done and has been included in appendix D.
$q\sim 1$
can be done and has been included in appendix D.
3 Sub-bounce dynamics and the RH problem
In this section, we use (2.4) and (2.6) to study the sub-bounce frequency response of the system. In particular, we will study the zonal flows in response to an externally applied quasi-static force perpendicular to the magnetic field. This approach has the simplification that GAMs are not excited but nevertheless contains all the zonal flow physics that is of interest. We note that RH obtained a sub-bounce response to the gyrokinetic equation, where they self consistently assumed drift ordering, small flows and short perpendicular wavenumber
![]() $k_{\bot }$
, such that
$k_{\bot }$
, such that
![]() $k_{\bot }\unicode[STIX]{x1D70C}\sim 1,\unicode[STIX]{x1D70C}$
being the Larmor radius. We will show that the RH zonal flows and the long wavelength RH coefficient Xiao, Catto & Molvig (Reference Xiao, Catto and Molvig2007) are obtained self-consistently from our approach.
$k_{\bot }\unicode[STIX]{x1D70C}\sim 1,\unicode[STIX]{x1D70C}$
being the Larmor radius. We will show that the RH zonal flows and the long wavelength RH coefficient Xiao, Catto & Molvig (Reference Xiao, Catto and Molvig2007) are obtained self-consistently from our approach.
We perform a linear analysis of the kinetic system (2.4), (2.6) with the electrostatic potential as a small perturbation. We start with an equilibrium,
![]() $F_{0}$
, with zero flow. From (2.6) we find that the equilibrium distribution function
$F_{0}$
, with zero flow. From (2.6) we find that the equilibrium distribution function
![]() $F_{0}$
satisfies
$F_{0}$
satisfies
which yields
![]() $F_{0}=F_{0}({\mathcal{E}})$
, where
$F_{0}=F_{0}({\mathcal{E}})$
, where
![]() ${\mathcal{E}}=(1/2)v_{\Vert }^{2}+\unicode[STIX]{x1D707}B$
is the energy. This
${\mathcal{E}}=(1/2)v_{\Vert }^{2}+\unicode[STIX]{x1D707}B$
is the energy. This
![]() $F_{0}$
also satisfies the (2.4) with
$F_{0}$
also satisfies the (2.4) with
![]() $\unicode[STIX]{x1D70F}_{\bot }=0$
. We transform from
$\unicode[STIX]{x1D70F}_{\bot }=0$
. We transform from
![]() $v_{\Vert }$
to
$v_{\Vert }$
to
![]() ${\mathcal{E}}$
coordinates. The perturbed distribution function,
${\mathcal{E}}$
coordinates. The perturbed distribution function,
![]() $\tilde{f}$
, satisfies the linearized DKE, which in energy coordinates is given by
$\tilde{f}$
, satisfies the linearized DKE, which in energy coordinates is given by
where
![]() $\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}}$
is the gradient operator at constant
$\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}}$
is the gradient operator at constant
![]() ${\mathcal{E}}$
, and we have used
${\mathcal{E}}$
, and we have used
![]() $v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}}(v_{\Vert })=-\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}_{\Vert }B$
. Since the force is weak, we look for a sub-bounce frequency solution according to the ordering
$v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}}(v_{\Vert })=-\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}_{\Vert }B$
. Since the force is weak, we look for a sub-bounce frequency solution according to the ordering
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t\sim \boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\sim F_{\bot }\ll v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }$
. Expanding
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t\sim \boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\sim F_{\bot }\ll v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }$
. Expanding
![]() $\tilde{f}$
as
$\tilde{f}$
as
![]() $\tilde{f}=\tilde{f}_{0}+\tilde{f}_{1}+\cdots \,$
in the smallness of
$\tilde{f}=\tilde{f}_{0}+\tilde{f}_{1}+\cdots \,$
in the smallness of
![]() $\unicode[STIX]{x2202}_{t}/\unicode[STIX]{x1D714}_{b}\ll 1$
, we obtain, to lowest order,
$\unicode[STIX]{x2202}_{t}/\unicode[STIX]{x1D714}_{b}\ll 1$
, we obtain, to lowest order,
To first order, equation (2.6) becomes
Annihilating the
![]() $\tilde{f}_{1}$
term by bounce averaging (discussed in Helander & Sigmar (Reference Helander and Sigmar2005)), denoted here by overbar as in
$\tilde{f}_{1}$
term by bounce averaging (discussed in Helander & Sigmar (Reference Helander and Sigmar2005)), denoted here by overbar as in
![]() $\overline{f}=\oint (\text{d}lf/v_{\Vert })/\!\oint (\text{d}l/v_{\Vert })$
, we get
$\overline{f}=\oint (\text{d}lf/v_{\Vert })/\!\oint (\text{d}l/v_{\Vert })$
, we get
![]() $\tilde{f}_{0}=\tilde{f}_{0}({\mathcal{E}})$
which can be set to zero since (3.3) is homogeneous. Solving for
$\tilde{f}_{0}=\tilde{f}_{0}({\mathcal{E}})$
which can be set to zero since (3.3) is homogeneous. Solving for
![]() $\tilde{f}_{1}$
from (3.4) we obtain
$\tilde{f}_{1}$
from (3.4) we obtain
where
![]() $g({\mathcal{E}})$
is yet to be determined and
$g({\mathcal{E}})$
is yet to be determined and
![]() $F_{0}^{\prime }\equiv \unicode[STIX]{x2202}_{{\mathcal{E}}}F_{0}$
. To second order we have,
$F_{0}^{\prime }\equiv \unicode[STIX]{x2202}_{{\mathcal{E}}}F_{0}$
. To second order we have,
Annihilation of (3.6) yields
![]() $\overline{\unicode[STIX]{x2202}_{t}\tilde{f}_{1}}=0$
, which gives
$\overline{\unicode[STIX]{x2202}_{t}\tilde{f}_{1}}=0$
, which gives
![]() $g=\overline{(v_{\Vert }/B)}$
. Thus, we get the RH solution for
$g=\overline{(v_{\Vert }/B)}$
. Thus, we get the RH solution for
![]() $\tilde{f}_{1}$
correct to first order (Xiao et al.
Reference Xiao, Catto and Molvig2007), viz.
$\tilde{f}_{1}$
correct to first order (Xiao et al.
Reference Xiao, Catto and Molvig2007), viz.
Let us now check for self-consistency of the above calculation, in particular the neglect of
![]() $E_{\Vert }$
. We can use
$E_{\Vert }$
. We can use
![]() $\tilde{f}_{0}$
and
$\tilde{f}_{0}$
and
![]() $\tilde{f}_{1}$
above to calculate the density. Since
$\tilde{f}_{1}$
above to calculate the density. Since
![]() $\tilde{f}_{0}=0$
, and the first order
$\tilde{f}_{0}=0$
, and the first order
![]() $\tilde{f}_{1}$
is antisymmetric in
$\tilde{f}_{1}$
is antisymmetric in
![]() $v_{\Vert }$
, density remains constant up to second order. Likewise, changes in parallel and perpendicular pressures are also zero because of parity. The elements of the electron pressure tensor can be used to a posteriori calculate
$v_{\Vert }$
, density remains constant up to second order. Likewise, changes in parallel and perpendicular pressures are also zero because of parity. The elements of the electron pressure tensor can be used to a posteriori calculate
![]() $E_{\Vert }$
, as defined in equation (49) of the Kulsrud (Reference Kulsrud1980) manuscript. (For massless electrons,
$E_{\Vert }$
, as defined in equation (49) of the Kulsrud (Reference Kulsrud1980) manuscript. (For massless electrons,
![]() $E_{\Vert }$
is given essentially by the generalized adiabatic electron response, viz.,
$E_{\Vert }$
is given essentially by the generalized adiabatic electron response, viz.,
![]() $neE_{\Vert }=-\boldsymbol{b}\unicode[STIX]{x1D735}\boldsymbol{ : }\boldsymbol{P}_{\boldsymbol{e}}$
.) We find that
$neE_{\Vert }=-\boldsymbol{b}\unicode[STIX]{x1D735}\boldsymbol{ : }\boldsymbol{P}_{\boldsymbol{e}}$
.) We find that
![]() $E_{\Vert }=0$
to lowest order and also zero to first order given the
$E_{\Vert }=0$
to lowest order and also zero to first order given the
![]() $f_{1}$
symmetry. This self-consistently justifies the neglect of
$f_{1}$
symmetry. This self-consistently justifies the neglect of
![]() $E_{\Vert }$
in our calculation above.
$E_{\Vert }$
in our calculation above.
3.1 Rosenbluth–Hinton
 $\Vert$
flows
$\Vert$
flows
We now calculate the parallel flow by taking the
![]() $v_{\Vert }$
moment of
$v_{\Vert }$
moment of
![]() $\tilde{f}=\tilde{f}_{0}+\,\tilde{f}_{1}$
. Since
$\tilde{f}=\tilde{f}_{0}+\,\tilde{f}_{1}$
. Since
![]() $\tilde{f}_{0}=0$
, we have
$\tilde{f}_{0}=0$
, we have
Until now, we have not done a large aspect ratio expansion. However, to evaluate the integrals and compare the leading-order scaling behaviour of the flows with respect to the trapped precession, we shall now consider the inverse aspect ratio
![]() $\unicode[STIX]{x1D716}$
as a small parameter. The analysis is straightforward and has been presented in detail by several authors (Xiao et al.
Reference Xiao, Catto and Molvig2007; Sugama & Watanabe Reference Sugama and Watanabe2009). Here we include a few details for completeness.
$\unicode[STIX]{x1D716}$
as a small parameter. The analysis is straightforward and has been presented in detail by several authors (Xiao et al.
Reference Xiao, Catto and Molvig2007; Sugama & Watanabe Reference Sugama and Watanabe2009). Here we include a few details for completeness.
In the large aspect ratio circular flux surface limit with
![]() $B=B_{0}(1-\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703})$
,
$B=B_{0}(1-\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703})$
,
![]() $\unicode[STIX]{x1D703}$
being the poloidal angle, we find that
$\unicode[STIX]{x1D703}$
being the poloidal angle, we find that
 $$\begin{eqnarray}\displaystyle \overline{\left(\frac{v_{\Vert }}{B}\right)}=\frac{\unicode[STIX]{x03C0}\sqrt{1-\unicode[STIX]{x1D706}(\unicode[STIX]{x1D716}+1)}}{2\text{K}\left(\displaystyle \frac{2\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}}{(\unicode[STIX]{x1D716}+1)\unicode[STIX]{x1D706}-1}\right)}\sqrt{2{\mathcal{E}}},\quad \int _{0}^{1/(1+\unicode[STIX]{x1D716})}\text{d}\unicode[STIX]{x1D706}\overline{\left(\frac{v_{\Vert }}{B}\right)}=\frac{2}{3}\sqrt{2{\mathcal{E}}}(1-1.6\unicode[STIX]{x1D716}^{3/2}+O(\unicode[STIX]{x1D716}^{2})),\hspace{-10.79993pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\left(\frac{v_{\Vert }}{B}\right)}=\frac{\unicode[STIX]{x03C0}\sqrt{1-\unicode[STIX]{x1D706}(\unicode[STIX]{x1D716}+1)}}{2\text{K}\left(\displaystyle \frac{2\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}}{(\unicode[STIX]{x1D716}+1)\unicode[STIX]{x1D706}-1}\right)}\sqrt{2{\mathcal{E}}},\quad \int _{0}^{1/(1+\unicode[STIX]{x1D716})}\text{d}\unicode[STIX]{x1D706}\overline{\left(\frac{v_{\Vert }}{B}\right)}=\frac{2}{3}\sqrt{2{\mathcal{E}}}(1-1.6\unicode[STIX]{x1D716}^{3/2}+O(\unicode[STIX]{x1D716}^{2})),\hspace{-10.79993pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where, K is the complete elliptic integral of the first kind and
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}B_{0}/{\mathcal{E}}$
is the pitch angle variable (Helander & Sigmar Reference Helander and Sigmar2005) with a range of
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}B_{0}/{\mathcal{E}}$
is the pitch angle variable (Helander & Sigmar Reference Helander and Sigmar2005) with a range of
![]() $(0,1/(1+\unicode[STIX]{x1D716}))$
. The lower limit corresponds to CPs with
$(0,1/(1+\unicode[STIX]{x1D716}))$
. The lower limit corresponds to CPs with
![]() $\unicode[STIX]{x1D707}=0$
and the upper limit corresponds to barely circulating particles on the separatrix with
$\unicode[STIX]{x1D707}=0$
and the upper limit corresponds to barely circulating particles on the separatrix with
![]() ${\mathcal{E}}=\unicode[STIX]{x1D707}B_{\text{max}}=\unicode[STIX]{x1D707}B_{0}(1+\unicode[STIX]{x1D716})$
. In terms of
${\mathcal{E}}=\unicode[STIX]{x1D707}B_{\text{max}}=\unicode[STIX]{x1D707}B_{0}(1+\unicode[STIX]{x1D716})$
. In terms of
![]() $\unicode[STIX]{x1D706}$
, we have
$\unicode[STIX]{x1D706}$
, we have
![]() $v_{\Vert }\,\text{d}^{3}v=2\unicode[STIX]{x03C0}(B/B_{0}){\mathcal{E}}\,\text{d}\unicode[STIX]{x1D706}\,\text{d}{\mathcal{E}}$
. Assuming
$v_{\Vert }\,\text{d}^{3}v=2\unicode[STIX]{x03C0}(B/B_{0}){\mathcal{E}}\,\text{d}\unicode[STIX]{x1D706}\,\text{d}{\mathcal{E}}$
. Assuming
![]() $F_{0}$
to be a Maxwellian and performing the energy integral
$F_{0}$
to be a Maxwellian and performing the energy integral
![]() ${\mathcal{E}}$
from
${\mathcal{E}}$
from
![]() $(0,\infty )$
, we obtain
$(0,\infty )$
, we obtain
where
![]() $I\unicode[STIX]{x1D711}^{\prime }/B$
can be seen to be of
$I\unicode[STIX]{x1D711}^{\prime }/B$
can be seen to be of
![]() $O(qU_{E}/\unicode[STIX]{x1D716})$
, which is the precession drift. We note that the parallel flow, (3.10), is smaller than the toroidal precession speed expected of the TPs, by a factor of
$O(qU_{E}/\unicode[STIX]{x1D716})$
, which is the precession drift. We note that the parallel flow, (3.10), is smaller than the toroidal precession speed expected of the TPs, by a factor of
![]() $\unicode[STIX]{x1D716}$
. In particular, given the large precession, we find a much larger angular momentum contribution from the TPs (even given the lower density fraction of this species). To examine this further, we calculate separately for trapped and circulating species the parallel flows resulting from the RH solution. Using (3.8) and integrating only over
$\unicode[STIX]{x1D716}$
. In particular, given the large precession, we find a much larger angular momentum contribution from the TPs (even given the lower density fraction of this species). To examine this further, we calculate separately for trapped and circulating species the parallel flows resulting from the RH solution. Using (3.8) and integrating only over
![]() ${\mathcal{E}}>\unicode[STIX]{x1D707}B_{\text{max}}$
, we get for circulating particles (CP)
${\mathcal{E}}>\unicode[STIX]{x1D707}B_{\text{max}}$
, we get for circulating particles (CP)
where we have used an expansion in
![]() $\unicode[STIX]{x1D716}$
. This flow speed is
$\unicode[STIX]{x1D716}$
. This flow speed is
![]() $O(qU_{E})$
as expected. Correspondingly, for the trapped particles (TP), we integrate inside the separatrix over
$O(qU_{E})$
as expected. Correspondingly, for the trapped particles (TP), we integrate inside the separatrix over
![]() $\unicode[STIX]{x1D707}B_{min}<{\mathcal{E}}<\unicode[STIX]{x1D707}B_{\text{max}}$
to get for the parallel flow,
$\unicode[STIX]{x1D707}B_{min}<{\mathcal{E}}<\unicode[STIX]{x1D707}B_{\text{max}}$
to get for the parallel flow,
The total parallel flow is obtained by summing the last two expressions, giving
in agreement with (3.10). Note that, we expect to see a large toroidal precession from the TPs. Instead, we find from (3.12), the flow of the TP to be
![]() $O(qU_{E})$
since the density of TP is
$O(qU_{E})$
since the density of TP is
![]() $O(\sqrt{\unicode[STIX]{x1D716}})$
. This is smaller than the toroidal precession drift of the TPs by a factor of
$O(\sqrt{\unicode[STIX]{x1D716}})$
. This is smaller than the toroidal precession drift of the TPs by a factor of
![]() $\unicode[STIX]{x1D716}$
. Further, if we calculate the poloidal velocity of the trapped particle fraction, we find
$\unicode[STIX]{x1D716}$
. Further, if we calculate the poloidal velocity of the trapped particle fraction, we find
the trapped particles seem to have a non-zero bounce averaged poloidal flow. This is puzzling, since for adiabatic changes we expect TPs to have a purely toroidal flow.
3.2 Angular momentum conservation and the effective mass
Inserting the parallel flow (3.10) into (2.4), we get the angular momentum equation in the form
From (3.15) we see that the factor multiplying
![]() $\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D711}}$
is the Rosenbluth–Hinton coefficient. As clarification, we note that we have calculated the RH coefficient using the angular momentum equation. An equivalent way of doing this would be to use quasineutrality of the charged species. In the former approach, which is also a statement of quasineutrality in axisymmetry, only linear terms in
$\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D711}}$
is the Rosenbluth–Hinton coefficient. As clarification, we note that we have calculated the RH coefficient using the angular momentum equation. An equivalent way of doing this would be to use quasineutrality of the charged species. In the former approach, which is also a statement of quasineutrality in axisymmetry, only linear terms in
![]() $v_{\Vert }$
are needed. In the latter approach, the calculation would have to be carried to a quadratic level (Xiao et al.
Reference Xiao, Catto and Molvig2007).
$v_{\Vert }$
are needed. In the latter approach, the calculation would have to be carried to a quadratic level (Xiao et al.
Reference Xiao, Catto and Molvig2007).
Equation (3.15) is of the form of Newton’s law
![]() $\unicode[STIX]{x1D70F}_{\bot }=Ma$
where the acceleration is the rate of change of
$\unicode[STIX]{x1D70F}_{\bot }=Ma$
where the acceleration is the rate of change of
![]() $U_{E}$
and
$U_{E}$
and
![]() $M$
is the effective mass. Thus, we can say the RH coefficient plays the role of an effective mass. The
$M$
is the effective mass. Thus, we can say the RH coefficient plays the role of an effective mass. The
![]() $(1+2q^{2})$
coefficient is the well-known Pfirsch–Schluter coefficient (Hassam & Kulsrud Reference Hassam and Kulsrud1978; Hirshman Reference Hirshman1978) arising from the circulating particles response. We see that
$(1+2q^{2})$
coefficient is the well-known Pfirsch–Schluter coefficient (Hassam & Kulsrud Reference Hassam and Kulsrud1978; Hirshman Reference Hirshman1978) arising from the circulating particles response. We see that
![]() $1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
is the dominant term. Using
$1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
is the dominant term. Using
![]() $\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}/(2\unicode[STIX]{x03C0})(1+\cos \unicode[STIX]{x1D703})^{3/2}\approx 1.2$
, it can be checked from (3.11), (3.12) that the averaged TP and CP flows are approximately in the ratio
$\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}/(2\unicode[STIX]{x03C0})(1+\cos \unicode[STIX]{x1D703})^{3/2}\approx 1.2$
, it can be checked from (3.11), (3.12) that the averaged TP and CP flows are approximately in the ratio
![]() $1.2:0.4$
. The effective mass contributions are, respectively,
$1.2:0.4$
. The effective mass contributions are, respectively,
![]() $1.2q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
due to the TPs and
$1.2q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
due to the TPs and
![]() $0.4q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
due to the CPs.
$0.4q^{2}/\sqrt{\unicode[STIX]{x1D716}}$
due to the CPs.
Given that we are doing a perturbative analysis, one might certainly question the validity of trapped particles staying trapped. However, we could consider very deeply trapped particles which cannot be detrapped easily. Moreover, it must be realized that we can make the dynamics arbitrarily slow by appropriately weakening
![]() $\unicode[STIX]{x1D70F}_{\bot }$
and thus approach a quasi-static equilibrium. In such a situation we do expect to have well confined trapped particles. In each case, the above analysis would point out to discrepancies in trapped particle flows and contribution to the effective mass.
$\unicode[STIX]{x1D70F}_{\bot }$
and thus approach a quasi-static equilibrium. In such a situation we do expect to have well confined trapped particles. In each case, the above analysis would point out to discrepancies in trapped particle flows and contribution to the effective mass.
In order to understand the discrepancy between the RH solution and the expected TP contribution to the flows and, possibly, effective mass, we will now take a different approach to solve the low frequency RH problem.
4 Shifted coordinates
As shown earlier, in axisymmetry we can rewrite the DKE as
where
![]() $f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. We reiterate that this equation is valid for large
$f=f(v_{\Vert },\unicode[STIX]{x1D707},\boldsymbol{x},t)$
. We reiterate that this equation is valid for large
![]() $q$
and with
$q$
and with
![]() $U_{E}$
ordered to be of the same order as
$U_{E}$
ordered to be of the same order as
![]() $v_{th}/q$
. It can be deduced from this equation, by examining the characteristics, that
$v_{th}/q$
. It can be deduced from this equation, by examining the characteristics, that
![]() ${\mathcal{E}}_{\ast }=(1/2)v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+I\unicode[STIX]{x1D711}^{\prime }(v_{\Vert }/B)$
is a constant of motion, as can be checked by a direct substitution into (4.1). Physically, the difference
${\mathcal{E}}_{\ast }=(1/2)v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+I\unicode[STIX]{x1D711}^{\prime }(v_{\Vert }/B)$
is a constant of motion, as can be checked by a direct substitution into (4.1). Physically, the difference
![]() $I\unicode[STIX]{x1D711}^{\prime }v_{\Vert }/B$
between
$I\unicode[STIX]{x1D711}^{\prime }v_{\Vert }/B$
between
![]() ${\mathcal{E}}_{\ast }$
and
${\mathcal{E}}_{\ast }$
and
![]() ${\mathcal{E}}$
is due to the electrostatic potential difference experienced by a particle undergoing a banana orbit. We have shown this in appendix A and it is also discussed elsewhere (Hassam Reference Hassam1996; Kagan & Catto Reference Kagan and Catto2008; Landreman & Catto Reference Landreman and Catto2010). Thus, any distribution function
${\mathcal{E}}$
is due to the electrostatic potential difference experienced by a particle undergoing a banana orbit. We have shown this in appendix A and it is also discussed elsewhere (Hassam Reference Hassam1996; Kagan & Catto Reference Kagan and Catto2008; Landreman & Catto Reference Landreman and Catto2010). Thus, any distribution function
![]() $f({\mathcal{E}}_{\ast })$
defines an equilibrium for kinetic MHD in an axisymmetric tokamak. Hence we shift to
$f({\mathcal{E}}_{\ast })$
defines an equilibrium for kinetic MHD in an axisymmetric tokamak. Hence we shift to
![]() $({\mathcal{E}}_{\ast },v_{\Vert \ast })$
coordinates, defined as follows:
$({\mathcal{E}}_{\ast },v_{\Vert \ast })$
coordinates, defined as follows:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{E}}_{\ast }=\frac{1}{2}v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+I\unicode[STIX]{x1D711}^{\prime }\frac{v_{\Vert }}{B}={\mathcal{E}}+\frac{I\unicode[STIX]{x1D711}^{\prime }v_{\Vert }}{B},\\ \displaystyle v_{\Vert \ast }=v_{\Vert }+\frac{I\unicode[STIX]{x1D711}^{\prime }}{B},\quad \text{d}^{3}v=\sum _{\unicode[STIX]{x1D70E}}\frac{B\,\text{d}\unicode[STIX]{x1D707}\,\text{d}{\mathcal{E}}_{\ast }}{|v_{\Vert \ast }|}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{E}}_{\ast }=\frac{1}{2}v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+I\unicode[STIX]{x1D711}^{\prime }\frac{v_{\Vert }}{B}={\mathcal{E}}+\frac{I\unicode[STIX]{x1D711}^{\prime }v_{\Vert }}{B},\\ \displaystyle v_{\Vert \ast }=v_{\Vert }+\frac{I\unicode[STIX]{x1D711}^{\prime }}{B},\quad \text{d}^{3}v=\sum _{\unicode[STIX]{x1D70E}}\frac{B\,\text{d}\unicode[STIX]{x1D707}\,\text{d}{\mathcal{E}}_{\ast }}{|v_{\Vert \ast }|}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Here,
![]() $\unicode[STIX]{x1D70E}=\text{sign }v_{\Vert \ast }$
denotes the three regions in energy space, namely, the trapped population and the rightward and leftward moving circulating particle populations. The coordinate
$\unicode[STIX]{x1D70E}=\text{sign }v_{\Vert \ast }$
denotes the three regions in energy space, namely, the trapped population and the rightward and leftward moving circulating particle populations. The coordinate
![]() $v_{\Vert \ast }$
is defined with respect to coordinates shifted downward in
$v_{\Vert \ast }$
is defined with respect to coordinates shifted downward in
![]() $v_{\Vert }$
.
$v_{\Vert }$
.
![]() ${\mathcal{E}}_{\ast }$
is then a downshifted energy-like coordinate, centred about
${\mathcal{E}}_{\ast }$
is then a downshifted energy-like coordinate, centred about
![]() $v_{\Vert \ast }=0$
. This shift, of size
$v_{\Vert \ast }=0$
. This shift, of size
![]() $\unicode[STIX]{x1D6E5}=I\unicode[STIX]{x1D711}^{\prime }/B\approx qU_{E}/\unicode[STIX]{x1D716}$
in
$\unicode[STIX]{x1D6E5}=I\unicode[STIX]{x1D711}^{\prime }/B\approx qU_{E}/\unicode[STIX]{x1D716}$
in
![]() $v_{\Vert }$
, is depicted in figure 3. In
$v_{\Vert }$
, is depicted in figure 3. In
![]() ${\mathcal{E}}_{\ast }$
coordinates, centred with respect to
${\mathcal{E}}_{\ast }$
coordinates, centred with respect to
![]() $v_{\Vert \ast }$
, the DKE, equation (2.5) or (4.1), becomes
$v_{\Vert \ast }$
, the DKE, equation (2.5) or (4.1), becomes
where
![]() $f=f({\mathcal{E}}_{\ast },\unicode[STIX]{x1D707},\unicode[STIX]{x1D713},\unicode[STIX]{x1D703},t)$
and
$f=f({\mathcal{E}}_{\ast },\unicode[STIX]{x1D707},\unicode[STIX]{x1D713},\unicode[STIX]{x1D703},t)$
and
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$
is at constant
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$
is at constant
![]() ${\mathcal{E}}_{\ast }$
. The angular momentum equation, also recast in
${\mathcal{E}}_{\ast }$
. The angular momentum equation, also recast in
![]() ${\mathcal{E}}_{\ast }$
coordinates, is now given by
${\mathcal{E}}_{\ast }$
coordinates, is now given by
In what follows, we shall use equations (4.2), (4.3), (4.4).

Figure 3. Contours of constant
![]() ${\mathcal{E}}$
(a) and
${\mathcal{E}}$
(a) and
![]() ${\mathcal{E}}_{\ast }$
(b). The downward shift is given by the precession drift
${\mathcal{E}}_{\ast }$
(b). The downward shift is given by the precession drift
![]() $(=I\unicode[STIX]{x1D711}^{\prime }/B\sim qU_{E}/\unicode[STIX]{x1D716})$
.
$(=I\unicode[STIX]{x1D711}^{\prime }/B\sim qU_{E}/\unicode[STIX]{x1D716})$
.
5 The sub-bounce problem revisited
To make contact with the RH problem, we begin by performing a
![]() $\unicode[STIX]{x2202}_{t}\ll \unicode[STIX]{x1D714}_{b}$
expansion, but allowing a large
$\unicode[STIX]{x2202}_{t}\ll \unicode[STIX]{x1D714}_{b}$
expansion, but allowing a large
![]() $U_{E}\sim v_{th}/q$
, which corresponds to a finite downward shift as shown in figure 3. This approach allows for a more transparent calculation. To dominant order, we have from (4.3)
$U_{E}\sim v_{th}/q$
, which corresponds to a finite downward shift as shown in figure 3. This approach allows for a more transparent calculation. To dominant order, we have from (4.3)
Annihilating the
![]() ${\unicode[STIX]{x1D735}_{\Vert }}_{{\mathcal{E}}_{\ast }}$
operator by bounce averaging gives a constraint equation for
${\unicode[STIX]{x1D735}_{\Vert }}_{{\mathcal{E}}_{\ast }}$
operator by bounce averaging gives a constraint equation for
![]() $f({\mathcal{E}}_{\ast },t)$
, viz.
$f({\mathcal{E}}_{\ast },t)$
, viz.
The constraint on
![]() $f$
introduces a
$f$
introduces a
![]() $\unicode[STIX]{x1D70E}$
dependence. Equation (5.2) and the angular momentum relation (4.4), with
$\unicode[STIX]{x1D70E}$
dependence. Equation (5.2) and the angular momentum relation (4.4), with
![]() $f=f({\mathcal{E}}_{\ast },t)$
, form a closed set for the nonlinear
$f=f({\mathcal{E}}_{\ast },t)$
, form a closed set for the nonlinear
![]() $\{f,\unicode[STIX]{x1D711}^{\prime }\}$
system. We now do a subsidiary expansion in small
$\{f,\unicode[STIX]{x1D711}^{\prime }\}$
system. We now do a subsidiary expansion in small
![]() $(I\unicode[STIX]{x1D711}^{\prime }/B)\ll v_{th}$
, denoting
$(I\unicode[STIX]{x1D711}^{\prime }/B)\ll v_{th}$
, denoting
![]() $f=f_{0}+f_{1}+\cdots \,$
(here, the subscript indices are not the same expansion parameter as in earlier sections). From (5.2), the corresponding lowest- and first-order equations are
$f=f_{0}+f_{1}+\cdots \,$
(here, the subscript indices are not the same expansion parameter as in earlier sections). From (5.2), the corresponding lowest- and first-order equations are
5.1 RH flows
We can now calculate the RH flows from (5.3). For general
![]() $(I\unicode[STIX]{x1D711}^{\prime }/B)/v_{th}$
, the dominant-order parallel flow for either the TP or the CP populations (or both) is
$(I\unicode[STIX]{x1D711}^{\prime }/B)/v_{th}$
, the dominant-order parallel flow for either the TP or the CP populations (or both) is
where, the integrals are to be taken over the appropriate populations and we have used the definition of
![]() $v_{\Vert \ast }$
as in (4.2). If we were to expand in small
$v_{\Vert \ast }$
as in (4.2). If we were to expand in small
![]() $\unicode[STIX]{x1D711}^{\prime }$
, correct to first order, we would insert both
$\unicode[STIX]{x1D711}^{\prime }$
, correct to first order, we would insert both
![]() $f=f_{0}+f_{1}$
in the right-hand side integral in (5.4). However, since
$f=f_{0}+f_{1}$
in the right-hand side integral in (5.4). However, since
![]() $f_{0}$
is independent of
$f_{0}$
is independent of
![]() $\unicode[STIX]{x1D70E}$
for both species, the lowest-order term, proportional to
$\unicode[STIX]{x1D70E}$
for both species, the lowest-order term, proportional to
![]() $\unicode[STIX]{x1D70E}|v_{\Vert \ast }|f_{0}$
, will vanish, by symmetry (with respect to the
$\unicode[STIX]{x1D70E}|v_{\Vert \ast }|f_{0}$
, will vanish, by symmetry (with respect to the
![]() ${\mathcal{E}}_{\ast }$
coordinates). To first order then, two terms must be retained: one from the
${\mathcal{E}}_{\ast }$
coordinates). To first order then, two terms must be retained: one from the
![]() $\unicode[STIX]{x1D711}^{\prime }$
term in the parenthesis and the other from the
$\unicode[STIX]{x1D711}^{\prime }$
term in the parenthesis and the other from the
![]() $f_{1}$
term. This yields the expression
$f_{1}$
term. This yields the expression
We emphasize that the second term in the integrand appears because of a ‘shift in the Jacobian’, and acts on the lowest order
![]() $f$
. In particular, note that even for small
$f$
. In particular, note that even for small
![]() $\unicode[STIX]{x1D711}^{\prime }$
, this term must be retained as it is of the same order as the preceding
$\unicode[STIX]{x1D711}^{\prime }$
, this term must be retained as it is of the same order as the preceding
![]() $f_{1}$
term. Inserting for
$f_{1}$
term. Inserting for
![]() $f_{1}$
in (5.5), we have
$f_{1}$
in (5.5), we have
where, for TPs, we recall that
![]() $\overline{(v_{\Vert \ast }/B)}=0$
. (Equation (5.6) can be compared with (3.8), the corresponding equation from the previous section; the latter equation does not have a Jacobian shift term.)
$\overline{(v_{\Vert \ast }/B)}=0$
. (Equation (5.6) can be compared with (3.8), the corresponding equation from the previous section; the latter equation does not have a Jacobian shift term.)
Since
![]() $\overline{(v_{\Vert \ast }/B)}=0$
for TPs, the TP parallel flow from (5.6) is
$\overline{(v_{\Vert \ast }/B)}=0$
for TPs, the TP parallel flow from (5.6) is
where
is the trapped particle density. This parallel flow is a rigid rotor flow and, we note, has an amplitude that corresponds precisely to the precession drift speed. We can also calculate the net poloidal velocity of the TPs,
using (5.7), and we find
This is zero as expected. Thus, as we can see, the previously discussed discrepancies in TP parallel flow and TP theta flow have been resolved; we note that the ‘Jacobian shift’ is responsible for resolving the discrepancies. Importance of an analogous shift in a time dependent problem has been recently shown by Burby (Reference Burby2016).
The CP flow can now be calculated from (5.6) assuming that the lowest-order distribution function is a Maxwellian. This gives us
 $$\begin{eqnarray}\displaystyle (nU)_{\Vert }^{\text{CP}} & = & \displaystyle n_{0}\frac{I\unicode[STIX]{x1D711}^{\prime }}{B_{0}}\left(\sqrt{\unicode[STIX]{x1D716}(1+\cos \unicode[STIX]{x1D703})}-2\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}^{3/2}\left(-1.6+\frac{(\cos \unicode[STIX]{x1D703}+\cos 2\unicode[STIX]{x1D703})}{2\sqrt{\cos \unicode[STIX]{x1D703}+1}}\right)+O(\unicode[STIX]{x1D716}^{2})\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (nU)_{\Vert }^{\text{CP}} & = & \displaystyle n_{0}\frac{I\unicode[STIX]{x1D711}^{\prime }}{B_{0}}\left(\sqrt{\unicode[STIX]{x1D716}(1+\cos \unicode[STIX]{x1D703})}-2\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}^{3/2}\left(-1.6+\frac{(\cos \unicode[STIX]{x1D703}+\cos 2\unicode[STIX]{x1D703})}{2\sqrt{\cos \unicode[STIX]{x1D703}+1}}\right)+O(\unicode[STIX]{x1D716}^{2})\right).\end{eqnarray}$$
Note that, to lowest order, the CP flow is a rigid rotor flow, equal and opposite to the TP flow. Thus from equations (5.11), (5.7) we see that to dominant order,
![]() $(nU)_{\Vert }^{\text{CP}}+(nU)_{\Vert }^{\text{TP}}\approx 0$
. This says that in the accounting of parallel flows for angular momentum, the large TP precession flow does not materialize as a large parallel flow since it is completely balanced by an oppositely directed CP flow. The
$(nU)_{\Vert }^{\text{CP}}+(nU)_{\Vert }^{\text{TP}}\approx 0$
. This says that in the accounting of parallel flows for angular momentum, the large TP precession flow does not materialize as a large parallel flow since it is completely balanced by an oppositely directed CP flow. The
![]() $\cos \unicode[STIX]{x1D703}$
term in the CP flow is the usual harmonic parallel flow. The net poloidal velocity of the CPs is:
$\cos \unicode[STIX]{x1D703}$
term in the CP flow is the usual harmonic parallel flow. The net poloidal velocity of the CPs is:
Hence the poloidal velocity of the CPs is basically the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow, consistent with expectations.
$\boldsymbol{E}\times \boldsymbol{B}$
flow, consistent with expectations.
Summing over the TP and CP flows, we get the total RH flow to be
Although the individual flows, equations (5.7), (5.11), differ from the ones obtained using standard neoclassical methods, equations (3.12), (3.11), the total flows, equations (5.13), (3.13) from our calculation, match the RH solution. Remarkably, the large TP precession flow is balanced by an equally large and oppositely directed flow from the barely CPs.
5.2 RH Effective mass
We now consider the effective mass coefficient. For this, we would insert
![]() $f_{0}+f_{1}$
just found into the second term of the angular momentum equation (4.4). The second term
$f_{0}+f_{1}$
just found into the second term of the angular momentum equation (4.4). The second term
is just the time derivative of the parallel flow, viz.,
![]() $\unicode[STIX]{x2202}_{t}\langle (I/B)(nU_{\Vert }^{\text{total}})\rangle$
. A general expression for the parallel flow (for small
$\unicode[STIX]{x2202}_{t}\langle (I/B)(nU_{\Vert }^{\text{total}})\rangle$
. A general expression for the parallel flow (for small
![]() $\unicode[STIX]{x1D711}^{\prime }$
) is given by (5.6). Inserting this expression as discussed, we obtain the angular momentum equation as
$\unicode[STIX]{x1D711}^{\prime }$
) is given by (5.6). Inserting this expression as discussed, we obtain the angular momentum equation as
Rearranging, we find
where,
 $$\begin{eqnarray}\displaystyle {\mathcal{D}} & = & \displaystyle \left\langle \left(\frac{1}{B^{2}}+\int _{\text{CP}}\sum _{\unicode[STIX]{x1D70E}}\frac{B\,\text{d}\unicode[STIX]{x1D707}\,\text{d}{\mathcal{E}}_{\ast }}{|v_{\Vert \ast }|n_{0}}\frac{v_{\Vert \ast }}{B}\overline{\left(\frac{v_{\Vert \ast }}{B}\right)}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}{\mathcal{E}}_{\ast }}\right)\right\rangle \left\langle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{I^{2}B^{2}}\right\rangle ^{-1}\nonumber\\ \displaystyle & {\approx} & \displaystyle {\displaystyle \frac{q^{2}}{\unicode[STIX]{x1D716}^{2}}}\langle nU_{\Vert }^{\text{total}}\rangle /(I\unicode[STIX]{x1D711}^{\prime }/B_{0}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}} & = & \displaystyle \left\langle \left(\frac{1}{B^{2}}+\int _{\text{CP}}\sum _{\unicode[STIX]{x1D70E}}\frac{B\,\text{d}\unicode[STIX]{x1D707}\,\text{d}{\mathcal{E}}_{\ast }}{|v_{\Vert \ast }|n_{0}}\frac{v_{\Vert \ast }}{B}\overline{\left(\frac{v_{\Vert \ast }}{B}\right)}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}{\mathcal{E}}_{\ast }}\right)\right\rangle \left\langle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{I^{2}B^{2}}\right\rangle ^{-1}\nonumber\\ \displaystyle & {\approx} & \displaystyle {\displaystyle \frac{q^{2}}{\unicode[STIX]{x1D716}^{2}}}\langle nU_{\Vert }^{\text{total}}\rangle /(I\unicode[STIX]{x1D711}^{\prime }/B_{0}),\end{eqnarray}$$
represents the added effective mass.
To illuminate the role of each species in the effective mass, we consider the individual effective mass contributions from the TPs and CPs. Using
![]() $\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}(\cos \unicode[STIX]{x1D703}+\cos 2\unicode[STIX]{x1D703})/(4\unicode[STIX]{x03C0}\sqrt{\cos \unicode[STIX]{x1D703}+1})\approx 0.15$
, the TP contribution to the effective mass coefficient can be shown to be
$\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}(\cos \unicode[STIX]{x1D703}+\cos 2\unicode[STIX]{x1D703})/(4\unicode[STIX]{x03C0}\sqrt{\cos \unicode[STIX]{x1D703}+1})\approx 0.15$
, the TP contribution to the effective mass coefficient can be shown to be
Thus the effective mass contribution from the TPs is
![]() ${\sim}O(q^{2}/\unicode[STIX]{x1D716}^{3/2})\gg 1$
as expected from our toy model. The CP contribution to the effective mass coefficient is
${\sim}O(q^{2}/\unicode[STIX]{x1D716}^{3/2})\gg 1$
as expected from our toy model. The CP contribution to the effective mass coefficient is
To lowest order this is equal and opposite to the TP effective mass. Thus the total effective mass is
![]() $1+1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}+O(q^{2})$
, consistent with the original RH calculation.
$1+1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}}+O(q^{2})$
, consistent with the original RH calculation.
5.3 Flows and effective masses for truncated distributions
We have seen that the cancellation of the rapid TP precession flow by an oppositely directed flow of barely CPs explains why the effective mass is smaller than that expected from the TPs alone. But this finding does not unequivocally address whether a distribution function of only TPs would result in the expected large effective mass. To address this, we consider the distribution function in (5.17) to be populated only for
![]() ${\mathcal{E}}_{\ast }<\unicode[STIX]{x1D707}B_{\text{max}}$
. For this case, the TP contribution to the effective mass can be seen from (5.18) to be independent of the details of the distribution. The contribution is found to be
${\mathcal{E}}_{\ast }<\unicode[STIX]{x1D707}B_{\text{max}}$
. For this case, the TP contribution to the effective mass can be seen from (5.18) to be independent of the details of the distribution. The contribution is found to be
![]() ${\sim}(q^{2}/\unicode[STIX]{x1D716}^{2})n^{\text{TP}}$
. Since there are no CPs,
${\sim}(q^{2}/\unicode[STIX]{x1D716}^{2})n^{\text{TP}}$
. Since there are no CPs,
![]() $n^{\text{TP}}=n$
. Therefore, we find the effective mass to be
$n^{\text{TP}}=n$
. Therefore, we find the effective mass to be
![]() $q^{2}/\unicode[STIX]{x1D716}^{2}$
, and the accompanying TP flows to be
$q^{2}/\unicode[STIX]{x1D716}^{2}$
, and the accompanying TP flows to be
To complete this line of reasoning, we have considered a distribution function with only energetic CPs, i.e. all particles considered to lie well above the separatrix region (
![]() ${\mathcal{E}}_{\ast }=\unicode[STIX]{x1D707}B_{0}(1+\unicode[STIX]{x1D716})$
) in phase space. The effective mass can be shown to be
${\mathcal{E}}_{\ast }=\unicode[STIX]{x1D707}B_{0}(1+\unicode[STIX]{x1D716})$
) in phase space. The effective mass can be shown to be
![]() $1+O(q^{2})$
. These results are consistent with fluid models where we get the oscillating Pfirsch–Schluter flows and the corresponding effective mass coefficient. We also find that unless we approach the separatrix, there are no
$1+O(q^{2})$
. These results are consistent with fluid models where we get the oscillating Pfirsch–Schluter flows and the corresponding effective mass coefficient. We also find that unless we approach the separatrix, there are no
![]() $\sqrt{\unicode[STIX]{x1D716}}$
terms.
$\sqrt{\unicode[STIX]{x1D716}}$
terms.
The above findings for TP and CP flows are fully consistent with our toy model equation (1.2) which shows the
![]() $O(q^{2}/\unicode[STIX]{x1D716}^{2})$
effective mass contribution from the trapped particle and the
$O(q^{2}/\unicode[STIX]{x1D716}^{2})$
effective mass contribution from the trapped particle and the
![]() $O(1)$
contribution from the freely circulating particle.
$O(1)$
contribution from the freely circulating particle.
6 The role of the barely circulating particles

Figure 4. Upgraded bead-on-wire toy model showing a particle of mass
![]() $m$
moving along a field line inclined at an angle
$m$
moving along a field line inclined at an angle
![]() $\unicode[STIX]{x1D6FC}\approx \unicode[STIX]{x1D716}/q$
to the toroidal direction. The field line moves rigidly under applied force
$\unicode[STIX]{x1D6FC}\approx \unicode[STIX]{x1D716}/q$
to the toroidal direction. The field line moves rigidly under applied force
![]() $F_{\bot }$
. The particle also feels the mirror force, modelled by the potential
$F_{\bot }$
. The particle also feels the mirror force, modelled by the potential
![]() $V(\unicode[STIX]{x1D703})$
, as it moves along
$V(\unicode[STIX]{x1D703})$
, as it moves along
![]() $\boldsymbol{B}$
.
$\boldsymbol{B}$
.
We have shown that the large trapped particle precession flow is cancelled to lowest order by an opposite flow from the circulating particles, so that there are no large composite flows of order
![]() $qU_{E}/\sqrt{\unicode[STIX]{x1D716}}$
. We would now like to understand the origin of the opposite flow. We show here that this flow is largely from a class of barely circulating particles. To demonstrate this, we begin with a more sophisticated toy model. Consider a particle on a rod as shown in figure 4. The generalized coordinates are
$qU_{E}/\sqrt{\unicode[STIX]{x1D716}}$
. We would now like to understand the origin of the opposite flow. We show here that this flow is largely from a class of barely circulating particles. To demonstrate this, we begin with a more sophisticated toy model. Consider a particle on a rod as shown in figure 4. The generalized coordinates are
![]() $(x=R_{0}\unicode[STIX]{x1D701},y=qR_{0}\unicode[STIX]{x1D703})$
, where
$(x=R_{0}\unicode[STIX]{x1D701},y=qR_{0}\unicode[STIX]{x1D703})$
, where
![]() $\unicode[STIX]{x1D703},\unicode[STIX]{x1D701}$
are analogous to the poloidal and toroidal angles. In addition to being constrained to move only along the rod, the particle also feels a force due to an applied potential
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D701}$
are analogous to the poloidal and toroidal angles. In addition to being constrained to move only along the rod, the particle also feels a force due to an applied potential
![]() $V(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D707}B(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D707}B_{0}(1-\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703})$
. Here, the force from the potential,
$V(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D707}B(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D707}B_{0}(1-\unicode[STIX]{x1D716}\cos \unicode[STIX]{x1D703})$
. Here, the force from the potential,
![]() $V(\unicode[STIX]{x1D703})$
, corresponds to the
$V(\unicode[STIX]{x1D703})$
, corresponds to the
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}_{\Vert }B$
force, the mirror force that the particle feels as it moves in
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}_{\Vert }B$
force, the mirror force that the particle feels as it moves in
![]() $\unicode[STIX]{x1D703}$
along
$\unicode[STIX]{x1D703}$
along
![]() $\boldsymbol{B}$
. Thus, while our previous model allowed only freely circulating particles and deeply trapped particles, our new model allows these but also allows barely circulating particles.
$\boldsymbol{B}$
. Thus, while our previous model allowed only freely circulating particles and deeply trapped particles, our new model allows these but also allows barely circulating particles.
The Lagrangian is given by,
where
![]() $c=(\int F_{\bot }\,\text{d}t)\sin \unicode[STIX]{x1D6FC}/(mR_{0})$
is the impulse due to the applied force
$c=(\int F_{\bot }\,\text{d}t)\sin \unicode[STIX]{x1D6FC}/(mR_{0})$
is the impulse due to the applied force
![]() $F_{\bot }$
. Here we use the impulse instead of work done by the force in the Lagrangian to manifestly preserve axisymmetry.
$F_{\bot }$
. Here we use the impulse instead of work done by the force in the Lagrangian to manifestly preserve axisymmetry.
The equation of motion is
which shows that our toy model is identical to a driven nonlinear pendulum (Henrard Reference Henrard2005). We can exploit this similarity to understand the particle trajectories in the presence of the external torque. Let us consider the case where
![]() $F_{\bot }$
is time independent. In this case the work and energy
$F_{\bot }$
is time independent. In this case the work and energy
![]() ${\mathcal{E}}$
of the driven pendulum is conserved. Thus,
${\mathcal{E}}$
of the driven pendulum is conserved. Thus,
Figure 5 shows the contours of constant
![]() ${\mathcal{E}}$
for non-zero
${\mathcal{E}}$
for non-zero
![]() $F_{\bot }$
. Note that for small
$F_{\bot }$
. Note that for small
![]() $F_{\bot }$
, most of the trajectories resemble the original trajectories of a torque-free pendulum. However now there exists a group of barely circulating particles near the separatrix (shown in red in figure 5), which can change directions so that the final direction is in the same sense as the applied torque.
$F_{\bot }$
, most of the trajectories resemble the original trajectories of a torque-free pendulum. However now there exists a group of barely circulating particles near the separatrix (shown in red in figure 5), which can change directions so that the final direction is in the same sense as the applied torque.

Figure 5. Phase portrait of a pendulum driven by
![]() $F_{\bot }$
. In black and blue we show oppositely moving freely circulating particle. In purple we show the orbit of a deeply trapped particle and in red we show a barely circulating particle preferentially changing direction in the presence of small
$F_{\bot }$
. In black and blue we show oppositely moving freely circulating particle. In purple we show the orbit of a deeply trapped particle and in red we show a barely circulating particle preferentially changing direction in the presence of small
![]() $F_{\bot }$
.
$F_{\bot }$
.
In order to make contact with the drift-kinetic system, lets now use the Hamiltonian description of the toy model. From the Lagrangian we calculate the canonical momenta,
Since the Lagrangian is independent of
![]() $\unicode[STIX]{x1D701}$
, the ‘toroidal angle’,
$\unicode[STIX]{x1D701}$
, the ‘toroidal angle’,
![]() $P_{\unicode[STIX]{x1D701}}$
must be a constant. The Hamiltonian
$P_{\unicode[STIX]{x1D701}}$
must be a constant. The Hamiltonian
![]() ${\mathcal{H}}$
, can now be constructed,
${\mathcal{H}}$
, can now be constructed,
where,
![]() $v_{\Vert \ast }\equiv qR_{0}\dot{\unicode[STIX]{x1D703}}=(P_{\unicode[STIX]{x1D703}}-q\cot \unicode[STIX]{x1D6FC}(P_{\unicode[STIX]{x1D701}}+cmR_{0}^{2}))/qm$
. We can now define
$v_{\Vert \ast }\equiv qR_{0}\dot{\unicode[STIX]{x1D703}}=(P_{\unicode[STIX]{x1D703}}-q\cot \unicode[STIX]{x1D6FC}(P_{\unicode[STIX]{x1D701}}+cmR_{0}^{2}))/qm$
. We can now define
![]() ${\mathcal{E}}_{\ast }=(1/2)v_{\Vert \ast }^{2}+\unicode[STIX]{x1D707}B(\unicode[STIX]{x1D703})$
and write down Liouville’s equation for this system in
${\mathcal{E}}_{\ast }=(1/2)v_{\Vert \ast }^{2}+\unicode[STIX]{x1D707}B(\unicode[STIX]{x1D703})$
and write down Liouville’s equation for this system in
![]() $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D701},{\mathcal{E}}_{\ast },P_{\unicode[STIX]{x1D701}}\}$
coordinates. We restrict ourselves to the ‘axisymmetric’ problem by choosing
$\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D701},{\mathcal{E}}_{\ast },P_{\unicode[STIX]{x1D701}}\}$
coordinates. We restrict ourselves to the ‘axisymmetric’ problem by choosing
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}=0$
(in axisymmetry there always exists a local frame). Thus we have,
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}=0$
(in axisymmetry there always exists a local frame). Thus we have,
Let us compare the Lioville’s equation (6.6) with the drift-kinetic equation (4.3). We note that, by making the identification
![]() $I\unicode[STIX]{x1D711}^{\prime }/B\Longleftrightarrow -R_{0}c\cot \unicode[STIX]{x1D6FC}$
, we obtain a one–one relation. This is perhaps not surprising because both equations describe conservation of phase space volume.
$I\unicode[STIX]{x1D711}^{\prime }/B\Longleftrightarrow -R_{0}c\cot \unicode[STIX]{x1D6FC}$
, we obtain a one–one relation. This is perhaps not surprising because both equations describe conservation of phase space volume.
Let us now try to understand the large cancellation of the RH flows. From the DKE–toy model equivalence, we see that
![]() $I\unicode[STIX]{x1D711}^{\prime }/B\propto -F_{\bot }$
. Figure 5 now corresponds to the case where
$I\unicode[STIX]{x1D711}^{\prime }/B\propto -F_{\bot }$
. Figure 5 now corresponds to the case where
![]() $I\unicode[STIX]{x1D711}^{\prime }/B>0$
. We have already seen that the trapped particles precess with speed
$I\unicode[STIX]{x1D711}^{\prime }/B>0$
. We have already seen that the trapped particles precess with speed
![]() $u_{\Vert }^{\text{TP}}\approx qU_{E}/\unicode[STIX]{x1D716}$
. Their net flow from equation (5.7) is
$u_{\Vert }^{\text{TP}}\approx qU_{E}/\unicode[STIX]{x1D716}$
. Their net flow from equation (5.7) is
![]() $(nu_{\Vert })^{\text{TP}}=-n\sqrt{\unicode[STIX]{x1D716}}I\unicode[STIX]{x1D711}^{\prime }/B$
which is negative in this case. The barely circulating particles on the other hand, have a similar density,
$(nu_{\Vert })^{\text{TP}}=-n\sqrt{\unicode[STIX]{x1D716}}I\unicode[STIX]{x1D711}^{\prime }/B$
which is negative in this case. The barely circulating particles on the other hand, have a similar density,
![]() $\sqrt{\unicode[STIX]{x1D716}}$
, but have an opposite flow
$\sqrt{\unicode[STIX]{x1D716}}$
, but have an opposite flow
![]() $n\sqrt{\unicode[STIX]{x1D716}}I\unicode[STIX]{x1D711}^{\prime }/B>0$
(see (5.11)). Thus the two flows cancel. A further explanation of the opposite flows is provided in the next section and in appendix D.
$n\sqrt{\unicode[STIX]{x1D716}}I\unicode[STIX]{x1D711}^{\prime }/B>0$
(see (5.11)). Thus the two flows cancel. A further explanation of the opposite flows is provided in the next section and in appendix D.
7 Sub-bounce dynamics in collisionless axisymmetric systems with sub-poloidal sonic flows
The analysis presented in § 5 was restricted to small flows. In this section, we present a nonlinear generalization of this analysis to finite but sub-poloidal sonic flows. We shall relax these constraints further in appendix D. Our main result in this section is to show that the collisionless RH flows and effective inertia arise because of two physical principles: conservation of angular momentum owing to axisymmetry, and conservation of
![]() $J_{\Vert }$
due to sub-bounce nature of the flows.
$J_{\Vert }$
due to sub-bounce nature of the flows.
We shall first show that the distribution function
![]() $f_{0}$
is a function of the second adiabatic invariant
$f_{0}$
is a function of the second adiabatic invariant
![]() $J_{\Vert }=\oint v_{\Vert }\text{d}l$
by solving (5.2) exactly. This is perhaps not surprising, since in the drift ordered sub-bounce kinetic system,
$J_{\Vert }=\oint v_{\Vert }\text{d}l$
by solving (5.2) exactly. This is perhaps not surprising, since in the drift ordered sub-bounce kinetic system,
![]() $J_{\Vert }$
is conserved (Medvedev et al.
Reference Medvedev, Diamond, Rosenbluth and Shevchenko1998), provided the forcing is adiabatic. Here we shall be content in restricting ourselves to sub-bounce axisymmetric systems. The existence of a second adiabatic invariant for kinetic MHD in more general settings has been discussed recently (Burby & Sengupta Reference Burby and Sengupta2017). The second adiabatic invariant
$J_{\Vert }$
is conserved (Medvedev et al.
Reference Medvedev, Diamond, Rosenbluth and Shevchenko1998), provided the forcing is adiabatic. Here we shall be content in restricting ourselves to sub-bounce axisymmetric systems. The existence of a second adiabatic invariant for kinetic MHD in more general settings has been discussed recently (Burby & Sengupta Reference Burby and Sengupta2017). The second adiabatic invariant
![]() $J_{\Vert }$
is defined by
$J_{\Vert }$
is defined by
We note that the
![]() $J_{\Vert }$
integral is done along a field line holding
$J_{\Vert }$
integral is done along a field line holding
![]() ${\mathcal{E}}_{\ast }$
fixed. Using
${\mathcal{E}}_{\ast }$
fixed. Using
![]() ${\mathcal{E}}_{\ast }=v_{\Vert }^{2}/2+\unicode[STIX]{x1D707}B+v_{\Vert }I\unicode[STIX]{x1D711}^{\prime }/B$
and
${\mathcal{E}}_{\ast }=v_{\Vert }^{2}/2+\unicode[STIX]{x1D707}B+v_{\Vert }I\unicode[STIX]{x1D711}^{\prime }/B$
and
![]() $v_{\Vert \ast }=v_{\Vert }+I\unicode[STIX]{x1D711}^{\prime }/B$
, we can show that
$v_{\Vert \ast }=v_{\Vert }+I\unicode[STIX]{x1D711}^{\prime }/B$
, we can show that
where the time derivative is done at fixed
![]() $(\unicode[STIX]{x1D707},{\mathcal{E}}_{\ast },\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
and
$(\unicode[STIX]{x1D707},{\mathcal{E}}_{\ast },\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
and
![]() ${\mathcal{E}}_{\ast }$
derivative is at constant
${\mathcal{E}}_{\ast }$
derivative is at constant
![]() $(\unicode[STIX]{x1D707},\unicode[STIX]{x1D703},\unicode[STIX]{x1D713},t)$
. We can now simplify (5.2) using the above properties of
$(\unicode[STIX]{x1D707},\unicode[STIX]{x1D703},\unicode[STIX]{x1D713},t)$
. We can now simplify (5.2) using the above properties of
![]() $J_{\Vert }$
.
$J_{\Vert }$
.
The last equation clearly implies
![]() $f_{0}=f_{0}(J_{\Vert })$
. Such a solution has been previously obtained by Kulsrud (Reference Kulsrud1961) treating
$f_{0}=f_{0}(J_{\Vert })$
. Such a solution has been previously obtained by Kulsrud (Reference Kulsrud1961) treating
![]() $U_{E}$
as a perturbation. Our result allows large flows.
$U_{E}$
as a perturbation. Our result allows large flows.
Note the crucial sigma dependence in the expression for
![]() $J_{\Vert }$
as noted earlier (Hastie, Taylor & Haas Reference Hastie, Taylor and Haas1967; Henrard Reference Henrard2005). There is no such sigma dependence in the trapped particle distribution because the second term averages out as
$J_{\Vert }$
as noted earlier (Hastie, Taylor & Haas Reference Hastie, Taylor and Haas1967; Henrard Reference Henrard2005). There is no such sigma dependence in the trapped particle distribution because the second term averages out as
![]() $\unicode[STIX]{x1D70E}=\pm 1$
for TPs. This means that the CP distribution is not symmetric with respect to
$\unicode[STIX]{x1D70E}=\pm 1$
for TPs. This means that the CP distribution is not symmetric with respect to
![]() $v_{\Vert \ast }=0$
.
$v_{\Vert \ast }=0$
.
In MHD ordering, the net flow is given by
![]() $\boldsymbol{U}=(U_{\Vert }/B)\boldsymbol{B}+\boldsymbol{U}_{\boldsymbol{E}}\text{ with }\boldsymbol{U}_{\boldsymbol{E}}=\boldsymbol{B}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})/B^{2}.$
In an axisymmetric system, using (2.3), we get the following expression for the net flow
$\boldsymbol{U}=(U_{\Vert }/B)\boldsymbol{B}+\boldsymbol{U}_{\boldsymbol{E}}\text{ with }\boldsymbol{U}_{\boldsymbol{E}}=\boldsymbol{B}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})/B^{2}.$
In an axisymmetric system, using (2.3), we get the following expression for the net flow
From the definition of
![]() $U_{\Vert }$
we obtain,
$U_{\Vert }$
we obtain,
Let us now consider the angular momentum conservation equation
where
![]() $\unicode[STIX]{x1D70F}_{\bot }$
is defined as in (2.4). Substituting for
$\unicode[STIX]{x1D70F}_{\bot }$
is defined as in (2.4). Substituting for
![]() $\boldsymbol{U}$
from (7.4) into (7.6) we get
$\boldsymbol{U}$
from (7.4) into (7.6) we get
In order to evaluate (7.7) we need an evolution equation for
![]() $n_{0}F$
. From (7.5) we get
$n_{0}F$
. From (7.5) we get
For the flows to be divergence free we need
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n\boldsymbol{U})=0$
which implies
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n\boldsymbol{U})=0$
which implies
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(nF)=0$
from (7.4) due to axisymmetry. From (7.8) we see that the factor
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(nF)=0$
from (7.4) due to axisymmetry. From (7.8) we see that the factor
![]() $v_{\Vert \ast }(\unicode[STIX]{x1D703})$
cancels out and the right side is only a function of
$v_{\Vert \ast }(\unicode[STIX]{x1D703})$
cancels out and the right side is only a function of
![]() $\unicode[STIX]{x1D713}$
after the
$\unicode[STIX]{x1D713}$
after the
![]() ${\mathcal{E}}_{\ast }$
and
${\mathcal{E}}_{\ast }$
and
![]() $\unicode[STIX]{x1D707}$
integrals are performed. Thus
$\unicode[STIX]{x1D707}$
integrals are performed. Thus
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(nF)=0$
is satisfied and the flows are indeed divergence free as expected for a stationary state.
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(nF)=0$
is satisfied and the flows are indeed divergence free as expected for a stationary state.
Using angular momentum conservation (7.7) and (7.8), we obtain the generalization of (5.17) for finite flow, showing a generalized effective mass,
where
![]() $f_{0}$
can depend nonlinearly on
$f_{0}$
can depend nonlinearly on
![]() $\unicode[STIX]{x1D711}$
. In the limit of small
$\unicode[STIX]{x1D711}$
. In the limit of small
![]() $U_{E}/v_{th}$
, we recover (5.17) and hence the RH coefficient
$U_{E}/v_{th}$
, we recover (5.17) and hence the RH coefficient
![]() $(1+1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}})$
in the large aspect ratio limit with an initial Maxwellian. The effective mass can also be written in terms of
$(1+1.6q^{2}/\sqrt{\unicode[STIX]{x1D716}})$
in the large aspect ratio limit with an initial Maxwellian. The effective mass can also be written in terms of
![]() $J_{\Vert }$
as shown in (D 7).
$J_{\Vert }$
as shown in (D 7).
Now let us try to understand the origin of the opposite flows from this point of view. Note that for small
![]() $(U_{E}/v_{\text{th}}),F$
is zero for TPs because the TP distribution function is an even function of
$(U_{E}/v_{\text{th}}),F$
is zero for TPs because the TP distribution function is an even function of
![]() $v_{\Vert \ast }$
. This ensures that the poloidal flow of TPs is zero and the parallel flow is due to the fast precession. Also from (7.9), we can see that the TPs always contribute the large
$v_{\Vert \ast }$
. This ensures that the poloidal flow of TPs is zero and the parallel flow is due to the fast precession. Also from (7.9), we can see that the TPs always contribute the large
![]() $q^{2}/\unicode[STIX]{x1D716}^{2}$
effective mass.
$q^{2}/\unicode[STIX]{x1D716}^{2}$
effective mass.
![]() $F$
is however non-zero and in fact different for the CPs above and below the separatrix. This breaks the up down symmetry dynamically, leading to differential parallel flow due to CPs. The fact that the CP flow must be opposite to the TPs also follow from the fact that
$F$
is however non-zero and in fact different for the CPs above and below the separatrix. This breaks the up down symmetry dynamically, leading to differential parallel flow due to CPs. The fact that the CP flow must be opposite to the TPs also follow from the fact that
![]() $J_{\Vert }$
must be conserved and that
$J_{\Vert }$
must be conserved and that
![]() $J_{\Vert }$
is initially small because of the initial up–down symmetry of the initial Maxwellian.
$J_{\Vert }$
is initially small because of the initial up–down symmetry of the initial Maxwellian.
8 Summary
If a tokamak plasma is set into motion with an initial radial electric field
![]() $E_{r}$
, the final state, after transients, is a much reduced
$E_{r}$
, the final state, after transients, is a much reduced
![]() $E_{r}$
and a parallel zonal flow consistent with angular momentum conservation. However, the well-known trapped particle precession angular momentum in the final
$E_{r}$
and a parallel zonal flow consistent with angular momentum conservation. However, the well-known trapped particle precession angular momentum in the final
![]() $E_{r}$
field is much larger than the zonal flow. We have shown in this paper that this apparent paradox is resolved by the fact that there are reverse flows from the barely passing particles that cancel the large momentum from the TP precession momentum. Mathematically, we show that, even for small perturbations, there is a linear shift in the Jacobian of the phase space volume element, from
$E_{r}$
field is much larger than the zonal flow. We have shown in this paper that this apparent paradox is resolved by the fact that there are reverse flows from the barely passing particles that cancel the large momentum from the TP precession momentum. Mathematically, we show that, even for small perturbations, there is a linear shift in the Jacobian of the phase space volume element, from
![]() $E_{r}$
, that accounts for the reverse flows and the cancellation. The effective mass for this system is the same as that obtained by Rosenbluth and Hinton (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) and Xiao et al. (Reference Xiao, Catto and Molvig2007). We have shown that sub-bounce axisymmetric kinetic MHD can be formulated in terms of the parallel adiabatic invariant
$E_{r}$
, that accounts for the reverse flows and the cancellation. The effective mass for this system is the same as that obtained by Rosenbluth and Hinton (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) and Xiao et al. (Reference Xiao, Catto and Molvig2007). We have shown that sub-bounce axisymmetric kinetic MHD can be formulated in terms of the parallel adiabatic invariant
![]() $J_{\Vert }$
much like the sub-bounce low flow drift-kinetic system. Rosenbluth–Hinton distribution function and the effective mass follows directly from
$J_{\Vert }$
much like the sub-bounce low flow drift-kinetic system. Rosenbluth–Hinton distribution function and the effective mass follows directly from
![]() $J_{\Vert }$
conservation in the long wavelength limit. This is expected even in the long wavelength low flow drift ordered kinetic systems.
$J_{\Vert }$
conservation in the long wavelength limit. This is expected even in the long wavelength low flow drift ordered kinetic systems.
Acknowledgements
The authors would like to thank the anonymous referees for their thorough, constructive and helpful reviews. We also acknowledge stimulating discussion with R. M. Kulsrud, T. M. Antonsen Jr. W. Dorland, J. F. Drake and M. Landreman. W.S. would also like to acknowledge helpful advice from J. J. Ramos, I. Pusztai and P. J. Catto. This research was funded by the US DOE.
Appendix A. Relation of
 ${\mathcal{E}}_{\ast }$
to toroidal angular momentum
${\mathcal{E}}_{\ast }$
to toroidal angular momentum
 $\unicode[STIX]{x1D713}_{\ast }$
$\unicode[STIX]{x1D713}_{\ast }$
We shall now clarify the meaning of the shifted energy variable
![]() ${\mathcal{E}}_{\ast }$
. It is well known (Kagan & Catto Reference Kagan and Catto2008) that in axisymmetry the conservation of canonical angular momentum leads to conservation of
${\mathcal{E}}_{\ast }$
. It is well known (Kagan & Catto Reference Kagan and Catto2008) that in axisymmetry the conservation of canonical angular momentum leads to conservation of
![]() $\unicode[STIX]{x1D713}_{\ast }$
defined as
$\unicode[STIX]{x1D713}_{\ast }$
defined as
where
![]() $\boldsymbol{v}$
is the velocity vector of particle of mass
$\boldsymbol{v}$
is the velocity vector of particle of mass
![]() $m$
and charge
$m$
and charge
![]() $e$
. The contribution of perpendicular velocities to
$e$
. The contribution of perpendicular velocities to
![]() $\unicode[STIX]{x1D713}_{\ast }$
average out except for
$\unicode[STIX]{x1D713}_{\ast }$
average out except for
![]() $U_{E}$
terms which are also negligible in our large sub-poloidal sonic ordering. The second term in
$U_{E}$
terms which are also negligible in our large sub-poloidal sonic ordering. The second term in
![]() $\unicode[STIX]{x1D713}_{\ast }$
is smaller than the first by a factor of
$\unicode[STIX]{x1D713}_{\ast }$
is smaller than the first by a factor of
![]() $\unicode[STIX]{x1D70C}_{\ast }(\equiv \unicode[STIX]{x1D70C}/L)$
and is related to the finite banana width.
$\unicode[STIX]{x1D70C}_{\ast }(\equiv \unicode[STIX]{x1D70C}/L)$
and is related to the finite banana width.
In a steady state collisionless plasma, total energy (kinetic plus electrostatic potential) is also conserved.
In drift ordering all the energy terms are one to one. However in MHD ordering, since
![]() $e\unicode[STIX]{x1D711}/T=1/\unicode[STIX]{x1D70C}\ast$
and
$e\unicode[STIX]{x1D711}/T=1/\unicode[STIX]{x1D70C}\ast$
and
![]() $\unicode[STIX]{x1D70C}_{\ast }\approx 0$
, the conserved quantities must be evaluated order by order. To lowest order thus we have
$\unicode[STIX]{x1D70C}_{\ast }\approx 0$
, the conserved quantities must be evaluated order by order. To lowest order thus we have
To next order,
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}_{\ast } & = & \displaystyle \frac{1}{2}(v_{\Vert }^{2}+\unicode[STIX]{x1D707}B)+\frac{e}{M}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})-\frac{e}{M}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713}_{\ast })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}(v_{\Vert }^{2}+\unicode[STIX]{x1D707}B)+\frac{I\unicode[STIX]{x1D711}^{\prime }}{B}=\text{const}.,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{\ast } & = & \displaystyle \frac{1}{2}(v_{\Vert }^{2}+\unicode[STIX]{x1D707}B)+\frac{e}{M}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})-\frac{e}{M}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713}_{\ast })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}(v_{\Vert }^{2}+\unicode[STIX]{x1D707}B)+\frac{I\unicode[STIX]{x1D711}^{\prime }}{B}=\text{const}.,\end{eqnarray}$$
where we have Taylor expanded
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})$
about
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})$
about
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\ast }+O(\unicode[STIX]{x1D70C}\ast )$
to obtain
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\ast }+O(\unicode[STIX]{x1D70C}\ast )$
to obtain
![]() ${\mathcal{E}}_{\ast }$
. Thus, it is clear that
${\mathcal{E}}_{\ast }$
. Thus, it is clear that
![]() ${\mathcal{E}}_{\ast }$
is indeed a shifted total energy, the shift being the potential difference across a banana width. It is important to note that in kinetic MHD,
${\mathcal{E}}_{\ast }$
is indeed a shifted total energy, the shift being the potential difference across a banana width. It is important to note that in kinetic MHD,
![]() $\unicode[STIX]{x1D713}$
is needed only to lowest order since the radial drifts are formally an order smaller than the parallel and the
$\unicode[STIX]{x1D713}$
is needed only to lowest order since the radial drifts are formally an order smaller than the parallel and the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drifts. Since
$\boldsymbol{E}\times \boldsymbol{B}$
drifts. Since
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\ast }$
to lowest order we are self-consistently ignoring
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\ast }$
to lowest order we are self-consistently ignoring
![]() $\dot{\unicode[STIX]{x1D713}}$
terms in the DKE. This does not interfere with energy conservation owing to
$\dot{\unicode[STIX]{x1D713}}$
terms in the DKE. This does not interfere with energy conservation owing to
![]() ${\mathcal{E}}_{\ast }$
. From the DKE it can be checked that for a time independent system,
${\mathcal{E}}_{\ast }$
. From the DKE it can be checked that for a time independent system,
![]() $\dot{\unicode[STIX]{x1D713}}=\dot{{\mathcal{E}}_{\ast }}=0$
, by direct substitution. Thus, equation (4.3) with the
$\dot{\unicode[STIX]{x1D713}}=\dot{{\mathcal{E}}_{\ast }}=0$
, by direct substitution. Thus, equation (4.3) with the
![]() $\unicode[STIX]{x2202}_{t}I\tilde{\unicode[STIX]{x1D711}}^{\prime }$
term is analogous to the standard drift ordered DKE (Hazeltine Reference Hazeltine1983) with the
$\unicode[STIX]{x2202}_{t}I\tilde{\unicode[STIX]{x1D711}}^{\prime }$
term is analogous to the standard drift ordered DKE (Hazeltine Reference Hazeltine1983) with the
![]() $(e/M)\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D711}}$
term.
$(e/M)\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D711}}$
term.
Appendix B. Vorticity equation in
 ${\mathcal{E}}$
and
${\mathcal{E}}$
and
 ${\mathcal{E}}_{\ast }$
coordinates
${\mathcal{E}}_{\ast }$
coordinates
We can derive the vorticity equation using
![]() $\langle \boldsymbol{j}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle =0$
. From Kulsrud’s equation (Reference Kulsrud1980) (46), it can be shown that
$\langle \boldsymbol{j}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle =0$
. From Kulsrud’s equation (Reference Kulsrud1980) (46), it can be shown that
In an axisymmetric system,
and we can show that
Now,
So,
Appendix C. Proof of equivalence of angular momentum and vorticity equation
Using the following identities,
the angular momentum conservation condition (4.4), simplifies to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}\left\langle n\frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}\unicode[STIX]{x1D711}^{\prime }\right\rangle -\unicode[STIX]{x1D70F}_{\bot } & = & \displaystyle \unicode[STIX]{x2202}_{t}\left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}f\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}\left(\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\right|_{{\mathcal{E}}_{\ast }}+\frac{\unicode[STIX]{x2202}I\unicode[STIX]{x1D711}^{\prime }}{\unicode[STIX]{x2202}t}\frac{v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}{\mathcal{E}}_{\ast }}\right)f\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}(-v_{\Vert \ast }\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}_{\ast }}\,f)\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{e}{M}\boldsymbol{v}_{\boldsymbol{d}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}f\right\rangle \quad \text{(integrating by parts)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}\left\langle n\frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}\unicode[STIX]{x1D711}^{\prime }\right\rangle -\unicode[STIX]{x1D70F}_{\bot } & = & \displaystyle \unicode[STIX]{x2202}_{t}\left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}f\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}\left(\left.\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\right|_{{\mathcal{E}}_{\ast }}+\frac{\unicode[STIX]{x2202}I\unicode[STIX]{x1D711}^{\prime }}{\unicode[STIX]{x2202}t}\frac{v_{\Vert }}{B}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}{\mathcal{E}}_{\ast }}\right)f\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{Iv_{\Vert }}{B}(-v_{\Vert \ast }\unicode[STIX]{x1D735}_{\Vert }|_{{\mathcal{E}}_{\ast }}\,f)\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \left\langle \int \text{d}^{3}v\frac{e}{M}\boldsymbol{v}_{\boldsymbol{d}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}f\right\rangle \quad \text{(integrating by parts)}.\end{eqnarray}$$
Appendix D.
 $J_{\Vert }$
invariance and the RH problem for arbitrary
$J_{\Vert }$
invariance and the RH problem for arbitrary
 $q$
and sub-poloidal sonic flows
$q$
and sub-poloidal sonic flows
So far we have presented a large
![]() $q$
ordering. In this section we shall present the general result for arbitrary
$q$
ordering. In this section we shall present the general result for arbitrary
![]() $q$
. We shall still assume flows to be smaller than the poloidal sound speed in order to avoid Alfvénic resonances (Hassam Reference Hassam1996). The
$q$
. We shall still assume flows to be smaller than the poloidal sound speed in order to avoid Alfvénic resonances (Hassam Reference Hassam1996). The
![]() $U_{E}^{2}$
term previously neglected in the DKE (2.1), is now kept. The
$U_{E}^{2}$
term previously neglected in the DKE (2.1), is now kept. The
![]() $E_{\Vert }$
term is also kept to ensure quasineutrality,
$E_{\Vert }$
term is also kept to ensure quasineutrality,
![]() $n_{e}=n_{i}$
, in the presence of large centrifugal forces. This motivates us to introduce
$n_{e}=n_{i}$
, in the presence of large centrifugal forces. This motivates us to introduce
![]() $\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D703})$
such that
![]() $E_{\Vert }=-\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D711}_{1}$
.
$E_{\Vert }=-\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D711}_{1}$
.
![]() $\boldsymbol{U}_{\boldsymbol{E}}$
depends only on the lowest-order electrostatic potential,
$\boldsymbol{U}_{\boldsymbol{E}}$
depends only on the lowest-order electrostatic potential,
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})$
, which is still a flux function. We shall assume adiabatic electrons. In axisymmetry the ion DKE (2.1) can be written as
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(\unicode[STIX]{x1D713})$
, which is still a flux function. We shall assume adiabatic electrons. In axisymmetry the ion DKE (2.1) can be written as
where the last two terms come from
![]() $-\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}$
and
$-\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{U}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}_{\boldsymbol{E}}$
and
![]() $(e/M)E_{\Vert }$
. It is straightforward to show that for finite
$(e/M)E_{\Vert }$
. It is straightforward to show that for finite
![]() $q$
,
$q$
,
![]() ${\mathcal{E}}_{\ast }$
is given by
${\mathcal{E}}_{\ast }$
is given by
In
![]() ${\mathcal{E}}_{\ast }$
coordinate we have
${\mathcal{E}}_{\ast }$
coordinate we have
where
![]() $\dot{{\mathcal{E}}_{\ast }}=v_{\Vert \ast }\unicode[STIX]{x2202}_{t}I\unicode[STIX]{x1D711}^{\prime }/B+\unicode[STIX]{x2202}_{t}(e\unicode[STIX]{x1D711}_{1}/m-R^{2}{\unicode[STIX]{x1D711}^{\prime }}^{2}/2)$
and
$\dot{{\mathcal{E}}_{\ast }}=v_{\Vert \ast }\unicode[STIX]{x2202}_{t}I\unicode[STIX]{x1D711}^{\prime }/B+\unicode[STIX]{x2202}_{t}(e\unicode[STIX]{x1D711}_{1}/m-R^{2}{\unicode[STIX]{x1D711}^{\prime }}^{2}/2)$
and
![]() $v_{\Vert \ast }=v_{\Vert }+I\unicode[STIX]{x1D711}^{\prime }/B$
.
$v_{\Vert \ast }=v_{\Vert }+I\unicode[STIX]{x1D711}^{\prime }/B$
.
As before, we investigate the sub-bounce zonal flow problem by expanding
![]() $f=f_{0}+f_{1}+\cdots \,$
and obtain the bounce averaged equation for
$f=f_{0}+f_{1}+\cdots \,$
and obtain the bounce averaged equation for
![]() $f_{0}$
$f_{0}$
Once again using
![]() $J_{\Vert }=\oint _{\ast }v_{\Vert }\text{d}l$
the above equation can be recast into
$J_{\Vert }=\oint _{\ast }v_{\Vert }\text{d}l$
the above equation can be recast into
Quasineutrality then gives us
![]() $\unicode[STIX]{x1D711}_{1}$
in terms of
$\unicode[STIX]{x1D711}_{1}$
in terms of
![]() $\unicode[STIX]{x1D711}^{\prime }$
. The flow and angular momentum equations in this limit are completely identical to the equations (7.5), (7.4), (7.7) derived earlier and
$\unicode[STIX]{x1D711}^{\prime }$
. The flow and angular momentum equations in this limit are completely identical to the equations (7.5), (7.4), (7.7) derived earlier and
Note that, since the only time dependence comes through
![]() $\unicode[STIX]{x1D711}^{\prime }$
,
$\unicode[STIX]{x1D711}^{\prime }$
,
![]() $\unicode[STIX]{x2202}_{t}J_{\Vert }$
is proportional to
$\unicode[STIX]{x2202}_{t}J_{\Vert }$
is proportional to
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\prime }$
. The final evolution equation for
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\prime }$
. The final evolution equation for
![]() $\unicode[STIX]{x1D711}^{\prime }$
is now given by
$\unicode[STIX]{x1D711}^{\prime }$
is now given by