Landau (Reference Landau1946) first realized that the singular behavior of the collisionless linearized kinetic equation describing weakly damped plasma waves could be resolved by Laplace transforming in time to solve a causal initial value problem. Subsequent collisionless work by Dawson (Reference Dawson1961), O’Neil (Reference O’Neil1965) and Villani (Reference Villani2014) provided additional insights into the linear and nonlinear temporal evolution of the resonant electrons. Here, the focus is on an applied steady state plasma wave where weak collisions must be retained to restore the regularity needed to avoid the singular behavior dealt with in the preceding formulations by focusing on temporal evolution. Then, the need to solve an initial value problem or invoke causality by Laplace transforming in time is removed. In this weak collision limit a narrow boundary layer resolves the singular behavior, and exactly recovers the collisionless results as long as the wave amplitude is small and the collision frequency finite. However, the deceptive collisionless behavior is removed once the collision frequency becomes small enough and/or the wave amplitude becomes sufficiently large that a nonlinear treatment is required. The nonlinear solution found herein for a monochromatic wave retains the island structure, but Landau’s results (Reference Landau1946) are no longer valid when the collision frequency goes to zero for a non-vanishing plasma wave amplitude. The collisional treatment remains valid as long as there are many electrons in a Debye sphere.

Consider a weakly dissipative plasma wave with an applied electric field

(1) \begin{equation}\vec {{E}}=\vec {{z}}\mathfrak{I}\textrm{m}[\tilde{{E}}{e}^{{i}{({k}_{||}}{z}-{\omega} {t})}]\approx \vec {{z}}{E}_{||}\sin ({k}_{||}{z}-{\omega} {t}),\end{equation}

where the wave frequency ${\omega}$ is very much larger than the collision frequency, $\vec {{z}}$ is a unit vector, $\tilde{{E}}$ is a complex amplitude, $\mathfrak{I}\textrm{m}$ denotes imaginary part and ${\omega}$ , ${k}_{||}$ and ${E}_{||}$ are positive with $ {k}_{||} $ the $z $ directed wave vector component. The steady state electron kinetic equation with the collision operator, ${C}\{{f}\}$ , retained is

(2) \begin{equation}\partial {f}/\partial {t}+\vec {{v}}\cdot \nabla {f}-({e}/{m})\vec {{E}}\cdot \nabla _{{v}}{f}={C}\{{f}\},\end{equation}

where f, e and m are the electron distribution function, charge magnitude, and mass. If the plasma is homogeneous with stationary ions and the electrons are a stationary Maxwellian ${f}_{0}({v})$ to lowest order, then ${C}\{{f}_{0}\}=0$ and the kinetic equation becomes

(3) \begin{equation}\partial {f}_{1}/\partial {t}+{v}_{||}\partial {f}_{1}/\partial {z}-({e}/{m})\vec {{E}}\cdot \vec {{z}}\partial ({f}_{0}+{f}_{1})/\partial {v}_{||}={C}\{{f}_{1}\},\end{equation}

where ${f}={f}_{0}+{f}_{1}$ , only spatial variation in z enters, and $\vec {{z}}\cdot \vec {{v}}={v}_{||}$ with ${v}^{2}={v}_{||}^{2}+{v}_{\bot }^{2}$ . The ordering allows $\partial {f}_{1}/\partial {v}_{||}\sim \partial {f}_{0}/\partial {v}_{||}$ to retain nonlinear behavior. The solution of this equation can be viewed as the weakly collisional, steady state counterpart of the collisionless, early temporal evolution model considered by O’Neil (Reference O’Neil1965).

The effects of resonant electrons, ${k}_{||}{v}_{||}\approx {\omega} \approx {\omega} _{{p}}$ , on the plasma or Langmuir wave are retained by this ordering, with the electron plasma frequency defined by ${\omega} _{{p}}^{2}=4{\pi} {e}^{2}{n}_{{e}}/{m}$ . For the weakly dissipative plasma waves of interest ${\omega} ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\gg 1,$ with ${v}_{{e}}=(2{T}_{{e}}/{m})^{1/2}$ the electron thermal speed. This inequality implies ${\omega} ^{2}/{k}_{||}^{2}\approx {v}_{||}^{2}\sim {v}^{2}\gg {v}_{{e}}^{2}$ are of interest in ${C}\{{f}_{1}\}$ . As a result, the high speed expansion ( ${v}^{2}\gg {v}_{{e}}^{2})$ of the collision operator

(4) \begin{align}{C}\{{f}_{1}\} & =\nabla _{{v}}\cdot \left\{\frac{{\nu} _{{e}}}{2{x}^{3}}\left[({v}^{2}\overleftrightarrow{I}-\vec {{v}}\vec {{v}})\cdot \nabla _{{v}}{f}_{1}+\frac{2{Tf}_{0}}{({Z}+1){m}}\nabla _{{v}}\left(\frac{{f}_{1}}{{f}_{0}}\right)\right]\right\}\nonumber\\&\approx \frac{{\nu} _{{e}}}{2{x}^{3}}\left[{v}_{\bot }^{2}+\frac{{v}_{{e}}^{2}}{({Z}+1)}\right]\frac{\partial ^{2}{f}_{1}}{\partial {v}_{||}^{2}},\end{align}

is adequate, where ${f}_{0}={n}_{{e}}{\pi} ^{-3/2}{v}_{{e}}^{-3}{e}^{-{{v}^{2}}/{v}_{{e}}^{2}}$ , ${x}={v}/{v}_{{e}}$ , ${\nu} _{{e}}=3\sqrt{{\pi} }({Z}+1){\nu} _{{ee}}/4$ and ${\nu} _{{ee}}=4\sqrt{2{\pi} }{e}^{4}{n}_{{e}}\mathcal{l}{n}{\Lambda} /3{m}^{1/2}{T}^{3/2}={\nu} _{{ei}}/{Z}$ , for a quasineutral plasma, with ${Z}$ the ion charge number, and a large Coulomb logarithm, , assuring there are many electrons in a Debye sphere. The final form is adequate for a resonance where rapid ${v}_{||}$ variation occurs in the thin collisional boundary layer. Collisions are negligible elsewhere.

Neglecting the nonlinear term leads to an inhomogeneous Airy equation with solution

(5) \begin{equation}\left.{f}_{1}\right| _{{\rm res}}=-\frac{{e}{\omega} {f}_{0}}{{T}({k}_{||}^{5}{v}_{\bot {z}}^{2}{\nu})^{1/3}}\mathfrak{I}\textrm{m}\left[\tilde{{E}}{e}^{{i}({{k}_{||}}{z}-{\omega} {t})}\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{is}{\tau} -{{\tau} ^{3}}/3}\right],\end{equation}

with ${s}=({k}_{||}/{v}_{\bot {z}}^{2}{\nu})^{1/3}({v}_{||}-{\omega} /{k}_{||})$ , ${\nu} ={\nu} _{{e}}/2{x}^{3}$ and ${v}_{\bot {z}}^{2}={v}_{\bot }^{2}+{v}_{{e}}^{2}/({Z}+1)$ . This solution can be checked by direct substitution and integration by parts, and is valid near ${v}_{||}\approx {\omega} /{k}_{||}$ . It retains collisions (via s) and slightly generalizes the earlier weak collisions solutions of Su & Oberman (Reference Su and Oberman1968), Johnston (Reference Johnston1971) and Auerbach (Reference Auerbach1977) by keeping ${v}_{\bot }^{2}$ dependence, and of Catto (Reference Catto2020) and Catto & Tolman (Reference Catto and Tolman2021) by keeping ${v}_{{e}}^{2}/({Z}+1)$ in ${v}_{\bot {z}}^{2}$ .

The collisional boundary-layer width of the resonance from ${s}=1$ is $({v}_{||}-{\omega} /{k}_{||})_{{\nu} }=$ $({\Delta} {v}_{||})_{{\nu} }=|{\nu} {v}_{\bot {z}}^{2}/{{k}_{||}}|^{1/3}$ . This corresponds to a normalized width $({\Delta} {v}_{||})_{{\nu} }/{v}_{{e}}\sim ({\nu} _{{e}}{k}_{||}^{2}{v}_{{e}}^{2}/{{\omega} ^{3}})^{1/3}$ and an effective resonant collision frequency ${{\nu} _{{\rm eff}}}\sim {{\nu} _{{e}}}[{v}_{{e}}/({\Delta} {v}_{||})_{{\nu} }]^{2}\gg {\nu} _{{e}}$ for ${v}_{\bot {z}}^{2}\sim {v}_{{e}}^{2}$ .

For $|{s}|\gg 1$ , $\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{is}{\tau} -{{\tau} ^{3}}/3}\rightarrow 1/{is}$ . As a result, away from resonance $\left.{f}_{1}\right| _{{\rm res}}$ matches the usual collisionless non-resonant solution

(6) \begin{equation}\left.{f}_{1}\right| _{{\rm non}}={eE}_{||}{v}_{||}{f}_{0}\cos {\phi} /{T}({{k}_{||}}{v}_{||}-{\omega}),\end{equation}

where ${\phi} \equiv {k}_{||}{z}-{\omega} {t}$ . The perturbed non-resonant density ${n}_{{\rm non}}=\left.\int {d}^{3}{vf}_{1}\right| _{{\rm non}}$ , is then calculated from the principal value integral by expanding for ${\omega} /{k}_{||}{v}_{||}\gg 1$ to obtain

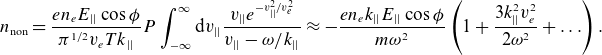(7) \begin{equation}{n}_{{\rm non}}=\frac{{en}_{{e}}{E}_{||}\cos {\phi} }{{\pi} ^{1/2}{v}_{{e}}{Tk}_{||}}{P}\int _{-{\infty }}^{{\infty }}{{\rm d}v}_{||}\frac{{{v}_{||}}{e}^{-{v}_{||}^{2}/{v}_{{e}}^{2}}}{{v}_{||}-{\omega} /{k}_{||}}\approx -\frac{{en}_{{e}}{k}_{||}{E}_{||}\cos {\phi} }{{m}{\omega} ^{2}}\left(1+\frac{3{k}_{||}^{2}{v}_{{e}}^{2}}{2{\omega} ^{2}}+\ldots \right).\end{equation}

The resonant contribution to the perturbed density, ${n}_{{\rm res}}=\left.\int {d}^{3}{vf}_{1}\right| _{{\rm res}}$ , is

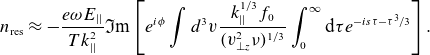(8) \begin{equation}{n}_{{\rm res}}\approx -\frac{{e}{\omega} {E}_{||}}{{Tk}_{||}^{2}}\mathfrak{I}\textrm{m}\left[{e}^{{i}{\phi} }\int {d}^{3}{v}\frac{{k}_{||}^{1/3}{f}_{0}}{({v}_{\bot {z}}^{2}{\nu})^{1/3}}\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{is}{\tau} -{{\tau} ^{3}}/3}\right].\end{equation}

The localization of the resonance makes it convenient to perform the ${v}_{||}$ integral first by letting ${\omega} /{k}_{||}\gg {w}\gg ({\Delta} {v}_{||})_{{\nu} }=|{\nu} {v}_{\bot {z}}^{2}/{{k}_{||}}|^{1/3}$ to find

(9) \begin{equation}\int _{-{w}}^{{w}}{\rm d}{u}\frac{{\rm d}{s}}{{\rm d}{u}}{f}_{0}\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{is}{\tau} -{{\tau} ^{3}}/3}\approx 2{f}_{0}({u}=0)\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{{\tau} ^{3}}/3}\frac{\sin ({W}{\tau})}{{\tau} }\approx {\pi} {f}_{0}({u}=0),\end{equation}

for ${u}={v}_{||}-{\omega} /{k}_{||}$ and ${W}\equiv ({k}_{||}/{v}_{\bot {z}}^{2}{\nu})^{1/3}{w}\gg 1$ . As a result, collisions cancel to yield

(10) \begin{equation}4{\pi} {en}_{{\rm res}}\approx -\frac{2{\pi} ^{1/2}{\omega} _{{p}}^{2}{\omega} {E}_{||}}{{k}_{||}^{2}{v}_{{e}}^{3}}{e}^{-{{\omega} ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}\sin {\phi},\end{equation}

due to the delta function character of ${\pi} ^{-1}\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{{\tau} ^{3}}/3}\cos ({s}{\tau})$ when integrated over s.

The perturbed Poisson equation, $\nabla \cdot \vec {{E}}=-4{\pi} {e}({n}_{{\rm non}}+{n}_{{\rm res}})$ , then gives

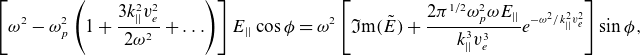(11) \begin{equation}\left[{{\omega} ^{2}}-{\omega} _{{p}}^{2}\left(1+\frac{3{k}_{||}^{2}{v}_{{e}}^{2}}{2{\omega} ^{2}}+\ldots\right)\right]{E}_{||}\cos {\phi} ={\omega} ^{2}\left[\mathfrak{I}\textrm{m}(\tilde{{E}})+\frac{2{\pi} ^{1/2}{\omega} _{{p}}^{2}\omega {E}_{||}}{{k}_{||}^{3}{v}_{{e}}^{3}}{e}^{-{{\omega} ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}\right]\sin {\phi},\end{equation}

where a small imaginary part of $\tilde{{E}}$ is required to balance the dissipation – as in the initial value Landau (Reference Landau1946) and collisional Auerbach (Reference Auerbach1977) solutions. Here, the temporal decay of Landau prescription is replaced by the need to provide power to maintain the steady state. To verify the preceding dispersion relation in a weakly collision kinetic simulation requires resolving parallel velocity scales of the order of $({\Delta} {v}_{||})_{{\nu} }=|{\nu} {v}_{\bot {z}}^{2}/{{k}_{||}}|^{1/3}\sim {v}_{{e}}({\nu} _{{e}}{k}_{||}^{2}{v}_{{e}}^{2}/{{\omega} ^{3}})^{1/3}$ .

The collisional power absorbed is evaluated using $\langle \ldots \rangle _{{\phi} }=\oint {\rm d}{\phi} (\ldots)/2{\pi}$ to find

(12) \begin{equation}{P}=-{eE}_{||}\left\langle \sin {\phi} \int {d}^{3}{vv}_{||}{f}_{1}\right\rangle _{{\phi} }\approx -({eE}_{||}{\omega} /{k}_{||})\left\langle \sin {\phi} \int {d}^{3}{v}\left.{f}_{1}\right| _{{\rm res}}\right\rangle _{{\phi} },\end{equation}

since $\left\langle \sin {\phi} \left.{f}_{1}\right| _{{\rm non}}\right\rangle _{{\phi} }=0$ and only the $\sin {\phi}$ term in $\left.{f}_{1}\right| _{{\rm res}}$ contributes. As a result

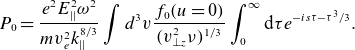(13) \begin{equation}{P}_{0}=\frac{{e}^{2}{E}_{||}^{2}{\omega} ^{2}}{{mv}_{{e}}^{2}{k}_{||}^{8/3}}\int {d}^{3}{v}\frac{{f}_{0}({u}=0)}{({v}_{\bot {z}}^{2}{\nu})^{1/3}}\int _{0}^{{\infty }}{\rm d}{\tau} {e}^{-{is}{\tau} -{{\tau} ^{3}}/3}.\end{equation}

Then ${d}^{3}{v}\rightarrow 2{\pi} {v}_{\bot }{\rm d}{v}_{\bot }{\rm d}{s}({v}_{\bot {z}}^{2}{\nu} /{k}_{||})^{1/3}$ leads to the usual ‘collisionless’ O’Neil (Reference O’Neil1965) result

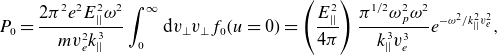(14) \begin{equation}{P}_{0}=\frac{2{{\pi} ^{2}}{e}^{2}{E}_{||}^{2}{\omega} ^{2}}{{mv}_{{e}}^{2}{k}_{||}^{3}}\int _{0}^{{\infty }}{\rm d}{v}_{\bot }{v}_{\bot }{f}_{0}({u}=0)=\left(\frac{{E}_{||}^{2}}{4{\pi} }\right)\frac{{\pi} ^{1/2}{\omega} _{{p}}^{2}{\omega} ^{2}}{{k}_{||}^{3}{v}_{{e}}^{3}}{e}^{-{{\omega} ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}},\end{equation}

even though collisions are crucial! But the absence is misleading as confirmed next.

The full nonlinear problem is considered for a monochromatic wave by allowing $\partial {f}_{1}/\partial {v}_{||}\sim \partial {f}_{0}/\partial {v}_{||}$ . Employing the phase ${\phi} ={k}_{||}{z}-{\omega} {t}$ , and noting ${v}_{\bot }$ enters as a parameter, the solution to the lowest order kinetic equation must be of the form ${f}_{1}={f}_{1}({\phi},{u})$ and satisfy

(15) \begin{equation}{k}_{||}{u}\partial {f}_{1}/\partial {\phi} -({eE}_{||}/{m})\sin {\phi} (\partial {f}_{0}/\partial {v}_{||}+\partial {f}_{1}/\partial {u})={\nu} {v}_{\bot {z}}^{2}\partial ^{2}{f}_{1}/\partial {u}^{2}.\end{equation}

Noticing $\partial {f}_{0}/\partial {v}_{||}\approx -({m}{\omega} /{Tk}_{||}){f}_{0}({u}=0)$ is a slowly varying function of ${v}_{||}$ , inserting

(16) \begin{equation}{f}_{1}={g}({u},{\phi})-({u}-{\sigma} {\alpha})\partial {f}_{0}/\partial {v}_{||},\end{equation}

where ${\sigma} ={u}/|{u}|=\pm 1$ or 0, and ${\alpha}$ is a constant speed to be determined, leads to

(17) \begin{equation}{k}_{||}{u}\partial {g}/\partial {\phi} -({eE}_{||}/{m})\sin {\phi} \partial {g}/\partial {u}={\nu} {v}_{\bot {z}}^{2}\partial ^{2}{g}/\partial {u}^{2}.\end{equation}

Letting

(18) \begin{equation}{j}=|{m}/{eE}_{||}{k}_{||}|^{1/2}{k}_{||}{u}=|{m}/{eE}_{||}{k}_{||}|^{1/2}({k}_{||}{v}_{||}-{\omega}),\end{equation}

and

(19) \begin{equation}{\varDelta} ={\nu} {k}_{||}^{2}{v}_{\bot {z}}^{2}|{m}/{eE}_{||}{k}_{||}|^{3/2}\propto {\nu} _{{ee}}/{E}_{||}^{3/2},\end{equation}

gives the equation to be the same as the one solved numerically by Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023),

(20) \begin{equation}{j}\frac{\partial {g}}{\partial {\phi} }-\sin {\phi} \frac{\partial {g}}{\partial {j}}={\varDelta} \frac{\partial ^{2}{g}}{\partial {j}^{2}}.\end{equation}

where ${\varDelta} \gt 0$ since ${v}_{\bot }^{2}\approx {v}^{2}-{\omega} ^{2}/{k}_{||}^{2}\gt 0$ in ${v}_{\bot {z}}^{2}$ . Their steady state solution is found by temporally evolving the full equation for g with a slow time derivative inserted.

The nonlinear equation treats the island structure as well as collisions. Taking j ∼ 1 gives the width of the velocity space island $({\Delta} {v}_{||})_{{is}}=({v}_{||}-{\omega} /{k}_{||})_{{is}}$ to be

(21) \begin{equation}({\Delta} {v}_{||})_{{is}}=|{eE}_{||}/{mk}_{||}|^{1/2}.\end{equation}

A linearized treatment is appropriate when the collisional boundary layer is wider than any island structure, requiring ${\varDelta} =[({\Delta} {v}_{||})_{{\nu} }/({\Delta} {v}_{||})_{{is}}]^{3}\gg 1$ . However, for a larger amplitude plasma wave in an extremely weak collisionality plasma, the ${\varDelta} \ll 1$ limit is of interest. This limit is considered next and will not lead to the Landau (Reference Landau1946) or Auerbach (Reference Auerbach1977) results.

The weak collision limit is different than the collisionless limit because the island structure must be retained. In this limit

(22) \begin{equation}1\gg |{eE}_{||}/{mk}_{||}{v}_{{e}}^{2}|^{3/2}\gg {\nu} /{{k}_{||}}{v}_{{e}}\sim {\nu} _{{e}}{k}_{||}^{2}{v}_{{e}}^{2}/{\omega} ^{3},\end{equation}

for ${v}_{\bot {z}}^{2}\sim {v}_{{e}}^{2}$ . The collisional boundary layers are now much narrower than the islands. They surround the separatrix between the bound (or librating) and unbound (or circulating) electron motion. All the dissipation occurs in these narrow boundary layers.

Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023) solved the nonlinear equation for g with slow temporal evolution for an astrophysical application. The steady skew symmetric solution satisfies

(23) \begin{equation}{g}({j},{\phi})=-{g}(-{j},-{\phi}).\end{equation}

An analytic treatment is possible for ${\varDelta} \ll 1$ by introducing the reduced constant of the motion

(24) \begin{equation}{h}({j},{\phi})={j}^{2}/2-\cos {\phi},\end{equation}

with h = 1 the location of the separatrix enclosed by a narrow collisional boundary layer separating the bound ( $-1 \lt h \lt 1$ ) and the unbound ( $h\gt 1$ ) electrons. The ${\varDelta} =0.001$ case shown in their figure 2(a) is reproduced here with their kind permission as figure 1. The reduced Hamiltonian allows the kinetic equation to be rewritten in terms of the new variables ${h},{\phi}$ as

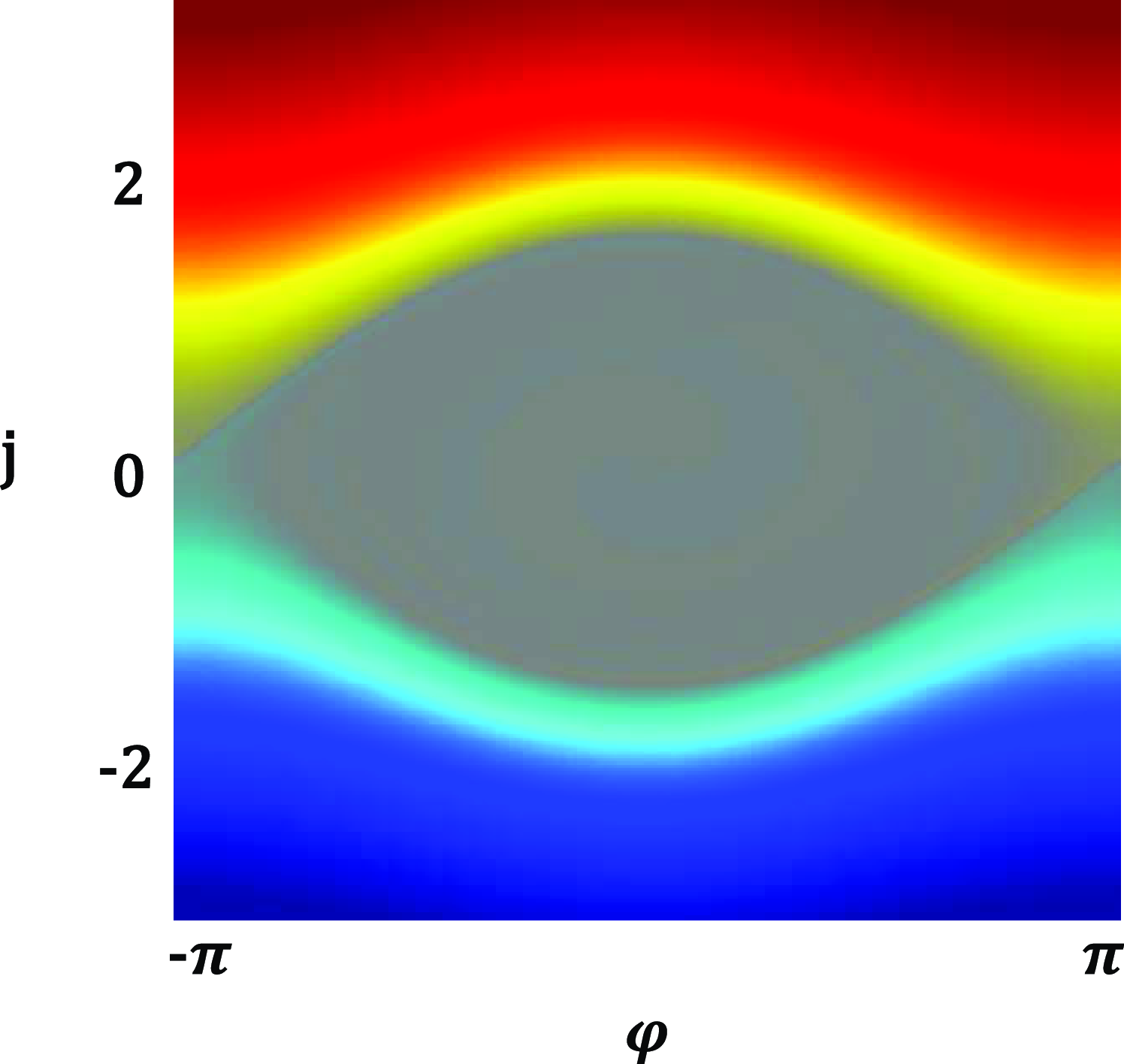
Figure 1. Contours of constant ${g}({j},{\varphi})$ , with the flattened bound region inside the separatrix at h = 1 and the two unbound regions above (in red and yellow) and below (in dark and light blue). Very narrow collisional boundary layers surround the separatrix at h = 1 for this ${\varDelta} =0.001$ case. (Reprinted with permission from Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023.)

(25) \begin{equation}\left.\frac{\partial {g}}{\partial {\phi} }\right| _{{h}}={\varDelta} \left.\frac{\partial }{\partial {h}}\right| _{{\phi} }\left({j}\left.\frac{\partial {g}}{\partial {h}}\right| _{{\phi} }\right).\end{equation}

The ${\varDelta} \ll 1$ limit allows a solution of the form ${g}={g}_{1}({h})+{g}_{2}({h},{\phi})+\cdots$ to be found. To lowest order $\partial {g}_{1}/\partial {\phi} |_{{h}}=0$ , while to next order

(26) \begin{equation}\left.\frac{\partial {g}_{2}}{\partial {\phi} }\right| _{{h}}={\varDelta} \left.\frac{\partial }{\partial {h}}\right| _{{\phi} }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right).\end{equation}

The solution to this equation, ${g}_{1}$ , must satisfy the collisional solubility constraint

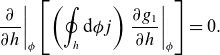(27) \begin{equation}\left.\frac{\partial }{\partial {h}}\right| _{{\phi} }\left[\left(\oint _{{h}}{\rm d}{\phi} {j}\right)\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right]=0.\end{equation}

It is independent of collisions, but its form is collisionally constrained. The partial solution of Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023) for ${\varDelta} \ll 1$ was completed by Catto (Reference Catto2025a ) for a stellarator application. It vanishes for bound orbits. For the unbound, $\int _{-{\pi} }^{{\pi} }{\rm d}{\varphi} {j}={\sigma} 8{k}^{-1}{E}({k})$ , with ${k}=\sqrt{2/({h}+1)}$ and E(k) a complete elliptic integral. To match ${f}_{1}$ to the non-resonant solution $\left.{f}_{1}\right| _{{\rm non}}$ as ${k}\rightarrow 0$

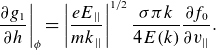(28) \begin{equation}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }=\left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{{\sigma} {\pi} {k}}{4{E}({k})}\frac{\partial {f}_{0}}{\partial {v}_{||}}.\end{equation}

Integrating from the separatrix at ${k}=1$ using ${\rm d}{h}=-4{\rm d}{k}/{k}^{3}$ leads to

\begin{equation*} {g}_{1}={\sigma} {\pi} \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\int _{{k}}^{1}\frac{{\rm d}{t}}{{t}^{2}{E}\left({t}\right)}\underset{{k}\rightarrow 0}{\rightarrow }{\sigma} \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{2}{{k}}-1.379-\frac{{k}}{2}+{O}\left({k}^{3}\right)\right] \end{equation*}

(29) \begin{equation}\approx \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[{j}-1.379{\sigma} -\frac{\cos {\phi} }{{j}}\right]=\left({u}-{\sigma} {\alpha} -\frac{{eE}_{||}\cos {\phi} }{{mk}_{||}{u}}\right)\frac{\partial {f}_{0}}{\partial {v}_{||}},\end{equation}

with ${j}=\pm \sqrt{2({h}+\cos {\phi})}=\pm (2/{k})\sqrt{1-{k}^{2}\sin ^{2}({\phi} /2)}$ , and ${\alpha} =1.379|{eE}_{||}/{m}{{k}_{||}}|^{1/2}$ now determined. The unbound solution satisfies ${g}_{1}\rightarrow 0$ at the separatrix (h = 1), but $\partial {g}_{1}/\partial {h}|_{{\varphi} }$ and $f_1$ step crossing it. The narrow, unresolved collisional boundary layer about the separatrix provides the smooth matching. Far from the resonance layer ${f}_{1}={g}_{1}-({u}-{\sigma} {\alpha})\partial {f}_{0}/\partial {v}_{||}\rightarrow ({eE}_{||}{f}_{0}/{k}_{||}{u})\cos {\phi} =\left.{f}_{1}\right| _{{\rm non}}$ as desired.

The power absorbed is evaluated using ${P}=-{eE}_{||}\langle \sin {\phi} \int {d}^{3}{vv}_{||}{f}_{1}\rangle _{{\phi} }$ . The details differ slightly from a recent lower hybrid current drive calculation (Catto Reference Catto2025b ) as the plasma wave evaluation is for an unmagnetized plasma. Using skew symmetry gives $\langle \int _{-{\infty }}^{{\infty }}\text{d}uu\sin{\phi} {f}_{1}({u},{\phi})\rangle _{{\phi} }=0$ . Integrating by parts using $2\sin {\phi} =-{\rm d}{j}^{2}/{\rm d}{\phi} |_{{h}}$ at fixed h, and inserting the kinetic equation leads to

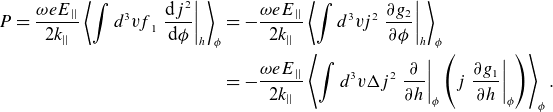(30) \begin{align}{P}=\frac{{\omega} {eE}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vf}_{1}\left.\frac{{\rm d}{j}^{2}}{{\rm d}{\phi} }\right| _{{h}}\right\rangle _{{\phi} } & = -\frac{{\omega} {eE}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vj}^{2}\left.\frac{\partial {g}_{2}}{\partial {\phi} }\right| _{{h}}\right\rangle _{{\phi} }\nonumber\\&=-\frac{{\omega} {eE}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{v}{\Delta} {j}^{2}\left.\frac{\partial }{\partial {h}}\right| _{{\phi} }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right)\right\rangle _{{\phi} }.\end{align}

In addition

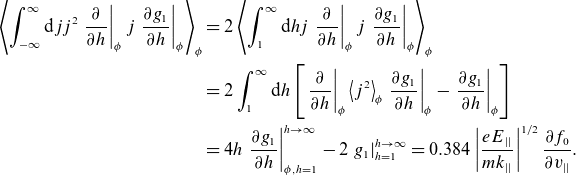(31) \begin{align} \left\langle \int _{-{\infty }}^{{\infty }}{\rm d}{jj}^{2}\left.\frac{\partial }{\partial {h}}\right| _{{\phi} }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right\rangle _{{\phi} } & =2\left\langle \int _{1}^{{\infty }}{\rm d}{hj}\left.\frac{\partial }{\partial {h}}\right| _{{\phi} }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right\rangle _{{\phi} }\nonumber\\&=2\int _{1}^{{\infty }}{\rm d}{h}\left[\left.\frac{\partial }{\partial {h}}\right| _{{\phi} }\left\langle {j}^{2}\right\rangle _{{\phi} }\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }-\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi} }\right]\nonumber\\&=4{h}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{{\phi},{h}=1}^{{h}\rightarrow {\infty }}-2\left.{g}_{1}\right| _{{h}=1}^{{h}\rightarrow {\infty }}=0.384\left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}.\end{align}

Using ${d}^{3}{v}\rightarrow 2{\pi} {v}_{\bot }{\rm d}{v}_{\bot }{\rm d}{j}/({\rm d}{j}/{\rm d}{u})$ and $\partial {f}_{0}/\partial {v}_{||}\approx -({m}{\omega} /{Tk}_{||}){f}_{0}({u}=0)$ , yields

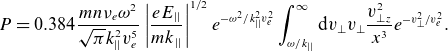(32) \begin{equation}{P}=0.384\frac{{mn}{\nu} _{{e}}{\omega} ^{2}}{\sqrt{{\pi} }{k}_{||}^{2}{v}_{{e}}^{5}}\left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}{e}^{-{{\omega} ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}\int _{{\omega} /{k}_{||}}^{{\infty }}{\rm d}{v}_{\bot }{v}_{\bot }\frac{{v}_{\bot {z}}^{2}}{{x}^{3}}{e}^{-{v}_{\bot }^{2}/{v}_{{e}}^{2}}.\end{equation}

The power absorbed for ${\omega} ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\gg 1$ is explicitly collisional and given by

(33) \begin{equation}{P}\approx 0.144({Z}+2){mnv}_{{e}}^{2}{\nu} _{{ee}}|{eE}_{||}{k}_{||}/{m}{\omega} ^{2}|^{1/2}{e}^{-{{\omega} ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}.\end{equation}

Normalizing ${P}$ to the result ${P}_{0}$ yields

(34) \begin{equation}\frac{{P}}{{P}_{0}}\approx 0.081({Z}+2)\frac{{\nu} _{{ee}}{k}_{||}^{5}{v}_{{e}}^{5}}{{\omega} ^{3}}\left|\frac{{m}}{{eE}_{||}{k}_{||}}\right|^{3/2}\sim {\varDelta}.\end{equation}

Consequently, Landau’s (Reference Landau1946) collisionless results do not hold as ${\nu} _{{ee}}\rightarrow 0$ for a finite ${E}_{||}$ .

Remarkably, the limits considered here demonstrate weak collisions play the key role in obtaining what is viewed as ‘collisionless Landau damping’ of a resonant plasma wave. The behavior is a characteristic of any kinetic equation involving a velocity space dependent resonance that must be resolved by diffusive collisions in a boundary layer. It is only when the collision frequency is very small and/or the amplitude becomes sufficiently large that departures from the deceptively looking ‘collisionless’ Landau (Reference Landau1946) limit arise. For a larger amplitude monochromatic plasma wave, nonlinearity occurs because of the appearance of island structure whose separatrix is enclosed by a very narrow collisional boundary layer that must be present – even as the collision frequency becomes very small. Consequently, this velocity space fine structure prevents Landau’s limit from being recovered in the limit of vanishing collision frequency for a plasma wave of non-vanishing amplitude. Moreover, energy must cascade to these ever finer velocity scales to be dissipated. The key role of collisions implies the seemingly ‘collisionless’ resonant Landau (Reference Landau1946) limit is actually a collisional plateau (or resonant plateau) regime, with ${\varDelta} \gt 1$ , located between the small ${\varDelta} \lt 1$ nonlinear regime treated here and a fully collisional plasma limit with ${\nu} _{{ee}}\gtrsim {\omega}$ . Thus, the Landau (Reference Landau1946) limit is valid when $1\gg {\nu} _{{ee}}/{\omega} \gg ({\omega} /{k}_{||}{v}_{{e}})^{2}|{eE}_{||}/{k}_{||}{T}_{{e}}|^{3/2}.$

Note added in proofs. François Waelbroeck has kindly brought to my attention a classic paper by Zakharov and Karpman (Reference Zakharov and Karpman1963) in which they solved the temporally evolving plasma wave problem of Landau but with collisions. The treatment in this paper solves the steady state driven plasma wave problem with collisions. Some details differ (like some details of the collision operator and the coefficient of the power absorbed in the weakly collisional, large plasma wave amplitude limit), but many other details are broadly the same. Their pioneering treatment should be consulted for full details.