We denote by KP_ the fragment of set-theory containing the axioms of extensionality, pairing, union and foundation as well as the schemas of ∆0-comprehension and ∆0-collection, that is: Kripke-Platek set-theory (KP) with the axiom of foundation in place of the ∈-induction schema. The theory KP is obtained by adding to KP_ the schema of ∈-induction
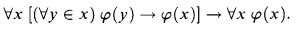
Using ∈-induction it is possible to prove the existence of the transi tive closure without appealing to the axiom of infinity (see, e.g., [1]). Vice versa, when a theory proves the existence of the transitive closure, some induction is immediately ensured (by foundation and comprehension). This is not true in general: e.g., the whole of Zermelo-Fraenkel set-theory without the axiom of infinity does not prove ∈-induction (in fact, it does not prove the existence of the transitive closure; see, e.g., [3]). Open-induction is the schema of ∈-induction restricted to open formulas. We prove the following theorem.
KP_ proves open-induction.
We reason in a fixed but arbitrary model of KP_ whom we refer to as the model. The language is extended with a name for every set in the model. We call this constants parameters. Let φ (x) be a satisfiable open-formula possibly depending on parameters and with no free variable but x. We show that φ(x) is satisfied by an ∈-minimal set, that is, a set a such that φ(a) and (∀x ∈ a) ¬φ(x). We assume that no ordinal satisfies φ(x), otherwise the existence of a ∈-minimal set follows from foundation and comprehension.