This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://ef.msp.org/submit/asl_jsl. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
It is well known that certain sentences corresponding to similar algebras are invariant under direct union; that is, are true of the direct union when true of each factor algebra. An axiomatizable class of similar algebras, such as the class of groups, is closed under direct union when each of its axioms is invariant. In this paper we shall determine a wide class of invariant sentences. We shall also be concerned with determining sentences which are true of a direct union provided they are true of some factor algebra. In the case where all the factor algebras are the same, a further result is obtained. In §2 it will be shown that these criteria are the only ones of their kind. Lemma 7 below may be of some independent interest.
We adopt the terminology and notation of McKinsey with the exception that the sign · will be used for conjunction. Expressions of the form ∼∊, where ∊ is an equation, will be called inequalities. In accordance with the analogy between conjunction and disjunction with product and sum respectively, we shall call α1, …, αn the terms of the disjunction
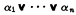
and the factors of the conjunction
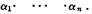
Every closed sentence is equivalent to a sentence in prenez normal form,
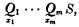
where x1, …, xm distinct individual variables, Q1, …, Qm are quantifiers, and the matrix S is an open sentence in which each of the variables x1, …, xm actually occurs. The sentence S may be written in either disjunctive normal form:
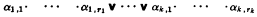
where αi,j is either an equation or an inequality, or in conjunctive normal form:
.
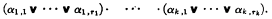