Professor C. I. Lewis, in Lewis and Langford's Symbolic logic, designates the system (S2) determined by the postulates used in Chapter VI—namely, 11.1–7 (B1–7) and

as the system of strict implication. For certain reasons, he prefers it to either the earlier system (S3) determined by the stronger set of postulates of his Survey of symbolic logic, as emended, namely, A1–7 and
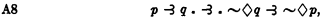
or the system (S1) determined by the weaker set of postulates B1–7 or A1–7.
But Lewis and others, following O. Becker, have also given consideration to systems which contain some additional principle effecting the reduction of complex modalities to simpler ones. Notable are the system (S4) determined by B1–7 plus
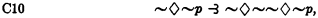
which includes (is stronger than) S3; and the system (S5) determined by B1–7 plus

which includes S4.
It seems worth while to investigate further the system of the Survey (emended), S3, which is intermediate between S2 and S4. This is the purpose of the present paper. We first prove some additional theorems in S2 and S3. These enable us to reduce all the complex modalities in S3 to a finite number, viz. 42; and it is shown that no further reduction is possible. Finally, several systems which include S3 are considered.