Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-30T14:40:31.742Z Has data issue: false hasContentIssue false
  • English
  • Français

VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS

Part of: Elliptic equations and systems Representations of solutions Partial differential equations

Published online by Cambridge University Press:  20 March 2024

FANG LIU  and
HONG SUN
FANG LIU*
Affiliation:
Department of Mathematics, School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, PR China
HONG SUN
Affiliation:
Department of Mathematics, School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, PR China e-mail: sunhong3721@163.com
*
e-mail: sdqdlf78@126.com, liufang78@njust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the singular boundary value problem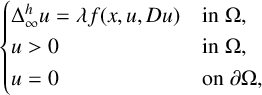

$$ \begin{align*} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{in}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega,\\ u=0 \quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$

where 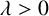$\lambda>0$ is a parameter, 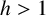$h>1$ and 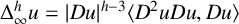$\Delta _\infty ^h u=|Du|^{h-3} \langle D^2uDu,Du \rangle $ is the highly degenerate and h-homogeneous operator related to the infinity Laplacian. The nonlinear term 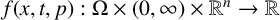$f(x,t,p):\Omega \times (0,\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}$ is a continuous function and may exhibit singularity at 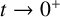$t\rightarrow 0^{+}$. We establish the comparison principle by the double variables method for the general equation 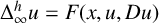$\Delta _\infty ^h u=F(x,u,Du)$ under some conditions on the term 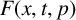$F(x,t,p)$. Then, we establish the existence of viscosity solutions to the singular boundary value problem in a bounded domain based on Perron’s method and the comparison principle. Finally, we obtain the existence result in the entire Euclidean space by the approximation procedure. In this procedure, we also establish the local Lipschitz continuity of the viscosity solution.

Keywords

infinity Laplaciansingular boundary value problemviscosity solutioncomparison principleexistence

MSC classification

Primary: 35D40: Viscosity solutions
Secondary: 35B51: Comparison principles 35J60: Nonlinear elliptic equations 35J70: Degenerate elliptic equations

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 3 , December 2024 , pp. 345 - 374
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Florica C. Cîrstea

This work was supported by the National Natural Science Foundation of China (No. 12141104)

References

Armstrong, S. and Smart, C., ‘An easy proof of Jensen’s theorem on the uniqueness of infinity harmonic functions’, Calc. Var. Partial Differential Equations 37 (2010), 381–384.CrossRefGoogle Scholar
Aronsson, G., ‘Minimization problems for the functional ${\sup }_{x}F\left(x,f(x),{f}^{\prime }(x)\right)$ ’, Ark. Mat. 6 (1965), 33–53.CrossRefGoogle Scholar
Aronsson, G., ‘Minimization problems for the functional ${\sup }_{x}F\left(x,f(x),{f}^{\prime }(x)\right)$ II’, Ark. Mat. 6 (1966), 409–431.Google Scholar
Aronsson, G., ‘Extension of functions satisfying Lipschitz conditions’, Ark. Mat. 6 (1967), 551–561.CrossRefGoogle Scholar
Aronsson, G., ‘Minimization problems for the functional ${\sup }_{x}F\left(x,f(x),{f}^{\prime }(x)\right)$ III’, Ark. Mat. 7 (1969), 509–512.CrossRefGoogle Scholar
Aronsson, G., Crandall, M. and Juutinen, P., ‘A tour of the theory of absolutely minimizing functions’, Bull. Amer. Math. Soc. (N.S.) 41 (2004), 439–505.CrossRefGoogle Scholar
Bhattacharya, T. and Mohammed, A., ‘On solutions to Dirichlet problems involving the infinity-Laplacian’, Adv. Calc. Var. 4 (2011), 445–487.CrossRefGoogle Scholar
Bhattacharya, T. and Mohammed, A., ‘Inhomogeneous Dirichlet problems involving the infinity-Laplacian’, Adv. Differential Equations 17(3) (2012), 225–266.CrossRefGoogle Scholar
Biset, T., Mebrate, B. and Mohammed, A., ‘A boundary-value problem for normalized Finsler infinity-Laplacian equations with singular nonhomogeneous terms’, Nonlinear Anal. 190 (2020), 111588.CrossRefGoogle Scholar
Biset, T. and Mohammed, A., ‘A singular boundary value problem for a degenerate elliptic PDE’, Nonlinear Anal. 119 (2015), 222–234.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V., ‘Uniqueness of the blow-up boundary solution of logistic equations with absorption’, C. R. Math. Acad. Sci. Paris 335 (2002), 447–452.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V., ‘Asymptotics for the blow-up boundary solution of the logistic equation with absorption’, C. R. Math. Acad. Sci. Paris 336 (2003), 231–236.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V., ‘Nonlinear problems with boundary blow-up: a Karamata regular variation theory approach’, Asymptot. Anal. 46 (2006), 275–298.Google Scholar
Crandall, M., ‘A visit with the $\infty$ -Laplacian equation’, Calc. Var. Partial Differential Equations 1927 (2008), 75–122.Google Scholar
Crandall, M. and Evans, L., ‘A remark on infinity harmonic functions’, Electron. J. Differ. Equ. Conf. 6 (2001), 123–129.Google Scholar
Crandall, M., Evans, L. and Gariepy, R., ‘Optimal Lipschitz extensions and the infinity Laplacian’, Calc. Var. Partial Differential Equations 13 (2001), 123–139.CrossRefGoogle Scholar
Crandall, M., Gunnarsson, G. and Wang, P., ‘Uniqueness of $\infty$ -harmonic functions and the eikonal equation’, Comm. Partial Differential Equations 32 (2007), 1587–1615.CrossRefGoogle Scholar
Crandall, M., Ishii, H. and Lions, P., ‘User’s guide to viscosity solutions of second order partial differential equations’, Bull. Amer. Math. Soc. (N.S.) 27 (1992), 1–67.CrossRefGoogle Scholar
Diaz, J., Morel, J. and Oswald, L., ‘An elliptic equation with singular nonlinearity’, Comm. Partial Differential Equations 12 (1987), 1333–1344.CrossRefGoogle Scholar
Esteban, R. and Vásquez, J., ‘On the equation of turbulent filtration in one-dimensional porous media’, Nonlinear Anal. 10(11) (1986), 1303–1325.CrossRefGoogle Scholar
Fulks, W. and Maybee, J., ‘A singular nonlinear equation’, Osaka J. Math. 12 (1960), 1–9.Google Scholar
Gomes, S., ‘On a singular nonlinear elliptic problem’, SIAM J. Math. Anal. 17 (1986), 1359–1369.CrossRefGoogle Scholar
Ishii, H., ‘Viscosity solutions of nonlinear partial differential equations’, Sugaku Expositions 9(2) (1996), 135–152.Google Scholar
Jensen, R., ‘Uniqueness of Lipschitz extensions minimizing the sup-norm of the gradient’, Arch. Ration. Mech. Anal. 123 (1993), 51–74.CrossRefGoogle Scholar
Li, C. and Liu, F., ‘Large solutions of a class of degenerate equations associated with infinity Laplacian’, Adv. Nonlinear Stud. 22 (2022), 67–87.CrossRefGoogle Scholar
Li, C. and Liu, F., ‘Viscosity solutions to the infinity Laplacian equation with lower terms’, Electron. J. Differ. Equ. 42 (2023), 1–23.Google Scholar
Liu, F., ‘The eigenvalue problem for a class of degenerate operators related to the normalized $p$ -Laplacian’, Discrete Contin. Dyn. Syst. Ser. B 27(5) (2022), 2701–2720.CrossRefGoogle Scholar
Liu, F., Tian, L. and Zhao, P., ‘A weighted eigenvalue problem of the degenerate operator associated with infinity Laplacian’, Nonlinear Anal. 200 (2020), 112001.CrossRefGoogle Scholar
Liu, F. and Yang, X., ‘Solutions to an inhomogeneous equation involving infinity-Laplacian’, Nonlinear Anal. 75 (2012), 5693–5701.CrossRefGoogle Scholar
López-Soriano, R., Navarro-Climent, J. and Rossi, J., ‘The infinity Laplacian with a transport term’, J. Math. Anal. Appl. 398 (2013), 752–765.CrossRefGoogle Scholar
Lu, G. and Wang, P., ‘Inhomogeneous infinity Laplace equation’, Adv. Math. 217 (2008), 1838–1868.CrossRefGoogle Scholar
Lu, G. and Wang, P., ‘A PDE perspective of the normalized infinity Laplacian’, Comm. Partial Differential Equations 33(10) (2008), 1788–1817.CrossRefGoogle Scholar
Mebrate, B. and Mohammed, A., ‘Infinity-Laplacian type equations and their associated Dirichlet problems’, Complex Var. Elliptic Equ. 65(7) (2020), 1139–1169.CrossRefGoogle Scholar
Mebrate, B. and Mohammed, A., ‘Comparison principles for infinity-Laplace equations in Finsler metrics’, Nonlinear Anal. 190 (2020), 111605.CrossRefGoogle Scholar
Mohammed, A., ‘Ground state solutions for singular semi-linear elliptic equations’, Nonlinear Anal. 71(3–4) (2009), 1276–1280.CrossRefGoogle Scholar
Mohammed, A., ‘Positive solutions of the p-Laplace equation with singular nonlinearity’, J. Math. Anal. Appl. 352(1) (2009), 234–245.CrossRefGoogle Scholar
Peres, Y., Pete, G. and Somersille, S., ‘Biased tug-of-war, the biased infinity Laplacian, and comparison with exponential cones’, Calc. Var. Partial Differential Equations 38(3–4) (2010), 541–564.CrossRefGoogle Scholar
Peres, Y., Schramm, O., Sheffield, S. and Wilson, D., ‘Tug-of-war and the infinity Laplacian’, J. Amer. Math. Soc. 22(1) (2009), 167–210.CrossRefGoogle Scholar
Santos, C., ‘On ground state solutions for singular and semi-linear problems including super-linear terms at infinity’, Nonlinear Anal. 71(12) (2009), 6038–6043.CrossRefGoogle Scholar