Article contents
Champ: a Cherednik algebra Magma package
Published online by Cambridge University Press: 01 April 2015
Abstract
We present a computer algebra package based onMagma for performing computations in rational Cherednik algebras with arbitrary parameters and in Verma modules for restricted rational Cherednik algebras. Part of this package is a new general Las Vegas algorithm for computing the head and the constituents of a module with simple head in characteristic zero, which we develop here theoretically. This algorithm is very successful when applied to Verma modules for restricted rational Cherednik algebras and it allows us to answer several questions posed by Gordon in some specific cases. We can determine the decomposition matrices of the Verma modules, the graded 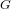 $G$ -module structure of the simple modules, and the Calogero–Moser families of the generic restricted rational Cherednik algebra for around half of the exceptional complex reflection groups. In this way we can also confirm Martino’s conjecture for several exceptional complex reflection groups.
$G$ -module structure of the simple modules, and the Calogero–Moser families of the generic restricted rational Cherednik algebra for around half of the exceptional complex reflection groups. In this way we can also confirm Martino’s conjecture for several exceptional complex reflection groups.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2015
References
- 12
- Cited by

