Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-59df476f6b-6b5bh Total loading time: 0.322 Render date: 2021-05-17T21:18:13.142Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": true, "newCiteModal": false, "newCitedByModal": true, "newEcommerce": true }
EnglishFrançais
LMS Journal of Computation and Mathematics LMS Journal of Computation and Mathematics

Article contents

Collecting relations for the number field sieve in 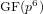$\text{GF}(p^{6})$

Part of: Finite fields and commutative rings (number-theoretic aspects) Computational number theory Number theory

Published online by Cambridge University Press:  26 August 2016

Pierrick Gaudry ,
Laurent Grémy  and
Marion Videau
Pierrick Gaudry
Affiliation:
INRIA, CNRS, Université de Lorraine, Nancy, France email pierrick.gaudry@loria.fr
Laurent Grémy
Affiliation:
INRIA, CNRS, Université de Lorraine, Nancy, France email laurent.gremy@loria.fr
Marion Videau
Affiliation:
Quarkslab, Paris, France INRIA, CNRS, Université de Lorraine, Nancy, France email marion.videau@loria.fr
Corresponding
E-mail address:
pierrick.gaudry@loria.fr
laurent.gremy@loria.fr
marion.videau@loria.fr
Save pdf (0.58 megabytes)Save pdf (0.58 mb)

Abstract

In order to assess the security of cryptosystems based on the discrete logarithm problem in non-prime finite fields, as are the torus-based or pairing-based ones, we investigate thoroughly the case in 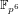$\mathbb{F}_{p^{6}}$ with the number field sieve. We provide new insights, improvements, and comparisons between different methods to select polynomials intended for a sieve in dimension 3 using a special- 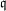$\mathfrak{q}$ strategy. We also take into account the Galois action to increase the relation productivity of the sieving phase. To validate our results, we ran several experiments and real computations for various polynomial selection methods and field sizes with our publicly available implementation of the sieve in dimension 3, with special- 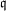$\mathfrak{q}$ and various enumeration strategies.

MSC classification

Primary: 11T71: Algebraic coding theory; cryptography 11Y40: Algebraic number theory computations 11-04: Explicit machine computation and programs (not the theory of computation or programming)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 332 - 350
Copyright
© The Author(s) 2016 

References

Bai, S., Brent, R. and Thomé, E., ‘Root optimization of polynomials in the number field sieve’, Math. Comp. 84 (2015) 2447–2457.CrossRefGoogle Scholar
Barbulescu, R., Gaudry, P., Guillevic, A. and Morain, F., ‘Improving NFS for the discrete logarithm problem in non-prime finite fields’, EUROCRYPT 2015 , Lecture Notes in Computer Science 9056 (eds Oswald, E. and Fischlin, M.; Springer, 2015) 129–155.Google Scholar
Barbulescu, R., Gaudry, P., Joux, A. and Thomé, E., ‘A heuristic quasi-polynomial algorithm for discrete logarithm in finite fields of small characteristic’, EUROCRYPT 2014 , Lecture Notes in Computer Science 8441 (eds Nguyen, P. and Oswald, E.; Springer, Berlin, Heidelberg, 2014) 1–16.Google Scholar
Barbulescu, R., Gaudry, P. and Kleinjung, T., ‘The tower number field sieve’, ASIACRYPT 2015 , Lecture Notes in Computer Science 9453 (eds Iwata, T. and Cheon, J. H.; Springer, Berlin, Heidelberg, 2015) 31–55.CrossRefGoogle Scholar
Barbulescu, R. and Lachand, A., ‘Some mathematical remarks on the polynomial selection in NFS’, Math. Comp., published online (2016), doi:10.1090/mcom/3112.Google Scholar
Barbulescu, R. and Pierrot, C., ‘The multiple number field sieve for medium and high characteristic finite fields’, LMS J. Comput. Math. 17 (2014) 230–246.CrossRefGoogle Scholar
Cohen, H., A course in algorithmic algebraic number theory , Graduate Texts in Mathematics 138 (Springer, Berlin, Heidelberg, 1993).CrossRefGoogle Scholar
Commeine, A. and Semaev, I., ‘An algorithm to solve the discrete logarithm problem with the number field sieve’, PKC 2006 , Lecture Notes in Computer Science 3958 (eds Yung, M., Dodis, Y., Kiayias, A. and Malkin, T.; Springer, Berlin, Heidelberg, 2006) 174–190.Google Scholar
Coppersmith, D., ‘Modifications to the number field sieve’, J. Cryptology 6 (1993) no. 3, 169–180.Google Scholar
Franke, J. and Kleinjung, T., ‘Continued fractions and lattice sieving’, SHARCS’05 – Special-purpose Hardware for Attacking Cryptographic Systems (2005), http://www.sharcs.org/.Google Scholar
Freeman, D., Scott, M. and Teske, E., ‘A taxonomy of pairing-friendly elliptic curves’, J. Cryptology 23 (2010) 224–280.CrossRefGoogle Scholar
González, Á., ‘Measurement of areas on a sphere using Fibonacci and latitude–longitude lattices’, Math. Geosci. (2010) 42–49.Google Scholar
Gordon, D. M., ‘Discrete logarithms in GF(p) using the number field sieve’, SIAM J. Discrete Math. 6 (1993) no. 1, 124–138.CrossRefGoogle Scholar
Guillevic, A., ‘Computing individual discrete logarithms faster in GF(p n ) with the NFS-DL algorithm’, ASIACRYPT 2015 , Lecture Notes in Computer Science 9452 (eds Iwata, T. and Cheon, J. H.; Springer, Berlin, Heidelberg, 2015) 149–173.CrossRefGoogle Scholar
Hanrot, G., Pujol, X. and Stehlé, D., ‘Algorithms for the shortest and closest lattice vector problems’, Coding and Cryptology — Third International Workshop, IWCC 2011 , Lecture Notes in Computer Science 6639 (eds Chee, Y. M., Guo, Z., Ling, S., Shao, F., Tang, Y., Wang, H. and Xing, C.; Springer, Berlin, Heidelberg, 2011) 159–190.Google Scholar
Hayasaka, K., Aoki, K., Kobayashi, T. and Takagi, T., ‘An experiment of number field sieve for discrete logarithm problem over GF(p 12 )’, Number theory and cryptography , Lecture Notes in Computer Science 8260 (eds Fischlin, M. and Katzenbeisser, S.; Springer, Berlin, Heidelberg, 2013) 108–120.Google Scholar
Hayasaka, K., Aoki, K., Kobayashi, T. and Takagi, T., ‘A construction of 3-dimensional lattice sieve for number field sieve over $\mathbb{F}_{p^{n}}$ ’, Cryptology ePrint Archive, 2015/1179, 2015.Google Scholar
Joux, A. and Lercier, R., ‘Improvements to the general number field sieve for discrete logarithms in prime fields’, Math. Comp. 72 (2003) no. 242, 953–967.CrossRefGoogle Scholar
Joux, A., Lercier, R., Smart, N. P. and Vercauteren, F., ‘The number field sieve in the medium prime case’, CRYPTO 2006 , Lecture Notes in Computer Science 4117 (ed. Dwork, C.; Springer, Berlin, Heidelberg, 2006) 326–344.CrossRefGoogle Scholar
Joux, A. and Pierrot, C., ‘The special number field sieve in F p n — application to pairing-friendly constructions’, Pairing 2013 , Lecture Notes in Computer Science 8365 (eds Cao, Z. and Zhang, F.; Springer, Cham, 2013) 45–61.Google Scholar
Kim, T. and Barbulescu, R., ‘Extended tower number field sieve: a new complexity for medium prime case’, CRYPTO 2016, Lecture Notes in Computer Science (Springer), to appear; Cryptology ePrint Archive, 2015/1027, 2015.Google Scholar
Kleinjung, T., ‘On polynomial selection for the general number field sieve’, Math. Comp. 75 (2006) 2037–2047.CrossRefGoogle Scholar
Lenstra, A. K. and Verheul, E. R., ‘The XTR public key system’, CRYPTO 2000 , Lecture Notes in Computer Science 1880 (ed. Bellare, M.; Springer, 2000) 1–19.Google Scholar
Murphy, B. A., ‘Polynomial selection for the number field sieve integer factorisation algorithm’, PhD Thesis, Australian National University, 1999.Google Scholar
Pierrot, C., ‘The multiple number field sieve with conjugation and generalized Joux–Lercier methods’, EUROCRYPT 2015 , Lecture Notes in Computer Science 9056 (eds Oswald, E. and Fischlin, M.; Springer, Berlin, Heidelberg, 2015) 156–170.Google Scholar
Pollard, J., ‘The lattice sieve’, The development of the number field sieve , Lecture Notes in Mathematics 1554 (eds Lenstra, A. K. and Lenstra, H. W. Jr.; Springer, Berlin, Heidelberg, 1993) 43–49.CrossRefGoogle Scholar
Rubin, K. and Silverberg, A., ‘Torus-based cryptography’, CRYPTO 2003 , Lecture Notes in Computer Science 2729 (ed. Boneh, D.; Springer, Berlin, Heidelberg, 2003) 349–365.CrossRefGoogle Scholar
Sarkar, P. and Singh, S., ‘New complexity trade-offs for the (multiple) number field sieve algorithm in non-prime fields’, EUROCRYPT 2016 , Lecture Notes in Computer Science 9665 (eds Fischlin, M. and Coron, J. S.; Springer, Berlin, Heidelberg, 2016) 429–458.CrossRefGoogle Scholar
Schirokauer, O., ‘Virtual logarithms’, J. Algorithms 57 (2005) 140–147.CrossRefGoogle Scholar
Schirokauer, O., ‘Discrete logarithms and local units’, Philos. Trans. A 345 (1993) no. 1676, 409–423.CrossRefGoogle Scholar
The CADO-NFS Development Team: CADO-NFS, an implementation of the number field sieve algorithm, 2015, http://cado-nfs.gforge.inria.fr/, release 2.2.0.Google Scholar
Zajac, P., ‘Discrete logarithm problem in degree six finite fields’, PhD Thesis, Slovak University of Technology, 2008, http://www.kaivt.elf.stuba.sk/kaivt/Vyskum/XTRDL.Google Scholar
Zajac, P., ‘On the use of the lattice sieve in the 3D NFS’, Tatra Mt. Math. Publ. 45 (2010) 161–172.Google Scholar
You have Access
6
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Collecting relations for the number field sieve in $\text{GF}(p^{6})$
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Collecting relations for the number field sieve in $\text{GF}(p^{6})$
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Collecting relations for the number field sieve in $\text{GF}(p^{6})$
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *