Article contents
The discrete logarithm problem for exponents of bounded height
Published online by Cambridge University Press: 01 August 2014
Abstract
Let 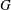 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a cyclic group written multiplicatively (and represented in some concrete way). Let
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a cyclic group written multiplicatively (and represented in some concrete way). Let  $n$ be a positive integer (much smaller than the order of
$n$ be a positive integer (much smaller than the order of 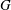 $G$). Let
$G$). Let 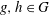 $g,h\in G$. The bounded height discrete logarithm problem is the task of finding positive integers
$g,h\in G$. The bounded height discrete logarithm problem is the task of finding positive integers  $a$ and
$a$ and 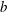 $b$ (if they exist) such that
$b$ (if they exist) such that 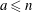 $a\leq n$,
$a\leq n$, 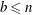 $b\leq n$ and
$b\leq n$ and 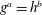 $g^a=h^b$. (Provided that
$g^a=h^b$. (Provided that 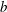 $b$ is coprime to the order of
$b$ is coprime to the order of 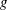 $g$, we have
$g$, we have 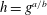 $h=g^{a/b}$ where
$h=g^{a/b}$ where 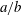 $a/b$ is a rational number of height at most
$a/b$ is a rational number of height at most  $n$. This motivates the terminology.)
$n$. This motivates the terminology.)
The paper provides a reduction to the two-dimensional discrete logarithm problem, so the bounded height discrete logarithm problem can be solved using a low-memory heuristic algorithm for the two-dimensional discrete logarithm problem due to Gaudry and Schost. The paper also provides a low-memory heuristic algorithm to solve the bounded height discrete logarithm problem in a generic group directly, without using a reduction to the two-dimensional discrete logarithm problem. This new algorithm is inspired by (but differs from) the Gaudry–Schost algorithm. Both algorithms use 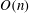 $O(n)$ group operations, but the new algorithm is faster and simpler than the Gaudry–Schost algorithm when used to solve the bounded height discrete logarithm problem. Like the Gaudry–Schost algorithm, the new algorithm can easily be carried out in a distributed fashion.
$O(n)$ group operations, but the new algorithm is faster and simpler than the Gaudry–Schost algorithm when used to solve the bounded height discrete logarithm problem. Like the Gaudry–Schost algorithm, the new algorithm can easily be carried out in a distributed fashion.
The bounded height discrete logarithm problem is relevant to a class of attacks on the privacy of a key establishment protocol recently published by EMVCo for comment. This protocol is intended to protect the communications between a chip-based payment card and a terminal using elliptic curve cryptography. The paper comments on the implications of these attacks for the design of any final version of the EMV protocol.
MSC classification
Information
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 148 - 156
- Copyright
- © The Author(s) 2014
References
- 1
- Cited by

