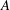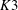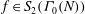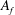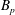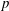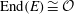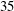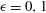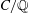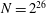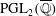Contents
Research Article
Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 1-13
-
- Article
-
- You have access
- Export citation
Examples of
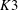 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation
Computing Galois representations of modular abelian surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 36-48
-
- Article
-
- You have access
- Export citation
A sieve algorithm based on overlattices
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 49-70
-
- Article
-
- You have access
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation
Approximating the densest sublattice from Rankin’s inequality
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 92-111
-
- Article
-
- You have access
- Export citation
Minimal models for
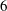 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 112-127
-
- Article
-
- You have access
- Export citation
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
The discrete logarithm problem for exponents of bounded height
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 148-156
-
- Article
-
- You have access
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
Finding roots in
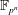 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 203-217
-
- Article
-
- You have access
- Export citation
Traps to the BGJT-algorithm for discrete logarithms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 218-229
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
On the computation of the determinant of vector-valued Siegel modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 247-256
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Tracking
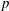 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-adic precision
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-adic precision
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 274-294
-
- Article
-
- You have access
- Export citation
Class number calculation using Siegel functions
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 295-302
-
- Article
-
- You have access
- Export citation
On the units generated by Weierstrass forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 303-313
-
- Article
-
- You have access
- Export citation
A census of quadratic post-critically finite rational functions defined over
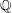 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation