Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T12:14:08.081Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit isogenies in quadratic time in any characteristic

Part of: Computational number theory Curves Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 August 2016

Luca De Feo Open the ORCID record for Luca De Feo [Opens in a new window] ,
Cyril Hugounenq ,
Jérôme Plût  and
Éric Schost
Luca De Feo
Affiliation:
LMV – UVSQ, 45 avenue des États-Unis, 78035 Versailles, France, email luca.de-feo@uvsq.fr
Cyril Hugounenq
Affiliation:
LMV – UVSQ, 45 avenue des États-Unis, 78035 Versailles, France email hugounenq@msn.com
Jérôme Plût
Affiliation:
ANSSI, 51, boulevard de La Tour-Maubourg, 75007 Paris, France email jerome.plut@ssi.gouv.fr
Éric Schost
Affiliation:
Cheriton School of Computer Science, University of Waterloo, Waterloo, ON, Canada N2L 3G1 email eschost@uwaterloo.ca

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider two ordinary elliptic curves 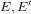$E,E^{\prime }$ defined over a finite field 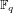$\mathbb{F}_{q}$ , and suppose that there exists an isogeny 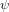$\unicode[STIX]{x1D713}$ between 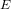$E$ and 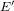$E^{\prime }$ . We propose an algorithm that determines 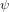$\unicode[STIX]{x1D713}$ from the knowledge of 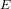$E$ , 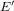$E^{\prime }$ and of its degree $r$ , by using the structure of the 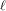$\ell$ -torsion of the curves (where  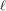$\ell$  is a prime different from the characteristic  $p$ of the base field). Our approach is inspired by a previous algorithm due to Couveignes, which involved computations using the $p$ -torsion on the curves. The most refined version of that algorithm, due to De Feo, has a complexity of 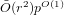 $\tilde{O} (r^{2})p^{O(1)}$ base field operations. On the other hand, the cost of our algorithm is 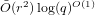$\tilde{O} (r^{2})\log (q)^{O(1)}$ , for a large class of inputs; this makes it an interesting alternative for the medium- and large-characteristic cases.

MSC classification

Primary: 11Y40: Algebraic number theory computations
Secondary: 11G20: Curves over finite and local fields 14H52: Elliptic curves

References

Atkin, A. O. L., ‘The number of points on an elliptic curve modulo a prime’, mail to the nmbrthry mailing list, 1988.Google Scholar
Atkin, A. O. L., ‘The number of points on an elliptic curve modulo a prime’, mail to the nmbrthry mailing list, 1991.Google Scholar
Bostan, A., Morain, F., Salvy, B. and Schost, É., ‘Fast algorithms for computing isogenies between elliptic curves’, Math. Comp. 77 (2008) no. 263, 1755–1778.Google Scholar
Bröker, R., Lauter, K. and Sutherland, A., ‘Modular polynomials via isogeny volcanoes’, Math. Comp. 81 (2012) no. 278, 1201–1231.Google Scholar
Charlap, L. S., Coley, R. and Robbins, D. P., ‘Enumeration of rational points on elliptic curves over finite fields’, Preprint, 1991.Google Scholar
Charles, D. X., Lauter, K. E. and Goren, E. Z., ‘Cryptographic hash functions from expander graphs’, J. Cryptology 22 (2009) no. 1, 93–113.Google Scholar
Couveignes, J.-M., ‘Quelques calculs en théorie des nombres’, PhD Thesis, Université de Bordeaux, 1994.Google Scholar
Couveignes, J.-M., ‘Computing l-Isogenies using the p-torsion’, ANTS-II: Proceedings of the Second International Symposium on Algorithmic Number Theory (Springer, London, 1996) 59–65.CrossRefGoogle Scholar
Couveignes, J.-M., ‘Isomorphisms between Artin–Schreier towers’, Math. Comp. 69 (2000) no. 232, 1625–1631.Google Scholar
De Feo, L., ‘Fast algorithms for computing isogenies between ordinary elliptic curves in small characteristic’, J. Number Theory 131 (2011) no. 5, 873–893.Google Scholar
De Feo, L., Doliskani, J. and Schost, É., ‘Fast algorithms for ℓ-adic towers over finite fields’, ISSAC’13: Proceedings of the 2013 International Symposium on Symbolic and Algebraic Computation (ACM, New York, 2013) 165–172.Google Scholar
De Feo, L., Jao, D. and Plût, J., ‘Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies’, J. Math. Cryptol. 8 (2014) no. 3, 209–247.Google Scholar
De Feo, L. and Schost, É., ‘Fast arithmetics in Artin–Schreier towers over finite fields’, J. Symbolic Comput. 47 (2012) no. 7, 771–792.Google Scholar
Doliskani, J. and Schost, É., ‘Computing in degree 2 k -extensions of finite fields of odd characteristic’, Des. Codes Cryptogr. 74 (2015) no. 3, 559–569.Google Scholar
Elkies, N. D., ‘Elliptic and modular curves over finite fields and related computational issues’, Computational perspectives on number theory (Chicago, IL, 1995) , Studies in Advanced Mathematics 7 (AMS International Press, Providence, RI, 1998) 21–76.Google Scholar
Enge, A. and Morain, F., ‘Fast decomposition of polynomials with known Galois group’, AAECC’03: Proceedings of the 15th International Conference on Applied Algebra, Algebraic Algorithms and Error-correcting Codes (Springer, Berlin, 2003) 254–264.Google Scholar
Fouquet, M. and Morain, F., ‘Isogeny volcanoes and the SEA algorithm’, Algorithmic number theory (Sydney, 2002) , Lecture Notes in Computer Science 2369 (Springer, Berlin, 2002).Google Scholar
Gallant, R. P., Lambert, R. J. and Vanstone, S. A., ‘Faster point multiplication on elliptic curves with efficient endomorphisms’, CRYPTO ’01: Proceedings of the 21st Annual International Cryptology Conference on Advances in Cryptology (Springer, London, 2001) 190–200.Google Scholar
Ionica, S. and Joux, A., ‘Pairing the volcano’, Math. Comp. 82 (2013) no. 281, 581–603.Google Scholar
Jao, D. and Soukharev, V., ‘Isogeny-based quantum-resistant undeniable signatures’, Post-Quantum Cryptography: 6th International Workshop, PQCrypto 2014 (Springer International Publishing, Waterloo, ON, 2014) 160–179.CrossRefGoogle Scholar
Kaltofen, E. and Shoup, V., ‘Fast polynomial factorization over high algebraic extensions of finite fields’, ISSAC’97: Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation (ACM, New York, 1997) 184–188.Google Scholar
Kohel, D., ‘Endomorphism rings of elliptic curves over finite fields’, PhD Thesis, University of California at Berkeley, 1996.Google Scholar
Lairez, P. and Vaccon, T., ‘On p-adic differential equations with separation of variables’, Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC’16 (ACM, New York, 2016) 319–323.Google Scholar
Lercier, R. and Sirvent, T., ‘On Elkies subgroups of ℓ-torsion points in elliptic curves defined over a finite field’, J. Théor. Nombres Bordeaux 20 (2008) no. 3, 783–797.Google Scholar
Longa, P. and Sica, F., ‘Four-dimensional Gallant–Lambert–Vanstone scalar multiplication’, J. Cryptology 27 (2014) no. 2, 248–283.Google Scholar
Maurer, M., Menezes, A. and Teske, E., ‘Analysis of the GHS Weil descent attack on the ECDLP over characteristic two finite fields of composite degree’, INDOCRYPT’01: Proceedings of the Second International Conference on Cryptology in India (Springer, Berlin, 2001) 195–213.Google Scholar
Miret, J. M., Moreno, R., Rio, A. and Valls, M., ‘Determining the 2-sylow subgroup of an elliptic curve over a finite field’, Math. Comp. 74 (2005) no. 249, 411–427.Google Scholar
The Sage Developers. ‘Sage Mathematics Software (version 7.1)’, 2016.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p ’, Math. Comp. 44 (1985) no. 170, 483–494.Google Scholar
Schoof, R., ‘Counting points on elliptic curves over finite fields’, J. Théor. Nombres Bordeaux 7 (1995) no. 1, 219–254.Google Scholar
Serre, J.-P., Cours d’arithmétique (Presses Universitaires de France, 1970).Google Scholar
Serre, J.-P., Arbres, amalgames, SL2 , Astérisque 46 (Société Mathématique de France, Paris, 1977).Google Scholar
Shparlinski, I. E. and Sutherland, A. V., ‘On the distribution of Atkin and Elkies primes’, Found. Comput. Math. 14 (2014) no. 2, 285–297.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves , Graduate Texts in Mathematics 106 (Springer, New York, 1992).Google Scholar
Stolbunov, A., ‘Constructing public-key cryptographic schemes based on class group action on a set of isogenous elliptic curves’, Adv. Math. Commun. 4 (2010) no. 2, 215–235.Google Scholar
Sutherland, A., ‘Isogeny volcanoes’, ANTS X: Proceedings of the Algorithmic Number Theory 10th International Symposium, vol. 1 (Mathematical Sciences Publishers, Berkerley, CA, 2013) 507–530.Google Scholar
Sutherland, A., ‘On the evaluation of modular polynomials’, ANTS X: Proceedings of the Algorithmic Number Theory 10th International Symposium, vol. 1 (Mathematical Sciences Publishers, Berkerley, CA, 2013) 531–555.Google Scholar
Tate, J., ‘Endomorphisms of abelian varieties over finite fields’, Invent. Math. 2 (1966) no. 2, 134–144.Google Scholar
Teske, E., ‘An elliptic curve trapdoor system’, J. Cryptology 19 (2006) no. 1, 115–133.Google Scholar
Vélu, J., ‘Isogénies entre courbes elliptiques’, C. R. Acad. Sci. Paris 273 (1971) 238–241.Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra (Cambridge University Press, New York, 1999).Google Scholar
von zur Gathen, J. and Shoup, V., ‘Computing Frobenius maps and factoring polynomials’, STOC ’92: Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing (ACM, New York, 1992) 97–105.CrossRefGoogle Scholar