Article contents
On families of 7- and 11-congruent elliptic curves
Published online by Cambridge University Press: 01 September 2014
Abstract
We use an invariant-theoretic method to compute certain twists of the modular curves 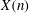 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}X(n)$ for
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}X(n)$ for 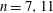 $n=7,11$ . Searching for rational points on these twists enables us to find non-trivial pairs of
$n=7,11$ . Searching for rational points on these twists enables us to find non-trivial pairs of  $n$ -congruent elliptic curves over
$n$ -congruent elliptic curves over 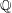 ${\mathbb{Q}}$ , that is, pairs of non-isogenous elliptic curves over
${\mathbb{Q}}$ , that is, pairs of non-isogenous elliptic curves over 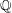 ${\mathbb{Q}}$ whose
${\mathbb{Q}}$ whose  $n$ -torsion subgroups are isomorphic as Galois modules. We also find a non-trivial pair of 11-congruent elliptic curves over
$n$ -torsion subgroups are isomorphic as Galois modules. We also find a non-trivial pair of 11-congruent elliptic curves over 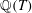 ${\mathbb{Q}}(T)$ , and hence give an explicit infinite family of non-trivial pairs of 11-congruent elliptic curves over
${\mathbb{Q}}(T)$ , and hence give an explicit infinite family of non-trivial pairs of 11-congruent elliptic curves over 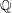 ${\mathbb{Q}}$ .
${\mathbb{Q}}$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2014
References
- 10
- Cited by

