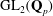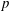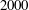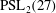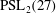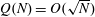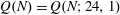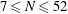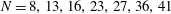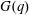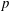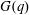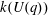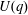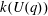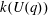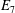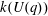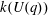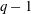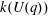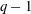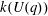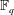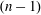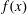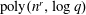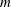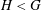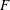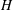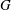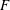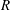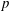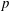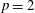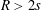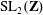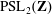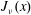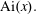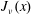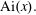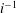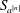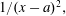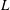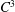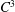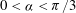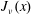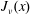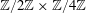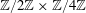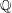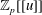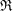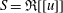Contents
Research Article
Computing fundamental domains for the Bruhat–Tits tree for
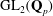 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 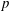 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
Classification of subgroups isomorphic to
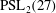 $\mathrm{PSL}_2(27)$ in the Monster
$\mathrm{PSL}_2(27)$ in the Monster
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 33-46
-
- Article
-
- You have access
- Export citation
Bounds for zeros of Meixner and Kravchuk polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 47-57
-
- Article
-
- You have access
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
Minimal genus and fibering of canonical surfaces via disk decomposition
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 77-108
-
- Article
-
- You have access
- Export citation
Calculating conjugacy classes in Sylow
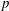 $p$ -subgroups of finite Chevalley groups of rank six and seven
$p$ -subgroups of finite Chevalley groups of rank six and seven
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 109-122
-
- Article
-
- You have access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
Computation of Galois groups of rational polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
Rational functions with maximal radius of absolute monotonicity
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 159-205
-
- Article
-
- You have access
- Export citation
Congruence testing for odd subgroups of the modular group
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 206-208
-
- Article
-
- You have access
- Export citation
Approximations for the Bessel and Airy functions with an explicit error term
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 209-225
-
- Article
-
- You have access
- Export citation
A note on magnitude bounds for the mask coefficients of the interpolatory Dubuc–Deslauriers subdivision scheme
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 226-232
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
Evaluating
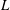 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 245-258
-
- Article
-
- You have access
- Export citation
A symmetric
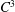 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 259-272
-
- Article
-
- You have access
- Export citation
On the Bessel function
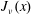 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 273-281
-
- Article
-
- You have access
- Export citation
High-rank elliptic curves with torsion
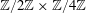 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 282-288
-
- Article
-
- You have access
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
Linear algebra over
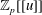 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation