Article contents
Wieferich pairs and Barker sequences, II
Published online by Cambridge University Press: 01 April 2014
Abstract
We show that if a Barker sequence of length 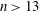 $n>13$ exists, then either n
$n>13$ exists, then either n  $=$ 3 979 201 339 721749 133 016 171 583 224 100, or
$=$ 3 979 201 339 721749 133 016 171 583 224 100, or 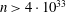 $n > 4\cdot 10^{33}$ . This improves the lower bound on the length of a long Barker sequence by a factor of nearly
$n > 4\cdot 10^{33}$ . This improves the lower bound on the length of a long Barker sequence by a factor of nearly 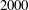 $2000$ . We also obtain eighteen additional integers
$2000$ . We also obtain eighteen additional integers 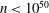 $n<10^{50}$ that cannot be ruled out as the length of a Barker sequence, and find more than 237 000 additional candidates
$n<10^{50}$ that cannot be ruled out as the length of a Barker sequence, and find more than 237 000 additional candidates 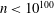 $n<10^{100}$ . These results are obtained by completing extensive searches for Wieferich prime pairs and using them, together with a number of arithmetic restrictions on
$n<10^{100}$ . These results are obtained by completing extensive searches for Wieferich prime pairs and using them, together with a number of arithmetic restrictions on  $n$ , to construct qualifying integers below a given bound. We also report on some updated computations regarding open cases of the circulant Hadamard matrix problem.
$n$ , to construct qualifying integers below a given bound. We also report on some updated computations regarding open cases of the circulant Hadamard matrix problem.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 11
- Cited by

