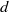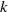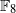Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Little, John B.
2013.
Remarks on generalized toric codes.
Finite Fields and Their Applications,
Vol. 24,
Issue. ,
p.
1.
Luo, Xue
Yau, Stephen S.-T.
Zhang, Mingyi
and
Zuo, Huaiqing
2015.
On classification of toric surface codes of low dimension.
Finite Fields and Their Applications,
Vol. 33,
Issue. ,
p.
90.
Little, John B.
2017.
Toric codes and finite geometries.
Finite Fields and Their Applications,
Vol. 45,
Issue. ,
p.
203.
Şahin, Mesut
2020.
Numerical Semigroups.
Vol. 40,
Issue. ,
p.
285.
Meyer, Kyle
Soprunov, Ivan
and
Soprunova, Jenya
2022.
$\mathbb{F}_q$-Zeros of Sparse Trivariate Polynomials and Toric 3-Fold Codes.
SIAM Journal on Applied Algebra and Geometry,
Vol. 6,
Issue. 3,
p.
432.
Nardi, Jade
2022.
Projective toric codes.
International Journal of Number Theory,
Vol. 18,
Issue. 01,
p.
179.
Baran, Esma
and
Şahin, Mesut
2023.
On parameterized toric codes.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 34,
Issue. 3,
p.
443.
Baldemir, Fadime
and
Şahin, Mesut
2023.
Calculating the Minimum Distance of a Toric Code via Algebraic Algorithms.
Mathematics in Computer Science,
Vol. 17,
Issue. 3-4,
Şahin, Mesut
2023.
Rational points of lattice ideals on a toric variety and toric codes.
Finite Fields and Their Applications,
Vol. 90,
Issue. ,
p.
102226.
Şahin, Mesut
and
Yayla, Oğuz
2024.
Codes on subgroups of weighted projective tori.
Designs, Codes and Cryptography,
Vol. 92,
Issue. 5,
p.
1201.