Ruzsa asked whether there exist Fourier-uniform subsets of 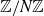$\mathbb Z/N\mathbb Z$ with density 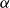$\alpha$ and 4-term arithmetic progression (4-AP) density at most 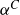$\alpha^C$, for arbitrarily large C. Gowers constructed Fourier uniform sets with density 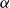$\alpha$ and 4-AP density at most 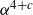$\alpha^{4+c}$ for some small constant 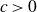$c \gt 0$. We show that an affirmative answer to Ruzsa’s question would follow from the existence of an 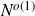$N^{o(1)}$-colouring of [N] without symmetrically coloured 4-APs. For a broad and natural class of constructions of Fourier-uniform subsets of 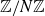$\mathbb Z/N\mathbb Z$, we show that Ruzsa’s question is equivalent to our arithmetic Ramsey question.

We prove analogous results for all even-length APs. For each odd 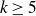$k\geq 5$, we show that there exist 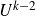$U^{k-2}$-uniform subsets of 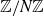$\mathbb Z/N\mathbb Z$ with density 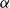$\alpha$ and k-AP density at most 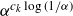$\alpha^{c_k \log(1/\alpha)}$. We also prove generalisations to arbitrary one-dimensional patterns.