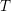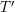Introduction and main results
In this paper, our aim is to prove a weak form of nearly Morita equivalence for mutations of (non-maximal) rigid objects in triangulated categories. Before recalling the case of cluster-tilting objects (see [Reference Buan, Marsh and ReitenBMR07]), we first give an example.
Let
![]() $Q$
be a linear orientation of the Dynkin diagram of type
$Q$
be a linear orientation of the Dynkin diagram of type
![]() $A_{3}$
. The Auslander–Reiten quiver of the acyclic cluster category
$A_{3}$
. The Auslander–Reiten quiver of the acyclic cluster category
![]() ${\mathcal{C}}_{Q}$
, defined in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06], is as follows:
${\mathcal{C}}_{Q}$
, defined in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06], is as follows:

The object
![]() $T=T_{1}\oplus T_{2}\oplus T_{3}$
is cluster-tilting. Its mutation at
$T=T_{1}\oplus T_{2}\oplus T_{3}$
is cluster-tilting. Its mutation at
![]() $T_{2}$
is the cluster-tilting object
$T_{2}$
is the cluster-tilting object
![]() $T^{\prime }=T_{1}\oplus T_{2}^{\ast }\oplus T_{3}$
. We write
$T^{\prime }=T_{1}\oplus T_{2}^{\ast }\oplus T_{3}$
. We write
![]() $\unicode[STIX]{x1D6E4}$
for the cluster-tilted algebra
$\unicode[STIX]{x1D6E4}$
for the cluster-tilted algebra
![]() $\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
, and
$\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
, and
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
for
$\unicode[STIX]{x1D6E4}^{\prime }$
for
![]() $\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
. Then, the two algebras
$\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
. Then, the two algebras
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
are related as follows.
$\unicode[STIX]{x1D6E4}^{\prime }$
are related as follows.
On the one hand, the functor
![]() ${\mathcal{C}}(T,-)$
induces an equivalence of categories
${\mathcal{C}}(T,-)$
induces an equivalence of categories
![]() ${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T)\simeq \operatorname{mod}\unicode[STIX]{x1D6E4}$
, where
${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T)\simeq \operatorname{mod}\unicode[STIX]{x1D6E4}$
, where
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}$
is the category of finitely generated left modules, and the Auslander–Reiten quiver of
$\operatorname{mod}\unicode[STIX]{x1D6E4}$
is the category of finitely generated left modules, and the Auslander–Reiten quiver of
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}$
is thus
$\operatorname{mod}\unicode[STIX]{x1D6E4}$
is thus

where
![]() $S_{2}={\mathcal{C}}(T,\unicode[STIX]{x1D6F4}T_{2}^{\ast })$
is the simple top of the projective indecomposable
$S_{2}={\mathcal{C}}(T,\unicode[STIX]{x1D6F4}T_{2}^{\ast })$
is the simple top of the projective indecomposable
![]() ${\mathcal{C}}(T,T_{2})$
.
${\mathcal{C}}(T,T_{2})$
.
On the other hand, the functor
![]() ${\mathcal{C}}(T^{\prime },-)$
induces an equivalence of categories
${\mathcal{C}}(T^{\prime },-)$
induces an equivalence of categories
![]() ${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })\simeq \operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }$
, and the Auslander–Reiten quiver of
${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })\simeq \operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }$
, and the Auslander–Reiten quiver of
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }$
is thus
$\operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }$
is thus

where
![]() $S_{2}^{\ast }={\mathcal{C}}(T^{\prime },\unicode[STIX]{x1D6F4}T_{2})$
is the simple top of the projective indecomposable
$S_{2}^{\ast }={\mathcal{C}}(T^{\prime },\unicode[STIX]{x1D6F4}T_{2})$
is the simple top of the projective indecomposable
![]() ${\mathcal{C}}(T^{\prime },T_{2}^{\ast })$
, where the two arrows starting at
${\mathcal{C}}(T^{\prime },T_{2}^{\ast })$
, where the two arrows starting at
![]() $S_{2}^{\ast }$
are identified, and where dots indicate zero relations.
$S_{2}^{\ast }$
are identified, and where dots indicate zero relations.
The two Auslander–Reiten quivers are not isomorphic; therefore,
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
are not Morita equivalent. However, they are not very far from being so: the difference in the Auslander–Reiten quivers comes from the simples
$\unicode[STIX]{x1D6E4}^{\prime }$
are not Morita equivalent. However, they are not very far from being so: the difference in the Auslander–Reiten quivers comes from the simples
![]() $S_{2}$
and
$S_{2}$
and
![]() $S_{2}^{\ast }$
.
$S_{2}^{\ast }$
.
The common Auslander–Reiten quiver of the categories
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}/(\operatorname{add}S_{2})$
and
$\operatorname{mod}\unicode[STIX]{x1D6E4}/(\operatorname{add}S_{2})$
and
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}/(\operatorname{add}S_{2}^{\ast })$
is thus
$\operatorname{mod}\unicode[STIX]{x1D6E4}/(\operatorname{add}S_{2}^{\ast })$
is thus

This phenomenon, proved in [Reference Buan, Marsh and ReitenBMR07], has been called “nearly Morita equivalence” by C. M. Ringel. Let us state the precise result.
Let
![]() $Q$
be an acyclic quiver, and let
$Q$
be an acyclic quiver, and let
![]() $T$
be a cluster-tilting object in the cluster category
$T$
be a cluster-tilting object in the cluster category
![]() ${\mathcal{C}}_{Q}$
. Let
${\mathcal{C}}_{Q}$
. Let
![]() $T^{\prime }=T/T_{k}\oplus T_{k}^{\ast }$
be the mutation of
$T^{\prime }=T/T_{k}\oplus T_{k}^{\ast }$
be the mutation of
![]() $T$
at an indecomposable summand
$T$
at an indecomposable summand
![]() $T_{k}$
; then,
$T_{k}$
; then,
![]() $T^{\prime }$
is also a cluster-tilting object. Let
$T^{\prime }$
is also a cluster-tilting object. Let
![]() $\unicode[STIX]{x1D6E4}$
(respectively,
$\unicode[STIX]{x1D6E4}$
(respectively,
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
) be the cluster-tilted algebra
$\unicode[STIX]{x1D6E4}^{\prime }$
) be the cluster-tilted algebra
![]() $\operatorname{End}_{{\mathcal{C}}_{Q}}(T)^{\text{op}}$
(respectively,
$\operatorname{End}_{{\mathcal{C}}_{Q}}(T)^{\text{op}}$
(respectively,
![]() $\operatorname{End}_{{\mathcal{C}}_{Q}}(T^{\prime })^{\text{op}}$
), and let
$\operatorname{End}_{{\mathcal{C}}_{Q}}(T^{\prime })^{\text{op}}$
), and let
![]() $S_{k}$
(respectively,
$S_{k}$
(respectively,
![]() $S_{k}^{\ast }$
) be the simple top of the projective indecomposable
$S_{k}^{\ast }$
) be the simple top of the projective indecomposable
![]() $\unicode[STIX]{x1D6E4}$
-module
$\unicode[STIX]{x1D6E4}$
-module
![]() ${\mathcal{C}}_{Q}(T,T_{k})$
(respectively, the simple top of the
${\mathcal{C}}_{Q}(T,T_{k})$
(respectively, the simple top of the
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
-module
$\unicode[STIX]{x1D6E4}^{\prime }$
-module
![]() ${\mathcal{C}}_{Q}(T^{\prime },T_{k}^{\ast })$
).
${\mathcal{C}}_{Q}(T^{\prime },T_{k}^{\ast })$
).
Then, by a result of [Reference Buan, Marsh and ReitenBMR07], the categories
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}/\operatorname{add}S_{k}$
and
$\operatorname{mod}\unicode[STIX]{x1D6E4}/\operatorname{add}S_{k}$
and
![]() $\operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }/\operatorname{add}S_{k}^{\ast }$
are equivalent. By [Reference YangYan12, Corollary 4.3], nearly Morita equivalence, in the more general setup of simple,
$\operatorname{mod}\unicode[STIX]{x1D6E4}^{\prime }/\operatorname{add}S_{k}^{\ast }$
are equivalent. By [Reference YangYan12, Corollary 4.3], nearly Morita equivalence, in the more general setup of simple,
![]() $2$
-periodic mutations of rigid objects (or rigid, Krull–Schmidt subcategories) in any triangulated category, follows from [Reference PlamondonPla11, Proposition 2.7].
$2$
-periodic mutations of rigid objects (or rigid, Krull–Schmidt subcategories) in any triangulated category, follows from [Reference PlamondonPla11, Proposition 2.7].
Our main aim in this paper is to prove an analogous result for any mutation of (non-maximal) rigid objects. Before explaining our results, let us have a look at an example that shows that one cannot expect these mutations to induce a nearly Morita equivalence in general.
Let
![]() $T=T_{1}\oplus T_{2}\oplus T_{3}$
be the rigid object of the acyclic cluster category
$T=T_{1}\oplus T_{2}\oplus T_{3}$
be the rigid object of the acyclic cluster category
![]() ${\mathcal{C}}={\mathcal{C}}_{A_{4}}$
given by
${\mathcal{C}}={\mathcal{C}}_{A_{4}}$
given by

and let
![]() $T^{\prime }=T_{1}\oplus T_{2}^{\ast }\oplus T_{3}$
be the rigid object obtained by mutating
$T^{\prime }=T_{1}\oplus T_{2}^{\ast }\oplus T_{3}$
be the rigid object obtained by mutating
![]() $T$
at the summand
$T$
at the summand
![]() $T_{2}$
. This means that
$T_{2}$
. This means that
![]() $\unicode[STIX]{x1D6F4}T_{2}^{\ast }$
is the cone of a minimal right
$\unicode[STIX]{x1D6F4}T_{2}^{\ast }$
is the cone of a minimal right
![]() $\operatorname{add}T/T_{2}$
-approximation of
$\operatorname{add}T/T_{2}$
-approximation of
![]() $T_{2}$
. In the example, there is a triangle
$T_{2}$
. In the example, there is a triangle
![]() $T_{2}^{\ast }\rightarrow T_{1}\rightarrow T_{2}\rightarrow \unicode[STIX]{x1D6F4}T_{2}^{\ast }$
. Let
$T_{2}^{\ast }\rightarrow T_{1}\rightarrow T_{2}\rightarrow \unicode[STIX]{x1D6F4}T_{2}^{\ast }$
. Let
![]() $\unicode[STIX]{x1D6EC}$
(respectively,
$\unicode[STIX]{x1D6EC}$
(respectively,
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
) be the algebra
$\unicode[STIX]{x1D6EC}^{\prime }$
) be the algebra
![]() $\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
$\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
![]() $\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
). Using results in [Reference Buan and MarshBM12, Reference Buan and MarshBM13] (see also [Reference Keller and ReitenKR07]), we can easily compute the Auslander–Reiten quivers of
$\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
). Using results in [Reference Buan and MarshBM12, Reference Buan and MarshBM13] (see also [Reference Keller and ReitenKR07]), we can easily compute the Auslander–Reiten quivers of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
and
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
and
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
:
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
:

The algebras
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
are not nearly Morita equivalent. On factoring out by
$\unicode[STIX]{x1D6EC}^{\prime }$
are not nearly Morita equivalent. On factoring out by
![]() $S_{2}$
(respectively,
$S_{2}$
(respectively,
![]() $S_{2}^{\ast }$
), we obtain the following Auslander–Reiten quivers:
$S_{2}^{\ast }$
), we obtain the following Auslander–Reiten quivers:

However, these algebras are not very far from being nearly Morita equivalent. Indeed, the Auslander–Reiten quivers differ by only one arrow. The corresponding morphism can be characterized in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
as being surjective with kernel in the subcategory
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
as being surjective with kernel in the subcategory
![]() $\operatorname{add}S_{2}$
.
$\operatorname{add}S_{2}$
.
Let
![]() ${\mathcal{C}}$
be an acyclic cluster category, and let
${\mathcal{C}}$
be an acyclic cluster category, and let
![]() $T$
be a rigid object in
$T$
be a rigid object in
![]() ${\mathcal{C}}$
. Let
${\mathcal{C}}$
. Let
![]() $T^{\prime }=T/T_{k}\oplus T_{k}^{\ast }$
be the mutation of
$T^{\prime }=T/T_{k}\oplus T_{k}^{\ast }$
be the mutation of
![]() $T$
at the summand
$T$
at the summand
![]() $T_{k}$
. Let
$T_{k}$
. Let
![]() $\unicode[STIX]{x1D6EC}$
(respectively,
$\unicode[STIX]{x1D6EC}$
(respectively,
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
) be the algebra
$\unicode[STIX]{x1D6EC}^{\prime }$
) be the algebra
![]() $\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
$\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
![]() $\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
), and let
$\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
), and let
![]() $S_{k}$
(respectively,
$S_{k}$
(respectively,
![]() $S_{k}^{\ast }$
) be the simple top of the projective indecomposable
$S_{k}^{\ast }$
) be the simple top of the projective indecomposable
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() ${\mathcal{C}}(T,T_{k})$
(respectively, the
${\mathcal{C}}(T,T_{k})$
(respectively, the
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-module
$\unicode[STIX]{x1D6EC}^{\prime }$
-module
![]() ${\mathcal{C}}(T^{\prime },T_{k}^{\ast })$
).
${\mathcal{C}}(T^{\prime },T_{k}^{\ast })$
).
As suggested by the example above, let us consider the class
![]() ${\mathcal{R}}$
of epimorphisms in
${\mathcal{R}}$
of epimorphisms in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
with kernels in
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
with kernels in
![]() $\operatorname{add}S_{k}$
, and the class
$\operatorname{add}S_{k}$
, and the class
![]() ${\mathcal{R}}^{\ast }$
of monomorphisms in
${\mathcal{R}}^{\ast }$
of monomorphisms in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
with cokernels in
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
with cokernels in
![]() $\operatorname{add}S_{k}^{\ast }$
.
$\operatorname{add}S_{k}^{\ast }$
.
Theorem A. There is an equivalence of categories
This result is not completely satisfactory since it does not resemble nearly Morita equivalence. The following remark will help in restating the theorem in a form that looks more like nearly Morita equivalence.
Let
![]() $M\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
. If there is a short exact sequence
$M\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
. If there is a short exact sequence
![]() $0\rightarrow S_{k}\rightarrow L\stackrel{f}{\rightarrow }M\rightarrow 0$
, the morphism
$0\rightarrow S_{k}\rightarrow L\stackrel{f}{\rightarrow }M\rightarrow 0$
, the morphism
![]() $f$
belongs to
$f$
belongs to
![]() ${\mathcal{R}}$
. Therefore, the objects
${\mathcal{R}}$
. Therefore, the objects
![]() $L$
and
$L$
and
![]() $M$
become isomorphic in the localization
$M$
become isomorphic in the localization
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{R}}}$
. This suggests that the objects having non-split extensions with
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{R}}}$
. This suggests that the objects having non-split extensions with
![]() $S_{k}$
can be removed from
$S_{k}$
can be removed from
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
without changing the localization. We thus define
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
without changing the localization. We thus define
![]() ${\mathcal{E}}$
to be the full subcategory of
${\mathcal{E}}$
to be the full subcategory of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
whose objects
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
whose objects
![]() $M$
satisfy
$M$
satisfy
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{k})=0$
. Dually, let
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{k})=0$
. Dually, let
![]() ${\mathcal{E}}^{\prime }$
be the full subcategory of
${\mathcal{E}}^{\prime }$
be the full subcategory of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
whose objects
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
whose objects
![]() $N$
satisfy
$N$
satisfy
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}^{\prime }}^{1}(S_{k}^{\ast },N)=0$
.
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}^{\prime }}^{1}(S_{k}^{\ast },N)=0$
.
It should be noted that
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{E}}^{\prime }$
are extension-closed in
${\mathcal{E}}^{\prime }$
are extension-closed in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
(respectively,
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
(respectively,
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
) and are thus exact categories.
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
) and are thus exact categories.
Theorem B. There is an equivalence of categories
Dually, there is an equivalence of categories
Combining the two theorems gives the following.
Corollary.
There is an equivalence of categories
This resembles nearly Morita equivalence except that, unlike in the cluster-tilting case, one has to restrict to an exact subcategory before killing the simple.
Unfortunately, these statements do not specialize to a nearly Morita equivalence in the cluster-tilting case: in the setup of [Reference Buan, Marsh and ReitenBMR07], we obtain a weaker statement.
The proofs of Theorems A and B are in Section 3.1 (but note that the proofs appear in reverse order to the above). In fact, we prove more general results than those mentioned above. First, we only assume the triangulated category
![]() ${\mathcal{C}}$
to be Krull–Schmidt, with a Serre functor. Second, we allow mutations at non-indecomposable summands. Our results hold, in particular, in any triangulated category in the following list (whose items overlap):
${\mathcal{C}}$
to be Krull–Schmidt, with a Serre functor. Second, we allow mutations at non-indecomposable summands. Our results hold, in particular, in any triangulated category in the following list (whose items overlap):
∙ Hom-finite generalized higher cluster categories (see [Reference AmiotAmi09, Reference GuoGuo11]);
∙ stable categories of maximal Cohen–Macaulay modules over an odd dimensional isolated hypersurface singularity (see [Reference Burban, Iyama, Keller and ReitenBIKR08]);
∙ cluster tubes (see [Reference Barot, Kussin and LenzingBKL08, Reference Buan, Marsh and VatneBMV10]…);
∙ (higher) cluster categories of type
 $A_{\infty }$
(see [Reference Holm and JørgensenHJ12, Reference Holm and Jørgensen.HJ13]);
$A_{\infty }$
(see [Reference Holm and JørgensenHJ12, Reference Holm and Jørgensen.HJ13]);∙ the triangulated orbit categories listed in [Reference AmiotAmi07];
∙ stable categories constructed from preprojective algebras in [Reference Geiß, Leclerc and SchröerGLS, Reference Geiß, Leclerc and SchröerGLS11]….
1 Setup and notation
We fix a field
![]() $k$
, and a Krull–Schmidt,
$k$
, and a Krull–Schmidt,
![]() $k$
-linear, Hom-finite, triangulated category
$k$
-linear, Hom-finite, triangulated category
![]() ${\mathcal{C}}$
, with suspension functor
${\mathcal{C}}$
, with suspension functor
![]() $\unicode[STIX]{x1D6F4}$
. An object
$\unicode[STIX]{x1D6F4}$
. An object
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}$
is called rigid if
${\mathcal{C}}$
is called rigid if
![]() $\operatorname{Ext}_{{\mathcal{C}}}^{1}(X,X)=0$
, where we write
$\operatorname{Ext}_{{\mathcal{C}}}^{1}(X,X)=0$
, where we write
![]() $\operatorname{Ext}_{{\mathcal{C}}}^{1}(X,Y)$
for
$\operatorname{Ext}_{{\mathcal{C}}}^{1}(X,Y)$
for
![]() ${\mathcal{C}}(X,\unicode[STIX]{x1D6F4}Y)$
. We write
${\mathcal{C}}(X,\unicode[STIX]{x1D6F4}Y)$
. We write
![]() $X^{\bot }$
for the right Hom-perp of
$X^{\bot }$
for the right Hom-perp of
![]() $X$
; that is, the subcategory of
$X$
; that is, the subcategory of
![]() ${\mathcal{C}}$
on objects
${\mathcal{C}}$
on objects
![]() $Y$
such that
$Y$
such that
![]() ${\mathcal{C}}(X,Y)=0$
. It should be noted that this notation differs from that used in [Reference Buan and MarshBM13], which we often cite; here, the Hom-perpendicular categories play a key role, so we use a different notation.
${\mathcal{C}}(X,Y)=0$
. It should be noted that this notation differs from that used in [Reference Buan and MarshBM13], which we often cite; here, the Hom-perpendicular categories play a key role, so we use a different notation.
Let
![]() $T\in {\mathcal{C}}$
be a basic rigid object. Let
$T\in {\mathcal{C}}$
be a basic rigid object. Let
![]() $R$
be a direct summand of
$R$
be a direct summand of
![]() $T$
, and write
$T$
, and write
![]() $T=\overline{T}\oplus R$
. Let
$T=\overline{T}\oplus R$
. Let
![]() $T^{\prime }$
be the object obtained from
$T^{\prime }$
be the object obtained from
![]() $T$
by replacing
$T$
by replacing
![]() $R$
by the negative shift
$R$
by the negative shift
![]() $R^{\ast }$
of the cone of a minimal right
$R^{\ast }$
of the cone of a minimal right
![]() $\operatorname{add}\overline{T}$
-approximation of
$\operatorname{add}\overline{T}$
-approximation of
![]() $R$
. We have a triangle
$R$
. We have a triangle
![]() $R^{\ast }\rightarrow B\rightarrow R\rightarrow \unicode[STIX]{x1D6F4}R^{\ast }$
, with
$R^{\ast }\rightarrow B\rightarrow R\rightarrow \unicode[STIX]{x1D6F4}R^{\ast }$
, with
![]() $B\in \operatorname{add}\overline{T}$
,
$B\in \operatorname{add}\overline{T}$
,
![]() $B\rightarrow R$
a minimal right
$B\rightarrow R$
a minimal right
![]() $\operatorname{add}\overline{T}$
-approximation, and
$\operatorname{add}\overline{T}$
-approximation, and
![]() $T^{\prime }=\overline{T}\oplus R^{\ast }$
. By [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.7],
$T^{\prime }=\overline{T}\oplus R^{\ast }$
. By [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.7],
![]() $\unicode[STIX]{x1D6F4}R^{\ast }\in \overline{T}^{\bot }$
. We assume that
$\unicode[STIX]{x1D6F4}R^{\ast }\in \overline{T}^{\bot }$
. We assume that
![]() $T^{\prime }$
is rigid. More precisely, we assume that
$T^{\prime }$
is rigid. More precisely, we assume that
![]() $R^{\ast }$
is rigid and that
$R^{\ast }$
is rigid and that
![]() $R^{\ast }$
belongs to
$R^{\ast }$
belongs to
![]() $^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
. By [Reference Iyama and YoshinoIY08, Proposition 2.6(1)] and [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.5],
$^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
. By [Reference Iyama and YoshinoIY08, Proposition 2.6(1)] and [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.5],
![]() $R$
and
$R$
and
![]() $R^{\ast }$
are basic and have the same number of indecomposable direct summands. We keep these assumptions throughout the paper.
$R^{\ast }$
are basic and have the same number of indecomposable direct summands. We keep these assumptions throughout the paper.
Remark.
We note that, if
![]() ${\mathcal{C}}$
is 2-Calabi–Yau, then
${\mathcal{C}}$
is 2-Calabi–Yau, then
![]() $T^{\prime }$
is automatically rigid (see [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Section 6]). However, WuZhong Yang kindly warned us that this is not true in general: Example 2.20 in [Reference Yang, Zhang and ZhuYZZ15] shows that
$T^{\prime }$
is automatically rigid (see [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Section 6]). However, WuZhong Yang kindly warned us that this is not true in general: Example 2.20 in [Reference Yang, Zhang and ZhuYZZ15] shows that
![]() $R^{\ast }$
might not be rigid. Moreover, even when
$R^{\ast }$
might not be rigid. Moreover, even when
![]() $R^{\ast }$
is rigid, it might not belong to
$R^{\ast }$
is rigid, it might not belong to
![]() $^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
. An example illustrating this latter phenomenon can be found in [Reference Yang and ZhuYZ15, Example 2.15]. In that example,
$^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
. An example illustrating this latter phenomenon can be found in [Reference Yang and ZhuYZ15, Example 2.15]. In that example,
![]() ${\mathcal{C}}$
is the 3-cluster category of type
${\mathcal{C}}$
is the 3-cluster category of type
![]() $A_{3}$
, which contains a cluster-tilting object
$A_{3}$
, which contains a cluster-tilting object
![]() $T$
. If
$T$
. If
![]() $R$
is any indecomposable summand of
$R$
is any indecomposable summand of
![]() $T$
, the (left) mutation of
$T$
, the (left) mutation of
![]() $T$
at
$T$
at
![]() $R$
gives an indecomposable rigid object
$R$
gives an indecomposable rigid object
![]() $R^{\ast }$
which belongs to
$R^{\ast }$
which belongs to
![]() $\unicode[STIX]{x1D6F4}^{-1}\overline{T}^{\bot }$
, but not to
$\unicode[STIX]{x1D6F4}^{-1}\overline{T}^{\bot }$
, but not to
![]() $^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
.
$^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
.
In some statements, we assume additionally that
![]() ${\mathcal{C}}$
has a Serre functor.
${\mathcal{C}}$
has a Serre functor.
We also need some more notation. If
![]() $X$
is an object in
$X$
is an object in
![]() ${\mathcal{C}}$
, we write
${\mathcal{C}}$
, we write
![]() $(X)$
for the ideal of morphisms factoring through the additive subcategory
$(X)$
for the ideal of morphisms factoring through the additive subcategory
![]() $\operatorname{add}X$
generated by
$\operatorname{add}X$
generated by
![]() $X$
. All modules considered are left modules.
$X$
. All modules considered are left modules.
We denote by
![]() ${\mathcal{C}}(T)$
the full subcategory of
${\mathcal{C}}(T)$
the full subcategory of
![]() ${\mathcal{C}}$
whose objects are the cones of morphisms
${\mathcal{C}}$
whose objects are the cones of morphisms
![]() $T_{1}\rightarrow T_{0}$
, where
$T_{1}\rightarrow T_{0}$
, where
![]() $T_{0},T_{1}\in \operatorname{add}T$
, and by
$T_{0},T_{1}\in \operatorname{add}T$
, and by
![]() $\overline{{\mathcal{C}}}(T)$
the full subcategory of
$\overline{{\mathcal{C}}}(T)$
the full subcategory of
![]() ${\mathcal{C}}$
whose objects are the cones of morphisms
${\mathcal{C}}$
whose objects are the cones of morphisms
![]() $\overline{T_{1}}\rightarrow T_{0}$
, where
$\overline{T_{1}}\rightarrow T_{0}$
, where
![]() $T_{0}\in \operatorname{add}T$
and
$T_{0}\in \operatorname{add}T$
and
![]() $\overline{T_{1}}\in \operatorname{add}\overline{T}$
.
$\overline{T_{1}}\in \operatorname{add}\overline{T}$
.
More generally, for any two full subcategories
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{B}}$
of
${\mathcal{B}}$
of
![]() ${\mathcal{C}}$
, we use the notation
${\mathcal{C}}$
, we use the notation
![]() ${\mathcal{A}}\ast {\mathcal{B}}$
for the full subcategory whose objects
${\mathcal{A}}\ast {\mathcal{B}}$
for the full subcategory whose objects
![]() $X$
are extensions of an object in
$X$
are extensions of an object in
![]() ${\mathcal{B}}$
by an object in
${\mathcal{B}}$
by an object in
![]() ${\mathcal{A}}$
(i.e.,
${\mathcal{A}}$
(i.e.,
![]() $X$
appears in a triangle
$X$
appears in a triangle
![]() $A\rightarrow X\rightarrow B\rightarrow \unicode[STIX]{x1D6F4}A$
with
$A\rightarrow X\rightarrow B\rightarrow \unicode[STIX]{x1D6F4}A$
with
![]() $A\in {\mathcal{A}}$
and
$A\in {\mathcal{A}}$
and
![]() $B\in {\mathcal{B}}$
). It follows from the octahedral axiom that the operation
$B\in {\mathcal{B}}$
). It follows from the octahedral axiom that the operation
![]() $\ast$
is associative. By abuse of notation, if
$\ast$
is associative. By abuse of notation, if
![]() $A,B$
are objects in
$A,B$
are objects in
![]() ${\mathcal{C}}$
, we write
${\mathcal{C}}$
, we write
![]() $A\ast B$
for
$A\ast B$
for
![]() $\operatorname{add}A\ast \operatorname{add}B$
.
$\operatorname{add}A\ast \operatorname{add}B$
.
Thus, one could also define
![]() ${\mathcal{C}}(T)$
and
${\mathcal{C}}(T)$
and
![]() $\overline{{\mathcal{C}}}(T)$
by
$\overline{{\mathcal{C}}}(T)$
by
![]() ${\mathcal{C}}(T)=T\ast \unicode[STIX]{x1D6F4}T$
and
${\mathcal{C}}(T)=T\ast \unicode[STIX]{x1D6F4}T$
and
![]() $\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}$
.
$\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}$
.
Remark.
Our results hold in the more general setup of rigid subcategories. We replace
![]() $\operatorname{add}T$
by a rigid subcategory
$\operatorname{add}T$
by a rigid subcategory
![]() ${\mathcal{T}}$
, with the following additional assumptions:
${\mathcal{T}}$
, with the following additional assumptions:
![]() ${\mathcal{T}}$
is contravariantly finite,
${\mathcal{T}}$
is contravariantly finite,
![]() $\overline{{\mathcal{T}}}$
is functorially finite, and
$\overline{{\mathcal{T}}}$
is functorially finite, and
![]() ${\mathcal{T}}^{\prime }$
is covariantly finite. This requires changing the functors of the form
${\mathcal{T}}^{\prime }$
is covariantly finite. This requires changing the functors of the form
![]() ${\mathcal{C}}(T,-)$
, taking values in the category
${\mathcal{C}}(T,-)$
, taking values in the category
![]() $\operatorname{mod}\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
, into functors of the form
$\operatorname{mod}\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
, into functors of the form
![]() ${\mathcal{C}}(?,-)|_{{\mathcal{T}}}$
, taking values in
${\mathcal{C}}(?,-)|_{{\mathcal{T}}}$
, taking values in
![]() $\operatorname{mod}{\mathcal{T}}$
, and replacing all references to [Reference Buan and MarshBM13] by references to [Reference BeligiannisBel13].
$\operatorname{mod}{\mathcal{T}}$
, and replacing all references to [Reference Buan and MarshBM13] by references to [Reference BeligiannisBel13].
2 Pseudo-Morita equivalence
2.1 Adjunctions
The methods used in this subsection are inspired by [Reference BeligiannisBel13, Reference Buan and MarshBM13, Reference Buan and MarshBM12], and much resemble results in [Reference NakaokaNak13, Section 3]. Indeed, [Reference NakaokaNak13, Corollary 3.8] applied to the twin cotorsion pair
![]() $(\unicode[STIX]{x1D6F4}\overline{T},\overline{T}^{\bot }),(\unicode[STIX]{x1D6F4}T^{\prime },{T^{\prime }}^{\bot })$
(where we use the notation from Section 2.2) gives the existence of a right adjoint to the fully faithful functor
$(\unicode[STIX]{x1D6F4}\overline{T},\overline{T}^{\bot }),(\unicode[STIX]{x1D6F4}T^{\prime },{T^{\prime }}^{\bot })$
(where we use the notation from Section 2.2) gives the existence of a right adjoint to the fully faithful functor
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\longrightarrow {\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })$
from which it is possible to deduce our Proposition 2.5. For the convenience of the reader, we nonetheless include a complete proof.
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\longrightarrow {\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })$
from which it is possible to deduce our Proposition 2.5. For the convenience of the reader, we nonetheless include a complete proof.
The subcategory
![]() ${\mathcal{C}}(T)$
is known to be contravariantly finite, by [Reference Buan and MarshBM13, Lemmas 3.3 and 3.6]. An analogous proof gives Lemma 2.2 below. We first need a definition.
${\mathcal{C}}(T)$
is known to be contravariantly finite, by [Reference Buan and MarshBM13, Lemmas 3.3 and 3.6]. An analogous proof gives Lemma 2.2 below. We first need a definition.
Definition 2.1. Let
![]() ${\mathcal{S}}$
be the set of morphisms
${\mathcal{S}}$
be the set of morphisms
![]() $X\stackrel{f}{\longrightarrow }Y$
in
$X\stackrel{f}{\longrightarrow }Y$
in
![]() ${\mathcal{C}}$
such that for any triangle
${\mathcal{C}}$
such that for any triangle
![]() $Z\rightarrow X\stackrel{f}{\rightarrow }Y\stackrel{g}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
we have
$Z\rightarrow X\stackrel{f}{\rightarrow }Y\stackrel{g}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
we have
![]() $Z\in \overline{T}^{\bot }$
and
$Z\in \overline{T}^{\bot }$
and
![]() $g\in (T^{\bot })$
.
$g\in (T^{\bot })$
.
Lemma 2.2.
(a) Let
 $X^{\prime }\stackrel{s}{\rightarrow }X$
be a morphism in
$X^{\prime }\stackrel{s}{\rightarrow }X$
be a morphism in
 ${\mathcal{S}}$
with
${\mathcal{S}}$
with
 $X^{\prime }\in \overline{{\mathcal{C}}}(T)$
. Then,
$X^{\prime }\in \overline{{\mathcal{C}}}(T)$
. Then,
 $s$
is a right
$s$
is a right
 $\overline{{\mathcal{C}}}(T)$
-approximation of
$\overline{{\mathcal{C}}}(T)$
-approximation of
 $X$
.
$X$
.(b) Each object
 $X$
in
$X$
in
 ${\mathcal{C}}$
has a right
${\mathcal{C}}$
has a right
 $\overline{{\mathcal{C}}}(T)$
-approximation
$\overline{{\mathcal{C}}}(T)$
-approximation
 $R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\rightarrow }X$
lying in
$R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\rightarrow }X$
lying in
 ${\mathcal{S}}$
.
${\mathcal{S}}$
.(c) The category
 $\overline{{\mathcal{C}}}(T)$
is a contravariantly finite subcategory of
$\overline{{\mathcal{C}}}(T)$
is a contravariantly finite subcategory of
 ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Proof. Suppose that
![]() $X^{\prime }\stackrel{s}{\rightarrow }X$
is a morphism in
$X^{\prime }\stackrel{s}{\rightarrow }X$
is a morphism in
![]() ${\mathcal{S}}$
with
${\mathcal{S}}$
with
![]() $X^{\prime }\in \overline{{\mathcal{C}}}(T)$
. Thus, we may complete
$X^{\prime }\in \overline{{\mathcal{C}}}(T)$
. Thus, we may complete
![]() $s$
to a triangle:
$s$
to a triangle:
where
![]() $g$
factors through
$g$
factors through
![]() $T^{\bot }$
, and
$T^{\bot }$
, and
![]() $\unicode[STIX]{x1D6F4}Z$
lies in
$\unicode[STIX]{x1D6F4}Z$
lies in
![]() $(\unicode[STIX]{x1D6F4}T)^{\bot }$
.
$(\unicode[STIX]{x1D6F4}T)^{\bot }$
.
Let
![]() $X^{\prime \prime }\stackrel{u}{\rightarrow }X$
be a morphism in
$X^{\prime \prime }\stackrel{u}{\rightarrow }X$
be a morphism in
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $X^{\prime \prime }$
lies in
$X^{\prime \prime }$
lies in
![]() $\overline{{\mathcal{C}}}(T)$
, so that there is a triangle
$\overline{{\mathcal{C}}}(T)$
, so that there is a triangle
![]() $U_{0}\stackrel{p}{\rightarrow }X^{\prime \prime }\rightarrow \unicode[STIX]{x1D6F4}\overline{U}_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{0}$
, with
$U_{0}\stackrel{p}{\rightarrow }X^{\prime \prime }\rightarrow \unicode[STIX]{x1D6F4}\overline{U}_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{0}$
, with
![]() $U_{0}\in \operatorname{add}T$
and
$U_{0}\in \operatorname{add}T$
and
![]() $\overline{U}_{1}\in \operatorname{add}\overline{T}$
. Since
$\overline{U}_{1}\in \operatorname{add}\overline{T}$
. Since
![]() $g$
factors through
$g$
factors through
![]() $T^{\bot }$
, and
$T^{\bot }$
, and
![]() $U_{0}\in \operatorname{add}T$
, we have
$U_{0}\in \operatorname{add}T$
, we have
![]() $gup=0$
, and therefore have the following commutative diagram whose rows are triangles:
$gup=0$
, and therefore have the following commutative diagram whose rows are triangles:

Moreover,
![]() $\unicode[STIX]{x1D6F4}Z$
lies in
$\unicode[STIX]{x1D6F4}Z$
lies in
![]() $(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
, and
$(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
, and
![]() $\unicode[STIX]{x1D6F4}\overline{U}_{1}$
is in
$\unicode[STIX]{x1D6F4}\overline{U}_{1}$
is in
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}$
, so the composition
$\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}$
, so the composition
![]() $gu=v\unicode[STIX]{x1D702}$
is zero. Thus, there is a morphism
$gu=v\unicode[STIX]{x1D702}$
is zero. Thus, there is a morphism
![]() $u^{\prime }$
such that
$u^{\prime }$
such that
![]() $u=su^{\prime }$
. Part (a) is shown.
$u=su^{\prime }$
. Part (a) is shown.
For part (b), let
![]() $X\in {\mathcal{C}}$
. Let
$X\in {\mathcal{C}}$
. Let
![]() $T_{0}^{X}\rightarrow X$
be a minimal right
$T_{0}^{X}\rightarrow X$
be a minimal right
![]() $\operatorname{add}T$
-approximation of
$\operatorname{add}T$
-approximation of
![]() $X$
. Complete it to a triangle
$X$
. Complete it to a triangle
![]() $Y\rightarrow T_{0}^{X}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}Y$
. Let
$Y\rightarrow T_{0}^{X}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}Y$
. Let
![]() $\overline{T}_{1}^{Y}\rightarrow Y$
be a minimal right
$\overline{T}_{1}^{Y}\rightarrow Y$
be a minimal right
![]() $\operatorname{add}\overline{T}$
-approximation of
$\operatorname{add}\overline{T}$
-approximation of
![]() $Y$
. Applying the octahedral axiom, we obtain the following diagram:
$Y$
. Applying the octahedral axiom, we obtain the following diagram:

Applying the functors
![]() ${\mathcal{C}}(T,-)$
and
${\mathcal{C}}(T,-)$
and
![]() ${\mathcal{C}}(\overline{T},-)$
to the triangles above shows that
${\mathcal{C}}(\overline{T},-)$
to the triangles above shows that
![]() $\unicode[STIX]{x1D6F4}Y\in T^{\bot }$
and
$\unicode[STIX]{x1D6F4}Y\in T^{\bot }$
and
![]() $Z\in \overline{T}^{\bot }$
. It should be noted that
$Z\in \overline{T}^{\bot }$
. It should be noted that
![]() $R_{0}X\in \overline{{\mathcal{C}}}(T)$
. Then, by part (a),
$R_{0}X\in \overline{{\mathcal{C}}}(T)$
. Then, by part (a),
![]() $\unicode[STIX]{x1D702}_{X}$
is a right
$\unicode[STIX]{x1D702}_{X}$
is a right
![]() $\overline{{\mathcal{C}}}(T)$
-approximation of
$\overline{{\mathcal{C}}}(T)$
-approximation of
![]() $X$
, and part (b) is shown. Part (c) follows immediately from part (b).◻
$X$
, and part (b) is shown. Part (c) follows immediately from part (b).◻
The following remark is stated as a lemma since it is used several times in the paper.
Lemma 2.3. Let
![]() $X\stackrel{f}{\longrightarrow }Y$
be a morphism in
$X\stackrel{f}{\longrightarrow }Y$
be a morphism in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $X\in \overline{{\mathcal{C}}}(T)$
, and assume that
$X\in \overline{{\mathcal{C}}}(T)$
, and assume that
![]() $f$
factors through
$f$
factors through
![]() $\overline{T}^{\bot }$
in
$\overline{T}^{\bot }$
in
![]() ${\mathcal{C}}$
. Then,
${\mathcal{C}}$
. Then,
![]() $f$
factors through
$f$
factors through
![]() $\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
.
$\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
.
Proof. Let
![]() $\overline{T}_{0}\stackrel{u}{\longrightarrow }X$
be a minimal right
$\overline{T}_{0}\stackrel{u}{\longrightarrow }X$
be a minimal right
![]() $\overline{T}$
-approximation of
$\overline{T}$
-approximation of
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}$
. Complete the morphism
${\mathcal{C}}$
. Complete the morphism
![]() $u$
to a triangle
$u$
to a triangle
![]() $\overline{T}_{0}\stackrel{u}{\rightarrow }X\stackrel{v}{\rightarrow }Z\rightarrow \unicode[STIX]{x1D6F4}\overline{T}_{0}$
in
$\overline{T}_{0}\stackrel{u}{\rightarrow }X\stackrel{v}{\rightarrow }Z\rightarrow \unicode[STIX]{x1D6F4}\overline{T}_{0}$
in
![]() ${\mathcal{C}}$
. As shown in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06] (apply the functor
${\mathcal{C}}$
. As shown in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06] (apply the functor
![]() ${\mathcal{C}}(\overline{T},-)$
to the triangle above), the cone
${\mathcal{C}}(\overline{T},-)$
to the triangle above), the cone
![]() $Z$
belongs to
$Z$
belongs to
![]() $\overline{T}^{\bot }$
. Moreover, the composition
$\overline{T}^{\bot }$
. Moreover, the composition
![]() $fu$
vanishes since
$fu$
vanishes since
![]() $f$
factors through
$f$
factors through
![]() $\overline{T}^{\bot }$
, and it follows that the morphism
$\overline{T}^{\bot }$
, and it follows that the morphism
![]() $f$
factors through
$f$
factors through
![]() $v$
. It remains to be checked that the object
$v$
. It remains to be checked that the object
![]() $Z$
lies in
$Z$
lies in
![]() $\overline{{\mathcal{C}}}(T)$
. The triangle above shows that
$\overline{{\mathcal{C}}}(T)$
. The triangle above shows that
![]() $Z\in \overline{{\mathcal{C}}}(T)\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}$
, and we have
$Z\in \overline{{\mathcal{C}}}(T)\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}$
, and we have
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{C}}}(T)\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T} & = & \displaystyle (\operatorname{add}T\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{add}T\ast (\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{add}T\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{C}}}(T)\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T} & = & \displaystyle (\operatorname{add}T\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{add}T\ast (\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T}\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{add}T\ast \operatorname{add}\unicode[STIX]{x1D6F4}\overline{T},\nonumber\end{eqnarray}$$
where the last equality holds since
![]() $\unicode[STIX]{x1D6F4}\overline{T}$
is rigid.◻
$\unicode[STIX]{x1D6F4}\overline{T}$
is rigid.◻
The following lemma, which is used in the proof of Proposition 2.5, is a particular case of [Reference Mac LaneML98, IV.1 Theorem 2(ii)].
Lemma 2.4. Let
![]() ${\mathcal{B}}$
be a category, and let
${\mathcal{B}}$
be a category, and let
![]() ${\mathcal{A}}$
be a full subcategory of
${\mathcal{A}}$
be a full subcategory of
![]() ${\mathcal{B}}$
. Suppose that, for any
${\mathcal{B}}$
. Suppose that, for any
![]() $B\in {\mathcal{B}}$
, there is an object
$B\in {\mathcal{B}}$
, there is an object
![]() $G_{0}B\in {\mathcal{A}}$
and a morphism
$G_{0}B\in {\mathcal{A}}$
and a morphism
![]() $G_{0}B\stackrel{\unicode[STIX]{x1D702}_{B}}{\longrightarrow }B$
such that for all
$G_{0}B\stackrel{\unicode[STIX]{x1D702}_{B}}{\longrightarrow }B$
such that for all
![]() $A\stackrel{f}{\longrightarrow }B$
with
$A\stackrel{f}{\longrightarrow }B$
with
![]() $A\in {\mathcal{A}}$
, the morphism
$A\in {\mathcal{A}}$
, the morphism
![]() $f$
lifts uniquely through
$f$
lifts uniquely through
![]() $\unicode[STIX]{x1D702}_{B}$
. Then, the inclusion
$\unicode[STIX]{x1D702}_{B}$
. Then, the inclusion
![]() ${\mathcal{A}}\subseteq {\mathcal{B}}$
has a right adjoint
${\mathcal{A}}\subseteq {\mathcal{B}}$
has a right adjoint
![]() $G:{\mathcal{B}}\rightarrow {\mathcal{A}}$
such that, for all
$G:{\mathcal{B}}\rightarrow {\mathcal{A}}$
such that, for all
![]() $B\in {\mathcal{B}}$
,
$B\in {\mathcal{B}}$
,
![]() $GB=G_{0}B$
.
$GB=G_{0}B$
.
The functor
![]() $G$
of the previous lemma is defined on arrows as follows. For any
$G$
of the previous lemma is defined on arrows as follows. For any
![]() $B\stackrel{b}{\longrightarrow }B^{\prime }$
in
$B\stackrel{b}{\longrightarrow }B^{\prime }$
in
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() $Gb$
is the unique lift through
$Gb$
is the unique lift through
![]() $\unicode[STIX]{x1D702}_{B^{\prime }}$
of the composition
$\unicode[STIX]{x1D702}_{B^{\prime }}$
of the composition
![]() $b\unicode[STIX]{x1D702}_{B}$
:
$b\unicode[STIX]{x1D702}_{B}$
:

The following proposition is inspired by [Reference BeligiannisBel13].
Proposition 2.5. The inclusion of
![]() $\overline{{\mathcal{C}}}(T)$
into
$\overline{{\mathcal{C}}}(T)$
into
![]() ${\mathcal{C}}$
induces a fully faithful functor
${\mathcal{C}}$
induces a fully faithful functor
![]() $\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))\stackrel{I}{\longrightarrow }{\mathcal{C}}/\overline{T}^{\bot }$
. Moreover, the functor
$\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))\stackrel{I}{\longrightarrow }{\mathcal{C}}/\overline{T}^{\bot }$
. Moreover, the functor
![]() $I$
admits an additive right adjoint
$I$
admits an additive right adjoint
![]() $R$
, such that, for all
$R$
, such that, for all
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}$
,
${\mathcal{C}}$
,
![]() $RX=R_{0}X$
, in the notation of Lemma 2.2.
$RX=R_{0}X$
, in the notation of Lemma 2.2.
Proof. The inclusion of
![]() $\overline{{\mathcal{C}}}(T)$
in
$\overline{{\mathcal{C}}}(T)$
in
![]() ${\mathcal{C}}$
induces a full functor:
${\mathcal{C}}$
induces a full functor:

We first check that the functor
![]() $I$
is faithful. This amounts to proving that if a morphism in
$I$
is faithful. This amounts to proving that if a morphism in
![]() $\overline{{\mathcal{C}}}(T)$
factors through
$\overline{{\mathcal{C}}}(T)$
factors through
![]() $\overline{T}^{\bot }$
in
$\overline{T}^{\bot }$
in
![]() ${\mathcal{C}}$
, then it already factors through
${\mathcal{C}}$
, then it already factors through
![]() $\overline{T}^{\bot }$
in
$\overline{T}^{\bot }$
in
![]() $\overline{{\mathcal{C}}}(T)$
. This follows from Lemma 2.3. In what follows, we identify
$\overline{{\mathcal{C}}}(T)$
. This follows from Lemma 2.3. In what follows, we identify
![]() $\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))$
with the image of
$\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))$
with the image of
![]() $\overline{{\mathcal{C}}}(T)$
in
$\overline{{\mathcal{C}}}(T)$
in
![]() ${\mathcal{C}}/(\overline{T}^{\bot })$
.
${\mathcal{C}}/(\overline{T}^{\bot })$
.
Next, we prove the existence of a right adjoint. For this, we use the particular case of [Reference Mac LaneML98, IV-1 Theorem 2(ii)], stated in Lemma 2.4.
Let
![]() $X\in {\mathcal{C}}$
. Consider the morphism
$X\in {\mathcal{C}}$
. Consider the morphism
![]() $R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\longrightarrow }X$
constructed in Lemma 2.2. We claim that
$R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\longrightarrow }X$
constructed in Lemma 2.2. We claim that
![]() $Q\unicode[STIX]{x1D702}_{X}$
is universal from
$Q\unicode[STIX]{x1D702}_{X}$
is universal from
![]() $I$
to
$I$
to
![]() $X$
, in the sense of MacLane; that is, any morphism in
$X$
, in the sense of MacLane; that is, any morphism in
![]() ${\mathcal{C}}/(\overline{T}^{\bot })$
from an object in
${\mathcal{C}}/(\overline{T}^{\bot })$
from an object in
![]() $\overline{{\mathcal{C}}}(T)$
to
$\overline{{\mathcal{C}}}(T)$
to
![]() $X$
factors uniquely through
$X$
factors uniquely through
![]() $Q\unicode[STIX]{x1D702}_{X}$
in
$Q\unicode[STIX]{x1D702}_{X}$
in
![]() ${\mathcal{C}}/(\overline{T}^{\bot })$
. Since
${\mathcal{C}}/(\overline{T}^{\bot })$
. Since
![]() $\unicode[STIX]{x1D702}_{X}$
is a right
$\unicode[STIX]{x1D702}_{X}$
is a right
![]() $\overline{{\mathcal{C}}}(T)$
-approximation of
$\overline{{\mathcal{C}}}(T)$
-approximation of
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}$
, its image
${\mathcal{C}}$
, its image
![]() $Q\unicode[STIX]{x1D702}_{X}$
is a right
$Q\unicode[STIX]{x1D702}_{X}$
is a right
![]() $\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))$
-approximation of
$\overline{{\mathcal{C}}}(T)/(\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T))$
-approximation of
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}/(\overline{T}^{\bot })$
, so that we only have to prove uniqueness.
${\mathcal{C}}/(\overline{T}^{\bot })$
, so that we only have to prove uniqueness.
Let
![]() $Y\in \overline{{\mathcal{C}}}(T)$
, and let
$Y\in \overline{{\mathcal{C}}}(T)$
, and let
![]() $Y\stackrel{u}{\longrightarrow }R_{0}X$
be a morphism in
$Y\stackrel{u}{\longrightarrow }R_{0}X$
be a morphism in
![]() ${\mathcal{C}}$
such that
${\mathcal{C}}$
such that
![]() $Q(\unicode[STIX]{x1D702}_{X}u)=0$
. Since the kernel of
$Q(\unicode[STIX]{x1D702}_{X}u)=0$
. Since the kernel of
![]() $Q$
is the ideal
$Q$
is the ideal
![]() $(\overline{T}^{\bot })$
of
$(\overline{T}^{\bot })$
of
![]() ${\mathcal{C}}$
, this means that the composition
${\mathcal{C}}$
, this means that the composition
![]() $\unicode[STIX]{x1D702}_{X}u$
factors through
$\unicode[STIX]{x1D702}_{X}u$
factors through
![]() $\overline{T}^{\bot }$
. Since its source belongs to
$\overline{T}^{\bot }$
. Since its source belongs to
![]() $\overline{{\mathcal{C}}}(T)$
, Lemma 2.3 shows that
$\overline{{\mathcal{C}}}(T)$
, Lemma 2.3 shows that
![]() $\unicode[STIX]{x1D702}_{X}u$
factors through
$\unicode[STIX]{x1D702}_{X}u$
factors through
![]() $\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
. Let
$\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
. Let
![]() $Y^{\prime }\in \overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
be such that the square
$Y^{\prime }\in \overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
be such that the square

commutes. Since
![]() $\unicode[STIX]{x1D702}_{X}$
is a right
$\unicode[STIX]{x1D702}_{X}$
is a right
![]() $\overline{{\mathcal{C}}}(T)$
-approximation, there exists a morphism
$\overline{{\mathcal{C}}}(T)$
-approximation, there exists a morphism
![]() $Y^{\prime }\stackrel{c}{\longrightarrow }R_{0}X$
with
$Y^{\prime }\stackrel{c}{\longrightarrow }R_{0}X$
with
![]() $b=\unicode[STIX]{x1D702}_{X}c$
. We have
$b=\unicode[STIX]{x1D702}_{X}c$
. We have
![]() $\unicode[STIX]{x1D702}_{X}(u-ca)=0$
, so that the morphism
$\unicode[STIX]{x1D702}_{X}(u-ca)=0$
, so that the morphism
![]() $u-ca$
factors through
$u-ca$
factors through
![]() $\unicode[STIX]{x1D6FC}$
. By construction,
$\unicode[STIX]{x1D6FC}$
. By construction,
![]() $Z\in \overline{T}^{\bot }$
; therefore, we have
$Z\in \overline{T}^{\bot }$
; therefore, we have
![]() $u\in (\overline{T}^{\bot })$
, which proves uniqueness.
$u\in (\overline{T}^{\bot })$
, which proves uniqueness.
Finally, we note that the functor
![]() $R$
is additive since it is the right adjoint of the additive functor
$R$
is additive since it is the right adjoint of the additive functor
![]() $I$
.◻
$I$
.◻
If the category admits a Serre functor
![]() $S$
, then a dual version of Proposition 2.5 will be of interest to us. We first note that applying to
$S$
, then a dual version of Proposition 2.5 will be of interest to us. We first note that applying to
![]() $ST^{\prime }$
the construction dual to that of
$ST^{\prime }$
the construction dual to that of
![]() $R_{0}$
gives, for any
$R_{0}$
gives, for any
![]() $X\in {\mathcal{C}}$
, a triangle
$X\in {\mathcal{C}}$
, a triangle
![]() $Z\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X\longrightarrow \unicode[STIX]{x1D6F4}Z$
, where
$Z\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X\longrightarrow \unicode[STIX]{x1D6F4}Z$
, where
![]() $L_{0}X$
belongs to
$L_{0}X$
belongs to
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
,
$\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
,
![]() $\unicode[STIX]{x1D700}_{X}$
is a minimal left
$\unicode[STIX]{x1D700}_{X}$
is a minimal left
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
-approximation,
$\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
-approximation,
![]() $\unicode[STIX]{x1D6FC}$
factors through
$\unicode[STIX]{x1D6FC}$
factors through
![]() $^{\bot }(ST^{\prime })=(T^{\prime })^{\bot }$
, and
$^{\bot }(ST^{\prime })=(T^{\prime })^{\bot }$
, and
![]() $\unicode[STIX]{x1D6F4}Z$
belongs to
$\unicode[STIX]{x1D6F4}Z$
belongs to
![]() $\overline{T}^{\bot }$
.
$\overline{T}^{\bot }$
.
Proposition 2.6. Assume that the category
![]() ${\mathcal{C}}$
has a Serre functor
${\mathcal{C}}$
has a Serre functor
![]() $S$
, and let
$S$
, and let
![]() $\text{}\underline{{\mathcal{C}}}(T^{\prime })$
be the full subcategory
$\text{}\underline{{\mathcal{C}}}(T^{\prime })$
be the full subcategory
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
of
$\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
of
![]() ${\mathcal{C}}$
. Then, the inclusion of
${\mathcal{C}}$
. Then, the inclusion of
![]() $\text{}\underline{{\mathcal{C}}}(T^{\prime })$
into
$\text{}\underline{{\mathcal{C}}}(T^{\prime })$
into
![]() ${\mathcal{C}}$
induces a fully faithful functor
${\mathcal{C}}$
induces a fully faithful functor
![]() $\text{}\underline{{\mathcal{C}}}(T^{\prime })/(\overline{T}^{\bot })\stackrel{J}{\longrightarrow }{\mathcal{C}}/(\overline{T}^{\bot })$
. Moreover, the functor
$\text{}\underline{{\mathcal{C}}}(T^{\prime })/(\overline{T}^{\bot })\stackrel{J}{\longrightarrow }{\mathcal{C}}/(\overline{T}^{\bot })$
. Moreover, the functor
![]() $J$
admits an additive left adjoint
$J$
admits an additive left adjoint
![]() $L$
, such that
$L$
, such that
![]() $LX=L_{0}X$
for all
$LX=L_{0}X$
for all
![]() $X\in {\mathcal{C}}$
.
$X\in {\mathcal{C}}$
.
The only reason why we assume the existence of a Serre functor here is that it converts a left perpendicular subcategory into a right perpendicular subcategory. This allows us to view both categories in Propositions 2.5 and 2.6 as subcategories of the same category
![]() ${\mathcal{C}}/(\overline{T}^{\bot })$
.
${\mathcal{C}}/(\overline{T}^{\bot })$
.
2.2 Main result
Our aim in this section is to prove that if
![]() ${\mathcal{C}}$
has a Serre functor then the categories
${\mathcal{C}}$
has a Serre functor then the categories
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $\overline{{\mathcal{C}}}(T)/(T)$
are equivalent (Theorem 2.9). This is then used in the next section in order to compare the module categories over the endomorphism algebras of
$\overline{{\mathcal{C}}}(T)/(T)$
are equivalent (Theorem 2.9). This is then used in the next section in order to compare the module categories over the endomorphism algebras of
![]() $T$
and
$T$
and
![]() $T^{\prime }$
.
$T^{\prime }$
.
We need the following key lemma, which is often used throughout the paper.
Lemma 2.7. We have:
(a)
 $\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
;
$\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
;(b)
 $\overline{{\mathcal{C}}}(T)\cap \overline{T}^{\bot }=\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
;
$\overline{{\mathcal{C}}}(T)\cap \overline{T}^{\bot }=\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
;(c) if
 ${\mathcal{C}}$
has a Serre functor
${\mathcal{C}}$
has a Serre functor
 $S$
, then
$S$
, then
 $(\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast ST^{\prime })\cap \overline{T}^{\bot }=\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}ST$
.
$(\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast ST^{\prime })\cap \overline{T}^{\bot }=\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}ST$
.
Proof. (a) The exchange triangle shows that
![]() $T\in \overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
. We thus have
$T\in \overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
. We thus have
 $$\begin{eqnarray}\displaystyle T\ast \unicode[STIX]{x1D6F4}\overline{T} & \subseteq & \displaystyle (\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime })\ast \unicode[STIX]{x1D6F4}\overline{T}\nonumber\\ \displaystyle & = & \displaystyle \overline{T}\ast (\unicode[STIX]{x1D6F4}T^{\prime }\ast \unicode[STIX]{x1D6F4}\overline{T})\nonumber\\ \displaystyle & = & \displaystyle \overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T\ast \unicode[STIX]{x1D6F4}\overline{T} & \subseteq & \displaystyle (\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime })\ast \unicode[STIX]{x1D6F4}\overline{T}\nonumber\\ \displaystyle & = & \displaystyle \overline{T}\ast (\unicode[STIX]{x1D6F4}T^{\prime }\ast \unicode[STIX]{x1D6F4}\overline{T})\nonumber\\ \displaystyle & = & \displaystyle \overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }.\nonumber\end{eqnarray}$$
The reverse inclusion is obtained by applying this inclusion to
![]() $\unicode[STIX]{x1D6F4}T^{\prime }$
(instead of
$\unicode[STIX]{x1D6F4}T^{\prime }$
(instead of
![]() $T$
) in the opposite category.
$T$
) in the opposite category.
(b) This immediately follows from (a).
(c) This also follows from (a):
Assume that
![]() ${\mathcal{C}}$
has a Serre functor
${\mathcal{C}}$
has a Serre functor
![]() $S$
. Recall that we write
$S$
. Recall that we write
![]() $\overline{{\mathcal{C}}}(T)$
(respectively,
$\overline{{\mathcal{C}}}(T)$
(respectively,
![]() $\text{}\underline{{\mathcal{C}}}(T^{\prime })$
) for the full subcategory
$\text{}\underline{{\mathcal{C}}}(T^{\prime })$
) for the full subcategory
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
(respectively,
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
(respectively,
![]() $\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast ST^{\prime }$
) of
$\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast ST^{\prime }$
) of
![]() ${\mathcal{C}}$
. By Propositions 2.5, 2.6 and Lemma 2.7, we have a pair of adjoint functors
${\mathcal{C}}$
. By Propositions 2.5, 2.6 and Lemma 2.7, we have a pair of adjoint functors
![]() $(G,H)$
, where
$(G,H)$
, where
![]() $G=LI$
and
$G=LI$
and
![]() $H=RJ$
. Since
$H=RJ$
. Since
![]() $I,J,L$
and
$I,J,L$
and
![]() $R$
are additive, so are
$R$
are additive, so are
![]() $G$
and
$G$
and
![]() $H$
.
$H$
.

Remark 2.8. We write
![]() $\unicode[STIX]{x1D70F}$
for the Auslander–Reiten translation
$\unicode[STIX]{x1D70F}$
for the Auslander–Reiten translation
![]() $\unicode[STIX]{x1D70F}=S\unicode[STIX]{x1D6F4}^{-1}$
(see [Reference Reiten and Van den BerghRvdB02, Section I.2]). Then, by Lemma 2.7, we have that
$\unicode[STIX]{x1D70F}=S\unicode[STIX]{x1D6F4}^{-1}$
(see [Reference Reiten and Van den BerghRvdB02, Section I.2]). Then, by Lemma 2.7, we have that
![]() $\text{}\underline{{\mathcal{C}}}(T^{\prime })=\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)$
.
$\text{}\underline{{\mathcal{C}}}(T^{\prime })=\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)$
.
Theorem 2.9. Assume that
![]() ${\mathcal{C}}$
has a Serre functor
${\mathcal{C}}$
has a Serre functor
![]() $S$
. Then the functors
$S$
. Then the functors
![]() $G$
and
$G$
and
![]() $H$
are quasi-inverse equivalences of categories. In particular, the categories
$H$
are quasi-inverse equivalences of categories. In particular, the categories
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $\overline{{\mathcal{C}}}(T)/(T)$
are equivalent.
$\overline{{\mathcal{C}}}(T)/(T)$
are equivalent.
Proof. The construction would be simplified if we had that, if
![]() $X$
belongs to
$X$
belongs to
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
, then the left
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
, then the left
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
-approximation
$\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}S\overline{T}\ast \operatorname{add}ST^{\prime }$
-approximation
![]() $X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X$
of
$X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X$
of
![]() $X$
(see Proposition 2.6 and the paragraph before it) is also a minimal right
$X$
(see Proposition 2.6 and the paragraph before it) is also a minimal right
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
![]() $L_{0}X$
. However, this cannot be expected to hold in general (take
$L_{0}X$
. However, this cannot be expected to hold in general (take
![]() $X$
to be
$X$
to be
![]() $\unicode[STIX]{x1D6F4}T^{\prime }$
, for instance).
$\unicode[STIX]{x1D6F4}T^{\prime }$
, for instance).
We can modify this approach in the following way. First, since the functors
![]() $G$
and
$G$
and
![]() $H$
are additive, we may assume that
$H$
are additive, we may assume that
![]() $X$
is indecomposable. This helps in proving that
$X$
is indecomposable. This helps in proving that
![]() $X$
is a summand of
$X$
is a summand of
![]() $R_{0}L_{0}X$
. Second, we add to
$R_{0}L_{0}X$
. Second, we add to
![]() $X$
a minimal right
$X$
a minimal right
![]() $\operatorname{add}(\unicode[STIX]{x1D6F4}T^{\prime })$
-approximation
$\operatorname{add}(\unicode[STIX]{x1D6F4}T^{\prime })$
-approximation
![]() $\unicode[STIX]{x1D6F4}T_{0}^{\prime }$
of
$\unicode[STIX]{x1D6F4}T_{0}^{\prime }$
of
![]() $L_{0}X$
. This is needed in order to get a right approximation of
$L_{0}X$
. This is needed in order to get a right approximation of
![]() $L_{0}X$
, while being harmless since the objects
$L_{0}X$
, while being harmless since the objects
![]() $X$
and
$X$
and
![]() $X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }$
are isomorphic in
$X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }$
are isomorphic in
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
.
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
.
Therefore, take an indecomposable object
![]() $X\in T\ast \unicode[STIX]{x1D6F4}\overline{T}$
, and assume that
$X\in T\ast \unicode[STIX]{x1D6F4}\overline{T}$
, and assume that
![]() $X$
does not belong to
$X$
does not belong to
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
(otherwise,
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
(otherwise,
![]() $X$
would be isomorphic to
$X$
would be isomorphic to
![]() $0$
in
$0$
in
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
). Consider the triangle
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
). Consider the triangle
![]() $Z\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X\stackrel{\unicode[STIX]{x1D6FD}}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
$Z\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D700}_{X}}{\longrightarrow }L_{0}X\stackrel{\unicode[STIX]{x1D6FD}}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
![]() ${\mathcal{C}}$
, constructed in the paragraph before Proposition 2.6, where
${\mathcal{C}}$
, constructed in the paragraph before Proposition 2.6, where
![]() $\unicode[STIX]{x1D6FC}\in ((T^{\prime })^{\bot })$
and
$\unicode[STIX]{x1D6FC}\in ((T^{\prime })^{\bot })$
and
![]() $\unicode[STIX]{x1D6F4}Z\in \overline{T}^{\bot }$
. Let
$\unicode[STIX]{x1D6F4}Z\in \overline{T}^{\bot }$
. Let
![]() $\unicode[STIX]{x1D6F4}T_{0}^{\prime }\stackrel{p}{\longrightarrow }L_{0}X$
be a minimal right
$\unicode[STIX]{x1D6F4}T_{0}^{\prime }\stackrel{p}{\longrightarrow }L_{0}X$
be a minimal right
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
-approximation of
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
-approximation of
![]() $L_{0}X$
in
$L_{0}X$
in
![]() ${\mathcal{C}}$
. We claim that
${\mathcal{C}}$
. We claim that
![]() $X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }\stackrel{[\unicode[STIX]{x1D700}_{X}p]}{\longrightarrow }L_{0}X$
is a right
$X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }\stackrel{[\unicode[STIX]{x1D700}_{X}p]}{\longrightarrow }L_{0}X$
is a right
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
![]() $L_{0}X$
in
$L_{0}X$
in
![]() ${\mathcal{C}}$
. Let
${\mathcal{C}}$
. Let
![]() $X^{\prime }\stackrel{f}{\longrightarrow }L_{0}X$
be a morphism in
$X^{\prime }\stackrel{f}{\longrightarrow }L_{0}X$
be a morphism in
![]() ${\mathcal{C}}$
, with
${\mathcal{C}}$
, with
![]() $X^{\prime }\in T\ast \unicode[STIX]{x1D6F4}\overline{T}$
. By assumption, there is a triangle
$X^{\prime }\in T\ast \unicode[STIX]{x1D6F4}\overline{T}$
. By assumption, there is a triangle
![]() $T_{1}^{\prime }\stackrel{a}{\longrightarrow }\overline{T}_{0}\stackrel{b}{\longrightarrow }X^{\prime }\stackrel{c}{\longrightarrow }\unicode[STIX]{x1D6F4}T_{1}^{\prime }$
in
$T_{1}^{\prime }\stackrel{a}{\longrightarrow }\overline{T}_{0}\stackrel{b}{\longrightarrow }X^{\prime }\stackrel{c}{\longrightarrow }\unicode[STIX]{x1D6F4}T_{1}^{\prime }$
in
![]() ${\mathcal{C}}$
, with
${\mathcal{C}}$
, with
![]() $T_{1}^{\prime }\in \operatorname{add}T^{\prime }$
and
$T_{1}^{\prime }\in \operatorname{add}T^{\prime }$
and
![]() $\overline{T}_{0}\in \operatorname{add}\overline{T}$
. Since
$\overline{T}_{0}\in \operatorname{add}\overline{T}$
. Since
![]() $\overline{T}_{0}$
is in
$\overline{T}_{0}$
is in
![]() $\operatorname{add}\overline{T}$
, and
$\operatorname{add}\overline{T}$
, and
![]() $\unicode[STIX]{x1D6F4}Z$
is in
$\unicode[STIX]{x1D6F4}Z$
is in
![]() $\overline{T}^{\bot }$
, the composition
$\overline{T}^{\bot }$
, the composition
![]() $\unicode[STIX]{x1D6FD}fb$
vanishes, and
$\unicode[STIX]{x1D6FD}fb$
vanishes, and
![]() $f$
induces a morphism of triangles:
$f$
induces a morphism of triangles:

Since
![]() $\unicode[STIX]{x1D6FC}$
factors through
$\unicode[STIX]{x1D6FC}$
factors through
![]() $(T^{\prime })^{\bot }$
, we have
$(T^{\prime })^{\bot }$
, we have
![]() $(-\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6FC})g=0$
, and there exists
$(-\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6FC})g=0$
, and there exists
![]() $\unicode[STIX]{x1D6F4}T_{1}^{\prime }\stackrel{u}{\longrightarrow }L_{0}X$
such that
$\unicode[STIX]{x1D6F4}T_{1}^{\prime }\stackrel{u}{\longrightarrow }L_{0}X$
such that
![]() $g=\unicode[STIX]{x1D6FD}u$
. This implies
$g=\unicode[STIX]{x1D6FD}u$
. This implies
![]() $\unicode[STIX]{x1D6FD}(f-uc)=0$
, so that there exists
$\unicode[STIX]{x1D6FD}(f-uc)=0$
, so that there exists
![]() $X^{\prime }\stackrel{v}{\longrightarrow }X$
such that
$X^{\prime }\stackrel{v}{\longrightarrow }X$
such that
![]() $f=uc+\unicode[STIX]{x1D700}_{X}v$
. The composition
$f=uc+\unicode[STIX]{x1D700}_{X}v$
. The composition
![]() $uc$
is in the ideal
$uc$
is in the ideal
![]() $(\unicode[STIX]{x1D6F4}T^{\prime })$
, and thus factors through
$(\unicode[STIX]{x1D6F4}T^{\prime })$
, and thus factors through
![]() $p$
; that is, there exists
$p$
; that is, there exists
![]() $w$
making the following square commute:
$w$
making the following square commute:

We thus have
![]() $f=[\unicode[STIX]{x1D700}_{X}\;p][\!\begin{smallmatrix}v\\ w\end{smallmatrix}\!]$
, and therefore the morphism
$f=[\unicode[STIX]{x1D700}_{X}\;p][\!\begin{smallmatrix}v\\ w\end{smallmatrix}\!]$
, and therefore the morphism
![]() $[\unicode[STIX]{x1D700}_{X}\;p]$
is a right
$[\unicode[STIX]{x1D700}_{X}\;p]$
is a right
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
![]() $L_{0}X$
in
$L_{0}X$
in
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Since also
![]() $R_{0}L_{0}X\stackrel{\unicode[STIX]{x1D702}_{L_{0}X}}{\longrightarrow }L_{0}X$
is a right
$R_{0}L_{0}X\stackrel{\unicode[STIX]{x1D702}_{L_{0}X}}{\longrightarrow }L_{0}X$
is a right
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation of
![]() $L_{0}X$
in
$L_{0}X$
in
![]() ${\mathcal{C}}$
, we can write
${\mathcal{C}}$
, we can write
![]() $R_{0}L_{0}X$
as a direct sum
$R_{0}L_{0}X$
as a direct sum
![]() $X^{\prime }\oplus X^{\prime \prime }$
, and
$X^{\prime }\oplus X^{\prime \prime }$
, and
![]() $\unicode[STIX]{x1D702}_{L_{0}X}=[\unicode[STIX]{x1D702}^{\prime }\;0]:X^{\prime }\oplus X^{\prime \prime }\rightarrow L_{0}X$
, where
$\unicode[STIX]{x1D702}_{L_{0}X}=[\unicode[STIX]{x1D702}^{\prime }\;0]:X^{\prime }\oplus X^{\prime \prime }\rightarrow L_{0}X$
, where
![]() $X^{\prime }\stackrel{\unicode[STIX]{x1D702}^{\prime }}{\longrightarrow }L_{0}X$
is a minimal right
$X^{\prime }\stackrel{\unicode[STIX]{x1D702}^{\prime }}{\longrightarrow }L_{0}X$
is a minimal right
![]() $T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation. Moreover, we have
$T\ast \unicode[STIX]{x1D6F4}\overline{T}$
-approximation. Moreover, we have
![]() $X^{\prime \prime }\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
, since in the triangle
$X^{\prime \prime }\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
, since in the triangle
![]() $Z^{\prime }\rightarrow X^{\prime }\oplus X^{\prime \prime }\rightarrow L_{0}X\rightarrow$
given by Lemma 2.2,
$Z^{\prime }\rightarrow X^{\prime }\oplus X^{\prime \prime }\rightarrow L_{0}X\rightarrow$
given by Lemma 2.2,
![]() $Z^{\prime }$
belongs to
$Z^{\prime }$
belongs to
![]() $\overline{T}^{\bot }$
, and
$\overline{T}^{\bot }$
, and
![]() $X^{\prime \prime }$
is a summand of
$X^{\prime \prime }$
is a summand of
![]() $Z^{\prime }$
. Thus,
$Z^{\prime }$
. Thus,
![]() $X^{\prime \prime }$
belongs to
$X^{\prime \prime }$
belongs to
![]() $\in \overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
, which is
$\in \overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
, which is
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7.
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7.
Now,
![]() $X^{\prime }$
is a summand of the approximation
$X^{\prime }$
is a summand of the approximation
![]() $X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }$
. Moreover,
$X\oplus \unicode[STIX]{x1D6F4}T_{0}^{\prime }$
. Moreover,
![]() $X^{\prime }$
contains
$X^{\prime }$
contains
![]() $X$
as a summand. Otherwise, we would have
$X$
as a summand. Otherwise, we would have
![]() $R_{0}L_{0}X\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
, which implies
$R_{0}L_{0}X\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
, which implies
![]() $L_{0}X\in \overline{T}^{\bot }\cap \text{}\underline{{\mathcal{C}}}(T^{\prime })=\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}ST^{\prime }$
(by applying the functor
$L_{0}X\in \overline{T}^{\bot }\cap \text{}\underline{{\mathcal{C}}}(T^{\prime })=\operatorname{add}\unicode[STIX]{x1D6F4}^{-1}ST^{\prime }$
(by applying the functor
![]() ${\mathcal{C}}(\overline{T},-)$
to the triangle
${\mathcal{C}}(\overline{T},-)$
to the triangle
![]() $Z^{\prime }\rightarrow R_{0}L_{0}X\rightarrow L_{0}X\rightarrow$
), which dually implies
$Z^{\prime }\rightarrow R_{0}L_{0}X\rightarrow L_{0}X\rightarrow$
), which dually implies
![]() $X\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
(note that we assumed
$X\in \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
(note that we assumed
![]() $X\notin \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
).
$X\notin \operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
).
As a consequence, given a lift

the image
![]() $\unicode[STIX]{x1D711}_{X}$
of
$\unicode[STIX]{x1D711}_{X}$
of
![]() $\widetilde{\unicode[STIX]{x1D711}}_{X}$
in
$\widetilde{\unicode[STIX]{x1D711}}_{X}$
in
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
, which is independent of the choice of
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
, which is independent of the choice of
![]() $\widetilde{\unicode[STIX]{x1D711}}_{X}$
by Proposition 2.5, is an isomorphism (and
$\widetilde{\unicode[STIX]{x1D711}}_{X}$
by Proposition 2.5, is an isomorphism (and
![]() $\unicode[STIX]{x1D700}_{X}$
is a minimal right
$\unicode[STIX]{x1D700}_{X}$
is a minimal right
![]() $\overline{{\mathcal{C}}}(T)$
-approximation of
$\overline{{\mathcal{C}}}(T)$
-approximation of
![]() $L_{0}X$
in
$L_{0}X$
in
![]() ${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })$
).
${\mathcal{C}}/(\unicode[STIX]{x1D6F4}T^{\prime })$
).
Let us check that we have defined a natural isomorphism
![]() $\unicode[STIX]{x1D711}:1\rightarrow HG$
.
$\unicode[STIX]{x1D711}:1\rightarrow HG$
.
Let
![]() $X\stackrel{f}{\longrightarrow }Y$
be a morphism in
$X\stackrel{f}{\longrightarrow }Y$
be a morphism in
![]() $\overline{{\mathcal{C}}}(T)$
. By construction, there is a diagram in
$\overline{{\mathcal{C}}}(T)$
. By construction, there is a diagram in
![]() ${\mathcal{C}}$
${\mathcal{C}}$

where we write
![]() $\unicode[STIX]{x1D702}$
for
$\unicode[STIX]{x1D702}$
for
![]() $\unicode[STIX]{x1D702}_{L_{0}Y}$
, and where the inner two triangles and the inner two squares commute. We thus have
$\unicode[STIX]{x1D702}_{L_{0}Y}$
, and where the inner two triangles and the inner two squares commute. We thus have
![]() $\unicode[STIX]{x1D702}(HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f)=0$
, and
$\unicode[STIX]{x1D702}(HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f)=0$
, and
![]() $HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
$HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
![]() $\overline{Z}\rightarrow R_{0}L_{0}Y$
in the triangle
$\overline{Z}\rightarrow R_{0}L_{0}Y$
in the triangle
![]() $\overline{Z}\rightarrow R_{0}L_{0}Y\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }L_{0}Y\rightarrow$
, where
$\overline{Z}\rightarrow R_{0}L_{0}Y\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }L_{0}Y\rightarrow$
, where
![]() $\overline{Z}\in \overline{T}^{\bot }$
. This shows that
$\overline{Z}\in \overline{T}^{\bot }$
. This shows that
![]() $HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
$HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
![]() $\overline{T}^{\bot }$
. Since
$\overline{T}^{\bot }$
. Since
![]() $X$
lies in
$X$
lies in
![]() $\overline{{\mathcal{C}}}(T)$
, we can apply Lemma 2.3. The morphism
$\overline{{\mathcal{C}}}(T)$
, we can apply Lemma 2.3. The morphism
![]() $HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
$HGf\circ \widetilde{\unicode[STIX]{x1D711}}_{X}-\widetilde{\unicode[STIX]{x1D711}}_{Y}\circ f$
factors through
![]() $\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
, which is
$\overline{T}^{\bot }\cap \overline{{\mathcal{C}}}(T)$
, which is
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7. As a consequence,
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7. As a consequence,
![]() $\unicode[STIX]{x1D711}$
is a natural transformation.
$\unicode[STIX]{x1D711}$
is a natural transformation.
By duality, there is a natural isomorphism
![]() $GH\rightarrow 1$
, and the functors
$GH\rightarrow 1$
, and the functors
![]() $G$
and
$G$
and
![]() $H$
are quasi-inverse equivalences of categories.◻
$H$
are quasi-inverse equivalences of categories.◻
2.3 A module-theoretic interpretation
In this section, we assume that
![]() ${\mathcal{C}}$
has a Serre functor
${\mathcal{C}}$
has a Serre functor
![]() $S$
. In this case, the assumptions of functorial finiteness (see Section 1) are automatically satisfied for all rigid objects (but have to be added in the case of rigid subcategories). We write
$S$
. In this case, the assumptions of functorial finiteness (see Section 1) are automatically satisfied for all rigid objects (but have to be added in the case of rigid subcategories). We write
![]() $D$
for the duality functor
$D$
for the duality functor
![]() $\operatorname{Hom}_{k}(-,k)$
. Recall that
$\operatorname{Hom}_{k}(-,k)$
. Recall that
![]() $T\in {\mathcal{C}}$
is a basic rigid object, and
$T\in {\mathcal{C}}$
is a basic rigid object, and
![]() $R$
is a direct summand of
$R$
is a direct summand of
![]() $T$
, with
$T$
, with
![]() $T=\overline{T}\oplus R$
. We write
$T=\overline{T}\oplus R$
. We write
![]() $\overline{T}=T_{1}\oplus \cdots \oplus T_{n}$
and
$\overline{T}=T_{1}\oplus \cdots \oplus T_{n}$
and
![]() $R=T_{n+1}\oplus \cdots \oplus T_{m}$
, where the
$R=T_{n+1}\oplus \cdots \oplus T_{m}$
, where the
![]() $T_{i}$
are indecomposable. Recall also that
$T_{i}$
are indecomposable. Recall also that
![]() $\unicode[STIX]{x1D6F4}R^{\ast }$
is the cone of a minimal right
$\unicode[STIX]{x1D6F4}R^{\ast }$
is the cone of a minimal right
![]() $\operatorname{add}\overline{T}$
-approximation of
$\operatorname{add}\overline{T}$
-approximation of
![]() $R$
. We have
$R$
. We have
![]() $T^{\prime }=\overline{T}\oplus R^{\ast }=T_{1}^{\prime }\oplus \cdots \oplus T_{m}^{\prime }$
, where
$T^{\prime }=\overline{T}\oplus R^{\ast }=T_{1}^{\prime }\oplus \cdots \oplus T_{m}^{\prime }$
, where
![]() $T_{i}^{\prime }=T_{i}$
if
$T_{i}^{\prime }=T_{i}$
if
![]() $i\leqslant n$
. Define
$i\leqslant n$
. Define
![]() $\unicode[STIX]{x1D6EC}$
(respectively,
$\unicode[STIX]{x1D6EC}$
(respectively,
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
) to be the endomorphism algebra
$\unicode[STIX]{x1D6EC}^{\prime }$
) to be the endomorphism algebra
![]() $\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
$\operatorname{End}_{{\mathcal{C}}}(T)^{\text{op}}$
(respectively,
![]() $\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
).
$\operatorname{End}_{{\mathcal{C}}}(T^{\prime })^{\text{op}}$
).
Let
![]() $S_{j}$
be the simple top of the indecomposable projective
$S_{j}$
be the simple top of the indecomposable projective
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() ${\mathcal{C}}(T,T_{j})$
, and let
${\mathcal{C}}(T,T_{j})$
, and let
![]() $S_{j}^{\prime }$
be the simple socle of the indecomposable injective
$S_{j}^{\prime }$
be the simple socle of the indecomposable injective
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-module
$\unicode[STIX]{x1D6EC}^{\prime }$
-module
![]() $D{\mathcal{C}}(\unicode[STIX]{x1D6F4}T_{j}^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })$
. We consider the exact categories
$D{\mathcal{C}}(\unicode[STIX]{x1D6F4}T_{j}^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })$
. We consider the exact categories
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{E}}^{\prime }$
defined as follows. The category
${\mathcal{E}}^{\prime }$
defined as follows. The category
![]() ${\mathcal{E}}$
(respectively,
${\mathcal{E}}$
(respectively,
![]() ${\mathcal{E}}^{\prime }$
) is the full subcategory of
${\mathcal{E}}^{\prime }$
) is the full subcategory of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
(respectively,
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
(respectively,
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
), whose objects
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
), whose objects
![]() $M$
(respectively,
$M$
(respectively,
![]() $N$
) satisfy
$N$
) satisfy
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{j})=0$
(respectively,
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{j})=0$
(respectively,
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}^{\prime }}^{1}(S_{j}^{\prime },N)=0$
) for all
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}^{\prime }}^{1}(S_{j}^{\prime },N)=0$
) for all
![]() $j>n$
.
$j>n$
.
Remark 2.10. For each indecomposable summand
![]() $R_{i}$
of
$R_{i}$
of
![]() $R$
, let
$R$
, let
![]() $R_{i}^{\ast }\rightarrow \overline{U}_{i}\rightarrow R_{i}\rightarrow \unicode[STIX]{x1D6F4}R_{i}^{\ast }$
be a triangle in
$R_{i}^{\ast }\rightarrow \overline{U}_{i}\rightarrow R_{i}\rightarrow \unicode[STIX]{x1D6F4}R_{i}^{\ast }$
be a triangle in
![]() ${\mathcal{C}}$
, with
${\mathcal{C}}$
, with
![]() $\overline{U}_{i}\rightarrow R_{i}$
a minimal right
$\overline{U}_{i}\rightarrow R_{i}$
a minimal right
![]() $\overline{T}$
-approximation. Then (as in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06]), the object
$\overline{T}$
-approximation. Then (as in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06]), the object
![]() $R_{i}^{\ast }$
is indecomposable. Moreover,
$R_{i}^{\ast }$
is indecomposable. Moreover,
![]() $\oplus _{i}{\overline{U}_{i}\rightarrow \oplus }_{i}R_{i}$
is a minimal right
$\oplus _{i}{\overline{U}_{i}\rightarrow \oplus }_{i}R_{i}$
is a minimal right
![]() $\overline{T}$
-approximation of
$\overline{T}$
-approximation of
![]() $R$
. As a consequence,
$R$
. As a consequence,
![]() $R^{\ast }$
is isomorphic to
$R^{\ast }$
is isomorphic to
![]() $\oplus _{i}R_{i}^{\ast }$
. This shows that the basic objects
$\oplus _{i}R_{i}^{\ast }$
. This shows that the basic objects
![]() $R$
and
$R$
and
![]() $R^{\ast }$
have the same number of indecomposable summands.
$R^{\ast }$
have the same number of indecomposable summands.
We can now restate Theorem 2.9 in module-theoretic terms.
Theorem 2.11. Suppose that
![]() ${\mathcal{C}}$
has a Serre functor. Then, there is an equivalence of categories
${\mathcal{C}}$
has a Serre functor. Then, there is an equivalence of categories
The proof is given later in this section. We note that, if
![]() ${\mathcal{C}}$
is 2-Calabi–Yau, then the modules
${\mathcal{C}}$
is 2-Calabi–Yau, then the modules
![]() $D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })$
and
$D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() ${\mathcal{C}}(T^{\prime },\unicode[STIX]{x1D6F4}R)$
are isomorphic. We also note that although the statement of the equivalence does not need a Serre functor, the existence is needed in the proof, in order to apply Theorem 2.9.
${\mathcal{C}}(T^{\prime },\unicode[STIX]{x1D6F4}R)$
are isomorphic. We also note that although the statement of the equivalence does not need a Serre functor, the existence is needed in the proof, in order to apply Theorem 2.9.
In order to prove Theorem 2.11, we need the following two lemmas.
Lemma 2.12. The functor
![]() ${\mathcal{C}}(T,-)$
induces a fully faithful functor
${\mathcal{C}}(T,-)$
induces a fully faithful functor
Its essential image is
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.
Proof. Let
![]() $X\stackrel{f}{\longrightarrow }Y$
be a morphism in
$X\stackrel{f}{\longrightarrow }Y$
be a morphism in
![]() ${\mathcal{C}}$
factoring through
${\mathcal{C}}$
factoring through
![]() $T^{\bot }$
. Recall that
$T^{\bot }$
. Recall that
![]() $\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}$
. Assume that
$\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}$
. Assume that
![]() $X$
belongs to
$X$
belongs to
![]() $\overline{{\mathcal{C}}}(T)$
, and let
$\overline{{\mathcal{C}}}(T)$
, and let
![]() $\overline{V}_{1}\rightarrow V_{0}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}\overline{V}_{1}$
be a triangle in
$\overline{V}_{1}\rightarrow V_{0}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}\overline{V}_{1}$
be a triangle in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $V_{0}\in \operatorname{add}T$
and
$V_{0}\in \operatorname{add}T$
and
![]() $\overline{V}_{1}\in \operatorname{add}\overline{T}$
. Since
$\overline{V}_{1}\in \operatorname{add}\overline{T}$
. Since
![]() $f$
factors through
$f$
factors through
![]() $T^{\bot }$
, the composition
$T^{\bot }$
, the composition
![]() $V_{0}\rightarrow X\rightarrow Y$
vanishes, and
$V_{0}\rightarrow X\rightarrow Y$
vanishes, and
![]() $f$
factors through
$f$
factors through
![]() $\unicode[STIX]{x1D6F4}\overline{V}_{1}$
. This implies that the first part of the lemma (the fullness of
$\unicode[STIX]{x1D6F4}\overline{V}_{1}$
. This implies that the first part of the lemma (the fullness of
![]() ${\mathcal{C}}(T,-)$
follows from [Reference Iyama and YoshinoIY08, Proposition 6.2] (see also [Reference Buan and MarshBM13, Lemma 4.3])).
${\mathcal{C}}(T,-)$
follows from [Reference Iyama and YoshinoIY08, Proposition 6.2] (see also [Reference Buan and MarshBM13, Lemma 4.3])).
For any
![]() $M$
in
$M$
in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
, let
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
, let
![]() $X\in {\mathcal{C}}(T)$
be such that
$X\in {\mathcal{C}}(T)$
be such that
![]() $X$
has no summands in
$X$
has no summands in
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T$
, and
$\operatorname{add}\unicode[STIX]{x1D6F4}T$
, and
![]() ${\mathcal{C}}(T,X)\simeq M$
. Let
${\mathcal{C}}(T,X)\simeq M$
. Let
![]() $U_{\unicode[STIX]{x1D6FD}}\rightarrow U_{\unicode[STIX]{x1D6FC}}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}U_{\unicode[STIX]{x1D6FD}}$
be a triangle with
$U_{\unicode[STIX]{x1D6FD}}\rightarrow U_{\unicode[STIX]{x1D6FC}}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}U_{\unicode[STIX]{x1D6FD}}$
be a triangle with
![]() $U_{\unicode[STIX]{x1D6FC}},U_{\unicode[STIX]{x1D6FD}}\in \operatorname{add}T$
and
$U_{\unicode[STIX]{x1D6FC}},U_{\unicode[STIX]{x1D6FD}}\in \operatorname{add}T$
and
![]() $U_{\unicode[STIX]{x1D6FC}}\rightarrow X$
right-minimal. Then,
$U_{\unicode[STIX]{x1D6FC}}\rightarrow X$
right-minimal. Then,
![]() ${\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FD}})\rightarrow {\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FC}})\rightarrow {\mathcal{C}}(T,X)\rightarrow 0$
is a minimal projective presentation of
${\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FD}})\rightarrow {\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FC}})\rightarrow {\mathcal{C}}(T,X)\rightarrow 0$
is a minimal projective presentation of
![]() ${\mathcal{C}}(T,X)$
, and the dimension of
${\mathcal{C}}(T,X)$
, and the dimension of
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{j})$
is the multiplicity of
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,S_{j})$
is the multiplicity of
![]() $P_{j}$
in
$P_{j}$
in
![]() ${\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FD}})$
.◻
${\mathcal{C}}(T,U_{\unicode[STIX]{x1D6FD}})$
.◻
Dually, we obtain the following.
Lemma 2.13. The functor
![]() $D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
induces a fully faithful functor
$D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
induces a fully faithful functor
Its essential image is
![]() ${\mathcal{E}}^{\prime }$
.
${\mathcal{E}}^{\prime }$
.
Proof. The proof is dual to that of Lemma 2.12. We use the description
![]() $\overline{{\mathcal{C}}}(T)=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
from Lemma 2.7, and note that any triangle
$\overline{{\mathcal{C}}}(T)=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
from Lemma 2.7, and note that any triangle
![]() $U_{1}^{\prime }\rightarrow \overline{U}_{0}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}U_{1}^{\prime }$
, where
$U_{1}^{\prime }\rightarrow \overline{U}_{0}\rightarrow X\rightarrow \unicode[STIX]{x1D6F4}U_{1}^{\prime }$
, where
![]() $U_{1}^{\prime }$
belongs to
$U_{1}^{\prime }$
belongs to
![]() $\operatorname{add}T^{\prime }$
, and
$\operatorname{add}T^{\prime }$
, and
![]() $\overline{U}_{0}$
belongs to
$\overline{U}_{0}$
belongs to
![]() $\operatorname{add}\overline{T}$
, gives rise to an injective co-presentation
$\operatorname{add}\overline{T}$
, gives rise to an injective co-presentation
![]() $0\rightarrow D{\mathcal{C}}(X,\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow D{\mathcal{C}}(\unicode[STIX]{x1D6F4}U_{1}^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow D{\mathcal{C}}(\unicode[STIX]{x1D6F4}\overline{U}_{0},\unicode[STIX]{x1D6F4}T^{\prime })$
.◻
$0\rightarrow D{\mathcal{C}}(X,\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow D{\mathcal{C}}(\unicode[STIX]{x1D6F4}U_{1}^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow D{\mathcal{C}}(\unicode[STIX]{x1D6F4}\overline{U}_{0},\unicode[STIX]{x1D6F4}T^{\prime })$
.◻
Proof of Theorem 2.11.
By Lemma 2.12, the functor
![]() ${\mathcal{C}}(T,-)$
induces an equivalence of categories from
${\mathcal{C}}(T,-)$
induces an equivalence of categories from
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})$
to
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})$
to
![]() ${\mathcal{E}}$
. Since
${\mathcal{E}}$
. Since
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
is isomorphic to
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
is isomorphic to
![]() $\big(\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})\big)/(\unicode[STIX]{x1D6F4}R^{\ast })$
, the functor
$\big(\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})\big)/(\unicode[STIX]{x1D6F4}R^{\ast })$
, the functor
![]() ${\mathcal{C}}(T,-)$
induces an equivalence of categories from
${\mathcal{C}}(T,-)$
induces an equivalence of categories from
![]() $\overline{{\mathcal{C}}}(T)/\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
to
$\overline{{\mathcal{C}}}(T)/\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
to
![]() ${\mathcal{E}}/\operatorname{add}{\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })$
. Dually, one can use Lemma 2.13 to notice that the functor
${\mathcal{E}}/\operatorname{add}{\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })$
. Dually, one can use Lemma 2.13 to notice that the functor
![]() $D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
induces an equivalence of categories from
$D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
induces an equivalence of categories from
![]() $(\overline{T}\ast T^{\prime })/\operatorname{add}T$
to
$(\overline{T}\ast T^{\prime })/\operatorname{add}T$
to
![]() ${\mathcal{E}}^{\prime }/\operatorname{add}D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })$
. The statement now follows from Theorem 2.9.◻
${\mathcal{E}}^{\prime }/\operatorname{add}D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })$
. The statement now follows from Theorem 2.9.◻
There are two particular cases of Theorem 2.11 that are worth noting. They are weak forms of nearly Morita equivalences that we call pseudo-Morita equivalences. They occur in the case where
![]() $R$
is indecomposable, that is
$R$
is indecomposable, that is
![]() $m=n+1$
, and we make this assumption for the rest of the section. It should be noted that
$m=n+1$
, and we make this assumption for the rest of the section. It should be noted that
![]() $R=T_{m}$
and
$R=T_{m}$
and
![]() $R^{\ast }=T_{m}^{\prime }$
.
$R^{\ast }=T_{m}^{\prime }$
.
Let
![]() $Q_{m}$
be the
$Q_{m}$
be the
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })={\mathcal{C}}(T,\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
appearing in Theorem 2.11. Similarly, we have the
${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })={\mathcal{C}}(T,\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
appearing in Theorem 2.11. Similarly, we have the
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-modules
$\unicode[STIX]{x1D6EC}^{\prime }$
-modules
![]() $Q_{m}^{\prime }=D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })=D{\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T^{\prime })$
. Then, we have the following.
$Q_{m}^{\prime }=D{\mathcal{C}}(R,\unicode[STIX]{x1D6F4}T^{\prime })=D{\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T^{\prime })$
. Then, we have the following.
Lemma 2.14. Suppose that
![]() $R$
is indecomposable. Let
$R$
is indecomposable. Let
![]() $e$
be the idempotent for
$e$
be the idempotent for
![]() $\unicode[STIX]{x1D6EC}$
corresponding to
$\unicode[STIX]{x1D6EC}$
corresponding to
![]() $T_{m}$
. Then, we have the isomorphism
$T_{m}$
. Then, we have the isomorphism
Furthermore,
![]() $Q_{m}$
is a simple object of
$Q_{m}$
is a simple object of
![]() ${\mathcal{E}}$
. Dually, let
${\mathcal{E}}$
. Dually, let
![]() $e^{\prime }$
be the idempotent for
$e^{\prime }$
be the idempotent for
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
corresponding to
$\unicode[STIX]{x1D6EC}^{\prime }$
corresponding to
![]() $\unicode[STIX]{x1D6F4}T_{m}^{\prime }$
. Then, we have the isomorphism
$\unicode[STIX]{x1D6F4}T_{m}^{\prime }$
. Then, we have the isomorphism
Furthermore,
![]() $Q_{m}^{\prime }$
is an indecomposable
$Q_{m}^{\prime }$
is an indecomposable
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-module and a simple object of
$\unicode[STIX]{x1D6EC}^{\prime }$
-module and a simple object of
![]() ${\mathcal{E}}^{\prime }$
.
${\mathcal{E}}^{\prime }$
.
Proof. The long exact sequences associated with the exchange triangle
![]() $T_{m}^{\prime }\rightarrow \overline{U}_{m}\rightarrow T_{m}\rightarrow \unicode[STIX]{x1D6F4}T_{m}^{\prime }$
of Remark 2.10 show that the functor
$T_{m}^{\prime }\rightarrow \overline{U}_{m}\rightarrow T_{m}\rightarrow \unicode[STIX]{x1D6F4}T_{m}^{\prime }$
of Remark 2.10 show that the functor
![]() ${\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
vanishes on
${\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
vanishes on
![]() $\operatorname{add}(\overline{T})$
, and that the
$\operatorname{add}(\overline{T})$
, and that the
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() ${\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
is isomorphic to the module
${\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T_{m}^{\prime })$
is isomorphic to the module
![]() ${\mathcal{C}}/(\operatorname{add}\overline{T})(T_{m},T_{m})$
. We thus have an isomorphism of
${\mathcal{C}}/(\operatorname{add}\overline{T})(T_{m},T_{m})$
. We thus have an isomorphism of
![]() $\unicode[STIX]{x1D6EC}$
-modules:
$\unicode[STIX]{x1D6EC}$
-modules:
Similarly, using the exchange triangle as above, we obtain an isomorphism between the
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-modules
$\unicode[STIX]{x1D6EC}^{\prime }$
-modules
![]() $D{\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T^{\prime })$
and
$D{\mathcal{C}}(T_{m},\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $D{\mathcal{C}}/(\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})(\unicode[STIX]{x1D6F4}T^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })$
, the latter being isomorphic to
$D{\mathcal{C}}/(\operatorname{add}\unicode[STIX]{x1D6F4}\overline{T})(\unicode[STIX]{x1D6F4}T^{\prime },\unicode[STIX]{x1D6F4}T^{\prime })$
, the latter being isomorphic to
![]() $Q_{m}^{\prime }$
.
$Q_{m}^{\prime }$
.
Since
![]() $Q_{m}$
is projective over
$Q_{m}$
is projective over
![]() $\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
, we have
$\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
, we have
and therefore
![]() $Q_{m}$
lies in
$Q_{m}$
lies in
![]() ${\mathcal{E}}$
. If
${\mathcal{E}}$
. If
![]() $N$
is a non-trivial submodule of
$N$
is a non-trivial submodule of
![]() $Q_{m}$
lying in
$Q_{m}$
lying in
![]() ${\mathcal{E}}$
, then
${\mathcal{E}}$
, then
![]() $N$
is also a
$N$
is also a
![]() $\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
-module satisfying
$\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
-module satisfying
![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}}^{1}(N,S_{m})=0$
. Since
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}}^{1}(N,S_{m})=0$
. Since
![]() $S_{m}$
is the only simple
$S_{m}$
is the only simple
![]() $\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
-module,
$\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
-module,
![]() $N$
is projective over
$N$
is projective over
![]() $\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
, so it must equal
$\unicode[STIX]{x1D6EC}(1-e)\unicode[STIX]{x1D6EC}$
, so it must equal
![]() $Q_{m}$
. It follows that
$Q_{m}$
. It follows that
![]() $Q_{m}$
is a simple object of the exact category
$Q_{m}$
is a simple object of the exact category
![]() ${\mathcal{E}}$
. Since
${\mathcal{E}}$
. Since
![]() ${\mathcal{E}}$
is closed under direct summands, it now follows that
${\mathcal{E}}$
is closed under direct summands, it now follows that
![]() $Q_{m}$
is an indecomposable
$Q_{m}$
is an indecomposable
![]() $\unicode[STIX]{x1D6EC}$
-module. The proofs of the duals of these last two statements are similar.◻
$\unicode[STIX]{x1D6EC}$
-module. The proofs of the duals of these last two statements are similar.◻
Corollary 2.15. Suppose that
![]() ${\mathcal{C}}$
satisfies the assumptions in Section 1 and that it has a Serre functor. Suppose further that
${\mathcal{C}}$
satisfies the assumptions in Section 1 and that it has a Serre functor. Suppose further that
![]() $R$
is indecomposable. Then, there is an equivalence of categories
$R$
is indecomposable. Then, there is an equivalence of categories
Corollary 2.16. Suppose that the assumptions in Corollary 2.15 hold, and, in addition, that the Gabriel quiver of
![]() $\unicode[STIX]{x1D6EC}$
has no loop at the vertex corresponding to
$\unicode[STIX]{x1D6EC}$
has no loop at the vertex corresponding to
![]() $R$
. Then, there is an equivalence of categories
$R$
. Then, there is an equivalence of categories
Proof. This is a particular case of Corollary 2.15. Indeed, by [Reference Iyama and YoshinoIY08, Proposition 2.6(1)],
![]() $R^{\ast }$
is also indecomposable and has no loop. This implies that
$R^{\ast }$
is also indecomposable and has no loop. This implies that
![]() $Q_{m}$
and
$Q_{m}$
and
![]() $Q_{m}^{\prime }$
are isomorphic to
$Q_{m}^{\prime }$
are isomorphic to
![]() $S_{m}$
and
$S_{m}$
and
![]() $S_{m}^{\prime }$
, respectively.◻
$S_{m}^{\prime }$
, respectively.◻
3 Localization
3.1 Notation and statement of main results
We continue with the assumptions and notation from Section 1. We do not assume here that
![]() ${\mathcal{C}}$
has a Serre functor, except in Corollary 3.5. Moreover, contrary to [Reference Buan and MarshBM13], we do not make any skeletal smallness assumption. This is because all of the localizations that we consider are shown to be equivalent to a subquotient of
${\mathcal{C}}$
has a Serre functor, except in Corollary 3.5. Moreover, contrary to [Reference Buan and MarshBM13], we do not make any skeletal smallness assumption. This is because all of the localizations that we consider are shown to be equivalent to a subquotient of
![]() ${\mathcal{C}}$
. Therefore, no set-theoretic difficulties arise, and the localizations we consider are all categories without passing to a higher universe.
${\mathcal{C}}$
. Therefore, no set-theoretic difficulties arise, and the localizations we consider are all categories without passing to a higher universe.
Recall that, by [Reference Keller and ReitenKR07, Reference Buan and MarshBM13], the functor
![]() ${\mathcal{C}}(T,-)$
induces an equivalence of categories from
${\mathcal{C}}(T,-)$
induces an equivalence of categories from
![]() ${\mathcal{C}}(T)/\unicode[STIX]{x1D6F4}T$
to
${\mathcal{C}}(T)/\unicode[STIX]{x1D6F4}T$
to
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
. In particular, it is dense and full when restricted to
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
. In particular, it is dense and full when restricted to
![]() ${\mathcal{C}}(T)$
.
${\mathcal{C}}(T)$
.
Definition 3.1. Let
![]() ${\mathcal{B}}$
be the full subcategory of
${\mathcal{B}}$
be the full subcategory of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
given by the (essential) image of
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
given by the (essential) image of
![]() $\overline{T}^{\bot }$
under
$\overline{T}^{\bot }$
under
![]() ${\mathcal{C}}(T,-)$
. Let
${\mathcal{C}}(T,-)$
. Let
![]() ${\mathcal{S}}_{{\mathcal{B}},0}$
be the class of all epimorphisms
${\mathcal{S}}_{{\mathcal{B}},0}$
be the class of all epimorphisms
![]() $f\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
whose kernel belongs to
$f\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
whose kernel belongs to
![]() ${\mathcal{B}}$
. Dually, we let
${\mathcal{B}}$
. Dually, we let
![]() ${\mathcal{B}}^{\prime }$
be the full subcategory of
${\mathcal{B}}^{\prime }$
be the full subcategory of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
given by the (essential) image of
$\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
given by the (essential) image of
![]() $\text{}^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
under
$\text{}^{\bot }\unicode[STIX]{x1D6F4}\overline{T}$
under
![]() $D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
, and set
$D{\mathcal{C}}(-,\unicode[STIX]{x1D6F4}T^{\prime })$
, and set
![]() ${\mathcal{S}}_{0,{\mathcal{B}}^{\prime }}$
to be the class of all monomorphisms
${\mathcal{S}}_{0,{\mathcal{B}}^{\prime }}$
to be the class of all monomorphisms
![]() $g\in \operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
whose cokernel belongs to
$g\in \operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime }$
whose cokernel belongs to
![]() ${\mathcal{B}}^{\prime }$
.
${\mathcal{B}}^{\prime }$
.
Let
![]() $F$
be the composition of the fully faithful functor
$F$
be the composition of the fully faithful functor
![]() $\overline{{\mathcal{C}}}(T)/\unicode[STIX]{x1D6F4}\overline{T}\rightarrow {\mathcal{C}}(T)/\unicode[STIX]{x1D6F4}T\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
and the localization functor
$\overline{{\mathcal{C}}}(T)/\unicode[STIX]{x1D6F4}\overline{T}\rightarrow {\mathcal{C}}(T)/\unicode[STIX]{x1D6F4}T\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
and the localization functor
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}\stackrel{L_{{\mathcal{S}}_{{\mathcal{B}},0}}}{\longrightarrow }(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. Then, since
$\operatorname{mod}\unicode[STIX]{x1D6EC}\stackrel{L_{{\mathcal{S}}_{{\mathcal{B}},0}}}{\longrightarrow }(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. Then, since
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })$
belongs to
${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })$
belongs to
![]() ${\mathcal{B}}$
, we have that
${\mathcal{B}}$
, we have that
![]() $F(\unicode[STIX]{x1D6F4}R^{\ast })\simeq 0$
in
$F(\unicode[STIX]{x1D6F4}R^{\ast })\simeq 0$
in
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. Hence,
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. Hence,
![]() $F$
induces a functor
$F$
induces a functor
![]() $\overline{F}$
as in the following diagram:
$\overline{F}$
as in the following diagram:

Our main aim in this section is to show that the following holds.
Theorem 3.2. The functor
![]() $\overline{F}:\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\longrightarrow (\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
is an equivalence of categories. Dually, there is an equivalence
$\overline{F}:\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\longrightarrow (\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
is an equivalence of categories. Dually, there is an equivalence
![]() $\overline{{\mathcal{C}}}(T)/(T)\longrightarrow (\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime })_{{\mathcal{S}}_{0,{\mathcal{B}}^{\prime }}}$
.
$\overline{{\mathcal{C}}}(T)/(T)\longrightarrow (\operatorname{mod}\unicode[STIX]{x1D6EC}^{\prime })_{{\mathcal{S}}_{0,{\mathcal{B}}^{\prime }}}$
.
This has two key corollaries, which we state below, after a lemma needed in the proof of the first one.
Lemma 3.3. For any object
![]() $M\in {\mathcal{B}}$
, there exists
$M\in {\mathcal{B}}$
, there exists
![]() $X\in {\mathcal{C}}(T)\cap \overline{T}^{\bot }$
such that
$X\in {\mathcal{C}}(T)\cap \overline{T}^{\bot }$
such that
![]() ${\mathcal{C}}(T,X)\simeq M$
.
${\mathcal{C}}(T,X)\simeq M$
.
Proof. For any object
![]() $M\in {\mathcal{B}}$
, there exists an object
$M\in {\mathcal{B}}$
, there exists an object
![]() $Y\in \overline{T}^{\bot }$
such that
$Y\in \overline{T}^{\bot }$
such that
![]() ${\mathcal{C}}(T,Y)\simeq M$
. By [Reference Buan and MarshBM13, Lemma 3.3], there is a triangle
${\mathcal{C}}(T,Y)\simeq M$
. By [Reference Buan and MarshBM13, Lemma 3.3], there is a triangle
![]() $Z\rightarrow X\rightarrow Y\stackrel{\unicode[STIX]{x1D700}}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
in
$Z\rightarrow X\rightarrow Y\stackrel{\unicode[STIX]{x1D700}}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
in
![]() ${\mathcal{C}}$
, where
${\mathcal{C}}$
, where
![]() $X\in {\mathcal{C}}(T)$
,
$X\in {\mathcal{C}}(T)$
,
![]() $Z\in T^{\bot }$
and
$Z\in T^{\bot }$
and
![]() $\unicode[STIX]{x1D700}\in (T^{\bot })$
. Then, we have
$\unicode[STIX]{x1D700}\in (T^{\bot })$
. Then, we have
![]() ${\mathcal{C}}(T,X)\simeq {\mathcal{C}}(T,Y)\simeq M$
, which can be seen by applying the functor
${\mathcal{C}}(T,X)\simeq {\mathcal{C}}(T,Y)\simeq M$
, which can be seen by applying the functor
![]() ${\mathcal{C}}(T,-)$
to the triangle above. Moreover,
${\mathcal{C}}(T,-)$
to the triangle above. Moreover,
![]() $X$
belongs to
$X$
belongs to
![]() $\overline{T}^{\bot }$
, since both
$\overline{T}^{\bot }$
, since both
![]() $Z$
and
$Z$
and
![]() $Y$
belong to
$Y$
belong to
![]() $\overline{T}^{\bot }$
.◻
$\overline{T}^{\bot }$
.◻
Corollary 3.4. There is an equivalence of categories
and, dually, an equivalence of categories
Proof. For the first statement, combine Theorem 3.2 with Lemma 2.12, and for the second statement, combine Theorem 3.2 with Lemma 2.13. ◻
Proof of Theorem B.
We set
![]() ${\mathcal{C}}$
to be an acyclic cluster category, and set
${\mathcal{C}}$
to be an acyclic cluster category, and set
![]() $T$
to be a rigid object in
$T$
to be a rigid object in
![]() ${\mathcal{C}}$
. We consider the case
${\mathcal{C}}$
. We consider the case
![]() $m=n+1$
and
$m=n+1$
and
![]() $R=T_{m}$
is indecomposable. As in the proofs of Corollaries 2.15 and 2.16,
$R=T_{m}$
is indecomposable. As in the proofs of Corollaries 2.15 and 2.16,
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })\simeq Q_{m}\simeq S_{m}$
in this case. In particular, there are no loops in the quiver of
${\mathcal{C}}(T,\unicode[STIX]{x1D6F4}R^{\ast })\simeq Q_{m}\simeq S_{m}$
in this case. In particular, there are no loops in the quiver of
![]() $\operatorname{End}_{{\mathcal{C}}}(T)$
at the vertex corresponding to
$\operatorname{End}_{{\mathcal{C}}}(T)$
at the vertex corresponding to
![]() $S_{m}$
.
$S_{m}$
.
By Lemma 3.3, we have
![]() ${\mathcal{B}}={\mathcal{C}}(T,\overline{T}^{\bot })={\mathcal{C}}(T,{\mathcal{C}}(T)\cap \overline{T}^{\bot })$
. For
${\mathcal{B}}={\mathcal{C}}(T,\overline{T}^{\bot })={\mathcal{C}}(T,{\mathcal{C}}(T)\cap \overline{T}^{\bot })$
. For
![]() $j=1,\ldots ,n+1$
, let
$j=1,\ldots ,n+1$
, let
![]() $P_{j}={\mathcal{C}}(T,T_{j})$
be the
$P_{j}={\mathcal{C}}(T,T_{j})$
be the
![]() $j$
th indecomposable projective in
$j$
th indecomposable projective in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then, an object
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then, an object
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}(T)$
lies in
${\mathcal{C}}(T)$
lies in
![]() $\overline{T}^{\bot }$
if and only if
$\overline{T}^{\bot }$
if and only if
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P_{j},{\mathcal{C}}(T,X))=0$
for
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P_{j},{\mathcal{C}}(T,X))=0$
for
![]() $j=1,2,\ldots ,n$
, which holds if and only if
$j=1,2,\ldots ,n$
, which holds if and only if
![]() ${\mathcal{C}}(T,X)$
lies in
${\mathcal{C}}(T,X)$
lies in
![]() $\operatorname{add}(S_{m})$
. It follows that
$\operatorname{add}(S_{m})$
. It follows that
![]() ${\mathcal{B}}=\operatorname{add}(S_{m})$
in this case, and hence
${\mathcal{B}}=\operatorname{add}(S_{m})$
in this case, and hence
![]() ${\mathcal{S}}_{{\mathcal{B}},0}$
coincides with the class
${\mathcal{S}}_{{\mathcal{B}},0}$
coincides with the class
![]() ${\mathcal{R}}$
of morphisms considered in the introduction. We see that the first statement in Theorem B follows from the first statement in Corollary 3.4. The second statement in Theorem B follows from the second statement in Corollary 3.4. ◻
${\mathcal{R}}$
of morphisms considered in the introduction. We see that the first statement in Theorem B follows from the first statement in Corollary 3.4. The second statement in Theorem B follows from the second statement in Corollary 3.4. ◻
Corollary 3.5. If the category
![]() ${\mathcal{C}}$
admits a Serre functor, then there is an equivalence of categories
${\mathcal{C}}$
admits a Serre functor, then there is an equivalence of categories
Proof of Theorem A.
Since an acyclic cluster category has a Serre functor, Theorem A follows from Corollary 3.5 and the observations in the proof of Theorem B above. ◻
We also use Theorem 3.2 to show that the categories
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
and
${\mathcal{C}}_{{\mathcal{S}}}$
and
![]() ${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
are isomorphic (Theorem 3.19). We also remark that Lemma 3.8 may be of independent interest.
${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
are isomorphic (Theorem 3.19). We also remark that Lemma 3.8 may be of independent interest.
3.2 Proof of Theorem 3.2
We show the first statement of the theorem. The second statement follows from a dual argument. In order to prove that
![]() $\overline{F}$
is full and dense, it is enough to prove that
$\overline{F}$
is full and dense, it is enough to prove that
![]() $F$
is full and dense. The functor
$F$
is full and dense. The functor
![]() $F$
is easily seen to be dense (Proposition 3.13). Showing that it is full requires a bit more work (Lemmas 3.8 and 3.9), and in order to do so we describe, in Lemma 3.11, the category
$F$
is easily seen to be dense (Proposition 3.13). Showing that it is full requires a bit more work (Lemmas 3.8 and 3.9), and in order to do so we describe, in Lemma 3.11, the category
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{B,0}}$
as a localization of
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{B,0}}$
as a localization of
![]() ${\mathcal{C}}$
. We then show that the functor
${\mathcal{C}}$
. We then show that the functor
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)$
induces a functor
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)$
induces a functor
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}\longrightarrow \operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
(Lemma 3.15). Composing
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}\longrightarrow \operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
(Lemma 3.15). Composing
![]() $F$
with this induced functor and applying results from [Reference Buan and MarshBM13] then gives us the faithfulness of
$F$
with this induced functor and applying results from [Reference Buan and MarshBM13] then gives us the faithfulness of
![]() $\overline{F}$
(Proposition 3.16).
$\overline{F}$
(Proposition 3.16).
Lemma 3.6. The full subcategory
![]() ${\mathcal{B}}$
of
${\mathcal{B}}$
of
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
is closed under taking images and submodules.
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
is closed under taking images and submodules.
Proof. Let
![]() $M\stackrel{u}{\rightarrow }N$
be a morphism in
$M\stackrel{u}{\rightarrow }N$
be a morphism in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then, there are objects
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then, there are objects
![]() $X,Y\in {\mathcal{C}}(T)$
such that
$X,Y\in {\mathcal{C}}(T)$
such that
![]() ${\mathcal{C}}(T,X)\simeq M$
and
${\mathcal{C}}(T,X)\simeq M$
and
![]() ${\mathcal{C}}(T,Y)\simeq N$
, and a morphism
${\mathcal{C}}(T,Y)\simeq N$
, and a morphism
![]() $f:X\rightarrow Y$
such that
$f:X\rightarrow Y$
such that
![]() ${\mathcal{C}}(T,f)\simeq u$
. We complete
${\mathcal{C}}(T,f)\simeq u$
. We complete
![]() $f$
to a triangle:
$f$
to a triangle:
If
![]() $M$
lies in
$M$
lies in
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() $u$
is an epimorphism, then, by Lemma 3.3, we may take
$u$
is an epimorphism, then, by Lemma 3.3, we may take
![]() $X$
in
$X$
in
![]() $\overline{T}^{\bot }$
, and, by [Reference Buan and MarshBM13, Lemma 2.5],
$\overline{T}^{\bot }$
, and, by [Reference Buan and MarshBM13, Lemma 2.5],
![]() $h$
factors through
$h$
factors through
![]() $T^{\bot }$
. If
$T^{\bot }$
. If
![]() $N$
lies in
$N$
lies in
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() $u$
is a monomorphism, then, by Lemma 3.3, we may take
$u$
is a monomorphism, then, by Lemma 3.3, we may take
![]() $Y$
in
$Y$
in
![]() $\overline{T}^{\bot }$
, and, by [Reference Buan and MarshBM13, Lemma 2.5],
$\overline{T}^{\bot }$
, and, by [Reference Buan and MarshBM13, Lemma 2.5],
![]() $f$
factors through
$f$
factors through
![]() $T^{\bot }$
.
$T^{\bot }$
.
In either case, the result follows from applying the functor
![]() ${\mathcal{C}}(\overline{T},-)$
to this triangle.◻
${\mathcal{C}}(\overline{T},-)$
to this triangle.◻
Proposition 3.7. The functor
![]() $F$
is dense.
$F$
is dense.
Proof. For any module
![]() $M\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
, let
$M\in \operatorname{mod}\unicode[STIX]{x1D6EC}$
, let
![]() $X$
be an object in
$X$
be an object in
![]() ${\mathcal{C}}(T)$
such that
${\mathcal{C}}(T)$
such that
![]() ${\mathcal{C}}(T,X)\simeq M$
. In Lemma 2.2, we constructed a triangle
${\mathcal{C}}(T,X)\simeq M$
. In Lemma 2.2, we constructed a triangle
![]() $Z\longrightarrow R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\longrightarrow }X\stackrel{g}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, with
$Z\longrightarrow R_{0}X\stackrel{\unicode[STIX]{x1D702}_{X}}{\longrightarrow }X\stackrel{g}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, with
![]() $R_{0}X\in \overline{{\mathcal{C}}}(T)$
,
$R_{0}X\in \overline{{\mathcal{C}}}(T)$
,
![]() $Z\in \overline{T}^{\bot }$
and
$Z\in \overline{T}^{\bot }$
and
![]() $g\in (T^{\bot })$
. We claim that the morphism
$g\in (T^{\bot })$
. We claim that the morphism
![]() $\unicode[STIX]{x1D702}_{X}$
is inverted in
$\unicode[STIX]{x1D702}_{X}$
is inverted in
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. There is an exact sequence in
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
. There is an exact sequence in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
:
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
:
Therefore, the morphism
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D702}_{X})$
is surjective, and
${\mathcal{C}}(T,\unicode[STIX]{x1D702}_{X})$
is surjective, and
![]() ${\mathcal{C}}(T,Z)$
surjects onto its kernel. Since
${\mathcal{C}}(T,Z)$
surjects onto its kernel. Since
![]() ${\mathcal{B}}$
is closed under images (Lemma 3.6), we may conclude that
${\mathcal{B}}$
is closed under images (Lemma 3.6), we may conclude that
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D702}_{X})$
belongs to
${\mathcal{C}}(T,\unicode[STIX]{x1D702}_{X})$
belongs to
![]() ${\mathcal{S}}_{{\mathcal{B}},0}$
, and the claim is shown. This shows that
${\mathcal{S}}_{{\mathcal{B}},0}$
, and the claim is shown. This shows that
![]() $M\simeq FR_{0}X$
in
$M\simeq FR_{0}X$
in
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
, and we are done.◻
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
, and we are done.◻
Lemma 3.8. Let
![]() $Z\stackrel{u}{\longrightarrow }X\stackrel{v}{\longrightarrow }Y\stackrel{\unicode[STIX]{x1D700}}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
be a triangle in
$Z\stackrel{u}{\longrightarrow }X\stackrel{v}{\longrightarrow }Y\stackrel{\unicode[STIX]{x1D700}}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
be a triangle in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $X,Y\in {\mathcal{C}}(T)$
and
$X,Y\in {\mathcal{C}}(T)$
and
![]() $\unicode[STIX]{x1D700}\in (T^{\bot })$
. Then,
$\unicode[STIX]{x1D700}\in (T^{\bot })$
. Then,
![]() $Z$
belongs to
$Z$
belongs to
![]() ${\mathcal{C}}(T)$
.
${\mathcal{C}}(T)$
.
Proof. Let
![]() $T^{Z}\stackrel{f}{\longrightarrow }Z$
be a minimal right
$T^{Z}\stackrel{f}{\longrightarrow }Z$
be a minimal right
![]() $\operatorname{add}T$
-approximation. Complete it to a triangle
$\operatorname{add}T$
-approximation. Complete it to a triangle
![]() $U\rightarrow T^{Z}\stackrel{f}{\rightarrow }Z\stackrel{\unicode[STIX]{x1D6FF}}{\rightarrow }\unicode[STIX]{x1D6F4}U$
. We note that, since
$U\rightarrow T^{Z}\stackrel{f}{\rightarrow }Z\stackrel{\unicode[STIX]{x1D6FF}}{\rightarrow }\unicode[STIX]{x1D6F4}U$
. We note that, since
![]() $f$
is an approximation and
$f$
is an approximation and
![]() $T$
is rigid, we have
$T$
is rigid, we have
![]() $\unicode[STIX]{x1D6F4}U\in T^{\bot }$
, as can be seen by applying the functor
$\unicode[STIX]{x1D6F4}U\in T^{\bot }$
, as can be seen by applying the functor
![]() ${\mathcal{C}}(T,-)$
to the triangle above, in a manner similar to that of [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.3]. (A more general version of this assertion can be found in [Reference JørgensenJør09, Lemma 2.1].)
${\mathcal{C}}(T,-)$
to the triangle above, in a manner similar to that of [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06, Lemma 6.3]. (A more general version of this assertion can be found in [Reference JørgensenJør09, Lemma 2.1].)
Since
![]() $Y$
belongs to
$Y$
belongs to
![]() ${\mathcal{C}}(T)$
, there is a triangle
${\mathcal{C}}(T)$
, there is a triangle
![]() $T_{1}^{Y}\rightarrow T_{0}^{Y}\stackrel{a}{\rightarrow }Y\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }\unicode[STIX]{x1D6F4}T_{1}^{Y}$
. By assumption, the composition
$T_{1}^{Y}\rightarrow T_{0}^{Y}\stackrel{a}{\rightarrow }Y\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }\unicode[STIX]{x1D6F4}T_{1}^{Y}$
. By assumption, the composition
![]() $\unicode[STIX]{x1D700}a$
vanishes, so that there is a morphism
$\unicode[STIX]{x1D700}a$
vanishes, so that there is a morphism
![]() $T_{0}^{Y}\stackrel{b}{\rightarrow }X$
such that
$T_{0}^{Y}\stackrel{b}{\rightarrow }X$
such that
![]() $a=vb$
. We thus have a morphism of triangles
$a=vb$
. We thus have a morphism of triangles

which we complete to a nine diagram

Since
![]() $\unicode[STIX]{x1D6F4}U\in T^{\bot }$
, the morphism
$\unicode[STIX]{x1D6F4}U\in T^{\bot }$
, the morphism
![]() $T_{1}^{Y}\rightarrow \unicode[STIX]{x1D6F4}U$
vanishes, and the top triangle splits. Thus,
$T_{1}^{Y}\rightarrow \unicode[STIX]{x1D6F4}U$
vanishes, and the top triangle splits. Thus,
![]() $U$
is a summand of
$U$
is a summand of
![]() $V$
, and it is enough to prove that
$V$
, and it is enough to prove that
![]() $V$
belongs to
$V$
belongs to
![]() $\operatorname{add}T$
. Since
$\operatorname{add}T$
. Since
![]() $X\in {\mathcal{C}}(T)$
, this amounts to proving that the morphism
$X\in {\mathcal{C}}(T)$
, this amounts to proving that the morphism
![]() $T^{Z}\oplus T_{0}^{Y}\rightarrow X$
is an
$T^{Z}\oplus T_{0}^{Y}\rightarrow X$
is an
![]() $\operatorname{add}T$
-approximation. Let us thus prove the latter statement. Let
$\operatorname{add}T$
-approximation. Let us thus prove the latter statement. Let
![]() $W\stackrel{g}{\longrightarrow }X$
be a morphism in
$W\stackrel{g}{\longrightarrow }X$
be a morphism in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $W\in \operatorname{add}T$
. (The morphisms are illustrated in the diagram below.) Then, the composition
$W\in \operatorname{add}T$
. (The morphisms are illustrated in the diagram below.) Then, the composition
![]() $\unicode[STIX]{x1D702}vg$
is zero, so that there is a morphism
$\unicode[STIX]{x1D702}vg$
is zero, so that there is a morphism
![]() $W\stackrel{c}{\longrightarrow }T_{0}^{Y}$
with
$W\stackrel{c}{\longrightarrow }T_{0}^{Y}$
with
![]() $vg=ac$
. This implies
$vg=ac$
. This implies
![]() $vg=vbc$
, and there is a morphism
$vg=vbc$
, and there is a morphism
![]() $W\stackrel{d}{\longrightarrow }Z$
such that
$W\stackrel{d}{\longrightarrow }Z$
such that
![]() $g-bc=ud$
. Now,
$g-bc=ud$
. Now,
![]() $f$
is an
$f$
is an
![]() $\operatorname{add}T$
-approximation, so that there is a morphism
$\operatorname{add}T$
-approximation, so that there is a morphism
![]() $W\stackrel{e}{\longrightarrow }T^{Z}$
satisfying
$W\stackrel{e}{\longrightarrow }T^{Z}$
satisfying
![]() $d=fe$
. The last two equalities give
$d=fe$
. The last two equalities give
![]() $g=ufe+bc=[uf\;b][\!\begin{smallmatrix}e\\ c\end{smallmatrix}\!]$
, and we have shown that
$g=ufe+bc=[uf\;b][\!\begin{smallmatrix}e\\ c\end{smallmatrix}\!]$
, and we have shown that
![]() $[uf\;b]$
is an
$[uf\;b]$
is an
![]() $\operatorname{add}T$
-approximation.◻
$\operatorname{add}T$
-approximation.◻
The following diagram shows the morphisms
![]() $g,b,c,d$
and
$g,b,c,d$
and
![]() $e$
.
$e$
.

Lemma 3.9. Let
![]() $Z\stackrel{f}{\longrightarrow }X$
be a morphism in
$Z\stackrel{f}{\longrightarrow }X$
be a morphism in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $Z\in {\mathcal{C}}(T)$
. Then,
$Z\in {\mathcal{C}}(T)$
. Then,
![]() ${\mathcal{C}}(T,f)$
factors through
${\mathcal{C}}(T,f)$
factors through
![]() ${\mathcal{B}}$
if and only if
${\mathcal{B}}$
if and only if
![]() $f$
factors through
$f$
factors through
![]() $\overline{T}^{\bot }$
.
$\overline{T}^{\bot }$
.
Proof. If
![]() $f$
belongs to the ideal
$f$
belongs to the ideal
![]() $(\overline{T}^{\bot })$
, then
$(\overline{T}^{\bot })$
, then
![]() ${\mathcal{C}}(T,f)$
factors through
${\mathcal{C}}(T,f)$
factors through
![]() ${\mathcal{B}}$
by the definition of
${\mathcal{B}}$
by the definition of
![]() ${\mathcal{B}}$
. Let us prove the converse. Since
${\mathcal{B}}$
. Let us prove the converse. Since
![]() $Z\in {\mathcal{C}}(T)$
, there is a triangle
$Z\in {\mathcal{C}}(T)$
, there is a triangle
![]() $T_{1}\rightarrow T_{0}\stackrel{g}{\rightarrow }Z\rightarrow \unicode[STIX]{x1D6F4}T_{1}$
in
$T_{1}\rightarrow T_{0}\stackrel{g}{\rightarrow }Z\rightarrow \unicode[STIX]{x1D6F4}T_{1}$
in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $T_{0},T_{1}\in \operatorname{add}T$
. Assume that
$T_{0},T_{1}\in \operatorname{add}T$
. Assume that
![]() ${\mathcal{C}}(T,f)$
belongs to
${\mathcal{C}}(T,f)$
belongs to
![]() $({\mathcal{B}})$
. Then, there exists
$({\mathcal{B}})$
. Then, there exists
![]() $U\in \overline{T}^{\bot }$
, and there exist maps
$U\in \overline{T}^{\bot }$
, and there exist maps
![]() ${\mathcal{C}}(T,Z)\stackrel{b}{\longrightarrow }{\mathcal{C}}(T,U)$
and
${\mathcal{C}}(T,Z)\stackrel{b}{\longrightarrow }{\mathcal{C}}(T,U)$
and
![]() ${\mathcal{C}}(T,U)\stackrel{a}{\longrightarrow }{\mathcal{C}}(T,X)$
such that
${\mathcal{C}}(T,U)\stackrel{a}{\longrightarrow }{\mathcal{C}}(T,X)$
such that
![]() ${\mathcal{C}}(T,f)=a\circ b$
.
${\mathcal{C}}(T,f)=a\circ b$
.
We would like to lift
![]() $a$
and
$a$
and
![]() $b$
to morphisms in the category
$b$
to morphisms in the category
![]() ${\mathcal{C}}$
. This cannot be done in general, since the functor
${\mathcal{C}}$
. This cannot be done in general, since the functor
![]() ${\mathcal{C}}(T,-)$
is not full. Fortunately, it is full when restricted to
${\mathcal{C}}(T,-)$
is not full. Fortunately, it is full when restricted to
![]() ${\mathcal{C}}(T)$
. We thus use [Reference Buan and MarshBM13, Lemma 3.3] in order to replace the object
${\mathcal{C}}(T)$
. We thus use [Reference Buan and MarshBM13, Lemma 3.3] in order to replace the object
![]() $U$
by an object
$U$
by an object
![]() $U^{\prime }$
whose image under
$U^{\prime }$
whose image under
![]() ${\mathcal{C}}(T,-)$
is isomorphic to that of
${\mathcal{C}}(T,-)$
is isomorphic to that of
![]() $U$
, but with the additional property that
$U$
, but with the additional property that
![]() $U^{\prime }$
is in
$U^{\prime }$
is in
![]() ${\mathcal{C}}(T)$
. Let us therefore apply [Reference Buan and MarshBM13, Lemma 3.3] so as to get triangles
${\mathcal{C}}(T)$
. Let us therefore apply [Reference Buan and MarshBM13, Lemma 3.3] so as to get triangles
![]() $Y_{U}\rightarrow U^{\prime }\rightarrow U\stackrel{\unicode[STIX]{x1D700}}{\rightarrow }\unicode[STIX]{x1D6F4}Y_{U}$
and
$Y_{U}\rightarrow U^{\prime }\rightarrow U\stackrel{\unicode[STIX]{x1D700}}{\rightarrow }\unicode[STIX]{x1D6F4}Y_{U}$
and
![]() $Y_{X}\rightarrow X^{\prime }\stackrel{u}{\rightarrow }X\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }\unicode[STIX]{x1D6F4}Y_{X}$
in
$Y_{X}\rightarrow X^{\prime }\stackrel{u}{\rightarrow }X\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }\unicode[STIX]{x1D6F4}Y_{X}$
in
![]() ${\mathcal{C}}$
, where
${\mathcal{C}}$
, where
![]() $U^{\prime },X^{\prime }$
belong to
$U^{\prime },X^{\prime }$
belong to
![]() ${\mathcal{C}}(T)$
, where
${\mathcal{C}}(T)$
, where
![]() $Y_{U},Y_{X}$
belong to
$Y_{U},Y_{X}$
belong to
![]() $T^{\bot }$
, and where the morphisms
$T^{\bot }$
, and where the morphisms
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $\unicode[STIX]{x1D702}$
factor through
$\unicode[STIX]{x1D702}$
factor through
![]() $T^{\bot }$
. Since
$T^{\bot }$
. Since
![]() $U$
is in
$U$
is in
![]() $\overline{T}^{\bot }$
and
$\overline{T}^{\bot }$
and
![]() $Y_{U}$
is in
$Y_{U}$
is in
![]() $T^{\bot }$
,
$T^{\bot }$
,
![]() $U^{\prime }$
is in
$U^{\prime }$
is in
![]() $\overline{T}^{\bot }$
as well.
$\overline{T}^{\bot }$
as well.
The modules
![]() ${\mathcal{C}}(T,U)$
and
${\mathcal{C}}(T,U)$
and
![]() ${\mathcal{C}}(T,U^{\prime })$
are isomorphic, and
${\mathcal{C}}(T,U^{\prime })$
are isomorphic, and
![]() ${\mathcal{C}}(T,u)$
is an isomorphism, so that there are morphisms
${\mathcal{C}}(T,u)$
is an isomorphism, so that there are morphisms
![]() ${\mathcal{C}}(T,Z)\stackrel{b^{\prime }}{\longrightarrow }{\mathcal{C}}(T,U^{\prime })$
and
${\mathcal{C}}(T,Z)\stackrel{b^{\prime }}{\longrightarrow }{\mathcal{C}}(T,U^{\prime })$
and
![]() ${\mathcal{C}}(T,U^{\prime })\stackrel{a^{\prime }}{\longrightarrow }{\mathcal{C}}(T,X^{\prime })$
satisfying
${\mathcal{C}}(T,U^{\prime })\stackrel{a^{\prime }}{\longrightarrow }{\mathcal{C}}(T,X^{\prime })$
satisfying
![]() ${\mathcal{C}}(T,u)\circ a^{\prime }\circ b^{\prime }={\mathcal{C}}(T,f)$
. Now, the objects
${\mathcal{C}}(T,u)\circ a^{\prime }\circ b^{\prime }={\mathcal{C}}(T,f)$
. Now, the objects
![]() $Z,U^{\prime }$
and
$Z,U^{\prime }$
and
![]() $X^{\prime }$
all belong to
$X^{\prime }$
all belong to
![]() ${\mathcal{C}}(T)$
, so that there exist morphisms
${\mathcal{C}}(T)$
, so that there exist morphisms
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D6FC})=a^{\prime }$
and
${\mathcal{C}}(T,\unicode[STIX]{x1D6FC})=a^{\prime }$
and
![]() ${\mathcal{C}}(T,\unicode[STIX]{x1D6FD})=b^{\prime }$
. We thus have the following diagram in
${\mathcal{C}}(T,\unicode[STIX]{x1D6FD})=b^{\prime }$
. We thus have the following diagram in
![]() ${\mathcal{C}}$
:
${\mathcal{C}}$
:

where the square
![]() $f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
commutes up to a summand in
$f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
commutes up to a summand in
![]() $T^{\bot }$
. Since
$T^{\bot }$
. Since
![]() $T_{0}\in \operatorname{add}T$
, the composition
$T_{0}\in \operatorname{add}T$
, the composition
![]() $(f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})g$
vanishes, and
$(f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})g$
vanishes, and
![]() $f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
factors through
$f-u\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
factors through
![]() $\unicode[STIX]{x1D6F4}T_{1}$
. This shows that
$\unicode[STIX]{x1D6F4}T_{1}$
. This shows that
![]() $f$
factors through
$f$
factors through
![]() $U^{\prime }\oplus \unicode[STIX]{x1D6F4}T_{1}$
, which belongs to
$U^{\prime }\oplus \unicode[STIX]{x1D6F4}T_{1}$
, which belongs to
![]() $\overline{T}^{\bot }$
, and we are done.◻
$\overline{T}^{\bot }$
, and we are done.◻
Definition 3.10. Let
![]() $\widetilde{{\mathcal{S}}}$
be the class of morphisms
$\widetilde{{\mathcal{S}}}$
be the class of morphisms
![]() $X\stackrel{s}{\longrightarrow }Y$
in
$X\stackrel{s}{\longrightarrow }Y$
in
![]() ${\mathcal{C}}$
such that, for any triangle
${\mathcal{C}}$
such that, for any triangle
![]() $Z\stackrel{f}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{g}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, we have
$Z\stackrel{f}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{g}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, we have
![]() $f\in (\overline{T}^{\bot })$
and
$f\in (\overline{T}^{\bot })$
and
![]() $g\in (T^{\bot })$
. It should be noted that this is a weaker property than that defining
$g\in (T^{\bot })$
. It should be noted that this is a weaker property than that defining
![]() ${\mathcal{S}}$
(where instead of the property
${\mathcal{S}}$
(where instead of the property
![]() $f\in (\overline{T}^{\bot })$
we had
$f\in (\overline{T}^{\bot })$
we had
![]() $Z\in \overline{T}^{\bot }$
). Therefore,
$Z\in \overline{T}^{\bot }$
). Therefore,
![]() ${\mathcal{S}}\subseteq \widetilde{{\mathcal{S}}}$
.
${\mathcal{S}}\subseteq \widetilde{{\mathcal{S}}}$
.
Let
![]() ${\mathcal{C}}\stackrel{L_{\widetilde{{\mathcal{S}}}}}{\longrightarrow }{\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
be the localization functor with respect to the class
${\mathcal{C}}\stackrel{L_{\widetilde{{\mathcal{S}}}}}{\longrightarrow }{\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
be the localization functor with respect to the class
![]() $\widetilde{{\mathcal{S}}}$
.
$\widetilde{{\mathcal{S}}}$
.
Lemma 3.11. There is a commutative diagram

where
![]() $G^{\prime }$
is an equivalence of categories.
$G^{\prime }$
is an equivalence of categories.
Proof. It is proved in [Reference Buan and MarshBM13] that the functor
![]() ${\mathcal{C}}(T,-):{\mathcal{C}}\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
is a localization functor for the class
${\mathcal{C}}(T,-):{\mathcal{C}}\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
is a localization functor for the class
![]() ${\mathcal{S}}_{T}$
of morphisms
${\mathcal{S}}_{T}$
of morphisms
![]() $X\stackrel{f}{\longrightarrow }Y$
such that, when completed to a triangle
$X\stackrel{f}{\longrightarrow }Y$
such that, when completed to a triangle
![]() $Z\stackrel{g}{\longrightarrow }X\stackrel{f}{\longrightarrow }Y\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, we have
$Z\stackrel{g}{\longrightarrow }X\stackrel{f}{\longrightarrow }Y\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
, we have
![]() $g,h\in (T^{\bot })$
. Since this class is contained in the class
$g,h\in (T^{\bot })$
. Since this class is contained in the class
![]() $\widetilde{{\mathcal{S}}}$
, it is enough to prove
$\widetilde{{\mathcal{S}}}$
, it is enough to prove
![]() ${\mathcal{C}}(T,\widetilde{{\mathcal{S}}})={\mathcal{S}}_{{\mathcal{B}},0}$
. Let
${\mathcal{C}}(T,\widetilde{{\mathcal{S}}})={\mathcal{S}}_{{\mathcal{B}},0}$
. Let
![]() $s$
be in
$s$
be in
![]() $\widetilde{{\mathcal{S}}}$
. There is a triangle
$\widetilde{{\mathcal{S}}}$
. There is a triangle
![]() $Z\stackrel{g}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
$Z\stackrel{g}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $g\in (\overline{T}^{\bot })$
and
$g\in (\overline{T}^{\bot })$
and
![]() $h\in (T^{\bot })$
. Applying the functor
$h\in (T^{\bot })$
. Applying the functor
![]() ${\mathcal{C}}(T,-)$
gives an exact sequence in
${\mathcal{C}}(T,-)$
gives an exact sequence in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
:
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
:
where
![]() ${\mathcal{C}}(T,g):{\mathcal{C}}(T,Z)\rightarrow {\mathcal{C}}(T,X)$
factors through some
${\mathcal{C}}(T,g):{\mathcal{C}}(T,Z)\rightarrow {\mathcal{C}}(T,X)$
factors through some
![]() $B\in {\mathcal{B}}$
. Thus,
$B\in {\mathcal{B}}$
. Thus,
![]() ${\mathcal{C}}(T,s)$
is an epimorphism, and its kernel is isomorphic to a quotient of a submodule of
${\mathcal{C}}(T,s)$
is an epimorphism, and its kernel is isomorphic to a quotient of a submodule of
![]() $B$
(see Remark 3.12 below). By Lemma 3.6, the subcategory
$B$
(see Remark 3.12 below). By Lemma 3.6, the subcategory
![]() ${\mathcal{B}}$
is stable under taking images and submodules, so that
${\mathcal{B}}$
is stable under taking images and submodules, so that
![]() ${\mathcal{C}}(T,s)$
belongs to
${\mathcal{C}}(T,s)$
belongs to
![]() ${\mathcal{S}}_{{\mathcal{B}},0}$
.
${\mathcal{S}}_{{\mathcal{B}},0}$
.
Conversely, let
![]() $0\rightarrow B\longrightarrow M\stackrel{f}{\longrightarrow }N\rightarrow 0$
be a short exact sequence in
$0\rightarrow B\longrightarrow M\stackrel{f}{\longrightarrow }N\rightarrow 0$
be a short exact sequence in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
, with
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
, with
![]() $B\in {\mathcal{B}}$
. There is a morphism
$B\in {\mathcal{B}}$
. There is a morphism
![]() $X\stackrel{s}{\longrightarrow }Y$
in
$X\stackrel{s}{\longrightarrow }Y$
in
![]() ${\mathcal{C}}$
, with
${\mathcal{C}}$
, with
![]() $X,Y\in {\mathcal{C}}(T)$
such that
$X,Y\in {\mathcal{C}}(T)$
such that
![]() ${\mathcal{C}}(T,s)\simeq f$
. Complete it to a triangle
${\mathcal{C}}(T,s)\simeq f$
. Complete it to a triangle
![]() $Z\stackrel{u}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{v}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
$Z\stackrel{u}{\longrightarrow }X\stackrel{s}{\longrightarrow }Y\stackrel{v}{\longrightarrow }\unicode[STIX]{x1D6F4}Z$
in
![]() ${\mathcal{C}}$
. Then,
${\mathcal{C}}$
. Then,
![]() $v\in (T^{\bot })$
since
$v\in (T^{\bot })$
since
![]() $f$
is an epimorphism, and
$f$
is an epimorphism, and
![]() ${\mathcal{C}}(T,u)$
factors through
${\mathcal{C}}(T,u)$
factors through
![]() $B$
since
$B$
since
![]() $su=0$
. Lemma 3.8 shows that
$su=0$
. Lemma 3.8 shows that
![]() $Z$
lies in
$Z$
lies in
![]() ${\mathcal{C}}(T)$
, and we can apply Lemma 3.9 to conclude that
${\mathcal{C}}(T)$
, and we can apply Lemma 3.9 to conclude that
![]() $u$
factors through
$u$
factors through
![]() $\overline{T}^{\bot }$
.◻
$\overline{T}^{\bot }$
.◻
Remark 3.12. Let
![]() $L\stackrel{g}{\longrightarrow }M\stackrel{f}{\longrightarrow }N$
be exact in an abelian category. Assume that the morphism
$L\stackrel{g}{\longrightarrow }M\stackrel{f}{\longrightarrow }N$
be exact in an abelian category. Assume that the morphism
![]() $g$
factors as
$g$
factors as
![]() $u\circ v$
through some object
$u\circ v$
through some object
![]() $B$
. Then, the kernel of
$B$
. Then, the kernel of
![]() $f$
is isomorphic to a quotient of a subobject of
$f$
is isomorphic to a quotient of a subobject of
![]() $B$
.
$B$
.
Proof. Let
![]() $K\stackrel{i}{\rightarrow }M$
be a kernel for
$K\stackrel{i}{\rightarrow }M$
be a kernel for
![]() $f$
. Since the sequence is exact, there is an epimorphism
$f$
. Since the sequence is exact, there is an epimorphism
![]() $L\stackrel{g^{\prime }}{\longrightarrow }K$
such that
$L\stackrel{g^{\prime }}{\longrightarrow }K$
such that
![]() $ig^{\prime }=g$
. The morphism
$ig^{\prime }=g$
. The morphism
![]() $v$
factors as in the following diagram:
$v$
factors as in the following diagram:

The composition
![]() $fujp=fg$
vanishes, so that
$fujp=fg$
vanishes, so that
![]() $fuj=0$
, and there is some
$fuj=0$
, and there is some
![]() $B^{\prime }\stackrel{q}{\longrightarrow }K$
so that
$B^{\prime }\stackrel{q}{\longrightarrow }K$
so that
![]() $iq=uj$
. It remains to show that
$iq=uj$
. It remains to show that
![]() $q$
is an epimorphism. Since
$q$
is an epimorphism. Since
![]() $i$
is a monomorphism, the equalities
$i$
is a monomorphism, the equalities
![]() $iqp=ujp=g=ig^{\prime }$
imply
$iqp=ujp=g=ig^{\prime }$
imply
![]() $qp=g^{\prime }$
. Since the morphism
$qp=g^{\prime }$
. Since the morphism
![]() $g^{\prime }$
is an epimorphism,
$g^{\prime }$
is an epimorphism,
![]() $q$
is an epimorphism also.◻
$q$
is an epimorphism also.◻
Proposition 3.13. The functor
![]() $F$
is full.
$F$
is full.
Proof. Let
![]() $X\in \overline{{\mathcal{C}}}(T)$
. Then, there is a triangle
$X\in \overline{{\mathcal{C}}}(T)$
. Then, there is a triangle
![]() $\overline{T}_{1}\stackrel{\unicode[STIX]{x1D6FD}}{\longrightarrow }T_{0}\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D6FE}}{\longrightarrow }\unicode[STIX]{x1D6F4}\overline{T}_{1}$
in
$\overline{T}_{1}\stackrel{\unicode[STIX]{x1D6FD}}{\longrightarrow }T_{0}\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X\stackrel{\unicode[STIX]{x1D6FE}}{\longrightarrow }\unicode[STIX]{x1D6F4}\overline{T}_{1}$
in
![]() ${\mathcal{C}}$
. Consider a hook diagram
${\mathcal{C}}$
. Consider a hook diagram

in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
, with
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
, with
![]() $U,V\in {\mathcal{C}}(T)$
and
$U,V\in {\mathcal{C}}(T)$
and
![]() ${\mathcal{C}}(T,s)\in {\mathcal{S}}_{{\mathcal{B}},0}$
. Let us prove that the morphism
${\mathcal{C}}(T,s)\in {\mathcal{S}}_{{\mathcal{B}},0}$
. Let us prove that the morphism
![]() ${\mathcal{C}}(T,f)$
lifts through the morphism
${\mathcal{C}}(T,f)$
lifts through the morphism
![]() ${\mathcal{C}}(T,s)$
. The proof of Lemma 3.11 shows that
${\mathcal{C}}(T,s)$
. The proof of Lemma 3.11 shows that
![]() $s$
belongs to
$s$
belongs to
![]() $\widetilde{{\mathcal{S}}}$
. We thus have a triangle
$\widetilde{{\mathcal{S}}}$
. We thus have a triangle
![]() $W\stackrel{g}{\longrightarrow }U\stackrel{s}{\longrightarrow }V\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}U$
in
$W\stackrel{g}{\longrightarrow }U\stackrel{s}{\longrightarrow }V\stackrel{h}{\longrightarrow }\unicode[STIX]{x1D6F4}U$
in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $g\in (\overline{T}^{\bot })$
and
$g\in (\overline{T}^{\bot })$
and
![]() $h\in (T^{\bot })$
. The composition
$h\in (T^{\bot })$
. The composition
![]() $hf\unicode[STIX]{x1D6FC}$
vanishes, so that
$hf\unicode[STIX]{x1D6FC}$
vanishes, so that
![]() $f$
induces a morphism of triangles
$f$
induces a morphism of triangles

The morphism
![]() $g$
factors through
$g$
factors through
![]() $\overline{T}^{\bot }$
, so that the composition
$\overline{T}^{\bot }$
, so that the composition
![]() $ga$
is zero, giving the existence of a morphism
$ga$
is zero, giving the existence of a morphism
![]() $b$
such that
$b$
such that
![]() $hb=v$
. The equalities
$hb=v$
. The equalities
![]() $hf=v\unicode[STIX]{x1D6FE}=hb\unicode[STIX]{x1D6FE}$
imply the existence of a morphism
$hf=v\unicode[STIX]{x1D6FE}=hb\unicode[STIX]{x1D6FE}$
imply the existence of a morphism
![]() $c$
such that
$c$
such that
![]() $f=b\unicode[STIX]{x1D6FE}+sc$
. Therefore,
$f=b\unicode[STIX]{x1D6FE}+sc$
. Therefore,
![]() ${\mathcal{C}}(T,s)\circ {\mathcal{C}}(T,c)={\mathcal{C}}(T,f)$
. We can conclude by induction on the number of hooks in a morphism from
${\mathcal{C}}(T,s)\circ {\mathcal{C}}(T,c)={\mathcal{C}}(T,f)$
. We can conclude by induction on the number of hooks in a morphism from
![]() ${\mathcal{C}}(T,X)$
to
${\mathcal{C}}(T,X)$
to
![]() ${\mathcal{C}}(T,Y)$
.◻
${\mathcal{C}}(T,Y)$
.◻
We write
![]() $U$
for
$U$
for
![]() ${\mathcal{C}}(T,\overline{T})$
. Define
${\mathcal{C}}(T,\overline{T})$
. Define
![]() $\overline{\unicode[STIX]{x1D6EC}}$
to be the endomorphism algebra of
$\overline{\unicode[STIX]{x1D6EC}}$
to be the endomorphism algebra of
![]() $U$
in
$U$
in
![]() $\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then,
$\operatorname{mod}\unicode[STIX]{x1D6EC}$
. Then,
![]() $\overline{\unicode[STIX]{x1D6EC}}\simeq \operatorname{End}_{{\mathcal{C}}}(\overline{T})$
.
$\overline{\unicode[STIX]{x1D6EC}}\simeq \operatorname{End}_{{\mathcal{C}}}(\overline{T})$
.
Lemma 3.14. The diagram

commutes up to a natural isomorphism.
Proof. For any
![]() $X\in \overline{{\mathcal{C}}}(T)$
, define a map
$X\in \overline{{\mathcal{C}}}(T)$
, define a map
![]() $\unicode[STIX]{x1D711}_{X}:{\mathcal{C}}(\overline{T},X)\longrightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6EC}}({\mathcal{C}}(T,\overline{T}),$
$\unicode[STIX]{x1D711}_{X}:{\mathcal{C}}(\overline{T},X)\longrightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6EC}}({\mathcal{C}}(T,\overline{T}),$
![]() ${\mathcal{C}}(T,X))$
by
${\mathcal{C}}(T,X))$
by
![]() $\unicode[STIX]{x1D711}_{X}(\unicode[STIX]{x1D6FC})={\mathcal{C}}(T,\unicode[STIX]{x1D6FC})$
. Then,
$\unicode[STIX]{x1D711}_{X}(\unicode[STIX]{x1D6FC})={\mathcal{C}}(T,\unicode[STIX]{x1D6FC})$
. Then,
![]() $\unicode[STIX]{x1D711}_{X}$
is
$\unicode[STIX]{x1D711}_{X}$
is
![]() $\overline{\unicode[STIX]{x1D6EC}}$
-linear, since
$\overline{\unicode[STIX]{x1D6EC}}$
-linear, since
![]() ${\mathcal{C}}(T,-)$
is a covariant functor, and it is an isomorphism, since
${\mathcal{C}}(T,-)$
is a covariant functor, and it is an isomorphism, since
![]() ${\mathcal{C}}(T,-):\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
is fully faithful. The transformation
${\mathcal{C}}(T,-):\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}\overline{T})\rightarrow \operatorname{mod}\unicode[STIX]{x1D6EC}$
is fully faithful. The transformation
![]() $\unicode[STIX]{x1D711}$
is easily seen to be natural. Let
$\unicode[STIX]{x1D711}$
is easily seen to be natural. Let
![]() $X\stackrel{f}{\longrightarrow }Y$
be a morphism in
$X\stackrel{f}{\longrightarrow }Y$
be a morphism in
![]() ${\mathcal{C}}$
. Write
${\mathcal{C}}$
. Write
![]() $f_{\ast }$
for the image of
$f_{\ast }$
for the image of
![]() $f$
under the functor
$f$
under the functor
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)\circ {\mathcal{C}}(T,-)$
. We have to check that
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)\circ {\mathcal{C}}(T,-)$
. We have to check that
![]() $\unicode[STIX]{x1D711}_{Y}\circ {\mathcal{C}}(\overline{T},f)=f_{\ast }\circ \unicode[STIX]{x1D711}_{X}$
. The left-hand side of this equality sends a morphism
$\unicode[STIX]{x1D711}_{Y}\circ {\mathcal{C}}(\overline{T},f)=f_{\ast }\circ \unicode[STIX]{x1D711}_{X}$
. The left-hand side of this equality sends a morphism
![]() $\overline{T}\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X$
to the map sending
$\overline{T}\stackrel{\unicode[STIX]{x1D6FC}}{\longrightarrow }X$
to the map sending
![]() $u\in {\mathcal{C}}(T,\overline{T})$
to
$u\in {\mathcal{C}}(T,\overline{T})$
to
![]() $(f\circ \unicode[STIX]{x1D6FC})\circ u$
, while the right-hand side sends
$(f\circ \unicode[STIX]{x1D6FC})\circ u$
, while the right-hand side sends
![]() $\unicode[STIX]{x1D6FC}$
to
$\unicode[STIX]{x1D6FC}$
to
![]() $u\mapsto f\circ (\unicode[STIX]{x1D6FC}\circ u)$
.◻
$u\mapsto f\circ (\unicode[STIX]{x1D6FC}\circ u)$
.◻
Lemma 3.15. The functor
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)$
induces a functor
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,-)$
induces a functor
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}\longrightarrow \operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
.
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}\longrightarrow \operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
.
Proof. Suppose that the morphism
![]() $f={\mathcal{C}}(T,s)$
lies in
$f={\mathcal{C}}(T,s)$
lies in
![]() ${\mathcal{S}}_{{\mathcal{B}},0}$
. Then,
${\mathcal{S}}_{{\mathcal{B}},0}$
. Then,
![]() $s$
belongs to
$s$
belongs to
![]() $\widetilde{{\mathcal{S}}}$
by Lemma 3.11. In particular,
$\widetilde{{\mathcal{S}}}$
by Lemma 3.11. In particular,
![]() $s$
is part of a triangle
$s$
is part of a triangle
![]() $(r,s,t)$
with
$(r,s,t)$
with
![]() $r,t\in (\overline{T}^{\bot })$
, so that
$r,t\in (\overline{T}^{\bot })$
, so that
![]() ${\mathcal{C}}(\overline{T},s)$
is an isomorphism (as proved in [Reference Buan and MarshBM13, Lemma 2.5]). Hence, by Lemma 3.14,
${\mathcal{C}}(\overline{T},s)$
is an isomorphism (as proved in [Reference Buan and MarshBM13, Lemma 2.5]). Hence, by Lemma 3.14,
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,f)$
is an isomorphism.◻
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(U,f)$
is an isomorphism.◻
Proposition 3.16. The functor
![]() $\overline{F}$
is faithful.
$\overline{F}$
is faithful.
Proof. Assume that
![]() $Fu=Fv$
for some
$Fu=Fv$
for some
![]() $u,v:X\rightarrow Y$
in
$u,v:X\rightarrow Y$
in
![]() $\overline{{\mathcal{C}}}(T)$
. Then, Lemmas 3.14 and 3.15 imply
$\overline{{\mathcal{C}}}(T)$
. Then, Lemmas 3.14 and 3.15 imply
![]() ${\mathcal{C}}(\overline{T},u)={\mathcal{C}}(\overline{T},v)$
, and [Reference Buan and MarshBM13, Lemma 2.3] implies
${\mathcal{C}}(\overline{T},u)={\mathcal{C}}(\overline{T},v)$
, and [Reference Buan and MarshBM13, Lemma 2.3] implies
![]() $u-v\in (\overline{T}^{\bot })$
. Since
$u-v\in (\overline{T}^{\bot })$
. Since
![]() $X$
belongs to
$X$
belongs to
![]() $\overline{{\mathcal{C}}}(T)=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
, there is a triangle
$\overline{{\mathcal{C}}}(T)=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
, there is a triangle
![]() $\overline{T}_{\unicode[STIX]{x1D6FC}}\stackrel{w}{\rightarrow }X\rightarrow \unicode[STIX]{x1D6F4}T_{\unicode[STIX]{x1D6FD}}^{\prime }\rightarrow$
, with
$\overline{T}_{\unicode[STIX]{x1D6FC}}\stackrel{w}{\rightarrow }X\rightarrow \unicode[STIX]{x1D6F4}T_{\unicode[STIX]{x1D6FD}}^{\prime }\rightarrow$
, with
![]() $\overline{T}_{\unicode[STIX]{x1D6FC}}\in \operatorname{add}\overline{T}$
and
$\overline{T}_{\unicode[STIX]{x1D6FC}}\in \operatorname{add}\overline{T}$
and
![]() $T_{\unicode[STIX]{x1D6FD}}^{\prime }\in \operatorname{add}T^{\prime }$
. The composition
$T_{\unicode[STIX]{x1D6FD}}^{\prime }\in \operatorname{add}T^{\prime }$
. The composition
![]() $(u-v)w$
vanishes, so that
$(u-v)w$
vanishes, so that
![]() $u-v\in (\unicode[STIX]{x1D6F4}T^{\prime })$
, and the functor
$u-v\in (\unicode[STIX]{x1D6F4}T^{\prime })$
, and the functor
![]() $\overline{F}$
is faithful.◻
$\overline{F}$
is faithful.◻
3.3 More localizations
In this section, we prove, under the assumptions as in Section 1, that the localizations
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
and
${\mathcal{C}}_{{\mathcal{S}}}$
and
![]() ${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
are isomorphic. We note that this result does not seem to follow easily from Lemma 3.11, as one would expect by analogy with [Reference Buan and MarshBM13, Section 4].
${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
are isomorphic. We note that this result does not seem to follow easily from Lemma 3.11, as one would expect by analogy with [Reference Buan and MarshBM13, Section 4].
Lemma 3.17. The full subcategory
![]() $\overline{{\mathcal{C}}}(T)$
of
$\overline{{\mathcal{C}}}(T)$
of
![]() ${\mathcal{C}}$
is stable under taking direct summands.
${\mathcal{C}}$
is stable under taking direct summands.
Proof. Let
![]() $X,X^{\prime }\in {\mathcal{C}}$
be so that
$X,X^{\prime }\in {\mathcal{C}}$
be so that
![]() $X\oplus X^{\prime }$
belongs to
$X\oplus X^{\prime }$
belongs to
![]() $\overline{{\mathcal{C}}}(T)$
. Let
$\overline{{\mathcal{C}}}(T)$
. Let
![]() $U_{0}\rightarrow X$
,
$U_{0}\rightarrow X$
,
![]() $V_{0}\rightarrow X^{\prime }$
be minimal right
$V_{0}\rightarrow X^{\prime }$
be minimal right
![]() $\operatorname{add}T$
-approximations. Then,
$\operatorname{add}T$
-approximations. Then,
![]() $U_{0}\oplus V_{0}\rightarrow X\oplus X^{\prime }$
is a minimal right
$U_{0}\oplus V_{0}\rightarrow X\oplus X^{\prime }$
is a minimal right
![]() $\operatorname{add}T$
-approximation. When completing it to a triangle
$\operatorname{add}T$
-approximation. When completing it to a triangle
![]() $W\rightarrow U_{0}\oplus V_{0}\rightarrow X\oplus X^{\prime }\rightarrow$
, we thus have
$W\rightarrow U_{0}\oplus V_{0}\rightarrow X\oplus X^{\prime }\rightarrow$
, we thus have
![]() $W\in \operatorname{add}\overline{T}$
. The nine lemma gives a commutative diagram whose rows and columns are triangles in
$W\in \operatorname{add}\overline{T}$
. The nine lemma gives a commutative diagram whose rows and columns are triangles in
![]() ${\mathcal{C}}$
:
${\mathcal{C}}$
:

We want to show that the triangle in the second row splits, which would then imply that
![]() $U_{1}$
and
$U_{1}$
and
![]() $V_{1}$
, being summands of
$V_{1}$
, being summands of
![]() $W$
, belong to
$W$
, belong to
![]() $\operatorname{add}\overline{T}$
. The composition
$\operatorname{add}\overline{T}$
. The composition
![]() $\unicode[STIX]{x1D6F4}^{-1}X^{\prime }\rightarrow V_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{1}$
is zero, so that the morphism
$\unicode[STIX]{x1D6F4}^{-1}X^{\prime }\rightarrow V_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{1}$
is zero, so that the morphism
![]() $V_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{1}$
factors through
$V_{1}\rightarrow \unicode[STIX]{x1D6F4}U_{1}$
factors through
![]() $V_{1}\rightarrow V_{0}$
. However, there are no non-zero morphisms from
$V_{1}\rightarrow V_{0}$
. However, there are no non-zero morphisms from
![]() $V_{0}$
to
$V_{0}$
to
![]() $\unicode[STIX]{x1D6F4}U_{1}$
, since
$\unicode[STIX]{x1D6F4}U_{1}$
, since
![]() $V_{0}\in \operatorname{add}T$
, and
$V_{0}\in \operatorname{add}T$
, and
![]() $\unicode[STIX]{x1D6F4}U_{1}$
is the cone of the right
$\unicode[STIX]{x1D6F4}U_{1}$
is the cone of the right
![]() $\operatorname{add}T$
-approximation
$\operatorname{add}T$
-approximation
![]() $U_{0}\rightarrow X$
.◻
$U_{0}\rightarrow X$
.◻
Lemma 3.18. Let
![]() $X$
and
$X$
and
![]() $Y$
be objects in
$Y$
be objects in
![]() $\overline{{\mathcal{C}}}(T)$
, and let
$\overline{{\mathcal{C}}}(T)$
, and let
![]() $X\stackrel{s}{\longrightarrow }Y$
be a morphism in
$X\stackrel{s}{\longrightarrow }Y$
be a morphism in
![]() $\widetilde{{\mathcal{S}}}$
. Then, there exist
$\widetilde{{\mathcal{S}}}$
. Then, there exist
![]() $\overline{U}\in \operatorname{add}\overline{T}$
, and morphisms
$\overline{U}\in \operatorname{add}\overline{T}$
, and morphisms
![]() $\unicode[STIX]{x1D6F4}\overline{U}\stackrel{c}{\longrightarrow }Y$
,
$\unicode[STIX]{x1D6F4}\overline{U}\stackrel{c}{\longrightarrow }Y$
,
![]() $Y\stackrel{a}{\longrightarrow }\unicode[STIX]{x1D6F4}\overline{U}$
and
$Y\stackrel{a}{\longrightarrow }\unicode[STIX]{x1D6F4}\overline{U}$
and
![]() $Y\stackrel{d}{\longrightarrow }X$
in
$Y\stackrel{d}{\longrightarrow }X$
in
![]() ${\mathcal{C}}$
such that
${\mathcal{C}}$
such that
(1) the morphism
 $X\oplus \unicode[STIX]{x1D6F4}\overline{U}\stackrel{[s\;c]}{\longrightarrow }Y$
is in
$X\oplus \unicode[STIX]{x1D6F4}\overline{U}\stackrel{[s\;c]}{\longrightarrow }Y$
is in
 ${\mathcal{S}}$
;
${\mathcal{S}}$
;(2) the image in
 ${\mathcal{C}}_{{\mathcal{S}}}$
of the morphism
${\mathcal{C}}_{{\mathcal{S}}}$
of the morphism
 $Y\stackrel{\left[\!\begin{smallmatrix}d\\ a\end{smallmatrix}\!\right]}{\longrightarrow }X\oplus \unicode[STIX]{x1D6F4}\overline{U}$
is inverse to
$Y\stackrel{\left[\!\begin{smallmatrix}d\\ a\end{smallmatrix}\!\right]}{\longrightarrow }X\oplus \unicode[STIX]{x1D6F4}\overline{U}$
is inverse to
 $[s\;c]$
.
$[s\;c]$
.
In particular, all morphisms in
![]() $\overline{{\mathcal{C}}}(T)$
that belong to
$\overline{{\mathcal{C}}}(T)$
that belong to
![]() $\widetilde{{\mathcal{S}}}$
are inverted by the localization functor
$\widetilde{{\mathcal{S}}}$
are inverted by the localization functor
![]() $L_{{\mathcal{S}}}:{\mathcal{C}}\rightarrow {\mathcal{C}}_{{\mathcal{S}}}$
.
$L_{{\mathcal{S}}}:{\mathcal{C}}\rightarrow {\mathcal{C}}_{{\mathcal{S}}}$
.
Proof. Let
![]() $X\stackrel{s}{\rightarrow }Y$
be a morphism in
$X\stackrel{s}{\rightarrow }Y$
be a morphism in
![]() $\widetilde{{\mathcal{S}}}$
, with
$\widetilde{{\mathcal{S}}}$
, with
![]() $X$
and
$X$
and
![]() $Y$
in
$Y$
in
![]() $\overline{{\mathcal{C}}}(T)$
. Complete it to a triangle
$\overline{{\mathcal{C}}}(T)$
. Complete it to a triangle
![]() $X\stackrel{s}{\rightarrow }Y\stackrel{v}{\rightarrow }\unicode[STIX]{x1D6F4}Z\stackrel{u}{\rightarrow }\unicode[STIX]{x1D6F4}X$
. We first show how to define the object
$X\stackrel{s}{\rightarrow }Y\stackrel{v}{\rightarrow }\unicode[STIX]{x1D6F4}Z\stackrel{u}{\rightarrow }\unicode[STIX]{x1D6F4}X$
. We first show how to define the object
![]() $\overline{U}$
and the morphisms
$\overline{U}$
and the morphisms
![]() $a,c,d$
. By assumption, the morphisms
$a,c,d$
. By assumption, the morphisms
![]() $v$
and
$v$
and
![]() $u$
factor through
$u$
factor through
![]() $T^{\bot }$
and
$T^{\bot }$
and
![]() $(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
, respectively. There is a triangle
$(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
, respectively. There is a triangle
![]() $\overline{U}\rightarrow U\stackrel{\unicode[STIX]{x1D6FC}}{\rightarrow }Y\stackrel{a}{\rightarrow }\unicode[STIX]{x1D6F4}\overline{U}$
, with
$\overline{U}\rightarrow U\stackrel{\unicode[STIX]{x1D6FC}}{\rightarrow }Y\stackrel{a}{\rightarrow }\unicode[STIX]{x1D6F4}\overline{U}$
, with
![]() $U\in \operatorname{add}T$
and
$U\in \operatorname{add}T$
and
![]() $\overline{U}\in \operatorname{add}\overline{T}$
. Since
$\overline{U}\in \operatorname{add}\overline{T}$
. Since
![]() $v$
is in
$v$
is in
![]() $(T^{\bot })$
, the composition
$(T^{\bot })$
, the composition
![]() $v\unicode[STIX]{x1D6FC}$
vanishes, and there is a morphism
$v\unicode[STIX]{x1D6FC}$
vanishes, and there is a morphism
![]() $b$
as in the diagram below, such that
$b$
as in the diagram below, such that
![]() $v=ba$
.
$v=ba$
.

The composition
![]() $ub$
also vanishes since
$ub$
also vanishes since
![]() $u$
factors through
$u$
factors through
![]() $(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
. Therefore, there is a morphism
$(\unicode[STIX]{x1D6F4}\overline{T})^{\bot }$
. Therefore, there is a morphism
![]() $c$
such that
$c$
such that
![]() $b=vc$
. Moreover, there is a morphism
$b=vc$
. Moreover, there is a morphism
![]() $d$
such that
$d$
such that
![]() $1_{Y}=sd+ca$
. Indeed, we have the equalities
$1_{Y}=sd+ca$
. Indeed, we have the equalities
![]() $vca=ba=v$
, so that
$vca=ba=v$
, so that
![]() $1_{Y}-ca$
factors through
$1_{Y}-ca$
factors through
![]() $s$
. Hence, the morphism
$s$
. Hence, the morphism
![]() $[s~c]:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow Y$
is a retraction.
$[s~c]:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow Y$
is a retraction.
Applying the octahedral axiom to the composition
yields the following commutative diagram whose rows and columns are triangles in
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.

Since
![]() $[s~c]$
is a retraction, the triangle in the lower row splits, and the morphism
$[s~c]$
is a retraction, the triangle in the lower row splits, and the morphism
![]() $\unicode[STIX]{x1D6F4}^{-1}Y\rightarrow Z^{\prime }$
is zero. Let
$\unicode[STIX]{x1D6F4}^{-1}Y\rightarrow Z^{\prime }$
is zero. Let
![]() $p$
be a morphism from
$p$
be a morphism from
![]() $\overline{T}$
to
$\overline{T}$
to
![]() $Z$
. Since
$Z$
. Since
![]() $s\in \widetilde{{\mathcal{S}}}$
,
$s\in \widetilde{{\mathcal{S}}}$
,
![]() $g$
factors through
$g$
factors through
![]() $\overline{T}^{\bot }$
, so
$\overline{T}^{\bot }$
, so
![]() $gp=0$
and therefore
$gp=0$
and therefore
![]() $p$
factors through
$p$
factors through
![]() $f$
. Since
$f$
. Since
![]() $kf=0$
,
$kf=0$
,
![]() $f$
factors through
$f$
factors through
![]() $h$
, and therefore
$h$
, and therefore
![]() $p$
factors through
$p$
factors through
![]() $h$
. Applying the functor
$h$
. Applying the functor
![]() ${\mathcal{C}}(\overline{T},-)$
to the triangle
${\mathcal{C}}(\overline{T},-)$
to the triangle
![]() $\overline{U}\rightarrow Z\rightarrow Z^{\prime }\rightarrow \unicode[STIX]{x1D6F4}\overline{U}$
gives
$\overline{U}\rightarrow Z\rightarrow Z^{\prime }\rightarrow \unicode[STIX]{x1D6F4}\overline{U}$
gives
![]() $Z^{\prime }\in \overline{T}^{\bot }$
. We have thus constructed a triangle
$Z^{\prime }\in \overline{T}^{\bot }$
. We have thus constructed a triangle
in
![]() ${\mathcal{C}}$
, where
${\mathcal{C}}$
, where
![]() $Z^{\prime }$
belongs to
$Z^{\prime }$
belongs to
![]() $\overline{T}^{\bot }$
. This implies (1).
$\overline{T}^{\bot }$
. This implies (1).
We now check (2). We have
![]() $[s\;c][\!\begin{smallmatrix}d\\ a\end{smallmatrix}\!]=1_{Y}$
in
$[s\;c][\!\begin{smallmatrix}d\\ a\end{smallmatrix}\!]=1_{Y}$
in
![]() ${\mathcal{C}}$
. Since
${\mathcal{C}}$
. Since
![]() $[s\;c]$
lies in
$[s\;c]$
lies in
![]() ${\mathcal{S}}$
by (1), it is invertible in
${\mathcal{S}}$
by (1), it is invertible in
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
, and (2) follows.
${\mathcal{C}}_{{\mathcal{S}}}$
, and (2) follows.
Finally, we check the last part of the statement. Let
![]() $\unicode[STIX]{x1D70B}:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow X$
be the first projection. Extending
$\unicode[STIX]{x1D70B}:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow X$
be the first projection. Extending
![]() $\unicode[STIX]{x1D70B}$
to a triangle in
$\unicode[STIX]{x1D70B}$
to a triangle in
![]() ${\mathcal{C}}$
, we have
${\mathcal{C}}$
, we have
Since
![]() $\unicode[STIX]{x1D6F4}\overline{U}\in \overline{T}^{\bot }$
, and the zero map factors through
$\unicode[STIX]{x1D6F4}\overline{U}\in \overline{T}^{\bot }$
, and the zero map factors through
![]() $T^{\bot }$
, we see that
$T^{\bot }$
, we see that
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{S}}$
. Furthermore,
$\unicode[STIX]{x1D70B}\in {\mathcal{S}}$
. Furthermore,
![]() $s\unicode[STIX]{x1D70B}=[s\,0]:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow Y$
, so
$s\unicode[STIX]{x1D70B}=[s\,0]:X\oplus \unicode[STIX]{x1D6F4}\overline{U}\rightarrow Y$
, so
![]() $s\unicode[STIX]{x1D70B}-[s\,c]=[0,-c]$
factors through
$s\unicode[STIX]{x1D70B}-[s\,c]=[0,-c]$
factors through
![]() $\unicode[STIX]{x1D6F4}\overline{U}$
, where
$\unicode[STIX]{x1D6F4}\overline{U}$
, where
![]() $\unicode[STIX]{x1D6F4}\overline{U}$
lies in
$\unicode[STIX]{x1D6F4}\overline{U}$
lies in
![]() $\unicode[STIX]{x1D6F4}T^{\prime }$
. Morphisms of the form
$\unicode[STIX]{x1D6F4}T^{\prime }$
. Morphisms of the form
![]() $A\oplus V\stackrel{[1\,0]}{\longrightarrow }A$
, with
$A\oplus V\stackrel{[1\,0]}{\longrightarrow }A$
, with
![]() $V\in \overline{T}^{\bot }$
, lie in
$V\in \overline{T}^{\bot }$
, lie in
![]() ${\mathcal{S}}$
. Hence, as in [Reference Buan and MarshBM13, Lemma 3.5],
${\mathcal{S}}$
. Hence, as in [Reference Buan and MarshBM13, Lemma 3.5],
![]() $L_{{\mathcal{S}}}(s)L_{{\mathcal{S}}}(\unicode[STIX]{x1D70B})=L_{{\mathcal{S}}}([s\,c])$
. Since
$L_{{\mathcal{S}}}(s)L_{{\mathcal{S}}}(\unicode[STIX]{x1D70B})=L_{{\mathcal{S}}}([s\,c])$
. Since
![]() $\unicode[STIX]{x1D70B},[s\,c]$
both lie in
$\unicode[STIX]{x1D70B},[s\,c]$
both lie in
![]() ${\mathcal{S}}$
, their images under
${\mathcal{S}}$
, their images under
![]() $L_{{\mathcal{S}}}$
are invertible in
$L_{{\mathcal{S}}}$
are invertible in
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
, and it follows that the image
${\mathcal{C}}_{{\mathcal{S}}}$
, and it follows that the image
![]() $L_{{\mathcal{S}}}(s)$
is also invertible in
$L_{{\mathcal{S}}}(s)$
is also invertible in
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
, as required.◻
${\mathcal{C}}_{{\mathcal{S}}}$
, as required.◻
For a morphism
![]() $f$
that is part of a triangle
$f$
that is part of a triangle
![]() $Z\stackrel{g}{\rightarrow }X\stackrel{f}{\rightarrow }Y\stackrel{h}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
, recall that
$Z\stackrel{g}{\rightarrow }X\stackrel{f}{\rightarrow }Y\stackrel{h}{\rightarrow }\unicode[STIX]{x1D6F4}Z$
, recall that
![]() $f$
belongs to the collection
$f$
belongs to the collection
![]() ${\mathcal{S}}$
if and only if
${\mathcal{S}}$
if and only if
![]() $Z$
belongs to
$Z$
belongs to
![]() $\overline{T}^{\bot }$
, and
$\overline{T}^{\bot }$
, and
![]() $h$
factors through
$h$
factors through
![]() $T^{\bot }$
, and that
$T^{\bot }$
, and that
![]() $f$
belongs to
$f$
belongs to
![]() $\widetilde{{\mathcal{S}}}$
if and only if
$\widetilde{{\mathcal{S}}}$
if and only if
![]() $g$
factors through
$g$
factors through
![]() $\overline{T}^{\bot }$
, and
$\overline{T}^{\bot }$
, and
![]() $h$
factors through
$h$
factors through
![]() $T^{\bot }$
.
$T^{\bot }$
.
Theorem 3.19. There is an isomorphism of categories
Proof. As proved in Lemma 3.11, the categories
![]() ${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
and
${\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
and
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
are equivalent. By Theorem 3.2, the category
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
are equivalent. By Theorem 3.2, the category
![]() $(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
is equivalent to
$(\operatorname{mod}\unicode[STIX]{x1D6EC})_{{\mathcal{S}}_{{\mathcal{B}},0}}$
is equivalent to
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
.
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
.
It is easy to check that any morphism of the form
![]() $X\oplus U\stackrel{[1\,0]}{\longrightarrow }X$
, with
$X\oplus U\stackrel{[1\,0]}{\longrightarrow }X$
, with
![]() $U\in \overline{T}^{\bot }$
, lies in
$U\in \overline{T}^{\bot }$
, lies in
![]() ${\mathcal{S}}$
. Hence, arguing as in [Reference Buan and MarshBM13, Lemma 3.5], if
${\mathcal{S}}$
. Hence, arguing as in [Reference Buan and MarshBM13, Lemma 3.5], if
![]() $u,v$
are any morphisms in
$u,v$
are any morphisms in
![]() ${\mathcal{C}}$
such that
${\mathcal{C}}$
such that
![]() $v$
factors through
$v$
factors through
![]() $\overline{T}^{\bot }$
, then
$\overline{T}^{\bot }$
, then
![]() $L_{{\mathcal{S}}}(u)=L_{{\mathcal{S}}}(u+v)$
. It follows that
$L_{{\mathcal{S}}}(u)=L_{{\mathcal{S}}}(u+v)$
. It follows that
![]() $L_{{\mathcal{S}}}$
induces a functor from
$L_{{\mathcal{S}}}$
induces a functor from
![]() $\overline{{\mathcal{C}}}(T)/(\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime })$
to
$\overline{{\mathcal{C}}}(T)/(\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime })$
to
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
, which we also denote by
${\mathcal{C}}_{{\mathcal{S}}}$
, which we also denote by
![]() $L_{{\mathcal{S}}}$
. Since
$L_{{\mathcal{S}}}$
. Since
![]() $\widetilde{{\mathcal{S}}}$
contains
$\widetilde{{\mathcal{S}}}$
contains
![]() ${\mathcal{S}}$
, the same argument applies to
${\mathcal{S}}$
, the same argument applies to
![]() $L_{\widetilde{{\mathcal{S}}}}$
. Furthermore, by the universal property of localization, the left-hand side of the diagram
$L_{\widetilde{{\mathcal{S}}}}$
. Furthermore, by the universal property of localization, the left-hand side of the diagram

commutes, where the functor
![]() ${\mathcal{C}}_{{\mathcal{S}}}\rightarrow {\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
is the identity on objects. The right-hand triangle commutes by Lemma 3.11 and (3.1). It is thus enough to show that the functor
${\mathcal{C}}_{{\mathcal{S}}}\rightarrow {\mathcal{C}}_{\widetilde{{\mathcal{S}}}}$
is the identity on objects. The right-hand triangle commutes by Lemma 3.11 and (3.1). It is thus enough to show that the functor
![]() $L_{{\mathcal{S}}}:\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow {\mathcal{C}}_{{\mathcal{S}}}$
is an equivalence of categories.
$L_{{\mathcal{S}}}:\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })\rightarrow {\mathcal{C}}_{{\mathcal{S}}}$
is an equivalence of categories.
The functor
![]() $L_{{\mathcal{S}}}$
is dense by Lemma 2.2.
$L_{{\mathcal{S}}}$
is dense by Lemma 2.2.
We next check that
![]() $L_{{\mathcal{S}}}$
is full. Let
$L_{{\mathcal{S}}}$
is full. Let
![]() $X,Y$
be objects of
$X,Y$
be objects of
![]() $\overline{{\mathcal{C}}}(T)$
, and let
$\overline{{\mathcal{C}}}(T)$
, and let
![]() $s:X\rightarrow Y$
be a morphism in
$s:X\rightarrow Y$
be a morphism in
![]() ${\mathcal{S}}$
. By part (2) of Lemma 3.18,
${\mathcal{S}}$
. By part (2) of Lemma 3.18,
![]() $sd=1_{Y}-ca$
, where
$sd=1_{Y}-ca$
, where
![]() $ca$
factors through
$ca$
factors through
![]() $\overline{T}^{\bot }$
. Arguing as above, we have that
$\overline{T}^{\bot }$
. Arguing as above, we have that
![]() $L_{{\mathcal{S}}}(s)L_{{\mathcal{S}}}(d)=L_{S}(1_{Y})$
, so
$L_{{\mathcal{S}}}(s)L_{{\mathcal{S}}}(d)=L_{S}(1_{Y})$
, so
![]() $L_{{\mathcal{S}}}(d)=L_{{\mathcal{S}}}(s)^{-1}$
. It follows that
$L_{{\mathcal{S}}}(d)=L_{{\mathcal{S}}}(s)^{-1}$
. It follows that
![]() $L_{{\mathcal{S}}}$
(on
$L_{{\mathcal{S}}}$
(on
![]() $\overline{{\mathcal{C}}}(T)/(\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime })$
) is full.
$\overline{{\mathcal{C}}}(T)/(\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime })$
) is full.
It thus remains to prove that
![]() $L_{{\mathcal{S}}}$
is faithful. Via the use of the functor
$L_{{\mathcal{S}}}$
is faithful. Via the use of the functor
![]() ${\mathcal{C}}(\overline{T},-)$
and of the category
${\mathcal{C}}(\overline{T},-)$
and of the category
![]() $\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
, this follows from results in [Reference Buan and MarshBM13]. Recall that we write
$\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
, this follows from results in [Reference Buan and MarshBM13]. Recall that we write
![]() $\overline{\unicode[STIX]{x1D6EC}}$
for the endomorphism algebra of
$\overline{\unicode[STIX]{x1D6EC}}$
for the endomorphism algebra of
![]() $\overline{T}$
in
$\overline{T}$
in
![]() ${\mathcal{C}}$
. The functor
${\mathcal{C}}$
. The functor
![]() ${\mathcal{C}}(\overline{T},-)$
from
${\mathcal{C}}(\overline{T},-)$
from
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
to
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
to
![]() $\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
inverts all morphisms in
$\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
inverts all morphisms in
![]() ${\mathcal{S}}$
, as proved in [Reference Buan and MarshBM13, Lemma 2.4]. By the universal property of localizations, there is a (unique) functor
${\mathcal{S}}$
, as proved in [Reference Buan and MarshBM13, Lemma 2.4]. By the universal property of localizations, there is a (unique) functor
![]() ${\mathcal{C}}_{{\mathcal{S}}}\stackrel{F^{\prime }}{\longrightarrow }\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
such that
${\mathcal{C}}_{{\mathcal{S}}}\stackrel{F^{\prime }}{\longrightarrow }\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
such that
![]() ${\mathcal{C}}(\overline{T},-)=F^{\prime }L_{{\mathcal{S}}}$
. Assume that the image under
${\mathcal{C}}(\overline{T},-)=F^{\prime }L_{{\mathcal{S}}}$
. Assume that the image under
![]() $L_{{\mathcal{S}}}$
of a morphism
$L_{{\mathcal{S}}}$
of a morphism
![]() $f$
in
$f$
in
![]() $\overline{{\mathcal{C}}}(T)$
is zero. Then,
$\overline{{\mathcal{C}}}(T)$
is zero. Then,
![]() $F^{\prime }L_{{\mathcal{S}}}(f)=0$
, so that
$F^{\prime }L_{{\mathcal{S}}}(f)=0$
, so that
![]() ${\mathcal{C}}(\overline{T},f)$
is zero in
${\mathcal{C}}(\overline{T},f)$
is zero in
![]() $\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
. By [Reference Buan and MarshBM13, Lemma 2.3], this implies that
$\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
. By [Reference Buan and MarshBM13, Lemma 2.3], this implies that
![]() $f$
factors through
$f$
factors through
![]() $\overline{T}^{\bot }$
. Since
$\overline{T}^{\bot }$
. Since
![]() $X$
is in
$X$
is in
![]() $\overline{{\mathcal{C}}}(T)$
, this implies, by Lemma 2.3, that
$\overline{{\mathcal{C}}}(T)$
, this implies, by Lemma 2.3, that
![]() $f$
factors through
$f$
factors through
![]() $\overline{{\mathcal{C}}}(T)\cap \overline{T}^{\bot }$
, which is
$\overline{{\mathcal{C}}}(T)\cap \overline{T}^{\bot }$
, which is
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7. Therefore,
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
by Lemma 2.7. Therefore,
![]() $f$
is zero in
$f$
is zero in
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
, and the functor
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
, and the functor
![]() $L_{{\mathcal{S}}}$
is faithful.◻
$L_{{\mathcal{S}}}$
is faithful.◻
Remark 3.20. The reader might wonder why our proof makes a detour through the category
![]() $\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
. One might think of a more direct proof as follows. Since we have an inclusion
$\operatorname{mod}\overline{\unicode[STIX]{x1D6EC}}$
. One might think of a more direct proof as follows. Since we have an inclusion
![]() ${\mathcal{S}}\subseteq \widetilde{{\mathcal{S}}}$
, it is enough to prove that every morphism in
${\mathcal{S}}\subseteq \widetilde{{\mathcal{S}}}$
, it is enough to prove that every morphism in
![]() $\widetilde{{\mathcal{S}}}$
is inverted in
$\widetilde{{\mathcal{S}}}$
is inverted in
![]() ${\mathcal{C}}_{{\mathcal{S}}}$
. This should easily follow from Lemma 3.18. Let
${\mathcal{C}}_{{\mathcal{S}}}$
. This should easily follow from Lemma 3.18. Let
![]() $X\stackrel{f}{\longrightarrow }Y$
be a morphism in
$X\stackrel{f}{\longrightarrow }Y$
be a morphism in
![]() $\widetilde{{\mathcal{S}}}$
. Then, there is a commutative diagram
$\widetilde{{\mathcal{S}}}$
. Then, there is a commutative diagram

where
![]() $R_{0}X,R_{0}Y$
are in
$R_{0}X,R_{0}Y$
are in
![]() $\overline{{\mathcal{C}}}(T)$
, and
$\overline{{\mathcal{C}}}(T)$
, and
![]() $\unicode[STIX]{x1D702}_{X},\unicode[STIX]{x1D702}_{Y}$
are in
$\unicode[STIX]{x1D702}_{X},\unicode[STIX]{x1D702}_{Y}$
are in
![]() ${\mathcal{S}}$
. It thus only remains to be checked that the morphism
${\mathcal{S}}$
. It thus only remains to be checked that the morphism
![]() $f^{\prime }$
can be chosen in
$f^{\prime }$
can be chosen in
![]() $\widetilde{{\mathcal{S}}}$
. If so, Lemma 3.18 would imply that
$\widetilde{{\mathcal{S}}}$
. If so, Lemma 3.18 would imply that
![]() $f^{\prime }$
is inverted by
$f^{\prime }$
is inverted by
![]() $L_{{\mathcal{S}}}$
. Since
$L_{{\mathcal{S}}}$
. Since
![]() $\unicode[STIX]{x1D702}_{X}$
and
$\unicode[STIX]{x1D702}_{X}$
and
![]() $\unicode[STIX]{x1D702}_{Y}$
are in
$\unicode[STIX]{x1D702}_{Y}$
are in
![]() ${\mathcal{S}}$
,
${\mathcal{S}}$
,
![]() $f$
would also be inverted by
$f$
would also be inverted by
![]() $L_{{\mathcal{S}}}$
. The problem here is that even though it is easily checked that
$L_{{\mathcal{S}}}$
. The problem here is that even though it is easily checked that
![]() $\widetilde{{\mathcal{S}}}$
is stable under composition,
$\widetilde{{\mathcal{S}}}$
is stable under composition,
![]() $\widetilde{{\mathcal{S}}}$
does not seem to satisfy the two-out-of-three property.
$\widetilde{{\mathcal{S}}}$
does not seem to satisfy the two-out-of-three property.
4 Examples
4.1 Mutating a cluster-tilting object at a loop
We consider the triangulated orbit category
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
(see [Reference KellerKel05]). Its Auslander–Reiten (AR) quiver is depicted in Figure 1. Copies of a fundamental domain are indicated by dashed lines. Let
$D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
(see [Reference KellerKel05]). Its Auslander–Reiten (AR) quiver is depicted in Figure 1. Copies of a fundamental domain are indicated by dashed lines. Let
![]() $T$
be the direct sum
$T$
be the direct sum
![]() $a\oplus b\oplus c$
. Then,
$a\oplus b\oplus c$
. Then,
![]() $T$
is a cluster-tilting object with a loop at
$T$
is a cluster-tilting object with a loop at
![]() $c$
.
$c$
.

Figure 1. The AR quiver of
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
; Example 4.1.
$D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
; Example 4.1.
Let
![]() $T^{\prime }$
be the cluster-tilting object obtained by mutating
$T^{\prime }$
be the cluster-tilting object obtained by mutating
![]() $T$
at
$T$
at
![]() $c$
. Since there is a triangle
$c$
. Since there is a triangle
![]() $s\rightarrow b\oplus b\rightarrow c\rightarrow$
, we have
$s\rightarrow b\oplus b\rightarrow c\rightarrow$
, we have
![]() $T^{\prime }=a\oplus b\oplus s$
. The indecomposable objects lying in
$T^{\prime }=a\oplus b\oplus s$
. The indecomposable objects lying in
![]() $\overline{{\mathcal{C}}}(T)$
are encircled (recall that
$\overline{{\mathcal{C}}}(T)$
are encircled (recall that
![]() $\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
). The objects
$\overline{{\mathcal{C}}}(T)=T\ast \unicode[STIX]{x1D6F4}\overline{T}=\overline{T}\ast \unicode[STIX]{x1D6F4}T^{\prime }$
). The objects
![]() $a,b,c$
(respectively,
$a,b,c$
(respectively,
![]() $n,q,r$
) belong to
$n,q,r$
) belong to
![]() $\overline{{\mathcal{C}}}(T)$
since they are in
$\overline{{\mathcal{C}}}(T)$
since they are in
![]() $\operatorname{add}T$
(respectively
$\operatorname{add}T$
(respectively
![]() $\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
). The remaining encircled objects are in
$\operatorname{add}\unicode[STIX]{x1D6F4}T^{\prime }$
). The remaining encircled objects are in
![]() $\overline{{\mathcal{C}}}(T)$
since there are triangles
$\overline{{\mathcal{C}}}(T)$
since there are triangles
![]() $a\rightarrow c\rightarrow d\rightarrow$
,
$a\rightarrow c\rightarrow d\rightarrow$
,
![]() $b\rightarrow c\rightarrow e\rightarrow$
,
$b\rightarrow c\rightarrow e\rightarrow$
,
![]() $a\rightarrow b\rightarrow g\rightarrow$
,
$a\rightarrow b\rightarrow g\rightarrow$
,
![]() $a\rightarrow c\rightarrow h\rightarrow$
,
$a\rightarrow c\rightarrow h\rightarrow$
,
![]() $a\oplus a\rightarrow c\rightarrow i\rightarrow$
,
$a\oplus a\rightarrow c\rightarrow i\rightarrow$
,
![]() $a\oplus b\rightarrow c\rightarrow j\rightarrow$
,
$a\oplus b\rightarrow c\rightarrow j\rightarrow$
,
![]() $b\rightarrow c\rightarrow l$
and
$b\rightarrow c\rightarrow l$
and
![]() $a\oplus b\rightarrow c\rightarrow m\rightarrow$
. The other four indecomposable objects are not in
$a\oplus b\rightarrow c\rightarrow m\rightarrow$
. The other four indecomposable objects are not in
![]() $\overline{{\mathcal{C}}}(T)$
since
$\overline{{\mathcal{C}}}(T)$
since
![]() $s$
is the shift of
$s$
is the shift of
![]() $c$
, and there are triangles
$c$
, and there are triangles
![]() $c\rightarrow c\rightarrow f\rightarrow$
,
$c\rightarrow c\rightarrow f\rightarrow$
,
![]() $a\oplus c\rightarrow c\rightarrow k\rightarrow$
and
$a\oplus c\rightarrow c\rightarrow k\rightarrow$
and
![]() $b\oplus c\rightarrow c\rightarrow p\rightarrow$
.
$b\oplus c\rightarrow c\rightarrow p\rightarrow$
.
By Theorem 2.9, the categories
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D70F}T)$
are equivalent. These two categories are illustrated in Figure 2.
$\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D70F}T)$
are equivalent. These two categories are illustrated in Figure 2.
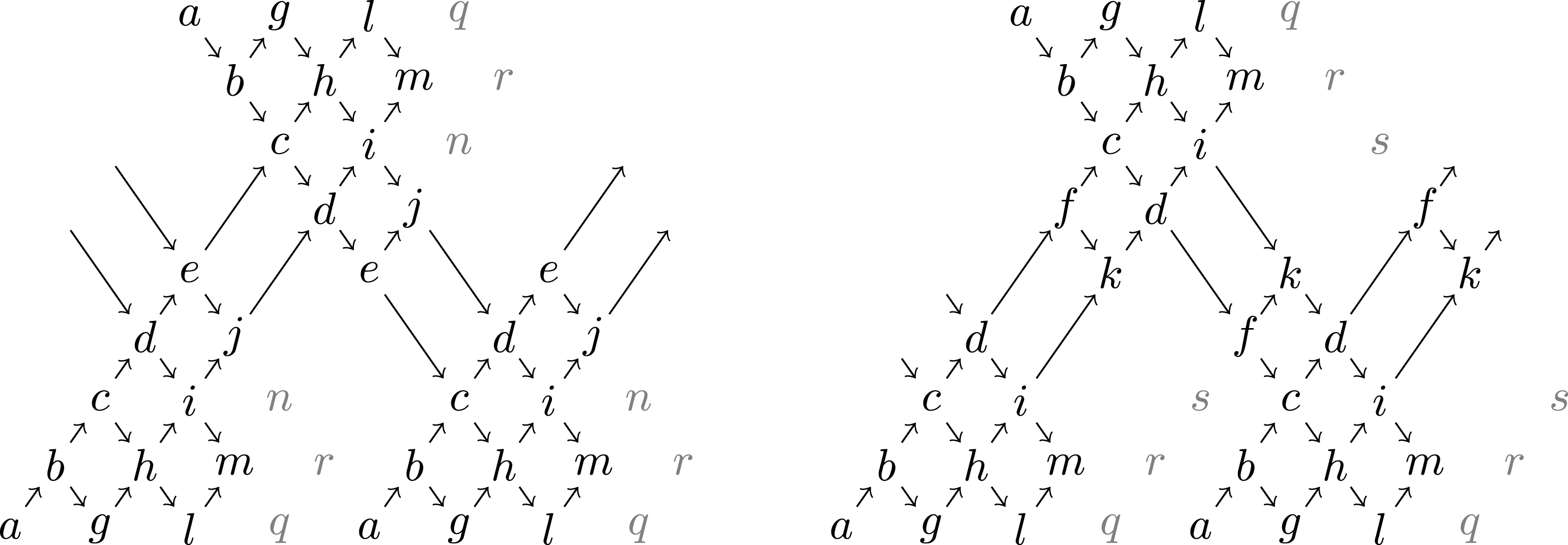
Figure 2. The categories
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D70F}T)$
; Example 4.1.
$\unicode[STIX]{x1D70F}\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D70F}T)$
; Example 4.1.
4.2 Mutating a rigid object at a loop
In the same category
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
as in the previous example, we now consider the rigid object
$D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
as in the previous example, we now consider the rigid object
![]() $T=a\oplus c$
. There is a triangle
$T=a\oplus c$
. There is a triangle
![]() $n\rightarrow a\oplus a\rightarrow c\rightarrow$
(see Figure 3), so that we can choose
$n\rightarrow a\oplus a\rightarrow c\rightarrow$
(see Figure 3), so that we can choose
![]() $T^{\prime }$
to be
$T^{\prime }$
to be
![]() $a\oplus n$
. Indecomposable objects in
$a\oplus n$
. Indecomposable objects in
![]() $\overline{{\mathcal{C}}}(T)$
are encircled. The shift of
$\overline{{\mathcal{C}}}(T)$
are encircled. The shift of
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $i\oplus q$
. Deleting either vertices labeled
$i\oplus q$
. Deleting either vertices labeled
![]() $a$
and
$a$
and
![]() $c$
, or vertices labeled
$c$
, or vertices labeled
![]() $i$
and
$i$
and
![]() $q$
, in the encircled part of the AR quiver yields isomorphic quivers, as depicted in Figure 4.
$q$
, in the encircled part of the AR quiver yields isomorphic quivers, as depicted in Figure 4.

Figure 3. The AR quiver of
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
; Example 4.2.
$D^{\text{b}}(\operatorname{mod}\text{A}_{9})/\unicode[STIX]{x1D70F}^{3}[1]$
; Example 4.2.

Figure 4. The categories
![]() $\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
$\overline{{\mathcal{C}}}(T)/(\unicode[STIX]{x1D6F4}T^{\prime })$
and
![]() $\overline{{\mathcal{C}}}(T)/(T)$
; Example 4.2.
$\overline{{\mathcal{C}}}(T)/(T)$
; Example 4.2.
4.3 Mutating at a non-indecomposable summand
In this example, we consider the triangulated orbit category
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{5})/\unicode[STIX]{x1D70F}^{-2}[1]$
(see [Reference KellerKel05]). It was shown in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06] that this category is a Krull–Schmidt, Hom-finite category with a Serre functor, and its AR quiver is depicted in Figure 5. As for the previous examples, we have not drawn the arrows. The two subquivers inside the dotted boxes have to be identified so as to match the two copies of
$D^{\text{b}}(\operatorname{mod}\text{A}_{5})/\unicode[STIX]{x1D70F}^{-2}[1]$
(see [Reference KellerKel05]). It was shown in [Reference Buan, Marsh, Reineke, Reiten and TodorovBMR+06] that this category is a Krull–Schmidt, Hom-finite category with a Serre functor, and its AR quiver is depicted in Figure 5. As for the previous examples, we have not drawn the arrows. The two subquivers inside the dotted boxes have to be identified so as to match the two copies of
![]() $a,b,c$
and
$a,b,c$
and
![]() $d$
. We choose rigid objects
$d$
. We choose rigid objects
![]() $T=a\oplus b\oplus c\oplus d$
and
$T=a\oplus b\oplus c\oplus d$
and
![]() $T^{\prime }=a\oplus b\oplus c^{\prime }\oplus d^{\prime }$
. Indecomposable objects in
$T^{\prime }=a\oplus b\oplus c^{\prime }\oplus d^{\prime }$
. Indecomposable objects in
![]() $\overline{{\mathcal{C}}}(T)$
are encircled. The indecomposable objects labeled
$\overline{{\mathcal{C}}}(T)$
are encircled. The indecomposable objects labeled
![]() $e,f,g,h$
are the shifts of
$e,f,g,h$
are the shifts of
![]() $a,b,c^{\prime },d^{\prime }$
, respectively. As predicted by Theorem 2.9, one obtains isomorphic quivers by deleting either vertices
$a,b,c^{\prime },d^{\prime }$
, respectively. As predicted by Theorem 2.9, one obtains isomorphic quivers by deleting either vertices
![]() $a,b,c,d$
or vertices
$a,b,c,d$
or vertices
![]() $e,f,g,h$
.
$e,f,g,h$
.
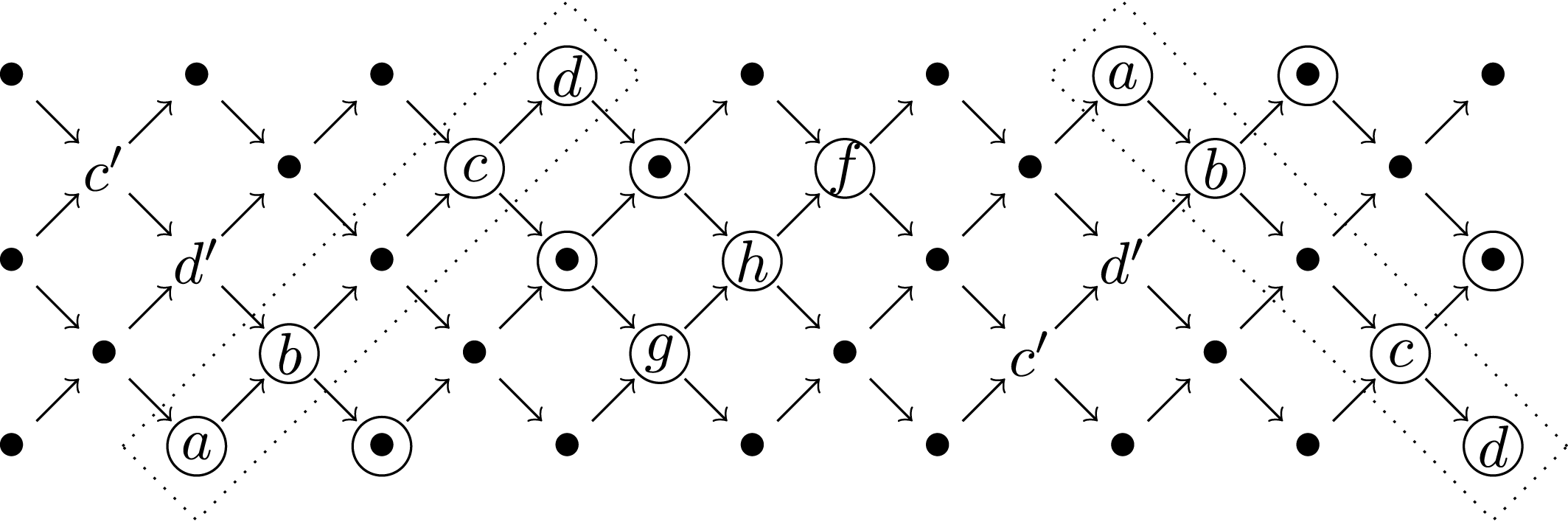
Figure 5. The AR quiver of
![]() $D^{\text{b}}(\operatorname{mod}\text{A}_{5})/\unicode[STIX]{x1D70F}^{-2}[1]$
; Example 4.3.
$D^{\text{b}}(\operatorname{mod}\text{A}_{5})/\unicode[STIX]{x1D70F}^{-2}[1]$
; Example 4.3.
Acknowledgments
The second author would like to thank the algebra team of the university of Leeds for a pleasant atmosphere when he was a postdoc there. Both authors are indebted to Apostolos Beligiannis for a preliminary version of [Reference BeligiannisBel13] which inspired the proofs of Section 2.1, and to Karin Baur who hosted their visits to the Institute for Mathematical Research (FIM) at the ETH Zürich, where this project was initiated. Both authors would like to thank an anonymous referee for a very careful reading, and gratefully acknowledge WuZhong Yang for raising an issue in our assumptions and for illustrating it with a clever example (see the remark above).