Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-30T23:29:52.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbations of norm-additive maps between continuous function spaces

Part of: Linear function spaces and their duals Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  10 October 2024

Longfa Sun  and
Yinghua Sun
Longfa Sun*
Affiliation:
Hebei Key Laboratory of Physics and Energy Technology, School of Mathematics and Physics, North China Electric Power University, Baoding, P. R. China
Yinghua Sun
Affiliation:
Hebei Key Laboratory of Physics and Energy Technology, School of Mathematics and Physics, North China Electric Power University, Baoding, P. R. China
*
Corresponding author: Longfa Sun, email: sun.longfa@ncepu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 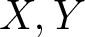$X, Y$ be two locally compact Hausdorff spaces and 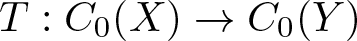$T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map, i.e.

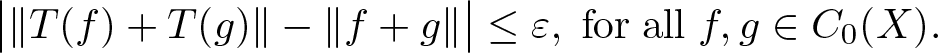\begin{equation*}\big|\|T(f)+T(g)\|-\|f+g\|\big|\leq \varepsilon,\;{\rm for\;all}\; f, g\in C_0(X).\end{equation*}

Then there exist a homeomorphism 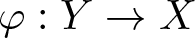$\varphi:Y\rightarrow X$ and a continuous function 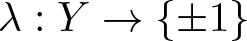$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that

\begin{equation*}|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).\end{equation*}

The estimate ‘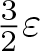$\frac{3}{2}\varepsilon$’ is optimal. And this result can be regarded as a new nonlinear extension of the Banach–Stone theorem.

Keywords

Banach–Stone theoremnorm-additive mapslinear isometriescontinuous function spacesstability

MSC classification

Primary: 46B04: Isometric theory of Banach spaces 46B20: Geometry and structure of normed linear spaces
Secondary: 46E15: Banach spaces of continuous, differentiable or analytic functions

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 4 , November 2024 , pp. 1099 - 1114
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amir, D., On isomorphisms of continuous function spaces, Israel J. Math. 3 (4) (1965), 205–210.CrossRefGoogle Scholar
Banach, S., Théorie des Opérations Lineaires Vol. 110, 2nd edn. (Chelsea Publishing Company, New York, 1963), .Google Scholar
Behrends, E., M-Structure and the Banach-Stone Theorem Vol. 736, 1st edn. Lecture Notes in Mathematics (Springer-Verlag Heidelberg, Berlin, 1979), .CrossRefGoogle Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric nonlinear functional analysis I. Amer. Math. Soc. Colloquium Publications, Volume 48 (Amer. Math. Soc, Providence, RI, 2000).Google Scholar
Cambern, M., A generalized Banach-Stone theorem, Proc. Amer. Math. Soc. 17 (2) (1966), 396–400.CrossRefGoogle Scholar
Cambern, M., On isomorphisms with small bound, Proc. Amer. Math. Soc. 18 (6) (1967), 1062–1066.CrossRefGoogle Scholar
Cambern, M., Isomorphisms of $C_0(Y)$ onto $C_0(X)$, Pacific J. Math. 35 (2) (1970), 307–312.CrossRefGoogle Scholar
Chen, L., Dong, Y. and Zheng, B., On norm-additive maps between the maximal groups of positive continuous functions, Result Math. 74 (2019), .CrossRefGoogle Scholar
Cohen, H. B., A bound-two isomorphism between C(X) Banach spaces, Proc. Amer. Math. Soc. 50 (1) (1975), 215–217.Google Scholar
Dong, Y., Li, L., Molnár, L. and Wong, N. -C., Transformations preserving the norm of means between positive cones of general and commutative $C^*$-algebras, J. Operator Theory 88 (2) (2022), 365–406.Google Scholar
Dutrieux, Y. and Kalton, N., Perturbations of isometries between C(K)-spaces, Studia Math. 166 (2) (2005), 181–197.CrossRefGoogle Scholar
Górak, R., Coarse version of the Banach-Stone theorem, J. Math. Anal. Appl. 377 (1) (2011), 406–413.CrossRefGoogle Scholar
Górak, R., Perturbations of isometries between Banach spaces, Studia Math. 207 (1) , 47–58.CrossRefGoogle Scholar
Galego, E. M. and , A. L. Porto da Silva, An optimal nonlinear extension of Banach-Stone theorem, J. Funct. Anal. 271 (8) (2016), 2166–2176.CrossRefGoogle Scholar
Garrido, M. I. and Jaramillo, J. A., Variations on the Banach-Stone theorem, Extracta Math. 17 (3) (2002), 351–383.Google Scholar
Hosseini, M. and Font, J. J., Real-linear isometries and jointly norm-additive maps on function algebras, Mediterr. J. Math. 13 (4) (2016), 1933–1948.CrossRefGoogle Scholar
Jarosz, K., Nonlinear generalizations of the Banach-Stone theorem, Studia Math. 93 (2) , 97–107.CrossRefGoogle Scholar
Mazur, S. and Ulam, S., Sur les transformations isométriques d’espaces vectoriels normés, C.R. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Molnár, L., Spectral characterization of Jordan-Segal isomorphisms of quantum observables, J. Operator Theory 83 (1) (2020), 179–195.CrossRefGoogle Scholar
Omladič, M. and , P. Šemrl, On non linear perturbations of isometries, Math. Ann. 303 (1) (1995), 617–628.CrossRefGoogle Scholar
Stone, M. H., Applications of the theory of Boolean rings to general topology, Trans. Amer. Math. Soc. 41 (3) (1937), 375–481.CrossRefGoogle Scholar
Tonev, T. and Yates, R., Norm-linear and norm-additive operators between uniform algebras, J. Math. Anal. Appl. 357 (1) (2009), 45–53.CrossRefGoogle Scholar
Vestfrid, I. A., Non-surjective coarse version of the Banach-Stone theorem, Ann. Funct. Anal. 11 (2020), 634–642.CrossRefGoogle Scholar