Article contents
Singular elliptic equations with nonlinearities of subcritical and critical growth
Published online by Cambridge University Press: 27 July 2022
Abstract
In this paper, we consider the problem $-\Delta u =-u^{-\beta }\chi _{\{u>0\}} + f(u)$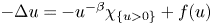 in $\Omega$
in $\Omega$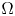 with $u=0$
with $u=0$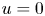 on $\partial \Omega$
on $\partial \Omega$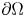 , where $0<\beta <1$
, where $0<\beta <1$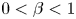 and $\Omega$
and $\Omega$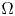 is a smooth bounded domain in $\mathbb {R}^{N}$
is a smooth bounded domain in $\mathbb {R}^{N}$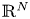 , $N\geq 2$
, $N\geq 2$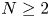 . We are able to solve this problem provided $f$
. We are able to solve this problem provided $f$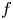 has subcritical growth and satisfy certain hypothesis. We also consider this problem with $f(s)=\lambda s+s^{\frac {N+2}{N-2}}$
has subcritical growth and satisfy certain hypothesis. We also consider this problem with $f(s)=\lambda s+s^{\frac {N+2}{N-2}}$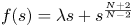 and $N\geq 3$
and $N\geq 3$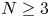 . In this case, we are able to obtain a solution for large values of $\lambda$
. In this case, we are able to obtain a solution for large values of $\lambda$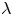 . We replace the singular function $u^{-\beta }$
. We replace the singular function $u^{-\beta }$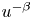 by a function $g_\epsilon (u)$
by a function $g_\epsilon (u)$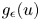 which pointwisely converges to $u^{-\beta }$
which pointwisely converges to $u^{-\beta }$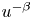 as $\epsilon \rightarrow 0$
as $\epsilon \rightarrow 0$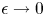 . The corresponding energy functional to the perturbed equation $-\Delta u + g_\epsilon (u) = f(u)$
. The corresponding energy functional to the perturbed equation $-\Delta u + g_\epsilon (u) = f(u)$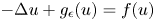 has a critical point $u_\epsilon$
has a critical point $u_\epsilon$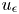 in $H_0^{1}(\Omega )$
in $H_0^{1}(\Omega )$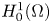 , which converges to a non-trivial non-negative solution of the original problem as $\epsilon \rightarrow 0$
, which converges to a non-trivial non-negative solution of the original problem as $\epsilon \rightarrow 0$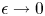 .
.
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 652 - 690
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 3
- Cited by


