Hostname: page-component-5b777bbd6c-v47t2 Total loading time: 0 Render date: 2025-06-21T03:47:46.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Strict Faber–Krahn-type inequality for the mixed local–nonlocal operator under polarization

Part of: Equations and inequalities involving nonlinear operators Manifolds Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  22 January 2025

K. Ashok Kumar Open the ORCID record for K. Ashok Kumar [Opens in a new window]  and
Nirjan Biswas Open the ORCID record for Nirjan Biswas [Opens in a new window]
K. Ashok Kumar*
Affiliation:
Tata Institute of Fundamental Research Centre for Applicable Mathematics, Bengaluru, Karnataka, India
Nirjan Biswas
Affiliation:
Tata Institute of Fundamental Research Centre for Applicable Mathematics, Bengaluru, Karnataka, India
*
Corresponding author: Nirjan Biswas, email: nirjan22@tifrbng.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

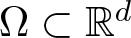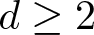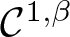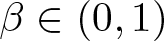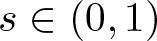Let $\Omega \subset \mathbb{R}^d$ with $d\geq 2$ be a bounded domain of class ${\mathcal C}^{1,\beta }$ for some $\beta \in (0,1)$. For $p\in (1, \infty )$ and $s\in (0,1)$, let 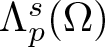$\Lambda ^s_{p}(\Omega )$ be the first eigenvalue of the mixed local–nonlocal operator 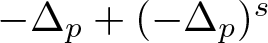$-\Delta _p+(-\Delta _p)^s$ in Ω with the homogeneous nonlocal Dirichlet boundary condition. We establish a strict Faber–Krahn-type inequality for 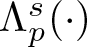$\Lambda _{p}^s(\cdot )$ under polarization. As an application of this strict inequality, we obtain the strict monotonicity of 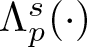$\Lambda _{p}^s(\cdot )$ over the annular domains and characterize the rigidity property of the balls in the classical Faber–Krahn inequality for 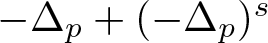$-\Delta _p+(-\Delta _p)^s$.

Keywords

mixed local–nonlocal operatorpolarizationsstrong comparison principlestrict Faber–Krahn inequalitystrong maximum principle

MSC classification

Primary: 35R11: Fractional partial differential equations 49Q10: Optimization of shapes other than minimal surfaces 47J10: Nonlinear spectral theory, nonlinear eigenvalue problems
Secondary: 35B51: Comparison principles
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlfors, L. V., Conformal Invariants: Topics in Geometric Function Theory. McGraw-Hill Series in Higher Mathematics (McGraw-Hill Book, New York-Düsseldorf-Johannesburg, 1973).Google Scholar
Alvino, A., Ferone, V. and Trombetti, G., On the properties of some nonlinear eigenvalues, SIAM J. Math. Anal. 29(2): (1998), 437–451 https://doi.org/10.1137/S0036141096302111.CrossRefGoogle Scholar
Anoop, T. V. and Ashok Kumar, K., Domain variations of the first eigenvalue via a strict Faber-Krahn-type inequality, Adv. Differ. Equ. 28(7-8): (2023), 537–568 https://doi.org/10.57262/ade028-0708-537.Google Scholar
Anoop, T. V., Ashok Kumar, K. and Kesavan, S., A shape variation result via the geometry of eigenfunctions, J. Differ. Equ. 298 (2021), 430–462. https://doi.org/10.1016/j.jde.2021.07.001.CrossRefGoogle Scholar
Ashok Kumar, K. and Biswas, N., Strict monotonicity of the first q-eigenvalue of the fractional p-Laplace operator over annuli, J. Geom. Anal. 34(3): (2024), https://doi.org/10.1007/s12220-023-01539-9.Google Scholar
Baernstein, A., II., A unified approach to symmetrization. In Partial Differential Equations of Elliptic Type (Cortona, 1992), Sympos. Math. Vol.XXXV, (Cambridge Univ. Press, Cambridge, 1994).Google Scholar
Beckner, W., Sobolev inequalities, the Poisson semigroup, and analysis on the sphere Sn, Proc. Nat. Acad. Sci. USA 89(11): (1992), 4816–4819 https://doi.org/10.1073/pnas.89.11.4816.CrossRefGoogle ScholarPubMed
Bhattacharya, T., A proof of the Faber-Krahn inequality for the first eigenvalue of the p-Laplacian, Ann. Mat. Pura Appl. (4) 177: (1999), 225–240 https://doi.org/10.1007/BF02505910.CrossRefGoogle Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E., Mixed local and nonlocal elliptic operators: regularity and maximum principles, Comm. Partial Differential Equations 47(3): (2022), 585–629 https://doi.org/10.1080/03605302.2021.1998908.CrossRefGoogle Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E., A Hong-Krahn-Szegö inequality for mixed local and nonlocal operators, Math. Eng. 5(1): (2023), https://doi.org/10.3934/mine.2023014.Google Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E., A Faber-Krahn inequality for mixed local and nonlocal operators, J. Anal. Math. 150(2): (2023b), 405–448 https://doi.org/10.1007/s11854-023-0272-5.CrossRefGoogle Scholar
Biagi, S., Mugnai, D. and Vecchi, E., A Brezis-Oswald approach for mixed local and nonlocal operators, Commun. Contemp. Math. 26(2): (2024), https://doi.org/10.1142/S0219199722500572.CrossRefGoogle Scholar
Biswas, N., Das, U. and Ghosh, M., On the optimization of the first weighted eigenvalue, Proc. R. Soc. Edinb. A 153(6): (2022), 1777–1804 https://doi.org/10.1017/prm.2022.60.CrossRefGoogle Scholar
Brasco, L. and Franzina, G., Convexity properties of Dirichlet integrals and Picone-type inequalities, Kodai Math. J. 37(3): (2014), 769–799 https://doi.org/10.2996/kmj/1414674621.CrossRefGoogle Scholar
Brasco, L., Lindgren, E. and Parini, E., The fractional Cheeger problem, Interfaces Free Bound. 16(3): (2014), 419–458 https://doi.org/10.4171/IFB/325.CrossRefGoogle Scholar
Brock, F., Positivity and radial symmetry of solutions to some variational problems in $\mathbb{R}^N$, J. Math. Anal. Appl. 296(1): (2004), 226–243 https://doi.org/10.1016/j.jmaa.2004.04.006.CrossRefGoogle Scholar
Brock, F. and Solynin, A. Y., An approach to symmetrization via polarization, Trans. Amer. Math. Soc. 352(4): (2000), 1759–1796 https://doi.org/10.1090/S0002-9947-99-02558-1.CrossRefGoogle Scholar
Buccheri, S., da Silva, J. V. and de Miranda, L. H., A system of local/nonlocal p-Laplacians: the eigenvalue problem and its asymptotic limit as $p\rightarrow\infty$, Asymptot. Anal. 128(2): (2022), 149–181 https://doi.org/10.3233/asy-211702.Google Scholar
Chorwadwala, A. M. H., Mahadevan, R. and Toledo, F., On the Faber-Krahn inequality for the Dirichlet p-Laplacian, ESAIM Control Optim. Calc. Var. 21(1): (2015), 60–72 https://doi.org/10.1051/cocv/2014017.CrossRefGoogle Scholar
Daners, D. and Kennedy, J., Uniqueness in the Faber-Krahn inequality for Robin problems, SIAM J. Math. Anal. 39(4): (2007/08), 1191–1207 https://doi.org/10.1137/060675629.CrossRefGoogle Scholar
De Filippis, C. and Mingione, G., Gradient regularity in mixed local and nonlocal problems, Math. Ann. 388 261–328 (2022), https://doi.org/10.1007/s00208-022-02512-7.CrossRefGoogle Scholar
Di Castro, A., Kuusi, T. and Palatucci, G., Local behavior of fractional p-minimizers, Ann. Inst. H. Poincaré C Anal. Non Linéaire 33(5): (2016), 1279–1299 https://doi.org/10.1016/j.anihpc.2015.04.003.CrossRefGoogle Scholar
Frank, R. L. and Seiringer, R., Non-linear ground state representations and sharp Hardy inequalities, J. Funct. Anal. 255(12): (2008), 3407–3430 https://doi.org/10.1016/j.jfa.2008.05.015.CrossRefGoogle Scholar
Kesavan, S., Some remarks on a result of Talenti, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 15(3): (1989)) 1988, 453–465. http://www.numdam.org/item?id=ASNSP_1988_4_15_3_453_0.Google Scholar
Sciunzi, B., Regularity and comparison principles for p-Laplace equations with vanishing source term, Commun. Contemp. Math. 16(6): (2014), https://doi.org/10.1142/S0219199714500138.CrossRefGoogle Scholar
Shang, B. and Zhang, C., A strong maximum principle for mixed local and nonlocal p-Laplace equations, Asymptot. Anal. 133(1-2): (2023), 1875–8576.Google Scholar
Solynin, A. Y., Continuous symmetrization via polarization, Algebra i Analiz 24(1): (2012), 157–222 https://doi.org/10.1090/S1061-0022-2012-01234-3.Google Scholar
Van Schaftingen, J., Symmetrization and minimax principles, Commun. Contemp. Math. 7(4): (2005), 463–481 https://doi.org/10.1142/S0219199705001817.CrossRefGoogle Scholar
Van Schaftingen, J., Universal approximation of symmetrizations by polarizations, Proc. Amer. Math. Soc. 134(1): (2006), 177–186 https://doi.org/10.1090/S0002-9939-05-08325-5.CrossRefGoogle Scholar
Weth, T., Symmetry of solutions to variational problems for nonlinear elliptic equations via reflection methods, Jahresber. Dtsch. Math.-Ver. 112(3): (2010), 119–158 https://doi.org/10.1365/s13291-010-0005-4.CrossRefGoogle Scholar
Wolontis, V., Properties of conformal invariants, Amer. J. Math. 74 (1952), 587–606 https://doi.org/10.2307/2372264.CrossRefGoogle Scholar