We study optimal dimensionless inequalities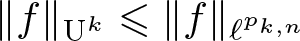

\begin{equation*} \|f\|_{\textrm{U}^k} \leqslant \|f\|_{\ell^{p_{k,n}}} \end{equation*}

that hold for all functions 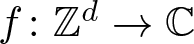$f\colon\mathbb{Z}^d\to\mathbb{C}$ supported in 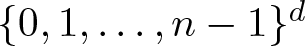$\{0,1,\ldots,n-1\}^d$ and estimates

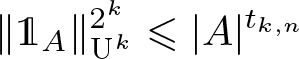\begin{equation*} \|\mathbb{1}_A\|_{\textrm{U}^k}^{2^k}\leqslant |A|^{t_{k,n}} \end{equation*}

that hold for all subsets A of the same discrete cubes. A general theory, analogous to the work of de Dios Pont, Greenfeld, Ivanisvili, and Madrid, is developed to show that the critical exponents are related by 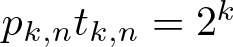$p_{k,n} t_{k,n} = 2^k$. This is used to prove the three main results of the article:

• • an explicit formula for 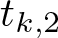$t_{k,2}$, which generalizes a theorem by Kane and Tao,

• • two-sided asymptotic estimates for 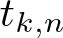$t_{k,n}$ as 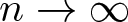$n\to\infty$ for a fixed 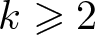$k\geqslant2$, which generalize a theorem by Shao, and

• • a precise asymptotic formula for 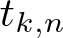$t_{k,n}$ as 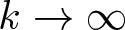$k\to\infty$ for a fixed 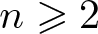$n\geqslant2$.