Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T09:09:52.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles

Part of: Representations of solutions Partial differential equations Stability theory Parabolic equations and systems

Published online by Cambridge University Press:  14 March 2024

Razvan Gabriel Iagar Open the ORCID record for Razvan Gabriel Iagar [Opens in a new window]  and
Philippe Laurençot Open the ORCID record for Philippe Laurençot [Opens in a new window]
Razvan Gabriel Iagar
Affiliation:
Departamento de Matemática Aplicada, Ciencia e Ingenieria de los Materiales y Tecnologia Electrónica, Universidad Rey Juan Carlos, Móstoles, 28933 Madrid, Spain (razvan.iagar@urjc.es)
Philippe Laurençot
Affiliation:
Laboratoire de Mathématiques (LAMA) UMR 5127, Université Savoie Mont Blanc, CNRS, F–73000 Chambéry, France (philippe.laurencot@univ-smb.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Existence of specific eternal solutions in exponential self-similar form to the following quasilinear diffusion equation with strong absorption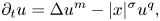

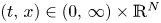\[ \partial_t u=\Delta u^m-|x|^{\sigma}u^q, \]
posed for $(t,\,x)\in (0,\,\infty )\times \mathbb {R}^N$, with $m>1$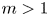, $q\in (0,\,1)$ 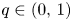and $\sigma =\sigma _c:=2(1-q)/ (m-1)$ is proved. Looking for radially symmetric solutions of the form
\[ u(t,x)={\rm e}^{-\alpha t}f(|x|\,{\rm e}^{\beta t}), \quad \alpha=\frac{2}{m-1}\beta, \]
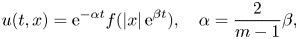
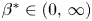we show that there exists a unique exponent $\beta ^*\in (0,\,\infty )$ for which there exists a one-parameter family $(u_A)_{A>0}$ 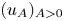of solutions with compactly supported and non-increasing profiles $(f_A)_{A>0}$ 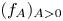satisfying $f_A(0)=A$ 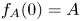and $f_A'(0)=0$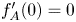. An important feature of these solutions is that they are bounded and do not vanish in finite time, a phenomenon which is known to take place for all non-negative bounded solutions when $\sigma \in (0,\,\sigma _c)$.

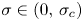Keywords

porous medium equationspatially inhomogeneous absorptioneternal solutionsexponential self-similarityglobal solutions

MSC classification

Primary: 35C06: Self-similar solutions
Secondary: 34D05: Asymptotic properties 35A24: Methods of ordinary differential equations 35B33: Critical exponents 35K65: Degenerate parabolic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 22
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullaev, U. G.. Instantaneous shrinking of the support of a solution of a nonlinear degenerate parabolic equation. Mat. Zametki 63 (1998), 323–331. (Russian). Translation in Math. Notes 63 (1998), 285–292.Google Scholar
Amann, H.. Ordinary differential equations. An introduction to nonlinear analysis. De Gruyter Studies in Mathematics, Vol. 13 (Walter de Gruyter, Berlin, 1990).CrossRefGoogle Scholar
Belaud, Y.. Time-vanishing properties of solutions of some degenerate parabolic equations with strong absorption. Adv. Nonlinear Stud. 1 (2001), 117–152.CrossRefGoogle Scholar
Belaud, Y. and Diaz, J. I.. Abstract results on the finite extinction time property: application to a singular parabolic equation. J. Convex Anal. 17 (2010), 827–860.Google Scholar
Belaud, Y. and Shishkov, A.. Extinction in a finite time for solutions of a class of quasilinear parabolic equations. Asymptot. Anal. 127 (2022), 97–119.Google Scholar
Bertoin, J.. Eternal solutions to Smoluchowski's coagulation equation with additive kernel and their probabilistic interpretations. Ann. Appl. Probab. 12 (2002), 547–564.CrossRefGoogle Scholar
Bobylev, A. V. and Cercignani, C.. Self-similar solutions of the Boltzmann equation and their applications. J. Stat. Phys. 106 (2002), 1039–1071.CrossRefGoogle Scholar
Bonacini, M., Niethammer, B. and Velázquez, J. J. L.. Self-similar solutions to coagulation equations with time-dependent tails: the case of homogeneity one. Arch. Ration. Mech. Anal. 233 (2019), 1–43.CrossRefGoogle Scholar
Cabannes, H.. Proof of the conjecture on ‘eternal’ positive solutions for a semi-continuous model of the Boltzmann equation. C.R. Acad. Sci., Paris, Sér. I, Math. 327 (1998), 217–222.CrossRefGoogle Scholar
Cantrell, R. S. and Cosner, C.. Spatial ecology via reaction-diffusion equations. Wiley Series in Mathematical and Computational Biology (Chichester: John Wiley & Sons, Ltd., 2003).Google Scholar
Chaves, M. and Vázquez, J. L.. Free boundary layer formation in nonlinear heat propagation. Commun. Partial Differ. Equ. 24 (1999), 1945–1965.CrossRefGoogle Scholar
Chaves, M., Vázquez, J. L. and Walias, M.. Optimal existence and uniqueness in a nonlinear diffusion-absorption equation with critical exponents. Proc. R. Soc. Edinburgh Sect. A 127 (1997), 217–242.CrossRefGoogle Scholar
Daskalopoulos, P. and Sesum, N.. Eternal solutions to the Ricci flow on $\mathbb {R}^2$. Int. Math. Res. Not. 2006 (2006), 83610.Google Scholar
Evans, L. C. and Knerr, B. F.. Instantaneous shrinking of the support of nonnegative solutions to certain nonlinear parabolic equations and variational inequalities. Ill. Math. J. 23 (1979), 153–166.Google Scholar
Galaktionov, V. A., Peletier, L. A. and Vázquez, J. L.. Asymptotics of the fast-diffusion equation with critical exponent. SIAM J. Math. Anal. 31 (2000), 1157–1174.CrossRefGoogle Scholar
Galaktionov, V. A. and Vázquez, J. L.. Extinction for a quasilinear heat equation with absorption I. Technique of intersection comparison. Commun. Partial Differ. Equ. 19 (1994), 1075–1106.CrossRefGoogle Scholar
Gilding, B. H. and Kersner, R.. Travelling waves in nonlinear diffusion-convection reaction. Prog. Nonlinear Differ. Equ. Appl., Vol. 60 (Basel: Birkhäuser, 2004).CrossRefGoogle Scholar
Hamilton, R. S.. Eternal solutions to the Ricci flow. J. Differ. Geom. 38 (1993), 1–11.CrossRefGoogle Scholar
Iagar, R. G. and Laurençot, Ph.. Eternal solutions to a singular diffusion equation with critical gradient absorption. Nonlinearity 26 (2013), 3169–3195.CrossRefGoogle Scholar
Iagar, R. G. and Laurençot, Ph.. Finite time extinction for a diffusion equation with spatially inhomogeneous strong absorption. Differ. Integr. Equ. 36 (2023), 1005–1016.Google Scholar
Iagar, R. G., Laurençot, Ph. and Sánchez, A.. Self-similar shrinking of supports and non-extinction for a nonlinear diffusion equation with strong nonhomogeneous absorption. Commun. Contemp. Math. (to appear). Preprint arxiv:2204.09307. doi: 10.1142/S0219199723500281.CrossRefGoogle Scholar
Iagar, R. G., Laurençot, Ph. and Sánchez, A.. Eternal solutions to a porous medium equation with strong nonhomogeneous absorption. Part II: dead-core profiles (Work in preparation, 2024).CrossRefGoogle Scholar
Iagar, R. G. and Sánchez, A.. Eternal solutions for a reaction-diffusion equation with weighted reaction. Discrete Contin. Dyn. Syst. 42 (2022), 1465–1491.CrossRefGoogle Scholar
Iagar, R. G. and Sánchez, A.. Anomalous self-similar solutions of exponential type for the subcritical fast diffusion equation with weighted reaction. Nonlinearity 35 (2022), 3385–3416.CrossRefGoogle Scholar
Kalasnikov, A. S.. The propagation of disturbances in problems of non-linear heat conduction with absorption. U.S.S.R. Comput. Math. Math. Phys. 14 (1975), 70–85.CrossRefGoogle Scholar
Kalashnikov, A. S.. Dependence of properties of solutions of parabolic equations on unbounded domains on the behavior of coefficients at infinity. Mat. Sb. 125 (1984), 398–409. (Russian). Translated Math. USSR Sb. 53 (1986), 399–410.Google Scholar
Kamin, S. and Peletier, L. A.. Large time behavior of solutions of the porous media equation with absorption. Isr. J. Math. 55 (1986), 129–146.CrossRefGoogle Scholar
Kamin, S., Peletier, L. A. and Vázquez, J. L.. Classification of singular solutions of a nonlinear heat equation. Duke Math. J. 58 (1989), 601–615.CrossRefGoogle Scholar
Kamin, S. and Ughi, M.. On the behavior as $t\to \infty$ of the solutions of the Cauchy problem for certain nonlinear parabolic equations. J. Math. Anal. Appl. 128 (1987), 456–469.CrossRefGoogle Scholar
Kamin, S. and Véron, L.. Existence and uniqueness of the very singular solution of the porous media equation with absorption. J. Anal. Math. 51 (1988), 245–258.CrossRefGoogle Scholar
Kwak, M.. A porous media equation with absorption. I. Long time behavior. J. Math. Anal. Appl. 223 (1998), 96–110.CrossRefGoogle Scholar
Leoni, G.. On very singular self-similar solutions for the porous media equation with absorption. Differ. Integr. Equ. 10 (1997), 1123–1140.Google Scholar
McLeod, J. B., Peletier, L. A. and Vázquez, J. L.. Solutions of a nonlinear ODE appearing in the theory of diffusion with absorption. Differ. Integr. Equ. 4 (1991), 1–14.Google Scholar
Peletier, L. A. and Terman, D.. A very singular solution of the porous media equation with absorption. J. Differ. Equ. 65 (1986), 396–410.CrossRefGoogle Scholar
Serre, D.. $L^1$-stability of nonlinear waves in scalar conservation laws. In Evolutionary Equations. Vol. I, Handb. Differ. Equ. (Amsterdam: North-Holland, 2004), pp. 473–553.CrossRefGoogle Scholar
Shi, P.. Self-similar very singular solution to a $p$-Laplacian equation with gradient absorption: existence and uniqueness. J. Southeast Univ. 20 (2004), 381–386.Google Scholar
Ye, H. and Yin, J.. Uniqueness of self-similar very singular solution for non-Newtonian polytropic filtration equations with gradient absorption. Electron. J. Differ. Equ. 2015 (2015), 1–9.Google Scholar