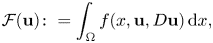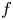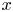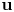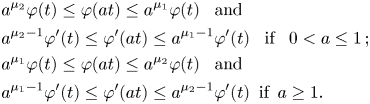1. Introduction
In this paper we study the partial regularity of minimizers of the integral functional
where ![]() $\Omega \subseteq \mathbb {R}^{n}$ is an open bounded set and
$\Omega \subseteq \mathbb {R}^{n}$ is an open bounded set and ![]() ${\bf u} : \Omega \rightarrow \mathbb {R}^{N}$, with
${\bf u} : \Omega \rightarrow \mathbb {R}^{N}$, with ![]() $n$,
$n$, ![]() $N\ge 2$; i.e., we consider vectorial minimizers of
$N\ge 2$; i.e., we consider vectorial minimizers of ![]() $\mathcal {F}$. The growth conditions we impose on
$\mathcal {F}$. The growth conditions we impose on ![]() $f=f(x,{\bf u},{\bf P})$ are quite general, being as they permit ‘general growth condition’ with respect to the gradient variable. This allows us to treat in a unified way the degenerate (when
$f=f(x,{\bf u},{\bf P})$ are quite general, being as they permit ‘general growth condition’ with respect to the gradient variable. This allows us to treat in a unified way the degenerate (when ![]() $p>2$) or singular (when
$p>2$) or singular (when ![]() $p<2$) behaviour. We assume with respect to
$p<2$) behaviour. We assume with respect to ![]() $x$ a weak VMO condition, uniformly in
$x$ a weak VMO condition, uniformly in ![]() $({\bf u},{\bf P})$, and continuity with respect to
$({\bf u},{\bf P})$, and continuity with respect to ![]() ${\bf u}$. Our main result, theorem 1.1, proves that a minimizer of (1.1) is locally Hölder continuous for any Hölder exponent
${\bf u}$. Our main result, theorem 1.1, proves that a minimizer of (1.1) is locally Hölder continuous for any Hölder exponent ![]() $0<\alpha <1$; i.e., if
$0<\alpha <1$; i.e., if ![]() ${\bf u}$ is a minimizer of (1.1), then
${\bf u}$ is a minimizer of (1.1), then ![]() ${\bf u}\in C_{\text {loc}}^{0,\alpha }(\Omega _0,\mathbb {R}^{N})$, where
${\bf u}\in C_{\text {loc}}^{0,\alpha }(\Omega _0,\mathbb {R}^{N})$, where ![]() $\Omega _0\subset \Omega$ is an open set of full measure specified in the statement of theorem 1.1 later in this section.
$\Omega _0\subset \Omega$ is an open set of full measure specified in the statement of theorem 1.1 later in this section.
1.1 Literature review
We begin by explaining how the study of functional (1.1) fits into the broader regularity theory research over the past many years. Before proceeding further, we point out that Mingione [Reference Mingione35] has provided a comprehensive account of the various areas of study within regularity theory for integral functionals and PDEs; it is an excellent reference for those wishing to read a broad overview of the various areas of interest within the larger realm of regularity theory.
As already mentioned we allow ![]() $f$ to satisfy a VMO-type condition with respect to
$f$ to satisfy a VMO-type condition with respect to ![]() $x$. More precisely the partial map
$x$. More precisely the partial map ![]() $\displaystyle x\mapsto ({f(x,{\bf u},{\bf P})})/({\varphi (|{\bf P}|)})$ satisfies a uniform VMO condition; here
$\displaystyle x\mapsto ({f(x,{\bf u},{\bf P})})/({\varphi (|{\bf P}|)})$ satisfies a uniform VMO condition; here ![]() $\varphi$ is an
$\varphi$ is an ![]() $N$-function—see condition (F4) later in this section for the precise formulation. As a consequence we allow a certain controlled discontinuous behaviour with respect to the spatial variable in the integrand of (1.1). We prove partial Hölder continuity for the local minimizers. The first paper who considered low order regularity (for variational integrals) was the one by Foss and Mingione [Reference Foss and Mingione23], where they were assuming continuity with respect to
$N$-function—see condition (F4) later in this section for the precise formulation. As a consequence we allow a certain controlled discontinuous behaviour with respect to the spatial variable in the integrand of (1.1). We prove partial Hölder continuity for the local minimizers. The first paper who considered low order regularity (for variational integrals) was the one by Foss and Mingione [Reference Foss and Mingione23], where they were assuming continuity with respect to ![]() $x$ and
$x$ and ![]() ${\bf u}$. Thereafter Kristensen and Mingione [Reference Kristensen and Mingione29] proved Hölder continuity for convex integral functionals with continuous coefficients for a fixed Hölder exponent depending on the dimension and the growth exponent. Stronger assumptions as Dini-type conditions [Reference Duzaar, Gastel and Mingione20] lead to partial
${\bf u}$. Thereafter Kristensen and Mingione [Reference Kristensen and Mingione29] proved Hölder continuity for convex integral functionals with continuous coefficients for a fixed Hölder exponent depending on the dimension and the growth exponent. Stronger assumptions as Dini-type conditions [Reference Duzaar, Gastel and Mingione20] lead to partial ![]() $C^{1}$-regularity. It is worth mentioning the uniform porosity of the singular set for Lipschitzian minimizers of quasiconvex functionals [Reference Kristensen and Mingione30].
$C^{1}$-regularity. It is worth mentioning the uniform porosity of the singular set for Lipschitzian minimizers of quasiconvex functionals [Reference Kristensen and Mingione30].
The space of functions with vanishing mean oscillation (VMO) has been introduced by Sarason in the realm of harmonic analysis, see [Reference Sarason37]. It has had several applications in connection with Hardy spaces, Riesz transforms or nonlinear commutators, see [Reference Iwaniec and Martin27, Reference Stein39] and references therein. In the early 90s, Chiarenza, Frasca and Longo [Reference Chiarenza, Frasca and Longo8] studied non-divergence form equations with VMO coefficients by means of singular integrals operators, see also [Reference Di Fazio and Ragusa18, Reference Di Fazio, Palagachev and Ragusa19].
The study of functionals satisfying a VMO-type condition has been broadened considerably over the past couple decades, see [Reference Danéćek and Viszus9, Reference Ragusa and Tachikawa38]. Recently, Bögelein, Duzaar, Habermann and Scheven [Reference Bögelein, Duzaar, Habermann and Scheven5] considered a functional of the form (1.1) under the assumption that ![]() $(x,{\bf u},{\bf P})\mapsto f(x,{\bf u},{\bf P})$ satisfies a type of VMO assumption in
$(x,{\bf u},{\bf P})\mapsto f(x,{\bf u},{\bf P})$ satisfies a type of VMO assumption in ![]() $x$, uniformly with respect to
$x$, uniformly with respect to ![]() ${\bf u}$ and
${\bf u}$ and ![]() ${\bf P}$; they further considered an analogous elliptic system of the form
${\bf P}$; they further considered an analogous elliptic system of the form ![]() $\nabla \cdot a(x,{\bf u},D{\bf u})=0$, in which, again, the coefficient
$\nabla \cdot a(x,{\bf u},D{\bf u})=0$, in which, again, the coefficient ![]() $a$ was assumed to satisfy a VMO-type condition with respect to its spatial coordinate. Moreover, the integral functional they studied was assumed to be quasi-convex. However, unlike our study, they assumed that the growth of
$a$ was assumed to satisfy a VMO-type condition with respect to its spatial coordinate. Moreover, the integral functional they studied was assumed to be quasi-convex. However, unlike our study, they assumed that the growth of ![]() $f$ with respect to
$f$ with respect to ![]() ${\bf P}$ was standard
${\bf P}$ was standard ![]() $p$-growth,
$p$-growth, ![]() $p\ge 2.$
$p\ge 2.$
Similarly, Bögelein [Reference Bögelein4] studied quasi-convex integral functionals in the vectorial case. But the assumed growth of the integrand with respect to the gradient was standard ![]() $p$-growth. It was also assumed that the map
$p$-growth. It was also assumed that the map ![]() $\displaystyle x\mapsto ({f(x,{\bf u},{\bf P})})/({(1+|{\bf P}|)^{p}})$ was VMO, uniformly with respect to
$\displaystyle x\mapsto ({f(x,{\bf u},{\bf P})})/({(1+|{\bf P}|)^{p}})$ was VMO, uniformly with respect to ![]() ${\bf u}$ and
${\bf u}$ and ![]() ${\bf P}$. Bögelein, Duzaar, Habermann and Scheven [Reference Bögelein, Duzaar, Habermann and Scheven6] made some similar assumptions when considering a system of PDEs involving the symmetric part of the gradient
${\bf P}$. Bögelein, Duzaar, Habermann and Scheven [Reference Bögelein, Duzaar, Habermann and Scheven6] made some similar assumptions when considering a system of PDEs involving the symmetric part of the gradient ![]() $D{\bf u}$, wherein the coefficients on the symmetric part were VMO.
$D{\bf u}$, wherein the coefficients on the symmetric part were VMO.
Goodrich [Reference Goodrich26] then further generalized, in part, the results of [Reference Bögelein, Duzaar, Habermann and Scheven5] by considering (1.1) in the case where ![]() $x\mapsto f(x,{\bf u},{\bf P})$ was VMO, uniformly with respect to
$x\mapsto f(x,{\bf u},{\bf P})$ was VMO, uniformly with respect to ![]() ${\bf u}$ and
${\bf u}$ and ![]() ${\bf P}$, and, furthermore, in which
${\bf P}$, and, furthermore, in which ![]() $f$ was only asymptotically convex.
$f$ was only asymptotically convex.
Next, the study of problems with general growth conditions has been initiated by Marcellini in a list of papers [Reference Marcellini32–Reference Marcellini and Papi34] and it is now very rich—see, e.g., [Reference Celada and Ok7, Reference De Filippis10, Reference Diening, Stroffolini and Verde15–Reference Diening, Lengeler, Stroffolini and Verde17, Reference Stroffolini40]. In particular, Marcellini and Papi proved the Lipschitz bound for a solution of an elliptic system of Uhlenbeck type with general growth. In view of comparison estimates, it is worth mentioning the paper [Reference Diening, Stroffolini and Verde15], where the ![]() $C^{1,\alpha }$ regularity is proven via an excess decay estimate. Very recently, De Filippis and Mingione have relaxed the hypotheses by considering also growth of exponential type (no
$C^{1,\alpha }$ regularity is proven via an excess decay estimate. Very recently, De Filippis and Mingione have relaxed the hypotheses by considering also growth of exponential type (no ![]() $\Delta _2$-condition) [Reference De Filippis and Mingione11].
$\Delta _2$-condition) [Reference De Filippis and Mingione11].
So, we see that many papers in recent years have treated either VMO-type coefficient problems or general growth problems. To our knowledge, it seems that the combination of these two generalities has not been considered as we do in this paper. Thus, the results of this paper significantly generalize many of the previously mentioned papers.
1.2 Strategy of the proof
We briefly explain the strategy of the proof of the main result. As a major difficulty with respect to the proof by Bögelein or Duzaar et al. in the ![]() $p$-setting, we can't rely on homogeneity of the function
$p$-setting, we can't rely on homogeneity of the function ![]() $\varphi$. In particular, an analogue of the Campanato excess
$\varphi$. In particular, an analogue of the Campanato excess
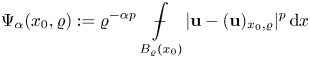 \begin{equation*} \Psi_\alpha(x_0,\varrho):=\varrho^{-\alpha p}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf u} - ({\bf u})_{x_0,\varrho}|^{p}\,\mathrm{d}x \end{equation*}
\begin{equation*} \Psi_\alpha(x_0,\varrho):=\varrho^{-\alpha p}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf u} - ({\bf u})_{x_0,\varrho}|^{p}\,\mathrm{d}x \end{equation*}defined there and playing a key role in the iteration process could not be easily handled in the Orlicz setting.
Our strategy is to find carefully the two quantities which play the role both in the non-degenerate and in the degenerate cases. The first leading quantity is the excess functional
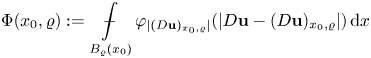 \begin{equation*} \Phi(x_0,\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi_{|({D{\bf u}})_{x_0,\varrho}|}(|D{\bf u}-({D{\bf u}})_{x_0,\varrho}|)\,\mathrm{d}x \end{equation*}
\begin{equation*} \Phi(x_0,\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi_{|({D{\bf u}})_{x_0,\varrho}|}(|D{\bf u}-({D{\bf u}})_{x_0,\varrho}|)\,\mathrm{d}x \end{equation*}(see (3.14)). In the non-degenerate case, when
we linearize the problem, via the ![]() $\mathcal {A}$-harmonic approximation [Reference Diening, Lengeler, Stroffolini and Verde17]. This procedure, exploiting assumptions (F4)–(F5) and a freezing technique (with respect to the variables
$\mathcal {A}$-harmonic approximation [Reference Diening, Lengeler, Stroffolini and Verde17]. This procedure, exploiting assumptions (F4)–(F5) and a freezing technique (with respect to the variables ![]() $x$ and
$x$ and ![]() ${\bf u}$) based on the Ekeland variational principle, provides a comparison map which is an almost minimizer of the frozen functional and whose gradient is
${\bf u}$) based on the Ekeland variational principle, provides a comparison map which is an almost minimizer of the frozen functional and whose gradient is ![]() $L^{1}$-close to that of the original minimizer (see lemma 3.8). Such comparison map is shown to be approximately
$L^{1}$-close to that of the original minimizer (see lemma 3.8). Such comparison map is shown to be approximately ![]() $\mathcal {A}$-harmonic, and this property is inherited by the minimizer itself via the comparison estimate. This allows to prove an excess-decay estimate, which, in turn, permits the iteration of the rescaled excess
$\mathcal {A}$-harmonic, and this property is inherited by the minimizer itself via the comparison estimate. This allows to prove an excess-decay estimate, which, in turn, permits the iteration of the rescaled excess ![]() $\frac {\Phi (x_0,\varrho )}{\varphi (|(D{\bf u})_{x_0,\varrho }|)}$ and of a ‘Morrey-type’ excess
$\frac {\Phi (x_0,\varrho )}{\varphi (|(D{\bf u})_{x_0,\varrho }|)}$ and of a ‘Morrey-type’ excess
 \begin{equation*} \Theta(x_0,\varrho):=\varrho\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right) \end{equation*}
\begin{equation*} \Theta(x_0,\varrho):=\varrho\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right) \end{equation*}
at each scale. Namely, there exists ![]() $\vartheta \in (0,1)$ such that, if the boundedness conditions
$\vartheta \in (0,1)$ such that, if the boundedness conditions
hold on some ball ![]() $B_\varrho (x_0)$, then
$B_\varrho (x_0)$, then
hold for every ![]() $m=0,1,\dots .$. Therefore,
$m=0,1,\dots .$. Therefore, ![]() $\Theta (x_0,\varrho )$ is the adequate excess playing the role of
$\Theta (x_0,\varrho )$ is the adequate excess playing the role of ![]() $\Psi _\alpha$ in our setting.
$\Psi _\alpha$ in our setting.
In the degenerate case, when
for some ![]() $\kappa <1$, we perform a different linearization procedure: the assumption (F7) coupled with an analogous freezing argument as before provides, now, the almost
$\kappa <1$, we perform a different linearization procedure: the assumption (F7) coupled with an analogous freezing argument as before provides, now, the almost ![]() $\varphi$-harmonicity of the minimizer via the application of the
$\varphi$-harmonicity of the minimizer via the application of the ![]() $\varphi$-harmonic approximation [Reference Diening, Stroffolini and Verde16] to the comparison map. The corresponding excess improvement implies that if the excess is small at radius
$\varphi$-harmonic approximation [Reference Diening, Stroffolini and Verde16] to the comparison map. The corresponding excess improvement implies that if the excess is small at radius ![]() $\varrho$ it is also small at some smaller radius
$\varrho$ it is also small at some smaller radius ![]() $\theta \varrho$, for
$\theta \varrho$, for ![]() $\theta <1$. The key point in this iteration process is that the boundedness of both the excess
$\theta <1$. The key point in this iteration process is that the boundedness of both the excess ![]() $\Phi$ and the Morrey excess
$\Phi$ and the Morrey excess ![]() $\Theta$ at some scale
$\Theta$ at some scale ![]() $\vartheta \theta ^{k_0}\varrho$ (‘switching radius’) under assumption (1.2) is satisfied exactly when the degenerate bound (1.3) fails and therefore we can proceed the iteration in the non-degenerate regime. Notice that, if on the one hand
$\vartheta \theta ^{k_0}\varrho$ (‘switching radius’) under assumption (1.2) is satisfied exactly when the degenerate bound (1.3) fails and therefore we can proceed the iteration in the non-degenerate regime. Notice that, if on the one hand ![]() $|(D{\bf u})_{x_0,\varrho }|$ might blow up in the iteration since we cannot expect
$|(D{\bf u})_{x_0,\varrho }|$ might blow up in the iteration since we cannot expect ![]() $C^{1}$-regularity, on the other hand the Morrey excess
$C^{1}$-regularity, on the other hand the Morrey excess ![]() $\Theta (x_0,\theta ^{k}\varrho )$ stays bounded, exactly as it should be for a
$\Theta (x_0,\theta ^{k}\varrho )$ stays bounded, exactly as it should be for a ![]() $C^{0,\alpha }$-regularity result. In addition, if at level
$C^{0,\alpha }$-regularity result. In addition, if at level ![]() $k_0$ the regime is non-degenerate, the behaviour stays non-degenerate at any subsequent level
$k_0$ the regime is non-degenerate, the behaviour stays non-degenerate at any subsequent level ![]() $k\geq k_0$, and the iteration can proceed. The smallness of
$k\geq k_0$, and the iteration can proceed. The smallness of ![]() $\Theta$ at any level ensures Hölder continuity of
$\Theta$ at any level ensures Hölder continuity of ![]() ${\bf u}$ in
${\bf u}$ in ![]() $x_0$ provided the excess functionals
$x_0$ provided the excess functionals ![]() $\Phi$ and
$\Phi$ and ![]() $\Theta$ are small at some initial radius
$\Theta$ are small at some initial radius ![]() $\varrho$ (actually, this holds in a neighbourhood of
$\varrho$ (actually, this holds in a neighbourhood of ![]() $x_0$, since these smallness conditions are open). Finally, it is then proven that such a smallness condition on the excesses is indeed satisfied on the complement of the set
$x_0$, since these smallness conditions are open). Finally, it is then proven that such a smallness condition on the excesses is indeed satisfied on the complement of the set ![]() $\Sigma _1\cup \Sigma _2$ of theorem 1.1.
$\Sigma _1\cup \Sigma _2$ of theorem 1.1.
1.3 Assumptions and statement of the main result
We list here the main assumptions on the integral functional that we are going to study throughout the paper. We assume that ![]() $\varphi :[0,\infty )\to [0,\infty )$ is an
$\varphi :[0,\infty )\to [0,\infty )$ is an ![]() $N$-function such that
$N$-function such that
(1)
 $\varphi \in C^{1}([0,\infty ))\cap C^{2}((0,\infty ))$;
$\varphi \in C^{1}([0,\infty ))\cap C^{2}((0,\infty ))$;(2)
 $0<\mu _1-1\leq \inf _{t>0}\frac {t\varphi ''(t)}{\varphi '(t)}\leq \sup _{t>0}\frac {t\varphi ''(t)}{\varphi '(t)}\leq \mu _2-1$, for suitable constants
$0<\mu _1-1\leq \inf _{t>0}\frac {t\varphi ''(t)}{\varphi '(t)}\leq \sup _{t>0}\frac {t\varphi ''(t)}{\varphi '(t)}\leq \mu _2-1$, for suitable constants  $1<\mu _1\leq \mu _2$.
$1<\mu _1\leq \mu _2$.
We may assume, without loss of generality, that ![]() $1<\mu _1<2<\mu _2$.
$1<\mu _1<2<\mu _2$.
For the precise notation and definitions, as well as the additional assumptions we will require on ![]() $\varphi$, we refer to § 2.
$\varphi$, we refer to § 2.
We assume the integrand ![]() $f:\Omega \times \mathbb {R}^{N}\times \mathbb {R}^{N\times n}\to \mathbb {R}$,
$f:\Omega \times \mathbb {R}^{N}\times \mathbb {R}^{N\times n}\to \mathbb {R}$, ![]() $f=f(x,{\bf u},{\bf P})$ to be Borel-measurable, such that the partial map
$f=f(x,{\bf u},{\bf P})$ to be Borel-measurable, such that the partial map ![]() ${\bf P}\to f(\cdot ,\cdot ,{\bf P})\in C^{1}(\mathbb {R}^{N\times n})\cap C^{2}(\mathbb {R}^{N\times n}\backslash \{{\bf 0}\})$. We will denote by
${\bf P}\to f(\cdot ,\cdot ,{\bf P})\in C^{1}(\mathbb {R}^{N\times n})\cap C^{2}(\mathbb {R}^{N\times n}\backslash \{{\bf 0}\})$. We will denote by ![]() $Df$ and
$Df$ and ![]() $D^{2}f$ the corresponding first and second gradients, respectively, for fixed
$D^{2}f$ the corresponding first and second gradients, respectively, for fixed ![]() $x$ and
$x$ and ![]() ${\bf u}$. We require
${\bf u}$. We require ![]() $f$ to comply with the following assumptions:
$f$ to comply with the following assumptions:
(F1) coercivity: there exists
 $\nu >0$ such that
uniformly in
$\nu >0$ such that
uniformly in \begin{equation*} \nu \varphi(|{\bf P}|)\le f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf 0}) \end{equation*}
\begin{equation*} \nu \varphi(|{\bf P}|)\le f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf 0}) \end{equation*} $x\in \Omega$ and
$x\in \Omega$ and  ${\bf u}\in \mathbb {R}^{N}$, for every
${\bf u}\in \mathbb {R}^{N}$, for every  ${\bf P}\in \mathbb {R}^{N\times n}$;
${\bf P}\in \mathbb {R}^{N\times n}$;(F2)
 $\varphi$-growth conditions with respect to the
$\varphi$-growth conditions with respect to the  ${\bf P}$ variable: there exists a constant
${\bf P}$ variable: there exists a constant  $L>0$ such that
uniformly in
$L>0$ such that
uniformly in \begin{equation*} |D f(x,{\bf u},{\bf P})|\le L \varphi'(|{\bf P}|),\quad |D^{2} f(x,{\bf u},{\bf P})|\le L \varphi''(|{\bf P}|), \end{equation*}
\begin{equation*} |D f(x,{\bf u},{\bf P})|\le L \varphi'(|{\bf P}|),\quad |D^{2} f(x,{\bf u},{\bf P})|\le L \varphi''(|{\bf P}|), \end{equation*} $x\in \Omega$ and
$x\in \Omega$ and  ${\bf u}\in \mathbb {R}^{N}$, for every
${\bf u}\in \mathbb {R}^{N}$, for every  ${\bf P}\in \mathbb {R}^{N\times n}$ with
${\bf P}\in \mathbb {R}^{N\times n}$ with  $|{\bf P}|\neq 0$;
$|{\bf P}|\neq 0$;(F3)
 $f$ is degenerate quasiconvex; i.e.,
for every
$f$ is degenerate quasiconvex; i.e.,
for every \begin{align*} & \int_{B}{f (x, {\bf u}, {\bf P}+D \boldsymbol {\eta}(y)) -f(x, {\bf u}, {\bf P})} \, \textrm{d} y\\ &\quad \geq \nu \int_{B}\varphi'' (\mu+ \vert{{\bf P}}\vert + \vert{D \boldsymbol \eta(y)}\vert)\, \vert{D \boldsymbol \eta(y)}\vert^{2} \, \textrm{d} y, \end{align*}
\begin{align*} & \int_{B}{f (x, {\bf u}, {\bf P}+D \boldsymbol {\eta}(y)) -f(x, {\bf u}, {\bf P})} \, \textrm{d} y\\ &\quad \geq \nu \int_{B}\varphi'' (\mu+ \vert{{\bf P}}\vert + \vert{D \boldsymbol \eta(y)}\vert)\, \vert{D \boldsymbol \eta(y)}\vert^{2} \, \textrm{d} y, \end{align*} $x \in \Omega$,
$x \in \Omega$,  ${\bf u} \in \mathbb {R}^{N}$, every ball
${\bf u} \in \mathbb {R}^{N}$, every ball  $B\subset \Omega$,
$B\subset \Omega$,  ${\bf P}\in \mathbb {R}^{N\times n}$ and
${\bf P}\in \mathbb {R}^{N\times n}$ and  $\boldsymbol \eta \in C^{\infty }_0(B, \mathbb {R}^{N})$,
$\boldsymbol \eta \in C^{\infty }_0(B, \mathbb {R}^{N})$,  $\mu \ge 0$;
$\mu \ge 0$;(F4) the function
 $x\mapsto f ( x, {\bf u}, {\bf P})/\varphi (|{\bf P}|)$ satisfies a VMO-condition, uniformly with respect to
$x\mapsto f ( x, {\bf u}, {\bf P})/\varphi (|{\bf P}|)$ satisfies a VMO-condition, uniformly with respect to  $({\bf u}, {\bf P})$:
where
$({\bf u}, {\bf P})$:
where \begin{equation*} {\vert{ f (x, {\bf u}, {\bf P})- (f({\cdot}, {\bf u}, {\bf P}))_{x_0, r}}\vert} \leq {v}_{x_0}(x, r) \varphi( |{\bf P}|),\quad \mbox{ for all} x\in B_r(x_0) \end{equation*}
\begin{equation*} {\vert{ f (x, {\bf u}, {\bf P})- (f({\cdot}, {\bf u}, {\bf P}))_{x_0, r}}\vert} \leq {v}_{x_0}(x, r) \varphi( |{\bf P}|),\quad \mbox{ for all} x\in B_r(x_0) \end{equation*} $x_0\in \Omega$,
$x_0\in \Omega$,  $r\in (0,1]$ and
$r\in (0,1]$ and  ${\bf P}\in \mathbb {R}^{N\times n}$ and
${\bf P}\in \mathbb {R}^{N\times n}$ and  ${v}_{x_0}:\mathbb {R}^{n}\times [0,1]\to [0,2L]$ are bounded functions such that
and
${v}_{x_0}:\mathbb {R}^{n}\times [0,1]\to [0,2L]$ are bounded functions such that
and \begin{equation*} \lim_{\varrho\to 0}{\mathcal{V}}(\varrho)=0 , \mbox{ where } {\mathcal{V}}(\varrho):=\sup_{x_0\in\Omega}\sup_{0< r\leq\varrho} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)}{v}_{x_0}(x,r)\,\mathrm{d}x, \end{equation*}
\begin{equation*} \lim_{\varrho\to 0}{\mathcal{V}}(\varrho)=0 , \mbox{ where } {\mathcal{V}}(\varrho):=\sup_{x_0\in\Omega}\sup_{0< r\leq\varrho} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)}{v}_{x_0}(x,r)\,\mathrm{d}x, \end{equation*} \begin{equation*} (f({\cdot}, {\bf u}, {\bf P}))_{x_0, r}:=\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)} f(x, {\bf u}, {\bf P})\,\mathrm{d}x\,; \end{equation*}
\begin{equation*} (f({\cdot}, {\bf u}, {\bf P}))_{x_0, r}:=\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)} f(x, {\bf u}, {\bf P})\,\mathrm{d}x\,; \end{equation*}(F5)
 $f$ is uniformly continuous with respect to the
$f$ is uniformly continuous with respect to the  ${\bf u}$ variable; i.e.,
where
${\bf u}$ variable; i.e.,
where \begin{equation*} {\vert{ f (x, {\bf u}, {\bf P})- f (x, {\bf u}_0, {\bf P})}\vert}\le L\omega ( |{\bf u}-{\bf u}_0|) \varphi(|{\bf P}|), \end{equation*}
\begin{equation*} {\vert{ f (x, {\bf u}, {\bf P})- f (x, {\bf u}_0, {\bf P})}\vert}\le L\omega ( |{\bf u}-{\bf u}_0|) \varphi(|{\bf P}|), \end{equation*} $\omega :[0,\infty )\to [0,1]$ is a nondecreasing, concave modulus of continuity; i.e.,
$\omega :[0,\infty )\to [0,1]$ is a nondecreasing, concave modulus of continuity; i.e.,  $\lim _{t\downarrow 0}\omega (t)=\omega (0)=0$.
$\lim _{t\downarrow 0}\omega (t)=\omega (0)=0$.(F6) the second derivatives
 $D^{2}f$ are Hölder continuous away from
$D^{2}f$ are Hölder continuous away from  $\bf {0}$ with some exponent
$\bf {0}$ with some exponent  $\beta _0 \in (0,1)$ such that uniformly in
$\beta _0 \in (0,1)$ such that uniformly in  $(x, {\bf u})$ and for
$(x, {\bf u})$ and for  $0<|{\bf P}|\le \frac 12 |{\bf Q}|$
$0<|{\bf P}|\le \frac 12 |{\bf Q}|$
 \begin{equation*} {\vert{ D^{2} f (x, {\bf u}, {\bf P})- D^{2} f (x, {\bf u}, {\bf P}+{\bf Q}) }\vert} \le c_0 \,\varphi' ({\vert{{\bf Q}}\vert}) \,{\vert{{\bf Q}}\vert}^{-\beta_0} {\vert{{\bf P}}\vert}^{\beta_0}\,; \end{equation*}
\begin{equation*} {\vert{ D^{2} f (x, {\bf u}, {\bf P})- D^{2} f (x, {\bf u}, {\bf P}+{\bf Q}) }\vert} \le c_0 \,\varphi' ({\vert{{\bf Q}}\vert}) \,{\vert{{\bf Q}}\vert}^{-\beta_0} {\vert{{\bf P}}\vert}^{\beta_0}\,; \end{equation*}(F7) the function
 ${\bf P} \to Df(x,{\bf u}, {{\bf P}})$ behaves asymptotically at
${\bf P} \to Df(x,{\bf u}, {{\bf P}})$ behaves asymptotically at  $0$ as the
$0$ as the  $\varphi$-Laplacian; i.e.,
uniformly in
$\varphi$-Laplacian; i.e.,
uniformly in \begin{equation*} \lim_{t\to 0} \frac{Df(x,{\bf u}, t {{\bf P}}) }{\varphi'(t)}= {{\bf P}}, \end{equation*}
\begin{equation*} \lim_{t\to 0} \frac{Df(x,{\bf u}, t {{\bf P}}) }{\varphi'(t)}= {{\bf P}}, \end{equation*} $\{{\bf P}\in \mathbb {R}^{N\times n}:\, |{\bf P}|=1\}$ and uniformly for all
$\{{\bf P}\in \mathbb {R}^{N\times n}:\, |{\bf P}|=1\}$ and uniformly for all  $x\in \Omega$ and
$x\in \Omega$ and  ${\bf u}\in \mathbb {R}^{N}$.
${\bf u}\in \mathbb {R}^{N}$.
Our main regularity result can be stated as follows. Note that the definition of ![]() ${\bf V}$ appearing in
${\bf V}$ appearing in ![]() $\Sigma _1$ can be found in (2.3).
$\Sigma _1$ can be found in (2.3).
Theorem 1.1 Let ![]() $\Omega \subset \mathbb {R}^{n}$ be an open bounded domain,
$\Omega \subset \mathbb {R}^{n}$ be an open bounded domain, ![]() $\varphi$ a convex function satisfying assumptions (φ1)–(φ3) and consider a minimizer
$\varphi$ a convex function satisfying assumptions (φ1)–(φ3) and consider a minimizer ![]() ${\bf u} \in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ to the functional (1.1) under assumptions (F1)–(F7). Then there exists an open subset
${\bf u} \in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ to the functional (1.1) under assumptions (F1)–(F7). Then there exists an open subset ![]() $\Omega _0 \subset \Omega$ such that
$\Omega _0 \subset \Omega$ such that
for every ![]() $\alpha \in (0,1)$. Moreover,
$\alpha \in (0,1)$. Moreover, ![]() $\Omega \setminus \Omega _0\subset \Sigma _1\cup \Sigma _2$ where
$\Omega \setminus \Omega _0\subset \Sigma _1\cup \Sigma _2$ where
 \begin{equation*} \begin{split} & \Sigma_1:=\left\{x_0\in\Omega:\, \mathop{\lim\inf}_{\varrho\searrow 0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\varrho}|}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x>0\right\},\\ & \Sigma_2:=\left\{x_0\in\Omega:\, \mathop{\lim\sup}_{\varrho\searrow 0}|(D{\bf u})_{x_0,\varrho}|={+}\infty\right\}. \end{split} \end{equation*}
\begin{equation*} \begin{split} & \Sigma_1:=\left\{x_0\in\Omega:\, \mathop{\lim\inf}_{\varrho\searrow 0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\varrho}|}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x>0\right\},\\ & \Sigma_2:=\left\{x_0\in\Omega:\, \mathop{\lim\sup}_{\varrho\searrow 0}|(D{\bf u})_{x_0,\varrho}|={+}\infty\right\}. \end{split} \end{equation*}2. Preliminaries and basic results
2.1 Some basic facts on  $N$–functions
$N$–functions
We recall here some elementary definitions and basic results about Orlicz functions. The following definitions and results can be found, e.g., in [Reference Adams1, Reference Bennett and Sharpley3, Reference Krasnosel'skií and Rutickií28, Reference Kufner, John and Fucik31].
A real-valued function ![]() $\varphi \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ is said to be an
$\varphi \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ is said to be an ![]() $N$-function if it is convex and satisfies the following conditions:
$N$-function if it is convex and satisfies the following conditions: ![]() $\varphi (0)=0$,
$\varphi (0)=0$, ![]() $\varphi$ admits the derivative
$\varphi$ admits the derivative ![]() $\varphi '$ and this derivative is right continuous, non-decreasing and satisfies
$\varphi '$ and this derivative is right continuous, non-decreasing and satisfies ![]() $\varphi '(0) = 0$,
$\varphi '(0) = 0$, ![]() $\varphi '(t)>0$ for
$\varphi '(t)>0$ for ![]() $t>0$, and
$t>0$, and ![]() $\lim _{t\to \infty } \varphi '(t)=\infty$.
$\lim _{t\to \infty } \varphi '(t)=\infty$.
We say that ![]() $\varphi$ satisfies the
$\varphi$ satisfies the ![]() $\Delta _2$-condition if there exists
$\Delta _2$-condition if there exists ![]() $c > 0$ such that for all
$c > 0$ such that for all ![]() $t \geq 0$ holds
$t \geq 0$ holds ![]() $\varphi (2t) \leq c\, \varphi (t)$. We denote the smallest possible such constant by
$\varphi (2t) \leq c\, \varphi (t)$. We denote the smallest possible such constant by ![]() $\Delta _2(\varphi )$. Since
$\Delta _2(\varphi )$. Since ![]() $\varphi (t) \leq \varphi (2t)$, the
$\varphi (t) \leq \varphi (2t)$, the ![]() $\Delta _2$-condition is equivalent to
$\Delta _2$-condition is equivalent to ![]() $\varphi (2t) \sim \varphi (t)$, where ‘
$\varphi (2t) \sim \varphi (t)$, where ‘![]() $\sim$’ indicates the equivalence between
$\sim$’ indicates the equivalence between ![]() $N$-functions.
$N$-functions.
By ![]() $L^{\varphi }$ and
$L^{\varphi }$ and ![]() $W^{1,\varphi }$ we denote the classical Orlicz and Orlicz-Sobolev spaces, i. e.
$W^{1,\varphi }$ we denote the classical Orlicz and Orlicz-Sobolev spaces, i. e. ![]() $f \in L^{\varphi }$ if and only if
$f \in L^{\varphi }$ if and only if ![]() $\int \varphi (|{f}|)\,\textrm {d}x < \infty$ and
$\int \varphi (|{f}|)\,\textrm {d}x < \infty$ and ![]() $f \in W^{1,\varphi }$ if and only if
$f \in W^{1,\varphi }$ if and only if ![]() $f, D f \in L^{\varphi }$. The space
$f, D f \in L^{\varphi }$. The space ![]() $W^{1,\varphi }_0(\Omega )$ will denote the closure of
$W^{1,\varphi }_0(\Omega )$ will denote the closure of ![]() $C^{\infty }_0(\Omega )$ in
$C^{\infty }_0(\Omega )$ in ![]() $W^{1,\varphi }(\Omega )$.
$W^{1,\varphi }(\Omega )$.
We define the function ![]() $(\varphi ')^{-1} \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ as
$(\varphi ')^{-1} \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ as
If ![]() $\varphi '$ is strictly increasing, then
$\varphi '$ is strictly increasing, then ![]() $(\varphi ')^{-1}$ is the inverse function of
$(\varphi ')^{-1}$ is the inverse function of ![]() $\varphi '$. Then
$\varphi '$. Then ![]() $\varphi ^{\ast } \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ with
$\varphi ^{\ast } \colon \mathbb {R}^{+}_0 \to \mathbb {R}^{+}_0$ with
is again an ![]() $N$-function and
$N$-function and ![]() $(\varphi ^{\ast })'(t) = (\varphi ')^{-1}(t)$ for
$(\varphi ^{\ast })'(t) = (\varphi ')^{-1}(t)$ for ![]() $t>0$.
$t>0$. ![]() $\varphi ^{\ast }$ is the Young-Fenchel-Yosida conjugate function of
$\varphi ^{\ast }$ is the Young-Fenchel-Yosida conjugate function of ![]() $\varphi$. Note that
$\varphi$. Note that ![]() $\varphi ^{*}(t)= \sup _{a \geq 0} (at - \varphi (a))$ and
$\varphi ^{*}(t)= \sup _{a \geq 0} (at - \varphi (a))$ and ![]() $(\varphi ^{\ast })^{\ast } = \varphi$. When both
$(\varphi ^{\ast })^{\ast } = \varphi$. When both ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi ^{*}$ satisfy
$\varphi ^{*}$ satisfy ![]() $\Delta _2$-condition, by elementary convex analysis it is easy to see that for all
$\Delta _2$-condition, by elementary convex analysis it is easy to see that for all ![]() $\delta >0$ there exists
$\delta >0$ there exists ![]() $c_\delta$ (only depending on
$c_\delta$ (only depending on ![]() $\Delta _2(\varphi )$ and
$\Delta _2(\varphi )$ and ![]() $\Delta _2(\varphi ^{\ast })$) such that for all
$\Delta _2(\varphi ^{\ast })$) such that for all ![]() $t, a \geq 0$ it holds that
$t, a \geq 0$ it holds that
Proposition 2.1 Let ![]() $\varphi$ be an
$\varphi$ be an ![]() $N$-function complying with (φ1) and (φ2). Then
$N$-function complying with (φ1) and (φ2). Then
(i) it holds that
(2.1)uniformly in \begin{equation} \varphi'(t) \sim t\,\varphi''(t) \end{equation}
\begin{equation} \varphi'(t) \sim t\,\varphi''(t) \end{equation} $t > 0$. The constants in (2.1) are called the characteristics of
$t > 0$. The constants in (2.1) are called the characteristics of  $\varphi$;
$\varphi$;(ii) it holds that
 \begin{equation*} \mu_1\leq \inf_{t>0}\frac{t\varphi'(t)}{\varphi(t)}\leq \sup_{t>0}\frac{t\varphi'(t)}{\varphi(t)}\leq\mu_2\,; \end{equation*}
\begin{equation*} \mu_1\leq \inf_{t>0}\frac{t\varphi'(t)}{\varphi(t)}\leq \sup_{t>0}\frac{t\varphi'(t)}{\varphi(t)}\leq\mu_2\,; \end{equation*}(iii) the mappings
are increasing and decreasing, respectively; \begin{equation*} t\in(0,+\infty)\to \frac{\varphi'(t)}{t^{\mu_1-1}},\, \frac{\varphi(t)}{t^{\mu_1}} \mbox{ and } t\in(0,+\infty)\to \frac{\varphi'(t)}{t^{\mu_2-1}},\, \frac{\varphi(t)}{t^{\mu_2}} \end{equation*}
\begin{equation*} t\in(0,+\infty)\to \frac{\varphi'(t)}{t^{\mu_1-1}},\, \frac{\varphi(t)}{t^{\mu_1}} \mbox{ and } t\in(0,+\infty)\to \frac{\varphi'(t)}{t^{\mu_2-1}},\, \frac{\varphi(t)}{t^{\mu_2}} \end{equation*}(iv) as for the functions
 $\varphi$ and
$\varphi$ and  $\varphi '$ applied to multiples of given arguments, the following inequalities hold for every
$\varphi '$ applied to multiples of given arguments, the following inequalities hold for every  $t\geq 0$:
$t\geq 0$:
 \begin{align*} & a^{\mu_2}\varphi(t) \leq \varphi(at) \leq a^{\mu_1}\varphi(t) \mbox{ and } \\ &a^{\mu_2-1}\varphi'(t) \leq \varphi'(at) \leq a^{\mu_1-1}\varphi'(t) \mbox{ if } 0< a\leq 1\,; \\ & a^{\mu_1}\varphi(t) \leq \varphi(at) \leq a^{\mu_2}\varphi(t) \mbox{ and } \\ &a^{\mu_1-1}\varphi'(t) \leq \varphi'(at) \leq a^{\mu_2-1}\varphi'(t) \mbox{ if } a\geq 1. \end{align*}
\begin{align*} & a^{\mu_2}\varphi(t) \leq \varphi(at) \leq a^{\mu_1}\varphi(t) \mbox{ and } \\ &a^{\mu_2-1}\varphi'(t) \leq \varphi'(at) \leq a^{\mu_1-1}\varphi'(t) \mbox{ if } 0< a\leq 1\,; \\ & a^{\mu_1}\varphi(t) \leq \varphi(at) \leq a^{\mu_2}\varphi(t) \mbox{ and } \\ &a^{\mu_1-1}\varphi'(t) \leq \varphi'(at) \leq a^{\mu_2-1}\varphi'(t) \mbox{ if } a\geq 1. \end{align*}
In particular, from (iv) it follows that both ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi ^{*}$ satisfy the
$\varphi ^{*}$ satisfy the ![]() $\Delta _2$-condition with constants
$\Delta _2$-condition with constants ![]() $\Delta _2(\varphi )$ and
$\Delta _2(\varphi )$ and ![]() $\Delta _2(\varphi ^{*})$ determined by
$\Delta _2(\varphi ^{*})$ determined by ![]() $\mu _1$ and
$\mu _1$ and ![]() $\mu _2$. We will denote by
$\mu _2$. We will denote by ![]() $\Delta _2({\varphi , \varphi ^{\ast }})$ constants depending on
$\Delta _2({\varphi , \varphi ^{\ast }})$ constants depending on ![]() $\Delta _2(\varphi )$ and
$\Delta _2(\varphi )$ and ![]() $\Delta _2(\varphi ^{*})$. Moreover, for
$\Delta _2(\varphi ^{*})$. Moreover, for ![]() $t>0$ we have
$t>0$ we have
We recall also that the following inequalities hold for the inverse function ![]() $\varphi ^{-1}$:
$\varphi ^{-1}$:
for every ![]() $t\geq 0$ with
$t\geq 0$ with ![]() $0< a\leq 1$. The same result holds also for
$0< a\leq 1$. The same result holds also for ![]() $a\geq 1$ by exchanging the role of
$a\geq 1$ by exchanging the role of ![]() $\mu _1$ and
$\mu _1$ and ![]() $\mu _2$.
$\mu _2$.
For given ![]() $\varphi$ we define the associated
$\varphi$ we define the associated ![]() $N$-function
$N$-function ![]() $\psi$ by
$\psi$ by
Notice that if ![]() $\varphi$ satisfies assumption (2.1), then also
$\varphi$ satisfies assumption (2.1), then also ![]() $\varphi ^{*}$,
$\varphi ^{*}$, ![]() $\psi$ and
$\psi$ and ![]() $\psi ^{*}$ satisfy this assumption.
$\psi ^{*}$ satisfy this assumption.
Define ![]() ${\bf V}\,:\, \mathbb {R}^{N\times n} \to \mathbb {R}^{N\times n}$ in the following way:
${\bf V}\,:\, \mathbb {R}^{N\times n} \to \mathbb {R}^{N\times n}$ in the following way:
It is easy to check that
uniformly in ![]() ${\bf Q} \in \mathbb {R}^{N\times n}$.
${\bf Q} \in \mathbb {R}^{N\times n}$.
Another important set of tools are the shifted ![]() $N$-functions
$N$-functions ![]() $\{\varphi _a \}_{a \ge 0}$ (see [Reference Diening and Ettwein12]). We define for
$\{\varphi _a \}_{a \ge 0}$ (see [Reference Diening and Ettwein12]). We define for ![]() $t\geq 0$
$t\geq 0$
We have the following relations:
 \begin{align} \varphi_a(t) &\sim \varphi'_a(t)\,t\,; \nonumber\\ \varphi_a(t) &\sim \varphi''(a+t)t^{2}\sim\frac{\varphi(a+t)}{(a+t)^{2}}t^{2}\sim \frac{\varphi'(a+t)}{a+t}t^{2}, \end{align}
\begin{align} \varphi_a(t) &\sim \varphi'_a(t)\,t\,; \nonumber\\ \varphi_a(t) &\sim \varphi''(a+t)t^{2}\sim\frac{\varphi(a+t)}{(a+t)^{2}}t^{2}\sim \frac{\varphi'(a+t)}{a+t}t^{2}, \end{align}
The families ![]() $\{\varphi _a \}_{a \ge 0}$ and
$\{\varphi _a \}_{a \ge 0}$ and ![]() $\{(\varphi _a)^{*} \}_{a \ge 0}$ satisfy the
$\{(\varphi _a)^{*} \}_{a \ge 0}$ satisfy the ![]() $\Delta _2$-condition uniformly in
$\Delta _2$-condition uniformly in ![]() $a \ge 0$. The connection between
$a \ge 0$. The connection between ![]() ${\bf V}$ and
${\bf V}$ and ![]() $\varphi _{a}$ (see [Reference Diening and Ettwein12]) is the following:
$\varphi _{a}$ (see [Reference Diening and Ettwein12]) is the following:
uniformly in ![]() ${\bf P}, {\bf Q} \in \mathbb {R}^{N\times n}$. The following lemma (see [Reference Diening and Kreuzer14, corollary 26]) deals with the change of shift for
${\bf P}, {\bf Q} \in \mathbb {R}^{N\times n}$. The following lemma (see [Reference Diening and Kreuzer14, corollary 26]) deals with the change of shift for ![]() $N$-functions.
$N$-functions.
Lemma 2.2 Let ![]() $\varphi$ be an
$\varphi$ be an ![]() $N$-function with
$N$-function with ![]() $\Delta _2(\varphi ),\Delta _2(\varphi ^{*})<\infty$. Then for any
$\Delta _2(\varphi ),\Delta _2(\varphi ^{*})<\infty$. Then for any ![]() $\eta >0$ there exists
$\eta >0$ there exists ![]() $c_\eta >0$, depending only on
$c_\eta >0$, depending only on ![]() $\eta$ and
$\eta$ and ![]() $\Delta _2(\varphi )$, such that for all
$\Delta _2(\varphi )$, such that for all ![]() ${\bf a}, {\bf b}\in \mathbb {R}^{d}$ and
${\bf a}, {\bf b}\in \mathbb {R}^{d}$ and ![]() $t\geq 0$
$t\geq 0$
We define the function ![]() ${\bf V}_a : \mathbb {R}^{N\times n}\to \mathbb {R}^{N\times n}$ for
${\bf V}_a : \mathbb {R}^{N\times n}\to \mathbb {R}^{N\times n}$ for ![]() $a\geq 0$ by
$a\geq 0$ by
where ![]() $\varphi _a$ is the shifted
$\varphi _a$ is the shifted ![]() $N$-function of
$N$-function of ![]() $\varphi$. Since
$\varphi$. Since ![]() $\varphi _0=\varphi$, we retrieve in (2.8) the function
$\varphi _0=\varphi$, we retrieve in (2.8) the function ![]() ${\bf V}$ for
${\bf V}$ for ![]() $a=0$. With the following lemma, we list some properties of functions
$a=0$. With the following lemma, we list some properties of functions ![]() ${\bf V}_a$ which will be useful in the sequel.
${\bf V}_a$ which will be useful in the sequel.
Lemma 2.3 Let ![]() $a\geq 0$ and
$a\geq 0$ and ![]() ${\bf V}_a$ be as above. Then for any
${\bf V}_a$ be as above. Then for any ![]() ${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$ a Young-type inequality holds:
${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$ a Young-type inequality holds:
where the constant ![]() $c$ depends only on
$c$ depends only on ![]() $\Delta _2(\varphi )$.
$\Delta _2(\varphi )$.
Let ![]() ${\bf {P}}_0,{\bf {P}}_1\in \mathbb {R}^{N\times n}$,
${\bf {P}}_0,{\bf {P}}_1\in \mathbb {R}^{N\times n}$, ![]() $\theta \in [0,1]$ and define
$\theta \in [0,1]$ and define ![]() ${\bf {P}}_{\theta }:=(1-\theta ){\bf {P}}_0+\theta {\bf {P}}_1$. Then the following result holds (see [Reference Diening and Ettwein12, lemma 20]).
${\bf {P}}_{\theta }:=(1-\theta ){\bf {P}}_0+\theta {\bf {P}}_1$. Then the following result holds (see [Reference Diening and Ettwein12, lemma 20]).
Lemma 2.4 Let ![]() $\varphi$ be a
$\varphi$ be a ![]() $N$-function with
$N$-function with ![]() $\Delta _2(\varphi , \varphi ^{*})<\infty .$ Then uniformly for all
$\Delta _2(\varphi , \varphi ^{*})<\infty .$ Then uniformly for all ![]() ${\bf {P}}_0,{\bf {P}}_1\in \mathbb {R}^{N\times n}$ with
${\bf {P}}_0,{\bf {P}}_1\in \mathbb {R}^{N\times n}$ with ![]() $|{\bf {P}}_0|+|{\bf {P}}_1|>0$ holds
$|{\bf {P}}_0|+|{\bf {P}}_1|>0$ holds
where the constants only depend on ![]() $\Delta _2(\varphi , \varphi ^{*}).$
$\Delta _2(\varphi , \varphi ^{*}).$
In view of the previous considerations, the same proposition holds true for the shifted functions, uniformly in ![]() $a\ge 0$.
$a\ge 0$.
From assumption (F2) we can easily infer an upper bound for ![]() $f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf Q})$, uniformly in
$f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf Q})$, uniformly in ![]() $x\in \Omega$ and
$x\in \Omega$ and ![]() ${\bf u}\in \mathbb {R}^{N}$, for every
${\bf u}\in \mathbb {R}^{N}$, for every ![]() ${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$; namely,
${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$; namely,
 \begin{equation} \begin{split} |f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf Q})| & \leq |{\bf P}-{\bf Q}|\int_0^{1} |Df(x,{\bf u},{\bf P}+t({\bf Q}-{\bf P}))|\,\mathrm{d}t \\ & \leq L|{\bf P}-{\bf Q}|\int_0^{1}\varphi'(|{\bf P}+t({\bf Q}-{\bf P})|)\,\mathrm{d}t \\ & \leq cL \varphi(|{\bf P}|+|{\bf Q}|). \end{split} \end{equation}
\begin{equation} \begin{split} |f(x,{\bf u},{\bf P})-f(x,{\bf u},{\bf Q})| & \leq |{\bf P}-{\bf Q}|\int_0^{1} |Df(x,{\bf u},{\bf P}+t({\bf Q}-{\bf P}))|\,\mathrm{d}t \\ & \leq L|{\bf P}-{\bf Q}|\int_0^{1}\varphi'(|{\bf P}+t({\bf Q}-{\bf P})|)\,\mathrm{d}t \\ & \leq cL \varphi(|{\bf P}|+|{\bf Q}|). \end{split} \end{equation}The following estimate is a consequence of (F2) and lemma 2.4 (see [Reference Diening, Lengeler, Stroffolini and Verde17, eq. (2.14)]):
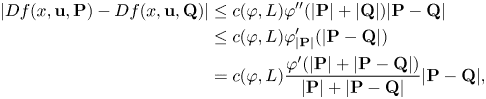 \begin{equation} \begin{split} |Df(x,{\bf u},{\bf P})-Df(x,{\bf u},{\bf Q})| & \leq c(\varphi,L) \varphi''(|{\bf P}|+|{\bf Q}|)|{\bf P}-{\bf Q}|\\ & \leq c(\varphi,L) \varphi'_{|{\bf P}|}(|{\bf P}-{\bf Q}|)\\ & = c(\varphi,L) \frac{\varphi'(|{\bf P}|+|{\bf P}-{\bf Q}|)}{|{\bf P}|+|{\bf P}-{\bf Q}|}|{\bf P}-{\bf Q}|, \end{split} \end{equation}
\begin{equation} \begin{split} |Df(x,{\bf u},{\bf P})-Df(x,{\bf u},{\bf Q})| & \leq c(\varphi,L) \varphi''(|{\bf P}|+|{\bf Q}|)|{\bf P}-{\bf Q}|\\ & \leq c(\varphi,L) \varphi'_{|{\bf P}|}(|{\bf P}-{\bf Q}|)\\ & = c(\varphi,L) \frac{\varphi'(|{\bf P}|+|{\bf P}-{\bf Q}|)}{|{\bf P}|+|{\bf P}-{\bf Q}|}|{\bf P}-{\bf Q}|, \end{split} \end{equation}
for every ![]() ${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$.
${\bf P}, {\bf Q}\in \mathbb {R}^{N\times n}$.
The following version of Sobolev-Poincaré inequality can be found in [Reference Diening and Ettwein12, lemma 7].
Theorem 2.5 Let ![]() $\varphi$ be an
$\varphi$ be an ![]() $N$-function with
$N$-function with ![]() $\Delta _2(\varphi ,\varphi ^{*})<+\infty$. Then there exist numbers
$\Delta _2(\varphi ,\varphi ^{*})<+\infty$. Then there exist numbers ![]() $\alpha =\alpha (n,\Delta _2(\varphi ,\varphi ^{*}))\in (0,1)$ and
$\alpha =\alpha (n,\Delta _2(\varphi ,\varphi ^{*}))\in (0,1)$ and ![]() $K=K(n,N,\Delta _2(\varphi ,\varphi ^{*}))>0$ such that the following holds. If
$K=K(n,N,\Delta _2(\varphi ,\varphi ^{*}))>0$ such that the following holds. If ![]() $B\subset \mathbb {R}^{n}$ is any ball with radius
$B\subset \mathbb {R}^{n}$ is any ball with radius ![]() $R$ and
$R$ and ![]() ${\bf w}\in W^{1,\varphi }(B,\mathbb {R}^{N})$, then
${\bf w}\in W^{1,\varphi }(B,\mathbb {R}^{N})$, then
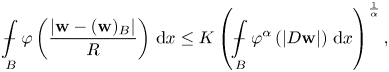 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_B \varphi\left(\frac{|{\bf w}-({\bf w})_B|}{R}\right)\,\mathrm{d}x\leq K \left(\mathop {\int\hskip -1,05em -\,} \limits_B \varphi^{\alpha}\left({|D{\bf w}|}\right)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}, \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_B \varphi\left(\frac{|{\bf w}-({\bf w})_B|}{R}\right)\,\mathrm{d}x\leq K \left(\mathop {\int\hskip -1,05em -\,} \limits_B \varphi^{\alpha}\left({|D{\bf w}|}\right)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}, \end{equation}
where 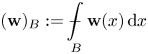 $\displaystyle ({\bf w})_B:=\mathop {\int\hskip -1,05em -\,} \limits_B {\bf w}(x)\,\mathrm {d}x$. Moreover, if
$\displaystyle ({\bf w})_B:=\mathop {\int\hskip -1,05em -\,} \limits_B {\bf w}(x)\,\mathrm {d}x$. Moreover, if ![]() ${\bf w}\in W^{1,\varphi }_0(B,\mathbb {R}^{N})$, then
${\bf w}\in W^{1,\varphi }_0(B,\mathbb {R}^{N})$, then
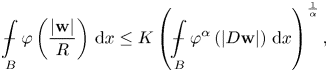 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \varphi\left(\frac{|{\bf w}|}{R}\right)\,\mathrm{d}x\leq K \left(\mathop {\int\hskip -1,05em -\,} \limits_B \varphi^{\alpha}\left({|D{\bf w}|}\right)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}, \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \varphi\left(\frac{|{\bf w}|}{R}\right)\,\mathrm{d}x\leq K \left(\mathop {\int\hskip -1,05em -\,} \limits_B \varphi^{\alpha}\left({|D{\bf w}|}\right)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}, \end{equation*}
where ![]() $K$ and
$K$ and ![]() $\alpha$ have the same dependencies as before.
$\alpha$ have the same dependencies as before.
2.2 Some useful lemmas
The following lemma, useful in order to re-absorb certain terms, is a variant of the classical [Reference Giusti25, lemma 6.1] (see [Reference Diening, Lengeler, Stroffolini and Verde17, lemma 3.1]).
Lemma 2.6 Let ![]() $\psi$ be an
$\psi$ be an ![]() $N$-function with
$N$-function with ![]() $\psi \in \Delta _2$, let
$\psi \in \Delta _2$, let ![]() $\varrho >0$ and
$\varrho >0$ and ![]() $h\in L^{\psi }(B_{\varrho }(x_0))$. Let
$h\in L^{\psi }(B_{\varrho }(x_0))$. Let ![]() $g:[r,\varrho ]\to \mathbb {R}$ be nonnegative and bounded such that for all
$g:[r,\varrho ]\to \mathbb {R}$ be nonnegative and bounded such that for all ![]() $r\leq s< t\leq \varrho$
$r\leq s< t\leq \varrho$
where ![]() $A,B,C\geq 0$,
$A,B,C\geq 0$, ![]() $\beta >0$ and
$\beta >0$ and ![]() $\theta \in [0,1)$. Then
$\theta \in [0,1)$. Then
 \begin{equation*} g\left(r\right)\leq c(\theta,\Delta_2(\psi),\beta)\left[A\int_{B_{\varrho}(x_0)}\psi\left(\frac{|h(y)|}{\varrho-r}\right)\,\mathrm{d}y + \frac{B}{(\varrho-r)^{\beta}}+C\right]. \end{equation*}
\begin{equation*} g\left(r\right)\leq c(\theta,\Delta_2(\psi),\beta)\left[A\int_{B_{\varrho}(x_0)}\psi\left(\frac{|h(y)|}{\varrho-r}\right)\,\mathrm{d}y + \frac{B}{(\varrho-r)^{\beta}}+C\right]. \end{equation*}The following lemma is useful to derive reverse Hölder estimates. It is a variant of the results by Gehring [Reference Gehring24] and Giaquinta-Modica [Reference Giusti25, theorem 6.6].
Lemma 2.7 Let ![]() $B_0\subset \mathbb {R}^{n}$ be a ball,
$B_0\subset \mathbb {R}^{n}$ be a ball, ![]() $f\in L^{1}(B_0)$, and
$f\in L^{1}(B_0)$, and ![]() $g\in L^{\sigma _0}(B_0)$ for some
$g\in L^{\sigma _0}(B_0)$ for some ![]() $\sigma _0>1$. Assume that for some
$\sigma _0>1$. Assume that for some ![]() $\theta \in (0,1)$,
$\theta \in (0,1)$, ![]() $c_1>0$ and all balls
$c_1>0$ and all balls ![]() $B$ with
$B$ with ![]() $2B\subset B_0$
$2B\subset B_0$
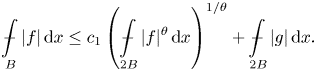 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B |f|\,\mathrm{d}x\leq c_1 \left(\mathop {\int\hskip -1,05em -\,} \limits_{2B}|f|^{\theta}\,\mathrm{d}x\right)^{1/\theta} + \mathop {\int\hskip -1,05em -\,} \limits_{2B}|g|\,\mathrm{d}x. \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B |f|\,\mathrm{d}x\leq c_1 \left(\mathop {\int\hskip -1,05em -\,} \limits_{2B}|f|^{\theta}\,\mathrm{d}x\right)^{1/\theta} + \mathop {\int\hskip -1,05em -\,} \limits_{2B}|g|\,\mathrm{d}x. \end{equation*}
Then there exist ![]() $\sigma _1>1$ and
$\sigma _1>1$ and ![]() $c_2>1$ such that
$c_2>1$ such that ![]() $g\in L^{\sigma _1}_\textrm {loc}(B)$ and for all
$g\in L^{\sigma _1}_\textrm {loc}(B)$ and for all ![]() $\sigma _2\in [1,\sigma _1]$
$\sigma _2\in [1,\sigma _1]$
 \begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B}|f|^{\sigma_2}\,\mathrm{d}x\right)^{1/{\sigma_2}}\leq c_2 \mathop {\int\hskip -1,05em -\,} \limits_{2B}|f|\,\mathrm{d}x + c_2 \left(\mathop {\int\hskip -1,05em -\,} \limits_{2B}|g|^{\sigma_2}\,\mathrm{d}x\right)^{1/{\sigma_2}}. \end{equation*}
\begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B}|f|^{\sigma_2}\,\mathrm{d}x\right)^{1/{\sigma_2}}\leq c_2 \mathop {\int\hskip -1,05em -\,} \limits_{2B}|f|\,\mathrm{d}x + c_2 \left(\mathop {\int\hskip -1,05em -\,} \limits_{2B}|g|^{\sigma_2}\,\mathrm{d}x\right)^{1/{\sigma_2}}. \end{equation*}2.3  $\mathcal {A}$-harmonic and
$\mathcal {A}$-harmonic and  $\varphi$-harmonic functions
$\varphi$-harmonic functions
Let ![]() $\mathcal {A}$ be a bilinear form on
$\mathcal {A}$ be a bilinear form on ![]() $\mathbb {R}^{N\times n}$. We say that
$\mathbb {R}^{N\times n}$. We say that ![]() $\mathcal {A}$ is strongly elliptic in the sense of Legendre-Hadamard if for all
$\mathcal {A}$ is strongly elliptic in the sense of Legendre-Hadamard if for all ![]() $\boldsymbol \xi \in \mathbb {R}^{N},\boldsymbol \zeta \in \mathbb {R}^{n}$ it holds that
$\boldsymbol \xi \in \mathbb {R}^{N},\boldsymbol \zeta \in \mathbb {R}^{n}$ it holds that
for some ![]() $L_{\mathcal {A}}\geq {{\kappa _{\!\mathcal {A}}}}>0$. We say that a Sobolev function
$L_{\mathcal {A}}\geq {{\kappa _{\!\mathcal {A}}}}>0$. We say that a Sobolev function ![]() ${\bf w}$ on a ball
${\bf w}$ on a ball ![]() $B_\varrho (x_0)$ is
$B_\varrho (x_0)$ is ![]() $\mathcal {A}$-harmonic on
$\mathcal {A}$-harmonic on ![]() $B_\varrho (x_0)$ if it satisfies
$B_\varrho (x_0)$ if it satisfies ![]() $-{ {\mathrm {div}}} (\mathcal {A}D {\bf w})=0$ in the sense of distributions; i.e.,
$-{ {\mathrm {div}}} (\mathcal {A}D {\bf w})=0$ in the sense of distributions; i.e.,
It is well known from the classical theory (see, e.g. [Reference Giusti25, chapter 10]) that ![]() ${\bf w}$ is smooth in the interior of
${\bf w}$ is smooth in the interior of ![]() $B_\varrho (x_0)$, and it satisfies the estimate
$B_\varrho (x_0)$, and it satisfies the estimate
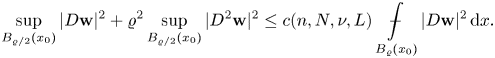 \begin{equation} \sup_{B_{\varrho/2}(x_0)}|D {\bf w}|^{2}+\varrho^{2} \sup_{B_{\varrho/2}(x_0)}|D^{2} {\bf w}|^{2}\leq c(n,N,\nu,L) \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|D{\bf w}|^{2}\,\mathrm{d}x. \end{equation}
\begin{equation} \sup_{B_{\varrho/2}(x_0)}|D {\bf w}|^{2}+\varrho^{2} \sup_{B_{\varrho/2}(x_0)}|D^{2} {\bf w}|^{2}\leq c(n,N,\nu,L) \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|D{\bf w}|^{2}\,\mathrm{d}x. \end{equation}
Let ![]() $\varphi$ be an Orlicz function. We say that a map
$\varphi$ be an Orlicz function. We say that a map ![]() ${\bf w}\in W^{1,\varphi }(B_\varrho (x_0),\mathbb {R}^{N})$ is
${\bf w}\in W^{1,\varphi }(B_\varrho (x_0),\mathbb {R}^{N})$ is ![]() $\varphi$-harmonic on
$\varphi$-harmonic on ![]() $B_\varrho (x_0)$ (see [Reference Diening, Stroffolini and Verde16]) if and only if
$B_\varrho (x_0)$ (see [Reference Diening, Stroffolini and Verde16]) if and only if
More precisely, ![]() $D{\bf w}$ and
$D{\bf w}$ and ![]() ${\bf V}(D{\bf w})$ are Hölder continuous due to the following decay estimate, see [Reference Diening, Stroffolini and Verde15].
${\bf V}(D{\bf w})$ are Hölder continuous due to the following decay estimate, see [Reference Diening, Stroffolini and Verde15].
Proposition 2.8 Let ![]() $\varphi$ be a convex function complying with (φ1), (φ2) and
$\varphi$ be a convex function complying with (φ1), (φ2) and
(φ3)
 \begin{align*} \hspace{0.5cm} & \varphi' \text{ is H}\unicode{x04E7}\text{lder continuous off the diagonal:} \hspace{1cm}\\ & \hspace{2cm} \left|\varphi''(s+t)-\varphi''(t)\right|\leq c_0\, \varphi'' (t)\, \bigg( \frac{\left|s\right|}{t} \bigg)^{\beta_0}, \quad \beta_0>0, \hspace{1cm}\\ & \text{ for all } t>0 \text{ and } s \in \mathbb{R} \text{ with } \left|s\right| < \frac{1}{2} t. \end{align*}
\begin{align*} \hspace{0.5cm} & \varphi' \text{ is H}\unicode{x04E7}\text{lder continuous off the diagonal:} \hspace{1cm}\\ & \hspace{2cm} \left|\varphi''(s+t)-\varphi''(t)\right|\leq c_0\, \varphi'' (t)\, \bigg( \frac{\left|s\right|}{t} \bigg)^{\beta_0}, \quad \beta_0>0, \hspace{1cm}\\ & \text{ for all } t>0 \text{ and } s \in \mathbb{R} \text{ with } \left|s\right| < \frac{1}{2} t. \end{align*}
Then there exist a constant ![]() $c\geq 1$ and an exponent
$c\geq 1$ and an exponent ![]() $\gamma _0 \in (0,1)$ depending only on
$\gamma _0 \in (0,1)$ depending only on ![]() $n,N$ and the characteristics of
$n,N$ and the characteristics of ![]() $\varphi$, such that the following statement holds true: whenever
$\varphi$, such that the following statement holds true: whenever ![]() ${\bf w} \in W^{1,\varphi }(B_{R}(x_0),\mathbb {R}^{N})$ is a weak solution of the system
${\bf w} \in W^{1,\varphi }(B_{R}(x_0),\mathbb {R}^{N})$ is a weak solution of the system
then for every ![]() $\tau \in (0,1)$ there hold
$\tau \in (0,1)$ there hold
 \begin{align*} &\sup_{B_{\tau R/2}(x_0)} \varphi({\vert{D {\bf w}}\vert})\leq c \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau R}(x_0)}} \varphi({\vert{D {\bf w}}\vert})\,\mathrm{d}x, \\ &\mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau R}(x_0)}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{x_0,{\tau R}}}\vert}^{2} \, \mathrm{d}x \\ &\quad \leq c \tau^{2 \gamma_0} \, \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_R(x_0)}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{x_0,R}}\vert}^{2} \, \mathrm{d}x. \end{align*}
\begin{align*} &\sup_{B_{\tau R/2}(x_0)} \varphi({\vert{D {\bf w}}\vert})\leq c \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau R}(x_0)}} \varphi({\vert{D {\bf w}}\vert})\,\mathrm{d}x, \\ &\mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau R}(x_0)}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{x_0,{\tau R}}}\vert}^{2} \, \mathrm{d}x \\ &\quad \leq c \tau^{2 \gamma_0} \, \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_R(x_0)}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{x_0,R}}\vert}^{2} \, \mathrm{d}x. \end{align*} This result can be viewed as the Orlicz version of the milestone theorem of Uhlenbeck [Reference Uhlenbeck41] for differential forms solving a ![]() $p$-harmonic system, see also [Reference Beck and Stroffolini2].
$p$-harmonic system, see also [Reference Beck and Stroffolini2].
2.4 Harmonic type approximation results
We recall here two different harmonic type approximation results. The first one is the ![]() $\mathcal {A}$-harmonic approximation: given a Sobolev function
$\mathcal {A}$-harmonic approximation: given a Sobolev function ![]() ${\bf u}$ on a ball
${\bf u}$ on a ball ![]() $B$, we want to find an
$B$, we want to find an ![]() $\mathcal {A}$-harmonic function
$\mathcal {A}$-harmonic function ![]() ${\bf w}$ which is ‘close’ to the function
${\bf w}$ which is ‘close’ to the function ![]() ${\bf u}$. It will be the
${\bf u}$. It will be the ![]() $\mathcal {A}$-harmonic function with the same boundary values as
$\mathcal {A}$-harmonic function with the same boundary values as ![]() ${\bf u}$; i.e., a Sobolev function
${\bf u}$; i.e., a Sobolev function ![]() ${\bf w}$ which satisfies
${\bf w}$ which satisfies
 \begin{equation} \begin{cases} -{{\mathrm{div}}} (\mathcal{A} D {\bf w})= 0 & \qquad\text{on } B \\ {\bf w}= {\bf u} & \qquad\text{on } \partial B \end{cases} \end{equation}
\begin{equation} \begin{cases} -{{\mathrm{div}}} (\mathcal{A} D {\bf w})= 0 & \qquad\text{on } B \\ {\bf w}= {\bf u} & \qquad\text{on } \partial B \end{cases} \end{equation}in the sense of distributions.
Setting ![]() ${\bf z} := {\bf w} - {\bf u}$, then (2.15) is equivalent to finding a Sobolev function
${\bf z} := {\bf w} - {\bf u}$, then (2.15) is equivalent to finding a Sobolev function ![]() ${\bf z}$ which satisfies
${\bf z}$ which satisfies
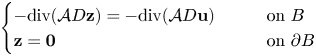 \begin{equation} \begin{cases} -{{\mathrm{div}}} (\mathcal{A} D {\bf z}) ={-}{{\mathrm{div}}}(\mathcal{A} D {\bf u}) & \qquad\text{on } B \\ {\bf z}= {{\mathbf{0}}} & \qquad\text{on } \partial B \end{cases} \end{equation}
\begin{equation} \begin{cases} -{{\mathrm{div}}} (\mathcal{A} D {\bf z}) ={-}{{\mathrm{div}}}(\mathcal{A} D {\bf u}) & \qquad\text{on } B \\ {\bf z}= {{\mathbf{0}}} & \qquad\text{on } \partial B \end{cases} \end{equation}in the sense of distributions.
The following ![]() $\mathcal {A}$-harmonic approximation result in the setting of Orlicz spaces has been proved in [Reference Diening, Lengeler, Stroffolini and Verde17, theorem 14].
$\mathcal {A}$-harmonic approximation result in the setting of Orlicz spaces has been proved in [Reference Diening, Lengeler, Stroffolini and Verde17, theorem 14].
Theorem 2.9 Let ![]() $B \subset \subset \Omega$ be a ball with radius
$B \subset \subset \Omega$ be a ball with radius ![]() $r_B$ and let
$r_B$ and let ![]() $\widetilde {B} \subset \Omega$ denote either
$\widetilde {B} \subset \Omega$ denote either ![]() $B$ or
$B$ or ![]() $2B$. Let
$2B$. Let ![]() $\mathcal {A}$ be a strongly elliptic (in the sense of Legendre-Hadamard) bilinear form on
$\mathcal {A}$ be a strongly elliptic (in the sense of Legendre-Hadamard) bilinear form on ![]() $\mathbb {R}^{N\times n}$. Let
$\mathbb {R}^{N\times n}$. Let ![]() $\psi$ be an N-function with
$\psi$ be an N-function with ![]() $\psi \in \Delta _2(\psi , \psi ^{*})$ and let
$\psi \in \Delta _2(\psi , \psi ^{*})$ and let ![]() $s>1$. Then for every
$s>1$. Then for every ![]() $\varepsilon >0$, there exists
$\varepsilon >0$, there exists ![]() $\delta >0$ only depending on
$\delta >0$ only depending on ![]() $n$,
$n$, ![]() $N$,
$N$, ![]() $\kappa _A$,
$\kappa _A$, ![]() $\lvert {\mathcal {A}}\rvert$,
$\lvert {\mathcal {A}}\rvert$, ![]() $\Delta _2(\psi ,\psi ^{*})$ and
$\Delta _2(\psi ,\psi ^{*})$ and ![]() $s>1$ such that the following holds. Let
$s>1$ such that the following holds. Let ![]() ${\bf u} \in W^{1,\psi }(\widetilde {B},\mathbb {R}^{N})$ be almost
${\bf u} \in W^{1,\psi }(\widetilde {B},\mathbb {R}^{N})$ be almost ![]() $\mathcal {A}$-harmonic on
$\mathcal {A}$-harmonic on ![]() $B$ in the sense that
$B$ in the sense that
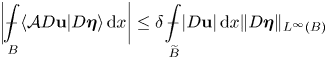 \begin{align} \bigg\lvert{\mathop {\int\hskip -1,05em -\,} \limits_B \langle\mathcal{A}D {\bf u} | D \boldsymbol\eta\rangle\,\mathrm{d}x}\bigg\rvert \leq \delta \mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \lvert{D {\bf u}}\rvert\,\mathrm{d}x \lVert{D \boldsymbol\eta}\rVert_{L^{\infty}(B)} \end{align}
\begin{align} \bigg\lvert{\mathop {\int\hskip -1,05em -\,} \limits_B \langle\mathcal{A}D {\bf u} | D \boldsymbol\eta\rangle\,\mathrm{d}x}\bigg\rvert \leq \delta \mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \lvert{D {\bf u}}\rvert\,\mathrm{d}x \lVert{D \boldsymbol\eta}\rVert_{L^{\infty}(B)} \end{align}
for all ![]() $\boldsymbol \eta \in C^{\infty }_0(B,\mathbb {R}^{N})$. Then the unique solution
$\boldsymbol \eta \in C^{\infty }_0(B,\mathbb {R}^{N})$. Then the unique solution ![]() ${\bf z} \in W^{1, \psi }_0(B,\mathbb {R}^{N})$ of (2.16) satisfies
${\bf z} \in W^{1, \psi }_0(B,\mathbb {R}^{N})$ of (2.16) satisfies
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \psi\bigg(\frac{\lvert{{\bf z}}\rvert}{r_B}\bigg)\,\mathrm{d}x + \mathop {\int\hskip -1,05em -\,} \limits_B \psi(\lvert{D {\bf z}}\rvert)\,\mathrm{d}x \leq \varepsilon \left(\bigg(\mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \big(\psi(\lvert{D {\bf u}}\rvert)\big)^{s} \,\mathrm{d}x\bigg)^{\frac 1s}+\mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \psi(\lvert{D {\bf u}}\rvert)\,\mathrm{d}x\right). \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \psi\bigg(\frac{\lvert{{\bf z}}\rvert}{r_B}\bigg)\,\mathrm{d}x + \mathop {\int\hskip -1,05em -\,} \limits_B \psi(\lvert{D {\bf z}}\rvert)\,\mathrm{d}x \leq \varepsilon \left(\bigg(\mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \big(\psi(\lvert{D {\bf u}}\rvert)\big)^{s} \,\mathrm{d}x\bigg)^{\frac 1s}+\mathop {\int\hskip -1,05em -\,} \limits_{\widetilde{B}} \psi(\lvert{D {\bf u}}\rvert)\,\mathrm{d}x\right). \end{equation*}Remark 2.10 We will exploit the previous approximation result in a slightly modified version. Indeed, following [Reference Celada and Ok7, lemma 2.7], under the additional assumption
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}} \psi(|D{\bf u}|)\,\mathrm{d}x \leq \left(\mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}} [\psi(|D{\bf u}|)]^{s}\,\mathrm{d}x\right)^{\frac{1}{s}}\leq \psi(\mu) \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}} \psi(|D{\bf u}|)\,\mathrm{d}x \leq \left(\mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}} [\psi(|D{\bf u}|)]^{s}\,\mathrm{d}x\right)^{\frac{1}{s}}\leq \psi(\mu) \end{equation*}
for some exponent ![]() $s>1$ and for a constant
$s>1$ and for a constant ![]() $\mu >0$, and (2.17) replaced by
$\mu >0$, and (2.17) replaced by
 \begin{equation*} \bigg\lvert{\mathop {\int\hskip -1,05em -\,} \limits_B \langle\mathcal{A}D {\bf u} | D \boldsymbol\eta\rangle\,\mathrm{d}x}\bigg\rvert \leq \delta \mu \lVert{D \boldsymbol\eta}\rVert_{L^{\infty}(B)}, \end{equation*}
\begin{equation*} \bigg\lvert{\mathop {\int\hskip -1,05em -\,} \limits_B \langle\mathcal{A}D {\bf u} | D \boldsymbol\eta\rangle\,\mathrm{d}x}\bigg\rvert \leq \delta \mu \lVert{D \boldsymbol\eta}\rVert_{L^{\infty}(B)}, \end{equation*}
it can be seen with minor changes in the proof that the unique solution ![]() ${\bf z} \in W^{1, \psi }_0(B,\mathbb {R}^{N})$ of (2.16) satisfies
${\bf z} \in W^{1, \psi }_0(B,\mathbb {R}^{N})$ of (2.16) satisfies
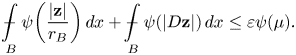 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \psi\bigg(\frac{\lvert{{\bf z}}\rvert}{r_B}\bigg)\,dx + \mathop {\int\hskip -1,05em -\,} \limits_B \psi(\lvert{D {\bf z}}\rvert)\,dx \leq \varepsilon \psi(\mu). \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_B \psi\bigg(\frac{\lvert{{\bf z}}\rvert}{r_B}\bigg)\,dx + \mathop {\int\hskip -1,05em -\,} \limits_B \psi(\lvert{D {\bf z}}\rvert)\,dx \leq \varepsilon \psi(\mu). \end{equation*} Now, moving on to ![]() $\varphi$-harmonic functions, the following
$\varphi$-harmonic functions, the following ![]() $\varphi$-harmonic approximation lemma ([Reference Diening, Stroffolini and Verde16, lemma 1.1]) is the extension to general convex functions of the
$\varphi$-harmonic approximation lemma ([Reference Diening, Stroffolini and Verde16, lemma 1.1]) is the extension to general convex functions of the ![]() $p$-harmonic approximation lemma [Reference Duzaar and Mingione21], [Reference Duzaar and Mingione22, lemma 1], and allows to approximate ‘almost
$p$-harmonic approximation lemma [Reference Duzaar and Mingione21], [Reference Duzaar and Mingione22, lemma 1], and allows to approximate ‘almost ![]() $\varphi$-harmonic’ functions by
$\varphi$-harmonic’ functions by ![]() $\varphi$-harmonic functions.
$\varphi$-harmonic functions.
Lemma 2.11 Let ![]() $\varphi$ satisfy assumption (2.1). For every
$\varphi$ satisfy assumption (2.1). For every ![]() $\varepsilon >0$ and
$\varepsilon >0$ and ![]() $\theta \in (0,1)$ there exists
$\theta \in (0,1)$ there exists ![]() $\delta >0$ which only depends on
$\delta >0$ which only depends on ![]() $\varepsilon$,
$\varepsilon$, ![]() $\theta$, and the characteristics of
$\theta$, and the characteristics of ![]() $\varphi$ such that the following holds. Let
$\varphi$ such that the following holds. Let ![]() $B\subset \mathbb {R}^{n}$ be a ball and let
$B\subset \mathbb {R}^{n}$ be a ball and let ![]() $\tilde {B}$ denote either
$\tilde {B}$ denote either ![]() $B$ or
$B$ or ![]() $2B$. If
$2B$. If ![]() ${\bf u}\in W^{1,\varphi }(\tilde {B},\mathbb {R}^{N})$ is almost
${\bf u}\in W^{1,\varphi }(\tilde {B},\mathbb {R}^{N})$ is almost ![]() $\varphi$-harmonic on a ball
$\varphi$-harmonic on a ball ![]() $B\subset \mathbb {R}^{n}$ in the sense that
$B\subset \mathbb {R}^{n}$ in the sense that
 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_B \left\langle\frac{\varphi'(|D{\bf u}|)}{|D{\bf u}|}D{\bf u}\biggl|D\boldsymbol\eta\right\rangle\,\mathrm{d}x \leq \delta\left(\mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}}\varphi(|D{\bf u}|)\,\mathrm{d}x+\varphi(\|D\boldsymbol\eta\|_\infty)\right) \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_B \left\langle\frac{\varphi'(|D{\bf u}|)}{|D{\bf u}|}D{\bf u}\biggl|D\boldsymbol\eta\right\rangle\,\mathrm{d}x \leq \delta\left(\mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}}\varphi(|D{\bf u}|)\,\mathrm{d}x+\varphi(\|D\boldsymbol\eta\|_\infty)\right) \end{equation}
for all ![]() $\boldsymbol \eta \in C^{\infty }_0(B,\mathbb {R}^{N})$, then the unique
$\boldsymbol \eta \in C^{\infty }_0(B,\mathbb {R}^{N})$, then the unique ![]() $\varphi$-harmonic
$\varphi$-harmonic ![]() ${\bf w}\in W^{1,\varphi }(B,\mathbb {R}^{N})$ with
${\bf w}\in W^{1,\varphi }(B,\mathbb {R}^{N})$ with ![]() ${\bf w}={\bf u}$ on
${\bf w}={\bf u}$ on ![]() $\partial B$ satisfies
$\partial B$ satisfies
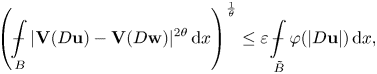 \begin{equation} \left(\mathop {\int\hskip -1,05em -\,} \limits_B |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2\theta}\,\mathrm{d}x\right)^{\frac{1}{\theta}}\leq \varepsilon \mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation}
\begin{equation} \left(\mathop {\int\hskip -1,05em -\,} \limits_B |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2\theta}\,\mathrm{d}x\right)^{\frac{1}{\theta}}\leq \varepsilon \mathop {\int\hskip -1,05em -\,} \limits_{\tilde{B}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation}
where ![]() ${\bf V}$ is as in (2.3).
${\bf V}$ is as in (2.3).
The estimate (2.19) can be improved when ![]() $\varphi (|D{\bf u}|)$ satisfies a reverse Hölder inequality as follows (see [Reference Celada and Ok7, corollary 2.10]).
$\varphi (|D{\bf u}|)$ satisfies a reverse Hölder inequality as follows (see [Reference Celada and Ok7, corollary 2.10]).
Lemma 2.12 Let ![]() $B\subset \mathbb {R}^{n}$ be a ball. Let
$B\subset \mathbb {R}^{n}$ be a ball. Let ![]() ${\bf u}\in W^{1,\varphi }(2B,\mathbb {R}^{N})$ be such that
${\bf u}\in W^{1,\varphi }(2B,\mathbb {R}^{N})$ be such that
 \begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B}\varphi^{s_1}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s_1}}\leq \tilde{c}_0 \mathop {\int\hskip -1,05em -\,} \limits_{2B}\varphi(|D{\bf u}|)\,\mathrm{d}x \end{equation*}
\begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B}\varphi^{s_1}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s_1}}\leq \tilde{c}_0 \mathop {\int\hskip -1,05em -\,} \limits_{2B}\varphi(|D{\bf u}|)\,\mathrm{d}x \end{equation*}
for ![]() $s_1>1$ and
$s_1>1$ and ![]() $\tilde {c}_0>0$. Then for every
$\tilde {c}_0>0$. Then for every ![]() $\varepsilon \in (0,1)$ there exists
$\varepsilon \in (0,1)$ there exists ![]() $\delta _0=\delta _0(n,N,\mu _1,\mu _2,s_1, \tilde {c}_0,\varepsilon )>0$ such that the following holds: if
$\delta _0=\delta _0(n,N,\mu _1,\mu _2,s_1, \tilde {c}_0,\varepsilon )>0$ such that the following holds: if ![]() ${\bf u}$ is almost
${\bf u}$ is almost ![]() $\varphi$-harmonic as in (2.18) with
$\varphi$-harmonic as in (2.18) with ![]() $\delta _0$ in place of
$\delta _0$ in place of ![]() $\delta$, then the unique
$\delta$, then the unique ![]() $\varphi$-harmonic function
$\varphi$-harmonic function ![]() ${\bf w}\in W^{1,\varphi }(B, \mathbb {R}^{N})$ such that
${\bf w}\in W^{1,\varphi }(B, \mathbb {R}^{N})$ such that ![]() ${\bf w}={\bf u}$ on
${\bf w}={\bf u}$ on ![]() $\partial B$ satisfies
$\partial B$ satisfies
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B} |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2}\,\mathrm{d}x\leq \varepsilon \mathop {\int\hskip -1,05em -\,} \limits_{2B}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B} |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2}\,\mathrm{d}x\leq \varepsilon \mathop {\int\hskip -1,05em -\,} \limits_{2B}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{equation*}3. Partial regularity for functionals
3.1 Caccioppoli inequalities and higher integrability results
As usual, the first step in proving a regularity theorem for the minimizers of integral functionals is to establish suitable Caccioppoli-type inequalities.
First, we state a ‘zero order’ Caccioppoli inequality. The proof is an adaptation to the ![]() $\varphi$-setting of [Reference Bögelein4, lemma 3.1], we then omit the details (see also [Reference Celada and Ok7, theorem 2.4]).
$\varphi$-setting of [Reference Bögelein4, lemma 3.1], we then omit the details (see also [Reference Celada and Ok7, theorem 2.4]).
Lemma 3.1 Let ![]() ${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ be a minimizer of the functional (1.1), under assumptions (F1)–(F2). Then, for every
${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ be a minimizer of the functional (1.1), under assumptions (F1)–(F2). Then, for every ![]() ${\bf u}_0\in \mathbb {R}^{N}$ and
${\bf u}_0\in \mathbb {R}^{N}$ and ![]() $x_0\in \Omega$ and all
$x_0\in \Omega$ and all ![]() $0<\varrho <\textrm {dist}(x_0,\partial \Omega )$ and
$0<\varrho <\textrm {dist}(x_0,\partial \Omega )$ and ![]() $r\in [\varrho /2,\varrho )$ there holds
$r\in [\varrho /2,\varrho )$ there holds
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi\left(\frac{|{\bf u} - {\bf u}_0|}{\varrho-r}\right)\,\mathrm{d}x \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi\left(\frac{|{\bf u} - {\bf u}_0|}{\varrho-r}\right)\,\mathrm{d}x \end{equation*}
for some constant ![]() $c=c(\varphi , L,\nu )>0$.
$c=c(\varphi , L,\nu )>0$.
From lemma 3.1 together with the Sobolev-Poincaré inequality (theorem 2.5) and Gehring's Lemma (lemma 2.7), one can infer in a standard way the following higher integrability result (see, e.g., [Reference Celada and Ok7, theorem 2.5]).
Lemma 3.2 There exist an exponent ![]() $s_0=s_0(n,N,\varphi ,L,\nu )>1$ and a constant
$s_0=s_0(n,N,\varphi ,L,\nu )>1$ and a constant ![]() $c$ depending only on
$c$ depending only on ![]() $n,N,\varphi ,L,\nu$ such that, if
$n,N,\varphi ,L,\nu$ such that, if ![]() ${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1), complying with (F1)–(F2), then the following holds: for every
${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1), complying with (F1)–(F2), then the following holds: for every ![]() $s\in (1,s_0]$, for any
$s\in (1,s_0]$, for any ![]() $x_0\in \Omega$, any radius
$x_0\in \Omega$, any radius ![]() $0<\varrho <{\rm dist}(x_0,\partial \Omega )$ and
$0<\varrho <{\rm dist}(x_0,\partial \Omega )$ and ![]() $r\in [\varrho /2,\varrho )$, one has
$r\in [\varrho /2,\varrho )$, one has
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s}(|D{\bf u}|)\,\mathrm{d}x \leq {c}\left(\frac{\varrho}{\varrho-r}\right)^{n(s-1)}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right)^{s}. \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s}(|D{\bf u}|)\,\mathrm{d}x \leq {c}\left(\frac{\varrho}{\varrho-r}\right)^{n(s-1)}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right)^{s}. \end{equation*}Another useful tool will be the following global higher integrability result on balls for minimizers of (1.1), which has been proven in the Orlicz setting for more general integrands in [Reference De Filippis10, lemma 4.3].
Lemma 3.3 Let ![]() ${\bf u}\in W^{1,\varphi }(B_r(x_0),\mathbb {R}^{N})$ be such that
${\bf u}\in W^{1,\varphi }(B_r(x_0),\mathbb {R}^{N})$ be such that ![]() $\varphi (|D{\bf u}|)\in L^{s_0}(B_r(x_0), \mathbb {R}^{N})$ for some
$\varphi (|D{\bf u}|)\in L^{s_0}(B_r(x_0), \mathbb {R}^{N})$ for some ![]() $s_0>1$. Then there exists an exponent
$s_0>1$. Then there exists an exponent ![]() $s=s(n,N,\varphi ,L,\nu ,s_0)\in (1,s_0]$ and a constant
$s=s(n,N,\varphi ,L,\nu ,s_0)\in (1,s_0]$ and a constant ![]() $c=c(n,N,\varphi ,L,\nu )$ such that, if
$c=c(n,N,\varphi ,L,\nu )$ such that, if ![]() ${\bf v}\in {\bf u}+W^{1,\varphi }_0(B_r(x_0),\mathbb {R}^{N})$ is a minimizer of the functional
${\bf v}\in {\bf u}+W^{1,\varphi }_0(B_r(x_0),\mathbb {R}^{N})$ is a minimizer of the functional ![]() $\mathcal {G}[{\bf v}]:=\int _{B_r(x_0)}g(D{\bf v})\,\mathrm {d}x$ with a
$\mathcal {G}[{\bf v}]:=\int _{B_r(x_0)}g(D{\bf v})\,\mathrm {d}x$ with a ![]() $C^{1}$-integrand
$C^{1}$-integrand ![]() $g:\mathbb {R}^{N\times n}\to \mathbb {R}$ complying with the growth assumptions
$g:\mathbb {R}^{N\times n}\to \mathbb {R}$ complying with the growth assumptions
for all ![]() $\boldsymbol \xi \in \mathbb {R}^{nN}$, then we have
$\boldsymbol \xi \in \mathbb {R}^{nN}$, then we have ![]() $\varphi (|D{\bf v}|)\in L^{s}(B_r(x_0),\mathbb {R}^{N})$ and
$\varphi (|D{\bf v}|)\in L^{s}(B_r(x_0),\mathbb {R}^{N})$ and
 \begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s}(|D{\bf v}|)\,\mathrm{d}x\right)^{\frac{1}{s}}\leq c\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s_0}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s_0}}. \end{equation*}
\begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s}(|D{\bf v}|)\,\mathrm{d}x\right)^{\frac{1}{s}}\leq c\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_r(x_0)} \varphi^{s_0}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s_0}}. \end{equation*}We have the following Caccioppoli inequality of second type for local minimizers of (1.1), involving affine functions.
Lemma 3.4 There exists a constant ![]() $c=c(n,N,\Delta _2(\varphi ),\nu ,L)>0$ such that, if
$c=c(n,N,\Delta _2(\varphi ),\nu ,L)>0$ such that, if ![]() ${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1) under assumptions (F1)–(F7), and
${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1) under assumptions (F1)–(F7), and ![]() $\boldsymbol \ell :\mathbb {R}^{n}\to \mathbb {R}^{N}$ is an affine function, say
$\boldsymbol \ell :\mathbb {R}^{n}\to \mathbb {R}^{N}$ is an affine function, say ![]() $\boldsymbol \ell (x):={\bf u}_0+{\bf Q}(x-x_0)$ for some
$\boldsymbol \ell (x):={\bf u}_0+{\bf Q}(x-x_0)$ for some ![]() ${\bf u}_0\in \mathbb {R}^{N}$ and
${\bf u}_0\in \mathbb {R}^{N}$ and ![]() ${\bf Q}\in \mathbb {R}^{N\times n}$, then for any ball
${\bf Q}\in \mathbb {R}^{N\times n}$, then for any ball ![]() $B_\varrho (x_0)\subseteq \Omega$ with
$B_\varrho (x_0)\subseteq \Omega$ with ![]() $\varrho \leq \varrho _0$ there holds
$\varrho \leq \varrho _0$ there holds
 \begin{align*} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-{\boldsymbol\ell}|}{\varrho}\right)\,\mathrm{d}x \\ &\qquad + c\varphi(|{\bf Q}|)\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+ [{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right] \end{align*}
\begin{align*} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-{\boldsymbol\ell}|}{\varrho}\right)\,\mathrm{d}x \\ &\qquad + c\varphi(|{\bf Q}|)\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+ [{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right] \end{align*}
for every ![]() $s\in (1,s_0]$ where
$s\in (1,s_0]$ where ![]() $s_0$ is that of lemma 3.2.
$s_0$ is that of lemma 3.2.
Proof. We follow the argument of [Reference Bögelein4, lemma 3.5] for functionals with ![]() $p$-growth, just mentioning how to obtain the analogous main estimates therein. We assume, without loss of generality, that
$p$-growth, just mentioning how to obtain the analogous main estimates therein. We assume, without loss of generality, that ![]() $x_0=0$. For radii
$x_0=0$. For radii ![]() $\frac {\varrho }{2}\leq r<\tau < t\leq \frac {3\varrho }{4}$ with
$\frac {\varrho }{2}\leq r<\tau < t\leq \frac {3\varrho }{4}$ with ![]() $\tau :=\frac {r+t}{2}$ we consider a cut-off function
$\tau :=\frac {r+t}{2}$ we consider a cut-off function ![]() $\eta \in C_0^{\infty }(B_\tau ;[0,1])$ such that
$\eta \in C_0^{\infty }(B_\tau ;[0,1])$ such that ![]() $\eta \equiv 1$ on
$\eta \equiv 1$ on ![]() $B_r$ and
$B_r$ and ![]() $|D\eta |\leq \frac {4}{t-r}$ on
$|D\eta |\leq \frac {4}{t-r}$ on ![]() $B_\tau$. Correspondingly, we define the functions
$B_\tau$. Correspondingly, we define the functions ![]() $\boldsymbol \xi :=\eta ({\bf u} - \boldsymbol \ell )\in W^{1,\varphi }(B_\tau ;\mathbb {R}^{N})$ and
$\boldsymbol \xi :=\eta ({\bf u} - \boldsymbol \ell )\in W^{1,\varphi }(B_\tau ;\mathbb {R}^{N})$ and ![]() $\boldsymbol \psi :=(1-\eta )({\bf u} - \boldsymbol \ell )\in W^{1,\varphi }(B_\tau ;\mathbb {R}^{N})$. Note that
$\boldsymbol \psi :=(1-\eta )({\bf u} - \boldsymbol \ell )\in W^{1,\varphi }(B_\tau ;\mathbb {R}^{N})$. Note that ![]() $\boldsymbol \ell +\boldsymbol \xi ={\bf u}-\boldsymbol \psi$. From the quasi-convexity assumption (F3), (2.4) and simple manipulations we obtain
$\boldsymbol \ell +\boldsymbol \xi ={\bf u}-\boldsymbol \psi$. From the quasi-convexity assumption (F3), (2.4) and simple manipulations we obtain
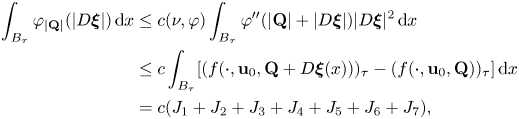 \begin{equation} \begin{split} \int_{B_\tau} \varphi_{|{\bf Q}|}(|D\boldsymbol\xi|)\,\mathrm{d}x & \leq c(\nu,\varphi)\int_{B_\tau} \varphi''(|{\bf Q}|+|D\boldsymbol\xi|)|D\boldsymbol\xi|^{2}\,\mathrm{d}x \\ & \leq c\int_{B_\tau}[(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\xi(x)))_\tau - (f({\cdot}, {\bf u}_0, {\bf Q}))_\tau]\,\mathrm{d}x \\ & = c(J_1+J_2+J_3+J_4+J_5+J_6+J_7), \end{split} \end{equation}
\begin{equation} \begin{split} \int_{B_\tau} \varphi_{|{\bf Q}|}(|D\boldsymbol\xi|)\,\mathrm{d}x & \leq c(\nu,\varphi)\int_{B_\tau} \varphi''(|{\bf Q}|+|D\boldsymbol\xi|)|D\boldsymbol\xi|^{2}\,\mathrm{d}x \\ & \leq c\int_{B_\tau}[(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\xi(x)))_\tau - (f({\cdot}, {\bf u}_0, {\bf Q}))_\tau]\,\mathrm{d}x \\ & = c(J_1+J_2+J_3+J_4+J_5+J_6+J_7), \end{split} \end{equation}where
 \begin{equation*} \begin{split} J_1 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, D{\bf u}(x)-D\boldsymbol\psi(x)))_\tau - (f({\cdot}, {\bf u}_0, D{\bf u}(x)))_\tau]\,\mathrm{d}x,\\ J_2 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, D{\bf u}(x)))_\tau - (f({\cdot}, {\bf u}(x), D{\bf u}(x)))_\tau]\,\mathrm{d}x, \\ J_3 & := \int_{B_\tau}[(f({\cdot}, {\bf u}(x), D{\bf u}(x)))_\tau - f(x, {\bf u}(x), D{\bf u}(x))]\,\mathrm{d}x, \\ J_4 & := \int_{B_\tau}[ f(x, {\bf u}(x), D{\bf u}(x)) - f(x, {\bf u}(x)-\boldsymbol\xi(x), D{\bf u}(x)-D\boldsymbol\xi(x))]\,\mathrm{d}x, \\ J_5 & := \int_{B_\tau}[f(x, {\bf u}(x)-\boldsymbol\xi(x), {\bf Q}+D\boldsymbol\psi(x))-f(x, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x))]\,\mathrm{d}x, \\ J_6 & := \int_{B_\tau}[f(x, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x))-(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x)))_\tau]\,\mathrm{d}x,\\ J_7 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x)))_\tau- (f({\cdot}, {\bf u}_0, {\bf Q}))_\tau]\,\mathrm{d}x. \end{split} \end{equation*}
\begin{equation*} \begin{split} J_1 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, D{\bf u}(x)-D\boldsymbol\psi(x)))_\tau - (f({\cdot}, {\bf u}_0, D{\bf u}(x)))_\tau]\,\mathrm{d}x,\\ J_2 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, D{\bf u}(x)))_\tau - (f({\cdot}, {\bf u}(x), D{\bf u}(x)))_\tau]\,\mathrm{d}x, \\ J_3 & := \int_{B_\tau}[(f({\cdot}, {\bf u}(x), D{\bf u}(x)))_\tau - f(x, {\bf u}(x), D{\bf u}(x))]\,\mathrm{d}x, \\ J_4 & := \int_{B_\tau}[ f(x, {\bf u}(x), D{\bf u}(x)) - f(x, {\bf u}(x)-\boldsymbol\xi(x), D{\bf u}(x)-D\boldsymbol\xi(x))]\,\mathrm{d}x, \\ J_5 & := \int_{B_\tau}[f(x, {\bf u}(x)-\boldsymbol\xi(x), {\bf Q}+D\boldsymbol\psi(x))-f(x, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x))]\,\mathrm{d}x, \\ J_6 & := \int_{B_\tau}[f(x, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x))-(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x)))_\tau]\,\mathrm{d}x,\\ J_7 & := \int_{B_\tau}[(f({\cdot}, {\bf u}_0, {\bf Q}+D\boldsymbol\psi(x)))_\tau- (f({\cdot}, {\bf u}_0, {\bf Q}))_\tau]\,\mathrm{d}x. \end{split} \end{equation*}
Now, we proceed to estimate each term above separately. From the minimizing property of ![]() ${\bf u}$ we infer that
${\bf u}$ we infer that ![]() $J_4\leq 0$, and by assumptions (F5) and (F4) we obtain the estimates
$J_4\leq 0$, and by assumptions (F5) and (F4) we obtain the estimates
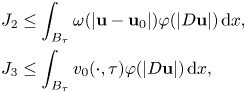 \begin{equation*} \begin{split} J_2 & \leq \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|)\varphi(|D{\bf u}|)\,\mathrm{d}x,\\ J_3 & \leq \int_{B_\tau} {v}_0({\cdot},\tau)\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{split} \end{equation*}
\begin{equation*} \begin{split} J_2 & \leq \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|)\varphi(|D{\bf u}|)\,\mathrm{d}x,\\ J_3 & \leq \int_{B_\tau} {v}_0({\cdot},\tau)\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{split} \end{equation*}
respectively. Again by exploiting property (F5), the monotonicity of ![]() $\omega$ and
$\omega$ and ![]() $\varphi$, and the fact that
$\varphi$, and the fact that
we can estimate ![]() $J_5$ as
$J_5$ as
 \begin{equation*} \begin{split} J_5 & \leq c(\varphi)\int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\varphi\left(|{\bf Q}|+|D{\bf u}|+\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\,\mathrm{d}x\\ & \leq c(\varphi) \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\left[\varphi(|{\bf Q}|+|D{\bf u}|)+\varphi\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right]\,\mathrm{d}x, \end{split} \end{equation*}
\begin{equation*} \begin{split} J_5 & \leq c(\varphi)\int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\varphi\left(|{\bf Q}|+|D{\bf u}|+\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\,\mathrm{d}x\\ & \leq c(\varphi) \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\left[\varphi(|{\bf Q}|+|D{\bf u}|)+\varphi\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right]\,\mathrm{d}x, \end{split} \end{equation*}whence, taking into account that by virtue of (2.5),
 \begin{equation} \begin{split} \varphi\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right) & \leq c\varphi_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)+c\varphi(|{\bf Q}|)\\ & \leq c(\varphi)\left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}+c\varphi(|{\bf Q}|) \end{split} \end{equation}
\begin{equation} \begin{split} \varphi\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right) & \leq c\varphi_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)+c\varphi(|{\bf Q}|)\\ & \leq c(\varphi)\left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}+c\varphi(|{\bf Q}|) \end{split} \end{equation}
and recalling that ![]() $\omega \leq 1$, we get
$\omega \leq 1$, we get
 \begin{align*} J_5&\leq c(\varphi) \left(\int_{B_\tau} \left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}\,\mathrm{d}x \right.\\ &\quad \left. + \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\varphi\left(|{\bf Q}|+|D{\bf u}|\right)\,\mathrm{d}x\right).\end{align*}
\begin{align*} J_5&\leq c(\varphi) \left(\int_{B_\tau} \left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}\,\mathrm{d}x \right.\\ &\quad \left. + \int_{B_\tau} \omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)\varphi\left(|{\bf Q}|+|D{\bf u}|\right)\,\mathrm{d}x\right).\end{align*}
For what concerns ![]() $J_6$, an analogous computation as for the estimate of
$J_6$, an analogous computation as for the estimate of ![]() $J_5$ based on (3.2) and the VMO assumption (F4) gives
$J_5$ based on (3.2) and the VMO assumption (F4) gives
 \begin{equation*} \begin{split} J_6 & \leq \int_{B_\tau} {v}_0({\cdot},\tau)\varphi(|{\bf Q}+D\boldsymbol\psi|)\,\mathrm{d}x \\ & \leq c(\Delta_2(\varphi)) \left(\int_{B_\tau} \left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}\,\mathrm{d}x + \int_{B_\tau} {v}_0({\cdot},\tau)\varphi\left(|{\bf Q}|+|D{\bf u}|\right)\,\mathrm{d}x\right). \end{split} \end{equation*}
\begin{equation*} \begin{split} J_6 & \leq \int_{B_\tau} {v}_0({\cdot},\tau)\varphi(|{\bf Q}+D\boldsymbol\psi|)\,\mathrm{d}x \\ & \leq c(\Delta_2(\varphi)) \left(\int_{B_\tau} \left|{\bf V}_{|{\bf Q}|}\left(\left|\frac{{\bf u}-\boldsymbol\ell}{t-\tau}\right|\right)\right|^{2}\,\mathrm{d}x + \int_{B_\tau} {v}_0({\cdot},\tau)\varphi\left(|{\bf Q}|+|D{\bf u}|\right)\,\mathrm{d}x\right). \end{split} \end{equation*}
The terms ![]() $J_1$ and
$J_1$ and ![]() $J_7$ can be combined together as
$J_7$ can be combined together as
 \begin{align*} J_7+J_1&= \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}\langle Df(y,{\bf u}_0,{\bf Q}+\theta D\boldsymbol\psi(x)) - Df(y,{\bf u}_0,{\bf Q})|D\boldsymbol\psi(x)\rangle\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x \\ & \quad + \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}\langle Df(y,{\bf u}_0,{\bf Q}) - Df(y,{\bf u}_0,D{\bf u}(x)\\ &\quad -(1-\theta)D\boldsymbol\psi(x))| D\boldsymbol\psi(x)\rangle\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x\\ & =: J'_7+J'_1. \end{align*}
\begin{align*} J_7+J_1&= \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}\langle Df(y,{\bf u}_0,{\bf Q}+\theta D\boldsymbol\psi(x)) - Df(y,{\bf u}_0,{\bf Q})|D\boldsymbol\psi(x)\rangle\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x \\ & \quad + \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}\langle Df(y,{\bf u}_0,{\bf Q}) - Df(y,{\bf u}_0,D{\bf u}(x)\\ &\quad -(1-\theta)D\boldsymbol\psi(x))| D\boldsymbol\psi(x)\rangle\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x\\ & =: J'_7+J'_1. \end{align*}
From the Cauchy-Schwarz inequality, (2.11) and the fact that ![]() $D\boldsymbol \psi ={\bf 0}$ on
$D\boldsymbol \psi ={\bf 0}$ on ![]() $B_r$ we infer
$B_r$ we infer
 \begin{equation*} \begin{split} J'_7 & \leq \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}|Df(y,{\bf u}_0,{\bf Q}+\theta D\boldsymbol\psi(x)) - Df(y,{\bf u}_0,{\bf Q})||D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}y\mathrm{d}x \\ & \leq c\int_{B_\tau}\int_0^{1}\varphi'_{|{\bf Q}|}(\theta |D\boldsymbol\psi(x)|)|D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}x \\ & \leq c\int_{B_\tau}\varphi_{|{\bf Q}|}(|D\boldsymbol\psi(x)|)\,\mathrm{d}x \leq c\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D\boldsymbol\psi(x))|^{2}\,\mathrm{d}x. \end{split} \end{equation*}
\begin{equation*} \begin{split} J'_7 & \leq \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}|Df(y,{\bf u}_0,{\bf Q}+\theta D\boldsymbol\psi(x)) - Df(y,{\bf u}_0,{\bf Q})||D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}y\mathrm{d}x \\ & \leq c\int_{B_\tau}\int_0^{1}\varphi'_{|{\bf Q}|}(\theta |D\boldsymbol\psi(x)|)|D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}x \\ & \leq c\int_{B_\tau}\varphi_{|{\bf Q}|}(|D\boldsymbol\psi(x)|)\,\mathrm{d}x \leq c\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D\boldsymbol\psi(x))|^{2}\,\mathrm{d}x. \end{split} \end{equation*}
We can estimate ![]() $J'_1$ analogously, by recalling that
$J'_1$ analogously, by recalling that ![]() $D{\bf u}-(1-\theta )D\boldsymbol \psi ={\bf Q}+D\boldsymbol \xi +\theta D\boldsymbol \psi$,
$D{\bf u}-(1-\theta )D\boldsymbol \psi ={\bf Q}+D\boldsymbol \xi +\theta D\boldsymbol \psi$, ![]() $D\boldsymbol \psi ={\bf 0}$ on
$D\boldsymbol \psi ={\bf 0}$ on ![]() $B_r$ and applying the triangle inequality for
$B_r$ and applying the triangle inequality for ![]() $\varphi '_{|{\bf Q}|}$, (2.11) and the Young's inequality (2.9). In this way we get
$\varphi '_{|{\bf Q}|}$, (2.11) and the Young's inequality (2.9). In this way we get
 \begin{align*} J'_1 & \leq \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}|Df(y,{\bf u}_0,{\bf Q}) - Df(y,{\bf u}_0,D{\bf u}(x)\\ &\quad -(1-\theta)D\boldsymbol\psi(x))||D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x \\ & \leq c\int_{B_\tau}\int_0^{1}\varphi'_{|{\bf Q}|}(|D\boldsymbol\xi+\theta D\boldsymbol\psi|)|D\boldsymbol\psi|\,\mathrm{d}\theta\,\mathrm{d}x \\ & \leq c \int_{B_\tau}\varphi'_{|{\bf Q}|}(|D\boldsymbol\psi|)|D\boldsymbol\psi|\,\mathrm{d}x + c \int_{B_\tau}\varphi'_{|{\bf Q}|}(|D\boldsymbol\xi|)|D\boldsymbol\psi|\,\mathrm{d}x\\ & \leq c\int_{B_\tau\backslash B_r}(|{\bf V}_{|{\bf Q}|}(D\boldsymbol\psi)|^{2}+|{\bf V}_{|{\bf Q}|}(D\boldsymbol\xi)|^{2})\,\mathrm{d}x. \end{align*}
\begin{align*} J'_1 & \leq \int_{B_\tau}\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\int_0^{1}|Df(y,{\bf u}_0,{\bf Q}) - Df(y,{\bf u}_0,D{\bf u}(x)\\ &\quad -(1-\theta)D\boldsymbol\psi(x))||D\boldsymbol\psi(x)|\,\mathrm{d}\theta\,\mathrm{d}y\,\mathrm{d}x \\ & \leq c\int_{B_\tau}\int_0^{1}\varphi'_{|{\bf Q}|}(|D\boldsymbol\xi+\theta D\boldsymbol\psi|)|D\boldsymbol\psi|\,\mathrm{d}\theta\,\mathrm{d}x \\ & \leq c \int_{B_\tau}\varphi'_{|{\bf Q}|}(|D\boldsymbol\psi|)|D\boldsymbol\psi|\,\mathrm{d}x + c \int_{B_\tau}\varphi'_{|{\bf Q}|}(|D\boldsymbol\xi|)|D\boldsymbol\psi|\,\mathrm{d}x\\ & \leq c\int_{B_\tau\backslash B_r}(|{\bf V}_{|{\bf Q}|}(D\boldsymbol\psi)|^{2}+|{\bf V}_{|{\bf Q}|}(D\boldsymbol\xi)|^{2})\,\mathrm{d}x. \end{align*}
Recalling the definitions of ![]() $\boldsymbol \xi$ and
$\boldsymbol \xi$ and ![]() $\boldsymbol \psi$, by a simple computation we find that
$\boldsymbol \psi$, by a simple computation we find that
whence
 \begin{align*} &\int_{B_\tau\backslash B_r} (\varphi_{|{\bf Q}|}(|D\boldsymbol\psi|) + \varphi_{|{\bf Q}|}(|D\boldsymbol\xi|))\,\mathrm{d}x\\ &\quad \leq c \int_{B_\tau\backslash B_r} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c\int_{B_\tau}\varphi_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\,\mathrm{d}x, \end{align*}
\begin{align*} &\int_{B_\tau\backslash B_r} (\varphi_{|{\bf Q}|}(|D\boldsymbol\psi|) + \varphi_{|{\bf Q}|}(|D\boldsymbol\xi|))\,\mathrm{d}x\\ &\quad \leq c \int_{B_\tau\backslash B_r} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c\int_{B_\tau}\varphi_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\,\mathrm{d}x, \end{align*}so that combining with the previous estimates we get
 \begin{equation*} J_1+J_7\leq c\left(\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\tau}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\right). \end{equation*}
\begin{equation*} J_1+J_7\leq c\left(\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\tau}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\right). \end{equation*}
Since ![]() $\boldsymbol \xi ={\bf u}-\boldsymbol \ell$ on
$\boldsymbol \xi ={\bf u}-\boldsymbol \ell$ on ![]() $B_r$ and
$B_r$ and ![]() $\tau \leq \varrho$, from (3.1) and the estimates for
$\tau \leq \varrho$, from (3.1) and the estimates for ![]() $J_1-J_7$ we obtain
$J_1-J_7$ we obtain
 \begin{align*} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq \tilde{c}\left(\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\right)\\ & \qquad + \tilde{c} \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x. \end{align*}
\begin{align*} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq \tilde{c}\left(\int_{B_\tau\backslash B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\right)\\ & \qquad + \tilde{c} \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x. \end{align*}Now, in a standard way we ‘fill the hole’ thus obtaining
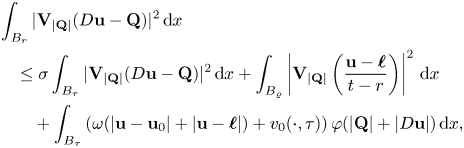 \begin{align} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \notag\\ & \quad \leq \sigma\int_{B_\tau}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\notag\\ & \qquad + \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x, \end{align}
\begin{align} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \notag\\ & \quad \leq \sigma\int_{B_\tau}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\notag\\ & \qquad + \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x, \end{align}
where ![]() $\sigma :=\frac {\tilde {c}}{\tilde {c}+1}<1$. In order to bound the latter term further, we exploit the higher integrability result of lemma 3.2. Thus, with fixed
$\sigma :=\frac {\tilde {c}}{\tilde {c}+1}<1$. In order to bound the latter term further, we exploit the higher integrability result of lemma 3.2. Thus, with fixed ![]() $s\in (1,s_0]$, as a consequence of Hölder's inequality, the concavity of
$s\in (1,s_0]$, as a consequence of Hölder's inequality, the concavity of ![]() $\omega$, the bounds
$\omega$, the bounds ![]() $\omega \leq 1$ and
$\omega \leq 1$ and ![]() ${v}_0\leq 2L$, and Jensen's inequality also we obtain
${v}_0\leq 2L$, and Jensen's inequality also we obtain
 \begin{align*} & \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x\\ & \quad \leq c |B_\tau|\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)^{\frac{s}{s-1}}\,\mathrm{d}x+\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}{v}_0({\cdot},\tau)^{\frac{s}{s-1}}\,\mathrm{d}x\right)^{1-\frac{1}{s}}\\ &\qquad \times\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\varphi^{s}(|{\bf Q}|)+\varphi^{s}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s}} \\ & \quad \leq c \tau^{n}\left(\frac{t}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_t}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{align*}
\begin{align*} & \int_{B_\tau} \left(\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)+{v}_0({\cdot},\tau)\right)\varphi(|{\bf Q}|+|D{\bf u}|)\,\mathrm{d}x\\ & \quad \leq c |B_\tau|\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\omega(|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|)^{\frac{s}{s-1}}\,\mathrm{d}x+\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}{v}_0({\cdot},\tau)^{\frac{s}{s-1}}\,\mathrm{d}x\right)^{1-\frac{1}{s}}\\ &\qquad \times\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau}\varphi^{s}(|{\bf Q}|)+\varphi^{s}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{s}} \\ & \quad \leq c \tau^{n}\left(\frac{t}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_t}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{align*}
where ![]() $c=c(n,N,\Delta _2(\varphi ),\nu ,L)$. This estimate, combined with (3.3) gives
$c=c(n,N,\Delta _2(\varphi ),\nu ,L)$. This estimate, combined with (3.3) gives
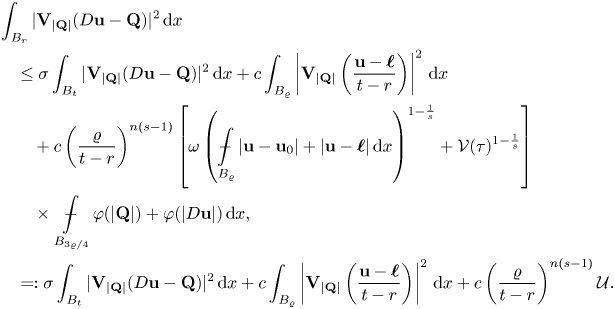 \begin{align*} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq \sigma\int_{B_t}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+c\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\\ & \qquad + c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x, \\ & \quad =: \sigma\int_{B_t}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+c\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x + c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\mathcal{U}. \end{align*}
\begin{align*} & \int_{B_r}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq \sigma\int_{B_t}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+c\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x\\ & \qquad + c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right]\\ &\qquad \times \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|{\bf Q}|)+\varphi(|D{\bf u}|)\,\mathrm{d}x, \\ & \quad =: \sigma\int_{B_t}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x+c\int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{t-r}\right)\right|^{2}\,\mathrm{d}x + c\left(\frac{\varrho}{t-r}\right)^{n(s-1)}\mathcal{U}. \end{align*}
Now, since the previous estimate holds for arbitrary radii ![]() $r,t$ such that
$r,t$ such that ![]() $\varrho /2\leq r< t\leq 3\varrho /4$, the constant
$\varrho /2\leq r< t\leq 3\varrho /4$, the constant ![]() $c$ depends only on
$c$ depends only on ![]() $n,N,\Delta _2(\varphi ),\nu ,L$ and
$n,N,\Delta _2(\varphi ),\nu ,L$ and ![]() $\sigma <1$, as a consequence of lemma 2.6 applied with
$\sigma <1$, as a consequence of lemma 2.6 applied with ![]() $\beta :=n(s-1)$ we obtain
$\beta :=n(s-1)$ we obtain
 \begin{equation} \int_{B_{\varrho/2}}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \leq c \int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x + c\mathcal{U}. \end{equation}
\begin{equation} \int_{B_{\varrho/2}}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \leq c \int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x + c\mathcal{U}. \end{equation}
In view of lemma 3.1 applied with ![]() $\varrho$ in place of
$\varrho$ in place of ![]() $t-s$ and from (3.2) we get
$t-s$ and from (3.2) we get
 \begin{equation*} \begin{split} \int_{B_{3\varrho/4}} \varphi(|D{\bf u}|)\,\mathrm{d}x & \leq c \int_{B_{\varrho}}\varphi\left(\left|\frac{{\bf u}-{\bf u}_0}{\varrho}\right|\right)\,\mathrm{d}x \\ & \leq c \int_{B_{\varrho}}\varphi\left(\left|\frac{{\bf u}-{\boldsymbol\ell}}{\varrho}\right|\right)\,\mathrm{d}x + c \varphi(|{\bf Q}|)\\ & \leq c\left[\int_{B_{\varrho}}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x + \varphi(|{\bf Q}|)\right], \end{split} \end{equation*}
\begin{equation*} \begin{split} \int_{B_{3\varrho/4}} \varphi(|D{\bf u}|)\,\mathrm{d}x & \leq c \int_{B_{\varrho}}\varphi\left(\left|\frac{{\bf u}-{\bf u}_0}{\varrho}\right|\right)\,\mathrm{d}x \\ & \leq c \int_{B_{\varrho}}\varphi\left(\left|\frac{{\bf u}-{\boldsymbol\ell}}{\varrho}\right|\right)\,\mathrm{d}x + c \varphi(|{\bf Q}|)\\ & \leq c\left[\int_{B_{\varrho}}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x + \varphi(|{\bf Q}|)\right], \end{split} \end{equation*}
which combined with (3.4) and using the fact that ![]() $\omega \leq 1$ as well as
$\omega \leq 1$ as well as ![]() ${\mathcal {V}}(\varrho )\leq 2L$ gives
${\mathcal {V}}(\varrho )\leq 2L$ gives
 \begin{align*} &\int_{B_{\varrho/2}}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq c \int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x \\ & \qquad + c\varrho^{n} \varphi(|{\bf Q}|)\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right], \end{align*}
\begin{align*} &\int_{B_{\varrho/2}}|{\bf V}_{|{\bf Q}|}(D{\bf u}-{\bf Q})|^{2}\,\mathrm{d}x \\ & \quad \leq c \int_{B_\varrho}\left|{\bf V}_{|{\bf Q}|}\left(\frac{{\bf u}-\boldsymbol\ell}{\varrho}\right)\right|^{2}\,\mathrm{d}x \\ & \qquad + c\varrho^{n} \varphi(|{\bf Q}|)\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}|{\bf u}-{\bf u}_0|+|{\bf u}-\boldsymbol\ell|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+{\mathcal{V}}(\tau)^{1-\frac{1}{s}}\right], \end{align*}
where ![]() $c=c(n,N,\Delta _2(\varphi ),\nu ,L)$. The Caccioppoli inequality then follows by taking means on both sides of the latter inequality.
$c=c(n,N,\Delta _2(\varphi ),\nu ,L)$. The Caccioppoli inequality then follows by taking means on both sides of the latter inequality.
We can apply lemma 3.4 to affine functions ![]() $\boldsymbol \ell _{x_0,r}(x):=({\bf u})_{x_0,\varrho }+{\bf Q}(x-x_0)$ for some
$\boldsymbol \ell _{x_0,r}(x):=({\bf u})_{x_0,\varrho }+{\bf Q}(x-x_0)$ for some ![]() ${\bf Q}\in \mathbb {R}^{N\times n}$, and the resulting Caccioppoli inequality can be compared with that of [Reference Celada and Ok7, theorem 3.1]. We notice that, apart from an extra VMO term due to assumption (F4), the dependence of the integrand
${\bf Q}\in \mathbb {R}^{N\times n}$, and the resulting Caccioppoli inequality can be compared with that of [Reference Celada and Ok7, theorem 3.1]. We notice that, apart from an extra VMO term due to assumption (F4), the dependence of the integrand ![]() $f$ also on
$f$ also on ![]() ${\bf u}$ implies that the remainder term inside
${\bf u}$ implies that the remainder term inside ![]() $\omega$; i.e.,
$\omega$; i.e.,
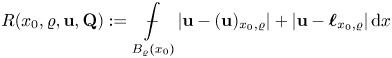 \begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}):=\displaystyle \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|+|{\bf u}-\boldsymbol\ell_{x_0,\varrho}|\,\mathrm{d}x \end{equation}
\begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}):=\displaystyle \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|+|{\bf u}-\boldsymbol\ell_{x_0,\varrho}|\,\mathrm{d}x \end{equation}
is, in general, non-monotone in the radius ![]() $\varrho$. Indeed, it can be estimated from above by the Morrey-type excess
$\varrho$. Indeed, it can be estimated from above by the Morrey-type excess
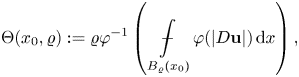 \begin{equation} \Theta(x_0,\varrho):=\varrho\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right), \end{equation}
\begin{equation} \Theta(x_0,\varrho):=\varrho\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right), \end{equation}
which fails to be monotone for small ![]() $\varrho$ (lemma 3.5(i)). This does not allow, in general, for an application of Gehring's lemma in order to infer an higher integrability result: for this purpose, a suitable ‘smallness’ regime (3.9) has to be imposed (lemma 3.5(ii)).
$\varrho$ (lemma 3.5(i)). This does not allow, in general, for an application of Gehring's lemma in order to infer an higher integrability result: for this purpose, a suitable ‘smallness’ regime (3.9) has to be imposed (lemma 3.5(ii)).
Lemma 3.5 Let ![]() $\boldsymbol \ell _{x_0,\varrho }$ be an affine function as above, and
$\boldsymbol \ell _{x_0,\varrho }$ be an affine function as above, and ![]() $R(x_0,\varrho ,{\bf u},\boldsymbol \ell _{x_0,\varrho })$ be defined as in (3.5). Then
$R(x_0,\varrho ,{\bf u},\boldsymbol \ell _{x_0,\varrho })$ be defined as in (3.5). Then
(i)
(3.7)In particular, if \begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \Theta(x_0,\varrho) + \varrho |{\bf Q}|. \end{equation}
\begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \Theta(x_0,\varrho) + \varrho |{\bf Q}|. \end{equation} ${\bf Q}=(D{\bf u})_{x_0,\varrho }$, we have
(3.8)
${\bf Q}=(D{\bf u})_{x_0,\varrho }$, we have
(3.8) \begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \Theta(x_0,\varrho) . \end{equation}
\begin{equation} R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \Theta(x_0,\varrho) . \end{equation}(ii) if the smallness assumption
(3.9)holds for some \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \leq \Lambda\varphi(|{\bf Q}|) \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \leq \Lambda\varphi(|{\bf Q}|) \end{equation} $\Lambda \in (0,1]$, then there exists a constant
$\Lambda \in (0,1]$, then there exists a constant  $c=c(\varphi )>0$ such that
(3.10)hence
$c=c(\varphi )>0$ such that
(3.10)hence \begin{equation} \left( \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|^{\mu_1}\,\mathrm{d}x \right)^{\frac{1}{\mu_1}} \leq c\Theta(x_0,\varrho) \leq c \varrho ( |{\bf Q}|)\,; \end{equation}
\begin{equation} \left( \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|^{\mu_1}\,\mathrm{d}x \right)^{\frac{1}{\mu_1}} \leq c\Theta(x_0,\varrho) \leq c \varrho ( |{\bf Q}|)\,; \end{equation} \[ R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \varrho ( |{\bf Q}|). \]
\[ R(x_0,\varrho,{\bf u},{\bf Q}) \leq c \varrho ( |{\bf Q}|). \]
Proof. (i) First, from Poincaré inequality and Jensen's inequality we obtain
 \begin{equation*} \varphi\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\,\mathrm{d}x\right) \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}
\begin{equation*} \varphi\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\,\mathrm{d}x\right) \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}whence
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} |{\bf u}-({\bf u})_{x_0,\varrho}|\,\mathrm{d}x \leq c \Theta(x_0,\varrho). \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} |{\bf u}-({\bf u})_{x_0,\varrho}|\,\mathrm{d}x \leq c \Theta(x_0,\varrho). \end{equation*}
Then, recalling the definition of ![]() $\boldsymbol \ell _{x_0,r}$, it is immediate to infer the estimate (3.7). As for (3.8), it follows from (3.7) since
$\boldsymbol \ell _{x_0,r}$, it is immediate to infer the estimate (3.7). As for (3.8), it follows from (3.7) since ![]() $\varrho |(D{\bf u})_{x_0,\varrho }|\leq c \Theta (x_0,\varrho )$.
$\varrho |(D{\bf u})_{x_0,\varrho }|\leq c \Theta (x_0,\varrho )$.
(ii) We note from (φ2) that ![]() $\varphi (t^{1/\mu _1})$ is convex for
$\varphi (t^{1/\mu _1})$ is convex for ![]() $t\ge 0$. Applying Jensen's inequality, the Poincaré type estimate in theorem 2.5 and the change-shift formula (2.7) with
$t\ge 0$. Applying Jensen's inequality, the Poincaré type estimate in theorem 2.5 and the change-shift formula (2.7) with ![]() ${\bf a}={\bf 0}$, and using assumption (3.9) , we obtain
${\bf a}={\bf 0}$, and using assumption (3.9) , we obtain
 \begin{align*} &\varphi\left(\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \left[\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right]^{\mu_1}\,\mathrm{d}x\right)^{\frac{1}{\mu_1}}\right) \\ & \quad \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c \varphi(|{\bf Q}|) \\ & \quad \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c\varphi(|{\bf Q}|) \leq \varphi(c(|{\bf Q}|)), \end{align*}
\begin{align*} &\varphi\left(\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \left[\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right]^{\mu_1}\,\mathrm{d}x\right)^{\frac{1}{\mu_1}}\right) \\ & \quad \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)} \varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c \varphi(|{\bf Q}|) \\ & \quad \leq c\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x + c\varphi(|{\bf Q}|) \leq \varphi(c(|{\bf Q}|)), \end{align*}
which yields (3.10) up to applying ![]() $\varphi ^{-1}$ to both sides.
$\varphi ^{-1}$ to both sides.
Now, we are in position to establish a ‘conditioned’ higher integrability result for ![]() $\varphi _{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)$, under the smallness assumption (3.9). The result follows as a consequence of Gehring's lemma with increasing supports (lemma 2.7):
$\varphi _{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)$, under the smallness assumption (3.9). The result follows as a consequence of Gehring's lemma with increasing supports (lemma 2.7):
Corollary 3.6 If ![]() ${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1) under assumptions (F1)–(F7), and
${\bf u}\in W^{1,\varphi }(\Omega ;\mathbb {R}^{N})$ is a minimizer of the functional (1.1) under assumptions (F1)–(F7), and ![]() ${\bf Q}\in \mathbb {R}^{N\times n}$ is such that (3.9) holds for some
${\bf Q}\in \mathbb {R}^{N\times n}$ is such that (3.9) holds for some ![]() $\Lambda \in (0,1]$, then there exist a constant
$\Lambda \in (0,1]$, then there exist a constant ![]() $c=c(n,N,\Delta _2(\varphi ),\nu , L)>0$ and
$c=c(n,N,\Delta _2(\varphi ),\nu , L)>0$ and ![]() $\sigma >1$ such that
$\sigma >1$ such that
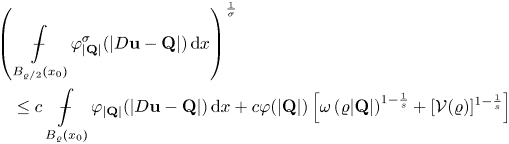 \begin{align} & \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \varphi_{|{\bf Q}|}^{\sigma}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\sigma}} \notag\\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x+ c\varphi(|{\bf Q}|)\left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ [{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right] \end{align}
\begin{align} & \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \varphi_{|{\bf Q}|}^{\sigma}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\sigma}} \notag\\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x+ c\varphi(|{\bf Q}|)\left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ [{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right] \end{align}
holds for every ![]() $s\in (1,s_0]$ where
$s\in (1,s_0]$ where ![]() $s_0$ is that of lemma 3.2.
$s_0$ is that of lemma 3.2.
Proof. Let ![]() $y\in \Omega$ and
$y\in \Omega$ and ![]() $r>0$ be such that
$r>0$ be such that ![]() $B_{2r}(y)\subset \subset B_\varrho (x_0)$. In view of lemma 3.4 applied with
$B_{2r}(y)\subset \subset B_\varrho (x_0)$. In view of lemma 3.4 applied with ![]() $\varrho =2r$,
$\varrho =2r$, ![]() $x_0=y$,
$x_0=y$, ![]() ${\bf u}_0=({\bf u})_{y,2r}$ and an arbitrary
${\bf u}_0=({\bf u})_{y,2r}$ and an arbitrary ![]() ${\bf Q}$, we obtain
${\bf Q}$, we obtain
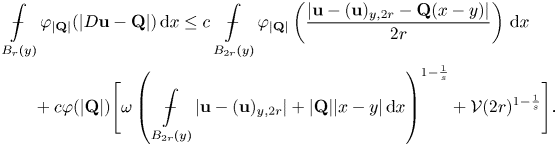 \begin{equation} \begin{aligned} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{r}(y)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)|}{2r}\right)\,\mathrm{d}x\\ & \qquad + c\varphi(|{\bf Q}|)\Bigg[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+ |{\bf Q}||x-y|\, \textrm{d} x\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(2r)^{1-\frac{1}{s}}\Bigg]. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{r}(y)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)|}{2r}\right)\,\mathrm{d}x\\ & \qquad + c\varphi(|{\bf Q}|)\Bigg[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+ |{\bf Q}||x-y|\, \textrm{d} x\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(2r)^{1-\frac{1}{s}}\Bigg]. \end{aligned} \end{equation}Here, we observe that
 \begin{equation*} \begin{split} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+ |{\bf Q}||x-y|\, \textrm{d} x & \le c \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x + c |{\bf Q}|r \\ & \le c \left(\frac{1}{\varrho|{\bf Q}|}\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x+1 \right) \varrho |{\bf Q}|, \end{split} \end{equation*}
\begin{equation*} \begin{split} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+ |{\bf Q}||x-y|\, \textrm{d} x & \le c \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x + c |{\bf Q}|r \\ & \le c \left(\frac{1}{\varrho|{\bf Q}|}\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x+1 \right) \varrho |{\bf Q}|, \end{split} \end{equation*}
which, recalling that ![]() $\omega (ct)\le c\omega (t)$ when
$\omega (ct)\le c\omega (t)$ when ![]() $c\ge 1$ since
$c\ge 1$ since ![]() $\omega$ is concave and
$\omega$ is concave and ![]() $\omega (0)=0$, yields
$\omega (0)=0$, yields
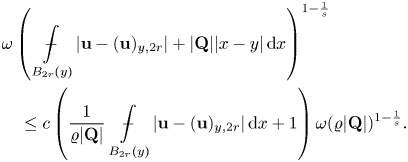 \begin{align*} &\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+|{\bf Q}||x-y|\, \textrm{d} x\right)^{1-\frac{1}{s}}\\ &\quad \le c \left(\frac{1}{\varrho|{\bf Q}|}\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x+1 \right) \omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}. \end{align*}
\begin{align*} &\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|+|{\bf Q}||x-y|\, \textrm{d} x\right)^{1-\frac{1}{s}}\\ &\quad \le c \left(\frac{1}{\varrho|{\bf Q}|}\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x+1 \right) \omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}. \end{align*}
Moreover, as ![]() $\unicode{x2A0D} _{B_{2r}(y)}{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)\,\textrm{d} x={\bf 0}$, by the Sobolev–Poincaré type inequality (2.12),
$\unicode{x2A0D} _{B_{2r}(y)}{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)\,\textrm{d} x={\bf 0}$, by the Sobolev–Poincaré type inequality (2.12),
 \[ \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)|}{r}\right)\,\mathrm{d}x \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}^{\alpha}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}} \]
\[ \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}\left(\frac{|{\bf u}-({\bf u})_{y,2r}-{\bf Q}(x-y)|}{r}\right)\,\mathrm{d}x \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}^{\alpha}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}} \]
for some ![]() $\alpha \in (0,1)$. Therefore, plugging the preceding two estimates into (3.12) and taking into account that
$\alpha \in (0,1)$. Therefore, plugging the preceding two estimates into (3.12) and taking into account that
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x \leq 2 \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{x_0,\varrho}|\, \textrm{d} x, \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{y,2r}|\, \textrm{d} x \leq 2 \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{x_0,\varrho}|\, \textrm{d} x, \end{equation*}we obtain
 \begin{align*} &\mathop {\int\hskip -1,05em -\,} \limits_{B_{r}(y)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \\ &\quad \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}^{\alpha}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}\\ &\qquad + c\frac{\varphi(|{\bf Q}|)\omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}}{\varrho|{\bf Q}|} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{x_0,\varrho}|\, \textrm{d} x+c\varphi(|{\bf Q}|)\\ &\qquad \times \left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(\varrho)^{1-\frac{1}{s}}\right].\end{align*}
\begin{align*} &\mathop {\int\hskip -1,05em -\,} \limits_{B_{r}(y)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x \\ &\quad \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)} \varphi_{|{\bf Q}|}^{\alpha}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}\\ &\qquad + c\frac{\varphi(|{\bf Q}|)\omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}}{\varrho|{\bf Q}|} \mathop {\int\hskip -1,05em -\,} \limits_{B_{2r}(y)}|{\bf u}-({\bf u})_{x_0,\varrho}|\, \textrm{d} x+c\varphi(|{\bf Q}|)\\ &\qquad \times \left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(\varrho)^{1-\frac{1}{s}}\right].\end{align*}
Now, since ![]() ${\bf u} -({\bf u})_{x_0,\varrho }\in L^{\mu _1}(B_{\varrho }(x_0))$, as a consequence of Gehring's lemma there exists
${\bf u} -({\bf u})_{x_0,\varrho }\in L^{\mu _1}(B_{\varrho }(x_0))$, as a consequence of Gehring's lemma there exists ![]() $\sigma =\sigma (n,N,\mu _1,\mu _2,\nu ,L)\in (1,\mu _1)$ such that
$\sigma =\sigma (n,N,\mu _1,\mu _2,\nu ,L)\in (1,\mu _1)$ such that
 \[ \begin{aligned} & \left( \mathop {\int\hskip -1,05em -\,} \limits_{B_{\rho/2}(x_0)} \varphi_{|{\bf Q}|}^{\sigma}(|D{\bf u} -{\bf Q}|)\,\mathrm{d}x \right)^{\frac{1}{\sigma}} \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\\ & \qquad + c\frac{ \varphi(|{\bf Q}|)\omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}}{\varrho|{\bf Q}|}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|^{\sigma}\, \textrm{d} x\right)^{\frac{1}{\sigma}}\\ &\qquad +c\varphi(|{\bf Q}|)\left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(\varrho)^{1-\frac{1}{s}}\right]. \end{aligned} \]
\[ \begin{aligned} & \left( \mathop {\int\hskip -1,05em -\,} \limits_{B_{\rho/2}(x_0)} \varphi_{|{\bf Q}|}^{\sigma}(|D{\bf u} -{\bf Q}|)\,\mathrm{d}x \right)^{\frac{1}{\sigma}} \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)} \varphi_{|{\bf Q}|}(|D{\bf u}-{\bf Q}|)\,\mathrm{d}x\\ & \qquad + c\frac{ \varphi(|{\bf Q}|)\omega(\varrho|{\bf Q}|)^{1-\frac{1}{s}}}{\varrho|{\bf Q}|}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}|{\bf u}-({\bf u})_{x_0,\varrho}|^{\sigma}\, \textrm{d} x\right)^{\frac{1}{\sigma}}\\ &\qquad +c\varphi(|{\bf Q}|)\left[\omega\left(\varrho|{\bf Q}|\right)^{1-\frac{1}{s}}+ {\mathcal{V}}(\varrho)^{1-\frac{1}{s}}\right]. \end{aligned} \] We conclude this section by introducing the excess functional and other tools useful in the sequel. Let ![]() $\boldsymbol L_{x_0,\varrho }:\mathbb {R}^{n}\to \mathbb {R}^{N}$ be the affine function associated to
$\boldsymbol L_{x_0,\varrho }:\mathbb {R}^{n}\to \mathbb {R}^{N}$ be the affine function associated to ![]() ${\bf u}$ defined as
${\bf u}$ defined as
where ![]() ${\bf Q}_{x_0,\varrho }:=(D{\bf u})_{x_0,\varrho }$. For
${\bf Q}_{x_0,\varrho }:=(D{\bf u})_{x_0,\varrho }$. For ![]() $x_0\in \Omega$ and
$x_0\in \Omega$ and ![]() $\varrho \in (0,\textrm {dist}(x_0,\partial \Omega ))$,
$\varrho \in (0,\textrm {dist}(x_0,\partial \Omega ))$, ![]() $\varrho \leq 1$, we define the excess functional as
$\varrho \leq 1$, we define the excess functional as
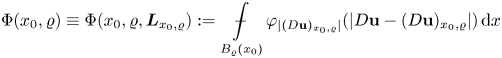 \begin{equation} \Phi(x_0,\varrho)\equiv\Phi(x_0,\varrho, \boldsymbol L_{x_0,\varrho}):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi_{|({D{\bf u}})_{x_0,\varrho}|}(|D{\bf u}-({D{\bf u}})_{x_0,\varrho}|)\,\mathrm{d}x \end{equation}
\begin{equation} \Phi(x_0,\varrho)\equiv\Phi(x_0,\varrho, \boldsymbol L_{x_0,\varrho}):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi_{|({D{\bf u}})_{x_0,\varrho}|}(|D{\bf u}-({D{\bf u}})_{x_0,\varrho}|)\,\mathrm{d}x \end{equation}and
 \begin{equation} \Psi(x_0,\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x. \end{equation}
\begin{equation} \Psi(x_0,\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}\varphi\left(\frac{|{\bf u}-({\bf u})_{x_0,\varrho}|}{\varrho}\right)\,\mathrm{d}x. \end{equation}Moreover, we define also
and
where ![]() $s\in (1,s_0]$ is the exponent of lemma 3.3 and
$s\in (1,s_0]$ is the exponent of lemma 3.3 and ![]() $\Theta (x_0,\varrho )$ is the excess defined in (3.6). Since
$\Theta (x_0,\varrho )$ is the excess defined in (3.6). Since ![]() $\omega \leq 1$ and
$\omega \leq 1$ and ![]() ${\mathcal {V}}(\varrho )\leq 2L$, we have that
${\mathcal {V}}(\varrho )\leq 2L$, we have that ![]() $H(x_0,\varrho ),\widetilde {H}(x_0,\varrho )\leq 1$, and
$H(x_0,\varrho ),\widetilde {H}(x_0,\varrho )\leq 1$, and
as a consequence of lemma 3.5(i). Under the smallness assumption ![]() $\Phi (x_0,\varrho )\leq \Lambda \varphi (|(D{\bf u})_{x_0,\varrho }|)$, by virtue of lemma 3.5(ii) there exists a constant
$\Phi (x_0,\varrho )\leq \Lambda \varphi (|(D{\bf u})_{x_0,\varrho }|)$, by virtue of lemma 3.5(ii) there exists a constant ![]() $\tilde {c}=\tilde {c}(\varphi )$ such that
$\tilde {c}=\tilde {c}(\varphi )$ such that
We can rewrite the Caccioppoli inequality (3.11) as
Note also that by (2.6) and, e.g., [Reference Diening, Kaplický and Schwarzacher13, lemma A.2] we have the following equivalence:
 \begin{equation*} \Phi(x_0,\varrho) \sim \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}(D{\bf u})-{\bf V}((D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x \sim \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}(D{\bf u})-({\bf V}(D{\bf u}))_{x_0,\varrho}|^{2}\,\mathrm{d}x. \end{equation*}
\begin{equation*} \Phi(x_0,\varrho) \sim \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}(D{\bf u})-{\bf V}((D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x \sim \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}(D{\bf u})-({\bf V}(D{\bf u}))_{x_0,\varrho}|^{2}\,\mathrm{d}x. \end{equation*} In the case ![]() $x_0=0$, we will use the shorthands
$x_0=0$, we will use the shorthands ![]() $\Phi (\varrho )$,
$\Phi (\varrho )$, ![]() $\Psi (\varrho )$,
$\Psi (\varrho )$, ![]() $\Theta (\varrho )$,
$\Theta (\varrho )$, ![]() $H(\varrho )$ and
$H(\varrho )$ and ![]() $\widetilde {H}(\varrho )$ in place of
$\widetilde {H}(\varrho )$ in place of ![]() $\Phi (0,\varrho )$,
$\Phi (0,\varrho )$, ![]() $\Psi (0,\varrho )$,
$\Psi (0,\varrho )$, ![]() $\Theta (0,\varrho )$,
$\Theta (0,\varrho )$, ![]() $H(0,\varrho )$ and
$H(0,\varrho )$ and ![]() $\widetilde {H}(0,\varrho )$, respectively.
$\widetilde {H}(0,\varrho )$, respectively.
3.2 Comparison maps via Ekeland's variational principle
The proof of the main results will require suitable comparison functions, which will be constructed with a freezing argument in the variables ![]() $(x,{\bf u})$ based on Ekeland's variational principle. We recall below a version of this classical tool, whose proof can be found, e.g., in [Reference Giusti25, theorem 5.6].
$(x,{\bf u})$ based on Ekeland's variational principle. We recall below a version of this classical tool, whose proof can be found, e.g., in [Reference Giusti25, theorem 5.6].
Lemma 3.7 (Ekeland's principle)
Let ![]() $(X,d)$ be a complete metric space, and assume that
$(X,d)$ be a complete metric space, and assume that ![]() $F : X\to [0,\infty ]$ be not identically
$F : X\to [0,\infty ]$ be not identically ![]() $\infty$ and lower semicontinuous with respect to the metric topology on
$\infty$ and lower semicontinuous with respect to the metric topology on ![]() $X$. If for some
$X$. If for some ![]() $u\in X$ and some
$u\in X$ and some ![]() $\kappa >0$, there holds
$\kappa >0$, there holds
then there exists ![]() $v\in X$ with the properties
$v\in X$ with the properties
Although a similar analysis in the Orlicz setting, for integrands ![]() $f=f(x,\boldsymbol \xi )$, has been performed in [Reference Celada and Ok7, theorem 3.3], we will follow a quite different argument, which refers to the case of
$f=f(x,\boldsymbol \xi )$, has been performed in [Reference Celada and Ok7, theorem 3.3], we will follow a quite different argument, which refers to the case of ![]() $p$-growth as in [Reference Bögelein4, lemma 3.7]. We will also specify the appropriate complete metric space
$p$-growth as in [Reference Bögelein4, lemma 3.7]. We will also specify the appropriate complete metric space ![]() $X$, which is not explicitly mentioned in [Reference Celada and Ok7, theorem 3.3].
$X$, which is not explicitly mentioned in [Reference Celada and Ok7, theorem 3.3].
To this aim, let ![]() $B_\varrho (x_0)\subseteq \Omega$ with
$B_\varrho (x_0)\subseteq \Omega$ with ![]() $\varrho \leq \varrho _0$ and set
$\varrho \leq \varrho _0$ and set
and
where ![]() $\widetilde {H}(x_0,\varrho )$ and
$\widetilde {H}(x_0,\varrho )$ and ![]() $\Psi (x_0,\varrho )$ are defined as in (3.17) and (3.15), respectively.
$\Psi (x_0,\varrho )$ are defined as in (3.17) and (3.15), respectively.
As for the complete metric space ![]() $(X,d)$, following [Reference Ok36, lemma 4.4] we consider
$(X,d)$, following [Reference Ok36, lemma 4.4] we consider
 \begin{equation*} X:=\left\{{\bf w}\in {\bf u}+W^{1,1}_0(B_{\varrho/2}(x_0)):\, \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho/2(x_0)}\varphi(|D{\bf w}|)\,\mathrm{d}x\leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho/2(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right\} \end{equation*}
\begin{equation*} X:=\left\{{\bf w}\in {\bf u}+W^{1,1}_0(B_{\varrho/2}(x_0)):\, \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho/2(x_0)}\varphi(|D{\bf w}|)\,\mathrm{d}x\leq \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho/2(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x\right\} \end{equation*}with the metric
 \begin{align*} &d({\bf w}_1,{\bf w}_2):= \frac{1}{c_*\varphi^{{-}1}(K(\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf w}_1-D{\bf w}_2|\,\mathrm{d}x, \end{align*}
\begin{align*} &d({\bf w}_1,{\bf w}_2):= \frac{1}{c_*\varphi^{{-}1}(K(\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf w}_1-D{\bf w}_2|\,\mathrm{d}x, \end{align*}
for ![]() ${\bf w}_1,{\bf w}_2\in{\bf u}+W_0^{1,1}(B_{\varrho/2(x_0)},\mathbb{R}^{N})$, and note that the functional
${\bf w}_1,{\bf w}_2\in{\bf u}+W_0^{1,1}(B_{\varrho/2(x_0)},\mathbb{R}^{N})$, and note that the functional
 \begin{equation} \mathcal{G}[{\bf w}]:= \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}g(D{\bf w})\,\mathrm{d}x \quad \mbox{ in } {\bf u}+W^{1,1}_0(B_{\varrho/2}(x_0),\mathbb{R}^{N}), \end{equation}
\begin{equation} \mathcal{G}[{\bf w}]:= \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}g(D{\bf w})\,\mathrm{d}x \quad \mbox{ in } {\bf u}+W^{1,1}_0(B_{\varrho/2}(x_0),\mathbb{R}^{N}), \end{equation}
is lower semicontinuous in the metric topology. We would get a comparison map ![]() ${\bf v}\in {\bf u} + W^{1,1}_0(B_{\varrho /2}({x}_0),\mathbb {R}^{N})$ by proving the following lemma.
${\bf v}\in {\bf u} + W^{1,1}_0(B_{\varrho /2}({x}_0),\mathbb {R}^{N})$ by proving the following lemma.
Lemma 3.8 Assume that ![]() ${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ is a minimizer of the functional (1.1), under assumptions (F1)–(F6). Then there exists a minimizer
${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ is a minimizer of the functional (1.1), under assumptions (F1)–(F6). Then there exists a minimizer ![]() ${\bf v}\in {\bf u} + W^{1,1}_0(B_{\varrho /2}({x}_0),\mathbb {R}^{N})$ of the functional
${\bf v}\in {\bf u} + W^{1,1}_0(B_{\varrho /2}({x}_0),\mathbb {R}^{N})$ of the functional
 \begin{equation*} \widetilde{\mathcal{G}}[{\bf w}]:= \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} g(D{\bf w})\,\mathrm{d}x + \frac{K(x_0,\varrho)}{\varphi^{{-}1}(K(x_0,\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf v}-D{\bf w}|\,\mathrm{d}x, \end{equation*}
\begin{equation*} \widetilde{\mathcal{G}}[{\bf w}]:= \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} g(D{\bf w})\,\mathrm{d}x + \frac{K(x_0,\varrho)}{\varphi^{{-}1}(K(x_0,\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf v}-D{\bf w}|\,\mathrm{d}x, \end{equation*}that satisfies
 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf v}-D{\bf u}|\,\mathrm{d}x \leq c_*\varphi^{{-}1}(K(x_0,\varrho)) \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D{\bf v}-D{\bf u}|\,\mathrm{d}x \leq c_*\varphi^{{-}1}(K(x_0,\varrho)) \end{equation}
for some constant ![]() $c_*=c_*(n,N,\Delta _2(\varphi ),\nu ,L)$. Moreover,
$c_*=c_*(n,N,\Delta _2(\varphi ),\nu ,L)$. Moreover, ![]() ${\bf v}$ fulfils the following Euler-Lagrange variational inequality:
${\bf v}$ fulfils the following Euler-Lagrange variational inequality:
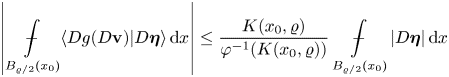 \begin{equation} \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}\langle Dg(D{\bf v})|D{\boldsymbol\eta}\rangle\,\mathrm{d}x\right|\leq \frac{K(x_0,\varrho)}{\varphi^{{-}1}(K(x_0,\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D\boldsymbol\eta|\,\mathrm{d}x \end{equation}
\begin{equation} \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}\langle Dg(D{\bf v})|D{\boldsymbol\eta}\rangle\,\mathrm{d}x\right|\leq \frac{K(x_0,\varrho)}{\varphi^{{-}1}(K(x_0,\varrho))}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}|D\boldsymbol\eta|\,\mathrm{d}x \end{equation}
for every ![]() $\boldsymbol \eta \in C^{\infty }_0(B_{\varrho /2}(x_0),\mathbb {R}^{N})$.
$\boldsymbol \eta \in C^{\infty }_0(B_{\varrho /2}(x_0),\mathbb {R}^{N})$.
Proof. We may assume, without loss of generality, that ![]() $x_0=0$ and, correspondingly, we use the shorthand
$x_0=0$ and, correspondingly, we use the shorthand ![]() $K(\varrho )$ for
$K(\varrho )$ for ![]() $K(0,\varrho )$. As a first remark, we recall that from lemma 3.1 with
$K(0,\varrho )$. As a first remark, we recall that from lemma 3.1 with ![]() $r=\frac {3}{4}\varrho$ we have
$r=\frac {3}{4}\varrho$ we have
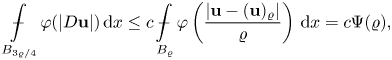 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi\left(\frac{|{\bf u} - ({\bf u})_\varrho|}{\varrho}\right)\,\mathrm{d}x = c\Psi(\varrho), \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi\left(\frac{|{\bf u} - ({\bf u})_\varrho|}{\varrho}\right)\,\mathrm{d}x = c\Psi(\varrho), \end{equation}
where ![]() $c=c(\Delta _2(\varphi ),L,\nu )$. We then denote by
$c=c(\Delta _2(\varphi ),L,\nu )$. We then denote by ![]() ${\tilde {\boldsymbol {v}}{\in }} X$ a minimizer of the functional (3.21) whose existence is ensured by the direct method under assumptions (F1)–(F2). From the minimality of
${\tilde {\boldsymbol {v}}{\in }} X$ a minimizer of the functional (3.21) whose existence is ensured by the direct method under assumptions (F1)–(F2). From the minimality of ![]() $\tilde {\boldsymbol {v}}$, assumption (F1) and (2.10) we get
$\tilde {\boldsymbol {v}}$, assumption (F1) and (2.10) we get
 \begin{equation} \begin{split} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x & \leq\frac{1}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}g(D\tilde{\boldsymbol{v}})-g({\bf 0})\,\mathrm{d}x\\ & \leq\frac{1}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}g(D{\bf u})-g({\bf 0})\,\mathrm{d}x\leq\frac{c(\varphi)L}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{split} \end{equation}
\begin{equation} \begin{split} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x & \leq\frac{1}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}g(D\tilde{\boldsymbol{v}})-g({\bf 0})\,\mathrm{d}x\\ & \leq\frac{1}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}g(D{\bf u})-g({\bf 0})\,\mathrm{d}x\leq\frac{c(\varphi)L}{\nu}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{split} \end{equation}
By the sublinearity of ![]() $\varphi$, the Poincaré inequality (theorem 2.5), Jensen's inequality and (3.24) this gives
$\varphi$, the Poincaré inequality (theorem 2.5), Jensen's inequality and (3.24) this gives
 \begin{align*} & \varphi\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \frac{|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|}{\varrho}\,\mathrm{d}x\right) \\ & \quad \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi\left(\frac{|\tilde{\boldsymbol{v}}-{\bf u}|}{\varrho}\right)\,\mathrm{d}x + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi\left(\frac{|{\bf u}-({\bf u})_\varrho|}{\varrho}\right)\,\mathrm{d}x\right) \\ & \quad \leq c\left[\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{\alpha}(|D\tilde{\boldsymbol{v}}-D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}} + \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{\alpha}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}\right] \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi(|D\tilde{\boldsymbol{v}}|) + \varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{align*}
\begin{align*} & \varphi\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \frac{|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|}{\varrho}\,\mathrm{d}x\right) \\ & \quad \leq c \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi\left(\frac{|\tilde{\boldsymbol{v}}-{\bf u}|}{\varrho}\right)\,\mathrm{d}x + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi\left(\frac{|{\bf u}-({\bf u})_\varrho|}{\varrho}\right)\,\mathrm{d}x\right) \\ & \quad \leq c\left[\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{\alpha}(|D\tilde{\boldsymbol{v}}-D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}} + \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{\alpha}(|D{\bf u}|)\,\mathrm{d}x\right)^{\frac{1}{\alpha}}\right] \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi(|D\tilde{\boldsymbol{v}}|) + \varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{align*}whence
 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|\,\mathrm{d}x\leq c \Theta(\varrho) \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|\,\mathrm{d}x\leq c \Theta(\varrho) \end{equation}
where ![]() $c=c(\varphi ,n,L,\nu )$. Moreover, as a consequence of the higher integrability results of both lemmas 3.2 and 3.3, together with (3.25) and (3.24), we infer the higher integrability result
$c=c(\varphi ,n,L,\nu )$. Moreover, as a consequence of the higher integrability results of both lemmas 3.2 and 3.3, together with (3.25) and (3.24), we infer the higher integrability result
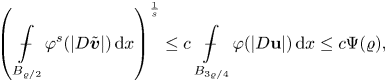 \begin{equation} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{s}(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x\right)^{\frac{1}{s}} \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|D{\bf u}|)\,\mathrm{d}x\leq c\Psi(\varrho), \end{equation}
\begin{equation} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \varphi^{s}(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x\right)^{\frac{1}{s}} \leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{3\varrho/4}}\varphi(|D{\bf u}|)\,\mathrm{d}x\leq c\Psi(\varrho), \end{equation}
where ![]() $c=c(n,N,\varphi ,\nu ,L)$ and
$c=c(n,N,\varphi ,\nu ,L)$ and ![]() $s=s(n,N,\varphi , \nu , L)\in (1,s_0]$.
$s=s(n,N,\varphi , \nu , L)\in (1,s_0]$.
Now we prove that ![]() ${\bf u}$ is an almost minimizer of the functional
${\bf u}$ is an almost minimizer of the functional ![]() $\mathcal {G}$. Indeed, from the minimality of
$\mathcal {G}$. Indeed, from the minimality of ![]() ${\bf u}$ and assumptions (F4), (F3) we get
${\bf u}$ and assumptions (F4), (F3) we get
 \begin{align*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] & \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] \\ & = \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}})-(f({\cdot},\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}}))_\varrho\,\mathrm{d}x \\ & \quad + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} ( f({\cdot},\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}}))_\varrho - (f({\cdot},({\bf u})_\varrho,D\tilde{\boldsymbol{v}}))_\varrho\,\mathrm{d}x \\ & \leq c(L)\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}[{v}_0({\cdot},\varrho)+\omega(|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|)] \varphi(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x. \end{align*}
\begin{align*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] & \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] \\ & = \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}})-(f({\cdot},\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}}))_\varrho\,\mathrm{d}x \\ & \quad + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} ( f({\cdot},\tilde{\boldsymbol{v}},D\tilde{\boldsymbol{v}}))_\varrho - (f({\cdot},({\bf u})_\varrho,D\tilde{\boldsymbol{v}}))_\varrho\,\mathrm{d}x \\ & \leq c(L)\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}[{v}_0({\cdot},\varrho)+\omega(|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|)] \varphi(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x. \end{align*}
Then, by using Jensen's inequality, the concavity and sub-linearity of ![]() $\omega$, (3.26) and (3.27), from the previous estimate we obtain
$\omega$, (3.26) and (3.27), from the previous estimate we obtain
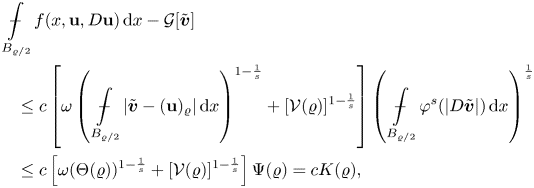 \begin{align} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] \notag\\ & \quad \leq c\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi^{s}(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x\right)^{\frac{1}{s}}\notag\\ & \quad \leq c \left[\omega(\Theta(\varrho))^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\Psi(\varrho) = c K(\varrho), \end{align}
\begin{align} & \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x - \mathcal{G}[\tilde{\boldsymbol{v}}] \notag\\ & \quad \leq c\left[\omega\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|\tilde{\boldsymbol{v}}-({\bf u})_\varrho|\,\mathrm{d}x\right)^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi^{s}(|D\tilde{\boldsymbol{v}}|)\,\mathrm{d}x\right)^{\frac{1}{s}}\notag\\ & \quad \leq c \left[\omega(\Theta(\varrho))^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\Psi(\varrho) = c K(\varrho), \end{align}
where ![]() $c=c(n,N,\Delta _2(\varrho ), \nu , L)$. Arguing similarly, we can estimate
$c=c(n,N,\Delta _2(\varrho ), \nu , L)$. Arguing similarly, we can estimate
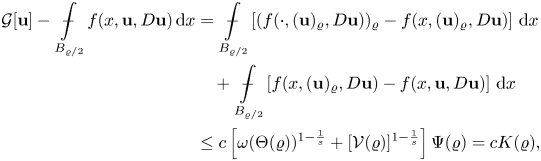 \begin{align} \mathcal{G}[{\bf u}]-\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x & = \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\left [(f({\cdot},({\bf u})_\varrho,D{\bf u}))_\varrho - f(x,({\bf u})_\varrho,D{\bf u})\right]\,\mathrm{d}x\notag\\ &\quad + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \left[f(x,({\bf u})_\varrho,D{\bf u}) - f(x,{\bf u},D{\bf u})\right]\,\mathrm{d}x \notag\\ & \leq c \left[\omega(\Theta(\varrho))^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\Psi(\varrho) = c K(\varrho), \end{align}
\begin{align} \mathcal{G}[{\bf u}]-\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}f(x,{\bf u},D{\bf u})\,\mathrm{d}x & = \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\left [(f({\cdot},({\bf u})_\varrho,D{\bf u}))_\varrho - f(x,({\bf u})_\varrho,D{\bf u})\right]\,\mathrm{d}x\notag\\ &\quad + \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} \left[f(x,({\bf u})_\varrho,D{\bf u}) - f(x,{\bf u},D{\bf u})\right]\,\mathrm{d}x \notag\\ & \leq c \left[\omega(\Theta(\varrho))^{1-\frac{1}{s}}+[{\mathcal{V}}(\varrho)]^{1-\frac{1}{s}}\right]\Psi(\varrho) = c K(\varrho), \end{align}
where the constant ![]() $c$ has the same dependencies as before. Adding term by term (3.28)–(3.29) and taking into account the minimality of
$c$ has the same dependencies as before. Adding term by term (3.28)–(3.29) and taking into account the minimality of ![]() $\tilde {\boldsymbol {v}}$, we infer
$\tilde {\boldsymbol {v}}$, we infer
for a constant ![]() $c_*=c_*(n, N, \Delta _2(\varphi ), \nu , L)$. Finally, Ekeland's variational principle (lemma 3.7) with the choice
$c_*=c_*(n, N, \Delta _2(\varphi ), \nu , L)$. Finally, Ekeland's variational principle (lemma 3.7) with the choice ![]() $\kappa =c_*K(\varrho )$ provides the existence of a function
$\kappa =c_*K(\varrho )$ provides the existence of a function ![]() ${{\bf v}\in X}$ with the desired property of minimality for the functional
${{\bf v}\in X}$ with the desired property of minimality for the functional ![]() $\widetilde {\mathcal {G}}$ and such that
$\widetilde {\mathcal {G}}$ and such that ![]() ${d({\bf u},{\bf v})\leq 1}$, which corresponds to (3.22). The inequality (3.23) follows from the validity of the associated Euler-Lagrange variational inequality for
${d({\bf u},{\bf v})\leq 1}$, which corresponds to (3.22). The inequality (3.23) follows from the validity of the associated Euler-Lagrange variational inequality for ![]() ${\bf v}$ in a standard way.
${\bf v}$ in a standard way.
3.3 Approximate  $\mathcal {A}$-harmonicity and
$\mathcal {A}$-harmonicity and  $\varphi$-harmonicity
$\varphi$-harmonicity
In this section, we provide two different linearization strategies for the minimization problem, along the lines of [Reference Bögelein4, section 3.2], where an analogous analysis has been performed for functionals with ![]() $p$-growth. On the one hand, with lemma 3.9 we will show that the minimizer
$p$-growth. On the one hand, with lemma 3.9 we will show that the minimizer ![]() ${\bf u}$ of
${\bf u}$ of ![]() $\mathcal {F}$ is an almost
$\mathcal {F}$ is an almost ![]() $\mathcal {A}$-harmonic function for a suitable elliptic bilinear form
$\mathcal {A}$-harmonic function for a suitable elliptic bilinear form ![]() $\mathcal {A}$. On the other hand, this
$\mathcal {A}$. On the other hand, this ![]() ${\bf u}$ turns out to be an almost
${\bf u}$ turns out to be an almost ![]() $\varphi$-harmonic function (see lemma 3.10). These results will allow us to apply the
$\varphi$-harmonic function (see lemma 3.10). These results will allow us to apply the ![]() $\mathcal {A}$-harmonic approximation lemma, respectively the
$\mathcal {A}$-harmonic approximation lemma, respectively the ![]() $\varphi$-harmonic approximation lemma. The proof will require, in both cases, the comparison maps obtained with lemma 3.8.
$\varphi$-harmonic approximation lemma. The proof will require, in both cases, the comparison maps obtained with lemma 3.8.
We start by proving the approximate ![]() $\mathcal {A}$-harmonicity of a minimizer to (1.1). To this aim, only assumptions (F1)–(F6) are required on
$\mathcal {A}$-harmonicity of a minimizer to (1.1). To this aim, only assumptions (F1)–(F6) are required on ![]() $f$.
$f$.
Let ![]() $\boldsymbol L_{x_0,\varrho }$ be the affine function associated to
$\boldsymbol L_{x_0,\varrho }$ be the affine function associated to ![]() ${\bf u}$ as in (3.13), which complies with
${\bf u}$ as in (3.13), which complies with ![]() $\boldsymbol L_{x_0,\varrho }(x_0)=({\bf u})_{x_0,\varrho }$ and
$\boldsymbol L_{x_0,\varrho }(x_0)=({\bf u})_{x_0,\varrho }$ and ![]() $D\boldsymbol L_{x_0,\varrho }=(D{\bf u})_{x_0,\varrho }=:{\bf Q}_{x_0,\varrho }$. We set
$D\boldsymbol L_{x_0,\varrho }=(D{\bf u})_{x_0,\varrho }=:{\bf Q}_{x_0,\varrho }$. We set
 \begin{equation*} \mathcal{A}:=\frac{D^{2}g((D{\bf u})_{x_0,\varrho})}{\varphi''(|(D{\bf u})_{x_0,\varrho}|)}\equiv \frac{\left(D^{2}f({\cdot}, ({\bf u})_{x_0,\varrho},(D{\bf u})_{x_0,\varrho})\right)_{x_0,\varrho}}{\varphi''(|(D{\bf u})_{x_0,\varrho}|)}. \end{equation*}
\begin{equation*} \mathcal{A}:=\frac{D^{2}g((D{\bf u})_{x_0,\varrho})}{\varphi''(|(D{\bf u})_{x_0,\varrho}|)}\equiv \frac{\left(D^{2}f({\cdot}, ({\bf u})_{x_0,\varrho},(D{\bf u})_{x_0,\varrho})\right)_{x_0,\varrho}}{\varphi''(|(D{\bf u})_{x_0,\varrho}|)}. \end{equation*} We point out that ![]() $\mathcal {A}$ defined above is a bilinear form on
$\mathcal {A}$ defined above is a bilinear form on ![]() $\mathbb {R}^{N\times n}$, satisfying the ellipticity assumption (2.13) by virtue of (F2) and (F3).
$\mathbb {R}^{N\times n}$, satisfying the ellipticity assumption (2.13) by virtue of (F2) and (F3).
Lemma 3.9 Let ![]() ${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ be a minimizer of the functional (1.1), under assumptions (F1)–(F6), and assume that for a ball
${\bf u}\in W^{1,\varphi }(\Omega ,\mathbb {R}^{N})$ be a minimizer of the functional (1.1), under assumptions (F1)–(F6), and assume that for a ball ![]() $B_\varrho (x_0)\subseteq \Omega$ the non-degeneracy assumptions
$B_\varrho (x_0)\subseteq \Omega$ the non-degeneracy assumptions
are satisfied. Then, ![]() ${\bf u}$ is approximately
${\bf u}$ is approximately ![]() $\mathcal {A}$-harmonic on the ball
$\mathcal {A}$-harmonic on the ball ![]() $B_{\varrho /2}(x_0)$, in the sense that there exists
$B_{\varrho /2}(x_0)$, in the sense that there exists ![]() $\beta _1=\beta _1(n,N,\mu _1,\mu _2,\nu ,L,\beta _0)\in (0,\frac {1}{2})$ such that
$\beta _1=\beta _1(n,N,\mu _1,\mu _2,\nu ,L,\beta _0)\in (0,\frac {1}{2})$ such that
 \begin{align} & \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \langle\mathcal{A}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|D\boldsymbol\eta\rangle\,\mathrm{d}x\right| \notag\\ & \quad \leq c |(D{\bf u})_{x_0,\varrho}|\|D\boldsymbol\eta\|_\infty\left\{[{H}(x_0,\varrho)]^{\beta_1}+\frac{\Phi(x_0,\varrho)}{\varphi(|(D{\bf u})_{x_0,\varrho}|)}+\left(\frac{\Phi(x_0,\varrho)}{\varphi(|(D{\bf u})_{x_0,\varrho}|)}\right)^{\frac{1+\beta_0}{2}}\right\} \end{align}
\begin{align} & \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)} \langle\mathcal{A}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|D\boldsymbol\eta\rangle\,\mathrm{d}x\right| \notag\\ & \quad \leq c |(D{\bf u})_{x_0,\varrho}|\|D\boldsymbol\eta\|_\infty\left\{[{H}(x_0,\varrho)]^{\beta_1}+\frac{\Phi(x_0,\varrho)}{\varphi(|(D{\bf u})_{x_0,\varrho}|)}+\left(\frac{\Phi(x_0,\varrho)}{\varphi(|(D{\bf u})_{x_0,\varrho}|)}\right)^{\frac{1+\beta_0}{2}}\right\} \end{align}
holds for every ![]() $\boldsymbol \eta \in C^{\infty }_c(B_{\varrho /2}(x_0),\mathbb {R}^{N})$ for some constant
$\boldsymbol \eta \in C^{\infty }_c(B_{\varrho /2}(x_0),\mathbb {R}^{N})$ for some constant ![]() $c = c(n,N,\mu _1, \mu _2,\nu , c_0, L)>0$, where
$c = c(n,N,\mu _1, \mu _2,\nu , c_0, L)>0$, where ![]() $\mu _1,\mu _2$ are the characteristics of
$\mu _1,\mu _2$ are the characteristics of ![]() $\varphi$ and
$\varphi$ and ![]() $c_0,\beta _0$ are the constants of assumption (F6).
$c_0,\beta _0$ are the constants of assumption (F6).
Proof. See [Reference Celada and Ok7, lemma 4.1].
If, in addition, ![]() $f$ complies also with (F7), we can show that each local minimizer of the functional
$f$ complies also with (F7), we can show that each local minimizer of the functional ![]() $\mathcal {F}({\bf u})$ (eq. (1.1)) is almost
$\mathcal {F}({\bf u})$ (eq. (1.1)) is almost ![]() $\varphi$-harmonic.
$\varphi$-harmonic.
For this, we preliminarily note (see [Reference Celada and Ok7, eq. (4.19)–(4.20)]) that assumption (F7) implies the following:
for every ![]() ${\bf P}\in \mathbb {R}^{N\times n}$ with
${\bf P}\in \mathbb {R}^{N\times n}$ with ![]() $0<|{\bf P}|\leq \sigma$, where the function
$0<|{\bf P}|\leq \sigma$, where the function ![]() $g$ has been introduced in (3.19).
$g$ has been introduced in (3.19).
We then have the following result.
Lemma 3.10 Let ![]() ${\bf u}\in W^{1,\varphi }_\textrm {loc}(\Omega ,\mathbb {R}^{N})$ be a local minimizer of the functional (1.1), and assume that
${\bf u}\in W^{1,\varphi }_\textrm {loc}(\Omega ,\mathbb {R}^{N})$ be a local minimizer of the functional (1.1), and assume that ![]() $f$ complies also with (F7). Then there exists
$f$ complies also with (F7). Then there exists ![]() $\beta _2=\beta _2(n,N,\mu _1,\mu _2,c_0,L)\in (0,\frac {1}{2})$ such that, for every
$\beta _2=\beta _2(n,N,\mu _1,\mu _2,c_0,L)\in (0,\frac {1}{2})$ such that, for every ![]() $\delta >0$ and for
$\delta >0$ and for ![]() $\sigma =\sigma (\delta )>0$ given by (3.31), the inequality
$\sigma =\sigma (\delta )>0$ given by (3.31), the inequality
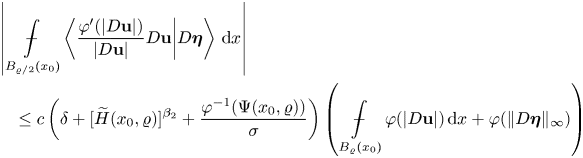 \begin{align*} & \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}\left\langle\frac{\varphi'(|D{\bf u}|)}{|D{\bf u}|}D{\bf u}\bigg|D\boldsymbol\eta\right\rangle\,\mathrm{d}x\right| \\ & \quad \leq c\left(\delta+[\widetilde{H}(x_0,\varrho)]^{\beta_2}+\frac{\varphi^{{-}1}(\Psi(x_0,\varrho))}{\sigma}\right) \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x+\varphi(\|D\boldsymbol\eta\|_\infty)\right) \end{align*}
\begin{align*} & \left|\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}(x_0)}\left\langle\frac{\varphi'(|D{\bf u}|)}{|D{\bf u}|}D{\bf u}\bigg|D\boldsymbol\eta\right\rangle\,\mathrm{d}x\right| \\ & \quad \leq c\left(\delta+[\widetilde{H}(x_0,\varrho)]^{\beta_2}+\frac{\varphi^{{-}1}(\Psi(x_0,\varrho))}{\sigma}\right) \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x+\varphi(\|D\boldsymbol\eta\|_\infty)\right) \end{align*}
holds for every ![]() $\boldsymbol \eta \in C^{\infty }_c(B_{\varrho /2}(x_0),\mathbb {R}^{N})$ for some constant
$\boldsymbol \eta \in C^{\infty }_c(B_{\varrho /2}(x_0),\mathbb {R}^{N})$ for some constant ![]() $c=c(n,N,\mu _1,\mu _2,c_0, \nu ,L)>0$.
$c=c(n,N,\mu _1,\mu _2,c_0, \nu ,L)>0$.
Proof. See [Reference Celada and Ok7, lemma 4.3].
3.4 Excess decay estimates: the non-degenerate regime
We start by establishing excess improvement estimates in the non-degenerate regime characterized by (3.33) below, i.e. the fact that ![]() $\Phi (x_0,\varrho )\leq c\varphi (|(D{\bf u})_{x_0,\varrho }|)$. The strategy of the proof is to exploit lemma 3.9 to approximate the given minimizer by
$\Phi (x_0,\varrho )\leq c\varphi (|(D{\bf u})_{x_0,\varrho }|)$. The strategy of the proof is to exploit lemma 3.9 to approximate the given minimizer by ![]() $\mathcal {A}$-harmonic functions, for which suitable decay estimates are available from theorem 2.9.
$\mathcal {A}$-harmonic functions, for which suitable decay estimates are available from theorem 2.9.
We introduce the hybrid excess functional
where ![]() $\beta _1$ is the exponent of lemma 3.9. Since
$\beta _1$ is the exponent of lemma 3.9. Since ![]() $\beta _1<1/2$ and
$\beta _1<1/2$ and ![]() $H(x_0,\varrho )\leq 1$, we deduce, in particular, that
$H(x_0,\varrho )\leq 1$, we deduce, in particular, that ![]() $H(x_0,\varrho )\leq [H(x_0,\varrho )]^{\beta _1}$. Thus, the Caccioppoli inequality (3.18) can be re-read as
$H(x_0,\varrho )\leq [H(x_0,\varrho )]^{\beta _1}$. Thus, the Caccioppoli inequality (3.18) can be re-read as
where ![]() $c=c(n,N,\mu _1,\mu _2,\nu ,L)$.
$c=c(n,N,\mu _1,\mu _2,\nu ,L)$.
Lemma 3.11 For every ![]() $\varepsilon \in (0,1)$ there exist
$\varepsilon \in (0,1)$ there exist ![]() $\delta _1,\delta _2\in (0,1]$, where
$\delta _1,\delta _2\in (0,1]$, where ![]() $\delta _i=\delta _i(n,N,\mu _1,\mu _2, \beta _0, \nu ,L,\varepsilon )$,
$\delta _i=\delta _i(n,N,\mu _1,\mu _2, \beta _0, \nu ,L,\varepsilon )$, ![]() $i=1,2$, with the following property: if
$i=1,2$, with the following property: if
then the excess improvement estimate
holds for every ![]() $\vartheta \in (0,1)$ for some constant
$\vartheta \in (0,1)$ for some constant ![]() $c_\textrm {dec}=c_\textrm {dec}(n,N,\mu _1,\mu _2,\nu ,L,c_1)>0$, where
$c_\textrm {dec}=c_\textrm {dec}(n,N,\mu _1,\mu _2,\nu ,L,c_1)>0$, where ![]() $\Phi _*$ is defined in (3.32).
$\Phi _*$ is defined in (3.32).
Proof. The proof follows the argument of [Reference Celada and Ok7, lemma 4.2]. We emphasize that corollary 3.6 is crucial in order to obtain the estimate
 \begin{align*} &\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\left[\frac{\varphi_{|{\bf Q}_{\varrho}|}(|D{\bf u}-{\bf Q}_{\varrho}|)}{\varphi(|{\bf Q}_{\varrho}|)}\right]^{s_0}\,\mathrm{d}x\right)^{\frac{1}{s_0}} \\ & \quad \leq \frac{c}{\varphi(|{\bf Q}_{\varrho}|)}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi_{|{\bf Q}_{\varrho}|}(|D{\bf u}-{\bf Q}_{\varrho}|)\,\mathrm{d}x + c[H(\varrho)]^{\beta_1}\\ & \quad \leq {c} \frac{\Phi_*(\varrho)}{\varphi(|{\bf Q}_{\varrho}|)}, \end{align*}
\begin{align*} &\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\left[\frac{\varphi_{|{\bf Q}_{\varrho}|}(|D{\bf u}-{\bf Q}_{\varrho}|)}{\varphi(|{\bf Q}_{\varrho}|)}\right]^{s_0}\,\mathrm{d}x\right)^{\frac{1}{s_0}} \\ & \quad \leq \frac{c}{\varphi(|{\bf Q}_{\varrho}|)}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi_{|{\bf Q}_{\varrho}|}(|D{\bf u}-{\bf Q}_{\varrho}|)\,\mathrm{d}x + c[H(\varrho)]^{\beta_1}\\ & \quad \leq {c} \frac{\Phi_*(\varrho)}{\varphi(|{\bf Q}_{\varrho}|)}, \end{align*}
which comes into play in applying the ![]() $\mathcal {A}$-harmonic approximation theorem in the modified version of remark 2.10.
$\mathcal {A}$-harmonic approximation theorem in the modified version of remark 2.10.
Lemma 3.12 Let ![]() $\vartheta \in (0,1)$, and assume that
$\vartheta \in (0,1)$, and assume that
where ![]() $c_{\mu _2}$ is the constant of the change of shift formula (2.7) with
$c_{\mu _2}$ is the constant of the change of shift formula (2.7) with ![]() $\eta =\frac {1}{2^{\mu _2+1}}$. Then it holds that
$\eta =\frac {1}{2^{\mu _2+1}}$. Then it holds that
Proof. As a consequence of (2.7) for ![]() $\eta =\frac {1}{2^{\mu _2+1}}$ and with (3.36) we get
$\eta =\frac {1}{2^{\mu _2+1}}$ and with (3.36) we get
 \begin{equation*} \begin{split} \varphi(|(D{\bf u})_{x_0,\varrho}-(D{\bf u})_{x_0,\vartheta\varrho}|) & \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_{\vartheta\varrho}(x_0)} \varphi(|D{\bf u} - (D{\bf u})_{x_0,\varrho}|)\,\mathrm{d}x \\ & \leq c_{\mu_2}\vartheta^{{-}n}\Phi(x_0,\varrho) + \frac{1}{2^{\mu_2+1}}\varphi(|(D{\bf u})_{x_0,\varrho}|) \\ & \leq \frac{1}{2^{\mu_2}} \varphi(|(D{\bf u})_{x_0,\varrho}|), \end{split} \end{equation*}
\begin{equation*} \begin{split} \varphi(|(D{\bf u})_{x_0,\varrho}-(D{\bf u})_{x_0,\vartheta\varrho}|) & \leq \mathop {\int\hskip -1,05em -\,} \limits_{B_{\vartheta\varrho}(x_0)} \varphi(|D{\bf u} - (D{\bf u})_{x_0,\varrho}|)\,\mathrm{d}x \\ & \leq c_{\mu_2}\vartheta^{{-}n}\Phi(x_0,\varrho) + \frac{1}{2^{\mu_2+1}}\varphi(|(D{\bf u})_{x_0,\varrho}|) \\ & \leq \frac{1}{2^{\mu_2}} \varphi(|(D{\bf u})_{x_0,\varrho}|), \end{split} \end{equation*}
whence, passing to ![]() $\varphi ^{-1}$ and taking into account (2.2), we obtain
$\varphi ^{-1}$ and taking into account (2.2), we obtain
Now,
whence (3.37) follows by re-absorbing the first term of the right-hand side into the left.
The excess-decay estimate (3.35) can be iterated, as the non-degeneracy conditions (3.33)–(3.34) are also satisfied on any smaller ball ![]() $B_{\vartheta ^{m}\varrho }(x_0)$,
$B_{\vartheta ^{m}\varrho }(x_0)$, ![]() $m\in \mathbb {N}$,
$m\in \mathbb {N}$, ![]() $\vartheta <1$.
$\vartheta <1$.
Lemma 3.13 Let ![]() $\Phi (x_0,\varrho )$ and
$\Phi (x_0,\varrho )$ and ![]() $\Theta (x_0,\varrho )$ be defined as in (3.14) and (3.6), respectively. Then there exist constants
$\Theta (x_0,\varrho )$ be defined as in (3.14) and (3.6), respectively. Then there exist constants ![]() $\delta _*$,
$\delta _*$, ![]() $\varepsilon _*$,
$\varepsilon _*$, ![]() $\varrho _*\in (0,1]$ and
$\varrho _*\in (0,1]$ and ![]() $\vartheta$ such that the following holds: if the conditions
$\vartheta$ such that the following holds: if the conditions
hold on ![]() $B_\varrho (x_0)\subseteq \Omega$ for
$B_\varrho (x_0)\subseteq \Omega$ for ![]() $\varrho \in (0,\varrho _*]$, then
$\varrho \in (0,\varrho _*]$, then
for every ![]() $m=0,1,\dots .$. As a consequence, for any
$m=0,1,\dots .$. As a consequence, for any ![]() $\alpha \in (0,1)$ the following Morrey-type estimate holds:
$\alpha \in (0,1)$ the following Morrey-type estimate holds:
for all ![]() $y\in B_{\varrho /2}(x_0)$ and
$y\in B_{\varrho /2}(x_0)$ and ![]() $r\in (0,\varrho /2]$.
$r\in (0,\varrho /2]$.
Proof. As usual, we omit the explicit dependence on ![]() $x_0$. Let
$x_0$. Let ![]() $\vartheta \in (0,1)$ be such that
$\vartheta \in (0,1)$ be such that
where ![]() $c_\textrm {dec}$ is the constant of lemma 3.11 depending only on
$c_\textrm {dec}$ is the constant of lemma 3.11 depending only on ![]() $n,N,\mu _1,\mu _2,\nu ,L,c_0$. Correspondingly, let
$n,N,\mu _1,\mu _2,\nu ,L,c_0$. Correspondingly, let ![]() $\delta _i=\delta _i(n,N,\mu _1,\mu _2,\beta _0,\nu ,L,\vartheta )$,
$\delta _i=\delta _i(n,N,\mu _1,\mu _2,\beta _0,\nu ,L,\vartheta )$, ![]() $i=1,2$ be the constants of lemma 3.11, applied with the choice
$i=1,2$ be the constants of lemma 3.11, applied with the choice ![]() $\varepsilon =\vartheta ^{n+2}$. We choose
$\varepsilon =\vartheta ^{n+2}$. We choose ![]() $\varepsilon _*>0$ such that
$\varepsilon _*>0$ such that
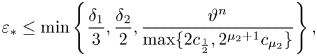 \begin{equation} \varepsilon_*\leq\min\left\{\frac{\delta_1}{3}, \frac{\delta_2}{2}, \frac{\vartheta^{n}}{\max\{2c_{\frac{1}{2}},2^{\mu_2+1} c_{\mu_2}\}}\right\}, \end{equation}
\begin{equation} \varepsilon_*\leq\min\left\{\frac{\delta_1}{3}, \frac{\delta_2}{2}, \frac{\vartheta^{n}}{\max\{2c_{\frac{1}{2}},2^{\mu_2+1} c_{\mu_2}\}}\right\}, \end{equation}
where ![]() $c_{\frac {1}{2}}$ is the constant in the change-shift formula (2.7) with
$c_{\frac {1}{2}}$ is the constant in the change-shift formula (2.7) with ![]() $\eta =\frac {1}{2}$, and we fix the constant
$\eta =\frac {1}{2}$, and we fix the constant ![]() $\delta _*>0$ so small that
$\delta _*>0$ so small that
 \begin{equation} \left(\frac{\omega(\delta_*)^{1-\frac{1}{s}}}{1+(2L)^{1-\frac{1}{s}}}\right)^{\beta_1}<\varepsilon_*. \end{equation}
\begin{equation} \left(\frac{\omega(\delta_*)^{1-\frac{1}{s}}}{1+(2L)^{1-\frac{1}{s}}}\right)^{\beta_1}<\varepsilon_*. \end{equation}
Moreover, we choose a radius ![]() $\varrho _*>0$ such that
$\varrho _*>0$ such that
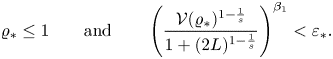 \begin{equation} \varrho_*\leq 1 \qquad \mbox{and} \qquad \left(\frac{\mathcal{V}(\varrho_*)^{1-\frac{1}{s}}}{1+(2L)^{1-\frac{1}{s}}}\right)^{\beta_1}<\varepsilon_*. \end{equation}
\begin{equation} \varrho_*\leq 1 \qquad \mbox{and} \qquad \left(\frac{\mathcal{V}(\varrho_*)^{1-\frac{1}{s}}}{1+(2L)^{1-\frac{1}{s}}}\right)^{\beta_1}<\varepsilon_*. \end{equation}
As a consequence, ![]() $\varepsilon _*$,
$\varepsilon _*$, ![]() $\delta _*$ and
$\delta _*$ and ![]() $\varrho _*$ have the same dependencies as
$\varrho _*$ have the same dependencies as ![]() $\delta _1$,
$\delta _1$, ![]() $\delta _2$. In addition,
$\delta _2$. In addition, ![]() $\delta _*$ depends also on
$\delta _*$ depends also on ![]() $\omega$, while
$\omega$, while ![]() $\varrho _*$ also on
$\varrho _*$ also on ![]() $\omega$ and
$\omega$ and ![]() $\mathcal {V}$.
$\mathcal {V}$.
We argue by induction on ![]() $m$. Since (3.39) are trivially true for
$m$. Since (3.39) are trivially true for ![]() $m=0$ by assumption (3.38), our aim is to show that if (3.39) holds for some
$m=0$ by assumption (3.38), our aim is to show that if (3.39) holds for some ![]() $m\geq 1$, then the corresponding inequalities hold with
$m\geq 1$, then the corresponding inequalities hold with ![]() $m+1$ in place of
$m+1$ in place of ![]() $m$. Setting
$m$. Setting
 \begin{equation*} E(B_{\vartheta^{m}\varrho}):=\mathop {\int\hskip -1,05em -\,} \limits_{B_{\vartheta^{m}\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}
\begin{equation*} E(B_{\vartheta^{m}\varrho}):=\mathop {\int\hskip -1,05em -\,} \limits_{B_{\vartheta^{m}\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}in order to prove the second inequalities in (3.39) it will suffice to show that
We have, with (3.39) at step ![]() $m$, the shift-change formula (2.7) with
$m$, the shift-change formula (2.7) with ![]() $\eta =\frac {1}{2}$ and (3.42), the estimate
$\eta =\frac {1}{2}$ and (3.42), the estimate
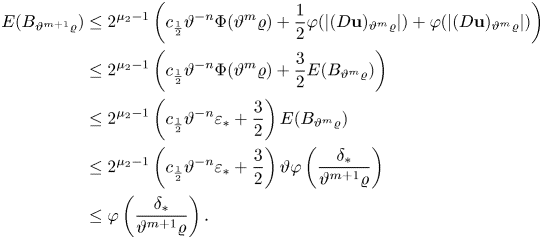 \begin{equation} \begin{split} E(B_{\vartheta^{m+1}\varrho}) & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n} \Phi(\vartheta^{m}\varrho) + \frac{1}{2}\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)+ \varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)\right)\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n} \Phi(\vartheta^{m}\varrho) +\frac{3}{2} E(B_{\vartheta^{m}\varrho})\right) \\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n}\varepsilon_*+\frac{3}{2}\right) E(B_{\vartheta^{m}\varrho})\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n}\varepsilon_*+\frac{3}{2}\right)\vartheta\varphi\left(\frac{\delta_*}{\vartheta^{m+1}\varrho}\right)\\ & \leq \varphi\left(\frac{\delta_*}{\vartheta^{m+1}\varrho}\right). \end{split} \end{equation}
\begin{equation} \begin{split} E(B_{\vartheta^{m+1}\varrho}) & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n} \Phi(\vartheta^{m}\varrho) + \frac{1}{2}\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)+ \varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)\right)\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n} \Phi(\vartheta^{m}\varrho) +\frac{3}{2} E(B_{\vartheta^{m}\varrho})\right) \\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n}\varepsilon_*+\frac{3}{2}\right) E(B_{\vartheta^{m}\varrho})\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\vartheta^{{-}n}\varepsilon_*+\frac{3}{2}\right)\vartheta\varphi\left(\frac{\delta_*}{\vartheta^{m+1}\varrho}\right)\\ & \leq \varphi\left(\frac{\delta_*}{\vartheta^{m+1}\varrho}\right). \end{split} \end{equation} Now, we prove by induction the first inequality in (3.39) for ![]() $m+1$. From (3.39) at step
$m+1$. From (3.39) at step ![]() $k$ and the choices of
$k$ and the choices of ![]() $\delta _*$ and
$\delta _*$ and ![]() $\varrho _*$ as in (3.43)–(3.44), we have
$\varrho _*$ as in (3.43)–(3.44), we have
 \begin{align*} &\frac{\Phi(\vartheta^{m}\varrho)}{{\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)}}\leq \varepsilon_*<3\varepsilon_*\leq\delta_1,\\ &[H(\vartheta^{m}\varrho)]^{\beta_1}<2\varepsilon_*\leq \delta_2, \end{align*}
\begin{align*} &\frac{\Phi(\vartheta^{m}\varrho)}{{\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|)}}\leq \varepsilon_*<3\varepsilon_*\leq\delta_1,\\ &[H(\vartheta^{m}\varrho)]^{\beta_1}<2\varepsilon_*\leq \delta_2, \end{align*}and
Then, by virtue of lemma 3.11 and lemma 3.12 applied with radius ![]() $\vartheta ^{m}\varrho$ in place of
$\vartheta ^{m}\varrho$ in place of ![]() $\varrho$, and recalling the choice of
$\varrho$, and recalling the choice of ![]() $\vartheta$ (3.41), we get
$\vartheta$ (3.41), we get
 \begin{equation*} \begin{split} \Phi(\vartheta^{m+1}\varrho)\leq 2c_\textrm{dec}\vartheta^{2}\Phi_*(\vartheta^{m}\varrho) & \leq 6c_\textrm{dec}\varepsilon_*\vartheta^{2}\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|) \\ & \leq \varepsilon_* \varphi(|(D{\bf u})_{\vartheta^{m+1}\varrho}|). \end{split} \end{equation*}
\begin{equation*} \begin{split} \Phi(\vartheta^{m+1}\varrho)\leq 2c_\textrm{dec}\vartheta^{2}\Phi_*(\vartheta^{m}\varrho) & \leq 6c_\textrm{dec}\varepsilon_*\vartheta^{2}\varphi(|(D{\bf u})_{\vartheta^{m}\varrho}|) \\ & \leq \varepsilon_* \varphi(|(D{\bf u})_{\vartheta^{m+1}\varrho}|). \end{split} \end{equation*} Finally, since the iteration starting from ![]() $m\,{=}\,0$ of the estimate
$m\,{=}\,0$ of the estimate ![]() $\varphi ^{-1}(E(B_{\vartheta ^{m+1}\varrho }))\leq 2^{\frac {\mu _2}{\mu _1}}\varphi ^{-1}(E(B_{\vartheta ^{m}\varrho }))$, obtained by (3.46) and (2.2), with (3.41) yields
$\varphi ^{-1}(E(B_{\vartheta ^{m+1}\varrho }))\leq 2^{\frac {\mu _2}{\mu _1}}\varphi ^{-1}(E(B_{\vartheta ^{m}\varrho }))$, obtained by (3.46) and (2.2), with (3.41) yields
and this estimate a fortiori holds if we consider ![]() $E(B_{\vartheta ^{m}\varrho }(y))$ for
$E(B_{\vartheta ^{m}\varrho }(y))$ for ![]() $y\in B_{\varrho /2}$ in place of
$y\in B_{\varrho /2}$ in place of ![]() $E(B_{\vartheta ^{m}\varrho })$, we deduce the Morrey-type estimate
$E(B_{\vartheta ^{m}\varrho })$, we deduce the Morrey-type estimate
for all ![]() $y\in B_{\varrho /2}$ and
$y\in B_{\varrho /2}$ and ![]() $r\leq \varrho /2$, which is equivalent to (3.40). The proof is now concluded.
$r\leq \varrho /2$, which is equivalent to (3.40). The proof is now concluded.
3.5 Excess decay estimate: the degenerate regime
In this section, with lemma 3.14 we will establish an excess improvement estimate for the degenerate case which is characterized by the fact that ![]() $\Phi (x_0,\varrho )$ is ‘large’ compared to
$\Phi (x_0,\varrho )$ is ‘large’ compared to ![]() $\varphi (|(D{\bf u})_{x_0,\varrho }|)$.
$\varphi (|(D{\bf u})_{x_0,\varrho }|)$.
In view of lemma 3.10, this will be achieved via the ![]() $\varphi$-harmonic approximation lemma (lemma 2.11) which allows to approximate the original minimizer by a
$\varphi$-harmonic approximation lemma (lemma 2.11) which allows to approximate the original minimizer by a ![]() $\varphi$-harmonic function. In this way, one can transfer the a priori estimates for
$\varphi$-harmonic function. In this way, one can transfer the a priori estimates for ![]() $\varphi$-harmonic functions (proposition 2.8) to the minimizer.
$\varphi$-harmonic functions (proposition 2.8) to the minimizer.
Lemma 3.14 Let ![]() $\gamma _0>0$ be the exponent of proposition 2.8. Then, for every
$\gamma _0>0$ be the exponent of proposition 2.8. Then, for every ![]() $0<\gamma <\gamma _0$ and every
$0<\gamma <\gamma _0$ and every ![]() $\kappa ,\mu \in (0,1)$ there exist
$\kappa ,\mu \in (0,1)$ there exist ![]() $\varepsilon _\#, \tau \in (0,1)$ and
$\varepsilon _\#, \tau \in (0,1)$ and ![]() $\varrho _\#\in (0,1]$ depending on
$\varrho _\#\in (0,1]$ depending on ![]() $n,N,\mu _1,\mu _2, c_0, \beta _0$,
$n,N,\mu _1,\mu _2, c_0, \beta _0$, ![]() $L,\nu ,\gamma ,\gamma _0,\mu$ and
$L,\nu ,\gamma ,\gamma _0,\mu$ and ![]() $\kappa$ (
$\kappa$ (![]() $\varepsilon _\#$ also depends on
$\varepsilon _\#$ also depends on ![]() $\tau$ and
$\tau$ and ![]() $\sigma (\delta )$, where
$\sigma (\delta )$, where ![]() $\delta$ satisfies (3.51) below, and
$\delta$ satisfies (3.51) below, and ![]() $\varrho _\#$ also depends on
$\varrho _\#$ also depends on ![]() $\omega$ and
$\omega$ and ![]() $\mathcal {V}$) with the following property: if
$\mathcal {V}$) with the following property: if
for ![]() $B_\varrho (x_0)\subseteq \Omega$ with
$B_\varrho (x_0)\subseteq \Omega$ with ![]() $\varrho \in (0,\varrho _\#]$, then
$\varrho \in (0,\varrho _\#]$, then
Proof. Without loss of generality, we assume that ![]() $x_0=0$ and, correspondingly, we use the abbreviations
$x_0=0$ and, correspondingly, we use the abbreviations ![]() $\Phi (\varrho )=\Phi (0,\varrho )$,
$\Phi (\varrho )=\Phi (0,\varrho )$, ![]() $\Psi (\varrho )=\Psi (0,\varrho )$,
$\Psi (\varrho )=\Psi (0,\varrho )$, ![]() $\Theta (\varrho )=\Theta (0,\varrho )$. Let
$\Theta (\varrho )=\Theta (0,\varrho )$. Let ![]() $0<\gamma <\gamma _0$ be fixed,
$0<\gamma <\gamma _0$ be fixed, ![]() $\tau \in (0,\frac {1}{2^{\mu _2}}]$ to be specified later, and we set
$\tau \in (0,\frac {1}{2^{\mu _2}}]$ to be specified later, and we set ![]() $\varepsilon :=\tau ^{2\gamma _0+n}$. Furthermore, let
$\varepsilon :=\tau ^{2\gamma _0+n}$. Furthermore, let ![]() $\delta _0=\delta _0(n,N,\varphi ,\nu ,L,\varepsilon )\in (0,1]$ be the constant according to the
$\delta _0=\delta _0(n,N,\varphi ,\nu ,L,\varepsilon )\in (0,1]$ be the constant according to the ![]() $\varphi$-harmonic approximation (lemma 2.11) with
$\varphi$-harmonic approximation (lemma 2.11) with ![]() $\theta$ the exponent of higher integrability as in (2.19).
$\theta$ the exponent of higher integrability as in (2.19).
Now, we have to check that ![]() ${\bf u}$ complies with (2.18), in order to apply lemma 2.11. From the Poincaré inequality, the shift change formula (2.7) with
${\bf u}$ complies with (2.18), in order to apply lemma 2.11. From the Poincaré inequality, the shift change formula (2.7) with ![]() $\eta =\kappa$ and (3.47) we have
$\eta =\kappa$ and (3.47) we have
 \begin{equation} \Psi(\varrho)\leq c_{P}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq 2^{\mu_2-1}c_{P} (c_{\kappa}+1+{\kappa}^{{-}1})\Phi(\varrho)\leq c_{P}c(\kappa,\mu_2)\varepsilon_\#, \end{equation}
\begin{equation} \Psi(\varrho)\leq c_{P}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x\leq 2^{\mu_2-1}c_{P} (c_{\kappa}+1+{\kappa}^{{-}1})\Phi(\varrho)\leq c_{P}c(\kappa,\mu_2)\varepsilon_\#, \end{equation}
where ![]() $c(\kappa ,\mu _2):=2^{\mu _2-1}(c_{\kappa }+1+{\kappa }^{-1})>1$. An analogous computation and the concavity of
$c(\kappa ,\mu _2):=2^{\mu _2-1}(c_{\kappa }+1+{\kappa }^{-1})>1$. An analogous computation and the concavity of ![]() $\varphi ^{-1}$ give
$\varphi ^{-1}$ give
 \begin{equation*} \begin{split} E(B_\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x & \leq \varphi\left(\varphi^{{-}1}\left(\frac{c(\kappa,\mu_2)\varepsilon_\#}{\varrho}\right)\right) \\ & \leq \varphi\left(\frac{(c(\kappa,\mu_2))^{\frac{1}{\mu_1}}\varphi^{{-}1}(\varepsilon_\#)}{\varrho}\right), \end{split} \end{equation*}
\begin{equation*} \begin{split} E(B_\varrho):=\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x & \leq \varphi\left(\varphi^{{-}1}\left(\frac{c(\kappa,\mu_2)\varepsilon_\#}{\varrho}\right)\right) \\ & \leq \varphi\left(\frac{(c(\kappa,\mu_2))^{\frac{1}{\mu_1}}\varphi^{{-}1}(\varepsilon_\#)}{\varrho}\right), \end{split} \end{equation*}whence
In applying lemma 3.10 we choose ![]() $\delta >0$ (which, in turn, determines
$\delta >0$ (which, in turn, determines ![]() $\sigma =\sigma (\delta )>0$ such that (3.31) holds) in such a way that
$\sigma =\sigma (\delta )>0$ such that (3.31) holds) in such a way that
where ![]() $c_*$ is the constant of lemma 3.10. Then, we choose
$c_*$ is the constant of lemma 3.10. Then, we choose ![]() $\varepsilon _\#<1$ such that
$\varepsilon _\#<1$ such that
 \begin{equation*} \varepsilon_\#\leq \min\left\{\frac{1}{c_{P}c(\kappa,\mu_2)}\varphi\left(\frac{\delta_0\sigma c_*}{4}\right), \varphi\left(\frac{\mu}{\tilde{c}(\kappa,\mu_1,\mu_2)}\right), \frac{\tau^{n}}{2 c_{\frac{1}{2}}}\varphi(\mu)\right\}, \end{equation*}
\begin{equation*} \varepsilon_\#\leq \min\left\{\frac{1}{c_{P}c(\kappa,\mu_2)}\varphi\left(\frac{\delta_0\sigma c_*}{4}\right), \varphi\left(\frac{\mu}{\tilde{c}(\kappa,\mu_1,\mu_2)}\right), \frac{\tau^{n}}{2 c_{\frac{1}{2}}}\varphi(\mu)\right\}, \end{equation*}so that, with (3.49)–(3.50), we have
We also determine a radius ![]() $\varrho _\#\in (0,1]$ according to
$\varrho _\#\in (0,1]$ according to
where ![]() $\beta _2$ is defined in lemma 3.10. Recalling the definition of
$\beta _2$ is defined in lemma 3.10. Recalling the definition of ![]() $\widetilde {H}(\varrho )$, for
$\widetilde {H}(\varrho )$, for ![]() $\varrho \leq \varrho _\#$ we then have
$\varrho \leq \varrho _\#$ we then have
For such choice of ![]() $\varepsilon _\#$ and
$\varepsilon _\#$ and ![]() $\varrho _\#$ it holds that
$\varrho _\#$ it holds that
so that, by lemma 2.11, there exists a unique ![]() $\varphi$-harmonic
$\varphi$-harmonic ![]() ${\bf w}\in W^{1,\varphi }(B_{\varrho /2},\mathbb {R}^{N})$ with
${\bf w}\in W^{1,\varphi }(B_{\varrho /2},\mathbb {R}^{N})$ with ![]() ${\bf w}={\bf u}$ on
${\bf w}={\bf u}$ on ![]() $\partial B_{\varrho /2}$ that satisfies
$\partial B_{\varrho /2}$ that satisfies
 \begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2\theta}\,\mathrm{d}x\right)^{\frac{1}{\theta}}\leq \tau^{2\gamma_0+n} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}
\begin{equation*} \left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}|{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2\theta}\,\mathrm{d}x\right)^{\frac{1}{\theta}}\leq \tau^{2\gamma_0+n} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation*}and
 \begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf w}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{equation*}
\begin{equation*} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf w}|)\,\mathrm{d}x\leq c \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}}\varphi(|D{\bf u}|)\,\mathrm{d}x. \end{equation*}Taking into account the higher integrability result of lemma 3.2, lemma 2.12 implies that
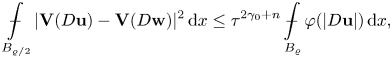 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2}\,\mathrm{d}x\leq \tau^{2\gamma_0+n} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho/2}} |{\bf V}(D{\bf u})-{\bf V}(D{\bf w})|^{2}\,\mathrm{d}x\leq \tau^{2\gamma_0+n} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}}\varphi(|D{\bf u}|)\,\mathrm{d}x, \end{equation}
and since ![]() $\tau <\frac {1}{2}$, from proposition 2.8 we also have
$\tau <\frac {1}{2}$, from proposition 2.8 we also have
Thus, with (3.52) and (3.53) we infer
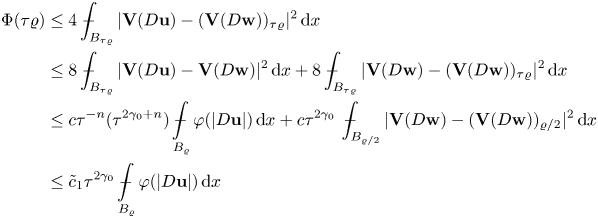 \begin{equation*} \begin{split} \Phi(\tau\varrho) & \leq 4 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf u})-({\bf V}(D {\bf w}))_{\tau\varrho}}\vert}^{2} \, \mathrm{d}x \\ & \leq 8 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf u})-{\bf V}(D {\bf w})}\vert}^{2} \, \mathrm{d}x + 8 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{\tau\varrho}}\vert}^{2} \, \mathrm{d}x \\ & \leq c\tau^{{-}n}(\tau^{2\gamma_0+n}) \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi(|D{\bf u}|)\,\mathrm{d}x + c \tau^{2 \gamma_0} \, \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\varrho/2}}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{\varrho/2}}\vert}^{2} \, \mathrm{d}x \\ & \leq \tilde{c}_1\tau^{2\gamma_0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi(|D{\bf u}|)\,\mathrm{d}x \end{split} \end{equation*}
\begin{equation*} \begin{split} \Phi(\tau\varrho) & \leq 4 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf u})-({\bf V}(D {\bf w}))_{\tau\varrho}}\vert}^{2} \, \mathrm{d}x \\ & \leq 8 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf u})-{\bf V}(D {\bf w})}\vert}^{2} \, \mathrm{d}x + 8 \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\tau\varrho}}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{\tau\varrho}}\vert}^{2} \, \mathrm{d}x \\ & \leq c\tau^{{-}n}(\tau^{2\gamma_0+n}) \mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi(|D{\bf u}|)\,\mathrm{d}x + c \tau^{2 \gamma_0} \, \mathop{\int\hskip -1,05em -\,}\nolimits_{\!\!\!\!{B_{\varrho/2}}} {\vert{{\bf V}(D{\bf w})-({\bf V}(D {\bf w}))_{\varrho/2}}\vert}^{2} \, \mathrm{d}x \\ & \leq \tilde{c}_1\tau^{2\gamma_0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho}\varphi(|D{\bf u}|)\,\mathrm{d}x \end{split} \end{equation*}
for some constant ![]() $\tilde {c}_1=\tilde {c}_1(n,N,\mu _1,\mu _2,c_1)>0$. Now, by virtue of the computation in (3.49) we conclude that
$\tilde {c}_1=\tilde {c}_1(n,N,\mu _1,\mu _2,c_1)>0$. Now, by virtue of the computation in (3.49) we conclude that
whence (3.48) follows if we choose ![]() $\tau$ such that
$\tau$ such that
 \begin{equation*} \tau\leq \left(\frac{1}{\tilde{c}_1c(\kappa,\mu_2)}\right)^{\frac{1}{2(\gamma_0-\gamma)}}. \end{equation*}
\begin{equation*} \tau\leq \left(\frac{1}{\tilde{c}_1c(\kappa,\mu_2)}\right)^{\frac{1}{2(\gamma_0-\gamma)}}. \end{equation*}
As for the second assertion in (3.48), the shift change formula (2.7) for ![]() $\eta =\frac {1}{2}$, with (3.47), (3.50) and the choice of
$\eta =\frac {1}{2}$, with (3.47), (3.50) and the choice of ![]() $\varepsilon _\#$ shows that
$\varepsilon _\#$ shows that
 \begin{equation*} \begin{split} E(B_{\tau\varrho})&:=\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\tau^{{-}n}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}} \varphi_{|(D{\bf u})_{\varrho}|}(|D{\bf u}-(D{\bf u})_{\varrho}|)\,\mathrm{d}x + \frac{3}{2}\varphi(|(D{\bf u})_{\varrho}|)\right) \\ & \leq 2^{\mu_2-1}\left(c_\frac{1}{2}\tau^{{-}n}\Phi(\varrho) +\frac{3}{2}E(B_{\varrho})\right)\\ & \leq 2^{\mu_2-1}\left(c_\frac{1}{2} \tau^{{-}n}\varepsilon_\#+\frac{3}{2}E(B_{\varrho})\right)\\ & \leq 2^{\mu_2}\tau\varphi\left(\frac{\mu}{\tau\varrho}\right) \end{split} \end{equation*}
\begin{equation*} \begin{split} E(B_{\tau\varrho})&:=\mathop {\int\hskip -1,05em -\,} \limits_{B_\tau\varrho} \varphi(|D{\bf u}|)\,\mathrm{d}x\\ & \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}\tau^{{-}n}\mathop {\int\hskip -1,05em -\,} \limits_{B_{\varrho}} \varphi_{|(D{\bf u})_{\varrho}|}(|D{\bf u}-(D{\bf u})_{\varrho}|)\,\mathrm{d}x + \frac{3}{2}\varphi(|(D{\bf u})_{\varrho}|)\right) \\ & \leq 2^{\mu_2-1}\left(c_\frac{1}{2}\tau^{{-}n}\Phi(\varrho) +\frac{3}{2}E(B_{\varrho})\right)\\ & \leq 2^{\mu_2-1}\left(c_\frac{1}{2} \tau^{{-}n}\varepsilon_\#+\frac{3}{2}E(B_{\varrho})\right)\\ & \leq 2^{\mu_2}\tau\varphi\left(\frac{\mu}{\tau\varrho}\right) \end{split} \end{equation*}
whence the assertion follows since ![]() $\tau \leq \frac {1}{2^{\mu _2}}$.
$\tau \leq \frac {1}{2^{\mu _2}}$.
3.6 Proof of theorem 1.1
Lemma 3.15 Under the assumptions of theorem 1.1, let ![]() $\alpha \in (0,1)$. Then there exist constants
$\alpha \in (0,1)$. Then there exist constants ![]() $\varepsilon _\#$,
$\varepsilon _\#$, ![]() $\delta _*$ and
$\delta _*$ and ![]() $\tilde {\varrho }$ such that the conditions
$\tilde {\varrho }$ such that the conditions
for ![]() $B_\varrho (x_0)\subseteq \Omega$ with
$B_\varrho (x_0)\subseteq \Omega$ with ![]() $\varrho \in (0,\tilde {\varrho }]$ imply
$\varrho \in (0,\tilde {\varrho }]$ imply
Proof. Without loss of generality, we assume that ![]() $x_0=0$ and, correspondingly, we omit the dependence on it. Let
$x_0=0$ and, correspondingly, we omit the dependence on it. Let ![]() $\varepsilon _*,\delta _*$,
$\varepsilon _*,\delta _*$, ![]() $\vartheta \in (0,1)$ and
$\vartheta \in (0,1)$ and ![]() $\varrho _*\in (0,1]$ be the constants of lemma 3.13. We then choose
$\varrho _*\in (0,1]$ be the constants of lemma 3.13. We then choose ![]() $\mu =\delta _*$ in lemma 3.14 leaving
$\mu =\delta _*$ in lemma 3.14 leaving ![]() $\kappa$ unchanged. This fixes the constants
$\kappa$ unchanged. This fixes the constants ![]() $\varepsilon _\#, \tau$ and
$\varepsilon _\#, \tau$ and ![]() $\varrho _\#$. We set
$\varrho _\#$. We set ![]() $\tilde {\varrho }:=\min \{\varrho _*,\varrho _\#\}$.
$\tilde {\varrho }:=\min \{\varrho _*,\varrho _\#\}$.
We introduce the set of integers
and we distinguish between the cases ![]() $\mathbb {S}=\mathbb {N}_0$ and
$\mathbb {S}=\mathbb {N}_0$ and ![]() $\mathbb {S}\neq \mathbb {N}_0$.
$\mathbb {S}\neq \mathbb {N}_0$.
The case ![]() $\mathbb {S}=\mathbb {N}_0$. We prove by induction that the bounds
$\mathbb {S}=\mathbb {N}_0$. We prove by induction that the bounds
hold for every ![]() $k\in \mathbb {N}_0$. The case
$k\in \mathbb {N}_0$. The case ![]() $k=0$ is trivial from the assumption (3.54). Now, since
$k=0$ is trivial from the assumption (3.54). Now, since ![]() $k\in \mathbb {S}=\mathbb {N}_0$, the assumption (3.47) of lemma 3.14 hold with
$k\in \mathbb {S}=\mathbb {N}_0$, the assumption (3.47) of lemma 3.14 hold with ![]() $\tau ^{k}\varrho$ in place of
$\tau ^{k}\varrho$ in place of ![]() $\varrho$. Then, an application of lemma 3.14 gives (3.56) for
$\varrho$. Then, an application of lemma 3.14 gives (3.56) for ![]() $k+1$ (recall that
$k+1$ (recall that ![]() $\tau <1$). The validity of (3.56) implies, as in lemma 3.13, that the Morrey-type estimate
$\tau <1$). The validity of (3.56) implies, as in lemma 3.13, that the Morrey-type estimate
holds for every ![]() $\alpha \in (0,1)$, for all
$\alpha \in (0,1)$, for all ![]() $y\in B_{\varrho /2}(x_0)$ and
$y\in B_{\varrho /2}(x_0)$ and ![]() $r\in (0,\varrho /2]$. For
$r\in (0,\varrho /2]$. For ![]() $y,z\in B_{\varrho /2}$, with
$y,z\in B_{\varrho /2}$, with ![]() $|y-z|\leq \varrho /4$ we estimate the telescopic sum
$|y-z|\leq \varrho /4$ we estimate the telescopic sum
 \begin{equation*} \frac{|{\bf u}(y)-{\bf u}(z)|}{|y-z|}\leq \sum_{j\in\mathbb{Z}}\frac{1}{2^{j}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\frac{|{\bf u}(x)-({\bf u})_j|}{|y-z|}\,\mathrm{d}x \leq \sum_{j\in\mathbb{Z}}\frac{1}{2^{j}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\frac{|{\bf u}(x)-({\bf u})_j|}{r_j}\,\mathrm{d}x, \end{equation*}
\begin{equation*} \frac{|{\bf u}(y)-{\bf u}(z)|}{|y-z|}\leq \sum_{j\in\mathbb{Z}}\frac{1}{2^{j}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\frac{|{\bf u}(x)-({\bf u})_j|}{|y-z|}\,\mathrm{d}x \leq \sum_{j\in\mathbb{Z}}\frac{1}{2^{j}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\frac{|{\bf u}(x)-({\bf u})_j|}{r_j}\,\mathrm{d}x, \end{equation*}
where ![]() $B_{r_j}:=B_{2^{1-j}|y-z|(y)}$ for
$B_{r_j}:=B_{2^{1-j}|y-z|(y)}$ for ![]() $j\geq 0$ and
$j\geq 0$ and ![]() $B_{r_j}:=B_{2^{1+j}|y-z|(z)}$ for
$B_{r_j}:=B_{2^{1+j}|y-z|(z)}$ for ![]() $j<0$. Now, with the Poincaré inequality we get
$j<0$. Now, with the Poincaré inequality we get
 \begin{equation*} \begin{split} \frac{|{\bf u}(y)-{\bf u}(z)|}{|y-z|}&\leq c\sum_{j\in\mathbb{Z}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}|D{\bf u}|\,\mathrm{d}x \\ & \leq c \sum_{j\in\mathbb{Z}}\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\varphi(|D{\bf u}|)\,\mathrm{d}x\right)\\ & \leq c \sum_{j\geq 0} \frac{\Theta(y,2^{1-j}|y-z|)}{2^{1-j}|y-z|} + c \sum_{j<0} \frac{\Theta(z,2^{1+j}|y-z|)}{2^{1+j}|y-z|}. \end{split} \end{equation*}
\begin{equation*} \begin{split} \frac{|{\bf u}(y)-{\bf u}(z)|}{|y-z|}&\leq c\sum_{j\in\mathbb{Z}}\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}|D{\bf u}|\,\mathrm{d}x \\ & \leq c \sum_{j\in\mathbb{Z}}\varphi^{{-}1}\left(\mathop {\int\hskip -1,05em -\,} \limits_{B_{r_j}}\varphi(|D{\bf u}|)\,\mathrm{d}x\right)\\ & \leq c \sum_{j\geq 0} \frac{\Theta(y,2^{1-j}|y-z|)}{2^{1-j}|y-z|} + c \sum_{j<0} \frac{\Theta(z,2^{1+j}|y-z|)}{2^{1+j}|y-z|}. \end{split} \end{equation*}Finally, with the estimate (3.57) we infer
 \begin{equation} \begin{split} |{\bf u}(y)-{\bf u}(z)| & \leq c \delta_* |y-z|^{\alpha}\varrho^{-\alpha} \left(\sum_{j\geq 0}2^{(\alpha-1)(1-j)}+\sum_{j<0}2^{(\alpha-1)(1+j)}\right)\\ & \leq c \delta_* |y-z|^{\alpha}\varrho^{-\alpha}, \end{split} \end{equation}
\begin{equation} \begin{split} |{\bf u}(y)-{\bf u}(z)| & \leq c \delta_* |y-z|^{\alpha}\varrho^{-\alpha} \left(\sum_{j\geq 0}2^{(\alpha-1)(1-j)}+\sum_{j<0}2^{(\alpha-1)(1+j)}\right)\\ & \leq c \delta_* |y-z|^{\alpha}\varrho^{-\alpha}, \end{split} \end{equation}
which, in particular, implies that ![]() ${\bf u}\in C^{0,\alpha }(\overline {B_{\varrho /2}})$.
${\bf u}\in C^{0,\alpha }(\overline {B_{\varrho /2}})$.
The case ![]() $\mathbb {S}\neq \mathbb {N}_0$. In this case, there exists
$\mathbb {S}\neq \mathbb {N}_0$. In this case, there exists ![]() $k_0:=\min \mathbb {N}\backslash \mathbb {S}$. Since
$k_0:=\min \mathbb {N}\backslash \mathbb {S}$. Since ![]() $k\in \mathbb {S}$ for any integer
$k\in \mathbb {S}$ for any integer ![]() $k< k_0$ we can iterate as in the case
$k< k_0$ we can iterate as in the case ![]() $\mathbb {S}=\mathbb {N}_0$ for
$\mathbb {S}=\mathbb {N}_0$ for ![]() $k=0,1,\dots ,k_0-1$ to infer that (3.56) holds for any
$k=0,1,\dots ,k_0-1$ to infer that (3.56) holds for any ![]() $k\leq k_0$. By the definition of
$k\leq k_0$. By the definition of ![]() $\mathbb {S}$ we have
$\mathbb {S}$ we have
which together with the second inequality in (3.56) with ![]() $k=k_0$ ensures that the assumptions (3.38) of lemma 3.13 are satisfied for
$k=k_0$ ensures that the assumptions (3.38) of lemma 3.13 are satisfied for ![]() $\varrho$ replaced by
$\varrho$ replaced by ![]() $\tau ^{k_0}\varrho$. Then, by virtue of this lemma, we have
$\tau ^{k_0}\varrho$. Then, by virtue of this lemma, we have
for every ![]() $m\in \mathbb {N}_0$.
$m\in \mathbb {N}_0$.
Now, we consider an arbitrary radius ![]() $r\in (0,\varrho ]$. If
$r\in (0,\varrho ]$. If ![]() $r\in (\tau ^{k_0}\varrho /2, \varrho ]$ we find
$r\in (\tau ^{k_0}\varrho /2, \varrho ]$ we find ![]() $0\leq k \leq k_0$ such that
$0\leq k \leq k_0$ such that ![]() $\tau ^{k+1}\leq r \leq \theta ^{k}$ and then we can argue as in the case
$\tau ^{k+1}\leq r \leq \theta ^{k}$ and then we can argue as in the case ![]() $\mathbb {S}=\mathbb {N}_0$. In the case
$\mathbb {S}=\mathbb {N}_0$. In the case ![]() $r\in (0,\tau ^{k_0}\varrho /2]$, instead, we find
$r\in (0,\tau ^{k_0}\varrho /2]$, instead, we find ![]() $m\in \mathbb {N}_0$ such that
$m\in \mathbb {N}_0$ such that ![]() $\vartheta ^{m+1}\tau ^{k_0}\varrho < r\leq \vartheta ^{m}\tau ^{k_0}\varrho$. Then arguing as in the proof of (3.40) and taking into account the second estimate in (3.59), we have
$\vartheta ^{m+1}\tau ^{k_0}\varrho < r\leq \vartheta ^{m}\tau ^{k_0}\varrho$. Then arguing as in the proof of (3.40) and taking into account the second estimate in (3.59), we have
for every ![]() $y\in B_{\vartheta ^{m}\tau ^{k_0}\varrho /2}\subseteq B_{\varrho /2}$ whence
$y\in B_{\vartheta ^{m}\tau ^{k_0}\varrho /2}\subseteq B_{\varrho /2}$ whence
At this point, we can argue as in the case ![]() $\mathbb {S}=\mathbb {N}_0$ for the proof of (3.58), whence (3.55) follows thus concluding the proof.
$\mathbb {S}=\mathbb {N}_0$ for the proof of (3.58), whence (3.55) follows thus concluding the proof.
Proof of theorem 1.1. Let ![]() $\varepsilon _\#$,
$\varepsilon _\#$, ![]() $\delta _*$ and
$\delta _*$ and ![]() $\tilde {\varrho }$ be the constants of lemma 3.15. Let
$\tilde {\varrho }$ be the constants of lemma 3.15. Let ![]() $\Sigma _1$ and
$\Sigma _1$ and ![]() $\Sigma _2$ be defined as in the statement of theorem 1.1. Note that, by Lebesgue's differentiation theorem, it holds that
$\Sigma _2$ be defined as in the statement of theorem 1.1. Note that, by Lebesgue's differentiation theorem, it holds that ![]() $|\Sigma _1\cup \Sigma _2|=0$. Thus, we are reduced to show that each
$|\Sigma _1\cup \Sigma _2|=0$. Thus, we are reduced to show that each ![]() $x_0\in \Omega \backslash (\Sigma _1\cup \Sigma _2)$ belongs to the set
$x_0\in \Omega \backslash (\Sigma _1\cup \Sigma _2)$ belongs to the set
where ![]() $U_{z_0}$ is an open neighbourhood of
$U_{z_0}$ is an open neighbourhood of ![]() $z_0$. For this, let
$z_0$. For this, let ![]() $x_0\in \Omega$ be such that both the conditions
$x_0\in \Omega$ be such that both the conditions
 \begin{align} &\mathop{\lim\inf}_{\varrho\searrow 0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\varrho}|}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x=0\,\mbox{ and }\notag\\ & m_{x_0}:=\mathop{\lim\sup}_{\varrho\searrow 0}|(D{\bf u})_{x_0,\varrho}|<{+}\infty \end{align}
\begin{align} &\mathop{\lim\inf}_{\varrho\searrow 0}\mathop {\int\hskip -1,05em -\,} \limits_{B_\varrho(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\varrho}|}(D{\bf u}-(D{\bf u})_{x_0,\varrho})|^{2}\,\mathrm{d}x=0\,\mbox{ and }\notag\\ & m_{x_0}:=\mathop{\lim\sup}_{\varrho\searrow 0}|(D{\bf u})_{x_0,\varrho}|<{+}\infty \end{align}hold.
We set
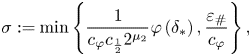 \begin{equation} \sigma:=\min\left\{\frac{1}{c_\varphi c_\frac{1}{2}2^{\mu_2}}\varphi\left({\delta_*}\right),\frac{\varepsilon_\#}{c_\varphi}\right\}, \end{equation}
\begin{equation} \sigma:=\min\left\{\frac{1}{c_\varphi c_\frac{1}{2}2^{\mu_2}}\varphi\left({\delta_*}\right),\frac{\varepsilon_\#}{c_\varphi}\right\}, \end{equation}
where the constants ![]() $c_\varphi$,
$c_\varphi$, ![]() $c_\frac {1}{2}$ are specified later and, correspondingly, with (3.60) we can find a radius
$c_\frac {1}{2}$ are specified later and, correspondingly, with (3.60) we can find a radius ![]() $\bar {\varrho }$ such that
$\bar {\varrho }$ such that
and
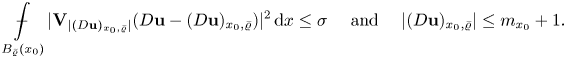 \begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x\leq\sigma\quad \mbox{ and }\quad |(D{\bf u})_{x_0,\bar{\varrho}}|\leq m_{x_0}+1. \end{equation}
\begin{equation} \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x\leq\sigma\quad \mbox{ and }\quad |(D{\bf u})_{x_0,\bar{\varrho}}|\leq m_{x_0}+1. \end{equation}Now, recalling that
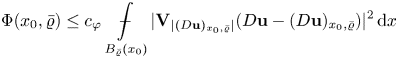 \begin{equation*} \Phi(x_0,\bar{\varrho})\leq c_\varphi \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x \end{equation*}
\begin{equation*} \Phi(x_0,\bar{\varrho})\leq c_\varphi \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x \end{equation*}
and observing that, as a consequence of the shift-change formula (2.7) with ![]() $\displaystyle \eta =\frac {1}{2}$, conditions (3.63) imply
$\displaystyle \eta =\frac {1}{2}$, conditions (3.63) imply
 \begin{equation*} \begin{split} &\mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq 2^{\mu_2-1}\left(c_\frac{1}{2} c_\varphi \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x+\frac{3}{2}\varphi(|(D{\bf u})_{x_0,\bar{\varrho}}|)\right)\\ & \quad \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}c_\varphi\sigma + \frac{3}{2}\varphi(m_{x_0}+1)\right) \leq \frac{1}{2}\varphi(\delta_*) + \frac{1}{2\bar{\varrho}}\varphi(\delta_*)\leq \varphi\left(\frac{\delta_*}{\bar{\varrho}}\right), \end{split} \end{equation*}
\begin{equation*} \begin{split} &\mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}\varphi(|D{\bf u}|)\,\mathrm{d}x \\ & \quad \leq 2^{\mu_2-1}\left(c_\frac{1}{2} c_\varphi \mathop {\int\hskip -1,05em -\,} \limits_{B_{\bar{\varrho}}(x_0)}|{\bf V}_{|(D{\bf u})_{x_0,\bar{\varrho}}|}(D{\bf u}-(D{\bf u})_{x_0,\bar{\varrho}})|^{2}\,\mathrm{d}x+\frac{3}{2}\varphi(|(D{\bf u})_{x_0,\bar{\varrho}}|)\right)\\ & \quad \leq 2^{\mu_2-1}\left(c_{\frac{1}{2}}c_\varphi\sigma + \frac{3}{2}\varphi(m_{x_0}+1)\right) \leq \frac{1}{2}\varphi(\delta_*) + \frac{1}{2\bar{\varrho}}\varphi(\delta_*)\leq \varphi\left(\frac{\delta_*}{\bar{\varrho}}\right), \end{split} \end{equation*}
with the choice of ![]() $\sigma$ (3.61), corresponding to the radius
$\sigma$ (3.61), corresponding to the radius ![]() $\bar {\varrho }\in (0,\tilde {\varrho }]$ as in (3.62) there holds
$\bar {\varrho }\in (0,\tilde {\varrho }]$ as in (3.62) there holds
By the absolute continuity of the integral, we can find an open neighbourhood ![]() $U_{x_0}$ of
$U_{x_0}$ of ![]() $x_0$ such that
$x_0$ such that
for every ![]() $x\in U_{x_0}$. We can apply lemma 3.15 at each point of
$x\in U_{x_0}$. We can apply lemma 3.15 at each point of ![]() $U_{x_0}$, proving that
$U_{x_0}$, proving that ![]() ${\bf u}\in C^{0,\alpha }(U_{x_0},\mathbb {R}^{N})$ for every
${\bf u}\in C^{0,\alpha }(U_{x_0},\mathbb {R}^{N})$ for every ![]() $\alpha \in (0,1)$. Thus,
$\alpha \in (0,1)$. Thus, ![]() $x_0\in \Omega _0$ and the proof is concluded.
$x_0\in \Omega _0$ and the proof is concluded.
Acknowledgments
G. Scilla has been supported by the Italian Ministry of Education, University and Research through the Project Variational methods for stationary and evolution problems with singularities and interfaces (PRIN 2017). The research of B. Stroffolini was supported by PRIN Project 2017TEXA3H.