Hostname: page-component-6bb9c88b65-dwch4 Total loading time: 0 Render date: 2025-07-17T22:37:23.316Z Has data issue: false hasContentIssue false
  • English
  • Français

A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N

Part of: Equations of mathematical physics and other areas of application Elliptic equations and systems Partial differential equations Higher-dimensional theory

Published online by Cambridge University Press:  17 February 2025

Alessandro Cannone Open the ORCID record for Alessandro Cannone [Opens in a new window]  and
Silvia Cingolani Open the ORCID record for Silvia Cingolani [Opens in a new window]
Alessandro Cannone
Affiliation:
Dipartimento di Matematica, Università degli Studi di Bari Aldo Moro Via Orabona 4, 70125 Bari, Italy (alessandro.cannone@uniba.it)
Silvia Cingolani*
Affiliation:
Dipartimento di Matematica, Università degli Studi di Bari Aldo Moro Via Orabona 4, 70125 Bari, Italy (silvia.cingolani@uniba.it) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In the article, we investigate Trudinger–Moser type inequalities in presence of logarithmic kernels in dimension N. A sharp threshold, depending on N, is detected for the existence of extremal functions or blow-up, where the domain is the ball or the entire space 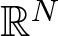$\mathbb{R}^N$. We also show that the extremal functions satisfy suitable Euler–Lagrange equations. When the domain is the entire space, such equations can be derived by a N-Laplacian Schrödinger equation strongly coupled with a higher order fractional Poisson’s equation. The results extends [16] to any dimension 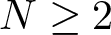$N \geq 2$.

Keywords

N dimensionextremal functionslogarithmic kernelthresholdTrudinger–Moser inequality

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 35Q40: PDEs in connection with quantum mechanics 31B10: Integral representations, integral operators, integral equations methods 35B33: Critical exponents

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 39
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abatangelo, N.. Very large solutions for the fractional Laplacian: Towards a fractional Keller-Osserman condition. Adv. Nonlinear Anal. 6 (2017), 383–405.CrossRefGoogle Scholar
Abatangelo, N., Jarohs, S. and Saldana, A.. Integral representation of solutions to higher-order fractional Dirichlet problems on balls. Commun. Contemp. Math. 20 (2018), .CrossRefGoogle Scholar
Beckner, W.. Sharp Sobolev inequalities on the sphere and the Moser-Trudinger inequality. Ann. of Math. (2) 138 (1993), 213–242.CrossRefGoogle Scholar
Berestycki, H. and Lions, P. L.. Nonlinear Scalar field equations, I. Existence of ground state. Arch. Rational Mech. Anal. 82 (1983), 313–346.CrossRefGoogle Scholar
Bonheure, D., Cingolani, S. and Secchi, S.. Concentration phenomena for the Schrödinger-Poisson system in $\mathbb{R}^2$. Discrete Contin. Dyn. Syst. Ser. S 14 (2021), 1631–1648.Google Scholar
Bonheure, D., Cingolani, S. and Van Schaftingen, J.. The logarithmic Choquard equation: Sharp asymptotics and nondegeneracy of the groundstate. J. Funct. Anal. 272 (2017), 5255–5281.CrossRefGoogle Scholar
Brasco, L., Gomez-Castro, D. and Vazquez, J. L.. Characterisation of homogeneous fractional Sobolev spaces. Calc. Var. Partial Differ. Equ. 60 (2021), .CrossRefGoogle Scholar
Bucur, C.. Some observations on the Green function for the ball in the fractional Laplace framework. Commun. Pure Appl. Anal. 15 (2016), 657–699.CrossRefGoogle Scholar
Bucur, C., Cassani, D. and Tarsi, C.. Quasilinear logarithmic Choquard equations with exponential growth in $\mathbb{R}^N$. J. Differ. Equ. 328 (2022), 261–294.CrossRefGoogle Scholar
Caglioti, E., Lions, P. L., Marchioro, C. and Pulvirenti, M.. A special class of stationary flows for two-dimensional Euler equations: A statistical mechanics description. Part II. Comm. Math. Phys. 174 (1995), 229–260.CrossRefGoogle Scholar
Cao, D. M.. Nontrivial solution of semilinear elliptic equation with critical exponent in $\mathbb{R}^2$. Comm. Partial Differ. Equ. 17 (1992), 407–435.CrossRefGoogle Scholar
Cassani, D., Liu, Z. and Romani, G.. Nonlocal planar Schrödinger-Poisson systems in the fractional Sobolev limiting case. J. Differ. Equ. 384 (2024), 214–269.CrossRefGoogle Scholar
Cassani, D., Liu, Z. and Romani, G.. Nonlocal Schrödinger-Poisson systems in $\mathbb{R}^N$. Preprint arxiv:2311.13424.Google Scholar
Cingolani, S. and Jeanjean, L.. Stationary solutions with prescribed L 2-norm for the planar Schrödinger-Poisson system. SIAM J. Math. Anal. 51 (2019), 3533–3568.CrossRefGoogle Scholar
Cingolani, S. and Weth, T.. On the planar Schrödinger-Poisson system. Ann. Inst. H. Poincaré Anal. Non LinéAire. 33 (2016), 169–197.CrossRefGoogle Scholar
Cingolani, S. and Weth, T.. Trudinger-Moser type inequality with logarithmic convolution potentials. J. Lond. Math. Soc. 105 (2022), 1897–1935.CrossRefGoogle Scholar
Cingolani, S., Weth, T. and Yu, M.. Extremal functions for the critical Trudinger-Moser inequality with logarithmic kernels. ESAIM: COCV 30 (2024), .Google Scholar
Dolbeault, J. and Perthame, B.. Optimal critical mass in the two dimensional Keller-Segel model in $\mathbb{R}^2$. C. R. Acad. Sci. Paris, Ser. I 339 (2004), 611–616.CrossRefGoogle Scholar
do Ó, J. M.. N-Laplacian equations in $\mathbb{R}^N$ with critical growth. Abstr. Appl. Anal. 2 (1997), 301–315.CrossRefGoogle Scholar
Du, M. and Weth, T.. Ground states and high energy solutions of the planar Schrödinger-Poisson system. Nonlinearity 30 (2017), 3492–3515.CrossRefGoogle Scholar
Galdi, G. P.. An introduction to the mathematical theory of the Navier-Stokes equations. Steady-state problems, Vol. 2, second edition (Springer Monographs in Mathematics, Springer, New York, 2011).CrossRefGoogle Scholar
Hyder, A.. Structure of conformal metrics on $\mathbb{R}^N$ with constant Q-curvature. Differ. Integral Equ. 32 (2019), 423–454.Google Scholar
Landkof, N. S.. Foundations of modern potential theory, Die Grundlehren der Mathematischen Wissenschaften, Vol. 180 (Springer-Verlag, New York-Heidelberg, 1972).Google Scholar
Li, Y. and Ruf, B.. A sharp Trudinger-Moser type inequality for unbounded domains in $\mathbb{R}^N$. Indiana Univ. Math. J. 57 (2008), .CrossRefGoogle Scholar
Lieb, E. H. and Loss, M.. Analysis, AMS 14, 2001.CrossRefGoogle Scholar
Lions, P. L.. The concentration-compactness principle in the calculus of variations. The limit case, part 1, Rev. Mat. Iberoam. 1 (1985), 145–201.CrossRefGoogle Scholar
Martinazzi, L., Classification of solutions to the higher order Liouville’s equation on $\mathbb{R}^{2m}$, Math. Z. 263 (2009), 307–329.CrossRefGoogle Scholar
Masaki, S.. Local existence and WKB approximation of solutions to Schrödinger-Poisson system in the two-dimensional whole space. Comm. Partial Differ. Equ. 35 (2010), 2253–2278.CrossRefGoogle Scholar
Masaki, S.. Energy solution to a Schrödinger-Poisson system in the two-dimensional whole space. SIAM J Math. Anal. 43 (2011) 2719-2731.CrossRefGoogle Scholar
Moser, J.. A sharp form of an inequality by N Trudinger, Ind. Univ. Math. 30 (1967), 473–484.Google Scholar
Ruf, B.. A sharp Trudinger-Moser type inequality for unbounded domains in $\mathbb{R}^2$. J. Funct. Anal. 219 (2005), 340–367.CrossRefGoogle Scholar
Samko, S., Kilbas, A. and Marichev, O.. Fractional integrals and derivatives (Gordon and Breach Science Publishers, Yverdon, 1993).Google Scholar
Stein, E.. Singular integrals and differentiability properties of functions, Vol. 30 (Princeton Mathematical Series, Princeton University Press, Princeton, NJ, 1970).Google Scholar
Stinga, P. R.. User’s guide to the fractional Laplacian and the method of semigroups. Handbook of fractional calculus with applications, Vol. 2, (De Gruyter, Berlin, 2019).Google Scholar
Stubbe, J.. Bound states of two-dimensional Schrödinger-Newton equations. arXiv 0807.4059v1 2008.Google Scholar
Stubbe, J. and Vuffray, M.. Bound states of the Schrödinger-Newton model in low dimensions. Nonlinear Anal. 73 (2010), 3171–3178.CrossRefGoogle Scholar
Suzuki, T.. Free energy and self-interacting particles, Progress in Nonlinear Differential Equations and Their Applications, Vol. 62 (Birkhäuser, Boston, 2005).Google Scholar
Trudinger, N. S.. On imbeddings into Orlicz spaces and some applications. J. Math. Mech. 75 (1980), 473–483.Google Scholar
Wolansky, G.. On steady distributions of self-attracting clusters under friction and fluctuations, Arch. Rational Mech. Anal. 119 (1992), 355–391.CrossRefGoogle Scholar