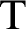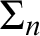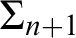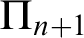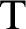1 Introduction
There has been a recent interest in hierarchical generalizations of classic incompleteness results [Reference Chao and Seraji5, Reference Kikuchi and Kurahashi23, Reference Kurahashi27, Reference Salehi and Seraji40]. A sample result, generalizing the Gödel–Rosser incompleteness theorem, and independently proved by both Kikuchi and Kurahashi [Reference Kikuchi and Kurahashi23] and Salehi and Seraji [Reference Salehi and Seraji40], is:
Theorem 1.1. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Sigma _n$
-sound extension of
$\Sigma _n$
-sound extension of
![]() $\mathrm {PA}$
. Then there is a
$\mathrm {PA}$
. Then there is a
![]() $\Pi _{n+1}$
sentence that is undecidable in
$\Pi _{n+1}$
sentence that is undecidable in
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
In this paper I argue that such hierarchical generalizations can often be obtained from the original proofs by replacing certain principles used in the proofs by appropriately formulated hierarchical versions, while the essence of the arguments remains the same. The hierarchical principles, once appropriately formulated, are in turn often provable by appropriate generalizations of the core concepts employed in the proofs of the ordinary ones, but even so, there is no single source to which to turn for them. Both Smoryński [Reference Smoryński45] and Beklemishev [Reference Beklemishev1] give good partial accounts of the syntactical side, and Poizat [Reference Poizat35] gives a hierarchical perspective on the basic model theory of arithmetic, including model-theoretic proofs of hierarchical versions of Gödel’s first and second incompleteness theorems. Still, I find certain aspects lacking. With this in mind, one aim of this paper is to collect a number of principles that may be useful to the reader who herself wishes to prove hierarchical incompleteness results without having to reinvent the wheel.
These principles are then put to use to prove a number of general incompleteness results for arithmetically definable extensions of fragments of
![]() $\mathrm {PA}$
. The goal is not to prove the sharpest or most general results (in fact some of the results follow from each other), but rather to exemplify how the hierarchical principles enter into more or less well-known proof methods. Even so, the results presented here improve on some results of Chao and Seraji [Reference Chao and Seraji5], Kikuchi and Kurahashi [Reference Kikuchi and Kurahashi23], and Salehi and Seraji [Reference Salehi and Seraji40], and sharpen some of Blanck [Reference Blanck3], Hamkins [Reference Hamkins18], Lindström [Reference Lindström28], and Woodin [Reference Woodin, Heller and Woodin48]. These sharpenings are in terms of gauging the amount of induction needed for the proofs, bringing the (in this particular sub-field largely ignored) fragments-of-arithmetic perspective to attention.
$\mathrm {PA}$
. The goal is not to prove the sharpest or most general results (in fact some of the results follow from each other), but rather to exemplify how the hierarchical principles enter into more or less well-known proof methods. Even so, the results presented here improve on some results of Chao and Seraji [Reference Chao and Seraji5], Kikuchi and Kurahashi [Reference Kikuchi and Kurahashi23], and Salehi and Seraji [Reference Salehi and Seraji40], and sharpen some of Blanck [Reference Blanck3], Hamkins [Reference Hamkins18], Lindström [Reference Lindström28], and Woodin [Reference Woodin, Heller and Woodin48]. These sharpenings are in terms of gauging the amount of induction needed for the proofs, bringing the (in this particular sub-field largely ignored) fragments-of-arithmetic perspective to attention.
In order to state the results in a more general form, I have chosen to consider only extensions of
![]() $\mathrm {I}\Delta _0 + \mathrm {exp}$
, although under the somewhat unusual name
$\mathrm {I}\Delta _0 + \mathrm {exp}$
, although under the somewhat unusual name
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
. This allows for formulating results for extensions of, e.g.,
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
. This allows for formulating results for extensions of, e.g.,
![]() $\mathrm {I}\Sigma _n + \mathrm {exp}$
, ensuring that partial satisfaction predicates are well behaved even for
$\mathrm {I}\Sigma _n + \mathrm {exp}$
, ensuring that partial satisfaction predicates are well behaved even for
![]() $n=0$
. While it is sometimes possible to push the background theory below
$n=0$
. While it is sometimes possible to push the background theory below
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
, I have refrained from doing so, to instead focus on the more general hierarchical picture.
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
, I have refrained from doing so, to instead focus on the more general hierarchical picture.
2 Notation and conventions
The expressions
![]() $\exists x \leq t \phi (x)$
and
$\exists x \leq t \phi (x)$
and
![]() $\forall x \leq t \phi (x)$
are used as shorthand for
$\forall x \leq t \phi (x)$
are used as shorthand for
![]() $\exists x (x \leq t \land \phi (x))$
and
$\exists x (x \leq t \land \phi (x))$
and
![]() $\forall x (x\leq t \rightarrow \phi (x))$
, where t is some term in the language of arithmetic. The initial quantifiers of these formulae are bounded and a formula containing only bounded quantifiers is a bounded formula. Let
$\forall x (x\leq t \rightarrow \phi (x))$
, where t is some term in the language of arithmetic. The initial quantifiers of these formulae are bounded and a formula containing only bounded quantifiers is a bounded formula. Let
![]() $\Delta _0 = \Sigma _0 = \Pi _0$
be the class of bounded formulae.
$\Delta _0 = \Sigma _0 = \Pi _0$
be the class of bounded formulae.
The arithmetical hierarchy is defined as follows. A formula is
![]() $\Sigma _{n+1}$
iff it is of the form
$\Sigma _{n+1}$
iff it is of the form
![]() $\exists x_1 \dots x_m \pi (x_1,\dots ,x_m)$
where
$\exists x_1 \dots x_m \pi (x_1,\dots ,x_m)$
where
![]() $\pi $
is a
$\pi $
is a
![]() $\Pi _n$
formula (that may contain other variables than
$\Pi _n$
formula (that may contain other variables than
![]() $x_1,\dots ,x_m$
). Similarly, a formula is
$x_1,\dots ,x_m$
). Similarly, a formula is
![]() $\Pi _{n+1}$
iff it is of the form
$\Pi _{n+1}$
iff it is of the form
![]() $\forall x_1 \dots x_m \sigma (x_1,\dots ,x_m)$
where
$\forall x_1 \dots x_m \sigma (x_1,\dots ,x_m)$
where
![]() $\sigma $
is a
$\sigma $
is a
![]() $\Sigma _n$
formula.
$\Sigma _n$
formula.
![]() $\Delta _n(\mathcal {M})$
(
$\Delta _n(\mathcal {M})$
(
![]() $\Delta _n(\mathrm {T})$
) is the set of
$\Delta _n(\mathrm {T})$
) is the set of
![]() $\Sigma _n$
formulae that are equivalent to
$\Sigma _n$
formulae that are equivalent to
![]() $\Pi _n$
formulae in a given model
$\Pi _n$
formulae in a given model
![]() $\mathcal {M}$
(theory
$\mathcal {M}$
(theory
![]() $\mathrm {T}$
). Throughout the paper
$\mathrm {T}$
). Throughout the paper
![]() $\Gamma $
denotes either
$\Gamma $
denotes either
![]() $\Sigma _{n+1}$
or
$\Sigma _{n+1}$
or
![]() $\Pi _{n+1}$
, and we always assume only that
$\Pi _{n+1}$
, and we always assume only that
![]() $n\geq 0$
.
$n\geq 0$
.
Theories are understood as sets of sentences, thought of as the set of nonlogical axioms of the theory.
![]() $\mathrm {I}\Sigma _n$
is the theory obtained by adding induction for
$\mathrm {I}\Sigma _n$
is the theory obtained by adding induction for
![]() $\Sigma _n$
formulae to Robinson’s arithmetic
$\Sigma _n$
formulae to Robinson’s arithmetic
![]() $\mathrm {Q}$
, while
$\mathrm {Q}$
, while
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
is
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
is
![]() $\mathrm {Q}$
plus
$\mathrm {Q}$
plus
![]() $\Sigma _0$
-induction plus an axiom stating that the exponentiation function is total. We assume that all theories denoted
$\Sigma _0$
-induction plus an axiom stating that the exponentiation function is total. We assume that all theories denoted
![]() $\mathrm {T}$
, etc., are consistent, arithmetically definable, extensions of
$\mathrm {T}$
, etc., are consistent, arithmetically definable, extensions of
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
.
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
.
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Gamma $
-sound iff for all
$\Gamma $
-sound iff for all
![]() $\Gamma $
sentences
$\Gamma $
sentences
![]() $\unicode{x3b3} $
, if
$\unicode{x3b3} $
, if
![]() $\mathrm {T} \vdash \unicode{x3b3} $
, then
$\mathrm {T} \vdash \unicode{x3b3} $
, then
![]() $\mathbb {N} \models \unicode{x3b3} $
. The converse implication is sometimes known as
$\mathbb {N} \models \unicode{x3b3} $
. The converse implication is sometimes known as
![]() $\Gamma $
-completeness: hence
$\Gamma $
-completeness: hence
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Gamma $
-complete iff for all
$\Gamma $
-complete iff for all
![]() $\Gamma $
sentences
$\Gamma $
sentences
![]() $\unicode{x3b3} $
, if
$\unicode{x3b3} $
, if
![]() $\mathbb {N} \models \unicode{x3b3} $
, then
$\mathbb {N} \models \unicode{x3b3} $
, then
![]() $\mathrm {T} \vdash \unicode{x3b3} $
.
$\mathrm {T} \vdash \unicode{x3b3} $
.
![]() $\mathrm {S}$
is
$\mathrm {S}$
is
![]() $\Gamma $
-conservative over
$\Gamma $
-conservative over
![]() $\mathrm {T}$
iff for all
$\mathrm {T}$
iff for all
![]() $\Gamma $
sentences
$\Gamma $
sentences
![]() $\unicode{x3b3} $
, if
$\unicode{x3b3} $
, if
![]() $\mathrm {S} \vdash \unicode{x3b3} $
, then
$\mathrm {S} \vdash \unicode{x3b3} $
, then
![]() $\mathrm {T} \vdash \unicode{x3b3} $
.
$\mathrm {T} \vdash \unicode{x3b3} $
.
We rely on a coding of finite sets and sequences in
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
, as developed by Hájek & Pudlák [Reference Hájek and Pudlák17, chap. I.1]. The set
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
, as developed by Hájek & Pudlák [Reference Hájek and Pudlák17, chap. I.1]. The set
![]() $\Sigma _0(X)$
is obtained by adding atomic formulae of the form
$\Sigma _0(X)$
is obtained by adding atomic formulae of the form
![]() $t \in X$
(where t is any term) and closing under propositional connectives and bounded quantifiers. The set
$t \in X$
(where t is any term) and closing under propositional connectives and bounded quantifiers. The set
![]() $\Sigma _1(X)$
is obtained from
$\Sigma _1(X)$
is obtained from
![]() $\Sigma _0(X)$
in the usual manner.
$\Sigma _0(X)$
in the usual manner.
Let
![]() $\varepsilon $
be Ackermann’s membership relation:
$\varepsilon $
be Ackermann’s membership relation:
![]() $n\varepsilon a$
expresses “the nth bit of the binary expansion of a is
$n\varepsilon a$
expresses “the nth bit of the binary expansion of a is
![]() $1$
.” In other words, a can be regarded as a code for the set consisting of all n such that
$1$
.” In other words, a can be regarded as a code for the set consisting of all n such that
![]() $n\varepsilon a$
. Then a is a z-piece of
$n\varepsilon a$
. Then a is a z-piece of
![]() $\phi (x)$
if
$\phi (x)$
if
![]() $\forall n < z (n\varepsilon a \leftrightarrow \phi (n))$
.
$\forall n < z (n\varepsilon a \leftrightarrow \phi (n))$
.
If
![]() $\phi (x)$
is any formula,
$\phi (x)$
is any formula,
![]() $\ulcorner \phi (x) \urcorner $
denotes the numeral for the Gödel number of
$\ulcorner \phi (x) \urcorner $
denotes the numeral for the Gödel number of
![]() $\phi (x)$
under some fixed Gödel numbering, but we make no typographical distinction between natural numbers and the corresponding numerals. We use Feferman’s dot notation
$\phi (x)$
under some fixed Gödel numbering, but we make no typographical distinction between natural numbers and the corresponding numerals. We use Feferman’s dot notation
![]() $\ulcorner \phi (\dot {x})\urcorner $
to represent the Gödel number of the sentence obtained by replacing the variable x with the actual value of x; hence x is free in
$\ulcorner \phi (\dot {x})\urcorner $
to represent the Gödel number of the sentence obtained by replacing the variable x with the actual value of x; hence x is free in
![]() $\ulcorner \phi (\dot {x})\urcorner $
. The notation
$\ulcorner \phi (\dot {x})\urcorner $
. The notation
![]() $:=$
is used to express equality between formulae. Let
$:=$
is used to express equality between formulae. Let
![]() $\top := 0 = 0$
and
$\top := 0 = 0$
and
![]() $\bot := \lnot \top $
. Let
$\bot := \lnot \top $
. Let
![]() $\phi ^0 := \lnot \phi $
and
$\phi ^0 := \lnot \phi $
and
![]() $\phi ^1 := \phi $
. Footnote
1
$\phi ^1 := \phi $
. Footnote
1
A relation X is numerated in
![]() $\mathrm {T}$
by a formula
$\mathrm {T}$
by a formula
![]() $\phi $
iff
$\phi $
iff
![]() $X = \{\langle k_1,\dots ,k_n \rangle \in \omega ^n : \mathrm {T} \vdash \phi (k_1,\dots ,k_n)\}$
, and binumerated by
$X = \{\langle k_1,\dots ,k_n \rangle \in \omega ^n : \mathrm {T} \vdash \phi (k_1,\dots ,k_n)\}$
, and binumerated by
![]() $\phi $
in
$\phi $
in
![]() $\mathrm {T}$
if
$\mathrm {T}$
if
![]() $\lnot \phi $
also numerates the complement of X. A relation X is correctly numerated by
$\lnot \phi $
also numerates the complement of X. A relation X is correctly numerated by
![]() $\phi $
if
$\phi $
if
![]() $\phi $
numerates X and for all
$\phi $
numerates X and for all
![]() $k_1,\dots ,k_n$
,
$k_1,\dots ,k_n$
,
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_n)$
iff
$\mathrm {T} \vdash \phi (k_1,\dots ,k_n)$
iff
![]() $\phi (k_1,\dots ,k_n)$
is true. A function f is strongly representable in
$\phi (k_1,\dots ,k_n)$
is true. A function f is strongly representable in
![]() $\mathrm {T}$
iff there is a formula
$\mathrm {T}$
iff there is a formula
![]() $\phi (x_1,\dots ,x_n,y)$
that numerates
$\phi (x_1,\dots ,x_n,y)$
that numerates
![]() $f(x_1,\dots ,x_n) = y$
in
$f(x_1,\dots ,x_n) = y$
in
![]() $\mathrm {T}$
, and moreover, if
$\mathrm {T}$
, and moreover, if
![]() $f(k_1,\dots ,k_n) = m$
, then
$f(k_1,\dots ,k_n) = m$
, then
![]() $\mathrm {T} \vdash \forall y (\phi (k_1,\dots ,k_n,y) \rightarrow y = m)$
.
$\mathrm {T} \vdash \forall y (\phi (k_1,\dots ,k_n,y) \rightarrow y = m)$
.
Given a formula
![]() $\tau (z)$
, let
$\tau (z)$
, let
![]() $\mathrm {Prf}_\tau (x,y)$
be a formula expressing “y is a proof of the formula x from the set of sentences satisfying
$\mathrm {Prf}_\tau (x,y)$
be a formula expressing “y is a proof of the formula x from the set of sentences satisfying
![]() $\tau (z)$
.” Let
$\tau (z)$
.” Let
![]() $\mathrm {Pr}_\tau (x)$
be the formula
$\mathrm {Pr}_\tau (x)$
be the formula
![]() $\exists y \mathrm {Prf}_\tau (x,y)$
, and let
$\exists y \mathrm {Prf}_\tau (x,y)$
, and let
![]() $\mathrm {Con}_\tau $
be the sentence
$\mathrm {Con}_\tau $
be the sentence
![]() $\lnot \mathrm {Pr}_\tau (\ulcorner \bot \urcorner )$
. Whenever
$\lnot \mathrm {Pr}_\tau (\ulcorner \bot \urcorner )$
. Whenever
![]() $\tau (z)$
is
$\tau (z)$
is
![]() $\Sigma _{n+1}$
,
$\Sigma _{n+1}$
,
![]() $\mathrm {Pr}_\tau (x)$
is equivalent to a
$\mathrm {Pr}_\tau (x)$
is equivalent to a
![]() $\Sigma _{n+1}$
formula in the real world. For any formula
$\Sigma _{n+1}$
formula in the real world. For any formula
![]() $\tau (x)$
, the notation
$\tau (x)$
, the notation
![]() $(\tau + z)(x)$
is used as shorthand for
$(\tau + z)(x)$
is used as shorthand for
![]() $\tau (x) \lor x = z$
. This convention is used in expressions such as
$\tau (x) \lor x = z$
. This convention is used in expressions such as
![]() $\mathrm {Prf}_{\tau + z}(x)$
.
$\mathrm {Prf}_{\tau + z}(x)$
.
Models of arithmetic are denoted
![]() $\mathcal {M}$
, etc., while the respective domains are denoted M, etc. The standard model is denoted
$\mathcal {M}$
, etc., while the respective domains are denoted M, etc. The standard model is denoted
![]() $\mathbb {N}$
and its domain is
$\mathbb {N}$
and its domain is
![]() $\omega $
. If
$\omega $
. If
![]() $\mathcal {M}$
is non-standard, then the standard system of
$\mathcal {M}$
is non-standard, then the standard system of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathrm {SSy}(\mathcal {M})$
, is the collection of sets
$\mathrm {SSy}(\mathcal {M})$
, is the collection of sets
![]() $X \subseteq \omega $
such that for some
$X \subseteq \omega $
such that for some
![]() $a \in M$
,
$a \in M$
,
![]() $X = \{ n \in \omega : \mathcal {M} \models n\varepsilon a\}$
. Then X is coded in
$X = \{ n \in \omega : \mathcal {M} \models n\varepsilon a\}$
. Then X is coded in
![]() $\mathcal {M}$
, and a is a code for X.
$\mathcal {M}$
, and a is a code for X.
A relation
![]() $X \subseteq M^n$
is
$X \subseteq M^n$
is
![]() $\Gamma $
-definable in
$\Gamma $
-definable in
![]() $\mathcal {M}$
(with parameters) iff there is a tuple
$\mathcal {M}$
(with parameters) iff there is a tuple
![]() $\overline {b}\in M$
and a formula
$\overline {b}\in M$
and a formula
![]() $\phi (x_1,\dots ,x_n, \overline {y}) \in \Gamma $
such that
$\phi (x_1,\dots ,x_n, \overline {y}) \in \Gamma $
such that
![]() $X = \{\langle m_1,\dots ,m_n \rangle \in M^n : \mathcal {M} \models \phi (m_1,\dots ,m_n,\overline {b})\}$
. Whenever this terminology is used without specifying a model
$X = \{\langle m_1,\dots ,m_n \rangle \in M^n : \mathcal {M} \models \phi (m_1,\dots ,m_n,\overline {b})\}$
. Whenever this terminology is used without specifying a model
![]() $\mathcal {M}$
, it is assumed that
$\mathcal {M}$
, it is assumed that
![]() $\mathcal {M} = \mathbb {N}$
. Thus, in particular, a
$\mathcal {M} = \mathbb {N}$
. Thus, in particular, a
![]() $\Gamma $
-definition of a theory
$\Gamma $
-definition of a theory
![]() $\mathrm {T}$
is a
$\mathrm {T}$
is a
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\tau (x)$
such that
$\tau (x)$
such that
![]() $\mathrm {T} = \{ \phi : \mathbb {N} \models \tau (\ulcorner \phi \urcorner ) \}$
.
$\mathrm {T} = \{ \phi : \mathbb {N} \models \tau (\ulcorner \phi \urcorner ) \}$
.
For each
![]() $\Gamma $
,
$\Gamma $
,
![]() $\mathrm {Th}_\Gamma (\mathcal {M})$
is the set of
$\mathrm {Th}_\Gamma (\mathcal {M})$
is the set of
![]() $\Gamma $
sentences true in
$\Gamma $
sentences true in
![]() $\mathcal {M}$
, that is, the set
$\mathcal {M}$
, that is, the set
![]() $\{ \phi \in \Gamma : \mathcal {M} \models \phi \}$
. If
$\{ \phi \in \Gamma : \mathcal {M} \models \phi \}$
. If
![]() $\mathcal {M}$
is a submodel of
$\mathcal {M}$
is a submodel of
![]() $\mathcal {N}$
, and for all
$\mathcal {N}$
, and for all
![]() $\overline {a} \in M$
and
$\overline {a} \in M$
and
![]() $\unicode{x3b3} (\overline {x}) \in \Gamma $
,
$\unicode{x3b3} (\overline {x}) \in \Gamma $
,
![]() $\mathcal {M} \models \unicode{x3b3} (\overline {a})$
iff
$\mathcal {M} \models \unicode{x3b3} (\overline {a})$
iff
![]() $\mathcal {N} \models \unicode{x3b3} (\overline {a})$
, then
$\mathcal {N} \models \unicode{x3b3} (\overline {a})$
, then
![]() $\mathcal {N}$
is a
$\mathcal {N}$
is a
![]() $\Gamma $
-elementary extension of
$\Gamma $
-elementary extension of
![]() $\mathcal {M}$
. If
$\mathcal {M}$
. If
![]() $\mathcal {M} \models \sigma $
for some
$\mathcal {M} \models \sigma $
for some
![]() $\Sigma _{n+1}$
sentence
$\Sigma _{n+1}$
sentence
![]() $\sigma $
, and
$\sigma $
, and
![]() $\mathcal {N}$
is a
$\mathcal {N}$
is a
![]() $\Sigma _n$
-elementary extension of
$\Sigma _n$
-elementary extension of
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\mathcal {N} \models \sigma $
.
$\mathcal {N} \models \sigma $
.
![]() $\mathcal {N}$
is an end-extension of
$\mathcal {N}$
is an end-extension of
![]() $\mathcal {M}$
(or, equivalently,
$\mathcal {M}$
(or, equivalently,
![]() $\mathcal {M}$
is an initial segment of
$\mathcal {M}$
is an initial segment of
![]() $\mathcal {N}$
) iff
$\mathcal {N}$
) iff
![]() $\mathcal {M}$
is a submodel of
$\mathcal {M}$
is a submodel of
![]() $\mathcal {N}$
, and whenever
$\mathcal {N}$
, and whenever
![]() $a \in M$
and
$a \in M$
and
![]() $b \in N$
, and
$b \in N$
, and
![]() $\mathcal {N}\models b < a$
, then
$\mathcal {N}\models b < a$
, then
![]() $b \in M$
.
$b \in M$
.
Let
![]() $\emptyset ^{(n)}$
denote the nth Turing jump of the empty set (see, e.g., [Reference Rogers39, p. 254]). For each n, let
$\emptyset ^{(n)}$
denote the nth Turing jump of the empty set (see, e.g., [Reference Rogers39, p. 254]). For each n, let
![]() $\langle \varphi _i^n : i \in \omega \rangle $
be an acceptable (in the sense of Rogers [Reference Rogers39, exercise 2.10]) enumeration of the functions that are recursively enumerable (r.e.) in
$\langle \varphi _i^n : i \in \omega \rangle $
be an acceptable (in the sense of Rogers [Reference Rogers39, exercise 2.10]) enumeration of the functions that are recursively enumerable (r.e.) in
![]() $\emptyset ^{(n)}$
; these are the partial n-recursive functions. For each partial n-recursive function
$\emptyset ^{(n)}$
; these are the partial n-recursive functions. For each partial n-recursive function
![]() $\varphi _e^n$
, let the eth n-r.e. set
$\varphi _e^n$
, let the eth n-r.e. set
![]() $W_e^n$
be the domain of
$W_e^n$
be the domain of
![]() $\varphi _e^n$
. If f is a function such that
$\varphi _e^n$
. If f is a function such that
![]() $f \simeq \varphi _e^n$
for some e, then e is an n-index for f.
$f \simeq \varphi _e^n$
for some e, then e is an n-index for f.
3 Preliminary principles
This section presents a number of suitably formulated principles that are useful in proving hierarchical incompleteness results of the kind given in Theorem 1.1. The basic versions of these principles can be found scattered across the literature, and none of them should be too surprising to the reader familiar with, e.g., Hájek and Pudlák [Reference Hájek and Pudlák17], Kaye [Reference Kaye22], Lindström [Reference Lindström29], and Smoryński [Reference Smoryński45].
The essence of the generalizations presented in this paper is that r.e. theories are replaced by
![]() $\Sigma _{n+1}$
-definable ones, and that the base theory is pushed down as far as it will go below
$\Sigma _{n+1}$
-definable ones, and that the base theory is pushed down as far as it will go below
![]() $\mathrm {PA}$
. On some occasions the theories have to satisfy additional constraints such as
$\mathrm {PA}$
. On some occasions the theories have to satisfy additional constraints such as
![]() $\Sigma _n$
-soundness or
$\Sigma _n$
-soundness or
![]() $\Pi _n$
-completeness for the generalization to go through, and whenever this is the case that will be pointed out explicitly.
$\Pi _n$
-completeness for the generalization to go through, and whenever this is the case that will be pointed out explicitly.
3.1 Basics, representability, recursion theory
Many textbooks in metamathematics rely on some version of the fact that Robinson’s arithmetic
![]() $\mathrm {Q}$
is
$\mathrm {Q}$
is
![]() $\Sigma _1$
-complete: it proves all true
$\Sigma _1$
-complete: it proves all true
![]() $\Sigma _1$
sentences. This has the consequence that every r.e. set can be numerated in
$\Sigma _1$
sentences. This has the consequence that every r.e. set can be numerated in
![]() $\mathrm {Q}$
by a
$\mathrm {Q}$
by a
![]() $\Sigma _1$
formula, which in turn allows for representing the theorem set of
$\Sigma _1$
formula, which in turn allows for representing the theorem set of
![]() $\mathrm {Q}$
in
$\mathrm {Q}$
in
![]() $\mathrm {Q}$
and proving the first incompleteness theorem. Many proofs of these facts rely on
$\mathrm {Q}$
and proving the first incompleteness theorem. Many proofs of these facts rely on
![]() $\Delta _0$
being closed under bounded quantification, and
$\Delta _0$
being closed under bounded quantification, and
![]() $\mathrm {Q}$
deciding all
$\mathrm {Q}$
deciding all
![]() $\Delta _0$
sentences.
$\Delta _0$
sentences.
Since the aim of this paper is to generalize incompleteness results to
![]() $\Sigma _{n+1}$
-definable theories rather than r.e. ones, there is a need for establishing a similar correspondence between
$\Sigma _{n+1}$
-definable theories rather than r.e. ones, there is a need for establishing a similar correspondence between
![]() $\Sigma _{n+1}$
-definable sets and theories sufficient to represent them. On these higher levels, the roles of
$\Sigma _{n+1}$
-definable sets and theories sufficient to represent them. On these higher levels, the roles of
![]() $\Delta _0$
and
$\Delta _0$
and
![]() $\mathrm {Q}$
are played by the classes
$\mathrm {Q}$
are played by the classes
![]() $\Sigma _0(\Sigma _{n})$
and the theories
$\Sigma _0(\Sigma _{n})$
and the theories
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, respectively. Establishing this relationship is the goal of this subsection.
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, respectively. Establishing this relationship is the goal of this subsection.
The following four observations (see, e.g., [Reference Smoryński43, lemma 0.3], [Reference Hájek16, lemma 2.2], [Reference Beklemishev1, lemma 2.9], [Reference Kikuchi and Kurahashi23, proposition 3.7]) serve as the starting point for the analogy between
![]() $\mathrm {Q}$
and
$\mathrm {Q}$
and
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.
Fact 3.2 (Basic properties of soundness and completeness).
-
1.
 $\mathrm {T}$
is consistent iff
$\mathrm {T}$
is consistent iff
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Sigma _0$
-sound.
$\Sigma _0$
-sound. -
2.
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Pi _n$
-complete iff
$\Pi _n$
-complete iff
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Sigma _{n+1}$
-complete.
$\Sigma _{n+1}$
-complete. -
3.
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Sigma _n$
-sound iff
$\Sigma _n$
-sound iff
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Pi _{n+1}$
-sound iff
$\Pi _{n+1}$
-sound iff
 $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
is consistent.
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
is consistent. -
4. If
 $\mathrm {T}$
is consistent and
$\mathrm {T}$
is consistent and
 $\Pi _n$
-complete, then
$\Pi _n$
-complete, then
 $\mathrm {T}$
is
$\mathrm {T}$
is
 $\Sigma _n$
-sound.
$\Sigma _n$
-sound.
While the usual formulation of Gödel’s theorem pertains to r.e., consistent theories, the hierarchically formulated Theorem 1.1 is stated for
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Sigma _n$
-sound theories. In light of the preceding fact, consistency and
$\Sigma _n$
-sound theories. In light of the preceding fact, consistency and
![]() $\Sigma _0$
-soundness are equivalent, so the ordinary statement fits nicely into the hierarchical statement of the theorem. However, inspection of the published proofs of Theorem 1.1 reveals that
$\Sigma _0$
-soundness are equivalent, so the ordinary statement fits nicely into the hierarchical statement of the theorem. However, inspection of the published proofs of Theorem 1.1 reveals that
![]() $\Pi _n$
-complete theories enter the argument in an indispensable way. In the proof by Kikuchi & Kurahashi [Reference Kikuchi and Kurahashi23],
$\Pi _n$
-complete theories enter the argument in an indispensable way. In the proof by Kikuchi & Kurahashi [Reference Kikuchi and Kurahashi23],
![]() $\Pi _n$
-completeness of
$\Pi _n$
-completeness of
![]() $\mathrm {T}$
can be explicitly assumed, since in the case where
$\mathrm {T}$
can be explicitly assumed, since in the case where
![]() $\mathrm {T}$
is not
$\mathrm {T}$
is not
![]() $\Pi _n$
-complete, it fails to prove all true
$\Pi _n$
-complete, it fails to prove all true
![]() $\Pi _n$
sentences and can hardly prove all true
$\Pi _n$
sentences and can hardly prove all true
![]() $\Pi _{n+1}$
sentences. By contrast, the proof by Salehi & Seraji [Reference Salehi and Seraji40] bypasses assuming
$\Pi _{n+1}$
sentences. By contrast, the proof by Salehi & Seraji [Reference Salehi and Seraji40] bypasses assuming
![]() $\Pi _n$
-completeness of
$\Pi _n$
-completeness of
![]() $\mathrm {T}$
by instead constructing a
$\mathrm {T}$
by instead constructing a
![]() $\Pi _{n+1}$
sentence that is independent of the
$\Pi _{n+1}$
sentence that is independent of the
![]() $\Pi _n$
-complete
$\Pi _n$
-complete
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, a theory whose consistency is guaranteed by the
$\mathrm {T} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, a theory whose consistency is guaranteed by the
![]() $\Sigma _n$
-soundness of
$\Sigma _n$
-soundness of
![]() $\mathrm {T}$
. That sentence is, a fortiori, also independent of
$\mathrm {T}$
. That sentence is, a fortiori, also independent of
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
The most conservative generalization of “r.e., consistent” is therefore “
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent” rather than “
$\Pi _n$
-complete, and consistent” rather than “
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Sigma _n$
-sound.” As is clear from Theorem 1.1, the assumption of
$\Sigma _n$
-sound.” As is clear from Theorem 1.1, the assumption of
![]() $\Pi _n$
-completeness of
$\Pi _n$
-completeness of
![]() $\mathrm {T}$
is sometimes excessively strong, and mere
$\mathrm {T}$
is sometimes excessively strong, and mere
![]() $\Sigma _n$
-soundness is indeed enough for some further applications as well. In those cases, the proofs rely on the consistency of
$\Sigma _n$
-soundness is indeed enough for some further applications as well. In those cases, the proofs rely on the consistency of
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, as in the proof by Salehi & Seraji [Reference Salehi and Seraji40]. In other cases, however, the
$\mathrm {T} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, as in the proof by Salehi & Seraji [Reference Salehi and Seraji40]. In other cases, however, the
![]() $\Pi _n$
-completeness is indispensable for the generalization to go through.Footnote
2
$\Pi _n$
-completeness is indispensable for the generalization to go through.Footnote
2
The analogy with regard to soundness and completeness therefore goes as follows. Since
![]() $\mathrm {Q}$
is
$\mathrm {Q}$
is
![]() $\Pi _0$
-complete, it is also
$\Pi _0$
-complete, it is also
![]() $\Sigma _{1}$
-complete, and since it is also consistent it follows that
$\Sigma _{1}$
-complete, and since it is also consistent it follows that
![]() $\mathrm {Q}$
is
$\mathrm {Q}$
is
![]() $\Sigma _0$
-sound and therefore also
$\Sigma _0$
-sound and therefore also
![]() $\Pi _1$
-sound. Now consider
$\Pi _1$
-sound. Now consider
![]() $\mathrm {Th}_{\Pi _n}(\mathbb {N})$
: This theory is
$\mathrm {Th}_{\Pi _n}(\mathbb {N})$
: This theory is
![]() $\Pi _n$
-complete and therefore also
$\Pi _n$
-complete and therefore also
![]() $\Sigma _{n+1}$
-complete; it is consistent and therefore
$\Sigma _{n+1}$
-complete; it is consistent and therefore
![]() $\Pi _{n+1}$
-sound.
$\Pi _{n+1}$
-sound.
The role of
![]() $\mathrm {I}\Sigma _n$
in the analogy between
$\mathrm {I}\Sigma _n$
in the analogy between
![]() $\mathrm {Q}$
and
$\mathrm {Q}$
and
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
becomes clear through the next fact. Its proof will take up most of the remainder of this subsection.
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
becomes clear through the next fact. Its proof will take up most of the remainder of this subsection.
Fact 3.3.
-
1. Every
 $\Sigma _n$
- (or
$\Sigma _n$
- (or
 $\Pi _n$
-) definable relation on
$\Pi _n$
-) definable relation on
 $\omega $
is binumerated by a
$\omega $
is binumerated by a
 $\Sigma _n$
(or
$\Sigma _n$
(or
 $\Pi _n$
) formula in
$\Pi _n$
) formula in
 $\mathrm {Q} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.
$\mathrm {Q} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
. -
2. Every
 $\Sigma _{n+1}$
-definable relation on
$\Sigma _{n+1}$
-definable relation on
 $\omega $
is numerated by a
$\omega $
is numerated by a
 $\Sigma _{n+1}$
formula in
$\Sigma _{n+1}$
formula in
 $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
. -
3. Every function from
 $\omega ^k$
to
$\omega ^k$
to
 $\omega $
that is recursive in
$\omega $
that is recursive in
 $\emptyset ^{(n)}$
is strongly representable by a
$\emptyset ^{(n)}$
is strongly representable by a
 $\Sigma _{n+1}$
formula (with particularly nice properties) in
$\Sigma _{n+1}$
formula (with particularly nice properties) in
 $\mathrm {I}\Sigma _{n} + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.Footnote
3
$\mathrm {I}\Sigma _{n} + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.Footnote
3
The first item is immediately seen to be true, since
![]() $\mathrm {Q} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
is consistent,
$\mathrm {Q} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
is consistent,
![]() $\Sigma _{n+1}$
-complete, and
$\Sigma _{n+1}$
-complete, and
![]() $\Pi _{n+1}$
-sound. The second and third items are elaborated on below, but first we need a few more stepping stones to help out in the constructions.
$\Pi _{n+1}$
-sound. The second and third items are elaborated on below, but first we need a few more stepping stones to help out in the constructions.
Fact 3.4 (Parametric diagonal lemma).
-
1. For every
 $\Gamma $
formula
$\Gamma $
formula
 $\unicode{x3b3} (x,y)$
, we can effectively find a
$\unicode{x3b3} (x,y)$
, we can effectively find a
 $\Gamma $
formula
$\Gamma $
formula
 $\xi (x)$
such that
$\xi (x)$
such that  $$ \begin{align*} \mathrm{Q} \vdash \forall x (\xi(x) \leftrightarrow \unicode{x3b3}(x,\ulcorner \xi\urcorner))\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{Q} \vdash \forall x (\xi(x) \leftrightarrow \unicode{x3b3}(x,\ulcorner \xi\urcorner))\text{.} \end{align*} $$
-
2. For every
 $\Gamma $
formula
$\Gamma $
formula
 $\unicode{x3b3} (x,y)$
, we can effectively find a
$\unicode{x3b3} (x,y)$
, we can effectively find a
 $\Gamma $
formula
$\Gamma $
formula
 $\xi (x)$
such that, for each k,
$\xi (x)$
such that, for each k,  $$ \begin{align*} \mathrm{Q} \vdash \xi(k) \leftrightarrow \unicode{x3b3}(k,\ulcorner \xi(k)\urcorner))\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{Q} \vdash \xi(k) \leftrightarrow \unicode{x3b3}(k,\ulcorner \xi(k)\urcorner))\text{.} \end{align*} $$
Bibliographical remark. Item 1. of the above is essentially due to Montague [Reference Montague33, lemma 1]. The proof by Ehrenfeucht and Feferman [Reference Ehrenfeucht and Feferman10, lemma 1] of 2. actually suffices to prove 1.; see also [Reference Smoryński44] for a discussion of the development of the diagonal lemma.
Fact 3.5 (Generalized Craig’s trick).
For any
![]() $\Sigma _{n+1}$
-definable theory
$\Sigma _{n+1}$
-definable theory
![]() $\mathrm {T}$
, defined by a
$\mathrm {T}$
, defined by a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\sigma (z)$
, there is a deductively equivalent theory
$\sigma (z)$
, there is a deductively equivalent theory
![]() $\mathrm {S}$
, defined by a formula
$\mathrm {S}$
, defined by a formula
![]() $\pi (x)$
that is
$\pi (x)$
that is
![]() $\Pi _n$
in
$\Pi _n$
in
![]() $\mathrm {I}\Sigma _n$
. Moreover,
$\mathrm {I}\Sigma _n$
. Moreover,
![]() $\mathrm {I}\Sigma _{n+1} \vdash \forall x (\mathrm {Pr}_\sigma (x) \leftrightarrow \mathrm {Pr}_\pi (x))$
.Footnote
4
$\mathrm {I}\Sigma _{n+1} \vdash \forall x (\mathrm {Pr}_\sigma (x) \leftrightarrow \mathrm {Pr}_\pi (x))$
.Footnote
4
Bibliographical remark. Craig’s [Reference Craig7] formulation pertains to r.e. theories, for which there exist deductively equivalent theories with primitive recursive definitions. An early hierarchical generalization is due to Grzegorczyk et al. [Reference Grzegorczyk, Mostowski and Ryll-Nardzewski14, theorem 2.2.C]. The hierarchical formulation presented here follows by inspection of a proof by Kurahashi [Reference Kurahashi27, proposition 9].
Convention. In light of Craig’s trick, we may assume that any
![]() $\Sigma _{n+1}$
-definable theory is in fact
$\Sigma _{n+1}$
-definable theory is in fact
![]() $\Pi _n$
-defined. In what follows, we write
$\Pi _n$
-defined. In what follows, we write
![]() $\mathrm {Prf}_{\mathrm {T}}(x,y)$
to denote (ambiguously) any formula
$\mathrm {Prf}_{\mathrm {T}}(x,y)$
to denote (ambiguously) any formula
![]() $\mathrm {Prf}_\tau (x,y)$
where
$\mathrm {Prf}_\tau (x,y)$
where
![]() $\tau $
is a
$\tau $
is a
![]() $\Pi _n$
binumeration of
$\Pi _n$
binumeration of
![]() $\mathrm {T}$
in
$\mathrm {T}$
in
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, and moreover, this formula can be assumed to be
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, and moreover, this formula can be assumed to be
![]() $\Pi _n$
. Consequently,
$\Pi _n$
. Consequently,
![]() $\Pr _{\mathrm {T}}(x)$
is
$\Pr _{\mathrm {T}}(x)$
is
![]() $\Sigma _{n+1}$
and
$\Sigma _{n+1}$
and
![]() $\mathrm {Con}_{\mathrm {T}}$
is
$\mathrm {Con}_{\mathrm {T}}$
is
![]() $\Pi _{n+1}$
in
$\Pi _{n+1}$
in
![]() $\mathrm {I}\Sigma _n$
.
$\mathrm {I}\Sigma _n$
.
Fact 3.6 [Reference Hájek and Pudlák17, lemmata I.2.9 and I.2.14 and theorem I.2.25].
-
1. In
 $\mathrm {I}\Sigma _n$
, both
$\mathrm {I}\Sigma _n$
, both
 $\Sigma _n$
and
$\Sigma _n$
and
 $\Pi _n$
are closed under bounded quantifiers.Footnote
5
$\Pi _n$
are closed under bounded quantifiers.Footnote
5
-
2.
 $\mathrm {I}\Sigma _n \vdash \mathrm {I}\Sigma _0(\Sigma _n)$
.
$\mathrm {I}\Sigma _n \vdash \mathrm {I}\Sigma _0(\Sigma _n)$
. -
3. Each
 $\Sigma _0(\Sigma _n)$
formula is
$\Sigma _0(\Sigma _n)$
formula is
 $\Delta _{n+1}$
in
$\Delta _{n+1}$
in
 $\mathrm {I}\Sigma _n$
.
$\mathrm {I}\Sigma _n$
.
All the pieces are now in place to prove a, sometimes useful, lemma from which Fact 3.3(2) follows immediately. The proof highlights the steps where induction and the additional truth from the standard model is required. For the statement of the lemma, recall that a relation X is correctly numerated by
![]() $\phi $
in
$\phi $
in
![]() $\mathrm {T}$
if
$\mathrm {T}$
if
![]() $\phi $
numerates X in
$\phi $
numerates X in
![]() $\mathrm {T}$
, and for all
$\mathrm {T}$
, and for all
![]() $k_1,\dots ,k_n$
,
$k_1,\dots ,k_n$
,
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_n)$
iff
$\mathrm {T} \vdash \phi (k_1,\dots ,k_n)$
iff
![]() $\phi (k_1,\dots ,k_n)$
is true.
$\phi (k_1,\dots ,k_n)$
is true.
Lemma 3.7. Let
![]() $\mathrm {T}$
be any
$\mathrm {T}$
be any
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent extension of
$\Pi _n$
-complete, and consistent extension of
![]() $\mathrm {I}\Sigma _n$
and let
$\mathrm {I}\Sigma _n$
and let
![]() $R(x_1,\dots ,x_m)$
be any
$R(x_1,\dots ,x_m)$
be any
![]() $\Sigma _{n+1}$
-definable relation. There is a
$\Sigma _{n+1}$
-definable relation. There is a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\phi (x_1,\dots ,x_m)$
that correctly numerates R in
$\phi (x_1,\dots ,x_m)$
that correctly numerates R in
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Proof. Let
![]() $\rho (x_1,\dots ,x_m)$
define R. We may assume that
$\rho (x_1,\dots ,x_m)$
define R. We may assume that
![]() $\rho (x_1,\dots ,x_m)$
is of the form
$\rho (x_1,\dots ,x_m)$
is of the form
![]() $\exists z \pi (x_1,\dots , x_m,z)$
with
$\exists z \pi (x_1,\dots , x_m,z)$
with
![]() $\pi \in \Pi _n$
. Let
$\pi \in \Pi _n$
. Let
![]() $\phi (x_1,\dots ,x_m)$
be such that, for all
$\phi (x_1,\dots ,x_m)$
be such that, for all
![]() $k_1,\dots ,k_m$
,
$k_1,\dots ,k_m$
,
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
proves
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
proves
Recall that if
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
-definable, then there is a deductively equivalent
$\Sigma _{n+1}$
-definable, then there is a deductively equivalent
![]() $\Pi _n$
definition of
$\Pi _n$
definition of
![]() $\mathrm {T}$
, and
$\mathrm {T}$
, and
![]() $\mathrm {Prf}_{\mathrm {T}}(x,y)$
is therefore equivalent to a
$\mathrm {Prf}_{\mathrm {T}}(x,y)$
is therefore equivalent to a
![]() $\Pi _n$
formula in
$\Pi _n$
formula in
![]() $\mathrm {I}\Sigma _n$
. Then
$\mathrm {I}\Sigma _n$
. Then
is a
![]() $\Sigma _0(\Sigma _n)$
formula, and is therefore, by Fact 3.6, equivalent to a
$\Sigma _0(\Sigma _n)$
formula, and is therefore, by Fact 3.6, equivalent to a
![]() $\Delta _{n+1}$
formula in
$\Delta _{n+1}$
formula in
![]() $\mathrm {I}\Sigma _n$
. It follows that
$\mathrm {I}\Sigma _n$
. It follows that
![]() $\phi $
is equivalent to a
$\phi $
is equivalent to a
![]() $\Sigma _{n+1}$
formula in
$\Sigma _{n+1}$
formula in
![]() $\mathrm {I}\Sigma _n$
.
$\mathrm {I}\Sigma _n$
.
Suppose
![]() $R(k_1,\dots ,k_m)$
. Then
$R(k_1,\dots ,k_m)$
. Then
![]() $\mathbb {N} \models \rho (k_1,\dots ,k_m)$
, so there is then an i such that
$\mathbb {N} \models \rho (k_1,\dots ,k_m)$
, so there is then an i such that
![]() $\mathbb {N} \models \pi (k_1,\dots ,k_m,i)$
. Since
$\mathbb {N} \models \pi (k_1,\dots ,k_m,i)$
. Since
![]() $\pi $
is
$\pi $
is
![]() $\Pi _n$
and
$\Pi _n$
and
![]() $\mathrm {Th}_{\Pi _n}(\mathbb {N})$
is
$\mathrm {Th}_{\Pi _n}(\mathbb {N})$
is
![]() $\Pi _n$
-complete, it follows that
$\Pi _n$
-complete, it follows that
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \pi (k_1,\dots ,k_m,i)$
. Suppose, for a contradiction, that
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \pi (k_1,\dots ,k_m,i)$
. Suppose, for a contradiction, that
![]() $\mathrm {T} \nvdash \phi (k_1,\dots ,k_m)$
. By Fact 3.3(1),
$\mathrm {T} \nvdash \phi (k_1,\dots ,k_m)$
. By Fact 3.3(1),
for all p. It follows that
so
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \phi (k_1,\dots ,k_m)$
, and
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \phi (k_1,\dots ,k_m)$
, and
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
.
$\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
.
Conversely, suppose
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
, and let p be a proof of
$\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
, and let p be a proof of
![]() $\phi (k_1,\dots ,k_m)$
in
$\phi (k_1,\dots ,k_m)$
in
![]() $\mathrm {T}$
. Then
$\mathrm {T}$
. Then
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Prf}_{\mathrm {T}}(\ulcorner \phi (k_1,\dots ,k_m)\urcorner , p)$
. It follows that
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Prf}_{\mathrm {T}}(\ulcorner \phi (k_1,\dots ,k_m)\urcorner , p)$
. It follows that
Suppose, for a contradiction, that
![]() $\lnot R(k_1,\dots ,k_m)$
. Then for all i,
$\lnot R(k_1,\dots ,k_m)$
. Then for all i,
It follows that
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \lnot \exists z < p \pi (k_1,\dots ,k_m,z)$
. We get
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \lnot \exists z < p \pi (k_1,\dots ,k_m,z)$
. We get
whence
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \lnot \phi (k_1,\dots ,k_m)$
, and
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \lnot \phi (k_1,\dots ,k_m)$
, and
![]() $\mathrm {T} \vdash \lnot \phi (k_1,\dots ,k_m)$
.
$\mathrm {T} \vdash \lnot \phi (k_1,\dots ,k_m)$
.
It remains to show that
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
iff
$\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
iff
![]() $\phi (k_1,\dots ,k_m)$
is true. The implication from right to left is trivial, since
$\phi (k_1,\dots ,k_m)$
is true. The implication from right to left is trivial, since
![]() $\phi $
is
$\phi $
is
![]() $\Sigma _{n+1}$
in
$\Sigma _{n+1}$
in
![]() $\mathrm {I}\Sigma _n$
and
$\mathrm {I}\Sigma _n$
and
![]() $\mathrm {Th}_{\Pi _n}(\mathbb {N})$
is
$\mathrm {Th}_{\Pi _n}(\mathbb {N})$
is
![]() $\Sigma _{n+1}$
-complete. For the other direction, suppose
$\Sigma _{n+1}$
-complete. For the other direction, suppose
![]() $\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
, and let p be the least such proof. Then
$\mathrm {T} \vdash \phi (k_1,\dots ,k_m)$
, and let p be the least such proof. Then
Suppose further that there is no
![]() $i < p$
such that
$i < p$
such that
![]() $\pi (k_1,\dots ,k_m,i)$
. Then, as before,
$\pi (k_1,\dots ,k_m,i)$
. Then, as before,
![]() $\mathrm {T} \vdash \lnot \phi (k_1,\dots ,k_m)$
, a contradiction. Thus there is an
$\mathrm {T} \vdash \lnot \phi (k_1,\dots ,k_m)$
, a contradiction. Thus there is an
![]() $i < p$
such that
$i < p$
such that
![]() $\pi (k_1,\dots ,k_m,i)$
is true. Since p is minimal,
$\pi (k_1,\dots ,k_m,i)$
is true. Since p is minimal,
![]() $\forall y \leq i \lnot \mathrm {Prf}_{\mathrm {T}}(\ulcorner \phi (k_1,\dots ,k_m)\urcorner ,y)$
, so
$\forall y \leq i \lnot \mathrm {Prf}_{\mathrm {T}}(\ulcorner \phi (k_1,\dots ,k_m)\urcorner ,y)$
, so
is true, and therefore
![]() $\phi (k_1,\dots ,k_m)$
is true, as desired.
$\phi (k_1,\dots ,k_m)$
is true, as desired.
Bibliographical remark. The correct representability of
![]() $\Sigma _1$
relations in
$\Sigma _1$
relations in
![]() $\mathrm {Q}$
is due to Ehrenfeucht and Feferman [Reference Ehrenfeucht and Feferman10]. The proof above mimics Lindström's [Reference Lindström29] version of Shepherdson's [Reference Shepherdson42] proof of the same result.
$\mathrm {Q}$
is due to Ehrenfeucht and Feferman [Reference Ehrenfeucht and Feferman10]. The proof above mimics Lindström's [Reference Lindström29] version of Shepherdson's [Reference Shepherdson42] proof of the same result.
Fact 3.3(2) follows directly from Lemma 3.7, and it only remains to give an argument for Fact 3.3(3). For this we need two more facts, the first being a version of Post’s theorem.
Fact 3.8 [Reference Post36].
A relation is
![]() $\Sigma _{n+1}$
iff it is r.e. in
$\Sigma _{n+1}$
iff it is r.e. in
![]() $\emptyset ^{(n)}$
.
$\emptyset ^{(n)}$
.
Fact 3.9 (The selection theorem).
For each
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\phi $
with exactly the variables
$\phi $
with exactly the variables
![]() $x_1,\dots ,x_k$
free, there is a
$x_1,\dots ,x_k$
free, there is a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\mathrm {Sel}\{\phi \}$
with exactly the same free variables, such that:
$\mathrm {Sel}\{\phi \}$
with exactly the same free variables, such that:
-
1.
 $\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_k(\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k) \rightarrow \phi (x_1,\dots ,x_k))$
;
$\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_k(\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k) \rightarrow \phi (x_1,\dots ,x_k))$
; -
2.
 $\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_k,z(\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k) \land \mathrm {Sel}\{\phi \}(x_1,\dots ,x_{k-1},z) \rightarrow x_k = z)$
;
$\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_k,z(\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k) \land \mathrm {Sel}\{\phi \}(x_1,\dots ,x_{k-1},z) \rightarrow x_k = z)$
; -
3.
 $\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_{k-1} (\exists x_k \phi (x_1,\dots ,x_k) \rightarrow \exists x_k \mathrm {Sel}\{\phi \}(x_1,\dots ,x_k))$
.
$\mathrm {I}\Sigma _n \vdash \forall x_1,\dots ,x_{k-1} (\exists x_k \phi (x_1,\dots ,x_k) \rightarrow \exists x_k \mathrm {Sel}\{\phi \}(x_1,\dots ,x_k))$
.
Proof sketch. We may assume that any given
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\phi (x_1,\dots ,x_k)$
is on the form
$\phi (x_1,\dots ,x_k)$
is on the form
![]() $\exists w \pi (x_1,\dots ,x_k,w)$
with
$\exists w \pi (x_1,\dots ,x_k,w)$
with
![]() $\pi \in \Pi _n$
. Let
$\pi \in \Pi _n$
. Let
![]() $(w)_i$
denote the ith element of the ordered pair coded by w, and define
$(w)_i$
denote the ith element of the ordered pair coded by w, and define
![]() $\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k)$
to be the formula
$\mathrm {Sel}\{\phi \}(x_1,\dots ,x_k)$
to be the formula
By Fact 3.6, this formula is equivalent in
![]() $\mathrm {I}\Sigma _n$
to a
$\mathrm {I}\Sigma _n$
to a
![]() $\Sigma _{n+1}$
formula. Using
$\Sigma _{n+1}$
formula. Using
![]() $\Sigma _n$
-induction, it is easy to check that it has the three desired properties.
$\Sigma _n$
-induction, it is easy to check that it has the three desired properties.
Bibliographical remark. Smoryński [Reference Smoryński45, theorem 0.6.9] provides a proof of the selection theorem for
![]() $n=0$
, and the generalization is straightforward. The numeration below of partial recursive functions is also based on the treatment in Section 0 of his book.
$n=0$
, and the generalization is straightforward. The numeration below of partial recursive functions is also based on the treatment in Section 0 of his book.
Fact 3.3(3) can now be established as follows: Let f be a k-ary partial n-recursive function; then the relation
![]() $f(x_1,\dots ,x_k) = y$
is
$f(x_1,\dots ,x_k) = y$
is
![]() $\Sigma _{n+1}$
by Fact 3.8. By Fact 3.3(2), this relation is correctly numerated in
$\Sigma _{n+1}$
by Fact 3.8. By Fact 3.3(2), this relation is correctly numerated in
![]() $\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
by some
$\mathrm {I}\Sigma _n + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
by some
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\psi (x_1,\dots ,x_k,y)$
. Finally, by Fact 3.9, f is strongly represented in
$\psi (x_1,\dots ,x_k,y)$
. Finally, by Fact 3.9, f is strongly represented in
![]() $\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
by the
$\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
by the
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(\ulcorner \psi \urcorner , x_1,\dots ,x_k, y)$
. This concludes the proof of Fact 3.3.
$\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(\ulcorner \psi \urcorner , x_1,\dots ,x_k, y)$
. This concludes the proof of Fact 3.3.
Convention. The partial n-recursive function with index e,
![]() $\varphi _e^n$
, can now be defined to be the function whose graph is defined by
$\varphi _e^n$
, can now be defined to be the function whose graph is defined by
![]() $\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(e, y_1, \dots , y_k, z)$
in
$\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(e, y_1, \dots , y_k, z)$
in
![]() $\mathbb {N}$
. The resulting enumeration is acceptable in the sense of Rogers [Reference Rogers39]. Whenever convenient,
$\mathbb {N}$
. The resulting enumeration is acceptable in the sense of Rogers [Reference Rogers39]. Whenever convenient,
![]() $\varphi _e^n(m_1,\dots ,m_i) = k$
is used as a shorthand for
$\varphi _e^n(m_1,\dots ,m_i) = k$
is used as a shorthand for
![]() $\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(e, m_1,\dots , m_i, k)$
.
$\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(e, m_1,\dots , m_i, k)$
.
To wrap up this subsection, we sketch a proof of a formalized version of the second recursion theorem.
Fact 3.10 (Formalized second recursion theorem).
Let
![]() $f : \omega ^2 \to \omega $
be n-recursive. There is an
$f : \omega ^2 \to \omega $
be n-recursive. There is an
![]() $e \in \omega $
such that
$e \in \omega $
such that
Proof. Let, by Fact 3.3(3),
![]() $\psi (x,y,z)$
be a
$\psi (x,y,z)$
be a
![]() $\Sigma _{n+1}$
formula strongly representing f in
$\Sigma _{n+1}$
formula strongly representing f in
![]() $\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
. Let, by Fact 3.4,
$\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
. Let, by Fact 3.4,
![]() $\unicode{x3b3} (y,z)$
be a formula such that
$\unicode{x3b3} (y,z)$
be a formula such that
Then
![]() $e= \ulcorner \unicode{x3b3} \urcorner $
is as desired.
$e= \ulcorner \unicode{x3b3} \urcorner $
is as desired.
The recursion theorem is usually deployed in the following manner. Define an n-recursive function
![]() $f(z,x)$
in stages, using z as a parameter; the resulting function may differ depending on the choice of z. By the recursion theorem, there is then an n-index e such that
$f(z,x)$
in stages, using z as a parameter; the resulting function may differ depending on the choice of z. By the recursion theorem, there is then an n-index e such that
![]() $\varphi _e^n(x)$
coincides with
$\varphi _e^n(x)$
coincides with
![]() $f(e,x)$
. This legitimates self-referential constructions where an index of f is being used in the construction of f itself.
$f(e,x)$
. This legitimates self-referential constructions where an index of f is being used in the construction of f itself.
Bibliographical remark. The recursion theorem is due to Kleene [Reference Kleene24, theorem XXVII]. Smoryński [Reference Smoryński45, theorem 0.6.12] shows how it can be formalized in (essentially)
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
for (
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
for (
![]() $0$
-)recursive functions.
$0$
-)recursive functions.
3.2 Strong provability predicates
A central piece in the proof of Gödel’s incompleteness theorem for r.e. theories
![]() $\mathrm {T}$
is the use of formal provability predicates
$\mathrm {T}$
is the use of formal provability predicates
![]() $\mathrm {Pr}_{\mathrm {T}}(x)$
, expressing “x is provable in
$\mathrm {Pr}_{\mathrm {T}}(x)$
, expressing “x is provable in
![]() $\mathrm {T}$
.” In the current setting, with
$\mathrm {T}$
.” In the current setting, with
![]() $\Sigma _{n+1}$
-definable theories in focus, the corresponding strong provability predicates
$\Sigma _{n+1}$
-definable theories in focus, the corresponding strong provability predicates
![]() $\Pr _{\mathrm {T},\Sigma _{n+1}}(x)$
express “x is provable in
$\Pr _{\mathrm {T},\Sigma _{n+1}}(x)$
express “x is provable in
![]() $\mathrm {T}$
from true
$\mathrm {T}$
from true
![]() $\Sigma _{n+1}$
sentences.”Footnote
6
To define these predicates, we first need to introduce partial satisfaction predicates.
$\Sigma _{n+1}$
sentences.”Footnote
6
To define these predicates, we first need to introduce partial satisfaction predicates.
Fact 3.11 (Partial satisfaction predicates).
For each k and
![]() $\Gamma $
, there is a
$\Gamma $
, there is a
![]() $k+1$
-ary
$k+1$
-ary
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\mathrm {Sat}_{\Gamma }(x,x_1,\dots ,x_k)$
such that for every
$\mathrm {Sat}_{\Gamma }(x,x_1,\dots ,x_k)$
such that for every
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\phi (x_1,\dots ,x_k)$
,
$\phi (x_1,\dots ,x_k)$
,
Hence there is also a
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\mathrm {Tr}_\Gamma (x)$
such that for every
$\mathrm {Tr}_\Gamma (x)$
such that for every
![]() $\Gamma $
sentence
$\Gamma $
sentence
![]() $\phi $
,
$\phi $
,
Bibliographical remark. Modern proofs of this fact are due to Hájek and Pudlák [Reference Hájek and Pudlák17] and Kaye [Reference Kaye22]. The use of partial satisfaction predicates, however, goes back to Hilbert and Bernays [Reference Hilbert and Bernays19].
Definition 3.12. Let, for each
![]() $\Gamma $
,
$\Gamma $
,
![]() $\mathrm {Prf}_{\mathrm {T},\Gamma }(x,y)$
be the formula
$\mathrm {Prf}_{\mathrm {T},\Gamma }(x,y)$
be the formula
Let
![]() $\mathrm {Pr}_{\mathrm {T},\Gamma }(x) := \exists y \mathrm {Prf}_{\mathrm {T},\Gamma }(x,y)$
, and let
$\mathrm {Pr}_{\mathrm {T},\Gamma }(x) := \exists y \mathrm {Prf}_{\mathrm {T},\Gamma }(x,y)$
, and let
![]() $\mathrm {Con}_{\mathrm {T},\Gamma } := \lnot \mathrm {Pr}_{\mathrm {T},\Gamma }(\ulcorner \bot \urcorner )$
.
$\mathrm {Con}_{\mathrm {T},\Gamma } := \lnot \mathrm {Pr}_{\mathrm {T},\Gamma }(\ulcorner \bot \urcorner )$
.
We are mainly interested in the predicates
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
. These provability predicates have many similarities with the usual provability predicate. Firstly, if
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
. These provability predicates have many similarities with the usual provability predicate. Firstly, if
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
-definable, then
$\Sigma _{n+1}$
-definable, then
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
is
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
is
![]() $\Sigma _{n+1}$
, and
$\Sigma _{n+1}$
, and
![]() $\mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
consequently
$\mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
consequently
![]() $\Pi _{n+1}$
. Secondly, they satisfy provable
$\Pi _{n+1}$
. Secondly, they satisfy provable
![]() $\Sigma _{n+1}$
-completeness and Löb’s derivability conditions. These notions also have their roots with Hilbert and Bernays [Reference Hilbert and Bernays19]; see also [Reference Feferman11, theorem 5.4 and corollary 5.5]. The versions presented here are extracted from [Reference Beklemishev1, propositions 2.10 and 2.11] and [Reference Smoryński45, lemma 3.3.7].
$\Sigma _{n+1}$
-completeness and Löb’s derivability conditions. These notions also have their roots with Hilbert and Bernays [Reference Hilbert and Bernays19]; see also [Reference Feferman11, theorem 5.4 and corollary 5.5]. The versions presented here are extracted from [Reference Beklemishev1, propositions 2.10 and 2.11] and [Reference Smoryński45, lemma 3.3.7].
Fact 3.13 (Provable
 $\Sigma _{m+1}$
-completeness).
$\Sigma _{m+1}$
-completeness).
Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable theory, and let
$\Sigma _{n+1}$
-definable theory, and let
![]() $\sigma (x_1,\dots ,x_k)$
be any
$\sigma (x_1,\dots ,x_k)$
be any
![]() $\Sigma _{m+1}$
formula. Then
$\Sigma _{m+1}$
formula. Then
Fact 3.14 (Löb conditions).
If
![]() $\mathrm {T}$
is a
$\mathrm {T}$
is a
![]() $\Sigma _{n+1}$
-definable extension of
$\Sigma _{n+1}$
-definable extension of
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
, then, for each
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
, then, for each
![]() $m\geq 0$
, and for all sentences
$m\geq 0$
, and for all sentences
![]() $\phi $
,
$\phi $
,
![]() $\psi $
,
$\psi $
,
-
L1. if
 $\mathrm {T}\vdash \phi $
, then
$\mathrm {T}\vdash \phi $
, then
 $\mathrm {I}\Sigma _n + \exp + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner )$
;
$\mathrm {I}\Sigma _n + \exp + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner )$
; -
L2.
 $\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner ) \land \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \rightarrow \psi \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \psi \urcorner )$
;
$\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner ) \land \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \rightarrow \psi \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \psi \urcorner )$
; -
L3.
 $\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner )\urcorner )$
.
$\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi \urcorner )\urcorner )$
.
Similar statements also hold for formulae:
-
L1’. if
 $\mathrm {T}\vdash \forall x \phi (x)$
, then
$\mathrm {T}\vdash \forall x \phi (x)$
, then
 $\mathrm {I}\Sigma _n + \exp + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \forall x \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner )$
;
$\mathrm {I}\Sigma _n + \exp + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \forall x \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner )$
; -
L2’.
 $\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \forall x (\mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner ) \land \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \rightarrow \psi (\dot {x})\urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \psi (\dot {x}) \urcorner ))$
;
$\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \forall x (\mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner ) \land \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \rightarrow \psi (\dot {x})\urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \psi (\dot {x}) \urcorner ))$
; -
L3’.
 $\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \forall x (\mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner )\urcorner ))$
.
$\mathrm {I}\Sigma _0 + \mathrm {exp} \vdash \forall x (\mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner ) \rightarrow \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \mathrm {Pr}_{\mathrm {T},\Sigma _{m+1}}(\ulcorner \phi (\dot {x}) \urcorner )\urcorner ))$
.
The stronger background theory used in items L1. and L1’. is enough to ensure the numerability of the
![]() $\Sigma _{n+1}$
-definable theory
$\Sigma _{n+1}$
-definable theory
![]() $\mathrm {T}$
. For r.e. theories
$\mathrm {T}$
. For r.e. theories
![]() $\mathrm {T}$
,
$\mathrm {T}$
,
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
suffices.
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
suffices.
We now turn our attention to the bounded provability predicates that feature prominently in the sequel. Consider again the
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
for a
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(x)$
for a
![]() $\Sigma _{n+1}$
-definable
$\Sigma _{n+1}$
-definable
![]() $\mathrm {T}$
. We may assume that there is a
$\mathrm {T}$
. We may assume that there is a
![]() $\Pi _n$
formula
$\Pi _n$
formula
![]() $\pi (x,y)$
such that
$\pi (x,y)$
such that
Let
 $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^k(x)$
be the formula
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^k(x)$
be the formula
![]() $\exists z \leq k \pi (x,z)$
.Footnote
7
Then, by Fact 3.6, this formula is
$\exists z \leq k \pi (x,z)$
.Footnote
7
Then, by Fact 3.6, this formula is
![]() $\Pi _n$
in
$\Pi _n$
in
![]() $\mathrm {I}\Sigma _n$
, and therefore decidable in
$\mathrm {I}\Sigma _n$
, and therefore decidable in
![]() $\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.Footnote
8
As a consequence, we have strong reflection properties for the bounded proof predicates.
$\mathrm {I}\Sigma _n + \mathrm {exp} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
.Footnote
8
As a consequence, we have strong reflection properties for the bounded proof predicates.
Fact 3.15 (Uniform small reflection).
Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable, consistent extension of
$\Sigma _{n+1}$
-definable, consistent extension of
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
. For each
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
. For each
![]() $\phi (x)$
and k, we have:
$\phi (x)$
and k, we have:
 $$ \begin{align*} \mathrm{I}\Sigma_n + \mathrm{exp} + \mathrm{Th}_{\Pi_{n}(\mathbb{N})}\vdash \forall x (\mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}^k(\ulcorner\phi(\dot{x})\urcorner) \rightarrow \phi(x))\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{I}\Sigma_n + \mathrm{exp} + \mathrm{Th}_{\Pi_{n}(\mathbb{N})}\vdash \forall x (\mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}^k(\ulcorner\phi(\dot{x})\urcorner) \rightarrow \phi(x))\text{.} \end{align*} $$
Bibliographical remark. A forerunner to this reflection principle is proved by Feferman [Reference Feferman12, lemma 2.18]. The generalization to
![]() $\Sigma _{n+1}$
-definable theories is straightforward; see also [Reference Hájek and Pudlák17, lemma III.4.40] for some middle ground: reflection for proofs from true
$\Sigma _{n+1}$
-definable theories is straightforward; see also [Reference Hájek and Pudlák17, lemma III.4.40] for some middle ground: reflection for proofs from true
![]() $\Sigma _{n+1}$
sentences for r.e. theories.
$\Sigma _{n+1}$
sentences for r.e. theories.
Fact 3.16 (Formalized small reflection).
Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable, consistent extension of
$\Sigma _{n+1}$
-definable, consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
. Then we have:
$\mathrm {I}\Sigma _{n+1}$
. Then we have:
 $$ \begin{align*} \mathrm{I}\Sigma_0 + \mathrm{exp} \vdash \forall \phi \forall z\mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}(\ulcorner \mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}^{\dot{z}}(\ulcorner \phi \urcorner) \rightarrow \phi\urcorner)\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{I}\Sigma_0 + \mathrm{exp} \vdash \forall \phi \forall z\mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}(\ulcorner \mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}^{\dot{z}}(\ulcorner \phi \urcorner) \rightarrow \phi\urcorner)\text{.} \end{align*} $$
Bibliographical remark. Verbrugge & Visser [Reference Verbrugge and Visser46] show how the small reflection principle can be formalized in (theories weaker than)
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
. I am grateful to one of the referees for pointing out a crucial error in an earlier statement of this fact.
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
. I am grateful to one of the referees for pointing out a crucial error in an earlier statement of this fact.
3.3 Model theory of arithmetic
The remainder of this section concerns the model theory of arithmetic, building up to a characterization of
![]() $\Pi _n$
-conservativity in the spirit of Orey, Hájek, Guaspari, and Lindström. A first step toward that goal is the following miniaturization of the arithmetized completeness theorem in the style of McAloon [Reference McAloon31, theorems 1.7 and 2.2].
$\Pi _n$
-conservativity in the spirit of Orey, Hájek, Guaspari, and Lindström. A first step toward that goal is the following miniaturization of the arithmetized completeness theorem in the style of McAloon [Reference McAloon31, theorems 1.7 and 2.2].
Fact 3.17 (The arithmetized completeness theorem).
Fix
![]() $m\leq n$
. If
$m\leq n$
. If
![]() $\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
, and
$\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
, and
![]() $\mathrm {T}$
is a theory that is
$\mathrm {T}$
is a theory that is
![]() $\Sigma _{n+1}$
-definable in
$\Sigma _{n+1}$
-definable in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M} \models \mathrm {Con}_{\mathrm {T},\Pi _m}$
, then there is a
$\mathcal {M} \models \mathrm {Con}_{\mathrm {T},\Pi _m}$
, then there is a
![]() $\Sigma _m$
-elementary end-extension of
$\Sigma _m$
-elementary end-extension of
![]() $\mathcal {M}$
satisfying
$\mathcal {M}$
satisfying
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
The proof of the arithmetized completeness theorem rests on the following version of the low basis theorem by Hájek & Pudlák [Reference Hájek and Pudlák17, corollary I.3.10(1)]:
Fact 3.18 (Low basis theorem).
Provably in
![]() $\mathrm {I}\Sigma _{n+1}$
, each dyadic unbounded
$\mathrm {I}\Sigma _{n+1}$
, each dyadic unbounded
![]() $\Delta _{n+1}$
tree has an unbounded
$\Delta _{n+1}$
tree has an unbounded
![]() $LL_{n+1}$
branch.
$LL_{n+1}$
branch.
Here, a tree is a set of finite binary sequences that is closed under taking initial segments. A branch through a tree is a subtree that is linearly ordered under the relation “being an initial segment of.” See [Reference Hájek and Pudlák17, chap. I.3(b)] for more details. A definition of the class
![]() $LL_{n+1}$
used in the statement of the low basis theorem can be found in [Reference Hájek and Pudlák17, chap. I.2(d)]. The only properties of
$LL_{n+1}$
used in the statement of the low basis theorem can be found in [Reference Hájek and Pudlák17, chap. I.2(d)]. The only properties of
![]() $LL_{n+1}$
sets that are used in the proof of the arithmetized completeness theorem are that
$LL_{n+1}$
sets that are used in the proof of the arithmetized completeness theorem are that
![]() $\mathrm {I}\Sigma _{n+1}$
proves induction for
$\mathrm {I}\Sigma _{n+1}$
proves induction for
![]() $\Sigma _1(LL_{n+1})$
sets, and that every set recursive in an
$\Sigma _1(LL_{n+1})$
sets, and that every set recursive in an
![]() $LL_{n+1}$
set is itself
$LL_{n+1}$
set is itself
![]() $LL_{n+1}$
[Reference Hájek and Pudlák17, I.2.78–79)].
$LL_{n+1}$
[Reference Hájek and Pudlák17, I.2.78–79)].
For the proof of the arithmetized completeness theorem, we also rely on
![]() $\mathrm {I}\Sigma _{n+1}$
being able to define formalized versions of syntactic and semantic notions such as “formula,” “term,” “theory,” “satisfaction,” and “model,” so that the relevant constructions can be carried out within
$\mathrm {I}\Sigma _{n+1}$
being able to define formalized versions of syntactic and semantic notions such as “formula,” “term,” “theory,” “satisfaction,” and “model,” so that the relevant constructions can be carried out within
![]() $\mathrm {I}\Sigma _{n+1}$
itself. The reader is again referred to [Reference Hájek and Pudlák17], especially Chapter I.4, for a detailed development of these concepts. The generalization to
$\mathrm {I}\Sigma _{n+1}$
itself. The reader is again referred to [Reference Hájek and Pudlák17], especially Chapter I.4, for a detailed development of these concepts. The generalization to
![]() $\Sigma _{n+1}$
-definable theories is straightforward, and fits safely within
$\Sigma _{n+1}$
-definable theories is straightforward, and fits safely within
![]() $\mathrm {I}\Sigma _{n+1}$
.
$\mathrm {I}\Sigma _{n+1}$
.
Proof of the arithmetized completeness theorem.
Fix
![]() $m\leq n$
. Let
$m\leq n$
. Let
![]() $\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
and let
$\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
and let
![]() $\mathrm {T}$
be a theory
$\mathrm {T}$
be a theory
![]() $\Sigma _{n+1}$
-definable in
$\Sigma _{n+1}$
-definable in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M}\models \mathrm {Con}_{\mathrm {T},\Pi _{m}}$
. Reason in
$\mathcal {M}\models \mathrm {Con}_{\mathrm {T},\Pi _{m}}$
. Reason in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
Since
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
and we have
$\Sigma _{n+1}$
and we have
![]() $\mathrm {I}\Sigma _{n+1}$
, we may assume
$\mathrm {I}\Sigma _{n+1}$
, we may assume
![]() $\mathrm {T}$
to be
$\mathrm {T}$
to be
![]() $\Pi _n$
-defined and Henkinized. Let
$\Pi _n$
-defined and Henkinized. Let
![]() $\psi _0,\psi _1,\dots $
be an enumeration of all sentences. Define a dyadic tree T by
$\psi _0,\psi _1,\dots $
be an enumeration of all sentences. Define a dyadic tree T by
![]() $s \in T$
iff there is no
$s \in T$
iff there is no
![]() $p \leq s $
such that p is a proof of contradiction in
$p \leq s $
such that p is a proof of contradiction in
![]() $\mathrm {T}$
from the true
$\mathrm {T}$
from the true
![]() $\Pi _{m}$
sentences plus
$\Pi _{m}$
sentences plus
 $\{ \psi _i^{(s)_i} : i < l(s)\}$
.
$\{ \psi _i^{(s)_i} : i < l(s)\}$
.
The proof relation for
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{m}}(\mathcal {M})$
is
$\mathrm {T} + \mathrm {Th}_{\Pi _{m}}(\mathcal {M})$
is
![]() $\Pi _{n}$
in
$\Pi _{n}$
in
![]() $\mathcal {M}$
, so the tree T is at most
$\mathcal {M}$
, so the tree T is at most
![]() $\Delta _{n+1}$
in
$\Delta _{n+1}$
in
![]() $\mathcal {M}$
. Then
$\mathcal {M}$
. Then
![]() $\mathrm {I}\Sigma _{n+1}$
suffices to show that T is unbounded, so by Fact 3.18 there is an unbounded
$\mathrm {I}\Sigma _{n+1}$
suffices to show that T is unbounded, so by Fact 3.18 there is an unbounded
![]() $LL_{n+1}$
branch
$LL_{n+1}$
branch
![]() $B = \{b_0,b_1,\dots \}$
through T.
$B = \{b_0,b_1,\dots \}$
through T.
Let
 $\hat {\mathrm {T}} = \{ \psi _i : b_i = 1\}$
. Then
$\hat {\mathrm {T}} = \{ \psi _i : b_i = 1\}$
. Then
![]() $\hat {\mathrm {T}}$
is recursive in the
$\hat {\mathrm {T}}$
is recursive in the
![]() $LL_{n+1}$
branch B, and is therefore
$LL_{n+1}$
branch B, and is therefore
![]() $LL_{n+1}$
itself. A term model
$LL_{n+1}$
itself. A term model
![]() $\mathcal {K}$
satisfying
$\mathcal {K}$
satisfying
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{m}}(\mathcal {M})$
can then be read off
$\mathrm {T} + \mathrm {Th}_{\Pi _{m}}(\mathcal {M})$
can then be read off
![]() $\hat {\mathrm {T}}$
in the usual way. Finally, note that
$\hat {\mathrm {T}}$
in the usual way. Finally, note that
![]() $\mathcal {K}$
is recursive in
$\mathcal {K}$
is recursive in
![]() $\hat {\mathrm {T}}$
and therefore
$\hat {\mathrm {T}}$
and therefore
![]() $LL_{n+1}$
. Using induction for
$LL_{n+1}$
. Using induction for
![]() $\Sigma _1(LL_{n+1})$
(provided by
$\Sigma _1(LL_{n+1})$
(provided by
![]() $\mathrm {I}\Sigma _{n+1}$
), we can now define an
$\mathrm {I}\Sigma _{n+1}$
), we can now define an
![]() $LL_{n+1}$
embedding f of
$LL_{n+1}$
embedding f of
![]() $\mathcal {M}$
onto an initial segment of
$\mathcal {M}$
onto an initial segment of
![]() $\mathcal {K}$
by letting
$\mathcal {K}$
by letting
![]() $f(0) = 0^{\mathcal {K}}$
and
$f(0) = 0^{\mathcal {K}}$
and
![]() $f(x+1) =$
the
$f(x+1) =$
the
![]() $\mathcal {K}$
-successor of
$\mathcal {K}$
-successor of
![]() $f(x)$
.
$f(x)$
.
The next few facts are used in the proof of the generalized Orey–Hájek characterization.
Fact 3.19 (Overspill).
Let
![]() $\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
. Suppose that
$\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
. Suppose that
![]() $a \in M$
and that
$a \in M$
and that
![]() $\phi (x,y)$
is a
$\phi (x,y)$
is a
![]() $\Sigma _0(\Sigma _{n+1})$
formula such that
$\Sigma _0(\Sigma _{n+1})$
formula such that
![]() $\mathcal {M} \models \phi (k,a)$
for all
$\mathcal {M} \models \phi (k,a)$
for all
![]() $k\in \omega $
. Then there is a
$k\in \omega $
. Then there is a
![]() $b \in M \setminus \omega $
such that
$b \in M \setminus \omega $
such that
![]() $\mathcal {M} \models \forall x \leq b \phi (x,a)$
.
$\mathcal {M} \models \forall x \leq b \phi (x,a)$
.
Bibliographical remark. The notion of overspill is originally due to Robinson [Reference Robinson38], while the hierarchical version stated here is from [Reference Hájek and Pudlák17, corollary IV.1.16].
Fact 3.20. If
![]() $\mathcal {M}$
is a non-standard model of
$\mathcal {M}$
is a non-standard model of
![]() $\mathrm {I}\Sigma _{n+1}$
, and
$\mathrm {I}\Sigma _{n+1}$
, and
![]() $\phi (x)$
is a
$\phi (x)$
is a
![]() $\Sigma _{n+1}$
formula which may include parameters from
$\Sigma _{n+1}$
formula which may include parameters from
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\{ k \in \omega : \mathcal {M} \models \phi (k)\}$
is coded in
$\{ k \in \omega : \mathcal {M} \models \phi (k)\}$
is coded in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
It follows that if
![]() $\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
, then
$\mathcal {M} \models \mathrm {I}\Sigma _{n+1}$
, then
![]() $\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
is coded in
$\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
is coded in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Fact 3.21 [Reference McAloon32], cf. [Reference D'Aquino8].
If
![]() $\mathcal {M}$
is a countable non-standard model of
$\mathcal {M}$
is a countable non-standard model of
![]() $\mathrm {I}\Delta _0$
, and
$\mathrm {I}\Delta _0$
, and
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _1$
-sound, then for every non-standard
$\Sigma _1$
-sound, then for every non-standard
![]() $c \in M$
, there is a non-standard initial segment of
$c \in M$
, there is a non-standard initial segment of
![]() $\mathcal {M}$
below c that is a model of
$\mathcal {M}$
below c that is a model of
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Fact 3.22 (Refined Friedman embedding theorem).
If
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are countable non-standard models of
$\mathcal {N}$
are countable non-standard models of
![]() $\mathrm {I}\Sigma _{n+1}$
then the following are equivalent:
$\mathrm {I}\Sigma _{n+1}$
then the following are equivalent:
-
1.
 $\mathcal {M}$
is embeddable as a
$\mathcal {M}$
is embeddable as a
 $\Sigma _n$
-elementary initial segment of
$\Sigma _n$
-elementary initial segment of
 $\mathcal {N}$
;
$\mathcal {N}$
; -
2.
 $\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {N})$
and
$\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {N})$
and
 $\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) \subseteq \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {N})$
.
$\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) \subseteq \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {N})$
.
Bibliographical remark. This refinement of Friedman’s [Reference Friedman, Mathias and Rogers13] embedding theorem for
![]() $n=0$
is due to Ressayre [Reference Ressayre and Simpson37, theorem 1.I] and Dimitracopoulos and Paris [Reference Dimitracopoulos and Paris9, corollary 2.4], independently. The hierarchical generalization is straightforward, and has been worked out by Cornaros [Reference Cornaros6, corollary 15].
$n=0$
is due to Ressayre [Reference Ressayre and Simpson37, theorem 1.I] and Dimitracopoulos and Paris [Reference Dimitracopoulos and Paris9, corollary 2.4], independently. The hierarchical generalization is straightforward, and has been worked out by Cornaros [Reference Cornaros6, corollary 15].
We are now ready to prove the final fact: an excerpt of a generalization of the Orey–Hájek–Guaspari–Lindström characterization of interpretability. For extensions of
![]() $\mathrm {PA}$
, the equivalence of 1. and 3. is due to Guaspari [Reference Guaspari15, theorem 6.5(1)]. The equivalence of 1. and 2. for finitely axiomatizable theories seems to have been known to experts for some time, while the equivalence of 2. and 3. for r.e. extensions of fragments of
$\mathrm {PA}$
, the equivalence of 1. and 3. is due to Guaspari [Reference Guaspari15, theorem 6.5(1)]. The equivalence of 1. and 2. for finitely axiomatizable theories seems to have been known to experts for some time, while the equivalence of 2. and 3. for r.e. extensions of fragments of
![]() $\mathrm {PA}$
is stated without proof by Blanck and Enayat [Reference Blanck and Enayat4, theorem 2.11]. With the previous facts of this section in place, the generalization to
$\mathrm {PA}$
is stated without proof by Blanck and Enayat [Reference Blanck and Enayat4, theorem 2.11]. With the previous facts of this section in place, the generalization to
![]() $\Sigma _{n+1}$
-definable theories presents no further difficulties.
$\Sigma _{n+1}$
-definable theories presents no further difficulties.
Fact 3.23 (OHGL characterization).
Let
![]() $\mathrm {S}$
and
$\mathrm {S}$
and
![]() $\mathrm {T}$
be
$\mathrm {T}$
be
![]() $\Sigma _{n+1}$
-definable, consistent extensions of
$\Sigma _{n+1}$
-definable, consistent extensions of
![]() $\mathrm {I}\Sigma _{n+1}$
, and suppose that
$\mathrm {I}\Sigma _{n+1}$
, and suppose that
![]() $\mathrm {S}$
is also
$\mathrm {S}$
is also
![]() $\Pi _n$
-complete. The following are equivalent:
$\Pi _n$
-complete. The following are equivalent:
-
1.
 $\mathrm {S}$
is
$\mathrm {S}$
is
 $\Pi _{n+1}$
-conservative over
$\Pi _{n+1}$
-conservative over
 $\mathrm {T}$
;
$\mathrm {T}$
; -
2. for all
 $k\in \omega $
,
$k\in \omega $
,
 $\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
;
$\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
; -
3. every countable model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $\mathrm {T}$
with
$\mathrm {T}$
with
 $\mathrm {S} \in \mathrm {SSy}(\mathcal {M})$
has a
$\mathrm {S} \in \mathrm {SSy}(\mathcal {M})$
has a
 $\Sigma _n$
-elementary extension to a model of
$\Sigma _n$
-elementary extension to a model of
 $\mathrm {S}$
.
$\mathrm {S}$
.
Proof. 1.
![]() $\Rightarrow $
2. Suppose that
$\Rightarrow $
2. Suppose that
![]() $\mathrm {S}$
is
$\mathrm {S}$
is
![]() $\Pi _{n+1}$
-conservative over
$\Pi _{n+1}$
-conservative over
![]() $\mathrm {T}$
. By Fact 3.15 and
$\mathrm {T}$
. By Fact 3.15 and
![]() $\Pi _n$
-completeness of
$\Pi _n$
-completeness of
![]() $\mathrm {S}$
,
$\mathrm {S}$
,
 $\mathrm {S} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
$\mathrm {S} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
![]() $k\in \omega $
. But
$k\in \omega $
. But
 $\mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
is at most
$\mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
is at most
![]() $\Pi _{n+1}$
, so
$\Pi _{n+1}$
, so
 $\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
$\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
![]() $k \in \omega $
.
$k \in \omega $
.
2.
![]() $\Rightarrow $
3. Suppose
$\Rightarrow $
3. Suppose
 $\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
$\mathrm {T} \vdash \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
for all
![]() $k \in \omega $
. Let
$k \in \omega $
. Let
![]() $\mathcal {M}$
be a countable model of
$\mathcal {M}$
be a countable model of
![]() $\mathrm {T}$
and suppose that
$\mathrm {T}$
and suppose that
![]() $\mathrm {S} \in \mathrm {SSy}(\mathcal {M})$
. Since
$\mathrm {S} \in \mathrm {SSy}(\mathcal {M})$
. Since
![]() $\mathrm {T}$
extends
$\mathrm {T}$
extends
![]() $\mathrm {I}\Sigma _{n+1}$
, it follows that
$\mathrm {I}\Sigma _{n+1}$
, it follows that
 $\mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
is at most
$\mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^k$
is at most
![]() $\Pi _{n+1}$
, and we can use overspill to get
$\Pi _{n+1}$
, and we can use overspill to get
 $\mathcal {M} \models \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^c$
for some non-standard
$\mathcal {M} \models \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}^c$
for some non-standard
![]() $c\in M$
. By Fact 3.21, there is a submodel
$c\in M$
. By Fact 3.21, there is a submodel
![]() $\mathcal {M}_0 \models \mathrm {PA}$
of
$\mathcal {M}_0 \models \mathrm {PA}$
of
![]() $\mathcal {M}$
, all of whose elements are below c, and there is some non-standard a below c that codes
$\mathcal {M}$
, all of whose elements are below c, and there is some non-standard a below c that codes
![]() $\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
. This ensures that
$\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
. This ensures that
![]() $\mathcal {M}_0 \models \mathrm {Con}_{\mathrm {S} + \{m:m\varepsilon a\}}$
, so Fact 3.17 guarantees the existence of an end-extension
$\mathcal {M}_0 \models \mathrm {Con}_{\mathrm {S} + \{m:m\varepsilon a\}}$
, so Fact 3.17 guarantees the existence of an end-extension
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathcal {M}_0$
, satisfying
$\mathcal {M}_0$
, satisfying
![]() $\mathrm {S} + \{m:m\varepsilon a\}$
and therefore also
$\mathrm {S} + \{m:m\varepsilon a\}$
and therefore also
![]() $\mathrm {S} + \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
.
$\mathrm {S} + \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M})$
.
At this point, the situation is that
![]() $\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {M}_0) = \mathrm {SSy}(\mathcal {K})$
,
$\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {M}_0) = \mathrm {SSy}(\mathcal {K})$
,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {K}$
are countable, and
$\mathcal {K}$
are countable, and
![]() $\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) \subseteq \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {K})$
. Then Fact 3.22 ensures that
$\mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) \subseteq \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {K})$
. Then Fact 3.22 ensures that
![]() $\mathcal {M}$
can be embedded as a
$\mathcal {M}$
can be embedded as a
![]() $\Sigma _n$
-elementary initial segment of
$\Sigma _n$
-elementary initial segment of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
3.
![]() $\Rightarrow $
1. Prove the contrapositive statement by assuming that
$\Rightarrow $
1. Prove the contrapositive statement by assuming that
![]() $\mathrm {S}$
is not
$\mathrm {S}$
is not
![]() $\Pi _{n+1}$
-conservative over
$\Pi _{n+1}$
-conservative over
![]() $\mathrm {T}$
. Then there is a
$\mathrm {T}$
. Then there is a
![]() $\Pi _{n+1}$
sentence
$\Pi _{n+1}$
sentence
![]() $\pi $
such that
$\pi $
such that
![]() $\mathrm {S} \vdash \pi $
but
$\mathrm {S} \vdash \pi $
but
![]() $\mathrm {T}+ \lnot \pi $
is consistent. Let
$\mathrm {T}+ \lnot \pi $
is consistent. Let
![]() $\mathcal {M} \models \mathrm {T}+ \lnot \pi $
. If
$\mathcal {M} \models \mathrm {T}+ \lnot \pi $
. If
![]() $\mathcal {K} \models \mathrm {S}$
were a
$\mathcal {K} \models \mathrm {S}$
were a
![]() $\Sigma _n$
-elementary extension of
$\Sigma _n$
-elementary extension of
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\mathcal {K}$
would satisfy both
$\mathcal {K}$
would satisfy both
![]() $\pi $
and
$\pi $
and
![]() $\lnot \pi $
, a contradiction.
$\lnot \pi $
, a contradiction.
4 Applications
The goal of this section is to prove a handful of hierarchical incompleteness results, using the tools we reviewed in the previous one. The first such result stems from Mostowski [Reference Mostowski34, theorem 2], who proved that whenever
![]() $\{\mathrm {T}_i: i \in \omega \}$
is an r.e. family of consistent, r.e. theories extending
$\{\mathrm {T}_i: i \in \omega \}$
is an r.e. family of consistent, r.e. theories extending
![]() $\mathrm {Q}$
, then there is a
$\mathrm {Q}$
, then there is a
![]() $\Pi _1$
formula that is simultaneously independent over these theories. Here, we understand the concept of an independent formula in the following way:
$\Pi _1$
formula that is simultaneously independent over these theories. Here, we understand the concept of an independent formula in the following way:
Definition 4.24. A formula
![]() $\xi (x)$
is independent over
$\xi (x)$
is independent over
![]() $\mathrm {T}$
if, for every
$\mathrm {T}$
if, for every
![]() $g : \omega \to \{0,1\}$
, the theory
$g : \omega \to \{0,1\}$
, the theory
 $\mathrm {T} + \{ \xi (k)^{g(k)}\}$
is consistent. Recall that
$\mathrm {T} + \{ \xi (k)^{g(k)}\}$
is consistent. Recall that
![]() $\xi (k)^0= \lnot \xi (k)$
and
$\xi (k)^0= \lnot \xi (k)$
and
![]() $\xi (k)^1 = \xi (k)$
.
$\xi (k)^1 = \xi (k)$
.
While one of Mostowski’s accomplishments was the simultaneous independence over a whole r.e. family of theories, this aspect of his result is deliberately ignored here. Instead, we focus on how to construct formulae independent over
![]() $\Sigma _{n+1}$
-definable theories.
$\Sigma _{n+1}$
-definable theories.
Theorem 4.25. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Sigma _n$
-sound extension of
$\Sigma _n$
-sound extension of
![]() $\mathrm {I}\Sigma _n + \mathrm {exp}$
. Then there is a
$\mathrm {I}\Sigma _n + \mathrm {exp}$
. Then there is a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\xi (x)$
that is independent over
$\xi (x)$
that is independent over
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Proof. Define a function
![]() $f(x)$
by the stipulation that
$f(x)$
by the stipulation that
![]() $f(m) = k$
iff there is a proof p of
$f(m) = k$
iff there is a proof p of
![]() $\varphi ^n_m(m) \neq k$
in
$\varphi ^n_m(m) \neq k$
in
![]() $\mathrm {T}$
, and for each
$\mathrm {T}$
, and for each
![]() $q<p$
and
$q<p$
and
![]() $k_0 \leq k$
, q is not a proof of
$k_0 \leq k$
, q is not a proof of
![]() $\varphi ^n_m(m) \neq k_0$
in
$\varphi ^n_m(m) \neq k_0$
in
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Since
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
-definable, there is a deductively equivalent
$\Sigma _{n+1}$
-definable, there is a deductively equivalent
![]() $\Pi _n$
-definition of
$\Pi _n$
-definition of
![]() $\mathrm {T}$
. Hence, the relation
$\mathrm {T}$
. Hence, the relation
![]() $f(x) = y$
is r.e. in
$f(x) = y$
is r.e. in
![]() $\emptyset ^{(n)}$
, and therefore partial n-recursive. Let e be an n-index for f, and let
$\emptyset ^{(n)}$
, and therefore partial n-recursive. Let e be an n-index for f, and let
![]() $\xi (x)$
be the formula
$\xi (x)$
be the formula
Since
![]() $\mathrm {T}$
extends
$\mathrm {T}$
extends
![]() $\mathrm {I}\Sigma _n$
, we may assume that both
$\mathrm {I}\Sigma _n$
, we may assume that both
![]() $\varphi ^n_x(y) = z$
and
$\varphi ^n_x(y) = z$
and
![]() $\xi (x)$
are equivalent in
$\xi (x)$
are equivalent in
![]() $\mathrm {T}$
to
$\mathrm {T}$
to
![]() $\Sigma _{n+1}$
formulae. The proof that
$\Sigma _{n+1}$
formulae. The proof that
![]() $\xi (x)$
is as desired has two parts. The first part shows that
$\xi (x)$
is as desired has two parts. The first part shows that
![]() $\mathrm {T} + \varphi ^n_e(e) = k$
is consistent for each
$\mathrm {T} + \varphi ^n_e(e) = k$
is consistent for each
![]() $k\in \omega $
.
$k\in \omega $
.
Suppose, for a contradiction, that
![]() $\mathrm {T} + \varphi ^n_e(e) = k$
is inconsistent for some
$\mathrm {T} + \varphi ^n_e(e) = k$
is inconsistent for some
![]() $k\in \omega $
. We may assume that k is the least such number. Then
$k\in \omega $
. We may assume that k is the least such number. Then
![]() $\mathrm {T} \vdash \varphi ^n_e(e) \neq k$
with some minimal proof p, so
$\mathrm {T} \vdash \varphi ^n_e(e) \neq k$
with some minimal proof p, so
![]() $f(e) = \varphi ^n_e(e) = k$
by definition. With
$f(e) = \varphi ^n_e(e) = k$
by definition. With
![]() $\mathrm {T}$
extending
$\mathrm {T}$
extending
![]() $\mathrm {I}\Sigma _n$
, we have
$\mathrm {I}\Sigma _n$
, we have
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N}) \vdash \varphi ^n_e(e) = k$
by Fact 3.3(3). But then
$\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N}) \vdash \varphi ^n_e(e) = k$
by Fact 3.3(3). But then
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is inconsistent, which by Fact 3.2 contradicts the assumption that
$\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is inconsistent, which by Fact 3.2 contradicts the assumption that
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _n$
-sound. Hence the theory
$\Sigma _n$
-sound. Hence the theory
![]() $\mathrm {T} + \varphi ^n_e(e) = k$
is consistent for any choice of
$\mathrm {T} + \varphi ^n_e(e) = k$
is consistent for any choice of
![]() $k \in \omega $
.
$k \in \omega $
.
In this final part of the proof, we show that
![]() $\xi (x)$
is independent over
$\xi (x)$
is independent over
![]() $\mathrm {T}$
. Let g be any function from
$\mathrm {T}$
. Let g be any function from
![]() $\omega $
to
$\omega $
to
![]() $\{0,1\}$
and let
$\{0,1\}$
and let
 $X = \{ \xi (k)^{g(k)} : k\in \omega \}$
. Let Y be any finite subset of X, and let Z be the set
$X = \{ \xi (k)^{g(k)} : k\in \omega \}$
. Let Y be any finite subset of X, and let Z be the set
![]() $\{k: \xi (k) \in Y\}$
. Let
$\{k: \xi (k) \in Y\}$
. Let
![]() $\zeta (x) := x \varepsilon a$
, where a is a code for the finite set Z; then
$\zeta (x) := x \varepsilon a$
, where a is a code for the finite set Z; then
![]() $\zeta $
binumerates Z in
$\zeta $
binumerates Z in
![]() $\mathrm {Q}$
.
$\mathrm {Q}$
.
Reason in the consistent theory
![]() $\mathrm {T} + \varphi ^n_e(e) = \ulcorner \zeta \urcorner $
:
$\mathrm {T} + \varphi ^n_e(e) = \ulcorner \zeta \urcorner $
:
If
![]() $\xi (x)$
, then
$\xi (x)$
, then
![]() $\varphi ^n_e(e) = z \land \mathrm {Sat}_{\Sigma _{n+1}}(z,x)$
for some z. But z is unique and
$\varphi ^n_e(e) = z \land \mathrm {Sat}_{\Sigma _{n+1}}(z,x)$
for some z. But z is unique and
![]() $\varphi ^n_e(e) = \ulcorner \zeta \urcorner $
, so
$\varphi ^n_e(e) = \ulcorner \zeta \urcorner $
, so
![]() $\mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x)$
and therefore
$\mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x)$
and therefore
![]() $\zeta (x)$
.
$\zeta (x)$
.
Conversely, observe that since
![]() $\varphi ^n_e(e) = \ulcorner \zeta \urcorner $
,
$\varphi ^n_e(e) = \ulcorner \zeta \urcorner $
,
![]() $\xi (x)$
follows from
$\xi (x)$
follows from
![]() $\zeta (x)$
by Fact 3.11 and
$\zeta (x)$
by Fact 3.11 and
![]() $\exists $
-introduction.
$\exists $
-introduction.
Hence the theory
![]() $\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x))$
is consistent. If
$\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x))$
is consistent. If
![]() $k \in Z$
, then
$k \in Z$
, then
![]() $\mathrm {T} \vdash \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,k)$
, so
$\mathrm {T} \vdash \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,k)$
, so
![]() $\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x)) \vdash \xi (k)$
, and similarly for
$\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x)) \vdash \xi (k)$
, and similarly for
![]() $k \notin Z$
. Hence the consistent theory
$k \notin Z$
. Hence the consistent theory
![]() $\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x))$
proves all the sentences in Y, so
$\mathrm {T} + \forall x (\xi (x) \leftrightarrow \mathrm {Sat}_{\Sigma _{n+1}}(\ulcorner \zeta \urcorner ,x))$
proves all the sentences in Y, so
![]() $\mathrm {T} + Y$
is consistent. By compactness, it follows that
$\mathrm {T} + Y$
is consistent. By compactness, it follows that
![]() $\mathrm {T} + X$
is consistent, and therefore
$\mathrm {T} + X$
is consistent, and therefore
![]() $\xi (x)$
is independent over
$\xi (x)$
is independent over
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
The Gödel–Rosser incompleteness Theorem 1.1 for arithmetically definable theories follows immediately from the result above. While the generalization to arithmetically definable theories is new, the basic idea of this proof is due to Kripke [Reference Kripke26, corollary 1.1], who used it to rederive Mostowski’s result from his own theorem on the existence of flexible formulae. Here, we understand flexibility in the following sense:
Definition 4.26. A formula
![]() $\unicode{x3b3} (x)$
is flexible for
$\unicode{x3b3} (x)$
is flexible for
![]() $\Gamma $
over
$\Gamma $
over
![]() $\mathrm {T}$
if, for every
$\mathrm {T}$
if, for every
![]() $\delta (x) \in \Gamma $
, the theory
$\delta (x) \in \Gamma $
, the theory
![]() $\mathrm {T} + \forall x (\unicode{x3b3} (x) \leftrightarrow \delta (x))$
is consistent.
$\mathrm {T} + \forall x (\unicode{x3b3} (x) \leftrightarrow \delta (x))$
is consistent.
The definitions used by Kripke obscure the original content of his theorem, but, in hindsight, his proof yields that for every consistent, r.e. extension
![]() $\mathrm {T}$
of
$\mathrm {T}$
of
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
, there is a
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
, there is a
![]() $\Sigma _{n+1}$
formula that is flexible for
$\Sigma _{n+1}$
formula that is flexible for
![]() $\Sigma _{n+1}$
over
$\Sigma _{n+1}$
over
![]() $\mathrm {T}$
. Striving for some unification, we derive a hierarchical version of Kripke’s theorem by generalizing a result of Lindström’s [Reference Lindström28, proposition 2]; which in turn is a generalization of both Mostowski’s and Kripke’s results, as well as of Scott’s famous lemma used to realize countable Scott sets as standard systems of models of
$\mathrm {T}$
. Striving for some unification, we derive a hierarchical version of Kripke’s theorem by generalizing a result of Lindström’s [Reference Lindström28, proposition 2]; which in turn is a generalization of both Mostowski’s and Kripke’s results, as well as of Scott’s famous lemma used to realize countable Scott sets as standard systems of models of
![]() $\mathrm {PA}$
[Reference Scott and Dekker41].
$\mathrm {PA}$
[Reference Scott and Dekker41].
Theorem 4.27. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable extension of
$\Sigma _{n+1}$
-definable extension of
![]() $\mathrm {I}\Sigma _{m} + \mathrm {exp}$
, with
$\mathrm {I}\Sigma _{m} + \mathrm {exp}$
, with
![]() $m\geq n$
. For every
$m\geq n$
. For every
![]() $\Sigma _m$
formula
$\Sigma _m$
formula
![]() $\phi (x)$
, there is a
$\phi (x)$
, there is a
![]() $\Sigma _{m+1}$
formula
$\Sigma _{m+1}$
formula
![]() $\unicode{x3b3} (x)$
such that for every
$\unicode{x3b3} (x)$
such that for every
![]() $g : \omega \to \{0,1\}$
, if
$g : \omega \to \{0,1\}$
, if
 $$ \begin{align*} \mathrm{T}_g = \mathrm{T} + \{ \phi(k) ^{g(k)}:k\in\omega\} \end{align*} $$
$$ \begin{align*} \mathrm{T}_g = \mathrm{T} + \{ \phi(k) ^{g(k)}:k\in\omega\} \end{align*} $$
is
![]() $\Sigma _n$
-sound, then
$\Sigma _n$
-sound, then
![]() $\unicode{x3b3} (x)$
is flexible for
$\unicode{x3b3} (x)$
is flexible for
![]() $\Sigma _{m+1}$
over
$\Sigma _{m+1}$
over
![]() $\mathrm {T}_g$
.
$\mathrm {T}_g$
.
Proof. Fix n and let
![]() $\phi (x) \in \Sigma _m$
, with
$\phi (x) \in \Sigma _m$
, with
![]() $m\geq n$
. Let
$m\geq n$
. Let
![]() $f(s,\ulcorner \eta \urcorner ) = \ulcorner \sigma \urcorner $
iff the following holds:
$f(s,\ulcorner \eta \urcorner ) = \ulcorner \sigma \urcorner $
iff the following holds:
-
1. s is binary sequence of length
 $k + 1$
;
$k + 1$
; -
2. there is a proof p of
 $\lnot \forall x (\eta (x) \leftrightarrow \sigma (x))$
in
$\lnot \forall x (\eta (x) \leftrightarrow \sigma (x))$
in
 $\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
;
$\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
; -
3. for every
 $q<p$
and any
$q<p$
and any
 $\ulcorner \sigma _0\urcorner \leq \ulcorner \sigma \urcorner $
, q is not a proof of
$\ulcorner \sigma _0\urcorner \leq \ulcorner \sigma \urcorner $
, q is not a proof of
 $\lnot \forall x (\eta (x) \leftrightarrow \sigma _0(x))$
in
$\lnot \forall x (\eta (x) \leftrightarrow \sigma _0(x))$
in
 $\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
.
$\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
.
Here
![]() $(s)_k$
denotes the kth element of the sequence s.
$(s)_k$
denotes the kth element of the sequence s.
Since
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
-definable, there is a deductively equivalent
$\Sigma _{n+1}$
-definable, there is a deductively equivalent
![]() $\Pi _n$
-definition of
$\Pi _n$
-definition of
![]() $\mathrm {T}$
. Hence, the relation
$\mathrm {T}$
. Hence, the relation
![]() $f(x,y) = z$
is r.e. in
$f(x,y) = z$
is r.e. in
![]() $\emptyset ^{(n)}$
, and therefore partial n-recursive. Let e be an n-index for f.
$\emptyset ^{(n)}$
, and therefore partial n-recursive. Let e be an n-index for f.
Let
 $\mathrm {Seq}_\phi (x)$
be the formula
$\mathrm {Seq}_\phi (x)$
be the formula
where
![]() $l(x)$
denotes the length of x (this is the formula “x is a
$l(x)$
denotes the length of x (this is the formula “x is a
![]() $l(x)$
-piece of
$l(x)$
-piece of
![]() $\phi $
”). Whenever
$\phi $
”). Whenever
![]() $\phi (x)$
is
$\phi (x)$
is
![]() $\Sigma _m$
,
$\Sigma _m$
,
 $\mathrm {Seq}_\phi (x)$
is
$\mathrm {Seq}_\phi (x)$
is
![]() $\Sigma _0(\Sigma _m)$
, and since
$\Sigma _0(\Sigma _m)$
, and since
![]() $\mathrm {T} \vdash \mathrm {I}\Sigma _m$
, it is
$\mathrm {T} \vdash \mathrm {I}\Sigma _m$
, it is
![]() $\Delta _{m+1}$
in
$\Delta _{m+1}$
in
![]() $\mathrm {T}$
. Let, by Fact 3.4,
$\mathrm {T}$
. Let, by Fact 3.4,
![]() $\unicode{x3b3} (x)$
be such that
$\unicode{x3b3} (x)$
be such that
 $$ \begin{align*} \mathrm{T} \vdash \forall x(\unicode{x3b3}(x) \leftrightarrow \exists s \exists z(\mathrm{Seq}_\phi(s) \land \varphi^n_e(s, \ulcorner \unicode{x3b3} \urcorner)= z \land \mathrm{Sat}_{\Sigma_{m+1}}(z,x)))\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{T} \vdash \forall x(\unicode{x3b3}(x) \leftrightarrow \exists s \exists z(\mathrm{Seq}_\phi(s) \land \varphi^n_e(s, \ulcorner \unicode{x3b3} \urcorner)= z \land \mathrm{Sat}_{\Sigma_{m+1}}(z,x)))\text{.} \end{align*} $$
Since
![]() $\mathrm {T} \vdash \mathrm {I}\Sigma _m$
and
$\mathrm {T} \vdash \mathrm {I}\Sigma _m$
and
![]() $m\geq n$
, the formula strongly representing f in
$m\geq n$
, the formula strongly representing f in
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is equivalent to a
$\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is equivalent to a
![]() $\Sigma _{n+1}$
formula in
$\Sigma _{n+1}$
formula in
![]() $\mathrm {T}$
. It follows that
$\mathrm {T}$
. It follows that
![]() $\unicode{x3b3} (x)$
is equivalent to a
$\unicode{x3b3} (x)$
is equivalent to a
![]() $\Sigma _{m+1}$
formula in
$\Sigma _{m+1}$
formula in
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Suppose, for a contradiction, that there is a
![]() $g : \omega \to \{0,1\}$
and a
$g : \omega \to \{0,1\}$
and a
![]() $\sigma (x) \in \Sigma _{m+1}$
such that
$\sigma (x) \in \Sigma _{m+1}$
such that
![]() $\mathrm {T}_g$
is
$\mathrm {T}_g$
is
![]() $\Sigma _n$
-sound, but
$\Sigma _n$
-sound, but
![]() $\mathrm {T}_g + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
is inconsistent. If there are more than one such
$\mathrm {T}_g + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
is inconsistent. If there are more than one such
![]() $\sigma (x)$
for a given g, consider the one with the least Gödel number. There is then an initial subsequence s of g, of length
$\sigma (x)$
for a given g, consider the one with the least Gödel number. There is then an initial subsequence s of g, of length
![]() $k+1$
for some k, such that p is a proof of
$k+1$
for some k, such that p is a proof of
![]() $\lnot \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
in
$\lnot \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
in
![]() $\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
. Let s be the initial subsequence of g corresponding to the least such p.
$\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
. Let s be the initial subsequence of g corresponding to the least such p.
It is now clear that neither p nor any
![]() $q <p$
can be a proof of
$q <p$
can be a proof of
![]() $\lnot \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma _0(x))$
in
$\lnot \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma _0(x))$
in
![]() $\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
for any formula
$\mathrm {T} + \phi (0)^{(s)_0} + \dots + \phi (k)^{(s)_k}$
for any formula
![]() $\sigma _0(x)$
whose Gödel number is less than
$\sigma _0(x)$
whose Gödel number is less than
![]() $ \ulcorner \sigma \urcorner $
. Hence, by definition,
$ \ulcorner \sigma \urcorner $
. Hence, by definition,
![]() $f(s,\ulcorner \unicode{x3b3} \urcorner ) = \ulcorner \sigma \urcorner $
, and by Fact 3.3,
$f(s,\ulcorner \unicode{x3b3} \urcorner ) = \ulcorner \sigma \urcorner $
, and by Fact 3.3,
By choice of s,
 $\mathrm {T}_g \vdash \mathrm {Seq}_\phi (\ulcorner s \urcorner )$
, so
$\mathrm {T}_g \vdash \mathrm {Seq}_\phi (\ulcorner s \urcorner )$
, so
![]() $\mathrm {T}_g + \mathrm {Th}_{\Pi _{n}}(\mathbb {N}) \vdash \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
by an argument similar to that in the proof of Theorem 4.25. Then
$\mathrm {T}_g + \mathrm {Th}_{\Pi _{n}}(\mathbb {N}) \vdash \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
by an argument similar to that in the proof of Theorem 4.25. Then
![]() $\mathrm {T}_g +\mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is inconsistent, contradicting the assumption that
$\mathrm {T}_g +\mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
is inconsistent, contradicting the assumption that
![]() $\mathrm {T}_g$
was
$\mathrm {T}_g$
was
![]() $\Sigma _n$
-sound.
$\Sigma _n$
-sound.
By choosing
![]() $\phi (x)$
as
$\phi (x)$
as
![]() $\top $
in the construction above, we obtain the expected hierarchical version of Kripke’s theorem. A similar, but not entirely correct, claim is made by Blanck [Reference Blanck3, theorem 4.8].
$\top $
in the construction above, we obtain the expected hierarchical version of Kripke’s theorem. A similar, but not entirely correct, claim is made by Blanck [Reference Blanck3, theorem 4.8].
Corollary 4.28. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Sigma _n$
-sound extension of
$\Sigma _n$
-sound extension of
![]() $\mathrm {I}\Sigma _n + \mathrm {exp}$
. For all
$\mathrm {I}\Sigma _n + \mathrm {exp}$
. For all
![]() $m\geq n$
, there is a
$m\geq n$
, there is a
![]() $\Sigma _{m+1}$
formula
$\Sigma _{m+1}$
formula
![]() $\unicode{x3b3} (x)$
that is flexible for
$\unicode{x3b3} (x)$
that is flexible for
![]() $\Sigma _{m+1}$
over
$\Sigma _{m+1}$
over
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Mostowski’s theorem for r.e. extensions of
![]() $\mathrm {I}\Sigma _0 + \mathrm {exp}$
then follows immediately by using the method described in the proof of Theorem 4.25. A similar argument also yields Scott’s lemma.
$\mathrm {I}\Sigma _0 + \mathrm {exp}$
then follows immediately by using the method described in the proof of Theorem 4.25. A similar argument also yields Scott’s lemma.
The next objective is to show how the hierarchical version of Kripke’s theorem can be formalized in
![]() $\Pi _n$
-complete extensions of
$\Pi _n$
-complete extensions of
![]() $\mathrm {I}\Sigma _{n+1}$
. A similar, but not entirely correct, claim is made by Blanck [Reference Blanck3, theorem 5.8]. The present proof is a minor modification of an argument of Blanck [Reference Blanck3, theorem 5.1].
$\mathrm {I}\Sigma _{n+1}$
. A similar, but not entirely correct, claim is made by Blanck [Reference Blanck3, theorem 5.8]. The present proof is a minor modification of an argument of Blanck [Reference Blanck3, theorem 5.1].
Theorem 4.29. Let
![]() $\mathrm {S}$
be a
$\mathrm {S}$
be a
![]() $\Pi _n$
-complete, consistent extension of
$\Pi _n$
-complete, consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
, and let
$\mathrm {I}\Sigma _{n+1}$
, and let
![]() $\mathrm {T}$
be
$\mathrm {T}$
be
![]() $\Sigma _{n+1}$
-definable. For all
$\Sigma _{n+1}$
-definable. For all
![]() $m \geq n$
, there is a
$m \geq n$
, there is a
![]() $\Sigma _{m+1}$
formula
$\Sigma _{m+1}$
formula
![]() $\unicode{x3b3} (x)$
such that:
$\unicode{x3b3} (x)$
such that:
-
1.
 $\mathrm {I}\Sigma _{n+1} \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
;
$\mathrm {I}\Sigma _{n+1} \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
; -
2. if
 $\sigma (x) \in \Sigma _{m+1}$
, then every model of
$\sigma (x) \in \Sigma _{m+1}$
, then every model of
 $\mathrm {S} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
has a
$\mathrm {S} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
has a
 $\Sigma _n$
-elementary extension to a model of
$\Sigma _n$
-elementary extension to a model of
 $\mathrm {T} + \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
.
$\mathrm {T} + \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
.
Proof. Fix n, and let
![]() $\phi (x,z)$
be the
$\phi (x,z)$
be the
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \varphi ^n_{\dot {x}}(\dot {x}) \neq \dot {z} \urcorner )$
. Let e be the Gödel number of
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \varphi ^n_{\dot {x}}(\dot {x}) \neq \dot {z} \urcorner )$
. Let e be the Gödel number of
![]() $\phi (x,z)$
.
$\phi (x,z)$
.
Recall that
![]() $\varphi ^n_x(y) = z$
is shorthand for
$\varphi ^n_x(y) = z$
is shorthand for
![]() $\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(x,y,z)$
. Therefore, by Fact 3.9(1) we have
$\mathrm {Sel}\{\mathrm {Sat}_{\Sigma _{n+1}}\}(x,y,z)$
. Therefore, by Fact 3.9(1) we have
so by construction of
![]() $\phi (x,z)$
and choice of e,
$\phi (x,z)$
and choice of e,
By Fact 3.13,
so (2) and (3) together with Fact 3.14 give
Now, observe that
 $$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \exists z \lnot \mathrm{Con}_{\mathrm{T} + \varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}} \leftrightarrow \exists z \mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}(\ulcorner \varphi^n_{e}(e) \neq \dot{z}\urcorner)\text{.} \end{align} $$
$$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \exists z \lnot \mathrm{Con}_{\mathrm{T} + \varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}} \leftrightarrow \exists z \mathrm{Pr}_{\mathrm{T},\Sigma_{n+1}}(\ulcorner \varphi^n_{e}(e) \neq \dot{z}\urcorner)\text{.} \end{align} $$
By construction of
![]() $\phi (x,z)$
, the right hand side of the equivalence of (5) is identical to
$\phi (x,z)$
, the right hand side of the equivalence of (5) is identical to
![]() $\exists z \phi (e,z)$
, and by Fact 3.11, we have
$\exists z \phi (e,z)$
, and by Fact 3.11, we have
Therefore, by Fact 3.9(3) and the convention on
![]() $\varphi ^n_{e}$
, (5) gives
$\varphi ^n_{e}$
, (5) gives
 $$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \exists z \lnot \mathrm{Con}_{\mathrm{T} + \varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}} \leftrightarrow \exists z (\varphi^n_{e}(e) = z)\text{.} \end{align} $$
$$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \exists z \lnot \mathrm{Con}_{\mathrm{T} + \varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}} \leftrightarrow \exists z (\varphi^n_{e}(e) = z)\text{.} \end{align} $$
Together with (4), this implies
 $$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \forall z (\mathrm{Con}_{\mathrm{T},\Sigma_{n+1}} \rightarrow \mathrm{Con}_{\mathrm{T}+\varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}})\text{.} \end{align} $$
$$ \begin{align} \mathrm{I}\Sigma_{n+1} \vdash \forall z (\mathrm{Con}_{\mathrm{T},\Sigma_{n+1}} \rightarrow \mathrm{Con}_{\mathrm{T}+\varphi^n_{e}(e) = \dot{z},\Sigma_{n+1}})\text{.} \end{align} $$
Then the
![]() $\Sigma _{m+1}$
formula
$\Sigma _{m+1}$
formula
![]() $\unicode{x3b3} (x) := \exists z (\varphi ^n_{e}(e) = z \land \mathrm {Sat}_{\Sigma _{m+1}}(z,x))$
is as desired, and the first part of the theorem follows directly from (4). For the second part, let
$\unicode{x3b3} (x) := \exists z (\varphi ^n_{e}(e) = z \land \mathrm {Sat}_{\Sigma _{m+1}}(z,x))$
is as desired, and the first part of the theorem follows directly from (4). For the second part, let
![]() $\mathcal {M}$
be any model of
$\mathcal {M}$
be any model of
![]() $\mathrm {S} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
, and let
$\mathrm {S} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
, and let
![]() $\sigma (x)$
be any
$\sigma (x)$
be any
![]() $\Sigma _{m+1}$
formula. By (8), we immediately get
$\Sigma _{m+1}$
formula. By (8), we immediately get
 $\mathcal {M} \models \mathrm {Con}_{\mathrm {T}+\varphi ^n_e(e) = \ulcorner \sigma \urcorner ,\Sigma _{n+1}}$
. Moreover, since
$\mathcal {M} \models \mathrm {Con}_{\mathrm {T}+\varphi ^n_e(e) = \ulcorner \sigma \urcorner ,\Sigma _{n+1}}$
. Moreover, since
![]() $\mathrm {S}$
is a
$\mathrm {S}$
is a
![]() $\Pi _n$
-complete extension of
$\Pi _n$
-complete extension of
![]() $\mathrm {I}\Sigma _{n+1}$
, and
$\mathrm {I}\Sigma _{n+1}$
, and
![]() $\mathrm {T}$
is
$\mathrm {T}$
is
![]() $\Sigma _{n+1}$
-definable, the theory
$\Sigma _{n+1}$
-definable, the theory
![]() $\mathrm {T} + \varphi ^n_e(e) = \ulcorner \sigma \urcorner $
is
$\mathrm {T} + \varphi ^n_e(e) = \ulcorner \sigma \urcorner $
is
![]() $\Sigma _{n+1}$
-definable in
$\Sigma _{n+1}$
-definable in
![]() $\mathcal {M}$
, using Craig’s trick. By Fact 3.17, there is then a
$\mathcal {M}$
, using Craig’s trick. By Fact 3.17, there is then a
![]() $\Sigma _{n}$
-elementary end-extension
$\Sigma _{n}$
-elementary end-extension
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathcal {M}$
that satisfies
$\mathcal {M}$
that satisfies
![]() $\mathrm {T} + \varphi ^n_e(e) = \ulcorner \sigma \urcorner $
. Since
$\mathrm {T} + \varphi ^n_e(e) = \ulcorner \sigma \urcorner $
. Since
![]() $\mathcal {K}$
satisfies
$\mathcal {K}$
satisfies
![]() $\varphi ^n_e(e) =\ulcorner \sigma \urcorner $
, it follows that
$\varphi ^n_e(e) =\ulcorner \sigma \urcorner $
, it follows that
![]() $\mathcal {K} \models \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
, as desired.
$\mathcal {K} \models \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
, as desired.
Corollary 4.30. Let
![]() $\mathrm {S}$
be a
$\mathrm {S}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent extension of
$\Pi _n$
-complete, and consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
, and let
$\mathrm {I}\Sigma _{n+1}$
, and let
![]() $\unicode{x3b3} (x)$
be as in the proof of Theorem 4.29. Then, for each
$\unicode{x3b3} (x)$
be as in the proof of Theorem 4.29. Then, for each
![]() $\sigma (x) \in \Sigma _{m+1}$
with
$\sigma (x) \in \Sigma _{m+1}$
with
![]() $m\geq n$
,
$m\geq n$
,
![]() $\mathrm {S} + \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
is
$\mathrm {S} + \forall x (\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
is
![]() $\Pi _{n+1}$
-conservative over
$\Pi _{n+1}$
-conservative over
![]() $\mathrm {S} + \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}$
.
$\mathrm {S} + \mathrm {Con}_{\mathrm {S},\Sigma _{n+1}}$
.
The next theorem has a different flavor than the earlier ones, and is a generalization of Woodin’s theorem on the universal algorithm [Reference Woodin, Heller and Woodin48]; see also [Reference Blanck and Enayat4, theorem 3.1]. A version for r.e. extensions of
![]() $\mathrm {PA}$
is independently due to Hamkins [Reference Hamkins18, theorem 18], and the proof presented here uses a method that I learned from Shavrukov. The particular Solovay-style construction used in the proof is similar to the ones used by Berarducci [Reference Berarducci2] and Japaridze [Reference Japaridze21].
$\mathrm {PA}$
is independently due to Hamkins [Reference Hamkins18, theorem 18], and the proof presented here uses a method that I learned from Shavrukov. The particular Solovay-style construction used in the proof is similar to the ones used by Berarducci [Reference Berarducci2] and Japaridze [Reference Japaridze21].
Theorem 4.31. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent extension of
$\Pi _n$
-complete, and consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
. There is a
$\mathrm {I}\Sigma _{n+1}$
. There is a
![]() $\Sigma _{n+1}$
-definable set
$\Sigma _{n+1}$
-definable set
![]() $W_e$
such that:
$W_e$
such that:
-
1.
 $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \text {``}W_e\text { is finite''}$
;
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \text {``}W_e\text { is finite''}$
; -
2.
 $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow W_e = \emptyset $
;
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow W_e = \emptyset $
; -
3. for each countable model
 $\mathcal {M} \models \mathrm {T}$
, if s is an
$\mathcal {M} \models \mathrm {T}$
, if s is an
 $\mathcal {M}$
-finite set such that
$\mathcal {M}$
-finite set such that
 $\mathcal {M} \models W_e \subseteq s$
, then there is a
$\mathcal {M} \models W_e \subseteq s$
, then there is a
 $\Sigma _n$
-elementary extension of
$\Sigma _n$
-elementary extension of
 $\mathcal {M}$
satisfying
$\mathcal {M}$
satisfying
 $\mathrm {T} + W_e = s$
.
$\mathrm {T} + W_e = s$
.
Proof. The set
![]() $W_e$
is defined (in
$W_e$
is defined (in
![]() $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
and in the real world) as follows, using the formalization of the recursion theorem (Fact 3.10). At the same time, an auxiliary function
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
and in the real world) as follows, using the formalization of the recursion theorem (Fact 3.10). At the same time, an auxiliary function
![]() $r(x)$
is defined.
$r(x)$
is defined.
Stage
![]() $0$
: Set
$0$
: Set
![]() $W_{e,0} = \emptyset $
, and
$W_{e,0} = \emptyset $
, and
![]() $r(0) = \infty $
.Footnote
9
$r(0) = \infty $
.Footnote
9
Stage
![]() $x+1$
: Suppose
$x+1$
: Suppose
![]() $r(x) = m$
. There are two cases:
$r(x) = m$
. There are two cases:
Case A: s is a finite set such that
![]() $s \supseteq W_{e,x}$
,
$s \supseteq W_{e,x}$
,
![]() $k < m$
, and x witnesses a
$k < m$
, and x witnesses a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\sigma (s)$
such that k is a proof in
$\sigma (s)$
such that k is a proof in
![]() $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
of
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
of
![]() $\forall t (\sigma (t) \rightarrow W_e \neq t)$
. Should there be more than one eligible candidate for either k or s, then choose the least such k, and then the least s corresponding to that k. Then set
$\forall t (\sigma (t) \rightarrow W_e \neq t)$
. Should there be more than one eligible candidate for either k or s, then choose the least such k, and then the least s corresponding to that k. Then set
![]() $W_{e,x+1} = s$
and
$W_{e,x+1} = s$
and
![]() $r(x+1) = k$
.
$r(x+1) = k$
.
Case B: Otherwise, set
![]() $W_{e,x+1} = W_{e,x}$
and
$W_{e,x+1} = W_{e,x}$
and
![]() $r(x+1) = m$
.
$r(x+1) = m$
.
Let
![]() $W_e = \bigcup _x W_{e,x}$
.
$W_e = \bigcup _x W_{e,x}$
.
To prove 1., reason as follows: Since the proof relation for
![]() $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
is
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
is
![]() $\Delta _{n+1}$
in
$\Delta _{n+1}$
in
![]() $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
,
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
,
![]() $W_e$
is r.e. in
$W_e$
is r.e. in
![]() $\emptyset ^{(n)}$
, and therefore
$\emptyset ^{(n)}$
, and therefore
![]() $\Sigma _{n+1}$
by Fact 3.8. Provably in
$\Sigma _{n+1}$
by Fact 3.8. Provably in
![]() $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, we have that
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})$
, we have that
![]() $W_{e,x+1} \supseteq W_{e,x}$
, and
$W_{e,x+1} \supseteq W_{e,x}$
, and
![]() $r(x+1) \leq r(x)$
, so by the
$r(x+1) \leq r(x)$
, so by the
![]() $\Sigma _{n+1}$
-least number principle (which is available thanks to
$\Sigma _{n+1}$
-least number principle (which is available thanks to
![]() $\Sigma _{n+1}$
-induction), there is a limit
$\Sigma _{n+1}$
-induction), there is a limit
![]() $R = \lim _x r(x)$
. For each x with
$R = \lim _x r(x)$
. For each x with
![]() $W_{e,x+1} \neq W_{e,x}$
,
$W_{e,x+1} \neq W_{e,x}$
,
![]() $\mathrm {I}\Sigma _{n+1}+ \mathrm {Th}_{\Pi _n}(\mathbb {N})$
proves
$\mathrm {I}\Sigma _{n+1}+ \mathrm {Th}_{\Pi _n}(\mathbb {N})$
proves
![]() $r(x+1) < r(x)$
, whence there can only be finitely many such x. So
$r(x+1) < r(x)$
, whence there can only be finitely many such x. So
![]() $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})\vdash \text {``}W_e \text { is finite.''}$
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N})\vdash \text {``}W_e \text { is finite.''}$
Note also that
![]() $\mathrm {T} \vdash R> k$
for all
$\mathrm {T} \vdash R> k$
for all
![]() $k \in \omega $
. To show this, fix
$k \in \omega $
. To show this, fix
![]() $k \in \omega $
and argue in
$k \in \omega $
and argue in
![]() $\mathrm {T}$
:
$\mathrm {T}$
:
Suppose
![]() $R \leq k$
. Let y be minimal such that
$R \leq k$
. Let y be minimal such that
![]() $r(y+1) = R$
. Then
$r(y+1) = R$
. Then
![]() $W_e = W_{e,y+1} = s$
for some s such that R is a proof in
$W_e = W_{e,y+1} = s$
for some s such that R is a proof in
![]() $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
of
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
of
![]() $\forall t (\sigma (t) \rightarrow W_e \neq t)$
, where
$\forall t (\sigma (t) \rightarrow W_e \neq t)$
, where
![]() $\sigma (s)$
is a true
$\sigma (s)$
is a true
![]() $\Sigma _{n+1}$
formula.
$\Sigma _{n+1}$
formula.
But, by Fact 3.15,
since
![]() $\forall t (\sigma (t) \rightarrow W_e \neq t)$
is proved from a true
$\forall t (\sigma (t) \rightarrow W_e \neq t)$
is proved from a true
![]() $\Sigma _{n+1}$
sentence with a proof not exceeding k, it must be true. Since
$\Sigma _{n+1}$
sentence with a proof not exceeding k, it must be true. Since
![]() $\sigma (s)$
is true,
$\sigma (s)$
is true,
![]() $W_e \neq s$
is also true, and the contradiction proves
$W_e \neq s$
is also true, and the contradiction proves
![]() $R> k$
.
$R> k$
.
To prove 2., argue for the contrapositive statement in
![]() $\mathrm {I}\Sigma _{n+1} +\mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
:
$\mathrm {I}\Sigma _{n+1} +\mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
:
If
![]() $W_e = s \neq \emptyset $
, then
$W_e = s \neq \emptyset $
, then
 $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^m(\ulcorner \forall t (\sigma (t) \rightarrow W_e \neq t)\urcorner )$
for some m and some true
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^m(\ulcorner \forall t (\sigma (t) \rightarrow W_e \neq t)\urcorner )$
for some m and some true
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\sigma (s)$
. The relation
$\sigma (s)$
. The relation
![]() $s \subseteq W_{e,x}$
is
$s \subseteq W_{e,x}$
is
![]() $\Delta _{n+1}$
by Fact 3.6(3), so
$\Delta _{n+1}$
by Fact 3.6(3), so
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \dot {s} \subseteq W_e \urcorner )$
follows by Fact 3.13. Now reason inside
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \dot {s} \subseteq W_e \urcorner )$
follows by Fact 3.13. Now reason inside
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}$
:
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}$
:
There is some
![]() $u = W_e$
with
$u = W_e$
with
![]() $u \supseteq s$
, so by construction,
$u \supseteq s$
, so by construction,
![]() $\sigma '(u)$
is true, and
$\sigma '(u)$
is true, and
 $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^k(\ulcorner \forall t (\sigma '(t) \rightarrow W_e \neq t)\urcorner )$
for some
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}^k(\ulcorner \forall t (\sigma '(t) \rightarrow W_e \neq t)\urcorner )$
for some
![]() $k\leq m$
and some
$k\leq m$
and some
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\sigma '(u)$
.
$\sigma '(u)$
.
Apply Fact 3.16, and continue reasoning inside
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}$
:
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}$
:
Then
![]() $\forall t (\sigma '(t) \rightarrow W_e \neq t)$
and
$\forall t (\sigma '(t) \rightarrow W_e \neq t)$
and
![]() $\sigma '(u)$
, so
$\sigma '(u)$
, so
![]() $W_e \neq u$
.
$W_e \neq u$
.
Then
![]() $\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \exists u(W_e = u \land W_e \neq u)\urcorner )$
, so Fact 3.14 gives
$\mathrm {Pr}_{\mathrm {T},\Sigma _{n+1}}(\ulcorner \exists u(W_e = u \land W_e \neq u)\urcorner )$
, so Fact 3.14 gives
![]() $\lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
as desired.
$\lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
as desired.
To prove 3., first fix
![]() $m \in \omega $
. By Fact 3.15, there is a proof k in
$m \in \omega $
. By Fact 3.15, there is a proof k in
![]() $\mathrm {T}$
of
$\mathrm {T}$
of
 $$ \begin{align*} \forall t (\mathrm{Pr}^m_{\mathrm{T}, \Sigma_{n+1}}(\ulcorner W_e \neq \dot{t} \urcorner) \rightarrow W_e \neq t)\text{.} \end{align*} $$
$$ \begin{align*} \forall t (\mathrm{Pr}^m_{\mathrm{T}, \Sigma_{n+1}}(\ulcorner W_e \neq \dot{t} \urcorner) \rightarrow W_e \neq t)\text{.} \end{align*} $$
Now reason in
![]() $\mathrm {T}$
:
$\mathrm {T}$
:
Consider any finite
![]() $s \supseteq W_e$
, and suppose x is a proof
$s \supseteq W_e$
, and suppose x is a proof
![]() $\leq m$
of
$\leq m$
of
![]() $W_e \neq s$
in
$W_e \neq s$
in
![]() $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
. Then
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathbb {N})$
. Then
![]() $s \supseteq W_{e,x+1}$
, and therefore
$s \supseteq W_{e,x+1}$
, and therefore
![]() $r(x+1) \leq k$
by construction of
$r(x+1) \leq k$
by construction of
![]() $r(x+1)$
: here
$r(x+1)$
: here
 $\mathrm {Pr}^m_{\mathrm {T}, \Sigma _{n+1}}(\ulcorner W_e \neq \dot {s} \urcorner )$
is
$\mathrm {Pr}^m_{\mathrm {T}, \Sigma _{n+1}}(\ulcorner W_e \neq \dot {s} \urcorner )$
is
![]() $\mathrm {I}\Sigma _{n+1}$
-equivalent to a true
$\mathrm {I}\Sigma _{n+1}$
-equivalent to a true
![]() $\Sigma _{n+1}$
sentence playing the role of
$\Sigma _{n+1}$
sentence playing the role of
![]() $\sigma (s)$
. But
$\sigma (s)$
. But
![]() $k < R \leq r(x+1)$
, and the contradiction proves
$k < R \leq r(x+1)$
, and the contradiction proves
 $\mathrm {Con}^m_{\mathrm {T} + W_e = \dot {s}, \Sigma _{n+1}}$
.
$\mathrm {Con}^m_{\mathrm {T} + W_e = \dot {s}, \Sigma _{n+1}}$
.
Therefore for all
![]() $m\in \omega $
,
$m\in \omega $
,
 $\mathrm {T} \vdash \forall s \supseteq W_e \,\, \mathrm {Con}^m_{\mathrm {T} + W_e=\dot {s}, \Sigma _{n+1}}$
.
$\mathrm {T} \vdash \forall s \supseteq W_e \,\, \mathrm {Con}^m_{\mathrm {T} + W_e=\dot {s}, \Sigma _{n+1}}$
.
For the final part of the proof, let
![]() $\mathcal {M}$
be any countable model of
$\mathcal {M}$
be any countable model of
![]() $\mathrm {T}$
, and let s be any
$\mathrm {T}$
, and let s be any
![]() $\mathcal {M}$
-finite set such that
$\mathcal {M}$
-finite set such that
![]() $\mathcal {M} \models W_e \subseteq s$
. Since
$\mathcal {M} \models W_e \subseteq s$
. Since
![]() $\mathrm {T}$
is a
$\mathrm {T}$
is a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _{n}$
-complete extension of
$\Pi _{n}$
-complete extension of
![]() $\mathrm {I}\Sigma _{n+1}$
, Facts 3.11 and 3.20 imply that
$\mathrm {I}\Sigma _{n+1}$
, Facts 3.11 and 3.20 imply that
![]() $\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) + W_e = s \in \mathrm {SSy}(\mathcal {M})$
. Since
$\mathrm {T} + \mathrm {Th}_{\Sigma _{n+1}}(\mathcal {M}) + W_e = s \in \mathrm {SSy}(\mathcal {M})$
. Since
 $\mathrm {T} \vdash \mathrm {Con}^m_{\mathrm {T} + W_e = \dot {s}, \Sigma _{n+1}}$
for all
$\mathrm {T} \vdash \mathrm {Con}^m_{\mathrm {T} + W_e = \dot {s}, \Sigma _{n+1}}$
for all
![]() $m\in \omega $
, Fact 3.23 guarantees the existence of a
$m\in \omega $
, Fact 3.23 guarantees the existence of a
![]() $\Sigma _n$
-elementary extension of
$\Sigma _n$
-elementary extension of
![]() $\mathcal {M}$
satisfying
$\mathcal {M}$
satisfying
![]() $\mathrm {T} + W_e = s$
, which concludes the proof of the theorem.
$\mathrm {T} + W_e = s$
, which concludes the proof of the theorem.
Corollary 4.32. With
![]() $\mathrm {T}$
as in Theorem 4.31,
$\mathrm {T}$
as in Theorem 4.31,
![]() $\lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
is
$\lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
is
![]() $\Pi _{n+1}$
-conservative over
$\Pi _{n+1}$
-conservative over
![]() $\mathrm {T}$
.
$\mathrm {T}$
.
Proof. Every countable model of
![]() $\mathrm {T}$
has a
$\mathrm {T}$
has a
![]() $\Sigma _n$
-elementary extension satisfying
$\Sigma _n$
-elementary extension satisfying
![]() $W_e \neq \emptyset $
, and therefore also
$W_e \neq \emptyset $
, and therefore also
![]() $\mathrm {T} + \lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
by the theorem. By Fact 3.23, the conclusion follows.Footnote
10
$\mathrm {T} + \lnot \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
by the theorem. By Fact 3.23, the conclusion follows.Footnote
10
The set
![]() $W_e$
defined in Theorem 4.31 can be used to prove results of a more Kripkean variety, by using the information contained in
$W_e$
defined in Theorem 4.31 can be used to prove results of a more Kripkean variety, by using the information contained in
![]() $W_e$
as codes for other sets. The next result is of this kind, and improves on Theorem 7.21 of [Reference Blanck3] by generalizing to arithmetically definable theories. A version for r.e. extensions of
$W_e$
as codes for other sets. The next result is of this kind, and improves on Theorem 7.21 of [Reference Blanck3] by generalizing to arithmetically definable theories. A version for r.e. extensions of
![]() $\mathrm {PA}$
is independently due to Hamkins [Reference Hamkins18, theorem 22(1)], who also noted that there is a very short proof of it from Theorem 4.31.
$\mathrm {PA}$
is independently due to Hamkins [Reference Hamkins18, theorem 22(1)], who also noted that there is a very short proof of it from Theorem 4.31.
Theorem 4.33. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent extension of
$\Pi _n$
-complete, and consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
. For all
$\mathrm {I}\Sigma _{n+1}$
. For all
![]() $m \geq n$
, there is a
$m \geq n$
, there is a
![]() $\Sigma _{m+2}$
formula
$\Sigma _{m+2}$
formula
![]() $\unicode{x3b3} (x)$
such that:
$\unicode{x3b3} (x)$
such that:
-
1.
 $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
;
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
; -
2. for every
 $\sigma (x) \in \Sigma _{m+2}$
, every countable model of
$\sigma (x) \in \Sigma _{m+2}$
, every countable model of
 $\mathrm {T}$
has a
$\mathrm {T}$
has a
 $\Sigma _n$
-elementary extension satisfying
$\Sigma _n$
-elementary extension satisfying
 $\mathrm {T} + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
.
$\mathrm {T} + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
.
Proof sketch. It is straightforward to adapt the construction in the proof of Theorem 4.31 to produce an
![]() $\mathcal {M}$
-finite binary sequence
$\mathcal {M}$
-finite binary sequence
![]() $S_e$
, rather than a set [Reference Blanck and Enayat4, Reference Hamkins18, Reference Woodin, Heller and Woodin48]. Assume an enumeration of
$S_e$
, rather than a set [Reference Blanck and Enayat4, Reference Hamkins18, Reference Woodin, Heller and Woodin48]. Assume an enumeration of
![]() $\Sigma _{m+2}$
formulae in which every
$\Sigma _{m+2}$
formulae in which every
![]() $\Sigma _{m+2}$
formula occurs infinitely often, and that every finite binary sequence codes such a formula. Let
$\Sigma _{m+2}$
formula occurs infinitely often, and that every finite binary sequence codes such a formula. Let
![]() $\unicode{x3b3} (x)$
be the formula
$\unicode{x3b3} (x)$
be the formula
![]() $\exists z (S_e = z \land \mathrm {Sat}_{\Sigma _{m+2}}(z,x))$
. Since
$\exists z (S_e = z \land \mathrm {Sat}_{\Sigma _{m+2}}(z,x))$
. Since
![]() $S_e = z$
is at most
$S_e = z$
is at most
![]() $\Sigma _{n+2}$
and
$\Sigma _{n+2}$
and
![]() $m \geq n$
, it follows that
$m \geq n$
, it follows that
![]() $\unicode{x3b3} (x)$
is
$\unicode{x3b3} (x)$
is
![]() $\Sigma _{m+2}$
.
$\Sigma _{m+2}$
.
Pick any
![]() $\sigma (x) \in \Sigma _{m+2}$
, let
$\sigma (x) \in \Sigma _{m+2}$
, let
![]() $\mathcal {M}$
be any countable model of
$\mathcal {M}$
be any countable model of
![]() $\mathrm {T}$
and let s be
$\mathrm {T}$
and let s be
![]() $S_e$
as calculated within
$S_e$
as calculated within
![]() $\mathcal {M}$
. By assumption on the enumeration of
$\mathcal {M}$
. By assumption on the enumeration of
![]() $\Sigma _{m+2}$
formulae, there is an
$\Sigma _{m+2}$
formulae, there is an
![]() $\mathcal {M}$
-finite sequence
$\mathcal {M}$
-finite sequence
![]() $t \supseteq s$
such that t codes
$t \supseteq s$
such that t codes
![]() $\ulcorner \sigma (x) \urcorner $
. By the sequence version of Theorem 4.31, there is a
$\ulcorner \sigma (x) \urcorner $
. By the sequence version of Theorem 4.31, there is a
![]() $\Sigma _n$
-elementary extension
$\Sigma _n$
-elementary extension
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathcal {M}$
in which
$\mathcal {M}$
in which
![]() $S_e =t$
. Then
$S_e =t$
. Then
![]() $\unicode{x3b3} (x)$
coincides with
$\unicode{x3b3} (x)$
coincides with
![]() $\sigma (x)$
in
$\sigma (x)$
in
![]() $\mathcal {K}$
, and therefore is as desired.
$\mathcal {K}$
, and therefore is as desired.
The question remains to which extent
![]() $m+2$
can be replaced by
$m+2$
can be replaced by
![]() $m+1$
in the statement of Theorem 4.33. Some partial answers are already available: Theorem 4.31 gives a positive answer restricted to
$m+1$
in the statement of Theorem 4.33. Some partial answers are already available: Theorem 4.31 gives a positive answer restricted to
![]() $\Sigma _{m+1}$
formulae
$\Sigma _{m+1}$
formulae
![]() $\sigma (x)$
whose extension is
$\sigma (x)$
whose extension is
![]() $\mathcal {M}$
-finite and for which
$\mathcal {M}$
-finite and for which
![]() $\mathcal {M} \models \forall x (\unicode{x3b3} (x) \rightarrow \sigma (x))$
, while Theorem 4.29 can be seen as giving a partial positive answer that is restricted to models of
$\mathcal {M} \models \forall x (\unicode{x3b3} (x) \rightarrow \sigma (x))$
, while Theorem 4.29 can be seen as giving a partial positive answer that is restricted to models of
![]() $\mathrm {T} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
. Blanck [Reference Blanck3, chap. 7.4] lists several other partial answers to this question in a setting where
$\mathrm {T} + \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}}$
. Blanck [Reference Blanck3, chap. 7.4] lists several other partial answers to this question in a setting where
![]() $\mathrm {T}$
is an r.e. extension of
$\mathrm {T}$
is an r.e. extension of
![]() $\mathrm {PA}$
and
$\mathrm {PA}$
and
![]() $n=0$
. By using the principles of Section 3 of the present paper, those constructions can be easily modified to give equally unsatisfactory answers in the present setting. The salient remaining question is as follows:
$n=0$
. By using the principles of Section 3 of the present paper, those constructions can be easily modified to give equally unsatisfactory answers in the present setting. The salient remaining question is as follows:
Question. Let
![]() $\mathrm {T}$
be a
$\mathrm {T}$
be a
![]() $\Sigma _{n+1}$
-definable,
$\Sigma _{n+1}$
-definable,
![]() $\Pi _n$
-complete, and consistent extension of
$\Pi _n$
-complete, and consistent extension of
![]() $\mathrm {I}\Sigma _{n+1}$
. Is there a
$\mathrm {I}\Sigma _{n+1}$
. Is there a
![]() $\Sigma _{n+1}$
formula
$\Sigma _{n+1}$
formula
![]() $\unicode{x3b3} (x)$
such that:
$\unicode{x3b3} (x)$
such that:
-
1.
 $\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
;
$\mathrm {I}\Sigma _{n+1} + \mathrm {Th}_{\Pi _n}(\mathbb {N}) \vdash \mathrm {Con}_{\mathrm {T},\Sigma _{n+1}} \rightarrow \forall x \lnot \unicode{x3b3} (x)$
; -
2. for every
 $\sigma (x) \in \Sigma _{n+1}$
, every countable model of
$\sigma (x) \in \Sigma _{n+1}$
, every countable model of
 $\mathrm {T} + \forall x(\unicode{x3b3} (x) \rightarrow \sigma (x))$
has a
$\mathrm {T} + \forall x(\unicode{x3b3} (x) \rightarrow \sigma (x))$
has a
 $\Sigma _n$
-elementary extension satisfying
$\Sigma _n$
-elementary extension satisfying
 $\mathrm {T} + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
?
$\mathrm {T} + \forall x(\unicode{x3b3} (x) \leftrightarrow \sigma (x))$
?
5 Discussion
By inspecting the results proved in Section 4, we see two classes of
![]() $\Sigma _{n+1}$
-definable theories emerging:
$\Sigma _{n+1}$
-definable theories emerging:
-
1.
 $\Sigma _n$
-sound extensions of
$\Sigma _n$
-sound extensions of
 $\mathrm {I}\Sigma _n + \mathrm {exp}$
; and
$\mathrm {I}\Sigma _n + \mathrm {exp}$
; and -
2.
 $\Pi _n$
-complete, consistent extensions of
$\Pi _n$
-complete, consistent extensions of
 $\mathrm {I}\Sigma _{n+1}$
.
$\mathrm {I}\Sigma _{n+1}$
.
As suggested by Theorem 1.1, theories in the first class are strong enough for some applications. These include the results of Salehi & Seraji [Reference Salehi and Seraji40] and Kikuchi & Kurahashi [Reference Kikuchi and Kurahashi23], together with Theorems 4.25 and 4.27 (and their corollaries) of the present paper. This success relies on the fact that
![]() $\Sigma _n$
-soundness of
$\Sigma _n$
-soundness of
![]() $\mathrm {T}$
guarantees the consistency of
$\mathrm {T}$
guarantees the consistency of
![]() $\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
, in which the n-recursive functions can be strongly represented by a formula that is
$\mathrm {T} + \mathrm {Th}_{\Pi _{n}}(\mathbb {N})$
, in which the n-recursive functions can be strongly represented by a formula that is
![]() $\Sigma _{n+1}$
in the presence of
$\Sigma _{n+1}$
in the presence of
![]() $\Sigma _n$
-induction.
$\Sigma _n$
-induction.
The second class of theories is required to prove results on
![]() $\Sigma _n$
-elementary extensions of models of
$\Sigma _n$
-elementary extensions of models of
![]() $\Sigma _{n+1}$
-definable theories, for example results on partial conservativity via the OHGL characterization (Theorem 4.29 and onward). In these cases,
$\Sigma _{n+1}$
-definable theories, for example results on partial conservativity via the OHGL characterization (Theorem 4.29 and onward). In these cases,
![]() $\Pi _n$
-completeness of
$\Pi _n$
-completeness of
![]() $\mathrm {T}$
ensures that every model
$\mathrm {T}$
ensures that every model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathrm {T}$
is a
$\mathrm {T}$
is a
![]() $\Sigma _n$
-elementary extension of the standard model, which in the presence of
$\Sigma _n$
-elementary extension of the standard model, which in the presence of
![]() $\Sigma _{n+1}$
-induction suffices for
$\Sigma _{n+1}$
-induction suffices for
![]() $\mathrm {T}$
to be
$\mathrm {T}$
to be
![]() $\Sigma _{n+1}$
-definable in
$\Sigma _{n+1}$
-definable in
![]() $\mathcal {M}$
by using Craig’s trick.
$\mathcal {M}$
by using Craig’s trick.
![]() $\Sigma _{n+1}$
-induction is also used to prove the arithmetized completeness theorem for
$\Sigma _{n+1}$
-induction is also used to prove the arithmetized completeness theorem for
![]() $\Sigma _{n+1}$
-definable theories, which is indispensable for constructing the
$\Sigma _{n+1}$
-definable theories, which is indispensable for constructing the
![]() $\Sigma _n$
-elementary extensions.
$\Sigma _n$
-elementary extensions.
The facts listed in Section 3 should be enough to derive hierarchical generalizations for arithmetically definable extensions of fragments of
![]() $\mathrm {PA}$
of many of the theorems in, e.g., Lindström’s classic Aspects of Incompleteness [Reference Lindström29]. As suggested by the results in the present paper, some of these generalizations would apply only to
$\mathrm {PA}$
of many of the theorems in, e.g., Lindström’s classic Aspects of Incompleteness [Reference Lindström29]. As suggested by the results in the present paper, some of these generalizations would apply only to
![]() $\Pi _n$
-complete theories, while in other cases mere
$\Pi _n$
-complete theories, while in other cases mere
![]() $\Sigma _n$
-soundness would do. Others might not be prone to such generalizations at all, as shown by Kurahashi [Reference Kurahashi27, theorem 11] and pointed out to me by one of the referees. In fact, it would be interesting to see which of the results in, say, the first five chapters of Aspects (where the results do not depend on
$\Sigma _n$
-soundness would do. Others might not be prone to such generalizations at all, as shown by Kurahashi [Reference Kurahashi27, theorem 11] and pointed out to me by one of the referees. In fact, it would be interesting to see which of the results in, say, the first five chapters of Aspects (where the results do not depend on
![]() $\mathrm {T}$
being essentially reflexive) that are prone to such generalizations, using these principles.
$\mathrm {T}$
being essentially reflexive) that are prone to such generalizations, using these principles.
Acknowledgments
This paper is based in part on some ideas that were left half-baked in the author’s doctoral thesis [Reference Blanck3], written under the supervision of Ali Enayat. In particular, not entirely correct claims similar to Corollary 4.28 and Theorem 4.29 have appeared there. I am grateful to Ali Enayat, Fredrik Engström, Joel David Hamkins, Aleksandre Maskharashvili, and Volodya Shavrukov for inspiration, discussion, and guidance. The comments of two excellent anonymous referees have greatly helped improve the paper by suggesting the correct statements of some of the theorems, and by weeding out a number of false claims in an earlier version of this paper.