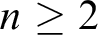1 Introduction
Frege [Reference Frege10–Reference Frege12] sought to derive the theorems of arithmetic from nothing but basic logical laws and definitions. Such a derivation, called a logicist derivation of arithmetic, would provide the ultimate foundation for our arithmetical knowledge. It would justify the theorems of arithmetic once and for all by deriving them from principles that needed no justification—principles that were either self-evident (‘basic logical laws’) or true simply by stipulation (‘definitions’).
By his own lights, Frege did not manage to give a logicist derivation of arithmetic. But he did show how to derive a very powerful system of arithmetic from a single, natural principle, known as Hume’s Principle (HP).Footnote 1 Informally, HP says, ‘The number of Fs is equal to the number of Gs iff there is a one–one correspondence between the Fs and the Gs.’ In second-order logic, HP is expressible as the universal closure of
where
![]() $\#$
is an operator that combines with monadic second-order variables
$\#$
is an operator that combines with monadic second-order variables
![]() $F,G$
to form terms of object type, and
$F,G$
to form terms of object type, and
![]() $ F \approx _R G$
abbreviates the statement that R is a one–one correspondence between the Fs and the Gs.Footnote
2
Then we have the following beautiful result:
$ F \approx _R G$
abbreviates the statement that R is a one–one correspondence between the Fs and the Gs.Footnote
2
Then we have the following beautiful result:
Theorem 1.1 (Frege’s Theorem)
The theorems of second-order arithmetic are derivable in second-order logic from HP together with eliminative definitions of natural number, zero, and successor.Footnote 3
Neo-Fregean logicists, preeminently Hale and Wright [Reference Hale and Wright14], argue that Frege’s Theorem already yields a logicist derivation of arithmetic. They claim that HP may be taken as an implicit definition of the operator
![]() $\#$
(‘the number of’) in purely logical terms.Footnote
4
Hale and Wright’s notion of implicit definition is deeply controversial. For our purposes, the main point is that Hale and Wright conceive of implicit definitions as true simply by stipulation [Reference Hale and Wright14, p. 117]. Such definitions need no justification. They are true by fiat. So, if Hale and Wright are correct, Frege’s Theorem does indeed yield a logicist derivation of arithmetic.
$\#$
(‘the number of’) in purely logical terms.Footnote
4
Hale and Wright’s notion of implicit definition is deeply controversial. For our purposes, the main point is that Hale and Wright conceive of implicit definitions as true simply by stipulation [Reference Hale and Wright14, p. 117]. Such definitions need no justification. They are true by fiat. So, if Hale and Wright are correct, Frege’s Theorem does indeed yield a logicist derivation of arithmetic.
Not just anything can be stipulated to be true. We cannot establish any new ‘substantive’ truths by fiat. No one could have established by fiat that the Morning Star is the Evening Star. Accordingly, it is natural to think that any legitimate stipulative definition must meet the following requirement, known as conservativeness:
Definition 1.2. Let T be a theory in a formal language L. Let
![]() $\Delta $
be a definition of one new sign, and let
$\Delta $
be a definition of one new sign, and let
![]() $L^+$
be the language obtained by adding that new sign to L. Assume that deductive systems for L and
$L^+$
be the language obtained by adding that new sign to L. Assume that deductive systems for L and
![]() $L^+$
have been specified. Then
$L^+$
have been specified. Then
![]() $\Delta $
is conservative over T iff any L-formula that is derivable
$\Delta $
is conservative over T iff any L-formula that is derivable
![]() $_{L^+}$
from
$_{L^+}$
from
![]() $T + \Delta $
is already derivable
$T + \Delta $
is already derivable
![]() $_{L}$
from T.
$_{L}$
from T.
Intuitively, a definition is conservative over our theory T just in case adding it to our theory does not yield any new theorems expressible entirely in old vocabulary. The definition does not settle any open questions that we already knew how to ask.
But HP is not conservative. More precisely, HP is not conservative over pure axiomatic second-order logic—which presumably ought to be the starting theory for aspiring logicists.Footnote 5 For HP proves a sentence DI in the language of pure second-order logic which says that the universe is Dedekind-infinite (‘there is a one–one mapping from the universe into itself that is not onto’). But DI is not a theorem of pure second-order logic. So, it seems that HP cannot be a legitimate stipulative definition. Call this the conservativeness problem for neo-Fregean logicism.
The conservativeness problem is robust. Definitions that are conservative over pure second-order logic seem to be mathematically very weak, and hence unable to provide a foundation for arithmetic. Furthermore, adding more basic logical laws won’t help unless those laws suffice to prove DI. But it seems like a tall order to prove the existence of infinitely many objects from basic logical laws alone.
Hale and Wright respond to the conservativeness problem by denying that stipulative definitions must be conservative in the sense of Definition 1.2. Roughly speaking, they hold that stipulative definitions need only satisfy a modified conservativeness requirement, known as Field-conservativeness.Footnote 6 We set out to explore a different approach. Is it possible to find a variant of HP that is conservative in the standard deductive sense—the sense of Definition 1.2?
A promising direction is suggested by Heck’s work on the Julius Caesar problem [Reference Heck15, Reference Heck16]. Heck reconstrues Hume’s Principle as introducing a new sort of singular term into the language. Call the reconstrued principle two-sorted Hume’s Principle (2HP), and the theory that results from supplementing 2HP with logical axioms for the expanded language, two-sorted Frege Arithmetic (2FA). The theory 2FA interprets second-order arithmetic in the numerical sort. In particular, 2FA proves that the numerical universe is Dedekind-infinite. But there is no obvious witness to non-conservativeness, because the numerical sort is not part of the base language. Indeed, it has been claimed that 2FA is conservative over pure second-order logic [Reference Burgess3, p. 237, n. 7].
In this paper we prove that 2FA is not conservative over pure second-order logic. In fact, we prove something stronger. Our strategy is based on the following little fact:
Lemma 1.3. Let T be a theory in a formal language L, and let A be any L-sentence. Suppose that a sentence
![]() $\Delta $
is not conservative over
$\Delta $
is not conservative over
![]() $T + A$
. Then
$T + A$
. Then
![]() $\Delta $
is not conservative over T.
$\Delta $
is not conservative over T.
Proof. Let
![]() $\varphi $
be an L-sentence such that
$\varphi $
be an L-sentence such that
![]() $T + A + \Delta \vdash \varphi $
, but
$T + A + \Delta \vdash \varphi $
, but
![]() $T + A \not \vdash \varphi $
. By the Deduction Theorem, we have
$T + A \not \vdash \varphi $
. By the Deduction Theorem, we have
![]() $T + \Delta \vdash A \rightarrow \varphi $
, but
$T + \Delta \vdash A \rightarrow \varphi $
, but
![]() $T \not \vdash A \rightarrow \varphi $
.
$T \not \vdash A \rightarrow \varphi $
.
In Section 7, we consider a theory w2FA that is much weaker than 2FA. We show that w2FA is non-conservative over pure second-order logic together with an axiom saying that the base universe is infinite.Footnote 7 In other words, even if we already know that there are infinitely many objects, w2FA tells us something new about them! Then from Lemma 1.3, it follows that w2FA, and hence 2FA, is non-conservative over pure second-order logic.
In Section 8, we show that for the weaker theory w2FA, the non-conservativeness vanishes if we strengthen the base theory in either of two natural ways. First, w2FA is conservative over third- or higher-order logic. Second, w2FA is conservative over second-order logic plus ‘the base universe is finite’.
In Section 9, we present a different proof that 2FA is not conservative over pure second-order logic. This proof shows that 2FA remains non-conservative over the stronger base theories discussed in the previous section. Specifically, we show that 2FA is not conservative over second-order logic plus ‘the base universe is finite’, and the proof of this fact generalizes to third- and higher-order logic.
In order to state and prove these results, we will need some preliminaries. In Section 2, we explain the logical setting for the paper: many-sorted axiomatic second-order logic. In Section 3, we explain how to construe Hume’s Principle in a many-sorted setting, and we define the theories w2FA and 2FA. In Section 4, we present some background material on first- and second-order arithmetic. In Section 5, we show how to formalize some facts about well-orderings and finiteness in second-order logic. In Section 6, we discuss the Fraenkel model, which is the minimal infinite model of pure second-order logic.
In Sections 7–9, we prove the main results. Lastly, in Section 10, we connect our work to the literature on Field-conservativeness and related notions. Our main result implies that in a one-sorted setting, HP is neither deductively Field-conservative nor deductively Caesar-neutral conservative over second- or higher-order logic. This answers some open problems raised by Shapiro and Weir [Reference Shapiro and Weir27, p. 298], Fine [Reference Fine9, p. 192, n. 1], and Studd [Reference Studd30, p. 597]. We conclude by mentioning some open problems of our own.
2 Many-sorted second-order logic
We work in axiomatic second-order logic with many sorts of singular terms and first-order variables. In this section we explain the logical framework in considerable generality.
In Section 2.1, we define ‘sort’. In Sections 2.2 and 2.3, we define second-order languages
![]() $\mathcal {L}_J[K]$
for any nonempty set of object sorts J and any set of constant symbols K. We present deductive systems and general semantics for these languages. In Section 2.4, we define the two many-sorted second-order languages that will be central to the rest of the paper, called the base language
$\mathcal {L}_J[K]$
for any nonempty set of object sorts J and any set of constant symbols K. We present deductive systems and general semantics for these languages. In Section 2.4, we define the two many-sorted second-order languages that will be central to the rest of the paper, called the base language
![]() $\mathcal {L} := \mathcal {L}_{\{0\}}[\varnothing ]$
and the expanded language
$\mathcal {L} := \mathcal {L}_{\{0\}}[\varnothing ]$
and the expanded language
![]() $\mathcal {L}^+ := \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n \}]$
.
$\mathcal {L}^+ := \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n \}]$
.
2.1 Sorts
Let J be any nonempty set of symbols. These symbols are called first-order sorts or object sorts.
Let
![]() $\mathit {Sorts}^2(J)$
be the set of all tuples
$\mathit {Sorts}^2(J)$
be the set of all tuples
![]() $\langle j_1, \dots , j_n \rangle $
with
$\langle j_1, \dots , j_n \rangle $
with
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $j_1, \dots , j_n \in J$
. These tuples are second-order relation sorts formed from J.
$j_1, \dots , j_n \in J$
. These tuples are second-order relation sorts formed from J.
Let
![]() $\mathit {Sorts}^3(J)$
be the set of all tuples
$\mathit {Sorts}^3(J)$
be the set of all tuples
![]() $\langle \tau _1, \dots , \tau _n \rangle $
with
$\langle \tau _1, \dots , \tau _n \rangle $
with
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\tau _1, \dots , \tau _n \in J \cup \mathit {Sorts}^2(J)$
, and with at least one of
$\tau _1, \dots , \tau _n \in J \cup \mathit {Sorts}^2(J)$
, and with at least one of
![]() $\tau _1, \dots , \tau _n$
belonging to
$\tau _1, \dots , \tau _n$
belonging to
![]() $\mathit {Sorts}^2(J)$
. These tuples are third-order relation sorts formed from J.
$\mathit {Sorts}^2(J)$
. These tuples are third-order relation sorts formed from J.
Let
![]() $\mathit {FnSorts}(J)$
be the set of all tuples
$\mathit {FnSorts}(J)$
be the set of all tuples
![]() $\langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle $
with
$\langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle $
with
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\tau _1, \ldots , \tau _n, \tau _{n+1} \in J \cup \mathit {Sorts}^2(J)$
. These tuples are function sorts formed from J.
$\tau _1, \ldots , \tau _n, \tau _{n+1} \in J \cup \mathit {Sorts}^2(J)$
. These tuples are function sorts formed from J.
Let
![]() $\mathit {Sorts}(J) = J \cup \mathit {Sorts}^2(J) \cup \mathit {Sorts}^3(J) \cup \mathit {FnSorts}(J)$
.
$\mathit {Sorts}(J) = J \cup \mathit {Sorts}^2(J) \cup \mathit {Sorts}^3(J) \cup \mathit {FnSorts}(J)$
.
Intuitively,
![]() $\langle \tau _1, \ldots , \tau _n \rangle $
is the sort of n-ary relations with arguments of sorts
$\langle \tau _1, \ldots , \tau _n \rangle $
is the sort of n-ary relations with arguments of sorts
![]() $\tau _1, \ldots , \tau _n$
, while
$\tau _1, \ldots , \tau _n$
, while
![]() $\langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle $
is the sort of n-ary functions with arguments of sorts
$\langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle $
is the sort of n-ary functions with arguments of sorts
![]() $\tau _1, \ldots , \tau _n$
and values of sort
$\tau _1, \ldots , \tau _n$
and values of sort
![]() $\tau _{n+1}$
.
$\tau _{n+1}$
.
Example 2.4. Suppose
![]() $J = \{0, 1\}$
. Then
$J = \{0, 1\}$
. Then
 $\langle 1, 1, 0 \rangle \in \mathit {Sorts}^2(J)$
,
$\langle 1, 1, 0 \rangle \in \mathit {Sorts}^2(J)$
,
 $\langle 0, 1, \langle 0, 1 \rangle \rangle \in \mathit {Sorts}^3(J)$
, and
$\langle 0, 1, \langle 0, 1 \rangle \rangle \in \mathit {Sorts}^3(J)$
, and
![]() $\langle \langle 0 \rangle; 1 \rangle \in \mathit {FnSorts}(J)$
.
$\langle \langle 0 \rangle; 1 \rangle \in \mathit {FnSorts}(J)$
.
In the languages
![]() $\mathcal {L}_J[K]$
, there will be no function variables and no third-order variables. We only allow variables of sorts
$\mathcal {L}_J[K]$
, there will be no function variables and no third-order variables. We only allow variables of sorts
![]() $\tau \in J \cup \mathit {Sorts}^2(J)$
. However, there may be constant symbols of any sort
$\tau \in J \cup \mathit {Sorts}^2(J)$
. However, there may be constant symbols of any sort
![]() $\tau \in \mathit {Sorts}(J)$
.
$\tau \in \mathit {Sorts}(J)$
.
2.2 Languages without constant symbols
For any set of object sorts J, we define the second-order language
![]() $\mathcal {L}_J$
as follows:
$\mathcal {L}_J$
as follows:
-
(i) The alphabet of
 $\mathcal {L}_J$
contains variables
$\mathcal {L}_J$
contains variables
 $x^j, y^j, z^j, \ldots $
for each object sort
$x^j, y^j, z^j, \ldots $
for each object sort
 $j \in J$
, and relation variables
$j \in J$
, and relation variables
 $X^{\tau }, Y^{\tau }, Z^{\tau }, \ldots $
for each second-order sort
$X^{\tau }, Y^{\tau }, Z^{\tau }, \ldots $
for each second-order sort
 $\tau \in \mathit {Sorts}^2(J)$
. There are no nonlogical constant symbols. The logical constants are
$\tau \in \mathit {Sorts}^2(J)$
. There are no nonlogical constant symbols. The logical constants are
 $\neg , \,{\rightarrow}, \forall , =$
.
$\neg , \,{\rightarrow}, \forall , =$
. -
(ii) The terms of sort
 $\tau $
are the variables of sort
$\tau $
are the variables of sort
 $\tau $
, for each
$\tau $
, for each
 $\tau \in J \cup \mathit {Sorts}^2(J)$
.
$\tau \in J \cup \mathit {Sorts}^2(J)$
. -
(iii) In atomic formulas, we require that the sorts match. More precisely, the atomic formulas are strings of the form
 $t_1^j = t_2^j$
and
$t_1^j = t_2^j$
and
 $T^{\langle j_1, \ldots , j_n \rangle } t_1^{j_1}, \dots , t_n^{j_n}$
, where each
$T^{\langle j_1, \ldots , j_n \rangle } t_1^{j_1}, \dots , t_n^{j_n}$
, where each
 $t^j$
is a term of sort
$t^j$
is a term of sort
 $j \in J$
, and
$j \in J$
, and
 $T^{\langle j_1, \ldots , j_n \rangle }$
is a term of sort
$T^{\langle j_1, \ldots , j_n \rangle }$
is a term of sort
 $\langle j_1, \ldots , j_n \rangle $
.
$\langle j_1, \ldots , j_n \rangle $
. -
(iv) If
 $\varphi , \psi $
are formulas and
$\varphi , \psi $
are formulas and
 $x^j, X^\tau $
are variables, then
$x^j, X^\tau $
are variables, then
 $ \neg \varphi $
,
$ \neg \varphi $
,
 $ \varphi \rightarrow \psi $
,
$ \varphi \rightarrow \psi $
,
 $ \forall x^j \varphi $
,
$ \forall x^j \varphi $
,
 $ \forall X^\tau \varphi $
are also formulas.
$ \forall X^\tau \varphi $
are also formulas.
The deductive system for
![]() $\mathcal {L}_J$
is essentially equivalent to Shapiro’s D2 minus the axiom schema of choice [Reference Shapiro26, pp. 66–67]. Compare [Reference Enderton8, pp. 112–113]. Its axioms are all closed universal generalizations of the formulas depicted in Table 1. For legibility, we suppress sorts. But note that x, y, and t must all be of the same sort, and X and T must be of the same sort. This requirement is induced by the formation rules of the language.
$\mathcal {L}_J$
is essentially equivalent to Shapiro’s D2 minus the axiom schema of choice [Reference Shapiro26, pp. 66–67]. Compare [Reference Enderton8, pp. 112–113]. Its axioms are all closed universal generalizations of the formulas depicted in Table 1. For legibility, we suppress sorts. But note that x, y, and t must all be of the same sort, and X and T must be of the same sort. This requirement is induced by the formation rules of the language.
Table 1
Deductive system for
![]() $\mathcal {L}_J$
.
$\mathcal {L}_J$
.

Let
![]() $\varphi , \psi $
be any formulas of
$\varphi , \psi $
be any formulas of
![]() $\mathcal {L}_J$
. Let
$\mathcal {L}_J$
. Let
![]() $x,y, X$
be variables, and
$x,y, X$
be variables, and
![]() $t,T$
be terms. (Note that
$t,T$
be terms. (Note that
![]() $x,y,t$
must all be of the same sort. Likewise, X and T must be of the same sort.) Let
$x,y,t$
must all be of the same sort. Likewise, X and T must be of the same sort.) Let
![]() $\varphi (t)$
be the result of substituting t for all free occurrences of x in
$\varphi (t)$
be the result of substituting t for all free occurrences of x in
![]() $\varphi $
. In (*), let
$\varphi $
. In (*), let
![]() $\alpha $
be any atomic formula of
$\alpha $
be any atomic formula of
![]() $\mathcal {L}_J$
, and let
$\mathcal {L}_J$
, and let
![]() $\alpha '$
be any formula obtained from
$\alpha '$
be any formula obtained from
![]() $\alpha $
by replacing zero or more occurrences of x with y. In Comprehension, we write
$\alpha $
by replacing zero or more occurrences of x with y. In Comprehension, we write
![]() $X \bar x$
to abbreviate
$X \bar x$
to abbreviate
 $X ^{\langle j_1, \ldots , j_n \rangle } x_1^{j_1} \cdots x_n^{j_n}$
.
$X ^{\langle j_1, \ldots , j_n \rangle } x_1^{j_1} \cdots x_n^{j_n}$
.
An
![]() $\mathcal {L}_J$
-prestructure
$\mathcal {L}_J$
-prestructure
![]() $\mathcal {M}$
is a collection of nonempty sets
$\mathcal {M}$
is a collection of nonempty sets
 $\{M_\tau : \tau \in J \cup \mathit {Sorts}^2(J) \}$
such that
$\{M_\tau : \tau \in J \cup \mathit {Sorts}^2(J) \}$
such that
![]() $M_{\langle j_1, \ldots , j_n \rangle } \subseteq \mathcal {P}(M_{j_1} \times \cdots \times M_{j_n})$
for all
$M_{\langle j_1, \ldots , j_n \rangle } \subseteq \mathcal {P}(M_{j_1} \times \cdots \times M_{j_n})$
for all
![]() $j_1, \ldots , j_n \in J$
. Satisfaction and truth in
$j_1, \ldots , j_n \in J$
. Satisfaction and truth in
![]() $\mathcal {M}$
are defined inductively, taking variables of sort
$\mathcal {M}$
are defined inductively, taking variables of sort
![]() $\tau $
to range over domain
$\tau $
to range over domain
![]() $M_\tau $
.
$M_\tau $
.
A general
![]() $\mathcal {L}_J$
-structure is an
$\mathcal {L}_J$
-structure is an
![]() $\mathcal {L}_J$
-prestructure in which the second-order comprehension axioms are satisfied. Our deductive system is sound and complete with respect to general
$\mathcal {L}_J$
-prestructure in which the second-order comprehension axioms are satisfied. Our deductive system is sound and complete with respect to general
![]() $\mathcal {L}_J$
-structures.
$\mathcal {L}_J$
-structures.
A standard
![]() $\mathcal {L}_J$
-structure
$\mathcal {L}_J$
-structure
![]() $\mathcal {M}$
is a general
$\mathcal {M}$
is a general
![]() $\mathcal {L}_J$
-structure in which
$\mathcal {L}_J$
-structure in which
![]() $M_{\langle j_1, \ldots , j_n \rangle }= \mathcal {P}(M_{j_1} \times \cdots \times M_{j_n})$
for all
$M_{\langle j_1, \ldots , j_n \rangle }= \mathcal {P}(M_{j_1} \times \cdots \times M_{j_n})$
for all
![]() $j_1, \ldots , j_n \in J$
. So, a standard
$j_1, \ldots , j_n \in J$
. So, a standard
![]() $\mathcal {L}_J$
-structure is fully specified by its object domains
$\mathcal {L}_J$
-structure is fully specified by its object domains
![]() $\{M_j : j \in J\}$
. Our deductive system is sound but not complete with respect to standard structures.
$\{M_j : j \in J\}$
. Our deductive system is sound but not complete with respect to standard structures.
2.3 Languages with constant symbols
We will now sketch how to add constant symbols to the languages
![]() $\mathcal {L}_J$
.
$\mathcal {L}_J$
.
For each
![]() $\tau \in \mathit {Sorts}(J)$
, let
$\tau \in \mathit {Sorts}(J)$
, let
![]() $K_\tau $
be a set of new symbols, called constant symbols. Each constant symbol is assigned to a particular sort
$K_\tau $
be a set of new symbols, called constant symbols. Each constant symbol is assigned to a particular sort
![]() $\tau $
, and is classified as an object, relation, or function constant accordingly. Assume that the
$\tau $
, and is classified as an object, relation, or function constant accordingly. Assume that the
![]() $K_\tau $
’s are pairwise disjoint, or use superscripts to keep track of sorts. Let
$K_\tau $
’s are pairwise disjoint, or use superscripts to keep track of sorts. Let
 $K = \bigcup _{\tau \in \mathit {Sorts}(J)} K_\tau $
.
$K = \bigcup _{\tau \in \mathit {Sorts}(J)} K_\tau $
.
Define the language
![]() $\mathcal {L}_J[K]$
as follows:
$\mathcal {L}_J[K]$
as follows:
-
(i) The alphabet of
 $\mathcal {L}_J[K]$
is the alphabet of
$\mathcal {L}_J[K]$
is the alphabet of
 $\mathcal {L}_J$
expanded by K.
$\mathcal {L}_J$
expanded by K. -
(ii) If
 $\tau \in J \cup \mathit {Sorts}^2(J)$
, the atomic terms of sort
$\tau \in J \cup \mathit {Sorts}^2(J)$
, the atomic terms of sort
 $\tau $
are the variables
$\tau $
are the variables
 $x^\tau $
and the constants in
$x^\tau $
and the constants in
 $K_\tau $
.
$K_\tau $
.If
 $\tau \in \mathit {Sorts}^3(J)$
, the atomic terms of sort
$\tau \in \mathit {Sorts}^3(J)$
, the atomic terms of sort
 $\tau $
are the constants in
$\tau $
are the constants in
 $K_\tau $
.
$K_\tau $
.If
 $\tau = \langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle \in \mathit {FnSorts}(J)$
, and
$\tau = \langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle \in \mathit {FnSorts}(J)$
, and
 $f^\tau \in K_\tau $
, and
$f^\tau \in K_\tau $
, and
 $t_1^{\tau _1}, \ldots , t_n^{\tau _n}$
are terms of the indicated sorts, then
$t_1^{\tau _1}, \ldots , t_n^{\tau _n}$
are terms of the indicated sorts, then
 $f^\tau t_1^{\tau _1} \cdots t_n^{\tau _n}$
is a term of sort
$f^\tau t_1^{\tau _1} \cdots t_n^{\tau _n}$
is a term of sort
 $\tau _{n+1}$
.
$\tau _{n+1}$
. -
(iii) The atomic formulas are defined as in
 $\mathcal {L}_J$
, except that we also allow atomic formulas of the form
$\mathcal {L}_J$
, except that we also allow atomic formulas of the form
 $T^{\tau } t_1^{\tau _1} \cdots t_n^{\tau _n}$
with
$T^{\tau } t_1^{\tau _1} \cdots t_n^{\tau _n}$
with
 $\tau = \langle \tau _1, \ldots , \tau _n \rangle \in \mathit {Sorts}^3(J)$
.
$\tau = \langle \tau _1, \ldots , \tau _n \rangle \in \mathit {Sorts}^3(J)$
. -
(iv) The inductive clauses generating the set of all formulas are unchanged.
The deductive system for
![]() $\mathcal {L}_J[K]$
is obtained from the deductive system for
$\mathcal {L}_J[K]$
is obtained from the deductive system for
![]() $\mathcal {L}_J$
by allowing
$\mathcal {L}_J$
by allowing
![]() $\varphi , \psi $
to range over
$\varphi , \psi $
to range over
![]() $\mathcal {L}_J[K]$
-formulas,
$\mathcal {L}_J[K]$
-formulas,
![]() $\alpha $
to range over atomic
$\alpha $
to range over atomic
![]() $\mathcal {L}_J[K]$
-formulas, and adding axioms of Extensionality analogous to the axioms of Identity.Footnote
8
$\mathcal {L}_J[K]$
-formulas, and adding axioms of Extensionality analogous to the axioms of Identity.Footnote
8
An
![]() $\mathcal {L}_J[K]$
-prestructure
$\mathcal {L}_J[K]$
-prestructure
![]() $\mathcal {M} = (\mathcal {S}, I)$
consists of an
$\mathcal {M} = (\mathcal {S}, I)$
consists of an
![]() $\mathcal {L}_J$
-prestructure
$\mathcal {L}_J$
-prestructure
![]() $\mathcal {S}$
together with an interpretation I of the constant symbols that meets the following three conditions:
$\mathcal {S}$
together with an interpretation I of the constant symbols that meets the following three conditions:
-
(i) If
 $c^j$
is an object constant of sort
$c^j$
is an object constant of sort
 $j \in J$
, then
$j \in J$
, then
 $I(c^j) \in M_j$
.
$I(c^j) \in M_j$
. -
(ii) If
 $R^\tau $
is a relation constant of sort
$R^\tau $
is a relation constant of sort
 $\tau = \langle \tau _1, \ldots , \tau _n \rangle \in \mathit {Sorts}^2(J) \cup \mathit {Sorts}^3(J)$
, then
$\tau = \langle \tau _1, \ldots , \tau _n \rangle \in \mathit {Sorts}^2(J) \cup \mathit {Sorts}^3(J)$
, then
 $I(R^\tau ) \in \mathcal {P}(M_{\tau _1} \times \cdots \times M_{\tau _n})$
.
$I(R^\tau ) \in \mathcal {P}(M_{\tau _1} \times \cdots \times M_{\tau _n})$
. -
(iii) If
 $f^\tau $
is a function constant of sort
$f^\tau $
is a function constant of sort
 $\tau = \langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle \in \mathit {FnSorts}(J)$
, then
$\tau = \langle \tau _1, \ldots , \tau _n; \tau _{n+1} \rangle \in \mathit {FnSorts}(J)$
, then
 $I(f^\tau )$
is a function from
$I(f^\tau )$
is a function from
 $M_{\tau _1} \times \cdots \times M_{\tau _{n}}$
into
$M_{\tau _1} \times \cdots \times M_{\tau _{n}}$
into
 $M_{\tau _{n+1}}$
.
$M_{\tau _{n+1}}$
.
General and standard
![]() $\mathcal {L}_J[K]$
-structures are defined analogously to
$\mathcal {L}_J[K]$
-structures are defined analogously to
![]() $\mathcal {L}_J$
-structures.
$\mathcal {L}_J$
-structures.
2.4 The languages
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\mathcal {L}^+$
$\mathcal {L}^+$
We now define the two languages that will be at the center of the rest of the paper.
Definition 2.5. The base language is
![]() $\mathcal {L} := \mathcal {L}_{\{0\}}$
.
$\mathcal {L} := \mathcal {L}_{\{0\}}$
.
Definition 2.6. The expanded language is
![]() $\mathcal {L}^+ := \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n\}]$
, where
$\mathcal {L}^+ := \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n\}]$
, where
![]() $\#_0$
and
$\#_0$
and
![]() $\#_n$
are function constants of sorts
$\#_n$
are function constants of sorts
![]() $\langle \langle 0 \rangle; n \rangle $
and
$\langle \langle 0 \rangle; n \rangle $
and
![]() $\langle \langle n \rangle; n \rangle $
, respectively.
$\langle \langle n \rangle; n \rangle $
, respectively.
The logical axioms for
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}^+$
will be denoted by
$\mathcal {L}^+$
will be denoted by
![]() $\mathit {Ax}_{\mathcal {L}}$
and
$\mathit {Ax}_{\mathcal {L}}$
and
![]() $\mathit {Ax}_{\mathcal {L}^+}$
, respectively.
$\mathit {Ax}_{\mathcal {L}^+}$
, respectively.
Some notational conventions:
-
(i) We generally drop the superscripts
 $0$
,
$0$
,
 $\langle 0 \rangle $
,
$\langle 0 \rangle $
,
 $\langle 0, 0 \rangle $
,
$\langle 0, 0 \rangle $
,
 $\ldots $
.
$\ldots $
. -
(ii) We generally write variables of sorts
 $\tau \in \{n\} \cup \mathit {Sorts}^2(\{n\})$
in boldface, and drop the superscripts n,
$\tau \in \{n\} \cup \mathit {Sorts}^2(\{n\})$
in boldface, and drop the superscripts n,
 $\langle n \rangle $
,
$\langle n \rangle $
,
 $\langle n, n \rangle $
,
$\langle n, n \rangle $
,
 $\cdots $
.
$\cdots $
. -
(iii) When we write second-order relation superscripts, we drop the angle brackets and commas. For example, we write
 $X^{n0}$
instead of
$X^{n0}$
instead of
 $X^{\langle n,0 \rangle }$
.
$X^{\langle n,0 \rangle }$
. -
(iv) We drop the subscripts from
 $\#_0$
and
$\#_0$
and
 $\#_n$
, writing
$\#_n$
, writing
 $\#$
for both.
$\#$
for both. -
(v) Following Frege, we refer to monadic relations as concepts.
3 Heck’s theory 2FA
Think of the base language
![]() $\mathcal {L}$
as our starting language, and
$\mathcal {L}$
as our starting language, and
![]() $\mathit {Ax}_{\mathcal {L}}$
as our starting theory. Heck [Reference Heck15], [Reference Heck16, pp. 150–151] reconstrues Hume’s Principle as introducing a new, numerical sort of object (sort n), together with a host of new second-order relation sorts. The operator
$\mathit {Ax}_{\mathcal {L}}$
as our starting theory. Heck [Reference Heck15], [Reference Heck16, pp. 150–151] reconstrues Hume’s Principle as introducing a new, numerical sort of object (sort n), together with a host of new second-order relation sorts. The operator
![]() $\#$
(‘the number of’) may be applied to a concept variable of either sort, yielding a singular term of the numerical sort.
$\#$
(‘the number of’) may be applied to a concept variable of either sort, yielding a singular term of the numerical sort.
Definition 3.7. Weak two-sorted Hume’s Principle (w2HP) is the universal closure of:
Here,
![]() $F^0 \approx _{R^{00}} G^0$
abbreviates the statement that
$F^0 \approx _{R^{00}} G^0$
abbreviates the statement that
![]() $R^{00}$
is a one–one correspondence between
$R^{00}$
is a one–one correspondence between
![]() $F^0$
and
$F^0$
and
![]() $G^0$
.
$G^0$
.
Intuitively, w2HP gives the criterion of identity for numbers belonging to base-sort concepts. It tells us how to count base-sort objects. But w2HP does not tell us how to count numbers. Since we do in fact count numbers, we are motivated to consider a stronger principle.
Definition 3.8.
Two-sorted Hume’s Principle (2HP) is the conjunction of the universal closures of the following three
![]() $\mathcal {L}^+$
-formulas:
$\mathcal {L}^+$
-formulas:
 $$ \begin{align*} \#F^0 = \#G^0 \ &\leftrightarrow \ \exists R^{00}(F^0 \approx_{R^{00}} G^0), \\ \# F^n = \# G^n \ &\leftrightarrow \ \exists R^{nn}(F^n \approx_{R^{nn}} G^n), \\ \# F^n = \# G^0 \ &\leftrightarrow \ \exists R^{n0}(F^n \approx_{R^{n0}} G^0). \end{align*} $$
$$ \begin{align*} \#F^0 = \#G^0 \ &\leftrightarrow \ \exists R^{00}(F^0 \approx_{R^{00}} G^0), \\ \# F^n = \# G^n \ &\leftrightarrow \ \exists R^{nn}(F^n \approx_{R^{nn}} G^n), \\ \# F^n = \# G^0 \ &\leftrightarrow \ \exists R^{n0}(F^n \approx_{R^{n0}} G^0). \end{align*} $$
The first line is w2HP. The second line gives the criterion of identity for numbers belonging to numerical concepts. The third line gives the mixed criterion of identity, which tells us (e.g.) whether the number of Julio-Claudian emperors equals the number of prime numbers less than 12.
Using our superscript-dropping conventions, we may write 2HP as follows:
 $$ \begin{align*} \#F = \#G \ &\leftrightarrow \ \exists R(F \approx_{R} G), \\ \# \mathbf{{F}} = \# \mathbf{{G}} \ &\leftrightarrow \ \exists \mathbf{{R}}(\mathbf{{F}} \approx_{\mathbf{{R}}} \mathbf{{G}}), \\ \# \mathbf{{F}} = \# G \ &\leftrightarrow \ \exists R^{n0}(\mathbf{{F}} \approx_{R^{n0}} G). \end{align*} $$
$$ \begin{align*} \#F = \#G \ &\leftrightarrow \ \exists R(F \approx_{R} G), \\ \# \mathbf{{F}} = \# \mathbf{{G}} \ &\leftrightarrow \ \exists \mathbf{{R}}(\mathbf{{F}} \approx_{\mathbf{{R}}} \mathbf{{G}}), \\ \# \mathbf{{F}} = \# G \ &\leftrightarrow \ \exists R^{n0}(\mathbf{{F}} \approx_{R^{n0}} G). \end{align*} $$
Definition 3.9.
Weak two-sorted Frege Arithmetic (w2FA) is the theory whose logical axioms are
![]() $\mathit {Ax}_{\mathcal {L}^+}$
and whose sole nonlogical axiom is
$\mathit {Ax}_{\mathcal {L}^+}$
and whose sole nonlogical axiom is
![]() $\mathrm{w2HP}$
.Footnote
9
In other words,
$\mathrm{w2HP}$
.Footnote
9
In other words,
Definition 3.10.
Two-sorted Frege Arithmetic (2FA) is the theory whose logical axioms are
![]() $\mathit {Ax}_{\mathcal {L}^+}$
and whose sole nonlogical axiom is
$\mathit {Ax}_{\mathcal {L}^+}$
and whose sole nonlogical axiom is
![]() $\mathrm{2HP}$
. In other words,
$\mathrm{2HP}$
. In other words,
Notice that the logical axioms of 2FA include full second-order comprehension for the expanded language. So, by Frege’s Theorem, 2FA interprets second-order arithmetic in the numerical sort. It follows that 2FA proves a sentence which says that the numerical universe is Dedekind-infinite. But this is not a witness to non-conservativeness, because the numerical sort is not part of the base language. Prima facie, it seems quite plausible that 2FA should be a conservative extension of
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
4 Arithmetic
We will study 2FA by comparing it with other, better-known systems of arithmetic. In Section 4.1, we describe the usual systems of first- and second-order arithmetic. In Section 4.2, we describe systems of arithmetic with no function symbols.
4.1 First- and second-order arithmetic
We begin with first-order arithmetic. For reference, see [Reference Hájek and Pudlák13, pp. 12–13, 28–29].
Definition 4.11. The language of Peano arithmetic,
![]() $L_{\mathrm{PA}}$
, is a classical first-order language with identity whose nonlogical vocabulary is
$L_{\mathrm{PA}}$
, is a classical first-order language with identity whose nonlogical vocabulary is
![]() $(0, S, \leq , +, \cdot )$
. Here, 0 is a constant symbol, S is a unary function symbol,
$(0, S, \leq , +, \cdot )$
. Here, 0 is a constant symbol, S is a unary function symbol,
![]() $\leq $
is a binary relation symbol, and
$\leq $
is a binary relation symbol, and
![]() $+,\cdot $
are binary function symbols.
$+,\cdot $
are binary function symbols.
Definition 4.12.
Robinson arithmetic, Q, is the theory in
![]() $L_{\mathrm{PA}}$
with the following eight axioms:
$L_{\mathrm{PA}}$
with the following eight axioms:
 $$ \begin{align*} & 0 \neq Sx, \\ & Sx = Sy \rightarrow x=y, \\ & x \neq 0 \rightarrow \exists y (x = Sy), \\ & x+0 = x, \\ & x+Sy = S(x+y), \\ & x \cdot 0 = 0, \\ & x \cdot Sy = (x \cdot y) + x,\\ & x \leq y \leftrightarrow \exists z (z + x = y). \end{align*} $$
$$ \begin{align*} & 0 \neq Sx, \\ & Sx = Sy \rightarrow x=y, \\ & x \neq 0 \rightarrow \exists y (x = Sy), \\ & x+0 = x, \\ & x+Sy = S(x+y), \\ & x \cdot 0 = 0, \\ & x \cdot Sy = (x \cdot y) + x,\\ & x \leq y \leftrightarrow \exists z (z + x = y). \end{align*} $$
Definition 4.13. Peano arithmetic, PA, is the result of adding to Q the following axiom schema of induction:
where
![]() $\varphi (x)$
is any formula of
$\varphi (x)$
is any formula of
![]() $L_{\mathrm{PA}}$
.
$L_{\mathrm{PA}}$
.
We write
![]() $(\forall x \leq t)(\cdots )$
to abbreviate
$(\forall x \leq t)(\cdots )$
to abbreviate
![]() $\forall x (x \leq t \rightarrow \cdots )$
, and similarly we write
$\forall x (x \leq t \rightarrow \cdots )$
, and similarly we write
![]() $(\exists x \leq t)(\cdots )$
. The quantifiers occurring in these expressions are said to be bounded.
$(\exists x \leq t)(\cdots )$
. The quantifiers occurring in these expressions are said to be bounded.
An
![]() $L_{\mathrm{PA}}$
-formula is called bounded, or
$L_{\mathrm{PA}}$
-formula is called bounded, or
![]() $\Sigma _0$
, if all quantifiers occurring in it are bounded.
$\Sigma _0$
, if all quantifiers occurring in it are bounded.
An
![]() $L_{\mathrm{PA}}$
-formula is called
$L_{\mathrm{PA}}$
-formula is called
![]() $\Sigma _n$
(
$\Sigma _n$
(
![]() $n \geq 0$
) if it consists of a string of n alternating unbounded quantifiers, the first of which is existential, followed by a bounded formula. That is, a
$n \geq 0$
) if it consists of a string of n alternating unbounded quantifiers, the first of which is existential, followed by a bounded formula. That is, a
![]() $\Sigma _n$
formula has the form
$\Sigma _n$
formula has the form
![]() $\exists x \forall y \exists z \forall w \cdots \theta $
, where
$\exists x \forall y \exists z \forall w \cdots \theta $
, where
![]() $\theta $
is bounded.
$\theta $
is bounded.
Definition 4.14. The theory
![]() $I\Sigma _n$
(
$I\Sigma _n$
(
![]() $n \geq 0$
) is the result of adding to Q the axiom schema of induction above, restricted to
$n \geq 0$
) is the result of adding to Q the axiom schema of induction above, restricted to
![]() $\Sigma _n$
formulas.
$\Sigma _n$
formulas.
We now turn our attention to second-order arithmetic. For reference, see [Reference Simpson28, pp. 2–5].
Definition 4.15. The language of second-order arithmetic,
![]() $L_2$
, is a two-sorted language consisting of all the vocabulary of
$L_2$
, is a two-sorted language consisting of all the vocabulary of
![]() $L_{\mathrm{PA}}$
, together with denumerably many monadic second-order variables
$L_{\mathrm{PA}}$
, together with denumerably many monadic second-order variables
![]() $X, Y, Z, \ldots $
and a second-order quantifier
$X, Y, Z, \ldots $
and a second-order quantifier
![]() $\forall X$
. The atomic formulas of
$\forall X$
. The atomic formulas of
![]() $L_2$
include all strings of the form
$L_2$
include all strings of the form
![]() $Xt$
, where t is a first-order term and X is a second-order variable.
$Xt$
, where t is a first-order term and X is a second-order variable.
The second-order variables of
![]() $L_2$
are usually called set variables, and the atomic formulas
$L_2$
are usually called set variables, and the atomic formulas
![]() $Xt$
are sometimes written
$Xt$
are sometimes written
![]() $t \in X$
. For our purposes, there is no difference between set variables and concept variables, and the predication relation
$t \in X$
. For our purposes, there is no difference between set variables and concept variables, and the predication relation
![]() $\in $
may be left implicit. Hence,
$\in $
may be left implicit. Hence,
![]() $L_2$
may be regarded as an expansion of the monadic fragment of
$L_2$
may be regarded as an expansion of the monadic fragment of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Definition 4.16.
Second-order arithmetic,
![]() $Z_2$
, is the theory in
$Z_2$
, is the theory in
![]() $L_2$
whose axioms are those of Q, together with the second-order induction axiom
$L_2$
whose axioms are those of Q, together with the second-order induction axiom
and the second-order comprehension scheme
for each formula
![]() $\varphi $
of
$\varphi $
of
![]() $L_2$
not containing X free. As usual,
$L_2$
not containing X free. As usual,
![]() $\varphi $
may contain parameters, i.e., free first- or second-order variables other than x.
$\varphi $
may contain parameters, i.e., free first- or second-order variables other than x.
4.2 First- and second-order arithmetic with no function symbols
In this section, we introduce an arithmetical language
![]() $L'$
in which successor, addition, and multiplication are rendered as relations (which may be only partially defined) instead of functions. This allows us to define
$L'$
in which successor, addition, and multiplication are rendered as relations (which may be only partially defined) instead of functions. This allows us to define
![]() $BA'$
, a weak system of arithmetic that does not assume the existence of infinitely many natural numbers. The main point of the section is to state Lemma 4.23 and prove Lemmas 4.25 and 4.28. We will use these lemmas in Section 9 only, so feel free to skip this section and return to it later.
$BA'$
, a weak system of arithmetic that does not assume the existence of infinitely many natural numbers. The main point of the section is to state Lemma 4.23 and prove Lemmas 4.25 and 4.28. We will use these lemmas in Section 9 only, so feel free to skip this section and return to it later.
For reference, see [Reference Hájek and Pudlák13, pp. 86–89, 233].
Definition 4.17. Let
![]() $L'$
be the classical first-order language with identity whose nonlogical vocabulary is
$L'$
be the classical first-order language with identity whose nonlogical vocabulary is
![]() $(0, S, \leq , A, M)$
. Here, 0 is a constant symbol, S and
$(0, S, \leq , A, M)$
. Here, 0 is a constant symbol, S and
![]() $\leq $
are binary relation symbols, and A and M are ternary relation symbols.
$\leq $
are binary relation symbols, and A and M are ternary relation symbols.
An
![]() $L'$
-formula is called bounded′, or
$L'$
-formula is called bounded′, or
![]() $\Sigma _0'$
, if it contains only bounded quantifiers.
$\Sigma _0'$
, if it contains only bounded quantifiers.
Definition 4.18.
![]() $BA'$
is the theory in
$BA'$
is the theory in
![]() $L'$
with the following axioms:
$L'$
with the following axioms:
-
1.
 $\leq $
is a discrete linear order with least element 0,
$\leq $
is a discrete linear order with least element 0, -
2.
 $Sxy$
iff y is the upper neighbor of x with respect to
$Sxy$
iff y is the upper neighbor of x with respect to
 $\leq $
,
$\leq $
, -
3. Definitions of A and M:
 $$ \begin{align*} & Ax0z\leftrightarrow z= x, \\ & Syy' \wedge Szz' \rightarrow (Axyz \leftrightarrow Axy'z'), \\ & Mx0z \leftrightarrow z=0, \\ & Syy' \wedge Azxz' \rightarrow (Mxyz \leftrightarrow Mxy'z'), \end{align*} $$
$$ \begin{align*} & Ax0z\leftrightarrow z= x, \\ & Syy' \wedge Szz' \rightarrow (Axyz \leftrightarrow Axy'z'), \\ & Mx0z \leftrightarrow z=0, \\ & Syy' \wedge Azxz' \rightarrow (Mxyz \leftrightarrow Mxy'z'), \end{align*} $$
-
4. Commutativity and associativity of A and M, distributivity, monotonicity of addition, monotonicity of multiplication by a positive number, and
 $x \leq y \leftrightarrow (\exists u \leq y) Axuy$
,
$x \leq y \leftrightarrow (\exists u \leq y) Axuy$
, -
5. Induction scheme for
 $\Sigma _0'$
formulas:
$\Sigma _0'$
formulas:  $$ \begin{align*}\varphi(0) \wedge \forall x \forall y (\varphi(x) \wedge Sxy \rightarrow \varphi(y)) \rightarrow \forall x \varphi(x). \end{align*} $$
$$ \begin{align*}\varphi(0) \wedge \forall x \forall y (\varphi(x) \wedge Sxy \rightarrow \varphi(y)) \rightarrow \forall x \varphi(x). \end{align*} $$
Definition 4.19.
![]() $I\Sigma _0'$
is the result of adding to
$I\Sigma _0'$
is the result of adding to
![]() $BA'$
axioms saying that
$BA'$
axioms saying that
![]() $S,A,M$
define total functions, namely
$S,A,M$
define total functions, namely
![]() $\forall x \exists y Sxy$
, etc.
$\forall x \exists y Sxy$
, etc.
An
![]() $L'$
-formula is called
$L'$
-formula is called
![]() $\Sigma _n'$
(
$\Sigma _n'$
(
![]() $n \geq 0$
) if it consists of a string of n alternating unbounded quantifiers, the first of which is existential, followed by a bounded
$n \geq 0$
) if it consists of a string of n alternating unbounded quantifiers, the first of which is existential, followed by a bounded
![]() $'$
formula.
$'$
formula.
Definition 4.20. The theory
![]() $I\Sigma _n'$
(
$I\Sigma _n'$
(
![]() $n \geq 0$
) is the result of adding to
$n \geq 0$
) is the result of adding to
![]() $I\Sigma _0'$
the axiom schema of induction above, extended to
$I\Sigma _0'$
the axiom schema of induction above, extended to
![]() $\Sigma _n'$
formulas.
$\Sigma _n'$
formulas.
We now state some useful facts about
![]() $BA'$
and its relatives.
$BA'$
and its relatives.
Definition 4.21. Let
![]() $\mathfrak {D}$
be the conjunction of the following three
$\mathfrak {D}$
be the conjunction of the following three
![]() $(L_{\mathrm{PA}} \cup L')$
-formulas:
$(L_{\mathrm{PA}} \cup L')$
-formulas:
 $$ \begin{align*} Sx = y \ &\leftrightarrow \ Sxy, \\ x + y = z \ &\leftrightarrow \ Axyz, \\ x \cdot y = z \ &\leftrightarrow \ Mxyz. \end{align*} $$
$$ \begin{align*} Sx = y \ &\leftrightarrow \ Sxy, \\ x + y = z \ &\leftrightarrow \ Axyz, \\ x \cdot y = z \ &\leftrightarrow \ Mxyz. \end{align*} $$
For each
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $x \doteq n$
abbreviate the
$x \doteq n$
abbreviate the
![]() $L'$
-formula
$L'$
-formula
Lemmas 4.22 and 4.23 tell us that the theories
![]() $I\Sigma _n$
and
$I\Sigma _n$
and
![]() $I\Sigma _n'$
are in a strong sense equivalent.
$I\Sigma _n'$
are in a strong sense equivalent.
Lemma 4.22. Let
![]() $n \geq 0$
. Then
$n \geq 0$
. Then
![]() $I\Sigma _n' + \mathfrak {D} \vdash I\Sigma _n$
, and conversely
$I\Sigma _n' + \mathfrak {D} \vdash I\Sigma _n$
, and conversely
![]() $I\Sigma _n + \mathfrak {D} \vdash I\Sigma _n'$
.
$I\Sigma _n + \mathfrak {D} \vdash I\Sigma _n'$
.
Lemma 4.23. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _n$
formula with
$\Sigma _n$
formula with
![]() $n \geq 1$
. Then there is a
$n \geq 1$
. Then there is a
![]() $\Sigma _n'$
formula
$\Sigma _n'$
formula
![]() $\varphi '$
with the same free variables as
$\varphi '$
with the same free variables as
![]() $\varphi $
such that
$\varphi $
such that
![]() $I\Sigma _n' + \mathfrak {D} \vdash \varphi \leftrightarrow \varphi '$
.
$I\Sigma _n' + \mathfrak {D} \vdash \varphi \leftrightarrow \varphi '$
.
For proof, see [Reference Hájek and Pudlák13, pp. 88–89].Footnote 10
Lemma 4.24.
![]() $I\Sigma _0'$
and
$I\Sigma _0'$
and
![]() $BA'$
prove the same bounded
$BA'$
prove the same bounded
![]() $'$
formulas.
$'$
formulas.
For proof, see [Reference Hájek and Pudlák13, p. 233].
Lemma 4.25. Let
![]() $\varphi (x_1, \ldots , x_k)$
be a bounded
$\varphi (x_1, \ldots , x_k)$
be a bounded
![]() $'$
formula, and let
$'$
formula, and let
![]() $a_1, \ldots , a_k \in \mathbb {N}$
be such that
$a_1, \ldots , a_k \in \mathbb {N}$
be such that
![]() $\mathbb {N} \vDash \varphi (a_1, \ldots , a_k)$
. Then
$\mathbb {N} \vDash \varphi (a_1, \ldots , a_k)$
. Then
Proof. Let
![]() $\psi $
be the
$\psi $
be the
![]() $L_{\mathrm{PA}}$
-formula obtained from
$L_{\mathrm{PA}}$
-formula obtained from
![]() $\varphi $
by replacing
$\varphi $
by replacing
![]() $Sxy$
,
$Sxy$
,
![]() $Axyz$
,
$Axyz$
,
![]() $Mxyz$
with
$Mxyz$
with
![]() $Sx = y$
,
$Sx = y$
,
![]() $x+y=z$
,
$x+y=z$
,
![]() $x \cdot y = z$
respectively. Observe that
$x \cdot y = z$
respectively. Observe that
![]() $\psi (S^{a_1}0, \ldots , S^{a_k}0)$
is a true bounded sentence of
$\psi (S^{a_1}0, \ldots , S^{a_k}0)$
is a true bounded sentence of
![]() $L_{\mathrm{PA}}$
.
$L_{\mathrm{PA}}$
.
Now we argue as follows:
 $$ \begin{align*} I\Sigma_0 &\vdash \psi(S^{a_1}0, \ldots, S^{a_k}0), \\ I\Sigma_0' + \mathfrak{D} &\vdash \psi(S^{a_1}0, \ldots, S^{a_k}0), \\ I\Sigma_0' + \mathfrak{D}&\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \psi(x_1, \ldots, x_k), \\ I\Sigma_0' + \mathfrak{D}&\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k), \\ I\Sigma_0' &\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k), \\ BA' &\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k). \end{align*} $$
$$ \begin{align*} I\Sigma_0 &\vdash \psi(S^{a_1}0, \ldots, S^{a_k}0), \\ I\Sigma_0' + \mathfrak{D} &\vdash \psi(S^{a_1}0, \ldots, S^{a_k}0), \\ I\Sigma_0' + \mathfrak{D}&\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \psi(x_1, \ldots, x_k), \\ I\Sigma_0' + \mathfrak{D}&\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k), \\ I\Sigma_0' &\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k), \\ BA' &\vdash x_1 \doteq a_1 \wedge \cdots \wedge x_k \doteq a_k \rightarrow \varphi(x_1, \ldots, x_k). \end{align*} $$
The first line holds because
![]() $I\Sigma _0$
proves all true bounded sentences.Footnote
11
The second line follows by Lemma 4.22. Regarding the third line, it is easy to check that for each
$I\Sigma _0$
proves all true bounded sentences.Footnote
11
The second line follows by Lemma 4.22. Regarding the third line, it is easy to check that for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
The fourth line follows by propositional logic, because
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
differ only by applications of the equivalences in
$\psi $
differ only by applications of the equivalences in
![]() $\mathfrak {D}$
. The fifth line follows because
$\mathfrak {D}$
. The fifth line follows because
![]() $I\Sigma _0' + \mathfrak {D}$
is conservative over
$I\Sigma _0' + \mathfrak {D}$
is conservative over
![]() $I\Sigma _0'$
for
$I\Sigma _0'$
for
![]() $L'$
-formulas. The sixth line follows by Lemma 4.24.
$L'$
-formulas. The sixth line follows by Lemma 4.24.
Lastly, we describe a system of second-order arithmetic without function symbols.
Definition 4.26. The language
![]() $L_2'$
is just like
$L_2'$
is just like
![]() $L_2$
, but with the vocabulary of
$L_2$
, but with the vocabulary of
![]() $L'$
replacing the vocabulary of
$L'$
replacing the vocabulary of
![]() $L_{\mathrm{PA}}$
.
$L_{\mathrm{PA}}$
.
Definition 4.27. Let
![]() $Z_2'$
be the theory in
$Z_2'$
be the theory in
![]() $L_2'$
whose axioms are those of
$L_2'$
whose axioms are those of
![]() $I\Sigma _0'$
, plus the second-order induction axiom
$I\Sigma _0'$
, plus the second-order induction axiom
and the second-order comprehension scheme for
![]() $L_2'$
.
$L_2'$
.
Lemma 4.28.
![]() $Z_2$
and
$Z_2$
and
![]() $Z_2'$
are mutually interpretable. Indeed,
$Z_2'$
are mutually interpretable. Indeed,
![]() $Z_2' + \mathfrak {D} \vdash Z_2$
, and conversely
$Z_2' + \mathfrak {D} \vdash Z_2$
, and conversely
![]() $Z_2 + \mathfrak {D} \vdash Z_2'$
.
$Z_2 + \mathfrak {D} \vdash Z_2'$
.
Proof. We argue that
![]() $Z_2' + \mathfrak {D} \vdash Z_2$
. The other direction is easy.
$Z_2' + \mathfrak {D} \vdash Z_2$
. The other direction is easy.
Observe that
![]() $(Z_2' + \mathfrak {D}) \vdash (I\Sigma _0' + \mathfrak {D}) \vdash I\Sigma _0 \vdash Q$
. Furthermore, the two ways of formulating the second-order induction axiom are equivalent in the presence of
$(Z_2' + \mathfrak {D}) \vdash (I\Sigma _0' + \mathfrak {D}) \vdash I\Sigma _0 \vdash Q$
. Furthermore, the two ways of formulating the second-order induction axiom are equivalent in the presence of
![]() $Sx=y \leftrightarrow Sxy$
.
$Sx=y \leftrightarrow Sxy$
.
It remains to show that
![]() $Z_2' + \mathfrak {D}$
proves the second-order comprehension scheme for
$Z_2' + \mathfrak {D}$
proves the second-order comprehension scheme for
![]() $L_2$
. Take any
$L_2$
. Take any
![]() $L_2$
-formula
$L_2$
-formula
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\psi $
be the formula obtained from
$\psi $
be the formula obtained from
![]() $\varphi $
by replacing each atomic predication
$\varphi $
by replacing each atomic predication
![]() $Xt$
with
$Xt$
with
![]() $\exists z(Xz \wedge z=t)$
, where z is a new variable. Then every non-atomic term in
$\exists z(Xz \wedge z=t)$
, where z is a new variable. Then every non-atomic term in
![]() $\psi $
occurs in an equation
$\psi $
occurs in an equation
![]() $t_1 = t_2$
. These equations are
$t_1 = t_2$
. These equations are
![]() $L_{\mathrm{PA}}$
-formulas. By Lemma 4.23,
$L_{\mathrm{PA}}$
-formulas. By Lemma 4.23,
![]() $Z_2' + \mathfrak {D}$
proves each
$Z_2' + \mathfrak {D}$
proves each
![]() $L_{\mathrm{PA}}$
-formula to be equivalent to an
$L_{\mathrm{PA}}$
-formula to be equivalent to an
![]() $L'$
-formula. So, there is an
$L'$
-formula. So, there is an
![]() $L_2'$
-formula
$L_2'$
-formula
![]() $\varphi '$
such that
$\varphi '$
such that
![]() $Z_2' + \mathfrak {D} \vdash \varphi \leftrightarrow \varphi '$
. Now apply second-order comprehension to
$Z_2' + \mathfrak {D} \vdash \varphi \leftrightarrow \varphi '$
. Now apply second-order comprehension to
![]() $\varphi '$
, and we are done.
$\varphi '$
, and we are done.
5 Well-orderings and finiteness
In this section, we define ‘well-ordering’ in
![]() $\mathcal {L}$
, and we note that
$\mathcal {L}$
, and we note that
![]() $\mathit {Ax}_{\mathcal {L}}$
proves that all well-orderings are comparable (Lemma 5.29). Then we define the notion of Stäckel-finiteness and prove the important lemma of induction on finite concepts (Lemma 5.32). We will use these lemmas throughout the paper.
$\mathit {Ax}_{\mathcal {L}}$
proves that all well-orderings are comparable (Lemma 5.29). Then we define the notion of Stäckel-finiteness and prove the important lemma of induction on finite concepts (Lemma 5.32). We will use these lemmas throughout the paper.
For simplicity, we work in
![]() $\mathcal {L}$
. However, these notions can easily be extended to
$\mathcal {L}$
. However, these notions can easily be extended to
![]() $\mathcal {L}^+$
.
$\mathcal {L}^+$
.
Let
![]() $\varnothing $
denote the empty concept. Let V denote the universal concept.
$\varnothing $
denote the empty concept. Let V denote the universal concept.
Let
![]() $Y \subseteq X$
abbreviate
$Y \subseteq X$
abbreviate
![]() $\forall x (Yx \rightarrow Xx)$
.
$\forall x (Yx \rightarrow Xx)$
.
Let ‘
![]() $(X,R)$
is a linear order’ abbreviate the formula
$(X,R)$
is a linear order’ abbreviate the formula
 $$ \begin{align*}\forall x \forall y(Rxy \wedge Ryx \rightarrow x=y) &\wedge \forall x \forall y \forall z (Rxy \wedge Ryz \rightarrow Rxz)\\ &\wedge \forall x \forall y(Xx \wedge Xy \leftrightarrow (Rxy \vee Ryx)). \end{align*} $$
$$ \begin{align*}\forall x \forall y(Rxy \wedge Ryx \rightarrow x=y) &\wedge \forall x \forall y \forall z (Rxy \wedge Ryz \rightarrow Rxz)\\ &\wedge \forall x \forall y(Xx \wedge Xy \leftrightarrow (Rxy \vee Ryx)). \end{align*} $$
In other words,
![]() $(X,R)$
is a linear order just in case R is an antisymmetric, transitive, total relation on X.
$(X,R)$
is a linear order just in case R is an antisymmetric, transitive, total relation on X.
Let ‘
![]() $(X,R)$
is well-founded’ abbreviate
$(X,R)$
is well-founded’ abbreviate
Say that
![]() $(X,R)$
is a well-ordering if
$(X,R)$
is a well-ordering if
![]() $(X,R)$
is a well-founded linear order.
$(X,R)$
is a well-founded linear order.
We say that two well-orderings
![]() $(X, \leq _X)$
and
$(X, \leq _X)$
and
![]() $(Y, \leq _Y)$
are order-isomorphic, denoted
$(Y, \leq _Y)$
are order-isomorphic, denoted
![]() $(X, \leq _X) \simeq _o (Y, \leq _Y)$
, just in case there is a bijection
$(X, \leq _X) \simeq _o (Y, \leq _Y)$
, just in case there is a bijection
![]() $f: X \to Y$
such that
$f: X \to Y$
such that
Strictly speaking, we should represent f as a relation, but we will go on using functional notation informally.
If
![]() $(X,R)$
is a well-ordering, let
$(X,R)$
is a well-ordering, let
![]() $X \upharpoonright a$
be the initial segment of
$X \upharpoonright a$
be the initial segment of
![]() $(X,R)$
up to a, defined by
$(X,R)$
up to a, defined by
We also regard
![]() $\varnothing $
as an initial segment of
$\varnothing $
as an initial segment of
![]() $(X,R)$
. An initial segment of
$(X,R)$
. An initial segment of
![]() $(X,R)$
is proper if it is not equal to X.
$(X,R)$
is proper if it is not equal to X.
Let
![]() $(X, \leq _X) <_o (Y, \leq _Y)$
abbreviate the statement that
$(X, \leq _X) <_o (Y, \leq _Y)$
abbreviate the statement that
![]() $(X, \leq _X)$
is order-isomorphic with a proper initial segment of
$(X, \leq _X)$
is order-isomorphic with a proper initial segment of
![]() $(Y, \leq _Y)$
.
$(Y, \leq _Y)$
.
We borrow the next lemma from [Reference Ebels-Duggan7, p. 611].
Lemma 5.29 (Comparability of well-orderings)
It is provable from
![]() $\mathit {Ax}_{\mathcal {L}}$
that any two well-orderings
$\mathit {Ax}_{\mathcal {L}}$
that any two well-orderings
![]() $(X,\leq _X)$
and
$(X,\leq _X)$
and
![]() $(Y,\leq _Y)$
are comparable, in the sense that exactly one of the following holds:
$(Y,\leq _Y)$
are comparable, in the sense that exactly one of the following holds:
Proof. Copy the usual set-theoretic proof [Reference Jech18, pp. 18–19].
We now define the notion of Stäckel-finiteness.
If R is a binary relation, let
![]() $R^{-1}$
be the converse of R, defined by
$R^{-1}$
be the converse of R, defined by
![]() $R^{-1}xy \leftrightarrow Ryx.$
$R^{-1}xy \leftrightarrow Ryx.$
Definition 5.30. Say that
![]() $(X,R)$
is a double well-ordering if
$(X,R)$
is a double well-ordering if
![]() $(X,R)$
and
$(X,R)$
and
![]() $(X,R^{-1})$
are both well-orderings.
$(X,R^{-1})$
are both well-orderings.
Say that X is Stäckel-finite, abbreviated
![]() $\mathit {Fin}(X)$
, if X admits a double well-ordering. That is,
$\mathit {Fin}(X)$
, if X admits a double well-ordering. That is,
Remark 5.31. The double well-ordering criterion is proposed as a definition of finiteness in [Reference Stäckel29]. The criterion is also discussed in [Reference Zermelo34, Reference Zermelo and Castelnuovo35]. For historical remarks, see [Reference Parsons25].
Stäckel-finiteness is strictly stronger than Dedekind-finiteness, in the sense that
 $$ \begin{align*} \mathit{Ax}_{\mathcal{L}} &\vdash \mathit{Fin}(X) \rightarrow \mathit{DFin}(X), \\ \mathit{Ax}_{\mathcal{L}} &\not\vdash \mathit{DFin}(X) \rightarrow \mathit{Fin}(X), \end{align*} $$
$$ \begin{align*} \mathit{Ax}_{\mathcal{L}} &\vdash \mathit{Fin}(X) \rightarrow \mathit{DFin}(X), \\ \mathit{Ax}_{\mathcal{L}} &\not\vdash \mathit{DFin}(X) \rightarrow \mathit{Fin}(X), \end{align*} $$
where of course
![]() $\mathit {DFin}(X)$
abbreviates that X is Dedekind-finite. Indeed,
$\mathit {DFin}(X)$
abbreviates that X is Dedekind-finite. Indeed,
![]() $\mathit {Fin}(X) \rightarrow \mathit {DFin}(X)$
is a version of the pigeonhole principle. It is provable from
$\mathit {Fin}(X) \rightarrow \mathit {DFin}(X)$
is a version of the pigeonhole principle. It is provable from
![]() $\mathit {Ax}_{\mathcal {L}}$
by induction on finite concepts (Lemma 5.32). On the other hand, the Fraenkel model (defined in Section 6) is a model of
$\mathit {Ax}_{\mathcal {L}}$
by induction on finite concepts (Lemma 5.32). On the other hand, the Fraenkel model (defined in Section 6) is a model of
![]() $\mathit {DFin}(V) + \neg \mathit {Fin}(V)$
, witnessing that
$\mathit {DFin}(V) + \neg \mathit {Fin}(V)$
, witnessing that
![]() $\mathit {Ax}_{\mathcal {L}} \not \vdash \mathit {DFin}(X) \rightarrow \mathit {Fin}(X)$
.
$\mathit {Ax}_{\mathcal {L}} \not \vdash \mathit {DFin}(X) \rightarrow \mathit {Fin}(X)$
.
Lastly, we show that
![]() $\mathit {Ax}_{\mathcal {L}}$
proves a principle of induction on Stäckel-finite concepts.
$\mathit {Ax}_{\mathcal {L}}$
proves a principle of induction on Stäckel-finite concepts.
Let
![]() $X \cup \{a\}$
be the concept defined by
$X \cup \{a\}$
be the concept defined by
Lemma 5.32 (Induction on finite concepts)
Let
![]() $\varphi (X)$
be any formula of
$\varphi (X)$
be any formula of
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\mathit {Ax}_{\mathcal {L}}$
proves the universal closure of
$\mathit {Ax}_{\mathcal {L}}$
proves the universal closure of
Proof. Assume the antecedent. Take any X such that
![]() $\mathit {Fin}(X)$
. Fix a double well-ordering
$\mathit {Fin}(X)$
. Fix a double well-ordering
![]() $(X,R)$
, and let Y be defined by
$(X,R)$
, and let Y be defined by
![]() $Yx \leftrightarrow (Xx \wedge \varphi (X \upharpoonright x))$
. It suffices to show that
$Yx \leftrightarrow (Xx \wedge \varphi (X \upharpoonright x))$
. It suffices to show that
![]() $Y=X$
.
$Y=X$
.
Suppose not. Since
![]() $(X,R)$
is a well-ordering, there is an R-least y such that
$(X,R)$
is a well-ordering, there is an R-least y such that
![]() $Xy \wedge \neg Yy$
. It is easy to see that y cannot be the R-least element of X. Since
$Xy \wedge \neg Yy$
. It is easy to see that y cannot be the R-least element of X. Since
![]() $(X,R^{-1})$
is a well-ordering, y has a unique
$(X,R^{-1})$
is a well-ordering, y has a unique
![]() $(X,R)$
-predecessor, call it z. By the minimality of y, we have
$(X,R)$
-predecessor, call it z. By the minimality of y, we have
![]() $Yz$
, and hence
$Yz$
, and hence
![]() $\varphi (X \upharpoonright z)$
. Also, it is easy to see that
$\varphi (X \upharpoonright z)$
. Also, it is easy to see that
![]() $\mathit {Fin}(X \upharpoonright z)$
. It follows that
$\mathit {Fin}(X \upharpoonright z)$
. It follows that
![]() $\varphi ( (X \upharpoonright z) \cup \{y\})$
, which is to say
$\varphi ( (X \upharpoonright z) \cup \{y\})$
, which is to say
![]() $\varphi (X \upharpoonright y)$
. But this contradicts our choice of y.
$\varphi (X \upharpoonright y)$
. But this contradicts our choice of y.
6 The Fraenkel model
In this section, we define the Fraenkel model and show that it is a model of
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
(Lemmas 6.38 and 6.39). Then we show that the relations occurring in the Fraenkel model are exactly the sets definable by Boolean combinations of equalities with object parameters (Lemma 6.40). We will make good use of these facts in Section 7.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
(Lemmas 6.38 and 6.39). Then we show that the relations occurring in the Fraenkel model are exactly the sets definable by Boolean combinations of equalities with object parameters (Lemma 6.40). We will make good use of these facts in Section 7.
We remark that Lemma 6.40 implies that the Fraenkel model is the minimal infinite model of
![]() $\mathit {Ax}_{\mathcal {L}}$
—i.e., it is a submodel of any infinite model of
$\mathit {Ax}_{\mathcal {L}}$
—i.e., it is a submodel of any infinite model of
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
Definition 6.33. Let
![]() $A \subseteq \mathbb {N}^n$
and
$A \subseteq \mathbb {N}^n$
and
![]() $E \subseteq \mathbb {N}$
. We say that E is a support of A if every permutation
$E \subseteq \mathbb {N}$
. We say that E is a support of A if every permutation
![]() $\pi : \mathbb {N} \to \mathbb {N}$
that fixes E pointwise fixes A setwise:
$\pi : \mathbb {N} \to \mathbb {N}$
that fixes E pointwise fixes A setwise:
Using the notation
![]() $\pi (A) = \{ ( \pi (x_1), \ldots , \pi (x_n) ) \in \mathbb {N}^n: ( x_1, \ldots , x_n ) \in A \}$
, we can restate this property as follows: for every permutation
$\pi (A) = \{ ( \pi (x_1), \ldots , \pi (x_n) ) \in \mathbb {N}^n: ( x_1, \ldots , x_n ) \in A \}$
, we can restate this property as follows: for every permutation
![]() $\pi :\mathbb {N}\to \mathbb {N}$
,
$\pi :\mathbb {N}\to \mathbb {N}$
,
Definition 6.34. A set
![]() $A \subseteq \mathbb {N}^n$
is symmetric if it has a finite support
$A \subseteq \mathbb {N}^n$
is symmetric if it has a finite support
![]() $E \subseteq \mathbb {N}$
.
$E \subseteq \mathbb {N}$
.
Definition 6.35. The Fraenkel model is the
![]() $\mathcal {L}$
-prestructure
$\mathcal {L}$
-prestructure
![]() $\mathcal {M}$
whose object universe is
$\mathcal {M}$
whose object universe is
![]() $\mathbb {N}$
, and whose n-ary relations are the symmetric subsets of
$\mathbb {N}$
, and whose n-ary relations are the symmetric subsets of
![]() $\mathbb {N}^n$
. That is, writing
$\mathbb {N}^n$
. That is, writing
![]() $M_n$
for
$M_n$
for
![]() $M_{\langle 0, \ldots , 0 \rangle } \ (n \text{ zeroes})$
,
$M_{\langle 0, \ldots , 0 \rangle } \ (n \text{ zeroes})$
,
 $$ \begin{align*} M_0 &= \mathbb{N}, \\ M_n &= \{A \subseteq \mathbb{N}^n: A \text{ is symmetric} \}. \end{align*} $$
$$ \begin{align*} M_0 &= \mathbb{N}, \\ M_n &= \{A \subseteq \mathbb{N}^n: A \text{ is symmetric} \}. \end{align*} $$
It is well known that
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathit {Ax}_{\mathcal {L}}$
(i.e., it is a general
$\mathit {Ax}_{\mathcal {L}}$
(i.e., it is a general
![]() $\mathcal {L}$
-structure) [Reference Väänänen and Zalta32]. However, we are not aware of any English-language source that gives the proof. For the reader’s convenience, we present the proof from [Reference Asser1] in the next two lemmas.
$\mathcal {L}$
-structure) [Reference Väänänen and Zalta32]. However, we are not aware of any English-language source that gives the proof. For the reader’s convenience, we present the proof from [Reference Asser1] in the next two lemmas.
Lemma 6.36. If
![]() $A \subseteq \mathbb {N}^n$
is symmetric, and
$A \subseteq \mathbb {N}^n$
is symmetric, and
![]() $\sigma :\mathbb {N} \to \mathbb {N}$
is any permutation, then
$\sigma :\mathbb {N} \to \mathbb {N}$
is any permutation, then
![]() $\sigma (A) \subseteq \mathbb {N}^n$
is also symmetric.
$\sigma (A) \subseteq \mathbb {N}^n$
is also symmetric.
Proof. Let E be a support for A. We show that
![]() $\sigma ^{-1}(E)$
is a support for
$\sigma ^{-1}(E)$
is a support for
![]() $\sigma (A)$
. Indeed, take any permutation
$\sigma (A)$
. Indeed, take any permutation
![]() $\pi :\mathbb {N} \to \mathbb {N}$
that fixes
$\pi :\mathbb {N} \to \mathbb {N}$
that fixes
![]() $\sigma ^{-1}(E)$
pointwise. Then the permutation
$\sigma ^{-1}(E)$
pointwise. Then the permutation
![]() $\sigma ^{-1} \pi \sigma : \mathbb {N} \to \mathbb {N}$
fixes E pointwise. So,
$\sigma ^{-1} \pi \sigma : \mathbb {N} \to \mathbb {N}$
fixes E pointwise. So,
![]() $(\sigma ^{-1} \pi \sigma )(A) = A$
, and hence
$(\sigma ^{-1} \pi \sigma )(A) = A$
, and hence
![]() $\pi (\sigma (A)) = \sigma (A)$
.
$\pi (\sigma (A)) = \sigma (A)$
.
Corollary 6.37. Each relation domain
![]() $M_n$
of the Fraenkel model is closed under the action (on
$M_n$
of the Fraenkel model is closed under the action (on
![]() $\mathbb {N}^n$
) of permutations of
$\mathbb {N}^n$
) of permutations of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Lemma 6.38. The Fraenkel model is a model of
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
Proof. Let
![]() $\mathcal {M}$
be the prestructure defined above. We show that
$\mathcal {M}$
be the prestructure defined above. We show that
![]() $\mathcal {M}$
satisfies Comprehension. Take any formula
$\mathcal {M}$
satisfies Comprehension. Take any formula
![]() $\varphi (\bar x, \bar b, \bar B)$
of
$\varphi (\bar x, \bar b, \bar B)$
of
![]() $\mathcal {L}$
, with free variables
$\mathcal {L}$
, with free variables
![]() $\bar x = (x_1, \ldots , x_n)$
and parameters
$\bar x = (x_1, \ldots , x_n)$
and parameters
 $\bar b = (b_1, \ldots , b_j)$
and
$\bar b = (b_1, \ldots , b_j)$
and
![]() $\bar B = (B_1, \ldots , B_k)$
drawn from
$\bar B = (B_1, \ldots , B_k)$
drawn from
![]() $\mathcal {M}$
. Say that
$\mathcal {M}$
. Say that
 $A = \{\bar a \in \mathbb {N}^n : \mathcal {M} \vDash \varphi (\bar a, \bar b, \bar B)\}$
. We show that
$A = \{\bar a \in \mathbb {N}^n : \mathcal {M} \vDash \varphi (\bar a, \bar b, \bar B)\}$
. We show that
![]() $A \in M_n$
.
$A \in M_n$
.
Since the relation parameters
![]() $\bar B$
are drawn from
$\bar B$
are drawn from
![]() $\mathcal {M}$
, each set
$\mathcal {M}$
, each set
![]() $B_i$
has a finite support
$B_i$
has a finite support
![]() $E_i$
(
$E_i$
(
![]() $i = 1, \ldots , k$
). Let
$i = 1, \ldots , k$
). Let
![]() $E = \{b_1, \ldots , b_j \} \cup E_1 \cup \cdots \cup E_k$
. Clearly, E is finite. We show that E is a support for A.
$E = \{b_1, \ldots , b_j \} \cup E_1 \cup \cdots \cup E_k$
. Clearly, E is finite. We show that E is a support for A.
Take any permutation
![]() $\pi : \mathbb {N} \to \mathbb {N}$
that fixes E pointwise, and take any
$\pi : \mathbb {N} \to \mathbb {N}$
that fixes E pointwise, and take any
![]() $\bar a = (a_1, \ldots , a_n) \in \mathbb {N}^n$
. We check that
$\bar a = (a_1, \ldots , a_n) \in \mathbb {N}^n$
. We check that
![]() $\bar a \in A \iff \pi (\bar a ) = ( \pi (a_1), \ldots , \pi (a_n) ) \in A$
. Indeed,
$\bar a \in A \iff \pi (\bar a ) = ( \pi (a_1), \ldots , \pi (a_n) ) \in A$
. Indeed,
 $$ \begin{align*} \bar a \in A &\iff \mathcal{M} \vDash \varphi(\bar a, \bar b, \bar B) \\ &\iff \mathcal{M} \vDash \varphi(\pi(\bar a), \pi(\bar b), \pi(\bar B))\\ &\iff \mathcal{M} \vDash \varphi(\pi(\bar a), \bar b, \bar B) \\ &\iff \pi(\bar a) \in A. \end{align*} $$
$$ \begin{align*} \bar a \in A &\iff \mathcal{M} \vDash \varphi(\bar a, \bar b, \bar B) \\ &\iff \mathcal{M} \vDash \varphi(\pi(\bar a), \pi(\bar b), \pi(\bar B))\\ &\iff \mathcal{M} \vDash \varphi(\pi(\bar a), \bar b, \bar B) \\ &\iff \pi(\bar a) \in A. \end{align*} $$
(Notation:
 $\pi (\bar b) = (\pi (b_1), \ldots , \pi (b_j))$
and
$\pi (\bar b) = (\pi (b_1), \ldots , \pi (b_j))$
and
![]() $\pi (\bar B) = (\pi (B_1), \ldots , \pi (B_k))$
. By Lemma 6.36, each
$\pi (\bar B) = (\pi (B_1), \ldots , \pi (B_k))$
. By Lemma 6.36, each
![]() $\pi (B_i)$
is a parameter from
$\pi (B_i)$
is a parameter from
![]() $\mathcal {M}$
.) The second step works because permuting everything uniformly doesn’t change any truth-values relative to any variable-assignment. This is easily proved by induction on formulas. The third step works because
$\mathcal {M}$
.) The second step works because permuting everything uniformly doesn’t change any truth-values relative to any variable-assignment. This is easily proved by induction on formulas. The third step works because
![]() $\pi $
fixes E pointwise, hence fixes all the parameters.
$\pi $
fixes E pointwise, hence fixes all the parameters.
Lemma 6.39. The Fraenkel model is a model of
![]() $\neg \mathit {Fin}(V)$
.
$\neg \mathit {Fin}(V)$
.
Proof. In fact, we will prove something stronger: the Fraenkel model does not contain any linear ordering of the universe.
Consider any relation
![]() $R \subseteq \mathbb {N}^2$
with finite support
$R \subseteq \mathbb {N}^2$
with finite support
![]() $E \subseteq \mathbb {N}$
. Suppose for sake of contradiction that R is a linear ordering of the universe. Since R is total, we may choose distinct
$E \subseteq \mathbb {N}$
. Suppose for sake of contradiction that R is a linear ordering of the universe. Since R is total, we may choose distinct
![]() $a,b \in \mathbb {N} \setminus E$
such that
$a,b \in \mathbb {N} \setminus E$
such that
![]() $Rab$
. Let
$Rab$
. Let
![]() $\pi $
be any permutation fixing E such that
$\pi $
be any permutation fixing E such that
![]() $\pi (a)=b$
and
$\pi (a)=b$
and
![]() $\pi (b)=a$
. Since E is a support of R, it follows that
$\pi (b)=a$
. Since E is a support of R, it follows that
![]() $Rba$
. But this contradicts the assumption that R is antisymmetric.
$Rba$
. But this contradicts the assumption that R is antisymmetric.
So,
![]() $\mathcal {M}$
contains no linear ordering of the universe. It follows that
$\mathcal {M}$
contains no linear ordering of the universe. It follows that
![]() $\mathcal {M}$
contains no double well-ordering of the universe, i.e.,
$\mathcal {M}$
contains no double well-ordering of the universe, i.e.,
![]() $\mathcal {M} \vDash \neg \mathit {Fin}(V)$
.
$\mathcal {M} \vDash \neg \mathit {Fin}(V)$
.
We close this section by giving a simple characterization of symmetric sets.
Lemma 6.40. Let
![]() $E \subseteq N$
be a finite set. A set
$E \subseteq N$
be a finite set. A set
![]() $A \subseteq N$
is symmetric with support E iff A is definable by Boolean combinations of equalities with parameters from E.
$A \subseteq N$
is symmetric with support E iff A is definable by Boolean combinations of equalities with parameters from E.
Proof. Define an equivalence relation
![]() $\sim _E$
on
$\sim _E$
on
![]() $\mathbb {N}^n$
, as follows:
$\mathbb {N}^n$
, as follows:
 $$ \begin{align*} (a_1, \ldots, a_n) \sim_E (b_1, \ldots, b_n) \iff [(&\forall i, j \leq n)(a_i = a_j \leftrightarrow b_i = b_j) \ \wedge \\ & (\forall e \in E)(\forall i \leq n)(a_i = e \leftrightarrow b_i = e)]. \end{align*} $$
$$ \begin{align*} (a_1, \ldots, a_n) \sim_E (b_1, \ldots, b_n) \iff [(&\forall i, j \leq n)(a_i = a_j \leftrightarrow b_i = b_j) \ \wedge \\ & (\forall e \in E)(\forall i \leq n)(a_i = e \leftrightarrow b_i = e)]. \end{align*} $$
In words:
![]() $\bar a \sim _E \bar b$
iff
$\bar a \sim _E \bar b$
iff
![]() $\bar a$
and
$\bar a$
and
![]() $\bar b$
are n-tuples with the same pattern of identity and distinctness which agree on members of E. It is easy to see that
$\bar b$
are n-tuples with the same pattern of identity and distinctness which agree on members of E. It is easy to see that
![]() $\sim _E$
really is an equivalence relation.
$\sim _E$
really is an equivalence relation.
(
![]() $\!{\implies}\kern-1pt\!$
). Suppose
$\!{\implies}\kern-1pt\!$
). Suppose
![]() $A \subseteq \mathbb {N}^n$
is symmetric with support E. Observe that A is a union of equivalence classes of
$A \subseteq \mathbb {N}^n$
is symmetric with support E. Observe that A is a union of equivalence classes of
![]() $\sim _E$
. Indeed, if
$\sim _E$
. Indeed, if
![]() $\bar a \sim _E \bar b$
, then there is a permutation
$\bar a \sim _E \bar b$
, then there is a permutation
![]() $\pi :\mathbb {N} \to \mathbb {N}$
fixing E such that
$\pi :\mathbb {N} \to \mathbb {N}$
fixing E such that
![]() $\pi (\bar a) = \bar b$
.
$\pi (\bar a) = \bar b$
.
Now, each equivalence class of
![]() $\sim _E$
is definable by a Boolean combination of equalities with parameters from E, of the following form:
$\sim _E$
is definable by a Boolean combination of equalities with parameters from E, of the following form:
 $$ \begin{align*}\bigwedge_{\substack{i, j \leq n \\ i \neq j}} (\neg) \ x_i = x_j \ \wedge \ \bigwedge_{\substack{ i \leq n \\ e \in E }} (\neg) \ x_i = e. \end{align*} $$
$$ \begin{align*}\bigwedge_{\substack{i, j \leq n \\ i \neq j}} (\neg) \ x_i = x_j \ \wedge \ \bigwedge_{\substack{ i \leq n \\ e \in E }} (\neg) \ x_i = e. \end{align*} $$
(The parenthesized negations may or may not be present in each conjunct.) Furthermore,
![]() $\sim _E$
has only finitely many equivalence classes, because there are only finitely many possible patterns of identity and distinctness among
$\sim _E$
has only finitely many equivalence classes, because there are only finitely many possible patterns of identity and distinctness among
![]() $x_1, \ldots , x_n$
and the members of E. Hence, A is definable by a disjunction of formulas like the one above.
$x_1, \ldots , x_n$
and the members of E. Hence, A is definable by a disjunction of formulas like the one above.
(
![]() $\Longleftarrow $
). Suppose A is definable by a Boolean combination of equalities with parameters from E. We show that A is symmetric with support E.
$\Longleftarrow $
). Suppose A is definable by a Boolean combination of equalities with parameters from E. We show that A is symmetric with support E.
Take any permutation
![]() $\pi :\mathbb {N}\to \mathbb {N}$
fixing E pointwise. That is, for all
$\pi :\mathbb {N}\to \mathbb {N}$
fixing E pointwise. That is, for all
![]() $x_i, x_j \in \mathbb {N}$
and
$x_i, x_j \in \mathbb {N}$
and
![]() $e \in E$
,
$e \in E$
,
 $$ \begin{align*} x_i = x_j \ &\leftrightarrow \ \pi(x_i) = \pi(x_j), \\ x_i = e \ &\leftrightarrow \ \pi(x_i) = e. \end{align*} $$
$$ \begin{align*} x_i = x_j \ &\leftrightarrow \ \pi(x_i) = \pi(x_j), \\ x_i = e \ &\leftrightarrow \ \pi(x_i) = e. \end{align*} $$
By induction on formulas, it is easy to see that
![]() $\mathbb {N} \vDash \varphi (\bar x, \bar e) \leftrightarrow \varphi (\pi (\bar x), \bar e)$
for any Boolean combination of equalities
$\mathbb {N} \vDash \varphi (\bar x, \bar e) \leftrightarrow \varphi (\pi (\bar x), \bar e)$
for any Boolean combination of equalities
![]() $\varphi (\bar x, \bar e)$
. Since A is defined by some such Boolean combination, it follows that
$\varphi (\bar x, \bar e)$
. Since A is defined by some such Boolean combination, it follows that
![]() $\pi (A) = A$
.
$\pi (A) = A$
.
Since
![]() $\pi $
was arbitrary, we conclude that A is symmetric with support E.
$\pi $
was arbitrary, we conclude that A is symmetric with support E.
7 The non-conservativeness of w2FA
In this section, we prove Theorem 7.47, which says that w2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
Here is the main idea of the proof. We have seen that
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
has a model whose relations are easy to describe in finitary terms (Section 6). Hence,
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
has a model whose relations are easy to describe in finitary terms (Section 6). Hence,
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
is a fairly weak theory; in fact it is mutually interpretable with first-order Peano arithmetic. (To show that
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
is a fairly weak theory; in fact it is mutually interpretable with first-order Peano arithmetic. (To show that
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
interprets PA, the trick is to code arithmetical statements as statements about finite concepts.) On the other hand, adding
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
interprets PA, the trick is to code arithmetical statements as statements about finite concepts.) On the other hand, adding
![]() $\mathrm{w2FA}$
to
$\mathrm{w2FA}$
to
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
results in a much stronger theory, one which proves that the numerical sort is Dedekind-infinite and hence interprets second-order arithmetic. Second-order arithmetic is not conservative over Peano arithmetic. By means of a carefully chosen interpretation, this non-conservativeness can be transferred to the theories of interest to us. For example,
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
results in a much stronger theory, one which proves that the numerical sort is Dedekind-infinite and hence interprets second-order arithmetic. Second-order arithmetic is not conservative over Peano arithmetic. By means of a carefully chosen interpretation, this non-conservativeness can be transferred to the theories of interest to us. For example,
![]() $\mathrm{w2FA} + \neg \mathit {Fin}(V)$
proves the interpretation of a consistency statement for Peano arithmetic, while
$\mathrm{w2FA} + \neg \mathit {Fin}(V)$
proves the interpretation of a consistency statement for Peano arithmetic, while
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
does not.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
does not.
Let
![]() $X \approx Y$
abbreviate that there is a bijection between X and Y, in which case we say that X and Y are equinumerous concepts.
$X \approx Y$
abbreviate that there is a bijection between X and Y, in which case we say that X and Y are equinumerous concepts.
If
![]() $Ryz$
is a binary relation, let
$Ryz$
is a binary relation, let
![]() $R_y$
be the concept defined by
$R_y$
be the concept defined by
![]() $R_y z \leftrightarrow Ryz$
. (This is terrible notation, but we only use it in the following definition.)
$R_y z \leftrightarrow Ryz$
. (This is terrible notation, but we only use it in the following definition.)
Definition 7.41. Define
![]() $\mathit {Succ}, \mathit {Leq}, \mathit {Add}, \mathit {Mult}$
as follows:
$\mathit {Succ}, \mathit {Leq}, \mathit {Add}, \mathit {Mult}$
as follows:
 $$ \begin{align*} \mathit{Succ}(X,Y) &\iff \exists a(\neg Xa \ \wedge\ Y \approx X\cup \{a\}), \\ \mathit{Leq}(X,Y) &\iff \exists X'(X \approx X' \ \wedge\ X' \subseteq Y), \\ \mathit{Add}(X,Y,Z) &\iff \exists Y' (Y \approx Y' \ \wedge\ X \cap Y' = \varnothing \ \wedge\ X \cup Y' \approx Z), \\ \mathit{Mult}(X,Y,Z) &\iff \exists R[ \forall y \forall z (Ryz \rightarrow (Yy \wedge Zz)) \wedge \forall y(Yy \rightarrow R_y \approx X) \\ & \quad \qquad \wedge \forall z(Zz \rightarrow \exists ! y Ryz) ]. \end{align*} $$
$$ \begin{align*} \mathit{Succ}(X,Y) &\iff \exists a(\neg Xa \ \wedge\ Y \approx X\cup \{a\}), \\ \mathit{Leq}(X,Y) &\iff \exists X'(X \approx X' \ \wedge\ X' \subseteq Y), \\ \mathit{Add}(X,Y,Z) &\iff \exists Y' (Y \approx Y' \ \wedge\ X \cap Y' = \varnothing \ \wedge\ X \cup Y' \approx Z), \\ \mathit{Mult}(X,Y,Z) &\iff \exists R[ \forall y \forall z (Ryz \rightarrow (Yy \wedge Zz)) \wedge \forall y(Yy \rightarrow R_y \approx X) \\ & \quad \qquad \wedge \forall z(Zz \rightarrow \exists ! y Ryz) ]. \end{align*} $$
In other words,
![]() $\mathit {Mult}(X,Y,Z)$
says that Z is equinumerous with the union of
$\mathit {Mult}(X,Y,Z)$
says that Z is equinumerous with the union of
![]() $|Y|$
disjoint copies of X.
$|Y|$
disjoint copies of X.
Definition 7.42. Define the translation
![]() $\alpha : L_2 \to \mathcal {L}^+$
as follows.
$\alpha : L_2 \to \mathcal {L}^+$
as follows.
Identify first-order variables of
![]() $L_{2}$
with base-sort concept variables of
$L_{2}$
with base-sort concept variables of
![]() $\mathcal {L}^+$
. Identify second-order variables of
$\mathcal {L}^+$
. Identify second-order variables of
![]() $L_2$
with numerical-sort concept variables of
$L_2$
with numerical-sort concept variables of
![]() $\mathcal {L}^+$
.
$\mathcal {L}^+$
.
Relativize
![]() $\forall x$
to the formula
$\forall x$
to the formula
![]() $\mathit {Fin}(X)$
.
$\mathit {Fin}(X)$
.
Relativize
![]() $\forall X$
to the formula
$\forall X$
to the formula
![]() $\mathit {FinNums}(\mathbf {X}) := \forall \mathbf {y}(\mathbf {X} \mathbf {y} \rightarrow \exists Y[\mathbf {y} = \#Y \wedge \mathit {Fin}(Y)])$
.
$\mathit {FinNums}(\mathbf {X}) := \forall \mathbf {y}(\mathbf {X} \mathbf {y} \rightarrow \exists Y[\mathbf {y} = \#Y \wedge \mathit {Fin}(Y)])$
.
Translate predication and equality as follows:
 $$ \begin{align*} (Xy)^\alpha &:= \mathbf{X}(\#Y), \\ (x=y)^\alpha &:= X \approx Y. \end{align*} $$
$$ \begin{align*} (Xy)^\alpha &:= \mathbf{X}(\#Y), \\ (x=y)^\alpha &:= X \approx Y. \end{align*} $$
Translate
![]() $0, S, \leq , +, \cdot $
as follows:
$0, S, \leq , +, \cdot $
as follows:
 $$ \begin{align*} (x=0)^\alpha &:= X = \varnothing, \\ (Sx = y)^\alpha &:= \mathit{Succ}(X,Y), \\ (x \leq y)^\alpha &:= \mathit{Leq}(X,Y), \\ (x+ y = z)^\alpha &:= \mathit{Add}(X,Y,Z), \\ (x \cdot y = z)^\alpha &:= \mathit{Mult}(X,Y,Z). \end{align*} $$
$$ \begin{align*} (x=0)^\alpha &:= X = \varnothing, \\ (Sx = y)^\alpha &:= \mathit{Succ}(X,Y), \\ (x \leq y)^\alpha &:= \mathit{Leq}(X,Y), \\ (x+ y = z)^\alpha &:= \mathit{Add}(X,Y,Z), \\ (x \cdot y = z)^\alpha &:= \mathit{Mult}(X,Y,Z). \end{align*} $$
We may extend this translation to all
![]() $L_2$
-formulas via the usual techniques for eliminating definite descriptions. For example, write
$L_2$
-formulas via the usual techniques for eliminating definite descriptions. For example, write
![]() $SSx = y$
as
$SSx = y$
as
![]() $\exists z(Sx = z \wedge Sz = y)$
, and so on.
$\exists z(Sx = z \wedge Sz = y)$
, and so on.
Lemma 7.43. Restricted to
![]() $L_{\mathrm{PA}}$
-formulas, the translation
$L_{\mathrm{PA}}$
-formulas, the translation
![]() $\alpha : L_2 \to \mathcal {L}^+$
is an interpretation of PA in
$\alpha : L_2 \to \mathcal {L}^+$
is an interpretation of PA in
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
Proof. Note that if
![]() $\varphi $
is an
$\varphi $
is an
![]() $L_{\mathrm{PA}}$
-formula, then
$L_{\mathrm{PA}}$
-formula, then
![]() $\varphi ^\alpha $
is an
$\varphi ^\alpha $
is an
![]() $\mathcal {L}$
-formula. We will show that
$\mathcal {L}$
-formula. We will show that
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
proves the
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
proves the
![]() $\alpha $
-translation of each axiom of PA, and also proves that
$\alpha $
-translation of each axiom of PA, and also proves that
![]() $\mathit {Succ}$
,
$\mathit {Succ}$
,
![]() $\mathit {Add}$
,
$\mathit {Add}$
,
![]() $\mathit {Mult}$
define total functions (up to
$\mathit {Mult}$
define total functions (up to
![]() $\approx $
).
$\approx $
).
First we prove that
![]() $\mathit {Succ}$
defines a total function (up to
$\mathit {Succ}$
defines a total function (up to
![]() $\approx $
). In other words, we show that for any Stäckel-finite concepts
$\approx $
). In other words, we show that for any Stäckel-finite concepts
![]() $X, Y, Z$
,
$X, Y, Z$
,
 $$ \begin{align*} & \exists W (\mathit{Fin}(W) \wedge \mathit{Succ}(X, W)), \\ &\mathit{Succ}(X, Y) \wedge \mathit{Succ}(X, Z) \rightarrow Y \approx Z. \end{align*} $$
$$ \begin{align*} & \exists W (\mathit{Fin}(W) \wedge \mathit{Succ}(X, W)), \\ &\mathit{Succ}(X, Y) \wedge \mathit{Succ}(X, Z) \rightarrow Y \approx Z. \end{align*} $$
We reason in
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
. For the first claim, take any concept X such that
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
. For the first claim, take any concept X such that
![]() $\mathit {Fin}(X)$
. Then X is not V. So, there exists a such that
$\mathit {Fin}(X)$
. Then X is not V. So, there exists a such that
![]() $\neg Xa$
. Then
$\neg Xa$
. Then
![]() $\mathit {Succ}(X, X \cup \{a\})$
, and it is easy to check that
$\mathit {Succ}(X, X \cup \{a\})$
, and it is easy to check that
![]() $\mathit {Fin}(X \cup \{a\})$
. This gives us the first claim. The second claim is obtained simply by unpacking the definition of
$\mathit {Fin}(X \cup \{a\})$
. This gives us the first claim. The second claim is obtained simply by unpacking the definition of
![]() $\mathit {Succ}$
.
$\mathit {Succ}$
.
We postpone the proofs that
![]() $\mathit {Add}$
and
$\mathit {Add}$
and
![]() $\mathit {Mult}$
define total functions (up to
$\mathit {Mult}$
define total functions (up to
![]() $\approx $
).
$\approx $
).
The
![]() $\alpha $
-translations of the axioms of Q can be expressed as follows (after eliminating definite descriptions in a convenient way). For any Stäckel-finite concepts
$\alpha $
-translations of the axioms of Q can be expressed as follows (after eliminating definite descriptions in a convenient way). For any Stäckel-finite concepts
![]() $X, Y, Z, Y', Z'$
,
$X, Y, Z, Y', Z'$
,
 $$ \begin{align*} & \neg \mathit{Succ}(X, \varnothing), \\ & \mathit{Succ}(X, Z) \wedge \mathit{Succ}(Y,Z) \rightarrow X \approx Y, \\ & \mathit{Add}(X, \varnothing, Z) \leftrightarrow Z \approx X, \\ & \mathit{Succ}(Y, Y') \rightarrow (\mathit{Add}(X,Y',Z') \leftrightarrow \exists Z [\mathit{Fin}(Z) \wedge \mathit{Add}(X, Y, Z) \wedge \mathit{Succ}(Z,Z')]), \\ & \mathit{Mult}(X, \varnothing, Z) \leftrightarrow Z = \varnothing, \\ & \mathit{Succ}(Y, Y') \rightarrow (\mathit{Mult}(X,Y',Z') \leftrightarrow \exists Z [\mathit{Fin}(Z) \wedge \mathit{Mult}(X, Y, Z) \wedge \mathit{Add}(Z,X,Z')]), \\ & \mathit{Leq}(X,Y) \leftrightarrow \exists Z (\mathit{Fin}(Z) \wedge \mathit{Add}(Z,X,Y)). \end{align*} $$
$$ \begin{align*} & \neg \mathit{Succ}(X, \varnothing), \\ & \mathit{Succ}(X, Z) \wedge \mathit{Succ}(Y,Z) \rightarrow X \approx Y, \\ & \mathit{Add}(X, \varnothing, Z) \leftrightarrow Z \approx X, \\ & \mathit{Succ}(Y, Y') \rightarrow (\mathit{Add}(X,Y',Z') \leftrightarrow \exists Z [\mathit{Fin}(Z) \wedge \mathit{Add}(X, Y, Z) \wedge \mathit{Succ}(Z,Z')]), \\ & \mathit{Mult}(X, \varnothing, Z) \leftrightarrow Z = \varnothing, \\ & \mathit{Succ}(Y, Y') \rightarrow (\mathit{Mult}(X,Y',Z') \leftrightarrow \exists Z [\mathit{Fin}(Z) \wedge \mathit{Mult}(X, Y, Z) \wedge \mathit{Add}(Z,X,Z')]), \\ & \mathit{Leq}(X,Y) \leftrightarrow \exists Z (\mathit{Fin}(Z) \wedge \mathit{Add}(Z,X,Y)). \end{align*} $$
(We drop the third axiom of Q, since it is redundant in PA.) It is tedious but straightforward to check that all of these claims are provable from
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
The previous step essentially provides us with recursive definitions of
![]() $\mathit {Add}$
and
$\mathit {Add}$
and
![]() $\mathit {Mult}$
. Using these recursive definitions, it is then easy to prove that
$\mathit {Mult}$
. Using these recursive definitions, it is then easy to prove that
![]() $\mathit {Add}$
and
$\mathit {Add}$
and
![]() $\mathit {Mult}$
define total functions (up to
$\mathit {Mult}$
define total functions (up to
![]() $\approx $
). For
$\approx $
). For
![]() $\mathit {Add}$
, we must show that for any Stäckel-finite concepts
$\mathit {Add}$
, we must show that for any Stäckel-finite concepts
![]() $X, Y, Z, W$
,
$X, Y, Z, W$
,
 $$ \begin{align*} & \exists U (\mathit{Fin}(U) \wedge \mathit{Add}(X, Y, U)), \\ & \mathit{Add}(X, Y, Z) \wedge \mathit{Add}(X, Y, W) \rightarrow Z \approx W. \end{align*} $$
$$ \begin{align*} & \exists U (\mathit{Fin}(U) \wedge \mathit{Add}(X, Y, U)), \\ & \mathit{Add}(X, Y, Z) \wedge \mathit{Add}(X, Y, W) \rightarrow Z \approx W. \end{align*} $$
Both of these claims are provable by induction on the finite concept Y (Lemma 5.32), using the recursive definition of
![]() $\mathit {Add}$
. The proof for
$\mathit {Add}$
. The proof for
![]() $\mathit {Mult}$
is similar.
$\mathit {Mult}$
is similar.
Lastly, the
![]() $\alpha $
-translation of the induction scheme of PA follows from induction on finite concepts (Lemma 5.32 again).
$\alpha $
-translation of the induction scheme of PA follows from induction on finite concepts (Lemma 5.32 again).
Lemma 7.44. The translation
![]() $\alpha : L_2 \to \mathcal {L}^+$
is an interpretation of
$\alpha : L_2 \to \mathcal {L}^+$
is an interpretation of
![]() $Z_2$
in
$Z_2$
in
![]() $\mathrm{w2FA} + \neg \mathit {Fin}(V)$
.
$\mathrm{w2FA} + \neg \mathit {Fin}(V)$
.
Proof. By Lemma 7.43, we already know that the
![]() $\alpha $
-translation is an interpretation of PA in
$\alpha $
-translation is an interpretation of PA in
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
, and hence in
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
, and hence in
![]() $\mathrm{w2FA} + \neg \mathit {Fin}(V)$
. It remains to check that
$\mathrm{w2FA} + \neg \mathit {Fin}(V)$
. It remains to check that
![]() $\mathrm{w2FA} + \neg \mathit {Fin}(V)$
proves the
$\mathrm{w2FA} + \neg \mathit {Fin}(V)$
proves the
![]() $\alpha $
-translations of the second-order induction and comprehension axioms.
$\alpha $
-translations of the second-order induction and comprehension axioms.
The translation of the second-order induction axiom is equivalent to
 $$ \begin{align*} & \mathbf{X}(\# \varnothing) \wedge \forall X \left ( \mathit{Fin}(X) \wedge \mathbf{X}(\#X) \wedge \mathit{Succ}(X, Y) \rightarrow \mathbf{X}(\#Y) \right ) \rightarrow \forall X \left ( \mathit{Fin}(X) \rightarrow \mathbf{X}(\#X) \right ). \end{align*} $$
$$ \begin{align*} & \mathbf{X}(\# \varnothing) \wedge \forall X \left ( \mathit{Fin}(X) \wedge \mathbf{X}(\#X) \wedge \mathit{Succ}(X, Y) \rightarrow \mathbf{X}(\#Y) \right ) \rightarrow \forall X \left ( \mathit{Fin}(X) \rightarrow \mathbf{X}(\#X) \right ). \end{align*} $$
This is easily proved by induction on finite concepts, generalized to
![]() $\mathcal {L}^+$
-formulas. The generalization is proved in the same way as Lemma 5.32.
$\mathcal {L}^+$
-formulas. The generalization is proved in the same way as Lemma 5.32.
The comprehension scheme translates as follows:
 $$ \begin{align*} \exists \mathbf{X} \left ( \mathit{FinNums}(\mathbf{X}) \wedge \forall Y \left( \mathit{Fin}(Y) \rightarrow \left ( \mathbf{X}(\#Y) \leftrightarrow \varphi^\alpha(Y) \right ) \right) \right ). \end{align*} $$
$$ \begin{align*} \exists \mathbf{X} \left ( \mathit{FinNums}(\mathbf{X}) \wedge \forall Y \left( \mathit{Fin}(Y) \rightarrow \left ( \mathbf{X}(\#Y) \leftrightarrow \varphi^\alpha(Y) \right ) \right) \right ). \end{align*} $$
To prove this in
![]() $\mathrm{w2FA} + \neg \mathit {Fin}(V)$
, apply comprehension (in
$\mathrm{w2FA} + \neg \mathit {Fin}(V)$
, apply comprehension (in
![]() $\mathcal {L}^+$
) to the formula
$\mathcal {L}^+$
) to the formula
 $$ \begin{align*}\exists Y \left ( \mathbf{x} = \#Y \wedge \mathit{Fin}(Y) \wedge \varphi^\alpha(Y) \right ). \end{align*} $$
$$ \begin{align*}\exists Y \left ( \mathbf{x} = \#Y \wedge \mathit{Fin}(Y) \wedge \varphi^\alpha(Y) \right ). \end{align*} $$
Then use w2FA and the fact that
![]() $\approx $
is a congruence with respect to
$\approx $
is a congruence with respect to
![]() $\varphi ^\alpha (Y)$
.
$\varphi ^\alpha (Y)$
.
We will now define a translation
![]() $\beta : \mathcal {L} \to L_{\mathrm{PA}}$
inspired by the Fraenkel model, and show that it is an interpretation of
$\beta : \mathcal {L} \to L_{\mathrm{PA}}$
inspired by the Fraenkel model, and show that it is an interpretation of
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
in PA.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
in PA.
Fix primitive recursive encodings of finite sets and sequences as natural numbers. For finite sequences, this amounts to specifying the following functions in
![]() $L_{\mathrm{PA}}$
:
$L_{\mathrm{PA}}$
:
-
(i) for each
 $n\in \mathbb {N}$
, a primitive recursive function
$n\in \mathbb {N}$
, a primitive recursive function
 $\langle x_1, \ldots , x_n \rangle $
, which codes this tuple as a single number,
$\langle x_1, \ldots , x_n \rangle $
, which codes this tuple as a single number, -
(ii) primitive recursive functions
 $\mathit {length}(s)$
and
$\mathit {length}(s)$
and
 $(s)_i$
, which return the length and the i-th element of the finite sequence coded by s.
$(s)_i$
, which return the length and the i-th element of the finite sequence coded by s.
We identify finite sets and sequences with their codes. We use the letter E for finite sets, and the letter s for finite sequences.
Fix a primitive recursive Gödel numbering of
![]() $L_{\mathrm{PA}}$
-formulas. We identify formulas with their Gödel numbers. For each formula
$L_{\mathrm{PA}}$
-formulas. We identify formulas with their Gödel numbers. For each formula
![]() $\varphi $
, let
$\varphi $
, let
![]() be a formal numeral that denotes (the Gödel number of)
be a formal numeral that denotes (the Gödel number of)
![]() $\varphi $
.
$\varphi $
.
Next, we describe
![]() $L_{\mathrm{PA}}$
-formulas
$L_{\mathrm{PA}}$
-formulas
![]() $\mathit {BoolEq}$
,
$\mathit {BoolEq}$
,
![]() $\mathit {BoolSat}$
,
$\mathit {BoolSat}$
,
![]() $\mathit {pad}_n$
representing certain primitive recursive relations and functions.
$\mathit {pad}_n$
representing certain primitive recursive relations and functions.
Let
![]() $\mathit {BoolEq}(x, y, E)$
just in case: x is a Boolean combination of
$\mathit {BoolEq}(x, y, E)$
just in case: x is a Boolean combination of
![]() $L_{\mathrm{PA}}$
-equalities with exactly y free variables and with constant symbols drawn from
$L_{\mathrm{PA}}$
-equalities with exactly y free variables and with constant symbols drawn from
![]() $\{S^e0: e\in E\}$
.
$\{S^e0: e\in E\}$
.
Let
![]() $\mathit {BoolSat}(x,s)$
just in case: x is a Boolean combination of
$\mathit {BoolSat}(x,s)$
just in case: x is a Boolean combination of
![]() $L_{\mathrm{PA}}$
-equalities that is satisfied when the i-th variable of
$L_{\mathrm{PA}}$
-equalities that is satisfied when the i-th variable of
![]() $L_{\mathrm{PA}}$
is assigned the value
$L_{\mathrm{PA}}$
is assigned the value
![]() $(s)_i$
, for all
$(s)_i$
, for all
![]() $i \leq length(s)$
. This is primitive recursive, because truth and satisfaction for bounded (
$i \leq length(s)$
. This is primitive recursive, because truth and satisfaction for bounded (
![]() $\Sigma _0$
) formulas are primitive recursive notions.
$\Sigma _0$
) formulas are primitive recursive notions.
For each
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\mathit {pad}_n(x_1, \ldots , x_n, y_1, \ldots , y_n)=s$
just in case: s is the shortest finite sequence whose
$\mathit {pad}_n(x_1, \ldots , x_n, y_1, \ldots , y_n)=s$
just in case: s is the shortest finite sequence whose
![]() $x_i$
-th element is
$x_i$
-th element is
![]() $y_i$
(for all
$y_i$
(for all
![]() $1 \leq i \leq n$
) and whose other elements are all zero.
$1 \leq i \leq n$
) and whose other elements are all zero.
Definition 7.45. Define the translation
![]() $\beta : \mathcal {L} \to L_{\mathrm{PA}}$
as follows.
$\beta : \mathcal {L} \to L_{\mathrm{PA}}$
as follows.
Let the variables of
![]() $L_{\mathrm{PA}}$
and the object variables of
$L_{\mathrm{PA}}$
and the object variables of
![]() $\mathcal {L}$
be enumerated by
$\mathcal {L}$
be enumerated by
![]() $v_1, v_2, v_3, \ldots $
.
$v_1, v_2, v_3, \ldots $
.
Translate each object variable
![]() $v_i$
of
$v_i$
of
![]() $\mathcal {L}$
by the even-numbered variable
$\mathcal {L}$
by the even-numbered variable
![]() $v_{2i}$
. Translate each relation variable X of
$v_{2i}$
. Translate each relation variable X of
![]() $\mathcal {L}$
by a distinct odd-numbered variable
$\mathcal {L}$
by a distinct odd-numbered variable
![]() $v_X \in \{v_1, v_3, v_5, \ldots \}$
. In the last clause, E is a fresh variable and n is the arity of X.
$v_X \in \{v_1, v_3, v_5, \ldots \}$
. In the last clause, E is a fresh variable and n is the arity of X.
 $$ \begin{align*} (X v_{i_1} \cdots v_{i_n})^\beta &:= \mathit{BoolSat}(v_{X}, \mathit{pad}_n(S^{i_1}0, \ldots, S^{i_n}0, v_{2i_1}, \ldots, v_{2i_n} ) ). \\ (v_i = v_j)^\beta &:= v_{2i} = v_{2j}. \\ (\varphi \rightarrow \psi)^\beta &:= \varphi^\beta \rightarrow \psi^\beta. \\ (\neg \varphi)^\beta &:= \neg \varphi^\beta. \\ (\forall v_i \ \varphi)^\beta &:= \forall v_{2i} \ \varphi^\beta. \\ (\forall X \ \varphi)^\beta &:= \forall v_{X} (\exists E \ \mathit{BoolEq}(v_{X}, S^n 0, E) \rightarrow \varphi^\beta). \end{align*} $$
$$ \begin{align*} (X v_{i_1} \cdots v_{i_n})^\beta &:= \mathit{BoolSat}(v_{X}, \mathit{pad}_n(S^{i_1}0, \ldots, S^{i_n}0, v_{2i_1}, \ldots, v_{2i_n} ) ). \\ (v_i = v_j)^\beta &:= v_{2i} = v_{2j}. \\ (\varphi \rightarrow \psi)^\beta &:= \varphi^\beta \rightarrow \psi^\beta. \\ (\neg \varphi)^\beta &:= \neg \varphi^\beta. \\ (\forall v_i \ \varphi)^\beta &:= \forall v_{2i} \ \varphi^\beta. \\ (\forall X \ \varphi)^\beta &:= \forall v_{X} (\exists E \ \mathit{BoolEq}(v_{X}, S^n 0, E) \rightarrow \varphi^\beta). \end{align*} $$
Lemma 7.46. The translation
![]() $\beta : \mathcal {L} \to L_{\mathrm{PA}}$
is an interpretation of
$\beta : \mathcal {L} \to L_{\mathrm{PA}}$
is an interpretation of
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
in PA.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
in PA.
Proof. It is easy to check that the
![]() $\beta $
-translation of any non-comprehension axiom is a theorem of first-order logic, and hence is provable in PA.Footnote
12
It remains to show that PA proves the
$\beta $
-translation of any non-comprehension axiom is a theorem of first-order logic, and hence is provable in PA.Footnote
12
It remains to show that PA proves the
![]() $\beta $
-translation of each comprehension axiom, and also that PA proves
$\beta $
-translation of each comprehension axiom, and also that PA proves
![]() $(\neg \mathit {Fin}(V))^\beta $
.
$(\neg \mathit {Fin}(V))^\beta $
.
The idea is to formalize the proofs of Lemmas 6.38, 6.39, and 6.40 in PA. The main obstacle is that we defined symmetric sets
![]() $A \subseteq \mathbb {N}^n$
in terms of arbitrary permutations of
$A \subseteq \mathbb {N}^n$
in terms of arbitrary permutations of
![]() $\mathbb {N}$
, and it is not obvious how to formalize those in PA. But in fact we do not need arbitrary permutations. Say that a permutation
$\mathbb {N}$
, and it is not obvious how to formalize those in PA. But in fact we do not need arbitrary permutations. Say that a permutation
![]() $\pi :\mathbb {N} \to \mathbb {N}$
is essentially finite if
$\pi :\mathbb {N} \to \mathbb {N}$
is essentially finite if
![]() $\pi (a) = a$
for all but finitely many
$\pi (a) = a$
for all but finitely many
![]() $a \in \mathbb {N}$
. If we go through Section 6, replacing ‘permutation’ with ‘essentially finite permutation’ everywhere, we get exactly the same model, and all the proofs still work.
$a \in \mathbb {N}$
. If we go through Section 6, replacing ‘permutation’ with ‘essentially finite permutation’ everywhere, we get exactly the same model, and all the proofs still work.
We formalize Lemma 6.40 as follows. Say that an
![]() $L_{\mathrm{PA}}$
-formula
$L_{\mathrm{PA}}$
-formula
![]() $\varphi (\bar x)$
is symmetric with support E just in case, for every essentially finite permutation
$\varphi (\bar x)$
is symmetric with support E just in case, for every essentially finite permutation
![]() $\pi $
,
$\pi $
,
Then we prove a theorem scheme in PA which says: ‘An
![]() $L_{\mathrm{PA}}$
-formula is symmetric iff there is a Boolean combination of equalities coextensive with it.’ More precisely, let
$L_{\mathrm{PA}}$
-formula is symmetric iff there is a Boolean combination of equalities coextensive with it.’ More precisely, let
![]() $\varphi (v_{i_1}, \ldots , v_{i_n})$
be any
$\varphi (v_{i_1}, \ldots , v_{i_n})$
be any
![]() $L_{\mathrm{PA}}$
-formula with exactly the free variables displayed. Then PA proves the following:
$L_{\mathrm{PA}}$
-formula with exactly the free variables displayed. Then PA proves the following:
![]() $\varphi (v_{i_1}, \ldots , v_{i_n})$
is symmetric with support E iff there exists y such that
$\varphi (v_{i_1}, \ldots , v_{i_n})$
is symmetric with support E iff there exists y such that
![]() $(\!{\implies}\!\kern-1pt)$
. We reason in PA. Suppose that
$(\!{\implies}\!\kern-1pt)$
. We reason in PA. Suppose that
![]() $\varphi (v_{i_1}, \ldots , v_{i_n})$
is symmetric with support E. Let
$\varphi (v_{i_1}, \ldots , v_{i_n})$
is symmetric with support E. Let
![]() $\psi _1, \ldots , \psi _m$
be all possible disjunctions of formulas of the form
$\psi _1, \ldots , \psi _m$
be all possible disjunctions of formulas of the form
 $$ \begin{align*}\bigwedge_{\substack{j,k \leq n \\ j \neq k}} (\neg) \ v_{i_j} = v_{i_k} \ \wedge \ \bigwedge_{\substack{ j \leq n \\ e \in E }} (\neg) \ v_{i_j} = S^e 0, \end{align*} $$
$$ \begin{align*}\bigwedge_{\substack{j,k \leq n \\ j \neq k}} (\neg) \ v_{i_j} = v_{i_k} \ \wedge \ \bigwedge_{\substack{ j \leq n \\ e \in E }} (\neg) \ v_{i_j} = S^e 0, \end{align*} $$
where parenthesized negations may or may not be present. Argue that
![]() $\bar x \sim _E \bar y \rightarrow (\varphi (\bar x) \leftrightarrow \varphi (\bar y))$
, and hence
$\bar x \sim _E \bar y \rightarrow (\varphi (\bar x) \leftrightarrow \varphi (\bar y))$
, and hence
Then observe that
![]() , for each
, for each
![]() $1 \leq i \leq m$
.Footnote
13
Reasoning by cases, we are done.
$1 \leq i \leq m$
.Footnote
13
Reasoning by cases, we are done.
For the
![]() $(\Longleftarrow )$
direction, copy the rest of the proof of Lemma 6.40.
$(\Longleftarrow )$
direction, copy the rest of the proof of Lemma 6.40.
Next, we formalize Lemma 6.38. We replace
![]() $\mathcal {M} \vDash \varphi $
(‘
$\mathcal {M} \vDash \varphi $
(‘
![]() $\mathcal {M}$
satisfies
$\mathcal {M}$
satisfies
![]() $\varphi $
’) with
$\varphi $
’) with
![]() $\varphi ^\beta $
throughout. For each
$\varphi ^\beta $
throughout. For each
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\bar x, \bar y, \bar Y)$
not containing X free, we wish to show that PA proves
$\varphi (\bar x, \bar y, \bar Y)$
not containing X free, we wish to show that PA proves
This basically says: ‘There is a Boolean combination of equalities coextensive with
![]() $\varphi (\bar x, \bar y, \bar Y)^\beta $
.’ By the formalized version of Lemma 6.40, it suffices to prove in PA that
$\varphi (\bar x, \bar y, \bar Y)^\beta $
.’ By the formalized version of Lemma 6.40, it suffices to prove in PA that
![]() $\varphi (\bar x, \bar y, \bar Y)^\beta $
is a symmetric
$\varphi (\bar x, \bar y, \bar Y)^\beta $
is a symmetric
![]() $L_{\mathrm{PA}}$
-formula. To do this, use induction on
$L_{\mathrm{PA}}$
-formula. To do this, use induction on
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\varphi (\bar x, \bar X)$
to prove the following theorem scheme in PA:
$\varphi (\bar x, \bar X)$
to prove the following theorem scheme in PA:
(This corresponds to our earlier observation that permuting everything uniformly doesn’t change any truth-values in
![]() $\mathcal {M}$
relative to any variable-assignment.) Then copy the rest of the proof of Lemma 6.38.
$\mathcal {M}$
relative to any variable-assignment.) Then copy the rest of the proof of Lemma 6.38.
In the same way, it is easy to formalize Lemma 6.39 in PA.
We are now ready to prove the first main theorem of the paper.
Theorem 7.47.
w2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {Fin}(V)$
.
Proof. Let
![]() $\mathit {Con}_{\mathrm{PA}}$
denote a standard consistency statement for PA. We claim that
$\mathit {Con}_{\mathrm{PA}}$
denote a standard consistency statement for PA. We claim that
![]() $(\mathit {Con}_{\mathrm{PA}})^\alpha $
is a witness to non-conservativeness. That is,
$(\mathit {Con}_{\mathrm{PA}})^\alpha $
is a witness to non-conservativeness. That is,
Proof of claim (1)
Write
![]() $\vartriangleright $
for ‘interprets’. From Lemmas 7.43 and 7.46, we have
$\vartriangleright $
for ‘interprets’. From Lemmas 7.43 and 7.46, we have
Suppose for a contradiction that
![]() $\mathit {Ax}_{\mathcal {L}} +\neg \mathit {Fin}(V) \vdash (\mathit {Con}_{\mathrm{PA}})^\alpha $
. Then
$\mathit {Ax}_{\mathcal {L}} +\neg \mathit {Fin}(V) \vdash (\mathit {Con}_{\mathrm{PA}})^\alpha $
. Then
![]() $\mathrm{PA} \vdash ((\mathit {Con}_{\mathrm{PA}})^\alpha )^\beta $
, and hence
$\mathrm{PA} \vdash ((\mathit {Con}_{\mathrm{PA}})^\alpha )^\beta $
, and hence
![]() $\mathrm{PA} \vartriangleright ^{\beta \circ \alpha } \mathrm{PA} + \mathit {Con}_{\mathrm{PA}}$
. However, by a strong version of Gödel’s second incompleteness theorem,
$\mathrm{PA} \vartriangleright ^{\beta \circ \alpha } \mathrm{PA} + \mathit {Con}_{\mathrm{PA}}$
. However, by a strong version of Gödel’s second incompleteness theorem,
![]() $\mathrm{PA} \not \vartriangleright (\mathrm{PA} + \mathit {Con}_{\mathrm{PA}})$
.Footnote
14
Contradiction.
$\mathrm{PA} \not \vartriangleright (\mathrm{PA} + \mathit {Con}_{\mathrm{PA}})$
.Footnote
14
Contradiction.
Proof of claim (2)
It is well known that
![]() $Z_2 \vdash \mathit {Con}_{\mathrm{PA}}$
. Hence, by Lemma 7.44,
$Z_2 \vdash \mathit {Con}_{\mathrm{PA}}$
. Hence, by Lemma 7.44,
Corollary 7.48.
w2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
For proof, see Lemma 1.3.
Corollary 7.49.
2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
8 w2FA is conservative over stronger base theories
It is surprising that w2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}}$
. However, the next two theorems establish some limits to the non-conservativeness of w2FA.
$\mathit {Ax}_{\mathcal {L}}$
. However, the next two theorems establish some limits to the non-conservativeness of w2FA.
Theorem 8.50. w2FA is conservative over third-order logic.
Proof. Let
![]() $\mathcal {L}^3$
be the third-order analog of the base language
$\mathcal {L}^3$
be the third-order analog of the base language
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\mathit {Ax}_{\mathcal {L}^3}$
denote the axioms of the deductive system for
$\mathit {Ax}_{\mathcal {L}^3}$
denote the axioms of the deductive system for
![]() $\mathcal {L}^3$
, including full third-order comprehension in the base sort. Note that w2FA still only includes second-order comprehension for the numerical sort.
$\mathcal {L}^3$
, including full third-order comprehension in the base sort. Note that w2FA still only includes second-order comprehension for the numerical sort.
Take any
![]() $\mathcal {L}^3$
-formula
$\mathcal {L}^3$
-formula
![]() $\varphi $
, and suppose that
$\varphi $
, and suppose that
![]() $\mathrm{w2FA} + \mathit {Ax}_{\mathcal {L}^3} \vdash \varphi $
. We show that
$\mathrm{w2FA} + \mathit {Ax}_{\mathcal {L}^3} \vdash \varphi $
. We show that
![]() $\mathit {Ax}_{\mathcal {L}^3} \vdash \varphi $
. Our strategy is to define an interpretation of w2FA in
$\mathit {Ax}_{\mathcal {L}^3} \vdash \varphi $
. Our strategy is to define an interpretation of w2FA in
![]() $\mathit {Ax}_{\mathcal {L}^3}$
that leaves
$\mathit {Ax}_{\mathcal {L}^3}$
that leaves
![]() $\mathcal {L}^3$
-sentences fixed (up to renaming of bound variables). Under such an interpretation, any derivation of
$\mathcal {L}^3$
-sentences fixed (up to renaming of bound variables). Under such an interpretation, any derivation of
![]() $\varphi $
from
$\varphi $
from
![]() $\mathrm{w2FA} + \mathit {Ax}_{\mathcal {L}^3}$
is transformed into a derivation of
$\mathrm{w2FA} + \mathit {Ax}_{\mathcal {L}^3}$
is transformed into a derivation of
![]() $\varphi $
from
$\varphi $
from
![]() $\mathit {Ax}_{\mathcal {L}^3}$
. The idea is to interpret each cardinality
$\mathit {Ax}_{\mathcal {L}^3}$
. The idea is to interpret each cardinality
![]() $\#X$
as the concept X from whence it came, with numerical-sort equality being interpreted as equinumerosity.
$\#X$
as the concept X from whence it came, with numerical-sort equality being interpreted as equinumerosity.
First, we define a pre-translation from variables of
![]() $\mathcal {L}^3 \cup \mathcal {L}^+$
into variables of
$\mathcal {L}^3 \cup \mathcal {L}^+$
into variables of
![]() $\mathcal {L}^3$
. Translate each variable of sort
$\mathcal {L}^3$
. Translate each variable of sort
![]() $\tau $
as a variable of sort
$\tau $
as a variable of sort
![]() $\tau ^*$
, where
$\tau ^*$
, where
 $$ \begin{align*} 0^* &:= 0, \\ n^* &:= \langle 0 \rangle, \\ \langle \tau_1, \ldots, \tau_k \rangle^* &:= \langle \tau_1^*, \ldots, \tau_k^* \rangle. \end{align*} $$
$$ \begin{align*} 0^* &:= 0, \\ n^* &:= \langle 0 \rangle, \\ \langle \tau_1, \ldots, \tau_k \rangle^* &:= \langle \tau_1^*, \ldots, \tau_k^* \rangle. \end{align*} $$
In other words,
![]() $\tau ^*$
is obtained from
$\tau ^*$
is obtained from
![]() $\tau $
by replacing each occurrence of n with
$\tau $
by replacing each occurrence of n with
![]() $\langle 0 \rangle $
.
$\langle 0 \rangle $
.
Set up the pre-translation so that distinct variables of
![]() $\mathcal {L}^3 \cup \mathcal {L}^+$
are translated as distinct variables of
$\mathcal {L}^3 \cup \mathcal {L}^+$
are translated as distinct variables of
![]() $\mathcal {L}^3$
. For example, let the base-sort concept variables be enumerated by
$\mathcal {L}^3$
. For example, let the base-sort concept variables be enumerated by
![]() $X_0, X_1, X_2, \ldots $
, and the numerical-sort object variables by
$X_0, X_1, X_2, \ldots $
, and the numerical-sort object variables by
![]() $\mathbf {{v}}_0, \mathbf {{v}}_1, \mathbf {{v}}_2, \ldots $
. Then let the pre-translations be
$\mathbf {{v}}_0, \mathbf {{v}}_1, \mathbf {{v}}_2, \ldots $
. Then let the pre-translations be
 $$ \begin{align*} X_i^* &:= X_{2i} , \\ \mathbf{{v}}_i^* &:= X_{2i+1}. \end{align*} $$
$$ \begin{align*} X_i^* &:= X_{2i} , \\ \mathbf{{v}}_i^* &:= X_{2i+1}. \end{align*} $$
Similarly for other sorts.
We now define the translation
![]() $*: \mathcal {L}^3 \cup \mathcal {L}^+ \to \mathcal {L}^3$
. In the first and last lines, let
$*: \mathcal {L}^3 \cup \mathcal {L}^+ \to \mathcal {L}^3$
. In the first and last lines, let
![]() $\tau = \langle \tau _1, \ldots , \tau _k \rangle $
be any second- or third-order sort. In the last line,
$\tau = \langle \tau _1, \ldots , \tau _k \rangle $
be any second- or third-order sort. In the last line,
![]() $\mathit {Cong}_\approx ((X^\tau )^*)$
is a metalinguistic abbreviation of the statement: ‘
$\mathit {Cong}_\approx ((X^\tau )^*)$
is a metalinguistic abbreviation of the statement: ‘
![]() $\approx $
is a congruence for the relevant argument-places of
$\approx $
is a congruence for the relevant argument-places of
![]() $(X^\tau )^*$
’, where the sort
$(X^\tau )^*$
’, where the sort
![]() $\tau $
determines which argument-places are relevant.
$\tau $
determines which argument-places are relevant.
 $$ \begin{align*} (X^\tau x_1^{\tau_1} \cdots x_k^{\tau_k})^* &:= (X^\tau)^* (x_1^{\tau_1})^* \cdots (x_k^{\tau_k})^*. \\ (x = y)^* &:= x^* = y^*. \\ (\mathbf{x} = \mathbf{y})^* &:= \mathbf{x}^* \approx \mathbf{y}^*. \\ (\mathbf{x} = \#X)^* &:= \mathbf{x}^* \approx X^*. \\ (\varphi \rightarrow \psi)^* &:= \varphi^* \rightarrow \psi^*. \\ (\neg \varphi)^* &:= \neg \varphi^*. \\ (\forall x \ \varphi)^* &= \forall x^* \ \varphi^*. \\ (\forall \mathbf{x} \ \varphi)^* &= \forall \mathbf{x}^* \ \varphi^*. \\ (\forall X^\tau \, \varphi)^* &= \begin{cases} \forall (X^\tau)^* \, \varphi^*, & \text{if } \tau \in \mathit{Sorts}^3(\{0\}), \\ \forall (X^\tau)^* (\mathit{Cong}_\approx((X^\tau)^*) \rightarrow \varphi^*), & \text{else.} \end{cases} \end{align*} $$
$$ \begin{align*} (X^\tau x_1^{\tau_1} \cdots x_k^{\tau_k})^* &:= (X^\tau)^* (x_1^{\tau_1})^* \cdots (x_k^{\tau_k})^*. \\ (x = y)^* &:= x^* = y^*. \\ (\mathbf{x} = \mathbf{y})^* &:= \mathbf{x}^* \approx \mathbf{y}^*. \\ (\mathbf{x} = \#X)^* &:= \mathbf{x}^* \approx X^*. \\ (\varphi \rightarrow \psi)^* &:= \varphi^* \rightarrow \psi^*. \\ (\neg \varphi)^* &:= \neg \varphi^*. \\ (\forall x \ \varphi)^* &= \forall x^* \ \varphi^*. \\ (\forall \mathbf{x} \ \varphi)^* &= \forall \mathbf{x}^* \ \varphi^*. \\ (\forall X^\tau \, \varphi)^* &= \begin{cases} \forall (X^\tau)^* \, \varphi^*, & \text{if } \tau \in \mathit{Sorts}^3(\{0\}), \\ \forall (X^\tau)^* (\mathit{Cong}_\approx((X^\tau)^*) \rightarrow \varphi^*), & \text{else.} \end{cases} \end{align*} $$
It is easy to check that the
![]() $*$
-translation of each axiom of w2FA is provable from
$*$
-translation of each axiom of w2FA is provable from
![]() $\mathit {Ax}_{\mathcal {L}^3}$
. So, the translation works.
$\mathit {Ax}_{\mathcal {L}^3}$
. So, the translation works.
To prove the next theorem, we need another little fact about conservativeness.
Lemma 8.51. Let T be a theory in a formal language L, and let A be any L-sentence. Suppose that a sentence
![]() $\Delta $
is conservative over
$\Delta $
is conservative over
![]() $T + A$
and is also conservative over
$T + A$
and is also conservative over
![]() $T + \neg A$
. Then
$T + \neg A$
. Then
![]() $\Delta $
is conservative over T.
$\Delta $
is conservative over T.
Proof. Take any
![]() $\varphi \in L$
, and suppose that
$\varphi \in L$
, and suppose that
![]() $T + \Delta \vdash \varphi $
. We show that
$T + \Delta \vdash \varphi $
. We show that
![]() $T \vdash \varphi $
. Indeed
$T \vdash \varphi $
. Indeed
 $$ \begin{align*} T + A + \Delta &\vdash \varphi, \\ T + A &\vdash \varphi, \\ T &\vdash A \rightarrow \varphi. \end{align*} $$
$$ \begin{align*} T + A + \Delta &\vdash \varphi, \\ T + A &\vdash \varphi, \\ T &\vdash A \rightarrow \varphi. \end{align*} $$
By the same reasoning, we also have
![]() $T \vdash \neg A \rightarrow \varphi $
. Hence,
$T \vdash \neg A \rightarrow \varphi $
. Hence,
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
Theorem 8.52.
w2FA is conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
.
Proof. Let
![]() $|V|=1$
abbreviate the formula
$|V|=1$
abbreviate the formula
![]() $\forall x \forall y \ x=y$
. By Lemma 8.51, we may divide into cases according to whether
$\forall x \forall y \ x=y$
. By Lemma 8.51, we may divide into cases according to whether
![]() $|V| = 1$
or
$|V| = 1$
or
![]() $|V| \neq 1$
. The rest of the proof is contained in Lemmas 8.53 and 8.54.
$|V| \neq 1$
. The rest of the proof is contained in Lemmas 8.53 and 8.54.
Lemma 8.53.
w2FA is conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
.
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
.
Proof. We follow the same strategy as in Theorem 8.50. That is, we show how to define an interpretation
![]() $\dagger $
of w2FA in
$\dagger $
of w2FA in
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
that leaves
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
that leaves
![]() $\mathcal {L}$
-sentences fixed (up to renaming of bound variables). The idea is to interpret cardinalities
$\mathcal {L}$
-sentences fixed (up to renaming of bound variables). The idea is to interpret cardinalities
![]() $\#X$
as pairs of base-sort objects. Specifically, we will fix distinct base-sort objects a and b, represent
$\#X$
as pairs of base-sort objects. Specifically, we will fix distinct base-sort objects a and b, represent
![]() $\# (V \upharpoonright x)$
as
$\# (V \upharpoonright x)$
as
![]() $(x, a)$
, and represent
$(x, a)$
, and represent
![]() $\#\varnothing $
as
$\#\varnothing $
as
![]() $(a,b)$
.
$(a,b)$
.
First, we define a pre-translation from variables of
![]() $\mathcal {L}^+$
into variables of
$\mathcal {L}^+$
into variables of
![]() $\mathcal {L}$
. Translate each variable of sort
$\mathcal {L}$
. Translate each variable of sort
![]() $\tau $
as a distinct variable or pair of variables of sort(s)
$\tau $
as a distinct variable or pair of variables of sort(s)
![]() $\tau ^\dagger $
, where
$\tau ^\dagger $
, where
 $$ \begin{align*} 0^\dagger &:= 0, \\ n^\dagger &:= 0, 0, \\ \langle \tau_1, \ldots, \tau_k \rangle^\dagger &:= \langle \tau_1^\dagger, \ldots, \tau_k^\dagger \rangle. \end{align*} $$
$$ \begin{align*} 0^\dagger &:= 0, \\ n^\dagger &:= 0, 0, \\ \langle \tau_1, \ldots, \tau_k \rangle^\dagger &:= \langle \tau_1^\dagger, \ldots, \tau_k^\dagger \rangle. \end{align*} $$
For example,
![]() $\langle n, 0, n \rangle ^\dagger = \langle 0,0,0,0,0\rangle $
and
$\langle n, 0, n \rangle ^\dagger = \langle 0,0,0,0,0\rangle $
and
![]() $\langle \langle n \rangle , n \rangle ^\dagger = \langle \langle 0,0 \rangle , 0,0\rangle $
.
$\langle \langle n \rangle , n \rangle ^\dagger = \langle \langle 0,0 \rangle , 0,0\rangle $
.
Set up the pre-translation so that no variable of
![]() $\mathcal {L}$
is ever used twice. For definiteness, let the base-sort object variables be enumerated by
$\mathcal {L}$
is ever used twice. For definiteness, let the base-sort object variables be enumerated by
![]() $v_0, v_1, v_2, \ldots $
, and the numerical-sort object variables by
$v_0, v_1, v_2, \ldots $
, and the numerical-sort object variables by
![]() $\mathbf {{v}}_0, \mathbf {{v}}_1, \mathbf {{v}}_2, \ldots $
. Then let the pre-translations of the object variables be
$\mathbf {{v}}_0, \mathbf {{v}}_1, \mathbf {{v}}_2, \ldots $
. Then let the pre-translations of the object variables be
 $$ \begin{align*} v_i^\dagger &:= v_{3i} ,\\ \mathbf{{v}}_i^\dagger &:= v_{3i+1} v_{3i+2}. \end{align*} $$
$$ \begin{align*} v_i^\dagger &:= v_{3i} ,\\ \mathbf{{v}}_i^\dagger &:= v_{3i+1} v_{3i+2}. \end{align*} $$
Similarly for second-order variables.
Now we define the interpretation
![]() $\dagger : \mathcal {L}^+ \to \mathcal {L}$
. Fix a well-ordering
$\dagger : \mathcal {L}^+ \to \mathcal {L}$
. Fix a well-ordering
![]() $\leq $
of V, and fix distinct base-sort objects
$\leq $
of V, and fix distinct base-sort objects
![]() $a \neq b$
. In the first and last lines, let
$a \neq b$
. In the first and last lines, let
![]() $\tau = \langle \tau _1, \ldots , \tau _k \rangle $
be any second-order sort.
$\tau = \langle \tau _1, \ldots , \tau _k \rangle $
be any second-order sort.
 $$ \begin{align*} (X^\tau x_1^{\tau_1} \cdots x_k^{\tau_k})^\dagger &:= (X^\tau)^\dagger (x_1^{\tau_1})^\dagger \cdots (x_k^{\tau_k})^\dagger. \\ (v_i = v_j)^\dagger &:= v_{3i} = v_{3j}. \\ (\mathbf{{v}}_i = \mathbf{{v}}_j)^\dagger &:= v_{3i+1} = v_{3j+1} \wedge v_{3i+2} = v_{3j+2}. \\ (\mathbf{{v}}_i = \#X)^\dagger &:= (X \approx (V \upharpoonright v_{3i+1}) \wedge v_{3i+2} = a) \vee (X = \varnothing \wedge v_{3i+1} = a \wedge v_{3i+2} = b). \\ (\varphi \rightarrow \psi)^\dagger &:= \varphi^\dagger \rightarrow \psi^\dagger. \\ (\neg \varphi)^\dagger &:= \neg \varphi^\dagger. \\ (\forall v_i \ \varphi)^\dagger &= \forall v_{3i} \ \varphi^\dagger. \\ (\forall \mathbf{{v}}_i \ \varphi)^\dagger &= \forall v_{3i+1}\forall v_{3i+2} \ \varphi^\dagger. \\ (\forall X^\tau \, \varphi)^\dagger &= \forall (X^\tau)^\dagger \, \varphi^\dagger. \end{align*} $$
$$ \begin{align*} (X^\tau x_1^{\tau_1} \cdots x_k^{\tau_k})^\dagger &:= (X^\tau)^\dagger (x_1^{\tau_1})^\dagger \cdots (x_k^{\tau_k})^\dagger. \\ (v_i = v_j)^\dagger &:= v_{3i} = v_{3j}. \\ (\mathbf{{v}}_i = \mathbf{{v}}_j)^\dagger &:= v_{3i+1} = v_{3j+1} \wedge v_{3i+2} = v_{3j+2}. \\ (\mathbf{{v}}_i = \#X)^\dagger &:= (X \approx (V \upharpoonright v_{3i+1}) \wedge v_{3i+2} = a) \vee (X = \varnothing \wedge v_{3i+1} = a \wedge v_{3i+2} = b). \\ (\varphi \rightarrow \psi)^\dagger &:= \varphi^\dagger \rightarrow \psi^\dagger. \\ (\neg \varphi)^\dagger &:= \neg \varphi^\dagger. \\ (\forall v_i \ \varphi)^\dagger &= \forall v_{3i} \ \varphi^\dagger. \\ (\forall \mathbf{{v}}_i \ \varphi)^\dagger &= \forall v_{3i+1}\forall v_{3i+2} \ \varphi^\dagger. \\ (\forall X^\tau \, \varphi)^\dagger &= \forall (X^\tau)^\dagger \, \varphi^\dagger. \end{align*} $$
In order to justify the interpretation of
![]() $\#$
, we must check that for each base concept X, there is a unique initial segment of
$\#$
, we must check that for each base concept X, there is a unique initial segment of
![]() $(V, \leq )$
that is equinumerous with X. For the existence claim, recall that
$(V, \leq )$
that is equinumerous with X. For the existence claim, recall that
![]() $\mathit {Ax}_{\mathcal {L}}$
proves that any two well-orderings are comparable (Lemma 5.29). In particular,
$\mathit {Ax}_{\mathcal {L}}$
proves that any two well-orderings are comparable (Lemma 5.29). In particular,
![]() $(X,\leq )$
is order-isomorphic with a segment of
$(X,\leq )$
is order-isomorphic with a segment of
![]() $(V, \leq )$
, and hence X is equinumerous with that segment. For the uniqueness claim, use the pigeonhole principle (Remark 5.31).
$(V, \leq )$
, and hence X is equinumerous with that segment. For the uniqueness claim, use the pigeonhole principle (Remark 5.31).
Now it is easy to check that the
![]() $\dagger $
-translation of each axiom of w2FA is provable from
$\dagger $
-translation of each axiom of w2FA is provable from
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
. So, the interpretation works.
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V) + |V| \neq 1$
. So, the interpretation works.
Lemma 8.54.
w2FA is conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + |V| = 1$
.
$\mathit {Ax}_{\mathcal {L}} + |V| = 1$
.
Proof. Observe that
![]() $\mathit {Ax}_{\mathcal {L}} + |V| = 1$
is a categorical theory, and hence it is a complete theory. So, the only way that w2FA could be non-conservative over
$\mathit {Ax}_{\mathcal {L}} + |V| = 1$
is a categorical theory, and hence it is a complete theory. So, the only way that w2FA could be non-conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + |V| = 1$
is if the combined theory
$\mathit {Ax}_{\mathcal {L}} + |V| = 1$
is if the combined theory
![]() $\mathrm{w2FA} + |V| = 1$
were inconsistent. But
$\mathrm{w2FA} + |V| = 1$
were inconsistent. But
![]() $\mathrm{w2FA} + |V| = 1$
is consistent: it has a model
$\mathrm{w2FA} + |V| = 1$
is consistent: it has a model
![]() $\mathcal {M}$
with object domains
$\mathcal {M}$
with object domains
![]() $M_0 = \{a\}$
and
$M_0 = \{a\}$
and
![]() $M_n = \{0,1\}$
and with
$M_n = \{0,1\}$
and with
![]() $I(\#)$
being the function mapping each base-sort concept to its cardinality.
$I(\#)$
being the function mapping each base-sort concept to its cardinality.
9 The non-conservativeness of 2FA
In the previous section, we established some limits to the non-conservativeness of w2FA. In this section, we will show that 2FA is more deeply non-conservative than w2FA. The main result is Theorem 9.67, which says that 2FA is non-conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
. Our proof of this result can be generalized to show that 2FA is non-conservative over pure axiomatic n-th order logic for any
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
. Our proof of this result can be generalized to show that 2FA is non-conservative over pure axiomatic n-th order logic for any
![]() $n \geq 2$
, or even over simple type theory.
$n \geq 2$
, or even over simple type theory.
Roughly, the idea is to construct a Gödel sentence for
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
. By a variation on Gödel’s first incompleteness theorem,
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
. By a variation on Gödel’s first incompleteness theorem,
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
does not prove its own Gödel sentence. On the other hand,
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
does not prove its own Gödel sentence. On the other hand,
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
does prove the Gödel sentence, because it is a powerful theory: it interprets second-order arithmetic in the new sort (and it is smart enough to relate that arithmetic to the Gödel sentence expressed in
$\mathrm{2FA} + \mathit {Fin}(V)$
does prove the Gödel sentence, because it is a powerful theory: it interprets second-order arithmetic in the new sort (and it is smart enough to relate that arithmetic to the Gödel sentence expressed in
![]() $\mathcal {L}$
).
$\mathcal {L}$
).
But
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
says that the universe is finite, so it cannot interpret Q. How, then, is it possible to pull off the Gödel argument? The trick is that
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
says that the universe is finite, so it cannot interpret Q. How, then, is it possible to pull off the Gödel argument? The trick is that
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
has arbitrarily large models. If
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
has arbitrarily large models. If
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
proved its own Gödel sentence, then any sufficiently large model would contain a witness to the paradoxical derivation, yielding a contradiction.
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
proved its own Gödel sentence, then any sufficiently large model would contain a witness to the paradoxical derivation, yielding a contradiction.
To implement this argument, it will be convenient to work with a definitional extension
![]() $T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
, which we now describe.
$T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
, which we now describe.
Definition 9.55. Let
![]() $\mathcal {L} \cup L' : = \mathcal {L}_{\{0\}}[\{0,S,\leq , A,M\}]$
.
$\mathcal {L} \cup L' : = \mathcal {L}_{\{0\}}[\{0,S,\leq , A,M\}]$
.
We identify variables of
![]() $L'$
with object variables of
$L'$
with object variables of
![]() $\mathcal {L}$
. Thus,
$\mathcal {L}$
. Thus,
-
•
 $0$
is a base object constant,
$0$
is a base object constant, -
• S and
 $\leq $
are constants of sort
$\leq $
are constants of sort
 $\langle 0, 0 \rangle $
,
$\langle 0, 0 \rangle $
, -
• A and M are constants of sort
 $\langle 0, 0, 0 \rangle $
.
$\langle 0, 0, 0 \rangle $
.
Let
![]() $\mathit {Ax}_{\mathcal {L} \cup L'}$
be the axioms of the deductive system for
$\mathit {Ax}_{\mathcal {L} \cup L'}$
be the axioms of the deductive system for
![]() $\mathcal {L} \cup L'$
.
$\mathcal {L} \cup L'$
.
Definition 9.56. Let
![]() $\Delta $
be the conjunction of the following
$\Delta $
be the conjunction of the following
![]() $(\mathcal {L}\cup L')$
-formulas:
$(\mathcal {L}\cup L')$
-formulas:
-
1.
 $(V,\leq )$
is a double well-ordering with least element
$(V,\leq )$
is a double well-ordering with least element
 $0$
,
$0$
, -
2.
 $Sxy$
iff y is the upper neighbor of x with respect to
$Sxy$
iff y is the upper neighbor of x with respect to
 $\leq $
,
$\leq $
, -
3. Definitions of A and M:
 $$ \begin{align*} & Ax0z\leftrightarrow z= x, \\ & Syy' \wedge Szz' \rightarrow (Axyz \leftrightarrow Axy'z'), \\ & Mx0z \leftrightarrow z=0, \\ & Syy' \wedge Azxz' \rightarrow (Mxyz \leftrightarrow Mxy'z'). \end{align*} $$
$$ \begin{align*} & Ax0z\leftrightarrow z= x, \\ & Syy' \wedge Szz' \rightarrow (Axyz \leftrightarrow Axy'z'), \\ & Mx0z \leftrightarrow z=0, \\ & Syy' \wedge Azxz' \rightarrow (Mxyz \leftrightarrow Mxy'z'). \end{align*} $$
Definition 9.57. Let
![]() $T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
.
$T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
.
Lemma 9.58.
![]() $T \vdash BA'$
.
$T \vdash BA'$
.
Proof. It is obvious that T proves the universal closures of the first three axioms of
![]() $BA'$
. Furthermore, since
$BA'$
. Furthermore, since
![]() $(V,\leq )$
is a well-ordering, we have induction for all
$(V,\leq )$
is a well-ordering, we have induction for all
![]() $(\mathcal {L} \cup L')$
-formulas. Using induction, it is easy to prove the universal closures of the remaining axioms of
$(\mathcal {L} \cup L')$
-formulas. Using induction, it is easy to prove the universal closures of the remaining axioms of
![]() $BA'$
.
$BA'$
.
We will now describe the construction of the Gödel sentence of T.
Fix a Gödel numbering of
![]() $\mathcal {L}\cup L'$
. We describe
$\mathcal {L}\cup L'$
. We describe
![]() $L_{\mathrm{PA}}$
-formulas
$L_{\mathrm{PA}}$
-formulas
![]() $\mathit {Der}_T$
,
$\mathit {Der}_T$
,
![]() $\mathit {diag}$
representing certain primitive recursive notions.
$\mathit {diag}$
representing certain primitive recursive notions.
Let
![]() $\mathit {Der}_T(x,y)$
just in case: x is the Gödel number of a T-derivation of a formula with Gödel number y.
$\mathit {Der}_T(x,y)$
just in case: x is the Gödel number of a T-derivation of a formula with Gödel number y.
Let
![]() $\mathit {diag}(x)=y$
be a function with the following property: if n is the Gödel number of an
$\mathit {diag}(x)=y$
be a function with the following property: if n is the Gödel number of an
![]() $(\mathcal {L} \cup L')$
-formula
$(\mathcal {L} \cup L')$
-formula
![]() $\theta (y)$
with exactly the free variable y, then
$\theta (y)$
with exactly the free variable y, then
(The notation
![]() $y \doteq {n}$
is from Definition 4.21.) Note that
$y \doteq {n}$
is from Definition 4.21.) Note that
![]() $\mathit {diag}$
is modeled on the Gödel diagonal function: in essence, it substitutes into a formula its own Gödel number.
$\mathit {diag}$
is modeled on the Gödel diagonal function: in essence, it substitutes into a formula its own Gödel number.
It is well known that recursive relations are
![]() $\Delta _1$
-definable in PA [Reference Hájek and Pudlák13, p. 18, theorem 0.45]. So, we may choose
$\Delta _1$
-definable in PA [Reference Hájek and Pudlák13, p. 18, theorem 0.45]. So, we may choose
![]() $\mathit {Der}_T$
and
$\mathit {Der}_T$
and
![]() $\mathit {diag}$
so that
$\mathit {diag}$
so that
![]() $\mathit {Der}_T(x, \mathit {diag}(y))$
is a
$\mathit {Der}_T(x, \mathit {diag}(y))$
is a
![]() $\Sigma _1$
formula. By Lemma 4.23, there is an equivalent
$\Sigma _1$
formula. By Lemma 4.23, there is an equivalent
![]() $\Sigma _1'$
formula
$\Sigma _1'$
formula
![]() $\varphi (x,y)$
of
$\varphi (x,y)$
of
![]() $L'$
such that, for any parameters
$L'$
such that, for any parameters
![]() $a,b \in \mathbb {N}$
,
$a,b \in \mathbb {N}$
,
Let p be the Gödel number of
![]() $\forall x \neg \varphi (x,y)$
. Then
$\forall x \neg \varphi (x,y)$
. Then
![]() , where G is the following sentence:
, where G is the following sentence:
We say that G is the Gödel sentence of the theory T.
Lemma 9.59. The theory
![]() $T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
does not prove its own Gödel sentence G.
$T = \mathit {Ax}_{\mathcal {L} \cup L'} + \mathit {Fin}(V) + \Delta $
does not prove its own Gödel sentence G.
Proof. Suppose for sake of contradiction that
![]() $T \vdash G$
. Let d be the Gödel number of a derivation of G. Then we have
$T \vdash G$
. Let d be the Gödel number of a derivation of G. Then we have
 $$ \begin{align*} & \mathbb{N} \vDash \mathit{Der}_T(S^d 0, \mathit{diag}(S^p 0)), \\ & \mathbb{N} \vDash \varphi(d,p). \end{align*} $$
$$ \begin{align*} & \mathbb{N} \vDash \mathit{Der}_T(S^d 0, \mathit{diag}(S^p 0)), \\ & \mathbb{N} \vDash \varphi(d,p). \end{align*} $$
Write
![]() $\varphi (x,y)$
as
$\varphi (x,y)$
as
![]() $\exists z \psi (x,y,z)$
, where
$\exists z \psi (x,y,z)$
, where
![]() $\psi $
is bounded
$\psi $
is bounded
![]() $'$
. Fix
$'$
. Fix
![]() $r \in \mathbb {N}$
such that
$r \in \mathbb {N}$
such that
![]() $\mathbb {N} \vDash \psi (d,p,r)$
. By Lemma 4.25 and the Generalization Theorem,
$\mathbb {N} \vDash \psi (d,p,r)$
. By Lemma 4.25 and the Generalization Theorem,
By Lemma 9.58,
It follows that
 $$ \begin{align*} T & \vdash \exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r}) \rightarrow \exists y(y \doteq {p} \wedge \exists x \exists z \psi(x,y,z)), \\ T & \vdash \exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r}) \rightarrow \neg G. \end{align*} $$
$$ \begin{align*} T & \vdash \exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r}) \rightarrow \exists y(y \doteq {p} \wedge \exists x \exists z \psi(x,y,z)), \\ T & \vdash \exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r}) \rightarrow \neg G. \end{align*} $$
We assumed that
![]() $T \vdash G$
. Hence,
$T \vdash G$
. Hence,
But T has arbitrarily large finite models. In particular,
![]() $\mathbb {N} \upharpoonright \max \{d,p,r\}$
is a model of T that satisfies
$\mathbb {N} \upharpoonright \max \{d,p,r\}$
is a model of T that satisfies
![]() $\exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r})$
. Contradiction.
$\exists x \exists y \exists z (x \doteq {d} \wedge y \doteq {p} \wedge z \doteq {r})$
. Contradiction.
Let us now turn our attention to what is provable in the stronger theory
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
.
$\mathrm{2FA} + \mathit {Fin}(V)$
.
Lemma 9.60.
2FA interprets
![]() $Z_2$
, and hence
$Z_2$
, and hence
![]() $Z_2'$
.
$Z_2'$
.
The proof is an easy variation on Frege’s Theorem.
It will be convenient to fix a particular interpretation of
![]() $Z_2$
and
$Z_2$
and
![]() $Z_2'$
in the numerical sort of 2FA.
$Z_2'$
in the numerical sort of 2FA.
Definition 9.61. Fix a translation
![]() $\gamma : L_2' \to \mathcal {L}^+$
which interprets
$\gamma : L_2' \to \mathcal {L}^+$
which interprets
![]() $Z_2'$
in the numerical sort of 2FA. The interpretants of the nonlogical vocabulary items of
$Z_2'$
in the numerical sort of 2FA. The interpretants of the nonlogical vocabulary items of
![]() $L_2'$
will be denoted by
$L_2'$
will be denoted by
![]() $\mathbf {{0}}$
,
$\mathbf {{0}}$
,
![]() $\mathbf {{S}}$
,
$\mathbf {{S}}$
,
![]() $\boldsymbol {\leq }$
,
$\boldsymbol {\leq }$
,
![]() $\mathbf {{A}}$
,
$\mathbf {{A}}$
,
![]() $\mathbf {{M}}$
. The universe of the interpretation is defined by the following formula
$\mathbf {{M}}$
. The universe of the interpretation is defined by the following formula
![]() $\mathbb {N}(\mathbf {x})$
:
$\mathbb {N}(\mathbf {x})$
:
Object quantifiers are relativized to
![]() $\mathbb {N}(\mathbf {x})$
. Set quantifiers are relativized to
$\mathbb {N}(\mathbf {x})$
. Set quantifiers are relativized to
![]() $\forall \mathbf {x} (\mathbf {X}\mathbf {x} \rightarrow \mathbb {N}(\mathbf {x}))$
.
$\forall \mathbf {x} (\mathbf {X}\mathbf {x} \rightarrow \mathbb {N}(\mathbf {x}))$
.
The interpretation of
![]() $Z_2$
in 2FA is obtained by extending the
$Z_2$
in 2FA is obtained by extending the
![]() $\gamma $
-translation so as to interpret
$\gamma $
-translation so as to interpret
![]() $Z_2' + \mathfrak {D}$
, where
$Z_2' + \mathfrak {D}$
, where
![]() $\mathfrak {D}$
consists of the definitions of
$\mathfrak {D}$
consists of the definitions of
![]() $S, +, \cdot $
in terms of
$S, +, \cdot $
in terms of
![]() $S,A,M$
(Definition 4.21).
$S,A,M$
(Definition 4.21).
The next two lemmas show that
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
is smart enough to relate the arithmetic in its base sort (
$\mathrm{2FA} + \mathit {Fin}(V)$
is smart enough to relate the arithmetic in its base sort (
![]() $BA'$
) with the arithmetic in its numerical sort (
$BA'$
) with the arithmetic in its numerical sort (
![]() $Z_2'$
).
$Z_2'$
).
To ease clutter, we will often write ‘
![]() $\mathrm{2FA} + \mathit {Fin}(V) \vdash \Delta \rightarrow \cdots $
’ when we really mean
$\mathrm{2FA} + \mathit {Fin}(V) \vdash \Delta \rightarrow \cdots $
’ when we really mean
![]() $\mathrm{2FA} + \mathit {Fin}(V) \vdash \forall (0, S, \leq , A, M) (\Delta \rightarrow \cdots )$
.
$\mathrm{2FA} + \mathit {Fin}(V) \vdash \forall (0, S, \leq , A, M) (\Delta \rightarrow \cdots )$
.
Lemma 9.62.
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
proves that the base universe is order-isomorphic with an initial segment of the natural numbers in the numerical sort:
$\mathrm{2FA} + \mathit {Fin}(V)$
proves that the base universe is order-isomorphic with an initial segment of the natural numbers in the numerical sort:
 $$ \begin{align*}\mathrm{2FA} + \mathit{Fin}(V) \vdash \Delta \rightarrow \exists \mathbf{{a}} \left ( (V, \leq) \simeq_o (\mathbb{N} \upharpoonright \mathbf{{a}}, \boldsymbol{\leq}) \right ). \end{align*} $$
$$ \begin{align*}\mathrm{2FA} + \mathit{Fin}(V) \vdash \Delta \rightarrow \exists \mathbf{{a}} \left ( (V, \leq) \simeq_o (\mathbb{N} \upharpoonright \mathbf{{a}}, \boldsymbol{\leq}) \right ). \end{align*} $$
Proof. We reason in
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
$\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
![]() $0,S,\leq , A, M$
, and suppose
$0,S,\leq , A, M$
, and suppose
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $(V, \leq )$
is a double well-ordering. Further, it is easy to show that
$(V, \leq )$
is a double well-ordering. Further, it is easy to show that
![]() $(\mathbb {N}, \boldsymbol {\leq })$
is a well-ordering.
$(\mathbb {N}, \boldsymbol {\leq })$
is a well-ordering.
By the comparability of well-orderings (Lemma 5.29, generalized to
![]() $\mathcal {L}^+$
), exactly one of the following holds:
$\mathcal {L}^+$
), exactly one of the following holds:
We can rule out the latter two options, because they imply that the converse of
![]() $(\mathbb {N}, \boldsymbol {\leq })$
is a well-ordering, which it isn’t. Hence,
$(\mathbb {N}, \boldsymbol {\leq })$
is a well-ordering, which it isn’t. Hence,
![]() $(V, \leq ) <_o (\mathbb {N}, \boldsymbol {\leq })$
. This is what we wanted.
$(V, \leq ) <_o (\mathbb {N}, \boldsymbol {\leq })$
. This is what we wanted.
For the next definition, fix
![]() $0,S,\leq , A, M$
, and suppose
$0,S,\leq , A, M$
, and suppose
![]() $\Delta $
. Also fix
$\Delta $
. Also fix
![]() $\mathbf {{a}}$
as in the statement of Lemma 9.62.
$\mathbf {{a}}$
as in the statement of Lemma 9.62.
Definition 9.63. Let
![]() $\delta : L' \to \mathcal {L}^+$
be a translation which is exactly like
$\delta : L' \to \mathcal {L}^+$
be a translation which is exactly like
![]() $\gamma $
, except that object quantifiers are relativized to
$\gamma $
, except that object quantifiers are relativized to
![]() $\mathbb {N} \upharpoonright \mathbf {{a}}$
, and we restrict the translation to first-order formulas. In other words,
$\mathbb {N} \upharpoonright \mathbf {{a}}$
, and we restrict the translation to first-order formulas. In other words,
 $$ \begin{align*} (x=0)^\delta &:= \mathbf{x} = \mathbf{{0}} , \\ (Sxy)^\delta &:= \mathbf{{S}}\mathbf{x}\mathbf{y} , \\ (x \leq y)^\delta &:= \mathbf{x} \boldsymbol{\leq} \mathbf{y}, \\ (Axyz)^\delta &:= \mathbf{{A}}\mathbf{x}\mathbf{y}\mathbf{z}, \\ (Mxyz)^\delta &:= \mathbf{{M}}\mathbf{x}\mathbf{y}\mathbf{z} ,\\ (x=y)^\delta &:= \mathbf{x} = \mathbf{y}, \\ (\varphi \rightarrow \psi)^\delta &:= \varphi^\delta \rightarrow \psi^\delta, \\ (\neg \varphi)^\delta &:= \neg \varphi^\delta, \\ (\forall x \ \varphi)^\delta &:= \forall \mathbf{x} ((\mathbb{N} \upharpoonright \mathbf{{a}})\mathbf{x} \rightarrow \varphi^\delta). \end{align*} $$
$$ \begin{align*} (x=0)^\delta &:= \mathbf{x} = \mathbf{{0}} , \\ (Sxy)^\delta &:= \mathbf{{S}}\mathbf{x}\mathbf{y} , \\ (x \leq y)^\delta &:= \mathbf{x} \boldsymbol{\leq} \mathbf{y}, \\ (Axyz)^\delta &:= \mathbf{{A}}\mathbf{x}\mathbf{y}\mathbf{z}, \\ (Mxyz)^\delta &:= \mathbf{{M}}\mathbf{x}\mathbf{y}\mathbf{z} ,\\ (x=y)^\delta &:= \mathbf{x} = \mathbf{y}, \\ (\varphi \rightarrow \psi)^\delta &:= \varphi^\delta \rightarrow \psi^\delta, \\ (\neg \varphi)^\delta &:= \neg \varphi^\delta, \\ (\forall x \ \varphi)^\delta &:= \forall \mathbf{x} ((\mathbb{N} \upharpoonright \mathbf{{a}})\mathbf{x} \rightarrow \varphi^\delta). \end{align*} $$
Lemma 9.64. For any formula
![]() $\varphi $
of
$\varphi $
of
![]() $L'$
,
$L'$
,
Proof. We reason in
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
$\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
![]() $0,S,\leq , A, M$
, and suppose
$0,S,\leq , A, M$
, and suppose
![]() $\Delta $
. By Lemma 9.62, there is an order-isomorphism
$\Delta $
. By Lemma 9.62, there is an order-isomorphism
![]() $f: V \to \mathbb {N} \upharpoonright \mathbf {{a}}$
. In other words, there is a bijection f such that
$f: V \to \mathbb {N} \upharpoonright \mathbf {{a}}$
. In other words, there is a bijection f such that
![]() $f(0) = \mathbf {{0}}$
and
$f(0) = \mathbf {{0}}$
and
We wish to prove corresponding statements for the other atomic formulas of
![]() $L'$
, namely,
$L'$
, namely,
 $$ \begin{align*} Sxy \ &\leftrightarrow \ \mathbf{{S}}f(x)f(y), \\ Axyz \ &\leftrightarrow \ \mathbf{{A}}f(x)f(y)f(z), \\ Mxyz \ &\leftrightarrow \ \mathbf{{M}}f(x)f(y)f(z). \end{align*} $$
$$ \begin{align*} Sxy \ &\leftrightarrow \ \mathbf{{S}}f(x)f(y), \\ Axyz \ &\leftrightarrow \ \mathbf{{A}}f(x)f(y)f(z), \\ Mxyz \ &\leftrightarrow \ \mathbf{{M}}f(x)f(y)f(z). \end{align*} $$
The first statement holds because S is definable in terms of
![]() $\leq $
:
$\leq $
:
 $$ \begin{align*} Sxy \ &\leftrightarrow \ y \text{ is the upper neighbor of } x \text{ with respect to} \leq \\ \ &\leftrightarrow \ \forall z((x \leq z \wedge x \neq z) \leftrightarrow y \leq z) \\ \ &\leftrightarrow \ \forall z((f(x) \leq f(z) \wedge f(x) \neq f(z)) \leftrightarrow f(y) \leq f(z)) \\ \ &\leftrightarrow \ \forall \mathbf{z} ((\mathbb{N} \upharpoonright \mathbf{{a}})\mathbf{z} \rightarrow [(f(x) \leq \mathbf{z} \wedge f(x) \neq \mathbf{z}) \leftrightarrow f(y) \leq \mathbf{z}]) \\ \ &\leftrightarrow \ f(y) \text{ is the upper neighbor of } f(x) \text{ with respect to} \boldsymbol{\leq} \\ \ &\leftrightarrow \ \mathbf{{S}} f(x)f(y). \end{align*} $$
$$ \begin{align*} Sxy \ &\leftrightarrow \ y \text{ is the upper neighbor of } x \text{ with respect to} \leq \\ \ &\leftrightarrow \ \forall z((x \leq z \wedge x \neq z) \leftrightarrow y \leq z) \\ \ &\leftrightarrow \ \forall z((f(x) \leq f(z) \wedge f(x) \neq f(z)) \leftrightarrow f(y) \leq f(z)) \\ \ &\leftrightarrow \ \forall \mathbf{z} ((\mathbb{N} \upharpoonright \mathbf{{a}})\mathbf{z} \rightarrow [(f(x) \leq \mathbf{z} \wedge f(x) \neq \mathbf{z}) \leftrightarrow f(y) \leq \mathbf{z}]) \\ \ &\leftrightarrow \ f(y) \text{ is the upper neighbor of } f(x) \text{ with respect to} \boldsymbol{\leq} \\ \ &\leftrightarrow \ \mathbf{{S}} f(x)f(y). \end{align*} $$
The second statement holds because A and
![]() $\mathbf {{A}}$
satisfy the same recursive definition along their respective well-orderings (Definition 4.18). So, by the recursion theorem, A and
$\mathbf {{A}}$
satisfy the same recursive definition along their respective well-orderings (Definition 4.18). So, by the recursion theorem, A and
![]() $\mathbf {{A}}$
are isomorphic. (If they are not isomorphic, then consider a counterexample where y is
$\mathbf {{A}}$
are isomorphic. (If they are not isomorphic, then consider a counterexample where y is
![]() $\leq $
-minimal and derive a contradiction.)
$\leq $
-minimal and derive a contradiction.)
The third statement holds for the same reason: M and
![]() $\mathbf {{M}}$
satisfy the same recursive definition along their respective well-orderings.
$\mathbf {{M}}$
satisfy the same recursive definition along their respective well-orderings.
By induction on formulas,
![]() $\varphi \leftrightarrow \varphi ^{\delta }$
for every
$\varphi \leftrightarrow \varphi ^{\delta }$
for every
![]() $L'$
-formula
$L'$
-formula
![]() $\varphi $
.
$\varphi $
.
In the next two lemmas, we show that 2FA formalizes the proof of Lemma 9.59.
Let
![]() $\varphi (x,y)$
,
$\varphi (x,y)$
,
![]() $\psi (x,y,z)$
, and G be the
$\psi (x,y,z)$
, and G be the
![]() $L'$
-formulas from Lemma 9.59.
$L'$
-formulas from Lemma 9.59.
Let
![]() $\mathbf {{p}}$
be a term in the numerical sort of
$\mathbf {{p}}$
be a term in the numerical sort of
![]() $\mathcal {L}^+$
that denotes the Gödel number of
$\mathcal {L}^+$
that denotes the Gödel number of
![]() $\forall x \neg \varphi (x,y)$
. In other words,
$\forall x \neg \varphi (x,y)$
. In other words,
![]() .
.
Let
![]() $\tilde G$
be the following formula in the numerical sort of
$\tilde G$
be the following formula in the numerical sort of
![]() $\mathcal {L}^+$
:
$\mathcal {L}^+$
:
Observe that
![]() $\mathrm{2FA} \vdash \tilde G \leftrightarrow G^\gamma $
. (This is because we chose the interpretations of
$\mathrm{2FA} \vdash \tilde G \leftrightarrow G^\gamma $
. (This is because we chose the interpretations of
![]() $Z_2$
and
$Z_2$
and
![]() $Z_2'$
to be compatible with one another. See Definition 9.61.) Intuitively,
$Z_2'$
to be compatible with one another. See Definition 9.61.) Intuitively,
![]() $\tilde G$
says: ‘The Gödel sentence for T is not derivable in T.’ In other words,
$\tilde G$
says: ‘The Gödel sentence for T is not derivable in T.’ In other words,
![]() $\tilde G$
formalizes the statement of Lemma 9.59.
$\tilde G$
formalizes the statement of Lemma 9.59.
It is well known that
![]() $Z_2$
formalizes Tarskian definitions of truth and satisfaction for
$Z_2$
formalizes Tarskian definitions of truth and satisfaction for
![]() $L_{\mathrm{PA}}$
[Reference Takeuti31, pp. 183–187]. In the same way, 2FA formalizes Tarskian definitions of truth and satisfaction for
$L_{\mathrm{PA}}$
[Reference Takeuti31, pp. 183–187]. In the same way, 2FA formalizes Tarskian definitions of truth and satisfaction for
![]() $L'$
with respect to the standard model
$L'$
with respect to the standard model
![]() $\mathbb {N}$
. Denote the truth predicate by
$\mathbb {N}$
. Denote the truth predicate by
![]() $\mathit {Tr}_{\mathbb {N}}(\mathbf {x})$
and the satisfaction predicate by
$\mathit {Tr}_{\mathbb {N}}(\mathbf {x})$
and the satisfaction predicate by
![]() $\mathit {Sat}_{\mathbb {N}}(\mathbf {x}, \mathbf {y})$
.
$\mathit {Sat}_{\mathbb {N}}(\mathbf {x}, \mathbf {y})$
.
Lemma 9.65. Let
![]() $\theta $
be an
$\theta $
be an
![]() $L'$
-formula whose free variables are among the first k free variables of
$L'$
-formula whose free variables are among the first k free variables of
![]() $L'$
. Then 2FA proves
$L'$
. Then 2FA proves
For proof, compare [Reference Takeuti31, pp. 186–187, proposition 18.12].
Lemma 9.66.
2FA
![]() $\vdash \tilde G.$
$\vdash \tilde G.$
Proof (sketch)
The idea is to formalize the proof of Lemma 9.59 in 2FA.
We reason in 2FA. Suppose
![]() $\neg \tilde G$
. Then there exists
$\neg \tilde G$
. Then there exists
![]() $\mathbf {{d}}$
such that
$\mathbf {{d}}$
such that
![]() $\varphi ^\gamma (\mathbf {{d}}, \mathbf {{p}})$
. By Lemma 9.65, we have
$\varphi ^\gamma (\mathbf {{d}}, \mathbf {{p}})$
. By Lemma 9.65, we have
![]() . Write
. Write
![]() $\varphi (x,y) = \exists z \psi (x,y,z)$
. Unpacking the definition of
$\varphi (x,y) = \exists z \psi (x,y,z)$
. Unpacking the definition of
![]() $\mathit {Sat}_{\mathbb {N}}$
, there exists
$\mathit {Sat}_{\mathbb {N}}$
, there exists
![]() $\mathbf {{r}}$
such that
$\mathbf {{r}}$
such that
![]() .
.
Formalize Lemma 4.25 to obtain
and so on, until we reach
Let
![]() $\mathbf {{m}} = \max \{\mathbf {{d}}, \mathbf {{p}}, \mathbf {{r}} \}$
. Argue that
$\mathbf {{m}} = \max \{\mathbf {{d}}, \mathbf {{p}}, \mathbf {{r}} \}$
. Argue that
![]() $\mathit {Der}_T$
is sound with respect to the semantics
$\mathit {Der}_T$
is sound with respect to the semantics
![]() $\mathit {Tr}_{\mathbb {N} \upharpoonright \mathbf {{m}}}$
, in the sense that
$\mathit {Tr}_{\mathbb {N} \upharpoonright \mathbf {{m}}}$
, in the sense that
Finally, check that
. Contradiction.
We are finally ready to prove the second main theorem of the paper.
Theorem 9.67.
2FA is not conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
.
$\mathit {Ax}_{\mathcal {L}} + \mathit {Fin}(V)$
.
Proof. We establish the following witness to non-conservativeness:
Proof of claim (3)
Suppose not. Then we have
 $$ \begin{align*} \mathit{Ax}_{\mathcal{L}} + \mathit{Fin}(V) \ &\vdash \ \forall (0,S,\leq,A,M) (\Delta \rightarrow G), \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) \ &\vdash \ \forall (0,S,\leq,A,M) (\Delta \rightarrow G), \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) \ &\vdash \ \Delta \rightarrow G, \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) + \Delta \ &\vdash \ G. \end{align*} $$
$$ \begin{align*} \mathit{Ax}_{\mathcal{L}} + \mathit{Fin}(V) \ &\vdash \ \forall (0,S,\leq,A,M) (\Delta \rightarrow G), \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) \ &\vdash \ \forall (0,S,\leq,A,M) (\Delta \rightarrow G), \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) \ &\vdash \ \Delta \rightarrow G, \\ \mathit{Ax}_{\mathcal{L} \cup L'} + \mathit{Fin}(V) + \Delta \ &\vdash \ G. \end{align*} $$
But this contradicts Lemma 9.59.
Proof of claim (4)
We reason in
![]() $\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
$\mathrm{2FA} + \mathit {Fin}(V)$
. Fix
![]() $0,S,\leq , A, M$
, and suppose
$0,S,\leq , A, M$
, and suppose
![]() $\Delta $
. Also fix
$\Delta $
. Also fix
![]() $\mathbf {{a}}$
as in the statement of Lemma 9.62. We show G.
$\mathbf {{a}}$
as in the statement of Lemma 9.62. We show G.
By Lemma 9.66, we have
![]() $\tilde G$
. Then we reason as follows:
$\tilde G$
. Then we reason as follows:
The first arrow holds because we set up the interpretations of
![]() $Z_2$
and
$Z_2$
and
![]() $Z_2'$
correctly (Definition 9.61). The second arrow holds by quantificational logic, using the fact that G is
$Z_2'$
correctly (Definition 9.61). The second arrow holds by quantificational logic, using the fact that G is
![]() $\Pi _1'$
. (The idea is that universal formulas are preserved when passing to a submodel.) The third arrow holds by Lemma 9.64. Hence, we obtain G.
$\Pi _1'$
. (The idea is that universal formulas are preserved when passing to a submodel.) The third arrow holds by Lemma 9.64. Hence, we obtain G.
By Lemma 1.3, this gives us another proof that 2FA is non-conservative over
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
By the same argument, we have:
Corollary 9.68.
2FA is not conservative over pure axiomatic n-th order logic, for any
![]() $n\geq 2$
.
$n\geq 2$
.
Corollary 9.69. 2FA is not conservative over simple type theory.
10 HP is not deductively Field-conservative
As we noted in the introduction, Hale and Wright hold that legitimate stipulative definitions need not be conservative in the standard deductive sense. They need only be Field-conservative, i.e., conservative over ‘previously recognized ontology’ [Reference Hale and Wright14, p. 133].
An abstraction principle is a purported implicit definition of a new operator
by means of a sentence of the form
where
![]() $\varphi (F,G)$
is an equivalence relation. In the special case of abstraction principles, Hale and Wright [Reference Hale and Wright14, p. 319, n. 21] adopt a precise formulation of Field-conservativeness, which we now describe.
$\varphi (F,G)$
is an equivalence relation. In the special case of abstraction principles, Hale and Wright [Reference Hale and Wright14, p. 319, n. 21] adopt a precise formulation of Field-conservativeness, which we now describe.
For any formula
![]() $\varphi $
, let
$\varphi $
, let
![]() $\varphi ^{A(x)}$
denote the relativization of
$\varphi ^{A(x)}$
denote the relativization of
![]() $\varphi $
to the formula
$\varphi $
to the formula
![]() $A(x)$
.Footnote
15
For any theory T, let
$A(x)$
.Footnote
15
For any theory T, let
 $T^{A(x)} = \{\varphi ^{A(x)}: \varphi \in T\}$
.
$T^{A(x)} = \{\varphi ^{A(x)}: \varphi \in T\}$
.
Definition 10.70. Let T be a theory in a formal language L. Let
![]() $\Delta $
be an abstraction principle introducing the new operator
$\Delta $
be an abstraction principle introducing the new operator
, and let
. Then
![]() $\Delta $
is Field-conservative over T if for every L-formula
$\Delta $
is Field-conservative over T if for every L-formula
![]() $\varphi $
,
$\varphi $
,

If L is a second- or higher-order language, then
![]() $\vDash $
denotes the consequence relation with respect to standard (full) semantics.
$\vDash $
denotes the consequence relation with respect to standard (full) semantics.
There are two differences between Field-conservativeness and standard deductive conservativeness. Firstly, Field-conservativeness involves relativizing some of the quantifiers to ‘non-abstracts’. Secondly, Field-conservativeness is formulated semantically rather than deductively.
Hale and Wright’s suggestion, then, is that abstraction principles need only be Field-conservative in order to be acceptable. Much of the neo-Fregean literature has followed Hale and Wright on this point, if only because there seemed to be no other way for the neo-Fregean project to get off the ground.Footnote 16
Following [Reference Weir33, pp. 21–22], we may distinguish some notions closely related to Field-conservativeness. See [Reference Cook and Linnebo6, Reference Weir33] for motivation and further discussion.
Definition 10.71. Let L,
![]() $L^+$
, T,
$L^+$
, T,
![]() $\Delta $
be as in Definition 10.70. Assume that deductive systems for L and
$\Delta $
be as in Definition 10.70. Assume that deductive systems for L and
![]() $L^+$
have been specified. Let P (for ‘previously recognized ontology’) be a new unary predicate symbol. Then:
$L^+$
have been specified. Let P (for ‘previously recognized ontology’) be a new unary predicate symbol. Then:
-
1.
 $\Delta $
is deductively Field-conservative over T iff for every L-formula
$\Delta $
is deductively Field-conservative over T iff for every L-formula
 $\varphi $
,
$\varphi $
, 
-
2.
 $\Delta $
is Caesar-neutral conservative over T iff for every L-formula
$\Delta $
is Caesar-neutral conservative over T iff for every L-formula
 $\varphi $
,
$\varphi $
,  $$ \begin{align*}T^{P} + \Delta \vDash \varphi^{P} \implies T \vDash \varphi. \end{align*} $$
$$ \begin{align*}T^{P} + \Delta \vDash \varphi^{P} \implies T \vDash \varphi. \end{align*} $$
-
3.
 $\Delta $
is deductively Caesar-neutral conservative over T iff for every L-formula
$\Delta $
is deductively Caesar-neutral conservative over T iff for every L-formula
 $\varphi $
,
$\varphi $
,  $$ \begin{align*}T^{P} + \Delta \vdash \varphi^{P} \implies T \vdash \varphi. \end{align*} $$
$$ \begin{align*}T^{P} + \Delta \vdash \varphi^{P} \implies T \vdash \varphi. \end{align*} $$
Weir [Reference Weir33, p. 24, theorem 4.1] proved that HP is both Field-conservative and Caesar-neutral conservative over pure second-order logic. It has remained an open question whether HP satisfies the deductive analogue of either of these conditions. Our results imply that it does not.Footnote 17
Theorem 10.72. HP is not deductively Caesar-neutral conservative over pure axiomatic second-order logic.
Proof. We proved that 2FA is not deductively conservative over pure axiomatic second-order logic
![]() $\mathit {Ax}_{\mathcal {L}}$
(Corollary 7.49). Let
$\mathit {Ax}_{\mathcal {L}}$
(Corollary 7.49). Let
![]() $\theta $
be an
$\theta $
be an
![]() $\mathcal {L}$
-sentence such that
$\mathcal {L}$
-sentence such that
![]() $\mathrm{2FA} \vdash \theta $
but
$\mathrm{2FA} \vdash \theta $
but
![]() $\mathit {Ax}_{\mathcal {L}} \not \vdash \theta $
. Let P be a new unary predicate symbol. It suffices to show that
$\mathit {Ax}_{\mathcal {L}} \not \vdash \theta $
. Let P be a new unary predicate symbol. It suffices to show that
 $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} \vdash \theta ^P$
.
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} \vdash \theta ^P$
.
Actually, we show that
 $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px \vdash \theta ^P$
. Since P is supposed to stand for ‘previously recognized ontology’, the hypothesis
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px \vdash \theta ^P$
. Since P is supposed to stand for ‘previously recognized ontology’, the hypothesis
![]() $\exists x Px$
merely reflects the fact that classical logic requires a nonempty domain. In any case, we can absorb the extra hypothesis by replacing
$\exists x Px$
merely reflects the fact that classical logic requires a nonempty domain. In any case, we can absorb the extra hypothesis by replacing
![]() $\theta $
with
$\theta $
with
![]() $\exists x (x=x) \rightarrow \theta $
.Footnote
18
$\exists x (x=x) \rightarrow \theta $
.Footnote
18
Let us define a translation
![]() from our two-sorted language
from our two-sorted language
![]() $\mathcal {L}^+ = \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n \}]$
into the one-sorted language
$\mathcal {L}^+ = \mathcal {L}_{\{0, n\}}[\{\#_0, \#_n \}]$
into the one-sorted language
![]() $\mathcal {L}[\{\#, P\}]$
. The idea is to relativize base-sort quantifiers to P and relativize numerical-sort quantifiers to
$\mathcal {L}[\{\#, P\}]$
. The idea is to relativize base-sort quantifiers to P and relativize numerical-sort quantifiers to
![]() $\mathit {Num}(x) := \exists F(x = \#F)$
.
$\mathit {Num}(x) := \exists F(x = \#F)$
.
First we define a pre-translation from variables of
![]() $\mathcal {L}^+$
into variables of
$\mathcal {L}^+$
into variables of
![]() $\mathcal {L}[\{\#, P\}]$
. (Compare Theorem 8.50.) Translate each variable of sort
$\mathcal {L}[\{\#, P\}]$
. (Compare Theorem 8.50.) Translate each variable of sort
![]() $\tau $
as a variable of sort
$\tau $
as a variable of sort
![]() , where
, where
![]() is obtained from
is obtained from
![]() $\tau $
by replacing each occurrence of n with
$\tau $
by replacing each occurrence of n with
![]() $0$
. Set up the pre-translation so that distinct variables of
$0$
. Set up the pre-translation so that distinct variables of
![]() $\mathcal {L}^+$
are translated as distinct variables of
$\mathcal {L}^+$
are translated as distinct variables of
![]() $\mathcal {L}[\{\#, P\}]$
.
$\mathcal {L}[\{\#, P\}]$
.
We now define the translation
. Let j be any object sort, and let
![]() $\tau = \langle j_1, \ldots , j_k \rangle $
be any second-order sort. Let
$\tau = \langle j_1, \ldots , j_k \rangle $
be any second-order sort. Let
![]() $\mathit {Num}(x) := \exists F(x = \#F)$
. Let
$\mathit {Num}(x) := \exists F(x = \#F)$
. Let
![]() $A_j$
be the relativization predicate for sort j:
$A_j$
be the relativization predicate for sort j:
 $$ \begin{align*}A_j(x) := \begin{cases} Px, & \text{ if } j=0, \\ \mathit{Num}(x), & \text{ if } j=n. \end{cases} \end{align*} $$
$$ \begin{align*}A_j(x) := \begin{cases} Px, & \text{ if } j=0, \\ \mathit{Num}(x), & \text{ if } j=n. \end{cases} \end{align*} $$
Then the translation runs as follows:

In other words, predication and equality are translated as themselves, both
![]() $\#_0$
and
$\#_0$
and
![]() $\#_n$
are translated as
$\#_n$
are translated as
![]() $\#$
, and quantifiers are relativized to P and
$\#$
, and quantifiers are relativized to P and
![]() $\mathit {Num}$
in the natural way.
$\mathit {Num}$
in the natural way.
We wish to show
 $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px \vdash \theta ^P$
. We have
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px \vdash \theta ^P$
. We have
![]() $\mathrm{2FA} \vdash \theta $
. Applying the -translation, we obtain
$\mathrm{2FA} \vdash \theta $
. Applying the -translation, we obtain

(The extra hypotheses serve to make the assumptions of our two-sorted notation explicit.) Notice that
is just
![]() $\theta ^P$
. So, it suffices to show that
$\theta ^P$
. So, it suffices to show that
![]() $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px$
proves all of the following:
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px$
proves all of the following:
-
•
 ,
, -
•
 $\exists x Px$
,
$\exists x Px$
, -
•
 $\exists x \mathit {Num}(x)$
,
$\exists x \mathit {Num}(x)$
, -
•
 $\forall X ((X \subseteq P \vee X \subseteq \mathit {Num}) \rightarrow \mathit {Num}(\# X))$
.
$\forall X ((X \subseteq P \vee X \subseteq \mathit {Num}) \rightarrow \mathit {Num}(\# X))$
.
The second, third, and fourth bullets are obvious. For the first bullet, we have

. Now,
merely consists of relativizations of the logical axioms
![]() $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]}$
. These relativizations are all provable from
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]}$
. These relativizations are all provable from
![]() $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \exists x Px + \exists x \mathit {Num}(x)$
.
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \exists x Px + \exists x \mathit {Num}(x)$
.
Similarly,
merely consists of relativizations of HP, such as
These are all provable from
![]() $\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px + \exists x \mathit {Num}(x)$
. The proof is complete.
$\mathit {Ax}_{\mathcal {L}[\{\#, P\}]} + \mathrm{HP} + \exists x Px + \exists x \mathit {Num}(x)$
. The proof is complete.
Corollary 10.73. HP is not deductively Field-conservative over pure axiomatic second-order logic.
Proof. Set
![]() $Px := \neg Num(x)$
in the proof of the previous theorem.
$Px := \neg Num(x)$
in the proof of the previous theorem.
The upshot is that it makes a very great difference for the neo-Fregean program whether conservativeness requirements are formulated deductively or semantically. There seems to be no deductive criterion of conservativeness on which HP, or any similar principle, is conservative. As a matter of fact, neo-Fregeans have tended to prefer semantic notions of conservativeness anyway. But it would be desirable to see more philosophical justification for the use of these semantic notions, given that the deductive alternatives simply don’t work.Footnote 19
By the way, just as our deductive conservativeness results in the two-sorted setting could easily be transferred to the one-sorted setting, so too, Weir’s semantic conservativeness results for HP can easily be transferred to the two-sorted setting. Say that
![]() $T_1$
is semantically conservative over
$T_1$
is semantically conservative over
![]() $T_0$
if every standard model of
$T_0$
if every standard model of
![]() $T_0$
can be expanded to a standard model of
$T_0$
can be expanded to a standard model of
![]() $T_1$
. Then we have the following result:
$T_1$
. Then we have the following result:
Theorem 10.74.
2FA is semantically conservative over
![]() $\mathit {Ax}_{\mathcal {L}}$
.
$\mathit {Ax}_{\mathcal {L}}$
.
Proof. Our argument is a simple adaptation of [Reference Weir33, p. 24, theorem 4.1].
Take any standard
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, with object domain
$\mathcal {M}$
, with object domain
![]() $M_0$
. We will show how to expand
$M_0$
. We will show how to expand
![]() $\mathcal {M}$
to a standard
$\mathcal {M}$
to a standard
![]() $\mathcal {L}^+$
-structure
$\mathcal {L}^+$
-structure
![]() $\mathcal {N}$
that satisfies 2HP.
$\mathcal {N}$
that satisfies 2HP.
To specify
![]() $\mathcal {N}$
, we have to specify object domains
$\mathcal {N}$
, we have to specify object domains
![]() $N_0$
and
$N_0$
and
![]() $N_n$
, and an interpretation I of the constant symbols
$N_n$
, and an interpretation I of the constant symbols
![]() $\#_0, \#_n$
.
$\#_0, \#_n$
.
Set
![]() $N_0 = M_0$
.
$N_0 = M_0$
.
Set
![]() $N_i = \varkappa \cup \{\varkappa \}$
, where
$N_i = \varkappa \cup \{\varkappa \}$
, where
![]() $\varkappa $
is the least infinite cardinal such that
$\varkappa $
is the least infinite cardinal such that
![]() $\varkappa \geq |N_0|$
.
$\varkappa \geq |N_0|$
.
Set
![]() $N_\tau = \mathcal {P}(N_{j_1} \times \cdots \times N_{j_m})$
for all other sorts
$N_\tau = \mathcal {P}(N_{j_1} \times \cdots \times N_{j_m})$
for all other sorts
![]() $\tau = \langle j_1, \ldots , j_m \rangle $
.
$\tau = \langle j_1, \ldots , j_m \rangle $
.
We claim that the cardinality of any base concept
![]() $A \in N_{\langle 0 \rangle }$
is a member of the numerical universe
$A \in N_{\langle 0 \rangle }$
is a member of the numerical universe
![]() $N_n$
. Indeed, take any
$N_n$
. Indeed, take any
![]() $A \in N_{\langle 0 \rangle }$
. Then
$A \in N_{\langle 0 \rangle }$
. Then
Further, we claim that the cardinality of any numerical concept
![]() $A \in N_{\langle n \rangle }$
is a member of the numerical universe
$A \in N_{\langle n \rangle }$
is a member of the numerical universe
![]() $N_n$
. Indeed, take any
$N_n$
. Indeed, take any
![]() $A \in N_{\langle n \rangle }$
. Then
$A \in N_{\langle n \rangle }$
. Then
Let
![]() $I(\#_0)$
be the function
$I(\#_0)$
be the function
![]() $N_{\langle 0 \rangle } \to N_n$
which maps each concept to its cardinality.
$N_{\langle 0 \rangle } \to N_n$
which maps each concept to its cardinality.
Let
![]() $I(\#_n)$
be the function
$I(\#_n)$
be the function
![]() $N_{\langle n \rangle } \to N_n$
which maps each concept to its cardinality.
$N_{\langle n \rangle } \to N_n$
which maps each concept to its cardinality.
Then
![]() $\mathcal {N}$
is a standard
$\mathcal {N}$
is a standard
![]() $\mathcal {L}^+$
-structure satisfying 2HP, and hence 2FA.
$\mathcal {L}^+$
-structure satisfying 2HP, and hence 2FA.
We conclude with some interesting open problems.
Problem 10.75. Is HP conservative over DI (
![]() $= \neg \mathit {DFin}(V)$
)?
$= \neg \mathit {DFin}(V)$
)?
Problem 10.76. Is w2FA conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {DFin}(V)$
?
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {DFin}(V)$
?
Problem 10.77. Is 2FA conservative over
![]() $\mathit {Ax}_{\mathcal {L}} + \neg \mathit {DFin}(V)$
?
$\mathit {Ax}_{\mathcal {L}} + \neg \mathit {DFin}(V)$
?
Problem 10.78. Is 2FA conservative over axiomatic third-order logic
![]() $+ \ \neg \mathit {Fin}(V)$
?
$+ \ \neg \mathit {Fin}(V)$
?
11 Acknowledgements
Thanks to Sophia Arbeiter, John Burgess, Sean Ebels-Duggan, Vivian Feldblyum, Warren Goldfarb, Anil Gupta, Alexander Johnstone, Daniel Kaplan, Benjamin Marschall, Thomas Ricketts, James Shaw, Sean Walsh, and Daniel Webber for helpful discussion. We are also grateful to Jouko Väänänen for providing us with a copy of Asser’s book, and to two anonymous referees for their constructive feedback.