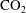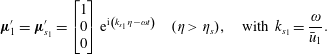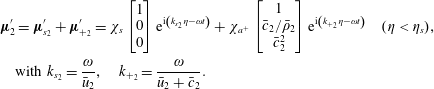1 Introduction
Dense vapours are single-phase gases featuring large heat capacities relative to their molecular weights. Examples are hydrocarbons, perfluorocarbons or siloxanes. They are of practical interest in energy-conversion cycles operating on low-temperature heat sources such as organic Rankine cycles (ORCs), where the expansion process may be performed in just one stage. Part of the expansion occurs close to the thermodynamic critical point (TCP), where the sound speed substantially decreases, making the expander flow highly supersonic (around Mach 3) and causing shockwaves to form in the expander. In the dense-vapour regime, close to the liquid–vapour equilibrium, the classical ideal-gas assumption has to be reconsidered to take into account the thermodynamic critical point and the so-called associated non-ideal-gas effects. This change of equation of state can have dramatic consequences on the hyperbolic part of the equations governing the motion of such fluids, giving rise to the formation of nonlinear waves which would be non-admissible (e.g. violating the entropy increase) in classical gas dynamics governed by an ideal-gas equation of state. The early works of Bethe (Reference Bethe1942), Zel’dovich (Reference Zel’dovich1946), Landau & Lifshitz (Reference Landau and Lifshitz1959), Thompson (Reference Thompson1971) and Thompson & Lambrakis (Reference Thompson and Lambrakis1973) set the theoretical basis for the conditions under which such non-classical effects can be observed in a single-phase fluid (often referred to as BZT fluid). The governing parameter to be used to address the question of non-classical gas dynamics is the so-called fundamental derivative of gas dynamics, first introduced by Hayes (Reference Hayes and Emmons1960),
where
![]() $\unicode[STIX]{x1D717}$
,
$\unicode[STIX]{x1D717}$
,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $s$
,
$s$
,
![]() $p$
and
$p$
and
![]() $c$
are the specific volume, the density, the specific entropy, the pressure and the isentropic speed of sound of the fluid. Classical gas dynamics occurs when
$c$
are the specific volume, the density, the specific entropy, the pressure and the isentropic speed of sound of the fluid. Classical gas dynamics occurs when
![]() $\unicode[STIX]{x1D6E4}>0$
; the isentropes in the
$\unicode[STIX]{x1D6E4}>0$
; the isentropes in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram are then convex and the only shockwaves satisfying the entropy-increase condition are compression shockwaves. Isentropic fans are then necessarily of expansion type. This classical nonlinear gas dynamics is sometimes referred to as positive nonlinearity and is found for every fluid in its ideal-gas limit. When
$(p,\unicode[STIX]{x1D717})$
-diagram are then convex and the only shockwaves satisfying the entropy-increase condition are compression shockwaves. Isentropic fans are then necessarily of expansion type. This classical nonlinear gas dynamics is sometimes referred to as positive nonlinearity and is found for every fluid in its ideal-gas limit. When
![]() $\unicode[STIX]{x1D6E4}<0$
(negative nonlinearity), the isentropes are concave in the
$\unicode[STIX]{x1D6E4}<0$
(negative nonlinearity), the isentropes are concave in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram and the only admissible shockwaves are rarefaction shockwaves, also called expansion shockwaves, and the isentropic fans are of compression type. The shock-formation process is much more complex for fluids featuring both
$(p,\unicode[STIX]{x1D717})$
-diagram and the only admissible shockwaves are rarefaction shockwaves, also called expansion shockwaves, and the isentropic fans are of compression type. The shock-formation process is much more complex for fluids featuring both
![]() $\unicode[STIX]{x1D6E4}>0$
and
$\unicode[STIX]{x1D6E4}>0$
and
![]() $\unicode[STIX]{x1D6E4}<0$
regions (mixed nonlinearity): in addition to compression shockwaves and rarefaction shockwaves, sonic shocks of compression or expansion type can form (the downstream velocity in the reference frame of the shock is then equal to the local sound speed) as well as double-sonic shocks for which both the upstream and downstream flows are sonic (see Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Sen Reference Cramer and Sen1986, Reference Cramer and Sen1987). Moreover, nonlinear waves can be of composite type, featuring two or three of these elementary waves. Thus, the Riemann problem for the Euler equations in the context of non-ideal gases is richer and much more complex than for ideal gases (Quartapelle et al.
Reference Quartapelle, Castelletti, Guardone and Quaranta2003). A comprehensive study of this problem can be found in Menikoff & Plohr (Reference Menikoff and Plohr1989).
$\unicode[STIX]{x1D6E4}<0$
regions (mixed nonlinearity): in addition to compression shockwaves and rarefaction shockwaves, sonic shocks of compression or expansion type can form (the downstream velocity in the reference frame of the shock is then equal to the local sound speed) as well as double-sonic shocks for which both the upstream and downstream flows are sonic (see Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Sen Reference Cramer and Sen1986, Reference Cramer and Sen1987). Moreover, nonlinear waves can be of composite type, featuring two or three of these elementary waves. Thus, the Riemann problem for the Euler equations in the context of non-ideal gases is richer and much more complex than for ideal gases (Quartapelle et al.
Reference Quartapelle, Castelletti, Guardone and Quaranta2003). A comprehensive study of this problem can be found in Menikoff & Plohr (Reference Menikoff and Plohr1989).
A fundamental outcome from the studies of Bethe (Reference Bethe1942), Zel’dovich (Reference Zel’dovich1946) and Thompson (Reference Thompson1971) is the possibility to observe a domain of finite size in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram featuring a
$(p,\unicode[STIX]{x1D717})$
-diagram featuring a
![]() $\unicode[STIX]{x1D6E4}<0$
in the vapour region surrounding the thermodynamical critical point (the BZT region). A sufficient condition of existence is that the dimensionless ratio between the specific heat capacity and the gas constant,
$\unicode[STIX]{x1D6E4}<0$
in the vapour region surrounding the thermodynamical critical point (the BZT region). A sufficient condition of existence is that the dimensionless ratio between the specific heat capacity and the gas constant,
![]() $c_{v}/R$
(measured in the dilute ideal-gas limit), is greater than a critical value which depends on the equation of state. Some molecules (e.g. siloxanes) feature
$c_{v}/R$
(measured in the dilute ideal-gas limit), is greater than a critical value which depends on the equation of state. Some molecules (e.g. siloxanes) feature
![]() $c_{v}/R$
values as large as
$c_{v}/R$
values as large as
![]() $10^{2}$
(Thompson & Lambrakis Reference Thompson and Lambrakis1973; Guardone & Argrow Reference Guardone and Argrow2005), and have attracted interest for a better understanding of gas dynamics in BZT fluids. Starting from the 1980s, significant effort has been made to extend the classical gas dynamics theory to BZT fluids. Most of these studies have focused on the mixed-nonlinearity effects on wave formation in idealised inviscid flow conditions (without any boundaries), yet have revealed significant departure from classical theory. Non-classical effects of progressively increasing interest for practical applications have been demonstrated, e.g. a shock-compression-strength limitation induced by an inviscid shock-splitting effect (Cramer Reference Cramer1989), a suppression of separation in viscous–inviscid shock boundary layer interactions (Cramer & Park Reference Cramer and Park1999) and a shock-free turbine blade in ORC turbines (Brown & Argrow Reference Brown and Argrow2000). Theoretical studies of the viscous shock structure also revealed strong non-classical effects close to
$10^{2}$
(Thompson & Lambrakis Reference Thompson and Lambrakis1973; Guardone & Argrow Reference Guardone and Argrow2005), and have attracted interest for a better understanding of gas dynamics in BZT fluids. Starting from the 1980s, significant effort has been made to extend the classical gas dynamics theory to BZT fluids. Most of these studies have focused on the mixed-nonlinearity effects on wave formation in idealised inviscid flow conditions (without any boundaries), yet have revealed significant departure from classical theory. Non-classical effects of progressively increasing interest for practical applications have been demonstrated, e.g. a shock-compression-strength limitation induced by an inviscid shock-splitting effect (Cramer Reference Cramer1989), a suppression of separation in viscous–inviscid shock boundary layer interactions (Cramer & Park Reference Cramer and Park1999) and a shock-free turbine blade in ORC turbines (Brown & Argrow Reference Brown and Argrow2000). Theoretical studies of the viscous shock structure also revealed strong non-classical effects close to
![]() $\unicode[STIX]{x1D6E4}=0$
, e.g. the occurrence of local extrema in Mach number and entropy in the shock structure and a non-monotonic behaviour of the shock thickness with respect to the shock strength even with constant transport coefficients (Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Crickenberger Reference Cramer and Crickenberger1991). With the development of numerical methods, the possibility of taking advantage of non-classical gas dynamics effects on problems from classical aerodynamics has been investigated (see Brown & Argrow Reference Brown and Argrow1997, Reference Brown and Argrow2000; Cinnella & Congedo Reference Cinnella and Congedo2007, Reference Cinnella and Congedo2008; Guardone, Parsani & Vigevano Reference Guardone, Parsani and Vigevano2007; Kluwick & Meyer Reference Kluwick and Meyer2011).
$\unicode[STIX]{x1D6E4}=0$
, e.g. the occurrence of local extrema in Mach number and entropy in the shock structure and a non-monotonic behaviour of the shock thickness with respect to the shock strength even with constant transport coefficients (Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Crickenberger Reference Cramer and Crickenberger1991). With the development of numerical methods, the possibility of taking advantage of non-classical gas dynamics effects on problems from classical aerodynamics has been investigated (see Brown & Argrow Reference Brown and Argrow1997, Reference Brown and Argrow2000; Cinnella & Congedo Reference Cinnella and Congedo2007, Reference Cinnella and Congedo2008; Guardone, Parsani & Vigevano Reference Guardone, Parsani and Vigevano2007; Kluwick & Meyer Reference Kluwick and Meyer2011).
Non-ideal-gas effects are also of potential importance in the stability problem of shock fronts subjected to small perturbations. D’yakov (Reference D’yakov1954) and Kontorovich (Reference Kontorovich1957) were the first to systematically investigate the response of an isolated shock to a small perturbation of its front for an arbitrary equation of state. Using a normal-mode decomposition, they confirmed the unconditional linear stability of isolated shock fronts under the assumption of the ideal-gas model. They built a one-parameter criterion, based on the equation of state, to address the question of stability. They showed that for a non-ideal-gas equation of state, there exist shocks that are linearly unstable to incoming perturbations. Remarkably, they demonstrated the existence of conditions under which a non-ideal-gas shock can sustain small perturbations of its front with no damping or growth of the initial disturbance. This regime is abusively called the ‘D’yakov–Kontorovich (DK) instability’ or regime of spontaneous acoustic emission (because of the emitted acoustic waves in the unperturbed flow, which is subsonic in the shock reference frame).
Since these early studies, non-ideal-gas effects on the linear stability of shocks have been investigated with modern and analytical methods (Erpenbeck Reference Erpenbeck1962; Bates Reference Bates2004). Deriving an equation for the Laplace transform of the shock-ripple amplitude, Bates (Reference Bates2004, Reference Bates2007) provided a convenient way of computing its time evolution for an arbitrary equation of state. He showed that in the stable-shock regime, a small corrugation of the front decreases with
![]() $t^{-3/2}$
, as for an ideal gas. While agreement with the D’yakov and Kontorovich theoretical results is achieved for the ‘isolated planar shockwave’ problem, Bates (Reference Bates2012, Reference Bates2015) also showed that the stability limits (expressed in terms of the D’yakov parameter) have to be reconsidered when a finite physical domain is taken into account (e.g. a moving piston). In particular, the ‘DK instability’ regime can simply disappear.
$t^{-3/2}$
, as for an ideal gas. While agreement with the D’yakov and Kontorovich theoretical results is achieved for the ‘isolated planar shockwave’ problem, Bates (Reference Bates2012, Reference Bates2015) also showed that the stability limits (expressed in terms of the D’yakov parameter) have to be reconsidered when a finite physical domain is taken into account (e.g. a moving piston). In particular, the ‘DK instability’ regime can simply disappear.
In most flows of interest, shockwaves travel through inhomogeneous fields such as turbulence. Despite the inherent nonlinear nature of such interactions, the linear framework is a powerful tool to address the fundamental question of the interaction of a shockwave with a turbulent flow. The linear interaction of waves with normal or oblique shocks has been studied primarily in ideal gases by Moore (Reference Moore1954) and Ribner (Reference Ribner1954, Reference Ribner1987), using a normal-mode decomposition (of plane sound waves and/or vorticity waves) of the small perturbation, in the context of acoustic generation. Ribner has demonstrated how turbulence intensities as low as 0.1 % could turn into a 120 dB noise level downstream of the shock. As aero-acoustic forcing in turbomachinery is a significant source of premature turbine-blade fatigue, this result showed the importance of shock/turbulence interaction and how the linear interaction analysis (LIA) is relevant in studying it, the most recent version of which may be found in Wouchuk, Huete & Velikovich (Reference Wouchuk, Huete and Velikovich2009) and Quadros, Sinha & Larsson (Reference Quadros, Sinha and Larsson2016a
,Reference Quadros, Sinha and Larsson
b
). This relevance has grown recently with favourable comparisons against state-of-the-art numerical simulations of the fully nonlinear interaction (Larsson & Lele Reference Larsson and Lele2009; Donzis Reference Donzis2012; Sinha Reference Sinha2012; Larsson, Bermejo-Moreno & Lele Reference Larsson, Bermejo-Moreno and Lele2013; Ryu & Livescu Reference Ryu and Livescu2014; Quadros et al.
Reference Quadros, Sinha and Larsson2016a
,Reference Quadros, Sinha and Larsson
b
). Lee, Lele & Moin (Reference Lee, Lele and Moin1997), Larsson & Lele (Reference Larsson and Lele2009), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013) and Ryu & Livescu (Reference Ryu and Livescu2014) demonstrated the ability of LIA to accurately predict the post-shock turbulent kinetic energy, which opened the way for turbulence modelling based on LIA. An exact analytical model of the interaction based on a closed form of several turbulent quantities extracted from the LIA was proposed by Wouchuk et al. (Reference Wouchuk, Huete and Velikovich2009). Sinha (Reference Sinha2012) formed a
![]() $k$
–
$k$
–
![]() $\unicode[STIX]{x1D716}$
model from the LIA formulation, improving the current modelling capabilities for both isotropic turbulence and complex flows with shockwaves. The LIA formulation of the shock interacting with oblique waves for an arbitrary equation of state was derived by McKenzie & Westphal (Reference McKenzie and Westphal1968). They provided an exact analytical formula for the acoustic generation/amplification factor through a shock impinged by an entropy/acoustic wave but without commenting on potential non-ideal-gas effects. Both analytical and numerical efforts towards the understanding of shock/turbulence interactions in non-ideal gases seem far behind what has been achieved for ideal gases. To the best of the authors’ knowledge, there does not exist any study of non-ideal-gas effects on the unsteady problem of a shock interacting with a perturbed flow field.
$\unicode[STIX]{x1D716}$
model from the LIA formulation, improving the current modelling capabilities for both isotropic turbulence and complex flows with shockwaves. The LIA formulation of the shock interacting with oblique waves for an arbitrary equation of state was derived by McKenzie & Westphal (Reference McKenzie and Westphal1968). They provided an exact analytical formula for the acoustic generation/amplification factor through a shock impinged by an entropy/acoustic wave but without commenting on potential non-ideal-gas effects. Both analytical and numerical efforts towards the understanding of shock/turbulence interactions in non-ideal gases seem far behind what has been achieved for ideal gases. To the best of the authors’ knowledge, there does not exist any study of non-ideal-gas effects on the unsteady problem of a shock interacting with a perturbed flow field.
The aim of this paper is to investigate the response of a shockwave travelling into a perturbed dense gas modelled with a non-ideal equation of state. The study is carried out by the LIA of a simple one-dimensional shockwave so as to focus on non-ideal-gas effects on the interaction. The first part is a derivation of the general Rankine–Hugoniot (RH) conditions, with a special discussion on the admissibility problem in the dense-gas region. In the second part, base flows satisfying the RH relations are used in a small-perturbation analysis. The response of shocks to an incoming supersonic entropy-mode perturbation is derived in the spirit of Ribner’s pioneering work. Explicit formulae are formulated in terms of thermodynamic properties. The amplification of entropy across the shock is commented on in § 4 and the generated acoustic field in § 5. A critical-point anomaly is found in the limiting case of
![]() $c_{v}/R\rightarrow +\infty$
. Strong non-ideal-gas effects on the unsteady shock perturbation problem are demonstrated for the first time with potentially large extrema of transmission factors (for large values of
$c_{v}/R\rightarrow +\infty$
. Strong non-ideal-gas effects on the unsteady shock perturbation problem are demonstrated for the first time with potentially large extrema of transmission factors (for large values of
![]() $c_{v}/R$
). Two distinct classes of non-ideal-gas effects are reported: near-critical-point and BZT effects. A convenient and new representation of the ‘D’yakov–Kontorovich instability’ locus in the
$c_{v}/R$
). Two distinct classes of non-ideal-gas effects are reported: near-critical-point and BZT effects. A convenient and new representation of the ‘D’yakov–Kontorovich instability’ locus in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram is provided, emphasising the importance of critical-point effects in the dense-gas regime. The new classes of unsteady non-ideal-gas effects, including the ‘DK instability’, are then assessed using the most accurate thermodynamic models for the siloxane D6 and toluene, providing a first insight towards the possibility of their experimental observation (§ 7).
$(p,\unicode[STIX]{x1D717})$
-diagram is provided, emphasising the importance of critical-point effects in the dense-gas regime. The new classes of unsteady non-ideal-gas effects, including the ‘DK instability’, are then assessed using the most accurate thermodynamic models for the siloxane D6 and toluene, providing a first insight towards the possibility of their experimental observation (§ 7).
2 Admissibility of compression shockwaves in non-ideal gases
This section recalls some well-known results on the shock-formation process in dense gases (Cramer & Kluwick Reference Cramer and Kluwick1984; Menikoff & Plohr Reference Menikoff and Plohr1989; Zamfirescu, Guardone & Colonna Reference Zamfirescu, Guardone and Colonna2008). An effort is made to formulate mathematical statements with geometric representations in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram in order to facilitate comments on the refraction properties introduced in the next section.
$(p,\unicode[STIX]{x1D717})$
-diagram in order to facilitate comments on the refraction properties introduced in the next section.
2.1 Jump conditions and shock adiabats
We consider an infinitely long shock tube in which a normal shockwave is propagating at constant velocity
![]() $\bar{u}_{s}$
in a gas modelled with an arbitrary equation of state. We assume a pressure and temperature field to be defined from a canonical equation of state of the form
$\bar{u}_{s}$
in a gas modelled with an arbitrary equation of state. We assume a pressure and temperature field to be defined from a canonical equation of state of the form
![]() $e_{s}(s,\unicode[STIX]{x1D717})$
, where
$e_{s}(s,\unicode[STIX]{x1D717})$
, where
![]() $e_{s}$
is the specific internal energy of the fluid (Menikoff & Plohr Reference Menikoff and Plohr1989). For simplicity, however, we will express the specific internal energy in terms of the pressure and the specific volume throughout the paper, i.e.
$e_{s}$
is the specific internal energy of the fluid (Menikoff & Plohr Reference Menikoff and Plohr1989). For simplicity, however, we will express the specific internal energy in terms of the pressure and the specific volume throughout the paper, i.e.
![]() $e(p,\unicode[STIX]{x1D717})$
. We are interested in the effect of a non-ideal equation of state on the refraction properties of the compression shockwaves emanating from the one-dimensional Euler equations. The integral form of these equations leads to the well-known Rankine–Hugoniot relations, satisfied across every discontinuity,
$e(p,\unicode[STIX]{x1D717})$
. We are interested in the effect of a non-ideal equation of state on the refraction properties of the compression shockwaves emanating from the one-dimensional Euler equations. The integral form of these equations leads to the well-known Rankine–Hugoniot relations, satisfied across every discontinuity,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{1}/\unicode[STIX]{x1D717}_{1}=u_{2}/\unicode[STIX]{x1D717}_{2},\\ p_{1}+{u_{1}}^{2}/\unicode[STIX]{x1D717}_{1}=p_{2}+{u_{2}}^{2}/\unicode[STIX]{x1D717}_{2},\\ e(p_{2},\unicode[STIX]{x1D717}_{2})-e(p_{1},\unicode[STIX]{x1D717}_{1})=(p_{2}+p_{1})(\unicode[STIX]{x1D717}_{1}-\unicode[STIX]{x1D717}_{2})/2,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{1}/\unicode[STIX]{x1D717}_{1}=u_{2}/\unicode[STIX]{x1D717}_{2},\\ p_{1}+{u_{1}}^{2}/\unicode[STIX]{x1D717}_{1}=p_{2}+{u_{2}}^{2}/\unicode[STIX]{x1D717}_{2},\\ e(p_{2},\unicode[STIX]{x1D717}_{2})-e(p_{1},\unicode[STIX]{x1D717}_{1})=(p_{2}+p_{1})(\unicode[STIX]{x1D717}_{1}-\unicode[STIX]{x1D717}_{2})/2,\end{array}\right\}\end{eqnarray}$$
where the subscripts
![]() $(\cdot )_{1}$
and
$(\cdot )_{1}$
and
![]() $(\cdot )_{2}$
stand for the uniform upstream and downstream states around the shock observed in a reference frame moving with the shock. The last equation has been obtained by combining both the momentum-balance and mass-conservation principles into the energy equation. Let us define a function
$(\cdot )_{2}$
stand for the uniform upstream and downstream states around the shock observed in a reference frame moving with the shock. The last equation has been obtained by combining both the momentum-balance and mass-conservation principles into the energy equation. Let us define a function
![]() $f$
such that
$f$
such that
![]() $f(\unicode[STIX]{x1D717}_{1},p_{1},\unicode[STIX]{x1D717}_{2},p_{2})=e(p_{2},\unicode[STIX]{x1D717}_{2})-e(p_{1},\unicode[STIX]{x1D717}_{1})-(p_{2}+p_{1})(\unicode[STIX]{x1D717}_{1}-\unicode[STIX]{x1D717}_{2})/2$
. From the implicit function theorem, we know that if
$f(\unicode[STIX]{x1D717}_{1},p_{1},\unicode[STIX]{x1D717}_{2},p_{2})=e(p_{2},\unicode[STIX]{x1D717}_{2})-e(p_{1},\unicode[STIX]{x1D717}_{1})-(p_{2}+p_{1})(\unicode[STIX]{x1D717}_{1}-\unicode[STIX]{x1D717}_{2})/2$
. From the implicit function theorem, we know that if
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}p_{2}(\unicode[STIX]{x1D717}_{1},p_{1},\unicode[STIX]{x1D717}_{2},p_{2})\neq 0$
, there exists a regular function
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}p_{2}(\unicode[STIX]{x1D717}_{1},p_{1},\unicode[STIX]{x1D717}_{2},p_{2})\neq 0$
, there exists a regular function
![]() $p_{h}$
such that
$p_{h}$
such that
![]() $p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1})$
. The existence condition can be expressed as
$p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1})$
. The existence condition can be expressed as
Introducing the Grüneisen parameter
![]() $G\equiv \unicode[STIX]{x1D717}\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}e\right)_{\unicode[STIX]{x1D717}}$
, the condition becomes
$G\equiv \unicode[STIX]{x1D717}\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}e\right)_{\unicode[STIX]{x1D717}}$
, the condition becomes
where
![]() $\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}\equiv \unicode[STIX]{x1D717}_{2}-\unicode[STIX]{x1D717}_{1}$
is the jump of specific volume across the discontinuity and
$\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}\equiv \unicode[STIX]{x1D717}_{2}-\unicode[STIX]{x1D717}_{1}$
is the jump of specific volume across the discontinuity and
![]() $G_{2}$
is the post-shock Grüneisen parameter. This condition defines the usual vertical asymptote of the Hugoniot curves in a single-phase gas for which the pressure goes to positive infinity in the
$G_{2}$
is the post-shock Grüneisen parameter. This condition defines the usual vertical asymptote of the Hugoniot curves in a single-phase gas for which the pressure goes to positive infinity in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram (see Cramer Reference Cramer1989). For a perfect gas, this singularity occurs at
$(p,\unicode[STIX]{x1D717})$
-diagram (see Cramer Reference Cramer1989). For a perfect gas, this singularity occurs at
![]() $\unicode[STIX]{x1D717}_{2}=\unicode[STIX]{x1D717}_{1}(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)$
. In what follows, we study shocks described by the right-hand-side branch of this vertical asymptote (defined by
$\unicode[STIX]{x1D717}_{2}=\unicode[STIX]{x1D717}_{1}(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)$
. In what follows, we study shocks described by the right-hand-side branch of this vertical asymptote (defined by
![]() $G_{2}+2\unicode[STIX]{x1D717}_{2}/\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}>0$
). Introducing the mass flow rate
$G_{2}+2\unicode[STIX]{x1D717}_{2}/\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}>0$
). Introducing the mass flow rate
![]() $j\equiv u_{1}/\unicode[STIX]{x1D717}_{1}=c_{1}M_{1}/\unicode[STIX]{x1D717}_{1}=c_{2}M_{2}/\unicode[STIX]{x1D717}_{2}$
(where
$j\equiv u_{1}/\unicode[STIX]{x1D717}_{1}=c_{1}M_{1}/\unicode[STIX]{x1D717}_{1}=c_{2}M_{2}/\unicode[STIX]{x1D717}_{2}$
(where
![]() $c$
and
$c$
and
![]() $M$
are the local sound speed and Mach number), the solution of (2.1) can then be expressed for a given upstream state as the intersection between the Rayleigh line (
$M$
are the local sound speed and Mach number), the solution of (2.1) can then be expressed for a given upstream state as the intersection between the Rayleigh line (
![]() ${\mathcal{R}}$
-line) and the Hugoniot line (
${\mathcal{R}}$
-line) and the Hugoniot line (
![]() ${\mathcal{H}}$
-line), defined in the
${\mathcal{H}}$
-line), defined in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram respectively as
$(p,\unicode[STIX]{x1D717})$
-diagram respectively as
These two curves have a simple interpretation in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram. For a given upstream state, the Hugoniot curve is the locus of all downstream thermodynamic states reachable via a discontinuity across which the total enthalpy can be conserved. For a given upstream state and Mach number, the
$(p,\unicode[STIX]{x1D717})$
-diagram. For a given upstream state, the Hugoniot curve is the locus of all downstream thermodynamic states reachable via a discontinuity across which the total enthalpy can be conserved. For a given upstream state and Mach number, the
![]() ${\mathcal{R}}$
-line is the locus of all downstream thermodynamic states satisfying the mass-conservation and momentum-balance principles. The slope of the Hugoniot curve on its right-hand-side branch is always negative for single-phase gases with
${\mathcal{R}}$
-line is the locus of all downstream thermodynamic states satisfying the mass-conservation and momentum-balance principles. The slope of the Hugoniot curve on its right-hand-side branch is always negative for single-phase gases with
![]() $G>0$
(Cramer Reference Cramer1989). The hypothesis that
$G>0$
(Cramer Reference Cramer1989). The hypothesis that
![]() $G>0$
will be made throughout this paper; this is representative of a substance that expands upon isobaric heating and is relevant for most of the single-phase gas behaviour of interest here. An important outcome is that isentropes do not cross each other in the
$G>0$
will be made throughout this paper; this is representative of a substance that expands upon isobaric heating and is relevant for most of the single-phase gas behaviour of interest here. An important outcome is that isentropes do not cross each other in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram and entropy increases towards higher pressures (Menikoff & Plohr Reference Menikoff and Plohr1989). For weak shocks, the curvature of the
$(p,\unicode[STIX]{x1D717})$
-diagram and entropy increases towards higher pressures (Menikoff & Plohr Reference Menikoff and Plohr1989). For weak shocks, the curvature of the
![]() ${\mathcal{H}}$
-line in the
${\mathcal{H}}$
-line in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram is given by the local sign of
$(p,\unicode[STIX]{x1D717})$
-diagram is given by the local sign of
![]() $\unicode[STIX]{x1D6E4}$
(Cramer Reference Cramer1989). Graphical solutions of the RH relations, read in the
$\unicode[STIX]{x1D6E4}$
(Cramer Reference Cramer1989). Graphical solutions of the RH relations, read in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram, can then be obtained (see figure 1). In most cases, there exist multiple weak solutions for a given upstream Mach number, and additional admissibility criteria must be expressed to select the waves that will not degenerate from the initial-value problem (scale-invariant initial data). This scale-invariant property is of fundamental importance in view of the perturbation analysis performed below. In the process of finding such a solution, the curvature of the
$(p,\unicode[STIX]{x1D717})$
-diagram, can then be obtained (see figure 1). In most cases, there exist multiple weak solutions for a given upstream Mach number, and additional admissibility criteria must be expressed to select the waves that will not degenerate from the initial-value problem (scale-invariant initial data). This scale-invariant property is of fundamental importance in view of the perturbation analysis performed below. In the process of finding such a solution, the curvature of the
![]() ${\mathcal{H}}$
-line plays a key role (Cramer & Kluwick Reference Cramer and Kluwick1984; Menikoff & Plohr Reference Menikoff and Plohr1989; Zamfirescu et al.
Reference Zamfirescu, Guardone and Colonna2008).
${\mathcal{H}}$
-line plays a key role (Cramer & Kluwick Reference Cramer and Kluwick1984; Menikoff & Plohr Reference Menikoff and Plohr1989; Zamfirescu et al.
Reference Zamfirescu, Guardone and Colonna2008).

Figure 1. Admissibility problem of classical and non-classical gas dynamics discussed in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram.
$(p,\unicode[STIX]{x1D717})$
-diagram.
2.2 Geometrical formulation of the admissibility problem in dense gases
Zamfirescu et al. (Reference Zamfirescu, Guardone and Colonna2008) have demonstrated the uniqueness of the Riemann problem in the context of dense gases using theoretical results from the general theory of conservation laws (Liu Reference Liu1975). In what follows, we detail the admissibility selection process for compression shockwaves in dense gases. We consider a gas with positive coefficient of thermal expansion, which implies
![]() $G>0$
, and arbitrary sign of
$G>0$
, and arbitrary sign of
![]() $\unicode[STIX]{x1D6E4}$
. For classical gas dynamics (positive nonlinearity), the
$\unicode[STIX]{x1D6E4}$
. For classical gas dynamics (positive nonlinearity), the
![]() ${\mathcal{H}}$
-lines are convex and the selection of self-similar solutions (only functions of
${\mathcal{H}}$
-lines are convex and the selection of self-similar solutions (only functions of
![]() $x/t$
) between weak solutions of the Euler equations is operated by the use of the Lax (Reference Lax1957) characteristic criterion (equivalent to the entropy-increase criterion), which also implies the Landau stability constraint on the wave orientation (i.e.
$x/t$
) between weak solutions of the Euler equations is operated by the use of the Lax (Reference Lax1957) characteristic criterion (equivalent to the entropy-increase criterion), which also implies the Landau stability constraint on the wave orientation (i.e.
![]() $M_{2}\leqslant 1\leqslant M_{1}$
). This criterion is still sufficient in the case of negative nonlinearity (the Hugoniot curves are then concave everywhere). However, when a finite region of mixed nonlinearity exists in the
$M_{2}\leqslant 1\leqslant M_{1}$
). This criterion is still sufficient in the case of negative nonlinearity (the Hugoniot curves are then concave everywhere). However, when a finite region of mixed nonlinearity exists in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram and is crossed by the Hugoniot locus, there usually are multiple solutions satisfying both the Landau and Lax conditions (Menikoff & Plohr Reference Menikoff and Plohr1989). The formulation of admissibility criteria for weak solutions of systems involving mixed nonlinearities has been studied in the context of general conservation laws; the corresponding wave solutions are then called locally linearly degenerated (Oleinik Reference Oleinik1959; Liu Reference Liu1976). The resulting criterion states that a shock is admissible if and only if its speed in the laboratory reference frame is greater than or at least equal to the speed of the fastest shock located on the Hugoniot branch joining the upstream thermodynamic state and the tested final state on the
$(p,\unicode[STIX]{x1D717})$
-diagram and is crossed by the Hugoniot locus, there usually are multiple solutions satisfying both the Landau and Lax conditions (Menikoff & Plohr Reference Menikoff and Plohr1989). The formulation of admissibility criteria for weak solutions of systems involving mixed nonlinearities has been studied in the context of general conservation laws; the corresponding wave solutions are then called locally linearly degenerated (Oleinik Reference Oleinik1959; Liu Reference Liu1976). The resulting criterion states that a shock is admissible if and only if its speed in the laboratory reference frame is greater than or at least equal to the speed of the fastest shock located on the Hugoniot branch joining the upstream thermodynamic state and the tested final state on the
![]() ${\mathcal{H}}$
-line. The Liu–Oleinik condition is a necessary condition for a dissipative structure to exist (Liu Reference Liu1976). It was used by Menikoff & Plohr (Reference Menikoff and Plohr1989) and Zhao et al. (Reference Zhao, Mentrelli, Ruggeri and Sugiyama2011) in the context of mixed nonlinearities in BZT fluids. Another admissibility criterion was also formulated by Lax (Reference Lax1971) (Lax’s generalised entropy condition) and used by Cramer (Reference Cramer1989) and Cramer & Crickenberger (Reference Cramer and Crickenberger1991) for dense gases. This condition asks for the segment of the
${\mathcal{H}}$
-line. The Liu–Oleinik condition is a necessary condition for a dissipative structure to exist (Liu Reference Liu1976). It was used by Menikoff & Plohr (Reference Menikoff and Plohr1989) and Zhao et al. (Reference Zhao, Mentrelli, Ruggeri and Sugiyama2011) in the context of mixed nonlinearities in BZT fluids. Another admissibility criterion was also formulated by Lax (Reference Lax1971) (Lax’s generalised entropy condition) and used by Cramer (Reference Cramer1989) and Cramer & Crickenberger (Reference Cramer and Crickenberger1991) for dense gases. This condition asks for the segment of the
![]() ${\mathcal{R}}$
-line connecting the upstream and downstream states of the shock to lie entirely above (compression shocks) or below (expansion shocks) the
${\mathcal{R}}$
-line connecting the upstream and downstream states of the shock to lie entirely above (compression shocks) or below (expansion shocks) the
![]() ${\mathcal{H}}$
-line. It is straightforward to see the equivalence between the two conditions in the context of shocks in BZT fluids.
${\mathcal{H}}$
-line. It is straightforward to see the equivalence between the two conditions in the context of shocks in BZT fluids.
Remarkably, all admissibility criteria can be conveniently read in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram. A useful relationship between the ratio of the slopes of the Hugoniot and Rayleigh lines at the downstream state and the downstream Mach number provides a way of graphically checking the Landau evolution criterion. This relation is obtained by combining a differentiation along the
$(p,\unicode[STIX]{x1D717})$
-diagram. A useful relationship between the ratio of the slopes of the Hugoniot and Rayleigh lines at the downstream state and the downstream Mach number provides a way of graphically checking the Landau evolution criterion. This relation is obtained by combining a differentiation along the
![]() ${\mathcal{H}}$
-line at constant upstream conditions with the Gibbs thermodynamic identity (Cramer Reference Cramer1989),
${\mathcal{H}}$
-line at constant upstream conditions with the Gibbs thermodynamic identity (Cramer Reference Cramer1989),
 $$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}p_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}_{2}}}-{\displaystyle \frac{\unicode[STIX]{x27E6}p\unicode[STIX]{x27E7}}{\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}}}={\displaystyle \frac{j^{2}}{{M_{2}}^{2}}}{\displaystyle \frac{{M_{2}}^{2}-1}{\left(1+{\displaystyle \frac{\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}}{2\unicode[STIX]{x1D717}_{2}}}G_{2}\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}p_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}_{2}}}-{\displaystyle \frac{\unicode[STIX]{x27E6}p\unicode[STIX]{x27E7}}{\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}}}={\displaystyle \frac{j^{2}}{{M_{2}}^{2}}}{\displaystyle \frac{{M_{2}}^{2}-1}{\left(1+{\displaystyle \frac{\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}}{2\unicode[STIX]{x1D717}_{2}}}G_{2}\right)}}.\end{eqnarray}$$
Therefore, on the right-hand-side branch of the
![]() ${\mathcal{H}}$
-line (where
${\mathcal{H}}$
-line (where
![]() $1+\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}G_{2}/(2\unicode[STIX]{x1D717}_{2})>0$
from earlier assumptions), the post-shock Mach number is subsonic if the slope of the
$1+\unicode[STIX]{x27E6}\unicode[STIX]{x1D717}\unicode[STIX]{x27E7}G_{2}/(2\unicode[STIX]{x1D717}_{2})>0$
from earlier assumptions), the post-shock Mach number is subsonic if the slope of the
![]() ${\mathcal{H}}$
-line is smaller (steeper down) than the slope of the
${\mathcal{H}}$
-line is smaller (steeper down) than the slope of the
![]() ${\mathcal{R}}$
-line and supersonic if it is greater. A sonic post-shock state is reached when the two curves are tangent. Figure 1 gives a picture of the admissibility problem for weak solutions of compression shocks (with upstream condition on point
${\mathcal{R}}$
-line and supersonic if it is greater. A sonic post-shock state is reached when the two curves are tangent. Figure 1 gives a picture of the admissibility problem for weak solutions of compression shocks (with upstream condition on point
![]() $\unicode[STIX]{x2460}$
) considered on Hugoniot curves representative of classical and non-classical gas dynamic. For the positive nonlinearity with convex
$\unicode[STIX]{x2460}$
) considered on Hugoniot curves representative of classical and non-classical gas dynamic. For the positive nonlinearity with convex
![]() ${\mathcal{H}}$
-line (or the negative nonlinearity with concave
${\mathcal{H}}$
-line (or the negative nonlinearity with concave
![]() ${\mathcal{H}}$
-line), the compression shocks starting at
${\mathcal{H}}$
-line), the compression shocks starting at
![]() $\unicode[STIX]{x2460}$
(or expansion shock starting at
$\unicode[STIX]{x2460}$
(or expansion shock starting at
![]() $\unicode[STIX]{x2461}$
) are the only discontinuities satisfying the entropy-increase criteria (and thus Landau’s wave orientation stability constraint); see figure 1(i). When a mixed nonlinearity is involved (see figure 1(ii–iii)), which is typical for dense gases near the TCP (Thompson & Lambrakis Reference Thompson and Lambrakis1973; Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Sen Reference Cramer and Sen1986), Lax’s entropy criterion is no longer guaranteed by the convexity property of the
$\unicode[STIX]{x2461}$
) are the only discontinuities satisfying the entropy-increase criteria (and thus Landau’s wave orientation stability constraint); see figure 1(i). When a mixed nonlinearity is involved (see figure 1(ii–iii)), which is typical for dense gases near the TCP (Thompson & Lambrakis Reference Thompson and Lambrakis1973; Cramer & Kluwick Reference Cramer and Kluwick1984; Cramer & Sen Reference Cramer and Sen1986), Lax’s entropy criterion is no longer guaranteed by the convexity property of the
![]() ${\mathcal{H}}$
-line. Let us consider the admissibility problem of compression shocks from upstream states with
${\mathcal{H}}$
-line. Let us consider the admissibility problem of compression shocks from upstream states with
![]() $\unicode[STIX]{x1D6E4}>0$
(point
$\unicode[STIX]{x1D6E4}>0$
(point
![]() $\unicode[STIX]{x2460}$
in figure 1(iii)), from which the
$\unicode[STIX]{x2460}$
in figure 1(iii)), from which the
![]() ${\mathcal{H}}$
-lines cross a
${\mathcal{H}}$
-lines cross a
![]() $\unicode[STIX]{x1D6E4}<0$
region and have their convexity changed. Two different situations may occur. If there is no sonic point on the
$\unicode[STIX]{x1D6E4}<0$
region and have their convexity changed. Two different situations may occur. If there is no sonic point on the
![]() ${\mathcal{H}}$
-line, then all compression shocks are admissible. If there exists a sonic point on the concave part of the
${\mathcal{H}}$
-line, then all compression shocks are admissible. If there exists a sonic point on the concave part of the
![]() ${\mathcal{H}}$
-line (point a in figure 1(iii) for which
${\mathcal{H}}$
-line (point a in figure 1(iii) for which
![]() $\unicode[STIX]{x1D6E4}<0$
), there exists a branch (from a to b) that violates Landau’s evolution criterion (the slope of the
$\unicode[STIX]{x1D6E4}<0$
), there exists a branch (from a to b) that violates Landau’s evolution criterion (the slope of the
![]() ${\mathcal{R}}$
-line being steeper down than that of the
${\mathcal{R}}$
-line being steeper down than that of the
![]() ${\mathcal{H}}$
-line). This branch corresponds to unstable waves that will not remain scale invariant. At b, the post-shock condition is again sonic. Branch b to c corresponds to compression shocks that satisfy the entropy-increase criterion (classical Lax criterion) and therefore Landau’s stability criterion but are still inadmissible by failure to fulfil the Liu–Oleinik criterion (or equivalently the general Lax criterion, see Lax Reference Lax1971). The solution of the Riemann problem with initial data taken on this branch is found to degenerate into a non-classical composite wave of type sonic shock/compression fan/shock (Cramer Reference Cramer1989) and is therefore not a suitable base flow. Branches
${\mathcal{H}}$
-line). This branch corresponds to unstable waves that will not remain scale invariant. At b, the post-shock condition is again sonic. Branch b to c corresponds to compression shocks that satisfy the entropy-increase criterion (classical Lax criterion) and therefore Landau’s stability criterion but are still inadmissible by failure to fulfil the Liu–Oleinik criterion (or equivalently the general Lax criterion, see Lax Reference Lax1971). The solution of the Riemann problem with initial data taken on this branch is found to degenerate into a non-classical composite wave of type sonic shock/compression fan/shock (Cramer Reference Cramer1989) and is therefore not a suitable base flow. Branches
![]() $\unicode[STIX]{x2460}$
to a and c to the highest pressure limit are admissible and remain scale invariant. A limiting case is found when a sonic point with
$\unicode[STIX]{x2460}$
to a and c to the highest pressure limit are admissible and remain scale invariant. A limiting case is found when a sonic point with
![]() $\unicode[STIX]{x1D6E4}=0$
exists on the
$\unicode[STIX]{x1D6E4}=0$
exists on the
![]() ${\mathcal{H}}$
-line, in which case all compression shocks are still admissible (see figure 1(ii)).
${\mathcal{H}}$
-line, in which case all compression shocks are still admissible (see figure 1(ii)).
Admissibility criteria for compression shockwaves are readily checked when plotting the post-shock Mach number against the pre-shock Mach number (see figure 1). Let us assume a positive value of the fundamental derivative of gas dynamics at the pre-shock state. For low enough pre-shock Mach number
![]() $M_{1}$
, the post-shock state is still with
$M_{1}$
, the post-shock state is still with
![]() $\unicode[STIX]{x1D6E4}>0$
and the post-shock Mach number
$\unicode[STIX]{x1D6E4}>0$
and the post-shock Mach number
![]() $M_{2}$
is a decreasing function of
$M_{2}$
is a decreasing function of
![]() $M_{1}$
(classical behaviour). If there exists a finite section on the Hugoniot curve with
$M_{1}$
(classical behaviour). If there exists a finite section on the Hugoniot curve with
![]() $\unicode[STIX]{x1D6E4}<0$
, it is possible to observe a non-monotonic variation of the post-shock Mach number with increasing shock strength, for post-shock states that lie after the first inflexion point on the
$\unicode[STIX]{x1D6E4}<0$
, it is possible to observe a non-monotonic variation of the post-shock Mach number with increasing shock strength, for post-shock states that lie after the first inflexion point on the
![]() ${\mathcal{H}}$
-line, see (2.5) (non-ideal-gas effect). The non-admissible branches a–b and b–c from figure 1(iii) are part of a loop in
${\mathcal{H}}$
-line, see (2.5) (non-ideal-gas effect). The non-admissible branches a–b and b–c from figure 1(iii) are part of a loop in
![]() $M_{2}(M_{1})$
, which is consistent with the expression of the Liu–Oleinik maximum wave speed criterion (for each point on the b–c branch there exists an intermediate point on the
$M_{2}(M_{1})$
, which is consistent with the expression of the Liu–Oleinik maximum wave speed criterion (for each point on the b–c branch there exists an intermediate point on the
![]() ${\mathcal{H}}$
-line with higher wave speed). In fact, it is the consequence of a change of variation of the
${\mathcal{H}}$
-line with higher wave speed). In fact, it is the consequence of a change of variation of the
![]() ${\mathcal{R}}$
-line slope (i.e. the mass flow rate
${\mathcal{R}}$
-line slope (i.e. the mass flow rate
![]() $j$
) when the post-shock state point is moving from sonic condition on the non-convex part of the
$j$
) when the post-shock state point is moving from sonic condition on the non-convex part of the
![]() ${\mathcal{H}}$
-line in the
${\mathcal{H}}$
-line in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram (red segment in figure 1(iii)). For the limiting case when a post-shock sonic state is reached for
$(p,\unicode[STIX]{x1D717})$
-diagram (red segment in figure 1(iii)). For the limiting case when a post-shock sonic state is reached for
![]() $\unicode[STIX]{x1D6E4}_{2}=0$
, the post-shock Mach number reaches a maximum of one with no inadmissible loop.
$\unicode[STIX]{x1D6E4}_{2}=0$
, the post-shock Mach number reaches a maximum of one with no inadmissible loop.
These different scenarios are illustrated in figure 2 using a van der Waals model of the PP10 gas for which
![]() $c_{v}/R=78.2$
(see appendix A). Pre-shock states at critical temperature but different upstream pressures are investigated. A behaviour in agreement with that of an ideal gas is obtained at low Mach numbers for low pressures (e.g.
$c_{v}/R=78.2$
(see appendix A). Pre-shock states at critical temperature but different upstream pressures are investigated. A behaviour in agreement with that of an ideal gas is obtained at low Mach numbers for low pressures (e.g.
![]() $p_{1}/p_{c}=0.13$
). A progressive departure from the ideal-gas-law behaviour is observed when the post-shock state reaches the TCP region. The divergence occurs at lower shock speeds (
$p_{1}/p_{c}=0.13$
). A progressive departure from the ideal-gas-law behaviour is observed when the post-shock state reaches the TCP region. The divergence occurs at lower shock speeds (
![]() $M_{1}$
) when the pre-shock state is brought closer to the TCP, corresponding to higher
$M_{1}$
) when the pre-shock state is brought closer to the TCP, corresponding to higher
![]() $p_{1}/p_{c}$
values on the critical isotherm (e.g.
$p_{1}/p_{c}$
values on the critical isotherm (e.g.
![]() $p_{1}/p_{c}=0.65$
). A local maximum in
$p_{1}/p_{c}=0.65$
). A local maximum in
![]() $M_{2}(M_{1})$
emerges above a given upstream pressure
$M_{2}(M_{1})$
emerges above a given upstream pressure
![]() $p_{1}/p_{c}$
(due to the mixed nonlinearity along the
$p_{1}/p_{c}$
(due to the mixed nonlinearity along the
![]() ${\mathcal{H}}$
-line) but does not necessarily imply the existence of a sonic post-shock state (see
${\mathcal{H}}$
-line) but does not necessarily imply the existence of a sonic post-shock state (see
![]() $p_{1}/p_{c}=0.45$
in figure 2
b). When a non-admissible path is found on the
$p_{1}/p_{c}=0.45$
in figure 2
b). When a non-admissible path is found on the
![]() ${\mathcal{H}}$
-line (thin lines in figure 2
b), the post-shock Mach number
${\mathcal{H}}$
-line (thin lines in figure 2
b), the post-shock Mach number
![]() $M_{2}$
becomes a discontinuous function of
$M_{2}$
becomes a discontinuous function of
![]() $M_{1}$
. Sonic-shock formation in van der Waals gases has been derived analytically in Cramer & Sen (Reference Cramer and Sen1987) and has been shown to be a direct consequence of the occurrence of states with
$M_{1}$
. Sonic-shock formation in van der Waals gases has been derived analytically in Cramer & Sen (Reference Cramer and Sen1987) and has been shown to be a direct consequence of the occurrence of states with
![]() $\unicode[STIX]{x1D6E4}<0$
on the
$\unicode[STIX]{x1D6E4}<0$
on the
![]() ${\mathcal{H}}$
-line. A line joining all double-sonic rarefaction pre-shock states has been derived for an arbitrary equation of state by Zamfirescu et al. (Reference Zamfirescu, Guardone and Colonna2008). Their discussion is restricted to rarefaction shockwaves which are very different as far as the admissibility problem is concerned. Indeed, double-sonic compression shocks are not admissible in general in single-phase gases with positive Grüneisen index (decreasing
${\mathcal{H}}$
-line. A line joining all double-sonic rarefaction pre-shock states has been derived for an arbitrary equation of state by Zamfirescu et al. (Reference Zamfirescu, Guardone and Colonna2008). Their discussion is restricted to rarefaction shockwaves which are very different as far as the admissibility problem is concerned. Indeed, double-sonic compression shocks are not admissible in general in single-phase gases with positive Grüneisen index (decreasing
![]() ${\mathcal{H}}$
-line in
${\mathcal{H}}$
-line in
![]() $(p,\unicode[STIX]{x1D717})$
-diagram); they fail to fulfil the Liu–Oleinik admissibility condition (Kluwick Reference Kluwick1993); while double-sonic rarefaction shocks are admissible. Therefore, post-shock sonic states necessarily occur when
$(p,\unicode[STIX]{x1D717})$
-diagram); they fail to fulfil the Liu–Oleinik admissibility condition (Kluwick Reference Kluwick1993); while double-sonic rarefaction shocks are admissible. Therefore, post-shock sonic states necessarily occur when
![]() $M_{1}\neq 1$
. Thus, the picture given by the four selected reduced pressures is representative of the general evolution of the post-shock Mach number for compression shockwaves with pre-shock states approaching the TCP. Thus, for a given upstream thermodynamic condition with
$M_{1}\neq 1$
. Thus, the picture given by the four selected reduced pressures is representative of the general evolution of the post-shock Mach number for compression shockwaves with pre-shock states approaching the TCP. Thus, for a given upstream thermodynamic condition with
![]() ${\mathcal{H}}$
-line featuring a discontinuous admissible path, there exists a mass flow rate for which the post-shock conditions (e.g. in a nozzle) change abruptly for arbitrarily small changes in upstream conditions.
${\mathcal{H}}$
-line featuring a discontinuous admissible path, there exists a mass flow rate for which the post-shock conditions (e.g. in a nozzle) change abruptly for arbitrarily small changes in upstream conditions.

Figure 2. Non-ideal-gas effects on the post-shock Mach number (for which
![]() $T_{1}=T_{c}$
) (a) and detailed view of the Mach number range up to
$T_{1}=T_{c}$
) (a) and detailed view of the Mach number range up to
![]() $1.5$
(b). The equivalent ideal-gas configuration is shown by dashed lines. The thin lines indicate the non-admissible paths.
$1.5$
(b). The equivalent ideal-gas configuration is shown by dashed lines. The thin lines indicate the non-admissible paths.
Scale-invariant admissible compression shocks originating from point
![]() $\unicode[STIX]{x2460}$
in figure 1 are used in the next section as the base flow in a small-perturbation analysis. As is first inferred here, a discontinuous admissible Hugoniot locus is a typical feature of non-ideal-gas dynamics and will have a significant impact on the refraction properties of shocks in non-ideal gases (e.g. BZT fluids).
$\unicode[STIX]{x2460}$
in figure 1 are used in the next section as the base flow in a small-perturbation analysis. As is first inferred here, a discontinuous admissible Hugoniot locus is a typical feature of non-ideal-gas dynamics and will have a significant impact on the refraction properties of shocks in non-ideal gases (e.g. BZT fluids).
2.3 Isothermal-shock limit
This paper makes frequent references to a hypothetical infinitely dense gas (i.e. a fluid with
![]() $c_{v}/R\rightarrow +\infty$
). This section provides a few comments relating to such a limit. For simplicity, fluids with constant isochoric heat capacities (polytropic gas) are considered.
$c_{v}/R\rightarrow +\infty$
). This section provides a few comments relating to such a limit. For simplicity, fluids with constant isochoric heat capacities (polytropic gas) are considered.
Let us assume that a finite change of internal energy is supplied, for instance through a shockwave (i.e. equal to the work done by the average pressure), to a ‘fluid’ parcel modelled with a theoretical infinite
![]() $c_{v}/R$
value (such a ‘fluid’ would be made of molecules with an infinite number of active degrees of freedom). It is clear from the definition
$c_{v}/R$
value (such a ‘fluid’ would be made of molecules with an infinite number of active degrees of freedom). It is clear from the definition
![]() $c_{v}\equiv (\unicode[STIX]{x2202}e/\unicode[STIX]{x2202}T)_{\unicode[STIX]{x1D717}}$
that a necessary condition for the internal energy to remain finite is that such change be following an isothermal process. Hence, the shock becomes an isothermal process. It should be noted that we recover the unphysical isothermal shockwave theoretical model of Stokes (Reference Stokes1848) (with the noticeable difference that the speed of sound in arbitrary media may change even at constant temperature). It is also well known that, in this limiting case, isentropes converge towards the isotherms in the
$c_{v}\equiv (\unicode[STIX]{x2202}e/\unicode[STIX]{x2202}T)_{\unicode[STIX]{x1D717}}$
that a necessary condition for the internal energy to remain finite is that such change be following an isothermal process. Hence, the shock becomes an isothermal process. It should be noted that we recover the unphysical isothermal shockwave theoretical model of Stokes (Reference Stokes1848) (with the noticeable difference that the speed of sound in arbitrary media may change even at constant temperature). It is also well known that, in this limiting case, isentropes converge towards the isotherms in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram (Thompson & Lambrakis Reference Thompson and Lambrakis1973; Cramer Reference Cramer1989). Thus, such ‘fluids’ have their
$(p,\unicode[STIX]{x1D717})$
-diagram (Thompson & Lambrakis Reference Thompson and Lambrakis1973; Cramer Reference Cramer1989). Thus, such ‘fluids’ have their
![]() ${\mathcal{H}}$
-lines coinciding with the isotherms, which are also the isentropes, in the
${\mathcal{H}}$
-lines coinciding with the isotherms, which are also the isentropes, in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram.
$(p,\unicode[STIX]{x1D717})$
-diagram.
Of course, isentropic or isothermal compression shocks have no physical meaning (Rankine Reference Rankine1870), and the limits should be seen as qualitatively inferring the behaviour of shocks for large and finite values of
![]() $c_{v}/R$
for which the entropy increases along the Hugoniot paths. A similar asymptotic argument was used by Thompson & Lambrakis (Reference Thompson and Lambrakis1973) to infer the existence of a negative
$c_{v}/R$
for which the entropy increases along the Hugoniot paths. A similar asymptotic argument was used by Thompson & Lambrakis (Reference Thompson and Lambrakis1973) to infer the existence of a negative
![]() $\unicode[STIX]{x1D6E4}$
region in the vapour-phase near-critical conditions for fluids with large molecular heat capacities.
$\unicode[STIX]{x1D6E4}$
region in the vapour-phase near-critical conditions for fluids with large molecular heat capacities.
3 Compression-shock refraction properties in dense gases
Following Ribner’s analysis (Ribner Reference Ribner1954), we first derive a small perturbation of the Euler equations for an arbitrary equation of state. A convenient basis suitable for analysis in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram is used here. The resulting eigenvector basis is then used to project small-amplitude waves in a linear interaction analysis with an admissible compression shockwave. It provides the refraction amplification/generation coefficients.
$(p,\unicode[STIX]{x1D717})$
-diagram is used here. The resulting eigenvector basis is then used to project small-amplitude waves in a linear interaction analysis with an admissible compression shockwave. It provides the refraction amplification/generation coefficients.
3.1 Small perturbation of 1D inviscid flows with arbitrary equations of state
The eigenmode basis of the Euler equations was first derived by Kovásznay (Reference Kovásznay1953) in the context of weak turbulence generated in a supersonic flow modelled with an ideal-gas equation of state. Small perturbations were found to propagate along an entropy mode, two acoustic (irrotational) modes and a divergence-free vortical mode. This idealised picture was used by many authors (Ribner Reference Ribner1954; Lee et al. Reference Lee, Lele and Moin1997; Larsson & Lele Reference Larsson and Lele2009; Sinha Reference Sinha2012) to address the question of compressibility effects on turbulence. A weakly nonlinear formulation of these interactions has also been provided (Chu & Kovásznay Reference Chu and Kovásznay1958).
For simplicity, a uniform one-dimensional flow is assumed here. A consequence is that no vortical mode will be considered and most of our attention focuses on non-ideal-gas effects on the generation of the acoustic field and the amplification of entropy waves at the shock. A small perturbation (
![]() $\unicode[STIX]{x1D700}\ll 1$
) is added to the piecewise uniform base flow (
$\unicode[STIX]{x1D700}\ll 1$
) is added to the piecewise uniform base flow (
![]() $\bar{\unicode[STIX]{x1D741}}$
),
$\bar{\unicode[STIX]{x1D741}}$
),
The flow perturbation satisfies the one-dimensional linearised Euler equations in non-dimensional form. Reference thermodynamic variables are taken at the TCP (see appendix A) and the velocity scale is chosen in accordance (
![]() $u_{ref}^{\ast }\equiv \sqrt{p_{c}^{\ast }/\unicode[STIX]{x1D70C}_{c}^{\ast }}$
), while a characteristic length scale is provided by the flow perturbation (
$u_{ref}^{\ast }\equiv \sqrt{p_{c}^{\ast }/\unicode[STIX]{x1D70C}_{c}^{\ast }}$
), while a characteristic length scale is provided by the flow perturbation (
![]() $\unicode[STIX]{x1D706}^{\ast }$
), resulting in
$\unicode[STIX]{x1D706}^{\ast }$
), resulting in
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}t}+\bar{\boldsymbol{A}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}x}=\mathbf{0}+o(\bar{\unicode[STIX]{x1D741}}\unicode[STIX]{x1D700}),\quad \text{where }\unicode[STIX]{x1D741}^{\prime }\equiv \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}^{\prime }\\ u^{\prime }\\ p^{\prime }\end{array}\right],\bar{\boldsymbol{A}}\equiv \left[\begin{array}{@{}ccc@{}}\bar{u} & \bar{\unicode[STIX]{x1D70C}} & 0\\ 0 & \bar{u} & 1/\bar{\unicode[STIX]{x1D70C}}\\ 0 & \bar{\unicode[STIX]{x1D70C}}\bar{c}^{2} & \bar{u}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}t}+\bar{\boldsymbol{A}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}x}=\mathbf{0}+o(\bar{\unicode[STIX]{x1D741}}\unicode[STIX]{x1D700}),\quad \text{where }\unicode[STIX]{x1D741}^{\prime }\equiv \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}^{\prime }\\ u^{\prime }\\ p^{\prime }\end{array}\right],\bar{\boldsymbol{A}}\equiv \left[\begin{array}{@{}ccc@{}}\bar{u} & \bar{\unicode[STIX]{x1D70C}} & 0\\ 0 & \bar{u} & 1/\bar{\unicode[STIX]{x1D70C}}\\ 0 & \bar{\unicode[STIX]{x1D70C}}\bar{c}^{2} & \bar{u}\end{array}\right].\end{eqnarray}$$
Solutions to (3.2) are sought in the form of plane travelling waves,
where
![]() $k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$
is the wavenumber and
$k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$
is the wavenumber and
![]() $\unicode[STIX]{x1D714}$
is a prescribed constant angular velocity (see § 3.2). Equation (3.2) reduces to the eigenvalue problem
$\unicode[STIX]{x1D714}$
is a prescribed constant angular velocity (see § 3.2). Equation (3.2) reduces to the eigenvalue problem
with
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D714}/k$
the eigenvalues of
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D714}/k$
the eigenvalues of
![]() $\bar{\boldsymbol{A}}$
. Each eigenvalue will have an associated unit eigenvector, denoted
$\bar{\boldsymbol{A}}$
. Each eigenvalue will have an associated unit eigenvector, denoted
![]() $\boldsymbol{e}$
,
$\boldsymbol{e}$
,
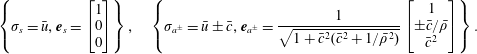 $$\begin{eqnarray}\left\{\unicode[STIX]{x1D70E}_{s}=\bar{u},\boldsymbol{e}_{s}=\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\right\},\quad \left\{\unicode[STIX]{x1D70E}_{a^{\pm }}=\bar{u}\pm \bar{c},\boldsymbol{e}_{a^{\pm }}={\displaystyle \frac{1}{\sqrt{1+\bar{c}^{2}(\bar{c}^{2}+1/\bar{\unicode[STIX]{x1D70C}}^{2})}}}\left[\begin{array}{@{}c@{}}1\\ \pm \bar{c}/\bar{\unicode[STIX]{x1D70C}}\\ \bar{c}^{2}\end{array}\right]\right\}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\left\{\unicode[STIX]{x1D70E}_{s}=\bar{u},\boldsymbol{e}_{s}=\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\right\},\quad \left\{\unicode[STIX]{x1D70E}_{a^{\pm }}=\bar{u}\pm \bar{c},\boldsymbol{e}_{a^{\pm }}={\displaystyle \frac{1}{\sqrt{1+\bar{c}^{2}(\bar{c}^{2}+1/\bar{\unicode[STIX]{x1D70C}}^{2})}}}\left[\begin{array}{@{}c@{}}1\\ \pm \bar{c}/\bar{\unicode[STIX]{x1D70C}}\\ \bar{c}^{2}\end{array}\right]\right\}.\qquad\end{eqnarray}$$

Figure 3. Dense-gas degeneracy of the eigenmode basis close to the TCP.
We recognise Kovásznay’s entropy eigenmode denoted by
![]() $(\cdot )_{s}$
and the right/left running acoustic eigenmodes
$(\cdot )_{s}$
and the right/left running acoustic eigenmodes
![]() $(\cdot )_{a^{\pm }}$
. The general wave solution of (3.2) can be represented as any linear combination of these three modes. The dependence on the equation of state is embedded in the speed of sound. It is of particular interest to notice that for fluids with molecules featuring a high number of degrees of freedom (typical for dense gas), the speed of sound decreases along an isentropic compression in the dense-gas region, down to a very low value near the TCP (Thompson & Lambrakis Reference Thompson and Lambrakis1973). This may come with a degeneracy of the basis, in which case a strong bias towards density fluctuation is expected. This is illustrated in figure 3, which represents the evolution of the unit eigenmode basis
$(\cdot )_{a^{\pm }}$
. The general wave solution of (3.2) can be represented as any linear combination of these three modes. The dependence on the equation of state is embedded in the speed of sound. It is of particular interest to notice that for fluids with molecules featuring a high number of degrees of freedom (typical for dense gas), the speed of sound decreases along an isentropic compression in the dense-gas region, down to a very low value near the TCP (Thompson & Lambrakis Reference Thompson and Lambrakis1973). This may come with a degeneracy of the basis, in which case a strong bias towards density fluctuation is expected. This is illustrated in figure 3, which represents the evolution of the unit eigenmode basis
![]() $(\boldsymbol{e}_{s},\boldsymbol{e}_{a^{+}},\boldsymbol{e}_{a^{-}})$
expressed in terms of the primitive variables
$(\boldsymbol{e}_{s},\boldsymbol{e}_{a^{+}},\boldsymbol{e}_{a^{-}})$
expressed in terms of the primitive variables
![]() $(\unicode[STIX]{x1D70C},u,p)$
for an isentropic process following the critical isentrope (the quarter unit sphere is represented for convenience). Thompson & Lambrakis (Reference Thompson and Lambrakis1973) have demonstrated the convergence of isentropes towards isotherms for large values of
$(\unicode[STIX]{x1D70C},u,p)$
for an isentropic process following the critical isentrope (the quarter unit sphere is represented for convenience). Thompson & Lambrakis (Reference Thompson and Lambrakis1973) have demonstrated the convergence of isentropes towards isotherms for large values of
![]() $c_{v}/R$
. In figure 3, both the critical isentrope and isotherm lines are represented for the PP10 gas with
$c_{v}/R$
. In figure 3, both the critical isentrope and isotherm lines are represented for the PP10 gas with
![]() $c_{v}/R=78.2$
, using a van der Waals equation of state (see appendix A). For an isentropic process in the dilute-gas limit (i.e. high specific volume) along the critical isentrope, the speed of sound is low (it vanishes for infinite specific volume) and the acoustic eigenvectors tend to be aligned with
$c_{v}/R=78.2$
, using a van der Waals equation of state (see appendix A). For an isentropic process in the dilute-gas limit (i.e. high specific volume) along the critical isentrope, the speed of sound is low (it vanishes for infinite specific volume) and the acoustic eigenvectors tend to be aligned with
![]() $[0,\pm u,0]$
. Thus, in the limit of infinite specific volume, the basis degenerates. The pressure and density fluctuations are then expected to be negligible compared with the velocity fluctuations. For an isentropic process in the high-pressure limit along the critical isentrope, the acoustic eigenvectors tend to align towards
$[0,\pm u,0]$
. Thus, in the limit of infinite specific volume, the basis degenerates. The pressure and density fluctuations are then expected to be negligible compared with the velocity fluctuations. For an isentropic process in the high-pressure limit along the critical isentrope, the acoustic eigenvectors tend to align towards
![]() $[0,0,p]$
and the velocity and density fluctuations are expected to be negligible compared with the pressure fluctuations. The basis also degenerates. These two limits are found in every equation of state; they match their ideal-gas asymptotic limits. For a dense gas close to the TCP where the sound speed is very small, the acoustic eigenvectors tend to align towards
$[0,0,p]$
and the velocity and density fluctuations are expected to be negligible compared with the pressure fluctuations. The basis also degenerates. These two limits are found in every equation of state; they match their ideal-gas asymptotic limits. For a dense gas close to the TCP where the sound speed is very small, the acoustic eigenvectors tend to align towards
![]() $[\unicode[STIX]{x1D70C},0,0]$
and both the pressure and velocity fluctuations are negligible relative to the density fluctuations. Once again, the eigenmode basis degenerates (for
$[\unicode[STIX]{x1D70C},0,0]$
and both the pressure and velocity fluctuations are negligible relative to the density fluctuations. Once again, the eigenmode basis degenerates (for
![]() $c_{v}/R\rightarrow +\infty$
) but with a triple-valued eigenvalue which is not possible in ideal gases. The black thick lines in figure 3 (right) illustrate paths of the eigenmode basis along the critical isentrope (from the dilute-gas to the high-pressure limit) for PP10. The linear interaction of these modes with a shockwave is investigated in the next section.
$c_{v}/R\rightarrow +\infty$
) but with a triple-valued eigenvalue which is not possible in ideal gases. The black thick lines in figure 3 (right) illustrate paths of the eigenmode basis along the critical isentrope (from the dilute-gas to the high-pressure limit) for PP10. The linear interaction of these modes with a shockwave is investigated in the next section.

Figure 4. Sketch of the entropy-mode refraction configuration. A one-dimensional shock travels at constant speed
![]() $\bar{u}_{s}$
through a fluid at rest (
$\bar{u}_{s}$
through a fluid at rest (
![]() $u_{R}=0$
) on which a periodic perturbation (in space, with periodicity
$u_{R}=0$
) on which a periodic perturbation (in space, with periodicity
![]() $\unicode[STIX]{x1D706}_{s_{1}}$
) is superimposed. The shock path
$\unicode[STIX]{x1D706}_{s_{1}}$
) is superimposed. The shock path
![]() $\unicode[STIX]{x1D701}(t)$
oscillates around the mean shock position
$\unicode[STIX]{x1D701}(t)$
oscillates around the mean shock position
![]() $\bar{u}_{s}t$
. The reference frame attached to the mean shock is denoted
$\bar{u}_{s}t$
. The reference frame attached to the mean shock is denoted
![]() $\unicode[STIX]{x1D702}(t)$
, and the actual shock position in that reference frame is denoted
$\unicode[STIX]{x1D702}(t)$
, and the actual shock position in that reference frame is denoted
![]() $\unicode[STIX]{x1D702}_{s}$
. (a) Spatio-temporal (
$\unicode[STIX]{x1D702}_{s}$
. (a) Spatio-temporal (
![]() $x$
–
$x$
–
![]() $t$
) diagram and (b) density profile in the reference frame moving with the mean shock position. The refracted density profile is the sum of entropic (with periodicity
$t$
) diagram and (b) density profile in the reference frame moving with the mean shock position. The refracted density profile is the sum of entropic (with periodicity
![]() $\unicode[STIX]{x1D706}_{s_{2}}$
) and downstream-propagating acoustic (with periodicity
$\unicode[STIX]{x1D706}_{s_{2}}$
) and downstream-propagating acoustic (with periodicity
![]() $\unicode[STIX]{x1D706}_{a_{2}^{+}}$
) perturbations.
$\unicode[STIX]{x1D706}_{a_{2}^{+}}$
) perturbations.
3.2 Linear shock-refraction properties with arbitrary equations of state
Let us consider a base flow consisting of an isolated one-dimensional compression shock whose compressed state is taken on the admissible branch defined in § 2 (upstream state
![]() $\bar{\unicode[STIX]{x1D741}}_{1}$
with
$\bar{\unicode[STIX]{x1D741}}_{1}$
with
![]() $M_{1}>1$
and downstream state
$M_{1}>1$
and downstream state
![]() $\bar{\unicode[STIX]{x1D741}}_{2}$
with
$\bar{\unicode[STIX]{x1D741}}_{2}$
with
![]() $M_{2}\leqslant 1$
). The shock is moving at a constant speed
$M_{2}\leqslant 1$
). The shock is moving at a constant speed
![]() $\bar{u}_{s}$
in the laboratory reference frame. Its position at time
$\bar{u}_{s}$
in the laboratory reference frame. Its position at time
![]() $t$
is set by the unique parameter
$t$
is set by the unique parameter
![]() $x_{s}(t)=\bar{u}_{s}t$
(assuming
$x_{s}(t)=\bar{u}_{s}t$
(assuming
![]() $x_{s}(0)=0$
). For simplicity, we introduce a new coordinate axis attached to the mean shock position
$x_{s}(0)=0$
). For simplicity, we introduce a new coordinate axis attached to the mean shock position
![]() $\unicode[STIX]{x1D702}=x-x_{s}$
and work in the reference frame attached to the moving shock. The uniform uncompressed side of the shock is perturbed with a prescribed small-amplitude wave, projected on the aforementioned eigenmode basis, which propagates through the shock discontinuity in the chosen reference frame. The compressed side and the shock front are therefore both perturbed. The fluctuating flow field satisfies the linearised Rankine–Hugoniot relations at the perturbed shock front. The linear-wave/shock interaction problem is solved by considering the most widely accepted methodology (D’yakov Reference D’yakov1954; Kontorovich Reference Kontorovich1957; McKenzie & Westphal Reference McKenzie and Westphal1968; Bates Reference Bates2004; Tumin Reference Tumin2008), which consists of taking as independent linear modes the incoming mode (entropy, upstream-propagating acoustic or downstream-propagating or acoustic), the refracted linear modes (one entropy and one downstream-propagating acoustic mode) and the unsteady shock displacement. The classical linearised Rankine–Hugoniot relations are solved at the shock front without additional surface tension terms (originated from inertial effects), as suggested by Lubchich & Pudovkin (Reference Lubchich and Pudovkin2004).
$\unicode[STIX]{x1D702}=x-x_{s}$
and work in the reference frame attached to the moving shock. The uniform uncompressed side of the shock is perturbed with a prescribed small-amplitude wave, projected on the aforementioned eigenmode basis, which propagates through the shock discontinuity in the chosen reference frame. The compressed side and the shock front are therefore both perturbed. The fluctuating flow field satisfies the linearised Rankine–Hugoniot relations at the perturbed shock front. The linear-wave/shock interaction problem is solved by considering the most widely accepted methodology (D’yakov Reference D’yakov1954; Kontorovich Reference Kontorovich1957; McKenzie & Westphal Reference McKenzie and Westphal1968; Bates Reference Bates2004; Tumin Reference Tumin2008), which consists of taking as independent linear modes the incoming mode (entropy, upstream-propagating acoustic or downstream-propagating or acoustic), the refracted linear modes (one entropy and one downstream-propagating acoustic mode) and the unsteady shock displacement. The classical linearised Rankine–Hugoniot relations are solved at the shock front without additional surface tension terms (originated from inertial effects), as suggested by Lubchich & Pudovkin (Reference Lubchich and Pudovkin2004).
The Rankine–Hugoniot conditions (2.1) are expressed at the shock position in the reference frame moving with the shock. A perturbation of this base flow (denoted with
![]() $\bar{.}$
) is now performed (with characteristic length scale
$\bar{.}$
) is now performed (with characteristic length scale
![]() $\unicode[STIX]{x1D706}$
). The instantaneous flow field is defined by parts as
$\unicode[STIX]{x1D706}$
). The instantaneous flow field is defined by parts as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D741}_{1}(\unicode[STIX]{x1D702},t)=\bar{\unicode[STIX]{x1D741}}_{1}(\unicode[STIX]{x1D702})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}_{1}^{\prime }(\unicode[STIX]{x1D702},t)+o(\unicode[STIX]{x1D700}\bar{\unicode[STIX]{x1D741}}_{1}(\unicode[STIX]{x1D702})),\quad \unicode[STIX]{x1D702}\in ]-\infty ,\unicode[STIX]{x1D702}_{s}(t)[,\\ \unicode[STIX]{x1D741}_{2}(\unicode[STIX]{x1D702},t)=\bar{\unicode[STIX]{x1D741}}_{2}(\unicode[STIX]{x1D702})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}_{2}^{\prime }(\unicode[STIX]{x1D702},t)+o(\unicode[STIX]{x1D700}\bar{\unicode[STIX]{x1D741}}_{2}(\unicode[STIX]{x1D702})),\quad \unicode[STIX]{x1D702}\in ]\unicode[STIX]{x1D702}_{s}(t),+\infty [,\\ \unicode[STIX]{x1D702}_{s}(t)=\unicode[STIX]{x1D700}\unicode[STIX]{x1D702}_{s}^{\prime }(t)+o(\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D741}_{1}(\unicode[STIX]{x1D702},t)=\bar{\unicode[STIX]{x1D741}}_{1}(\unicode[STIX]{x1D702})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}_{1}^{\prime }(\unicode[STIX]{x1D702},t)+o(\unicode[STIX]{x1D700}\bar{\unicode[STIX]{x1D741}}_{1}(\unicode[STIX]{x1D702})),\quad \unicode[STIX]{x1D702}\in ]-\infty ,\unicode[STIX]{x1D702}_{s}(t)[,\\ \unicode[STIX]{x1D741}_{2}(\unicode[STIX]{x1D702},t)=\bar{\unicode[STIX]{x1D741}}_{2}(\unicode[STIX]{x1D702})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}_{2}^{\prime }(\unicode[STIX]{x1D702},t)+o(\unicode[STIX]{x1D700}\bar{\unicode[STIX]{x1D741}}_{2}(\unicode[STIX]{x1D702})),\quad \unicode[STIX]{x1D702}\in ]\unicode[STIX]{x1D702}_{s}(t),+\infty [,\\ \unicode[STIX]{x1D702}_{s}(t)=\unicode[STIX]{x1D700}\unicode[STIX]{x1D702}_{s}^{\prime }(t)+o(\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}),\end{array}\right\}\end{eqnarray}$$
and
![]() $\bar{\unicode[STIX]{x1D741}}_{1}$
and
$\bar{\unicode[STIX]{x1D741}}_{1}$
and
![]() $\bar{\unicode[STIX]{x1D741}}_{2}$
are solutions to the algebraic system of (2.1).
$\bar{\unicode[STIX]{x1D741}}_{2}$
are solutions to the algebraic system of (2.1).
In what follows, the shock is perturbed by an entropy mode (density fluctuations without velocity and pressure fluctuations) and a boundary value problem is solved at the shock front. This approach is different from the linear stability analysis of the shock front (D’yakov Reference D’yakov1954; Kontorovich Reference Kontorovich1957; Bates Reference Bates2004) in the literature. Here, the linear refraction properties (wave transmission coefficients) of compression shocks are solved when the shocks are continuously forced with an entropy mode of prescribed angular velocity (
![]() $\unicode[STIX]{x1D714}$
is real and constant). The shock is considered to be a true discontinuity and to be continuously forced, consistent with the choice of a constant
$\unicode[STIX]{x1D714}$
is real and constant). The shock is considered to be a true discontinuity and to be continuously forced, consistent with the choice of a constant
![]() $\unicode[STIX]{x1D714}$
value. The general form of the problem can be summarised as follows.
$\unicode[STIX]{x1D714}$
value. The general form of the problem can be summarised as follows.
-
(i) On the upstream supersonic side of the shock lies the continuous forcing by a unitary entropy mode,
(3.7) $$\begin{eqnarray}\unicode[STIX]{x1D741}_{1}^{\prime }=\unicode[STIX]{x1D741}_{s_{1}}^{\prime }=\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\text{e}^{\text{i}\left(k_{s_{1}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}\quad (\unicode[STIX]{x1D702}>\unicode[STIX]{x1D702}_{s}),\quad \text{with }k_{s_{1}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D741}_{1}^{\prime }=\unicode[STIX]{x1D741}_{s_{1}}^{\prime }=\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\text{e}^{\text{i}\left(k_{s_{1}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}\quad (\unicode[STIX]{x1D702}>\unicode[STIX]{x1D702}_{s}),\quad \text{with }k_{s_{1}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{1}}.\end{eqnarray}$$
-
(ii) On the downstream subsonic side of the shock lie both the post-shock entropy and acoustic modes leaving the shock,
(3.8) $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D741}_{2}^{\prime }=\unicode[STIX]{x1D741}_{s_{2}}^{\prime }+\unicode[STIX]{x1D741}_{+_{2}}^{\prime }=\unicode[STIX]{x1D712}_{s}\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\text{e}^{\text{i}\left(k_{s_{2}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}+\unicode[STIX]{x1D712}_{a^{+}}\left[\begin{array}{@{}c@{}}1\\ \bar{c}_{2}/\bar{\unicode[STIX]{x1D70C}}_{2}\\ \bar{c}_{2}^{2}\end{array}\right]\text{e}^{\text{i}\left(k_{+_{2}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}\quad (\unicode[STIX]{x1D702}<\unicode[STIX]{x1D702}_{s}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{with }k_{s_{2}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{2}},\quad k_{+_{2}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{2}+\bar{c}_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D741}_{2}^{\prime }=\unicode[STIX]{x1D741}_{s_{2}}^{\prime }+\unicode[STIX]{x1D741}_{+_{2}}^{\prime }=\unicode[STIX]{x1D712}_{s}\left[\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right]\text{e}^{\text{i}\left(k_{s_{2}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}+\unicode[STIX]{x1D712}_{a^{+}}\left[\begin{array}{@{}c@{}}1\\ \bar{c}_{2}/\bar{\unicode[STIX]{x1D70C}}_{2}\\ \bar{c}_{2}^{2}\end{array}\right]\text{e}^{\text{i}\left(k_{+_{2}}\unicode[STIX]{x1D702}-\unicode[STIX]{x1D714}t\right)}\quad (\unicode[STIX]{x1D702}<\unicode[STIX]{x1D702}_{s}),\nonumber\\ \displaystyle & & \displaystyle \quad \text{with }k_{s_{2}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{2}},\quad k_{+_{2}}=\frac{\unicode[STIX]{x1D714}}{\bar{u}_{2}+\bar{c}_{2}}.\end{eqnarray}$$
-
(iii) The velocity of the shock oscillations is given by
(3.9) $$\begin{eqnarray}u_{s}^{\prime }\equiv {\displaystyle \frac{\text{d}\unicode[STIX]{x1D702}_{s}^{\prime }}{\text{d}t}}=\unicode[STIX]{x1D6FF}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}.\end{eqnarray}$$
$$\begin{eqnarray}u_{s}^{\prime }\equiv {\displaystyle \frac{\text{d}\unicode[STIX]{x1D702}_{s}^{\prime }}{\text{d}t}}=\unicode[STIX]{x1D6FF}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}.\end{eqnarray}$$
The boundary conditions at the shock front are used to obtain analytic expressions for both the entropy-mode amplification
![]() $\unicode[STIX]{x1D712}_{s}$
and the acoustic-mode generation
$\unicode[STIX]{x1D712}_{s}$
and the acoustic-mode generation
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
coefficients for a general equation of state (see appendix B).
$\unicode[STIX]{x1D712}_{a^{+}}$
coefficients for a general equation of state (see appendix B).
4 Post-shock amplification of an incoming entropy mode
Dense-gas effects on the shock-induced entropy-mode amplification are analysed here. Solving a boundary value problem at the shock front gives the expression for the entropy-mode amplification coefficient for an arbitrary equation of state (see appendix B),
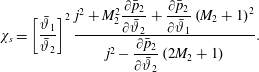 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{s}=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\left(M_{2}+1\right)^{2}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{s}=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\left(M_{2}+1\right)^{2}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{eqnarray}$$
4.1 Dense-gas shocks with an infinite
 $c_{v}/R$
value
$c_{v}/R$
value
It can be shown that the value of
![]() $\unicode[STIX]{x1D712}_{s}$
for a post-shock state at the critical point (with
$\unicode[STIX]{x1D712}_{s}$
for a post-shock state at the critical point (with
![]() $c_{v}/R\rightarrow +\infty$
) goes to positive infinity (see appendix C). It is conjectured that for finite and large values of
$c_{v}/R\rightarrow +\infty$
) goes to positive infinity (see appendix C). It is conjectured that for finite and large values of
![]() $c_{v}/R$
, compression shocks with near-TCP post-shock states featuring finite and large values of
$c_{v}/R$
, compression shocks with near-TCP post-shock states featuring finite and large values of
![]() $\unicode[STIX]{x1D712}_{s}$
can exist. This is illustrated hereafter using a van der Waals model. It is important to stress that this limiting case has no physical meaning. The question of shock admissibility must be addressed before commenting on the post-shock transmission coefficients. For
$\unicode[STIX]{x1D712}_{s}$
can exist. This is illustrated hereafter using a van der Waals model. It is important to stress that this limiting case has no physical meaning. The question of shock admissibility must be addressed before commenting on the post-shock transmission coefficients. For
![]() $c_{v}/R\rightarrow +\infty$
, the horizontal tangent point at the TCP on the isothermal
$c_{v}/R\rightarrow +\infty$
, the horizontal tangent point at the TCP on the isothermal
![]() ${\mathcal{H}}$
-line cannot be a Landau-admissible compression post-shock state as the post-shock Mach number is then singular (due to the vanishing sound speed as a result of the isentropes coinciding with the isotherms). A subset of (arbitrarily) large but finite values of
${\mathcal{H}}$
-line cannot be a Landau-admissible compression post-shock state as the post-shock Mach number is then singular (due to the vanishing sound speed as a result of the isentropes coinciding with the isotherms). A subset of (arbitrarily) large but finite values of
![]() $\unicode[STIX]{x1D712}_{s}$
is instead expected in the subset of admissible shocks with post-shock states near the critical point when
$\unicode[STIX]{x1D712}_{s}$
is instead expected in the subset of admissible shocks with post-shock states near the critical point when
![]() $c_{v}/R$
is made larger and larger.
$c_{v}/R$
is made larger and larger.
The sensitivity of
![]() $\unicode[STIX]{x1D712}_{s}$
to near-critical post-shock conditions when the limit
$\unicode[STIX]{x1D712}_{s}$
to near-critical post-shock conditions when the limit
![]() $c_{v}/R\rightarrow +\infty$
is reached is provided for a van der Waals gas (see figure 5). The diagrams represent contour plots of
$c_{v}/R\rightarrow +\infty$
is reached is provided for a van der Waals gas (see figure 5). The diagrams represent contour plots of
![]() $\unicode[STIX]{x1D712}_{s}$
obtained for shocks with low (figure 5
a) and higher (figure 5
b) upstream reduced pressures. Hugoniot lines (black lines) are drawn for shocks with a constant upstream reduced pressure, set to
$\unicode[STIX]{x1D712}_{s}$
obtained for shocks with low (figure 5
a) and higher (figure 5
b) upstream reduced pressures. Hugoniot lines (black lines) are drawn for shocks with a constant upstream reduced pressure, set to
![]() $p_{1}/p_{c}=0.13$
(figure 5
a) and
$p_{1}/p_{c}=0.13$
(figure 5
a) and
![]() $p_{1}/p_{c}=0.55$
(figure 5
b), and for different reduced specific volumes starting from the critical temperature to supercritical temperatures. Isolines of upstream Mach numbers are also shown. They correspond to the required shock speed to reach the corresponding post-shock thermodynamic state on the
$p_{1}/p_{c}=0.55$
(figure 5
b), and for different reduced specific volumes starting from the critical temperature to supercritical temperatures. Isolines of upstream Mach numbers are also shown. They correspond to the required shock speed to reach the corresponding post-shock thermodynamic state on the
![]() ${\mathcal{H}}$
-lines. All
${\mathcal{H}}$
-lines. All
![]() ${\mathcal{H}}$
-lines (which coincide with the isotherms here) start from the horizontal
${\mathcal{H}}$
-lines (which coincide with the isotherms here) start from the horizontal
![]() $M_{1}=1$
line for the two given upstream pressures. For large values of the upstream specific volume, the linear isotherms in the
$M_{1}=1$
line for the two given upstream pressures. For large values of the upstream specific volume, the linear isotherms in the
![]() $(\log p,\log \unicode[STIX]{x1D717})$
-diagram for the ideal-gas model are recovered. Along these dilute-gas isotherms,
$(\log p,\log \unicode[STIX]{x1D717})$
-diagram for the ideal-gas model are recovered. Along these dilute-gas isotherms,
![]() $\unicode[STIX]{x1D712}_{s}$
is a monotonically increasing function of
$\unicode[STIX]{x1D712}_{s}$
is a monotonically increasing function of
![]() $M_{1}$
(for this range of upstream Mach numbers). A large local maximum of
$M_{1}$
(for this range of upstream Mach numbers). A large local maximum of
![]() $\unicode[STIX]{x1D712}_{s}$
is then observed along every isotherm when the post-shock states reach near-TCP conditions. The value of the local maximum along each isotherm increases with lower pre-shock pressures and can be made arbitrarily large in the infinitely dense gas limit. The upstream Mach numbers (
$\unicode[STIX]{x1D712}_{s}$
is then observed along every isotherm when the post-shock states reach near-TCP conditions. The value of the local maximum along each isotherm increases with lower pre-shock pressures and can be made arbitrarily large in the infinitely dense gas limit. The upstream Mach numbers (
![]() $M_{1}$
) corresponding to these local maxima in
$M_{1}$
) corresponding to these local maxima in
![]() $\unicode[STIX]{x1D712}_{s}$
decrease for increasing upstream pressures. For
$\unicode[STIX]{x1D712}_{s}$
decrease for increasing upstream pressures. For
![]() $p_{1}/p_{c}=0.55$
, large entropy-amplification coefficients are found for relatively weak shocks (
$p_{1}/p_{c}=0.55$
, large entropy-amplification coefficients are found for relatively weak shocks (
![]() $M_{1}\approx 1.3$
). For both reduced pressures,
$M_{1}\approx 1.3$
). For both reduced pressures,
![]() $\unicode[STIX]{x1D712}_{s}$
is singular at the TCP; the maximum values obtained in the subset of admissible post-shock states (points not enclosed by the green line) are of order
$\unicode[STIX]{x1D712}_{s}$
is singular at the TCP; the maximum values obtained in the subset of admissible post-shock states (points not enclosed by the green line) are of order
![]() $10^{3}$
and
$10^{3}$
and
![]() $10^{1}$
respectively.
$10^{1}$
respectively.

Figure 5. The divergence of the entropy-amplification factor at the TCP;
![]() $(p,\unicode[STIX]{x1D717})$
-diagram of
$(p,\unicode[STIX]{x1D717})$
-diagram of
![]() $\unicode[STIX]{x1D712}_{s}$
isocontours and
$\unicode[STIX]{x1D712}_{s}$
isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for
${\mathcal{H}}$
-lines (solid black lines) for
![]() $c_{v}/R\rightarrow +\infty$
using the van der Waals model (appendix A). Upstream Mach numbers (
$c_{v}/R\rightarrow +\infty$
using the van der Waals model (appendix A). Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line. Strong non-ideal-gas amplifications of the incoming entropy modes are found for realistic pre-shock Mach numbers (
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line. Strong non-ideal-gas amplifications of the incoming entropy modes are found for realistic pre-shock Mach numbers (
![]() $M_{1}<3.0$
).
$M_{1}<3.0$
).
The use of the van der Waals analytical equation of state (EOS) in the isothermal infinitely dense gas limit is convenient to isolate the TCP compressibility effects from other TCP behaviours (e.g. large change of heat capacities). Indeed, it is clear from figure 5 that the stronger the local deformation of the isotherm in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram is the higher the entropy-amplification factor is. At the TCP, the critical isotherm eventually features a saddle point and the transmission factor diverges. This plateauing of the isotherms close to the TCP, and thus of the isentropes, indicates a decrease of the speed of sound (eventually vanishing at the TCP in this limit). This typical dense-gas compressible property comes with a tendency towards degeneracy of the linearised Kovásznay eigenmode basis (see the general discussion in § 3.1). Figure 6 illustrates the ‘trajectory’ of normalised slow and fast post-shock acoustic eigenvectors in a quarter unit sphere representation for increasing pre-shock Mach numbers along the critical isotherm. The two upstream pressures (blue lines) from figure 5 are considered together with the equivalent ideal-gas ‘trajectories’ (black). The non-admissible post-shock region is indicated in light blue. A larger non-admissible part is expected as the upstream state is approaching the TCP and the negative-
$(p,\unicode[STIX]{x1D717})$
-diagram is the higher the entropy-amplification factor is. At the TCP, the critical isotherm eventually features a saddle point and the transmission factor diverges. This plateauing of the isotherms close to the TCP, and thus of the isentropes, indicates a decrease of the speed of sound (eventually vanishing at the TCP in this limit). This typical dense-gas compressible property comes with a tendency towards degeneracy of the linearised Kovásznay eigenmode basis (see the general discussion in § 3.1). Figure 6 illustrates the ‘trajectory’ of normalised slow and fast post-shock acoustic eigenvectors in a quarter unit sphere representation for increasing pre-shock Mach numbers along the critical isotherm. The two upstream pressures (blue lines) from figure 5 are considered together with the equivalent ideal-gas ‘trajectories’ (black). The non-admissible post-shock region is indicated in light blue. A larger non-admissible part is expected as the upstream state is approaching the TCP and the negative-
![]() $\unicode[STIX]{x1D6E4}$
region. The singularity for which the eigenbasis degenerates towards a density-fluctuation orientation is found at the TCP, as expected. The ideal-gas eigenmode basis only degenerates towards velocity (for low upstream reduced pressures) and pressure (for post-shock pressures going to infinity) fluctuations. Once again, these two singularities are also recovered for a non-ideal gas considered in the same limits. Finally, the eigenmode basis corresponding to a pre-shock Mach number that brings the post-shock state close to a maximum of
$\unicode[STIX]{x1D6E4}$
region. The singularity for which the eigenbasis degenerates towards a density-fluctuation orientation is found at the TCP, as expected. The ideal-gas eigenmode basis only degenerates towards velocity (for low upstream reduced pressures) and pressure (for post-shock pressures going to infinity) fluctuations. Once again, these two singularities are also recovered for a non-ideal gas considered in the same limits. Finally, the eigenmode basis corresponding to a pre-shock Mach number that brings the post-shock state close to a maximum of
![]() $\unicode[STIX]{x1D712}_{s}$
on the admissible part of the
$\unicode[STIX]{x1D712}_{s}$
on the admissible part of the
![]() ${\mathcal{H}}$
-lines is illustrated for the two upstream pressures. These results are investigated for finite values of the parameter
${\mathcal{H}}$
-lines is illustrated for the two upstream pressures. These results are investigated for finite values of the parameter
![]() $c_{v}/R$
in the following two sections.
$c_{v}/R$
in the following two sections.

Figure 6. Post-shock normalised Kovásznay eigenmode basis evolution along the critical
![]() ${\mathcal{H}}$
-line for
${\mathcal{H}}$
-line for
![]() $c_{v}/R\rightarrow +\infty$
using the van der Waals model. The admissible path is shown in dark blue while the non-admissible path is represented in light blue. The corresponding ideal-gas eigenmode basis evolution is shown in black.
$c_{v}/R\rightarrow +\infty$
using the van der Waals model. The admissible path is shown in dark blue while the non-admissible path is represented in light blue. The corresponding ideal-gas eigenmode basis evolution is shown in black.
4.2 Dense-gas shocks with finite
 $c_{v}/R$
values
$c_{v}/R$
values
Results for a van der Waals gas with a large value of
![]() $c_{v}/R=78.2$
(corresponding to the PP10 gas) are reported for
$c_{v}/R=78.2$
(corresponding to the PP10 gas) are reported for
![]() ${\mathcal{H}}$
-lines featuring at most one or two sonic points.
${\mathcal{H}}$
-lines featuring at most one or two sonic points.
4.2.1 Hugoniot lines with at most one sonic point: a selectivity effect
A key feature of the result obtained in the infinite dense-gas limit is the plateauing of the
![]() ${\mathcal{H}}$
-line in the
${\mathcal{H}}$
-line in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram when the post-shock state approaches the TCP. In this diagram, the local changes of both the
$(p,\unicode[STIX]{x1D717})$
-diagram when the post-shock state approaches the TCP. In this diagram, the local changes of both the
![]() ${\mathcal{H}}$
-line slope and the post-shock Mach number (which appear explicitly in the amplification coefficient, see (4.1)) are indeed directly linked to the sound speed.
${\mathcal{H}}$
-line slope and the post-shock Mach number (which appear explicitly in the amplification coefficient, see (4.1)) are indeed directly linked to the sound speed.
For a given ideal gas (e.g. a given
![]() $\unicode[STIX]{x1D6FE}$
), the density, velocity and pressure jumps can be parametrised by the upstream Mach number
$\unicode[STIX]{x1D6FE}$
), the density, velocity and pressure jumps can be parametrised by the upstream Mach number
![]() $M_{1}$
without any other dependence with respect to the upstream conditions. As a result,
$M_{1}$
without any other dependence with respect to the upstream conditions. As a result,
![]() ${\mathcal{H}}$
-lines drawn in the
${\mathcal{H}}$
-lines drawn in the
![]() $(\log p,\log \unicode[STIX]{x1D717})$
-diagram for a given upstream pressure and different upstream specific volumes are deduced one from another simply by a translation along the
$(\log p,\log \unicode[STIX]{x1D717})$
-diagram for a given upstream pressure and different upstream specific volumes are deduced one from another simply by a translation along the
![]() $\log \unicode[STIX]{x1D717}$
-axis. When a non-ideal equation of state is used instead, the jump properties are not simply functions of
$\log \unicode[STIX]{x1D717}$
-axis. When a non-ideal equation of state is used instead, the jump properties are not simply functions of
![]() $M_{1}$
but also depend on the upstream thermodynamic state, making the
$M_{1}$
but also depend on the upstream thermodynamic state, making the
![]() ${\mathcal{H}}$
-lines a two degrees of freedom map in this diagram (see figure 7
a). For high upstream specific volumes, when the gas is in its ideal-gas asymptotic limit, the van der Waals
${\mathcal{H}}$
-lines a two degrees of freedom map in this diagram (see figure 7
a). For high upstream specific volumes, when the gas is in its ideal-gas asymptotic limit, the van der Waals
![]() ${\mathcal{H}}$
-lines match those obtained for the equivalent ideal gas (i.e. with
${\mathcal{H}}$
-lines match those obtained for the equivalent ideal gas (i.e. with
![]() $\unicode[STIX]{x1D6FE}=1.013$
for PP10). For post-shock states near the TCP region, the
$\unicode[STIX]{x1D6FE}=1.013$
for PP10). For post-shock states near the TCP region, the
![]() ${\mathcal{H}}$
-lines lean towards the critical isotherm (depicted with a thick blue line passing through the TCP) and depart from the ideal-gas
${\mathcal{H}}$
-lines lean towards the critical isotherm (depicted with a thick blue line passing through the TCP) and depart from the ideal-gas
![]() ${\mathcal{H}}$
-lines (this is expected for large
${\mathcal{H}}$
-lines (this is expected for large
![]() $c_{v}/R$
values). The main consequence of this deformation of the
$c_{v}/R$
values). The main consequence of this deformation of the
![]() ${\mathcal{H}}$
-lines is that results obtained in the infinitely dense-gas limit are recovered even at finite
${\mathcal{H}}$
-lines is that results obtained in the infinitely dense-gas limit are recovered even at finite
![]() $c_{v}/R$
values, i.e.
$c_{v}/R$
values, i.e.
![]() $\unicode[STIX]{x1D712}_{s}$
has a local maximum along
$\unicode[STIX]{x1D712}_{s}$
has a local maximum along
![]() ${\mathcal{H}}$
-lines passing near the TCP.
${\mathcal{H}}$
-lines passing near the TCP.
The same trend towards degeneracy as that for infinitely dense gases is seen for the eigenmode basis along the critical
![]() ${\mathcal{H}}$
-line (see figure 7
b). For this finite value of
${\mathcal{H}}$
-line (see figure 7
b). For this finite value of
![]() $c_{v}/R$
, the local maximum of
$c_{v}/R$
, the local maximum of
![]() $\unicode[STIX]{x1D712}_{s}$
on the critical
$\unicode[STIX]{x1D712}_{s}$
on the critical
![]() ${\mathcal{H}}$
-line matches the point on the quarter unit sphere for which the basis is the most density-oriented. Interestingly, there exists another local maximum of
${\mathcal{H}}$
-line matches the point on the quarter unit sphere for which the basis is the most density-oriented. Interestingly, there exists another local maximum of
![]() $\unicode[STIX]{x1D712}_{s}$
in the dilute-gas limit. Its value is reached for a large value of the pre-shock Mach number (
$\unicode[STIX]{x1D712}_{s}$
in the dilute-gas limit. Its value is reached for a large value of the pre-shock Mach number (
![]() $M_{1}=12$
) and matches the pre-shock Mach number for which the equivalent ideal-gas eigenmode basis is the most oriented towards density fluctuations.
$M_{1}=12$
) and matches the pre-shock Mach number for which the equivalent ideal-gas eigenmode basis is the most oriented towards density fluctuations.
For dense gases, the local changes of shock adiabat near the TCP are the result of both the high number of degrees of freedom in the gas molecules (which implies high values of
![]() $c_{v}/R$
which in turn brings the
$c_{v}/R$
which in turn brings the
![]() ${\mathcal{H}}$
-line close to the isotherm) and the increase of inter-molecular interactions between particles near the TCP (the saddle point of the isotherm at the TCP being a consequence of these interactions). However, the present results are not fundamentally restricted to dense-gas dynamics, and any additional source term in the energy equation that may create a similar deformation of the Hugoniot path can potentially reproduce the conditions observed here for dense gases close to the TCP (e.g. ionisation, see Griffiths, Sandeman & Hornung Reference Griffiths, Sandeman and Hornung1976).
${\mathcal{H}}$
-line close to the isotherm) and the increase of inter-molecular interactions between particles near the TCP (the saddle point of the isotherm at the TCP being a consequence of these interactions). However, the present results are not fundamentally restricted to dense-gas dynamics, and any additional source term in the energy equation that may create a similar deformation of the Hugoniot path can potentially reproduce the conditions observed here for dense gases close to the TCP (e.g. ionisation, see Griffiths, Sandeman & Hornung Reference Griffiths, Sandeman and Hornung1976).

Figure 7. Strong near-critical entropy-mode amplification coefficient for
![]() $p_{1}/p_{c}=0.13$
. (a) The
$p_{1}/p_{c}=0.13$
. (a) The
![]() $\unicode[STIX]{x1D712}_{s}$
isocontours and
$\unicode[STIX]{x1D712}_{s}$
isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for the PP10 gas using the van der Waals model (appendix A). The
${\mathcal{H}}$
-lines (solid black lines) for the PP10 gas using the van der Waals model (appendix A). The
![]() $M_{1}$
values needed to reach the corresponding thermodynamic state on the
$M_{1}$
values needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines in the dilute-gas limit are represented by thick grey lines. The
${\mathcal{H}}$
-lines in the dilute-gas limit are represented by thick grey lines. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. (b) Acoustic eigenmode ‘trajectories’ along the
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. (b) Acoustic eigenmode ‘trajectories’ along the
![]() ${\mathcal{H}}$
-line with
${\mathcal{H}}$
-line with
![]() $T_{1}=T_{c}$
. The vectors represent the basis when
$T_{1}=T_{c}$
. The vectors represent the basis when
![]() $M_{1}=3.10$
. The corresponding ideal-gas path is shown in black.
$M_{1}=3.10$
. The corresponding ideal-gas path is shown in black.
Dense-gas effects on the entropy-mode amplification are made clear from figure 8, which represents the evolution of
![]() $\unicode[STIX]{x1D712}_{s}$
along the critical
$\unicode[STIX]{x1D712}_{s}$
along the critical
![]() ${\mathcal{H}}$
-line (
${\mathcal{H}}$
-line (
![]() $T_{1}=T_{c}$
) for increasing upstream Mach numbers. The non-ideal-gas value of
$T_{1}=T_{c}$
) for increasing upstream Mach numbers. The non-ideal-gas value of
![]() $\unicode[STIX]{x1D712}_{s}$
is similar to the corresponding ideal-gas value for small values of the upstream Mach number, which is expected at low upstream reduced pressure and critical temperature. It is in agreement with the results from figure 7, which illustrates the weak dependence of the eigenmode basis with respect to the equation of state at low Mach number for those upstream conditions. When the downstream state reaches near-TCP conditions, the non-ideal-gas value of
$\unicode[STIX]{x1D712}_{s}$
is similar to the corresponding ideal-gas value for small values of the upstream Mach number, which is expected at low upstream reduced pressure and critical temperature. It is in agreement with the results from figure 7, which illustrates the weak dependence of the eigenmode basis with respect to the equation of state at low Mach number for those upstream conditions. When the downstream state reaches near-TCP conditions, the non-ideal-gas value of
![]() $\unicode[STIX]{x1D712}_{s}$
can be one order of magnitude higher than the ideal-gas value (for this choice of
$\unicode[STIX]{x1D712}_{s}$
can be one order of magnitude higher than the ideal-gas value (for this choice of
![]() $c_{v}/R$
and upstream pressure and temperature). This large isolated value of
$c_{v}/R$
and upstream pressure and temperature). This large isolated value of
![]() $\unicode[STIX]{x1D712}_{s}$
will have an influence on the (linear) interaction of shocks with arbitrary incoming perturbations. Indeed, in the linear framework, small fluctuations are expected to be strongly amplified by dense-gas shocks with unperturbed Mach number close to the local maximum in figure 8 (i.e. around
$\unicode[STIX]{x1D712}_{s}$
will have an influence on the (linear) interaction of shocks with arbitrary incoming perturbations. Indeed, in the linear framework, small fluctuations are expected to be strongly amplified by dense-gas shocks with unperturbed Mach number close to the local maximum in figure 8 (i.e. around
![]() $M_{1}=3.1$
). However, for a small change in the base flow (e.g. by modification of the nozzle geometry), any small perturbation would be significantly less amplified due to the sharp drop of
$M_{1}=3.1$
). However, for a small change in the base flow (e.g. by modification of the nozzle geometry), any small perturbation would be significantly less amplified due to the sharp drop of
![]() $\unicode[STIX]{x1D712}_{s}$
around this local maximum. The resulting refracted perturbed flow can then be strongly selected from the incoming perturbed flow based on a small change in the base flow. This one-dimensional dense-gas selectivity effect is likely to have a significant impact even at higher dimensions, as the one-dimensional results set the behaviour of shock-normal perturbations regardless of the dimension considered (in the linear regime). This non-ideal-gas effect is to be added to the degeneracy of the post-shock eigenmode basis, which forces the post-shock energy to be propagating along a direction more aligned with density fluctuations in the
$\unicode[STIX]{x1D712}_{s}$
around this local maximum. The resulting refracted perturbed flow can then be strongly selected from the incoming perturbed flow based on a small change in the base flow. This one-dimensional dense-gas selectivity effect is likely to have a significant impact even at higher dimensions, as the one-dimensional results set the behaviour of shock-normal perturbations regardless of the dimension considered (in the linear regime). This non-ideal-gas effect is to be added to the degeneracy of the post-shock eigenmode basis, which forces the post-shock energy to be propagating along a direction more aligned with density fluctuations in the
![]() $(\unicode[STIX]{x1D70C},u,p)$
space.
$(\unicode[STIX]{x1D70C},u,p)$
space.
It is worth mentioning that large extrema of
![]() $\unicode[STIX]{x1D712}_{s}$
come with strong contractions in wavelengths (see figure 8
b). This contraction effect can be much stronger than the usual contraction observed in ideal gases. The higher values of
$\unicode[STIX]{x1D712}_{s}$
come with strong contractions in wavelengths (see figure 8
b). This contraction effect can be much stronger than the usual contraction observed in ideal gases. The higher values of
![]() $\unicode[STIX]{x1D712}_{s}$
also suggest that nonlinear interactions may be more important than in ideal gases. This may have significant consequences on the evolution of the turbulence kinetic energy behind the shock near the TCP. With the decrease of the post-shock characteristic length scales, viscous effects play a greater role in the post-shock evolution of the turbulent kinetic energy, indirectly promoting kinetic energy dissipation.
$\unicode[STIX]{x1D712}_{s}$
also suggest that nonlinear interactions may be more important than in ideal gases. This may have significant consequences on the evolution of the turbulence kinetic energy behind the shock near the TCP. With the decrease of the post-shock characteristic length scales, viscous effects play a greater role in the post-shock evolution of the turbulent kinetic energy, indirectly promoting kinetic energy dissipation.

Figure 8. The TCP effects on the refracted entropy-mode properties (
![]() $p_{1}/p_{c}=0.13$
,
$p_{1}/p_{c}=0.13$
,
![]() $T_{1}=T_{c}$
and
$T_{1}=T_{c}$
and
![]() $c_{v}/R=78.2$
). Ideal gas is shown by dashed lines. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
$c_{v}/R=78.2$
). Ideal gas is shown by dashed lines. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
4.2.2 Hugoniot lines with two sonic points: discontinuous discontinuities
In this section, we investigate the mixed-nonlinearity effects on the evolution of
![]() $\unicode[STIX]{x1D712}_{s}$
. Near-TCP upstream pressures are thus considered. Figure 9 illustrates how the
$\unicode[STIX]{x1D712}_{s}$
. Near-TCP upstream pressures are thus considered. Figure 9 illustrates how the
![]() ${\mathcal{H}}$
-lines starting at
${\mathcal{H}}$
-lines starting at
![]() $p_{1}/p_{c}=0.55$
and
$p_{1}/p_{c}=0.55$
and
![]() $T_{1}=T_{c}$
depart from their dilute ideal-gas limit towards the dense-gas isothermal limit close to the TCP. Discrepancies with the ideal-gas model are seen for low supersonic Mach numbers
$T_{1}=T_{c}$
depart from their dilute ideal-gas limit towards the dense-gas isothermal limit close to the TCP. Discrepancies with the ideal-gas model are seen for low supersonic Mach numbers
![]() $M_{1}\in [1,2]$
, as expected (see § 2.2). The importance of the critical-point vicinity of the upstream pressure in the discussion of non-admissibility can be appreciated by comparing the two isothermal limits for low upstream pressures (see figure 5
a) and near-critical-point upstream pressures (see figure 5
b). A larger non-admissible region is obtained for near-critical upstream pressures for which the
$M_{1}\in [1,2]$
, as expected (see § 2.2). The importance of the critical-point vicinity of the upstream pressure in the discussion of non-admissibility can be appreciated by comparing the two isothermal limits for low upstream pressures (see figure 5
a) and near-critical-point upstream pressures (see figure 5
b). A larger non-admissible region is obtained for near-critical upstream pressures for which the
![]() ${\mathcal{H}}$
-line is more likely to feature a sonic point (Zamfirescu et al.
Reference Zamfirescu, Guardone and Colonna2008), which is fundamental in the discussion of the admissibility problem (see § 2). In particular, the
${\mathcal{H}}$
-line is more likely to feature a sonic point (Zamfirescu et al.
Reference Zamfirescu, Guardone and Colonna2008), which is fundamental in the discussion of the admissibility problem (see § 2). In particular, the
![]() $p_{1}/p_{c}=0.55$
and
$p_{1}/p_{c}=0.55$
and
![]() $T_{1}=T_{c}$
$T_{1}=T_{c}$
![]() ${\mathcal{H}}$
-line crosses a region of mixed nonlinearity, which produces two sonic points and consequently a non-admissible path (see figure 9
b). Therefore, a jump in refraction properties is expected on the admissible part of this
${\mathcal{H}}$
-line crosses a region of mixed nonlinearity, which produces two sonic points and consequently a non-admissible path (see figure 9
b). Therefore, a jump in refraction properties is expected on the admissible part of this
![]() ${\mathcal{H}}$
-line. This is illustrated with the jump on the quarter unit sphere operated by the post-shock Kovásznay eigenmode basis (see figure 9
b).
${\mathcal{H}}$
-line. This is illustrated with the jump on the quarter unit sphere operated by the post-shock Kovásznay eigenmode basis (see figure 9
b).

Figure 9. Discontinuous entropy-mode amplification factor for
![]() $p_{1}/p_{c}=0.55$
. (a) The
$p_{1}/p_{c}=0.55$
. (a) The
![]() $\unicode[STIX]{x1D712}_{s}$
isocontours and
$\unicode[STIX]{x1D712}_{s}$
isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for the PP10 gas using the van der Waals model (appendix A). The
${\mathcal{H}}$
-lines (solid black lines) for the PP10 gas using the van der Waals model (appendix A). The
![]() $M_{1}$
values needed to reach the corresponding thermodynamic state on the
$M_{1}$
values needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines in the dilute-gas limit are represented by thick grey lines. The
${\mathcal{H}}$
-lines in the dilute-gas limit are represented by thick grey lines. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is delimited with a green line. (b) Eigenmode basis ‘trajectory’ along the critical
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is delimited with a green line. (b) Eigenmode basis ‘trajectory’ along the critical
![]() ${\mathcal{H}}$
-line (
${\mathcal{H}}$
-line (
![]() $T_{1}=T_{c}$
) with vectors for
$T_{1}=T_{c}$
) with vectors for
![]() $M_{1}=1.30$
. The non-admissible path is shown in light blue. The corresponding ideal-gas path is shown in black.
$M_{1}=1.30$
. The non-admissible path is shown in light blue. The corresponding ideal-gas path is shown in black.
The main consequence on the entropy-amplification factor is the corresponding discontinuity of
![]() $\unicode[STIX]{x1D712}_{s}$
with respect to
$\unicode[STIX]{x1D712}_{s}$
with respect to
![]() $M_{1}$
when the admissible part of the
$M_{1}$
when the admissible part of the
![]() ${\mathcal{H}}$
-line is considered. This can be seen in figure 10(a,b), where a jump in the entropy-amplification factor is seen for different upstream pressures at
${\mathcal{H}}$
-line is considered. This can be seen in figure 10(a,b), where a jump in the entropy-amplification factor is seen for different upstream pressures at
![]() $M_{1}=1.29$
and
$M_{1}=1.29$
and
![]() $M_{1}=1.16$
respectively. Thus, for pre-shock conditions close enough to the TCP for the
$M_{1}=1.16$
respectively. Thus, for pre-shock conditions close enough to the TCP for the
![]() ${\mathcal{H}}$
-line to feature two sonic points, there exists a critical mass flow rate for which a negligible change in operating conditions would lead to significant modifications of the refracted-flow properties. As was shown previously (see figure 2), the discontinuity of the refraction coefficients occurs at lower upstream Mach number
${\mathcal{H}}$
-line to feature two sonic points, there exists a critical mass flow rate for which a negligible change in operating conditions would lead to significant modifications of the refracted-flow properties. As was shown previously (see figure 2), the discontinuity of the refraction coefficients occurs at lower upstream Mach number
![]() $M_{1}$
as the reduced pressure
$M_{1}$
as the reduced pressure
![]() $p_{1}/p_{c}$
approaches the critical point, and the corresponding discontinuity can become larger (corresponding to a larger jump in the density coordinate of the acoustic eigenmode basis). A consequence is that for near-critical conditions, a non-classical selective behaviour is expected for weak shocks. The difference between the classical ideal-gas entropy mode and the non-classical non-ideal-gas one is striking for those weak shocks for which the ideal-gas scenario hardly amplifies incoming entropy waves. This result could have potentially great impact on the transmission properties of eddy shocklets commonly found in weakly compressible turbulent flows, considering that near the TCP, entropy wave/shock interactions are more likely to occur as density perturbations dominate over pressure fluctuations.
$p_{1}/p_{c}$
approaches the critical point, and the corresponding discontinuity can become larger (corresponding to a larger jump in the density coordinate of the acoustic eigenmode basis). A consequence is that for near-critical conditions, a non-classical selective behaviour is expected for weak shocks. The difference between the classical ideal-gas entropy mode and the non-classical non-ideal-gas one is striking for those weak shocks for which the ideal-gas scenario hardly amplifies incoming entropy waves. This result could have potentially great impact on the transmission properties of eddy shocklets commonly found in weakly compressible turbulent flows, considering that near the TCP, entropy wave/shock interactions are more likely to occur as density perturbations dominate over pressure fluctuations.

Figure 10. Discontinuous entropy-mode amplification factor for
![]() $T_{1}=T_{c}$
. The equivalent ideal-gas configuration is shown with dashed lines. The non-admissible path is shown in light blue. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
$T_{1}=T_{c}$
. The equivalent ideal-gas configuration is shown with dashed lines. The non-admissible path is shown in light blue. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
5 Post-shock acoustic generation from an incoming entropy mode
The post-shock acoustic-generation coefficient obtained from the refraction of an incoming entropy mode is recalled here (see appendix B):
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{a^{+}}=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}M_{2}^{2}{\displaystyle \frac{{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{a^{+}}=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}M_{2}^{2}{\displaystyle \frac{{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{eqnarray}$$
5.1 Dense-gas shocks with an infinite
 $c_{v}/R$
value
$c_{v}/R$
value
Following the same reasoning as for the asymptotic limit of
![]() $\unicode[STIX]{x1D712}_{s}$
, it can be shown that the value of
$\unicode[STIX]{x1D712}_{s}$
, it can be shown that the value of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
at the critical point goes to negative infinity. The same precaution as the one taken near the singularity of
$\unicode[STIX]{x1D712}_{a^{+}}$
at the critical point goes to negative infinity. The same precaution as the one taken near the singularity of
![]() $\unicode[STIX]{x1D712}_{s}$
has to be considered for the admissibility problem of shocks near the TCP. The isothermal limit suggests two main non-ideal-gas effects on the post-shock acoustic emission produced from incoming entropy perturbations. The first one is a similar selective effect to the one observed in the entropy-mode amplification case. This can be seen in figure 11(a), where large variations of
$\unicode[STIX]{x1D712}_{s}$
has to be considered for the admissibility problem of shocks near the TCP. The isothermal limit suggests two main non-ideal-gas effects on the post-shock acoustic emission produced from incoming entropy perturbations. The first one is a similar selective effect to the one observed in the entropy-mode amplification case. This can be seen in figure 11(a), where large variations of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
are expected for post-shock states near the TCP. The second one is the negative value of the limit, which suggests an anti-correlation (phase shift of
$\unicode[STIX]{x1D712}_{a^{+}}$
are expected for post-shock states near the TCP. The second one is the negative value of the limit, which suggests an anti-correlation (phase shift of
![]() $\unicode[STIX]{x03C0}$
) of the post-shock acoustic emitted field and the post-shock entropy mode (density/temperature fluctuations) at the shock front. This effect is present for both low and high upstream pressure (see figure 11
a,b), but affects a wider area in the
$\unicode[STIX]{x03C0}$
) of the post-shock acoustic emitted field and the post-shock entropy mode (density/temperature fluctuations) at the shock front. This effect is present for both low and high upstream pressure (see figure 11
a,b), but affects a wider area in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram near the TCP when the pre-shock state is closer to the TCP.
$(p,\unicode[STIX]{x1D717})$
-diagram near the TCP when the pre-shock state is closer to the TCP.

Figure 11. The
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
isocontours and
$\unicode[STIX]{x1D712}_{a^{+}}$
isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for
${\mathcal{H}}$
-lines (solid black lines) for
![]() $c_{v}/R\rightarrow +\infty$
using the van der Waals model (appendix A). Upstream Mach numbers (
$c_{v}/R\rightarrow +\infty$
using the van der Waals model (appendix A). Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line.
5.2 Selective acoustic emission
Results for finite values of
![]() $c_{v}/R$
are now considered (see figure 12). A good agreement with the theoretical infinitely dense-gas limit can be obtained for the van der Waals equation with
$c_{v}/R$
are now considered (see figure 12). A good agreement with the theoretical infinitely dense-gas limit can be obtained for the van der Waals equation with
![]() $c_{v}/R=78.2$
(PP10 gas). The local maxima of
$c_{v}/R=78.2$
(PP10 gas). The local maxima of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
along the
$\unicode[STIX]{x1D712}_{a^{+}}$
along the
![]() ${\mathcal{H}}$
-lines starting at
${\mathcal{H}}$
-lines starting at
![]() $p_{1}/p_{c}=0.13$
are indeed very similar to their ‘isothermal’ limits apart from the loss of the anti-correlation region and the non-admissible region. For the near-TCP upstream state, however (see figure 12
b), there exist both a non-admissible region (due to the presence of two sonic points on the
$p_{1}/p_{c}=0.13$
are indeed very similar to their ‘isothermal’ limits apart from the loss of the anti-correlation region and the non-admissible region. For the near-TCP upstream state, however (see figure 12
b), there exist both a non-admissible region (due to the presence of two sonic points on the
![]() ${\mathcal{H}}$
-lines when approaching the TCP) and an anti-correlation region. As was observed with the evolution of
${\mathcal{H}}$
-lines when approaching the TCP) and an anti-correlation region. As was observed with the evolution of
![]() $\unicode[STIX]{x1D712}_{s}$
for different upstream pressures, non-ideal-gas effects are related to weaker shocks if the upstream pressure is increased from
$\unicode[STIX]{x1D712}_{s}$
for different upstream pressures, non-ideal-gas effects are related to weaker shocks if the upstream pressure is increased from
![]() $p_{1}/p_{c}=0.13$
to
$p_{1}/p_{c}=0.13$
to
![]() $p_{1}/p_{c}=0.55$
and are more pronounced at critical temperature (i.e.
$p_{1}/p_{c}=0.55$
and are more pronounced at critical temperature (i.e.
![]() $T_{1}=T_{c}$
) for single-phase flows.
$T_{1}=T_{c}$
) for single-phase flows.

Figure 12. Non-ideal selective acoustic emission;
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
isocontours and
$\unicode[STIX]{x1D712}_{a^{+}}$
isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for
${\mathcal{H}}$
-lines (solid black lines) for
![]() $c_{v}/R=78.2$
using the van der Waals model (appendix A). Upstream Mach numbers (
$c_{v}/R=78.2$
using the van der Waals model (appendix A). Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. The near-TCP non-admissible region is enclosed within the region delimited by the green line.
Figure 13(a) illustrates the evolution of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
for increasing Mach number for a pre-shock state at
$\unicode[STIX]{x1D712}_{a^{+}}$
for increasing Mach number for a pre-shock state at
![]() $p_{1}/p_{c}=0.13$
and
$p_{1}/p_{c}=0.13$
and
![]() $T_{1}=T_{c}$
. The value of
$T_{1}=T_{c}$
. The value of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
is plotted alongside the value of the generated acoustic wavelength. The local maximum of
$\unicode[STIX]{x1D712}_{a^{+}}$
is plotted alongside the value of the generated acoustic wavelength. The local maximum of
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
matches the local maximum of the acoustic wavelength compression ratio (see figure 13
b). The generated acoustic wavelengths are then more likely to be sensitive to wave steepening than their ideal-gas counterparts (for the same value of
$\unicode[STIX]{x1D712}_{a^{+}}$
matches the local maximum of the acoustic wavelength compression ratio (see figure 13
b). The generated acoustic wavelengths are then more likely to be sensitive to wave steepening than their ideal-gas counterparts (for the same value of
![]() $M_{1}$
), which could have a great impact on compressibility effects in turbulent flows. However, these short wavelengths are more prone to viscous damping.
$M_{1}$
), which could have a great impact on compressibility effects in turbulent flows. However, these short wavelengths are more prone to viscous damping.

Figure 13. Acoustic-generation coefficient and wavelength (obtained from the
![]() $k_{+_{2}}/k_{s_{1}}$
ratio) for
$k_{+_{2}}/k_{s_{1}}$
ratio) for
![]() $p_{1}/p_{c}=0.13$
,
$p_{1}/p_{c}=0.13$
,
![]() $T_{1}=T_{c}$
. The equivalent ideal-gas configuration is shown with dashed lines. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
$T_{1}=T_{c}$
. The equivalent ideal-gas configuration is shown with dashed lines. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
As was seen for
![]() $\unicode[STIX]{x1D712}_{s}$
at higher upstream pressure, shocklets can exhibit discontinuous refraction properties with respect to
$\unicode[STIX]{x1D712}_{s}$
at higher upstream pressure, shocklets can exhibit discontinuous refraction properties with respect to
![]() $M_{1}$
. This is also the case as far as the acoustic generation is concerned (see figure 14
a). Another important aspect of near-TCP shocklets is the appearance of an anti-correlation region (
$M_{1}$
. This is also the case as far as the acoustic generation is concerned (see figure 14
a). Another important aspect of near-TCP shocklets is the appearance of an anti-correlation region (
![]() $\unicode[STIX]{x1D712}_{a^{+}}<0$
), and the generated acoustic mode is thus beating out of phase (phase shift of
$\unicode[STIX]{x1D712}_{a^{+}}<0$
), and the generated acoustic mode is thus beating out of phase (phase shift of
![]() $\unicode[STIX]{x03C0}$
, see (3.8)) with the refracted entropy mode at the front, making the corresponding shocklets very different from their ideal-gas counterparts, for which
$\unicode[STIX]{x03C0}$
, see (3.8)) with the refracted entropy mode at the front, making the corresponding shocklets very different from their ideal-gas counterparts, for which
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
is always positive. Once again, the admissible path along a given Hugoniot is very important to comment on the refraction properties, and can complicate the evolution of the refraction coefficients. An example of this non-intuitive evolution can be seen for the shocks at
$\unicode[STIX]{x1D712}_{a^{+}}$
is always positive. Once again, the admissible path along a given Hugoniot is very important to comment on the refraction properties, and can complicate the evolution of the refraction coefficients. An example of this non-intuitive evolution can be seen for the shocks at
![]() $p_{1}/p_{c}=0.65$
, for which the resulting
$p_{1}/p_{c}=0.65$
, for which the resulting
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
discontinuity is small (see figure 14
b) despite a significant jump in
$\unicode[STIX]{x1D712}_{a^{+}}$
discontinuity is small (see figure 14
b) despite a significant jump in
![]() $\unicode[STIX]{x1D712}_{s}$
(see figure 10
b).
$\unicode[STIX]{x1D712}_{s}$
(see figure 10
b).

Figure 14. Discontinuous acoustic-generation coefficients (
![]() $T_{1}=T_{c}$
). The equivalent ideal-gas configuration is shown with dashed lines. The non-admissible path is shown in light blue. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
$T_{1}=T_{c}$
). The equivalent ideal-gas configuration is shown with dashed lines. The non-admissible path is shown in light blue. The thick lines indicate the range of Mach numbers for which the DK instability is expected (to be discussed later).
5.3 On the possibility of ‘silent’ interactions normal to the shock front

Figure 15. On the possibility of silent shocks; the
![]() $\unicode[STIX]{x1D712}_{a^{+}}=0$
line coloured by the magnitude of
$\unicode[STIX]{x1D712}_{a^{+}}=0$
line coloured by the magnitude of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
(high value in red, low value in light blue). The line joining the maximum value of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
(high value in red, low value in light blue). The line joining the maximum value of
![]() $\unicode[STIX]{x1D712}_{s}$
is also shown (white dashed line). Upstream Mach numbers (
$\unicode[STIX]{x1D712}_{s}$
is also shown (white dashed line). Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines starting at
${\mathcal{H}}$
-lines starting at
![]() $p_{1}/p_{c}=0.55$
(a) and
$p_{1}/p_{c}=0.55$
(a) and
![]() $p_{1}/p_{c}=0.65$
(b) are represented by the thin green lines with labels. The near-TCP non-admissible region is enclosed within the region delimited by the thick green line. The contours represent the local speed of sound normalised by its TCP value (
$p_{1}/p_{c}=0.65$
(b) are represented by the thin green lines with labels. The near-TCP non-admissible region is enclosed within the region delimited by the thick green line. The contours represent the local speed of sound normalised by its TCP value (
![]() $c_{v}/R=78.2$
). The
$c_{v}/R=78.2$
). The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
The sign change of the acoustic-generation coefficient for some of the
![]() ${\mathcal{H}}$
-lines considered implies that there exist mass flow rates (or
${\mathcal{H}}$
-lines considered implies that there exist mass flow rates (or
![]() $M_{1}$
values) for which
$M_{1}$
values) for which
![]() $\unicode[STIX]{x1D712}_{a^{+}}=0$
. Therefore, shocks with no generated acoustic waves following an entropy-mode refraction are possible. This result contrasts with that of ideal gases (for which perturbations normal to the shock front always generate an acoustic field) and could significantly affect shock/turbulence interaction properties. In most cases, for a given upstream pressure, two values of the upstream Mach number can give
$\unicode[STIX]{x1D712}_{a^{+}}=0$
. Therefore, shocks with no generated acoustic waves following an entropy-mode refraction are possible. This result contrasts with that of ideal gases (for which perturbations normal to the shock front always generate an acoustic field) and could significantly affect shock/turbulence interaction properties. In most cases, for a given upstream pressure, two values of the upstream Mach number can give
![]() $\unicode[STIX]{x1D712}_{a^{+}}=0$
(see figure 15). A broader view is provided by figure 15, in which the effect of the thermodynamic upstream state is investigated by increasing the upstream temperature at constant upstream pressure following the same methodology as for the previous
$\unicode[STIX]{x1D712}_{a^{+}}=0$
(see figure 15). A broader view is provided by figure 15, in which the effect of the thermodynamic upstream state is investigated by increasing the upstream temperature at constant upstream pressure following the same methodology as for the previous
![]() $(p,\unicode[STIX]{x1D717})$
-diagram analysis. The subdomain of the
$(p,\unicode[STIX]{x1D717})$
-diagram analysis. The subdomain of the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram inside which
$(p,\unicode[STIX]{x1D717})$
-diagram inside which
![]() ${\mathcal{H}}$
-lines feature at least one shock with
${\mathcal{H}}$
-lines feature at least one shock with
![]() $\unicode[STIX]{x1D712}_{a^{+}}=0$
is considered. Upstream Mach numbers are indicated only for this subdomain. The post-shock values corresponding to vanishing
$\unicode[STIX]{x1D712}_{a^{+}}=0$
is considered. Upstream Mach numbers are indicated only for this subdomain. The post-shock values corresponding to vanishing
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
are represented on a line coloured with the local value of
$\unicode[STIX]{x1D712}_{a^{+}}$
are represented on a line coloured with the local value of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a+}/\unicode[STIX]{x2202}M_{1}$
(low values in light blue, high values in red). The post-shock state giving the maximum value of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a+}/\unicode[STIX]{x2202}M_{1}$
(low values in light blue, high values in red). The post-shock state giving the maximum value of
![]() $\unicode[STIX]{x1D712}_{s}$
is also represented with a dashed white line. As expected from § 4, the local maximum of
$\unicode[STIX]{x1D712}_{s}$
is also represented with a dashed white line. As expected from § 4, the local maximum of
![]() $\unicode[STIX]{x1D712}_{s}$
is closely related to the local minimum of the sound speed, which in turn strongly deforms the Kovásznay eigenmode basis towards density perturbation. Regions of low values of
$\unicode[STIX]{x1D712}_{s}$
is closely related to the local minimum of the sound speed, which in turn strongly deforms the Kovásznay eigenmode basis towards density perturbation. Regions of low values of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
on the isoline of vanishing
$\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
on the isoline of vanishing
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
can be identified for both upstream pressures (for instance at
$\unicode[STIX]{x1D712}_{a^{+}}$
can be identified for both upstream pressures (for instance at
![]() $M_{1}\approx 1.5$
and
$M_{1}\approx 1.5$
and
![]() $\unicode[STIX]{x1D717}_{1}/\unicode[STIX]{x1D717}_{c}\approx 4.0$
for
$\unicode[STIX]{x1D717}_{1}/\unicode[STIX]{x1D717}_{c}\approx 4.0$
for
![]() $p_{1}/p_{c}=0.55$
). These shockwaves may be of interest for practical applications aiming at reducing the generation of noise induced by the refraction of a density perturbation (e.g. ORC turbine expanders).
$p_{1}/p_{c}=0.55$
). These shockwaves may be of interest for practical applications aiming at reducing the generation of noise induced by the refraction of a density perturbation (e.g. ORC turbine expanders).
6 About the D’yakov and Kontorovich criteria and potential 2D effects
The previous sections were aimed at presenting the peculiar properties of the one-dimensional shock-refraction problem for dense gases in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram, which is found to be convenient to represent non-ideal-gas effects induced by the TCP. In this section, known two-dimensional stability results in non-ideal gas are presented in this diagram along with the importance of admissibility. The initial-value problem of linear stability of shocks subjected to a prescribed perturbation of their front has been conveniently expressed by D’yakov and Kontorovich (D’yakov Reference D’yakov1954; Kontorovich Reference Kontorovich1957; Swan & Fowles Reference Swan and Fowles1975) for an arbitrary equation of state by using the unique scalar parameter
$(p,\unicode[STIX]{x1D717})$
-diagram, which is found to be convenient to represent non-ideal-gas effects induced by the TCP. In this section, known two-dimensional stability results in non-ideal gas are presented in this diagram along with the importance of admissibility. The initial-value problem of linear stability of shocks subjected to a prescribed perturbation of their front has been conveniently expressed by D’yakov and Kontorovich (D’yakov Reference D’yakov1954; Kontorovich Reference Kontorovich1957; Swan & Fowles Reference Swan and Fowles1975) for an arbitrary equation of state by using the unique scalar parameter
They showed that shocks are stable if
Another important result from their linear stability analysis is the occurrence of undamped acoustic waves from the perturbed front when
This last relation is never fulfilled for an ideal gas (Bates Reference Bates2000) but can be satisfied when a non-ideal EOS is used. Although the theoretical prediction of this neutrally stable acoustic emission was derived in 1954, the first attempt to observe it numerically was provided by Bates (Reference Bates2000), who intended to produce a shock radiating undamped acoustic waves from its front (using a van der Waals EOS). Apart from a possible experimental observation in ionising blast waves (Nilson et al.
Reference Nilson, Mangles, Willingale, Kaluza, Thomas, Tatarakis, Najmudin, Clarke, Lancaster and Karsch2009), to the best of authors’ knowledge, there has been no experimental evidence of DK acoustic emission, especially in single-phase gases. Even though the expression for the condition of occurrence is rather simple provided that
![]() ${\mathcal{H}}$
-lines can be extracted from the EOS, a practical representation of these conditions for single-phase non-ideal gases would be valuable and is currently missing in the literature.
${\mathcal{H}}$
-lines can be extracted from the EOS, a practical representation of these conditions for single-phase non-ideal gases would be valuable and is currently missing in the literature.
Figure 16 represents a set of
![]() ${\mathcal{H}}$
-lines originating at a constant upstream pressure (
${\mathcal{H}}$
-lines originating at a constant upstream pressure (
![]() $p_{1}/p_{c}=0.13$
in figure 16
a and
$p_{1}/p_{c}=0.13$
in figure 16
a and
![]() $p_{1}/p_{c}=0.80$
in figure 16
b) and for different increasing upstream temperatures starting at
$p_{1}/p_{c}=0.80$
in figure 16
b) and for different increasing upstream temperatures starting at
![]() $T_{1}=T_{c}$
. The
$T_{1}=T_{c}$
. The
![]() ${\mathcal{H}}$
-lines are plotted in the
${\mathcal{H}}$
-lines are plotted in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram together with the liquid–vapour two-phase region for a van der Waals gas (see appendix A). At each downstream point on a given
$(p,\unicode[STIX]{x1D717})$
-diagram together with the liquid–vapour two-phase region for a van der Waals gas (see appendix A). At each downstream point on a given
![]() ${\mathcal{H}}$
-line, the DK parameter (6.1) is computed and the points that fulfil the acoustic emission condition (6.3) are coloured in dark blue in figure 16. The DK acoustic emission is expected to occur close to the TCP where the equation of state departs from the dilute ideal-gas limit. With this representation in the
${\mathcal{H}}$
-line, the DK parameter (6.1) is computed and the points that fulfil the acoustic emission condition (6.3) are coloured in dark blue in figure 16. The DK acoustic emission is expected to occur close to the TCP where the equation of state departs from the dilute ideal-gas limit. With this representation in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram, the effect of the TCP is clearly seen for both upstream pressures. Indeed, the DK acoustic emission regime is found for shocks whose post-shock states are in the supercritical region close to the TCP. The shocks with low upstream pressures (see figure 16
a) feature a larger ‘DK area’ than the shocks with near-critical upstream pressures, which may not be intuitive. Remarkably, the ‘DK area’ covers a large portion of the
$(p,\unicode[STIX]{x1D717})$
-diagram, the effect of the TCP is clearly seen for both upstream pressures. Indeed, the DK acoustic emission regime is found for shocks whose post-shock states are in the supercritical region close to the TCP. The shocks with low upstream pressures (see figure 16
a) feature a larger ‘DK area’ than the shocks with near-critical upstream pressures, which may not be intuitive. Remarkably, the ‘DK area’ covers a large portion of the
![]() ${\mathcal{H}}$
-lines with one-dimensional non-ideal-gas effects commented on in the previous sections. The dynamic response of shocks under incoming supersonic perturbation in this region is far from the ideal-gas response. Furthermore, a significant portion of the ‘DK area’ is found to be non-admissible at high upstream pressure (the inadmissible part being the area enclosed by the magenta line). This is a consequence of the
${\mathcal{H}}$
-lines with one-dimensional non-ideal-gas effects commented on in the previous sections. The dynamic response of shocks under incoming supersonic perturbation in this region is far from the ideal-gas response. Furthermore, a significant portion of the ‘DK area’ is found to be non-admissible at high upstream pressure (the inadmissible part being the area enclosed by the magenta line). This is a consequence of the
![]() ${\mathcal{H}}$
-line crossing the BZT region. The BZT effects thus result in a narrower observable ‘DK area’, which could make any attempt to observe it experimentally very difficult.
${\mathcal{H}}$
-line crossing the BZT region. The BZT effects thus result in a narrower observable ‘DK area’, which could make any attempt to observe it experimentally very difficult.

Figure 16. The (
![]() $p,\unicode[STIX]{x1D717}$
)-diagram with the DK regions (dark blue) around the critical point plotted on the Hugoniot locus (black lines). The region enclosed by the magenta line in (b) indicates the non-admissible portions of the adiabats. Upstream Mach numbers (
$p,\unicode[STIX]{x1D717}$
)-diagram with the DK regions (dark blue) around the critical point plotted on the Hugoniot locus (black lines). The region enclosed by the magenta line in (b) indicates the non-admissible portions of the adiabats. Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the green lines with labels. The
${\mathcal{H}}$
-lines are represented by the green lines with labels. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
7 Towards experimental observations
In the previous sections, the van der Waals cubic equation of state is used to illustrate the one-dimensional shock-refraction properties near the TCP. Analytical expressions for the transmission factors are then obtained. While the dense-gas region is known to be qualitatively well captured by the van der Waals model, stronger limitations are expected in the vicinity of the TCP where analytic EOSs fail to predict the qualitatively correct behaviour of the fluid. Nevertheless, the current theoretical framework does not depend on a specific choice of EOS. The peculiar shock-refraction properties near the TCP are indeed found to result from (i) the sound-speed reduction along isentropic compressions (resulting in a peculiar deformation of Kovásznay’s eigenmode basis) and (ii) the occurrence of a negative-
![]() $\unicode[STIX]{x1D6E4}$
region in the vapour phase (producing jumps of transmission factors along
$\unicode[STIX]{x1D6E4}$
region in the vapour phase (producing jumps of transmission factors along
![]() ${\mathcal{H}}$
-lines featuring non-admissible paths). These properties are well reproduced by predictive thermodynamic models.
${\mathcal{H}}$
-lines featuring non-admissible paths). These properties are well reproduced by predictive thermodynamic models.
In this section, a step towards the experimental observation of the current theoretical findings is carried out. Shock-refraction properties are computed for siloxane D6 and toluene. Fluids of the siloxane family are identified as promising fluids for experimental observation of non-ideal-gas compressible fluid dynamics near the TCP (Colonna, Guardone & Nannan Reference Colonna, Guardone and Nannan2007) and have recently been targeted as working fluids in newly designed experimental facilities aiming at reproducing these conditions (Guardone, Spinelli & Dossena Reference Guardone, Spinelli and Dossena2013; Spinelli et al.
Reference Spinelli, Guardone, Cozzi, Carmine, Cheli, Zocca, Gaetani and Dossena2015; Head et al.
Reference Head, De Servi, Casati, Pini and Colonna2016). Toluene has a simpler molecular complexity (lower value of
![]() $c_{v}/R$
in the ideal-gas limit) compared with siloxane D6 and is currently used as a working fluid in ORC turbines (Colonna et al.
Reference Colonna, Casati, Trapp, Mathijssen, Larjola, Turunen-Saaresti and Uusitalo2015; Rinaldi, Pecnik & Colonna Reference Rinaldi, Pecnik and Colonna2016). The thermodynamic model considered here is the 12-parameter Span–Wagner (SW) (Span Reference Span2000) functional form EOS developed for siloxanes by Colonna, Nannan & Guardone (Reference Colonna, Nannan and Guardone2008) and for toluene by Lemmon & Span (Reference Lemmon and Span2006). It is among the most accurate thermodynamic models for these fluids and it was used in the design process of the experimental facilities mentioned above. A well-known practical limitation of near-TCP experimental observations of complex fluid dynamics is the thermal degradation of the corresponding molecules close to the critical temperature (Colonna et al.
Reference Colonna, Nannan and Guardone2008). For this reason, the isotherm corresponding to experimental estimates of the thermal stability limits for the two previously mentioned fluids is represented in the following results. For both the siloxane D6 and the toluene this limit is set to
$c_{v}/R$
in the ideal-gas limit) compared with siloxane D6 and is currently used as a working fluid in ORC turbines (Colonna et al.
Reference Colonna, Casati, Trapp, Mathijssen, Larjola, Turunen-Saaresti and Uusitalo2015; Rinaldi, Pecnik & Colonna Reference Rinaldi, Pecnik and Colonna2016). The thermodynamic model considered here is the 12-parameter Span–Wagner (SW) (Span Reference Span2000) functional form EOS developed for siloxanes by Colonna, Nannan & Guardone (Reference Colonna, Nannan and Guardone2008) and for toluene by Lemmon & Span (Reference Lemmon and Span2006). It is among the most accurate thermodynamic models for these fluids and it was used in the design process of the experimental facilities mentioned above. A well-known practical limitation of near-TCP experimental observations of complex fluid dynamics is the thermal degradation of the corresponding molecules close to the critical temperature (Colonna et al.
Reference Colonna, Nannan and Guardone2008). For this reason, the isotherm corresponding to experimental estimates of the thermal stability limits for the two previously mentioned fluids is represented in the following results. For both the siloxane D6 and the toluene this limit is set to
![]() $673~\text{K}$
(Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008).
$673~\text{K}$
(Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008).

Figure 17. Shock-transmission-factor isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for
${\mathcal{H}}$
-lines (solid black lines) for
![]() $p_{1}/p_{c}=0.13$
. Upstream Mach numbers (
$p_{1}/p_{c}=0.13$
. Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The fluid is the siloxane D6 modelled using the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The fluid is the siloxane D6 modelled using the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
The well-established program REFPROP (Lemmon, Huber & McLinden Reference Lemmon, Huber and McLinden2013) is used to compute the thermodynamic properties of the fluids. The computation of
![]() ${\mathcal{H}}$
-lines is performed through numerical integration of the nonlinear system of (2.1), and the derivatives needed in the computation of the transmission factors are evaluated numerically. The results for the post-shock entropy-mode amplification and acoustic-mode generation factors are reported in figure 17 for the siloxane D6 with
${\mathcal{H}}$
-lines is performed through numerical integration of the nonlinear system of (2.1), and the derivatives needed in the computation of the transmission factors are evaluated numerically. The results for the post-shock entropy-mode amplification and acoustic-mode generation factors are reported in figure 17 for the siloxane D6 with
![]() $p_{1}/p_{c}=0.13$
. As suggested by the asymptotic analysis (appendix C), for this complex fluid with a large isochoric heat capacity (
$p_{1}/p_{c}=0.13$
. As suggested by the asymptotic analysis (appendix C), for this complex fluid with a large isochoric heat capacity (
![]() $c_{v}/R\approx 170$
near the TCP), both the entropy-mode amplification and the acoustic-mode generation factors feature a large extremum along
$c_{v}/R\approx 170$
near the TCP), both the entropy-mode amplification and the acoustic-mode generation factors feature a large extremum along
![]() ${\mathcal{H}}$
-lines for post-shock states near the TCP. The picture provided by the van der Waals model is found to be robust, and within the thermal stability limit of the fluid, when compared with the predictive SW model from Colonna et al. (Reference Colonna, Nannan and Guardone2008). For the conditions considered, the extreme amplification of entropy modes is in fact stronger for the siloxane D6 modelled with the SW EOS than for the PP10 modelled with the van der Waals EOS. The different
${\mathcal{H}}$
-lines for post-shock states near the TCP. The picture provided by the van der Waals model is found to be robust, and within the thermal stability limit of the fluid, when compared with the predictive SW model from Colonna et al. (Reference Colonna, Nannan and Guardone2008). For the conditions considered, the extreme amplification of entropy modes is in fact stronger for the siloxane D6 modelled with the SW EOS than for the PP10 modelled with the van der Waals EOS. The different
![]() $c_{v}/R$
values, together with differences in the isotherm maps close to the TCP, result in
$c_{v}/R$
values, together with differences in the isotherm maps close to the TCP, result in
![]() ${\mathcal{H}}$
-lines that are more affected by the TCP for the siloxane D6 than what the van der Waals model captures. This can be appreciated with the evolution of Kovásznay’s eigenmode basis on the quarter unit sphere (figure 18), from which a stronger tendency towards degeneracy is observed for the siloxane D6 modelled with the SW EOS than when modelled with the analytical EOS (resulting in a stronger amplification factor, see figure 18
a). This observation is also consistent with the existence of a non-ideal region of negative
${\mathcal{H}}$
-lines that are more affected by the TCP for the siloxane D6 than what the van der Waals model captures. This can be appreciated with the evolution of Kovásznay’s eigenmode basis on the quarter unit sphere (figure 18), from which a stronger tendency towards degeneracy is observed for the siloxane D6 modelled with the SW EOS than when modelled with the analytical EOS (resulting in a stronger amplification factor, see figure 18
a). This observation is also consistent with the existence of a non-ideal region of negative
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
values (see figure 17
b) close to the TCP, a feature observed at higher upstream pressure for the PP10 modelled with the van der Waals EOS. The non-ideal selective behaviour of the compression shockwave is therefore stronger when the SW model is used. While it is well known that the van der Waals model overestimates the negative-
$\unicode[STIX]{x1D712}_{a^{+}}$
values (see figure 17
b) close to the TCP, a feature observed at higher upstream pressure for the PP10 modelled with the van der Waals EOS. The non-ideal selective behaviour of the compression shockwave is therefore stronger when the SW model is used. While it is well known that the van der Waals model overestimates the negative-
![]() $\unicode[STIX]{x1D6E4}$
region in the
$\unicode[STIX]{x1D6E4}$
region in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram and therefore the BZT effects, the new class of non-ideal properties considered in this study can be stronger for predictive models. The discontinuous refraction properties (‘discontinuous discontinuities’) are intrinsically linked to the negative-
$(p,\unicode[STIX]{x1D717})$
-diagram and therefore the BZT effects, the new class of non-ideal properties considered in this study can be stronger for predictive models. The discontinuous refraction properties (‘discontinuous discontinuities’) are intrinsically linked to the negative-
![]() $\unicode[STIX]{x1D6E4}$
region. Although theoretically observable (see figure 19), their practical observation is expected to be as challenging as the observation of BZT effects. Finally, the selective behaviour of shockwaves is also recovered for fluids with molecules with moderate numbers of active degrees of freedom and therefore featuring larger thermal stability limits (see
$\unicode[STIX]{x1D6E4}$
region. Although theoretically observable (see figure 19), their practical observation is expected to be as challenging as the observation of BZT effects. Finally, the selective behaviour of shockwaves is also recovered for fluids with molecules with moderate numbers of active degrees of freedom and therefore featuring larger thermal stability limits (see
![]() $\unicode[STIX]{x1D712}_{s}$
and
$\unicode[STIX]{x1D712}_{s}$
and
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
for toluene in figure 20).
$\unicode[STIX]{x1D712}_{a^{+}}$
for toluene in figure 20).

Figure 18. Comparison of technical and analytical EOS refraction properties. (a) Evolution of the entropy-mode amplification factor with pre-shock Mach numbers. The thick line indicates the range of Mach numbers for which the DK instability is expected. (b) Eigenmode basis evolution along the
![]() ${\mathcal{H}}$
-line. The pre-shock state is fixed to
${\mathcal{H}}$
-line. The pre-shock state is fixed to
![]() $p_{1}/p_{c}=0.13$
and
$p_{1}/p_{c}=0.13$
and
![]() $T_{1}/T_{c}=0.94$
in both panels. The blue line represents the data obtained for the siloxane D6 modelled with the SW EOS while the light blue and black lines represent the results obtained for the corresponding van der Waals and ideal-gas models respectively, with the same pre-shock conditions and
$T_{1}/T_{c}=0.94$
in both panels. The blue line represents the data obtained for the siloxane D6 modelled with the SW EOS while the light blue and black lines represent the results obtained for the corresponding van der Waals and ideal-gas models respectively, with the same pre-shock conditions and
![]() $c_{v}/R=102$
. The vectors correspond to pre-shock conditions with
$c_{v}/R=102$
. The vectors correspond to pre-shock conditions with
![]() $M_{1}=2.81$
for which the
$M_{1}=2.81$
for which the
![]() $\unicode[STIX]{x1D712}_{s}$
value for the siloxane D6 is approximately equal to
$\unicode[STIX]{x1D712}_{s}$
value for the siloxane D6 is approximately equal to
![]() $350$
.
$350$
.
Another important class of results illustrated with the van der Waals model is the non-ideal acoustic-generation properties. As shown in figure 21, good qualitative agreement is found between the siloxane D6 modelled with the SW model and the PP10 results modelled with the van der Waals EOS. Both the ‘DK spontaneous acoustic emission’ and the silent shock property are found within the thermal stability limit of the molecules, opening the way to their potential experimental observations.

Figure 19. Discontinuous transmission factors in the siloxane D6 for
![]() ${\mathcal{H}}$
-lines crossing the negative-
${\mathcal{H}}$
-lines crossing the negative-
![]() $\unicode[STIX]{x1D6E4}$
region (
$\unicode[STIX]{x1D6E4}$
region (
![]() $p_{1}/p_{c}=0.800$
,
$p_{1}/p_{c}=0.800$
,
![]() $T_{1}/T_{c}=0.986$
). The non-admissible path is shown in light blue. The thick line indicates the range of Mach numbers for which the DK instability is expected. The fluid is modelled with the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The corresponding ideal-gas model (
$T_{1}/T_{c}=0.986$
). The non-admissible path is shown in light blue. The thick line indicates the range of Mach numbers for which the DK instability is expected. The fluid is modelled with the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The corresponding ideal-gas model (
![]() $c_{v}/R=102$
) is represented by dashed black lines.
$c_{v}/R=102$
) is represented by dashed black lines.

Figure 20. The
![]() $\unicode[STIX]{x1D712}_{s}$
(a) and
$\unicode[STIX]{x1D712}_{s}$
(a) and
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
(b) isocontours and
$\unicode[STIX]{x1D712}_{a^{+}}$
(b) isocontours and
![]() ${\mathcal{H}}$
-lines (solid black lines) for
${\mathcal{H}}$
-lines (solid black lines) for
![]() $p_{1}/p_{c}=0.20$
in toluene. Upstream Mach numbers (
$p_{1}/p_{c}=0.20$
in toluene. Upstream Mach numbers (
![]() $M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
$M_{1}$
) indicating the shock speed needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
${\mathcal{H}}$
-lines are represented by the black dashed lines with labels. Ideal-gas
![]() ${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The fluid is modelled with the 12-parameter SW functional form EOS developed by Lemmon & Span (Reference Lemmon and Span2006). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
${\mathcal{H}}$
-lines (thick grey lines) are represented in the dilute-gas limit. The fluid is modelled with the 12-parameter SW functional form EOS developed by Lemmon & Span (Reference Lemmon and Span2006). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively.

Figure 21. Non-ideal acoustic generation in the siloxane D6 (
![]() $p_{1}/p_{c}=0.55$
). Upstream Mach numbers (
$p_{1}/p_{c}=0.55$
). Upstream Mach numbers (
![]() $M_{1}$
) needed to reach the corresponding thermodynamic state on the
$M_{1}$
) needed to reach the corresponding thermodynamic state on the
![]() ${\mathcal{H}}$
-lines are represented by the light blue lines (a) and light green lines (b) with labels. The fluid is the D6 siloxane modelled with the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
${\mathcal{H}}$
-lines are represented by the light blue lines (a) and light green lines (b) with labels. The fluid is the D6 siloxane modelled with the 12-parameter SW functional form EOS developed by Colonna et al. (Reference Colonna, Nannan and Guardone2008). The isotherm corresponding to the thermal stability limit (Angelino & Invernizzi Reference Angelino and Invernizzi1993; Colonna et al.
Reference Colonna, Nannan and Guardone2008) is indicated by a thick red line. The
![]() $\unicode[STIX]{x1D6E4}=0$
and
$\unicode[STIX]{x1D6E4}=0$
and
![]() $T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. (a) The ‘DK regions’ are shown by thick blue lines along the
$T=T_{c}$
isolines are represented with thick orange and thick blue lines respectively. (a) The ‘DK regions’ are shown by thick blue lines along the
![]() ${\mathcal{H}}$
-lines (thin black lines). (b) The
${\mathcal{H}}$
-lines (thin black lines). (b) The
![]() $\unicode[STIX]{x1D712}_{a^{+}}=0$
line coloured by the magnitude of
$\unicode[STIX]{x1D712}_{a^{+}}=0$
line coloured by the magnitude of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
(high value in red, low value in light blue). The line joining the maximum value of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{a^{+}}/\unicode[STIX]{x2202}M_{1}$
(high value in red, low value in light blue). The line joining the maximum value of
![]() $\unicode[STIX]{x1D712}_{s}$
is also shown (dashed white line). The contours represent the local speed of sound.
$\unicode[STIX]{x1D712}_{s}$
is also shown (dashed white line). The contours represent the local speed of sound.
8 Summary
A small-perturbation analysis of one-dimensional compression shockwaves subjected to incoming entropy waves has been performed for gases modelled with a non-ideal EOS. A general formalism that does not depend on a specific choice of EOS has been used. The discussion has focused primarily on molecularly complex fluids (featuring large values of
![]() $c_{v}/R$
), brought near their vapour–liquid critical point (TCP), and for which the isentrope and shock-adiabat maps converge towards the isotherm map in the
$c_{v}/R$
), brought near their vapour–liquid critical point (TCP), and for which the isentrope and shock-adiabat maps converge towards the isotherm map in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram. Although this convergence leads to well-known non-classical gas dynamics (BZT fluids), it was shown here that peculiar shock-refraction properties may also be expected.
$(p,\unicode[STIX]{x1D717})$
-diagram. Although this convergence leads to well-known non-classical gas dynamics (BZT fluids), it was shown here that peculiar shock-refraction properties may also be expected.
Entropy (density) fluctuations are found to be extremely and selectively amplified by shocks whose post-shock states lie in the supercritical region close to the TCP. Amplification ratios hundreds of times larger than for the corresponding (i.e. same
![]() $c_{v}/R$
and upstream Mach number) ideal gas are demonstrated using both the van der Waals EOS and the SW EOS for the siloxane D6. This is due to a tendency of Kovásznay’s acoustic eigenmode vectors to lean towards the entropy eigenvector near the TCP (as a consequence of a local minimum in the speed of sound). Similar results are obtained for the generated acoustic mode. The near degeneracy of the eigenmode basis is very local in the
$c_{v}/R$
and upstream Mach number) ideal gas are demonstrated using both the van der Waals EOS and the SW EOS for the siloxane D6. This is due to a tendency of Kovásznay’s acoustic eigenmode vectors to lean towards the entropy eigenvector near the TCP (as a consequence of a local minimum in the speed of sound). Similar results are obtained for the generated acoustic mode. The near degeneracy of the eigenmode basis is very local in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram, making both the post-shock entropy amplification and the acoustic generation from entropy waves very sensitive to any change in the incoming mass flow rate (or, equivalently, the incoming Mach number
$(p,\unicode[STIX]{x1D717})$
-diagram, making both the post-shock entropy amplification and the acoustic generation from entropy waves very sensitive to any change in the incoming mass flow rate (or, equivalently, the incoming Mach number
![]() $M_{1}$
). This provides the corresponding shockwaves with selective refraction properties with respect to the incoming fluctuating Mach number. It should be noted that these selective amplification properties are not restricted to BZT fluids (
$M_{1}$
). This provides the corresponding shockwaves with selective refraction properties with respect to the incoming fluctuating Mach number. It should be noted that these selective amplification properties are not restricted to BZT fluids (
![]() $\unicode[STIX]{x1D6E4}<0$
region) and also apply to convex shock adiabats, including ideal gases under extreme (but non-physical) conditions (e.g. Mach 15 in figure 7). The proximity of a critical point (non-ideal-gas effect) exacerbates and shifts this phenomenon to low and attainable supersonic conditions which are relevant to ORC turbines.
$\unicode[STIX]{x1D6E4}<0$
region) and also apply to convex shock adiabats, including ideal gases under extreme (but non-physical) conditions (e.g. Mach 15 in figure 7). The proximity of a critical point (non-ideal-gas effect) exacerbates and shifts this phenomenon to low and attainable supersonic conditions which are relevant to ORC turbines.
Most of the paper focuses on impinging entropy modes, which are more relevant to ORC turbines. The flow is indeed close to the critical point only near the nozzle throat, where the near degeneracy of the eigenmode basis can produce large density fluctuations, which can then be convected through the expansion and interact with the fishbone (oblique) shock pattern forming at the trailing edge of the nozzle, with the end result (refracted field) then sent into the turbine blade. Such shocks are around the Mach 2 mark with similar pre-shock states (
![]() $p_{1}/p_{c}\approx 0.5$
and near-critical temperature) to the ones studied here. Therefore, these results demonstrate that strong density fluctuations coming out from the fishbone shocks are a possibility in real applications, and can impart unsteady loads to the downstream turbine blades.
$p_{1}/p_{c}\approx 0.5$
and near-critical temperature) to the ones studied here. Therefore, these results demonstrate that strong density fluctuations coming out from the fishbone shocks are a possibility in real applications, and can impart unsteady loads to the downstream turbine blades.
With respect to locally non-convex shock adiabats (e.g. BZT fluids), the admissibility problem takes a non-classical form and gives rise to discontinuous admissible paths in the phase diagram. Consequently, all of the shock-refraction properties are discontinuous functions of the upstream Mach number
![]() $M_{1}$
. This applies, in particular, to both the entropy-amplification and acoustic-generation coefficients (following the impingement of the shock by an entropy mode). The presence of jumps in the shock-refraction properties is a unique feature of locally non-convex shock adiabats, and translates in practice to major modifications of the refracted-field properties in response to a minute change in the upstream conditions (i.e. Mach number). This was shown to occur in low supersonic regimes and could be relevant to both dense-gas nozzle flows and energy transfers in compressible turbulent flows featuring compression eddy shocklets (e.g. mixing layers, jets).
$M_{1}$
. This applies, in particular, to both the entropy-amplification and acoustic-generation coefficients (following the impingement of the shock by an entropy mode). The presence of jumps in the shock-refraction properties is a unique feature of locally non-convex shock adiabats, and translates in practice to major modifications of the refracted-field properties in response to a minute change in the upstream conditions (i.e. Mach number). This was shown to occur in low supersonic regimes and could be relevant to both dense-gas nozzle flows and energy transfers in compressible turbulent flows featuring compression eddy shocklets (e.g. mixing layers, jets).
Finally, shocks with their downstream state in close proximity to the TCP were shown to exhibit unusual acoustic properties. Unlike ideal gases, negative generation coefficients were found to be physically possible (indicative of an out-of-phase beating with the entropy mode). Remarkably, this sign change was shown to offer the possibility of finding ‘silent’ shocks for which no post-shock acoustic field is produced (following a perturbation normal to the shock front). This is to contrast to the so-called ‘D’yakov–Kontorovich spontaneous acoustic emission’ expected to occur in two or three dimensions but not yet observed experimentally. One difficulty in observing the spontaneous acoustic emission was shown to relate to the observation that the required conditions can be those of non-admissible shocks, with low subcritical pressures and near-critical temperatures offering more opportunities to observe this phenomenon.
The new class of non-ideal shock properties reported here has also been assessed with predictive thermodynamic models (SW EOS), giving a first insight towards their possible experimental observation. While the use of an analytical EOS (van der Waals model) may overestimate BZT effects, it can, on the contrary, severely underpredict unsteady non-ideal-gas effects close to the TCP.
While the above discussion is limited to dense gases in the vapour region close to the TCP, the theoretical results derived in this paper are general and are applicable to any EOS through the properties of both the shock-adiabat map in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram and the speed of sound. In particular, substances with locally non-convex shock adiabats are expected to mirror the above results, as for instance with shocks entering the vapour–liquid equilibrium region where negative nonlinearities are known to occur.
$(p,\unicode[STIX]{x1D717})$
-diagram and the speed of sound. In particular, substances with locally non-convex shock adiabats are expected to mirror the above results, as for instance with shocks entering the vapour–liquid equilibrium region where negative nonlinearities are known to occur.
The general one-dimensional framework provided in this paper has led to the identification of a new class of non-ideal-gas shock/perturbation interaction properties near the TCP. However, important multidimensional aspects have not been taken into account (vorticity mode, directivity effects and non-propagative post-shock acoustic), and will be thoroughly commented on in an upcoming paper.
Acknowledgements
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grants EP/L021676/1 and EP/K503733/1.
Appendix A. The van der Waals model
Throughout the paper, the refraction properties of compression shocks are illustrated by using a van der Waals EOS. This thermodynamic model is a prototypical choice to model a TCP. It can be seen as a simple model to take into account particles of finite size and with long-range interactions. In the van der Waals polytropic gas model, the complexity of the molecules constituting the gas is only taken into account by the parameter
![]() $c_{v}/R$
(Guardone & Argrow Reference Guardone and Argrow2005). In non-dimensional form, the EOS is given by
$c_{v}/R$
(Guardone & Argrow Reference Guardone and Argrow2005). In non-dimensional form, the EOS is given by
and the internal energy by
where
![]() $p$
,
$p$
,
![]() $T$
,
$T$
,
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $e$
are non-dimensional quantities (
$e$
are non-dimensional quantities (
![]() $p=p^{\ast }/p_{c}^{\ast }$
,
$p=p^{\ast }/p_{c}^{\ast }$
,
![]() $T=T^{\ast }/T_{c}^{\ast }$
,
$T=T^{\ast }/T_{c}^{\ast }$
,
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x1D717}^{\ast }/\unicode[STIX]{x1D717}_{c}^{\ast }$
and
$\unicode[STIX]{x1D717}=\unicode[STIX]{x1D717}^{\ast }/\unicode[STIX]{x1D717}_{c}^{\ast }$
and
![]() $e=e^{\ast }/(p_{c}^{\ast }\unicode[STIX]{x1D717}_{c}^{\ast })$
, where
$e=e^{\ast }/(p_{c}^{\ast }\unicode[STIX]{x1D717}_{c}^{\ast })$
, where
![]() $(\cdot )^{\ast }$
are dimensional quantities).
$(\cdot )^{\ast }$
are dimensional quantities).
Appendix B. Shock-refraction eigenvalue problem
The Rankine–Hugoniot relations in the laboratory reference frame are
where
![]() $u_{s}$
is the shock speed in the laboratory reference frame,
$u_{s}$
is the shock speed in the laboratory reference frame,
![]() $e_{t}$
is the total energy (i.e.
$e_{t}$
is the total energy (i.e.
![]() $e_{t}\equiv e+u^{2}/2$
) and
$e_{t}\equiv e+u^{2}/2$
) and
![]() $\unicode[STIX]{x27E6}f\unicode[STIX]{x27E7}\equiv f(\unicode[STIX]{x1D701}^{+},t)-f(\unicode[STIX]{x1D701}^{-},t)$
(with
$\unicode[STIX]{x27E6}f\unicode[STIX]{x27E7}\equiv f(\unicode[STIX]{x1D701}^{+},t)-f(\unicode[STIX]{x1D701}^{-},t)$
(with
![]() $\unicode[STIX]{x1D701}$
the shock position in time). Moving to the reference frame attached to the shock, equation (B 1) becomes (after some re-arrangement)
$\unicode[STIX]{x1D701}$
the shock position in time). Moving to the reference frame attached to the shock, equation (B 1) becomes (after some re-arrangement)
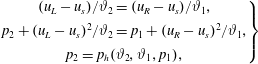 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(u_{L}-u_{s})/\unicode[STIX]{x1D717}_{2}=(u_{R}-u_{s})/\unicode[STIX]{x1D717}_{1},\\ p_{2}+(u_{L}-u_{s})^{2}/\unicode[STIX]{x1D717}_{2}=p_{1}+(u_{R}-u_{s})^{2}/\unicode[STIX]{x1D717}_{1},\\ p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1}),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(u_{L}-u_{s})/\unicode[STIX]{x1D717}_{2}=(u_{R}-u_{s})/\unicode[STIX]{x1D717}_{1},\\ p_{2}+(u_{L}-u_{s})^{2}/\unicode[STIX]{x1D717}_{2}=p_{1}+(u_{R}-u_{s})^{2}/\unicode[STIX]{x1D717}_{1},\\ p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1}),\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D717}_{1}$
and
$\unicode[STIX]{x1D717}_{1}$
and
![]() $p_{1}$
are the specific volume and pressure in front of the shock (in the reference frame attached to the shock, i.e.
$p_{1}$
are the specific volume and pressure in front of the shock (in the reference frame attached to the shock, i.e.
![]() $\unicode[STIX]{x1D717}_{1}=1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701}^{+},t)$
and
$\unicode[STIX]{x1D717}_{1}=1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701}^{+},t)$
and
![]() $p_{1}=p(\unicode[STIX]{x1D701}^{+},t)$
in (B 1)), and
$p_{1}=p(\unicode[STIX]{x1D701}^{+},t)$
in (B 1)), and
![]() $\unicode[STIX]{x1D717}_{2}$
and
$\unicode[STIX]{x1D717}_{2}$
and
![]() $p_{2}$
are the specific volume and pressure behind the shock (in the reference frame attached to the shock, i.e.
$p_{2}$
are the specific volume and pressure behind the shock (in the reference frame attached to the shock, i.e.
![]() $\unicode[STIX]{x1D717}_{2}=1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701}^{-},t)$
and
$\unicode[STIX]{x1D717}_{2}=1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D701}^{-},t)$
and
![]() $p_{2}=p(\unicode[STIX]{x1D701}^{-},t)$
in (B 1), see figure 4). The last equation in (B 2) stipulates that the post-shock pressure
$p_{2}=p(\unicode[STIX]{x1D701}^{-},t)$
in (B 1), see figure 4). The last equation in (B 2) stipulates that the post-shock pressure
![]() $p_{2}$
must be on the shock adiabat
$p_{2}$
must be on the shock adiabat
![]() $p_{h}$
. The variables
$p_{h}$
. The variables
![]() $u_{R}$
and
$u_{R}$
and
![]() $u_{L}$
represent the fluid velocity in the laboratory reference frame upstream and downstream of the discontinuity (i.e.
$u_{L}$
represent the fluid velocity in the laboratory reference frame upstream and downstream of the discontinuity (i.e.
![]() $u_{R}=u(\unicode[STIX]{x1D701}^{+},t)$
and
$u_{R}=u(\unicode[STIX]{x1D701}^{+},t)$
and
![]() $u_{L}=u(\unicode[STIX]{x1D701}^{-},t)$
in (B 1)). It should be noted that the reference frame attached to the shock is not inertial and a body force should be added. However, the shock in this work is viewed as a true discontinuity, making it massless, and is unaffected by inertial effects. This precludes the use of a modified pressure as suggested by Lubchich & Pudovkin (Reference Lubchich and Pudovkin2004).
$u_{L}=u(\unicode[STIX]{x1D701}^{-},t)$
in (B 1)). It should be noted that the reference frame attached to the shock is not inertial and a body force should be added. However, the shock in this work is viewed as a true discontinuity, making it massless, and is unaffected by inertial effects. This precludes the use of a modified pressure as suggested by Lubchich & Pudovkin (Reference Lubchich and Pudovkin2004).
We now wish to distinguish the actual shock position
![]() $\unicode[STIX]{x1D701}(t)$
from the one it would have in the absence of perturbations
$\unicode[STIX]{x1D701}(t)$
from the one it would have in the absence of perturbations
![]() $x_{s}(t)$
. Denoting the shock speed in the absence of a perturbation by
$x_{s}(t)$
. Denoting the shock speed in the absence of a perturbation by
![]() $\bar{u}_{s}$
, and assuming it to be constant with
$\bar{u}_{s}$
, and assuming it to be constant with
![]() $x_{s}(0)=0$
, then
$x_{s}(0)=0$
, then
![]() $x_{s}(t)=\bar{u}_{s}t$
. For any given time
$x_{s}(t)=\bar{u}_{s}t$
. For any given time
![]() $t$
, the perturbed shock is a distance
$t$
, the perturbed shock is a distance
![]() $\unicode[STIX]{x1D702}_{s}$
away from the position it assumes in the absence of the perturbation; hence,
$\unicode[STIX]{x1D702}_{s}$
away from the position it assumes in the absence of the perturbation; hence,
![]() $\unicode[STIX]{x1D701}=x_{s}+\unicode[STIX]{x1D702}_{s}$
and
$\unicode[STIX]{x1D701}=x_{s}+\unicode[STIX]{x1D702}_{s}$
and
![]() $u_{s}=\bar{u}_{s}+\text{d}\unicode[STIX]{x1D702}_{s}/\text{d}t=\bar{u}_{s}+\dot{\unicode[STIX]{x1D702}}_{s}$
. Following the small-perturbation analysis introduced in (3.6), equation (B 2) becomes
$u_{s}=\bar{u}_{s}+\text{d}\unicode[STIX]{x1D702}_{s}/\text{d}t=\bar{u}_{s}+\dot{\unicode[STIX]{x1D702}}_{s}$
. Following the small-perturbation analysis introduced in (3.6), equation (B 2) becomes
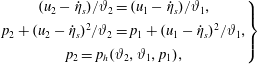 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(u_{2}-\dot{\unicode[STIX]{x1D702}}_{s})/\unicode[STIX]{x1D717}_{2}=(u_{1}-\dot{\unicode[STIX]{x1D702}}_{s})/\unicode[STIX]{x1D717}_{1},\\ p_{2}+(u_{2}-\dot{\unicode[STIX]{x1D702}}_{s})^{2}/\unicode[STIX]{x1D717}_{2}=p_{1}+(u_{1}-\dot{\unicode[STIX]{x1D702}}_{s})^{2}/\unicode[STIX]{x1D717}_{1},\\ p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1}),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(u_{2}-\dot{\unicode[STIX]{x1D702}}_{s})/\unicode[STIX]{x1D717}_{2}=(u_{1}-\dot{\unicode[STIX]{x1D702}}_{s})/\unicode[STIX]{x1D717}_{1},\\ p_{2}+(u_{2}-\dot{\unicode[STIX]{x1D702}}_{s})^{2}/\unicode[STIX]{x1D717}_{2}=p_{1}+(u_{1}-\dot{\unicode[STIX]{x1D702}}_{s})^{2}/\unicode[STIX]{x1D717}_{1},\\ p_{2}=p_{h}(\unicode[STIX]{x1D717}_{2},\unicode[STIX]{x1D717}_{1},p_{1}),\end{array}\right\}\end{eqnarray}$$
where
![]() $u_{1}=u_{R}-\bar{u}_{s}$
and
$u_{1}=u_{R}-\bar{u}_{s}$
and
![]() $u_{2}=u_{L}-\bar{u}_{s}$
.
$u_{2}=u_{L}-\bar{u}_{s}$
.
The perturbation (3.1), initially written in the laboratory reference frame, can be written about the shock position at a given time
![]() $t$
following a series expansion of
$t$
following a series expansion of
![]() $\unicode[STIX]{x1D741}$
around
$\unicode[STIX]{x1D741}$
around
![]() $\unicode[STIX]{x1D702}\equiv x-x_{s}=0$
,
$\unicode[STIX]{x1D702}\equiv x-x_{s}=0$
,
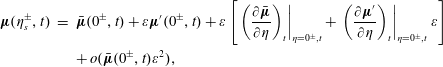 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D741}(\unicode[STIX]{x1D702}_{s}^{\pm },t) & = & \displaystyle \bar{\unicode[STIX]{x1D741}}(0^{\pm },t)+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}^{\prime }(0^{\pm },t)+\unicode[STIX]{x1D700}\left[\left.\left(\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D741}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)_{t}\right|_{\unicode[STIX]{x1D702}=0^{\pm },t}+\left.\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)_{t}\right|_{\unicode[STIX]{x1D702}=0^{\pm },t}\unicode[STIX]{x1D700}\right]\nonumber\\ \displaystyle & & \displaystyle +\,o(\bar{\unicode[STIX]{x1D741}}(0^{\pm },t)\unicode[STIX]{x1D700}^{2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D741}(\unicode[STIX]{x1D702}_{s}^{\pm },t) & = & \displaystyle \bar{\unicode[STIX]{x1D741}}(0^{\pm },t)+\unicode[STIX]{x1D700}\unicode[STIX]{x1D741}^{\prime }(0^{\pm },t)+\unicode[STIX]{x1D700}\left[\left.\left(\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D741}}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)_{t}\right|_{\unicode[STIX]{x1D702}=0^{\pm },t}+\left.\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D741}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right)_{t}\right|_{\unicode[STIX]{x1D702}=0^{\pm },t}\unicode[STIX]{x1D700}\right]\nonumber\\ \displaystyle & & \displaystyle +\,o(\bar{\unicode[STIX]{x1D741}}(0^{\pm },t)\unicode[STIX]{x1D700}^{2}),\end{eqnarray}$$
where all
![]() $\pm$
stand for the left/right values of the discontinuous quantities at the shock front. For the assumed piecewise uniform base flow (
$\pm$
stand for the left/right values of the discontinuous quantities at the shock front. For the assumed piecewise uniform base flow (
![]() $\left.\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D741}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\right|_{0^{\pm },t}=\mathbf{0}$
), the linearised Rankine–Hugoniot jump conditions can be expressed at
$\left.\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D741}}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\right|_{0^{\pm },t}=\mathbf{0}$
), the linearised Rankine–Hugoniot jump conditions can be expressed at
![]() $\unicode[STIX]{x1D702}=0$
(instead of
$\unicode[STIX]{x1D702}=0$
(instead of
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{s}$
) without missing first-order terms.
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{s}$
) without missing first-order terms.
Injecting (3.6) into (B 3) and retaining only first-order terms in
![]() $\unicode[STIX]{x1D700}$
gives the linearised version of the Rankine–Hugoniot conditions to be satisfied by linear waves across discontinuities for an arbitrary medium,
$\unicode[STIX]{x1D700}$
gives the linearised version of the Rankine–Hugoniot conditions to be satisfied by linear waves across discontinuities for an arbitrary medium,
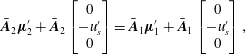 $$\begin{eqnarray}\bar{\boldsymbol{A}}_{2}\unicode[STIX]{x1D741}_{2}^{\prime }+\bar{\boldsymbol{A}}_{2}\left[\begin{array}{@{}c@{}}0\\ -u_{s}^{\prime }\\ 0\end{array}\right]=\bar{\boldsymbol{A}}_{1}\unicode[STIX]{x1D741}_{1}^{\prime }+\bar{\boldsymbol{A}}_{1}\left[\begin{array}{@{}c@{}}0\\ -u_{s}^{\prime }\\ 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\bar{\boldsymbol{A}}_{2}\unicode[STIX]{x1D741}_{2}^{\prime }+\bar{\boldsymbol{A}}_{2}\left[\begin{array}{@{}c@{}}0\\ -u_{s}^{\prime }\\ 0\end{array}\right]=\bar{\boldsymbol{A}}_{1}\unicode[STIX]{x1D741}_{1}^{\prime }+\bar{\boldsymbol{A}}_{1}\left[\begin{array}{@{}c@{}}0\\ -u_{s}^{\prime }\\ 0\end{array}\right],\end{eqnarray}$$
with
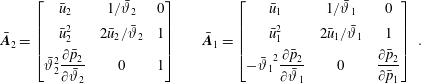 $$\begin{eqnarray}\begin{array}{@{}cc@{}}\bar{\boldsymbol{A}}_{2}=\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & 1/\bar{\unicode[STIX]{x1D717}}_{2} & 0\\ \bar{u}_{2}^{2} & 2\bar{u}_{2}/\bar{\unicode[STIX]{x1D717}}_{2} & 1\\ \bar{\unicode[STIX]{x1D717}}_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & 1\end{array}\right] & \quad \bar{\boldsymbol{A}}_{1}=\left[\begin{array}{@{}ccc@{}}\bar{u}_{1} & 1/\bar{\unicode[STIX]{x1D717}}_{1} & 0\\ \bar{u}_{1}^{2} & 2\bar{u}_{1}/\bar{\unicode[STIX]{x1D717}}_{1} & 1\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}} & 0 & {\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}\end{array}\right]\end{array}.\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cc@{}}\bar{\boldsymbol{A}}_{2}=\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & 1/\bar{\unicode[STIX]{x1D717}}_{2} & 0\\ \bar{u}_{2}^{2} & 2\bar{u}_{2}/\bar{\unicode[STIX]{x1D717}}_{2} & 1\\ \bar{\unicode[STIX]{x1D717}}_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & 1\end{array}\right] & \quad \bar{\boldsymbol{A}}_{1}=\left[\begin{array}{@{}ccc@{}}\bar{u}_{1} & 1/\bar{\unicode[STIX]{x1D717}}_{1} & 0\\ \bar{u}_{1}^{2} & 2\bar{u}_{1}/\bar{\unicode[STIX]{x1D717}}_{1} & 1\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}} & 0 & {\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}\end{array}\right]\end{array}.\end{eqnarray}$$
The waves in (3.7)–(3.8) have to satisfy the boundary conditions at
![]() $\unicode[STIX]{x1D702}=0$
, namely the linearised Rankine–Hugoniot conditions (B 5). Taking into account a change of variables from
$\unicode[STIX]{x1D702}=0$
, namely the linearised Rankine–Hugoniot conditions (B 5). Taking into account a change of variables from
![]() $(\unicode[STIX]{x1D70C},u,p)$
to
$(\unicode[STIX]{x1D70C},u,p)$
to
![]() $(\unicode[STIX]{x1D717},u,p)$
, the resulting linear system expressed in the eigenmode basis is
$(\unicode[STIX]{x1D717},u,p)$
, the resulting linear system expressed in the eigenmode basis is
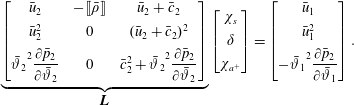 $$\begin{eqnarray}\underbrace{\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & -\unicode[STIX]{x27E6}\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x27E7} & \bar{u}_{2}+\bar{c}_{2}\\ \bar{u}_{2}^{2} & 0 & (\bar{u}_{2}+\bar{c}_{2})^{2}\\ {\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & \bar{c}_{2}^{2}+{\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\end{array}\right]}_{\displaystyle \boldsymbol{L}}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\\ \unicode[STIX]{x1D6FF}\\ \unicode[STIX]{x1D712}_{a^{+}}\end{array}\right]=\left[\begin{array}{@{}c@{}}\bar{u}_{1}\\ \bar{u}_{1}^{2}\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\underbrace{\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & -\unicode[STIX]{x27E6}\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x27E7} & \bar{u}_{2}+\bar{c}_{2}\\ \bar{u}_{2}^{2} & 0 & (\bar{u}_{2}+\bar{c}_{2})^{2}\\ {\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & \bar{c}_{2}^{2}+{\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\end{array}\right]}_{\displaystyle \boldsymbol{L}}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\\ \unicode[STIX]{x1D6FF}\\ \unicode[STIX]{x1D712}_{a^{+}}\end{array}\right]=\left[\begin{array}{@{}c@{}}\bar{u}_{1}\\ \bar{u}_{1}^{2}\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\end{array}\right].\end{eqnarray}$$
The problem has a unique solution if and only if
![]() $\unicode[STIX]{x1D6E5}=\text{det}(\boldsymbol{L})\neq 0$
, i.e.
$\unicode[STIX]{x1D6E5}=\text{det}(\boldsymbol{L})\neq 0$
, i.e.
Introducing the D’yakov parameter
![]() $h\equiv j^{2}/(\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2})$
, we find that the system has a solution if and only if
$h\equiv j^{2}/(\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2})$
, we find that the system has a solution if and only if
which is satisfied in a single-phase flow with
![]() $G>0$
. Indeed, the slope of the
$G>0$
. Indeed, the slope of the
![]() ${\mathcal{H}}$
-line in the (
${\mathcal{H}}$
-line in the (
![]() $p,\unicode[STIX]{x1D717}$
)-diagram (
$p,\unicode[STIX]{x1D717}$
)-diagram (
![]() $\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}$
) is then always negative (Cramer Reference Cramer1989) and
$\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}$
) is then always negative (Cramer Reference Cramer1989) and
![]() $2M_{2}+1>0$
. We can then invert the system and obtain the entropy-mode amplification factor (
$2M_{2}+1>0$
. We can then invert the system and obtain the entropy-mode amplification factor (
![]() $\unicode[STIX]{x1D712}_{s}$
) and the acoustic-mode generation factor (
$\unicode[STIX]{x1D712}_{s}$
) and the acoustic-mode generation factor (
![]() $\unicode[STIX]{x1D712}_{a^{+}}$
),
$\unicode[STIX]{x1D712}_{a^{+}}$
),
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\left(M_{2}+1\right)^{2}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}},\\ \unicode[STIX]{x1D712}_{a^{+}}=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}M_{2}^{2}{\displaystyle \frac{{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\left(M_{2}+1\right)^{2}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}},\\ \unicode[STIX]{x1D712}_{a^{+}}=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}M_{2}^{2}{\displaystyle \frac{{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{array}\right\}\end{eqnarray}$$
Following the same methodology, one can obtain the entropy-mode generation factor
![]() $(\unicode[STIX]{x1D712}_{s}^{\pm })$
and the acoustic-mode amplification factor
$(\unicode[STIX]{x1D712}_{s}^{\pm })$
and the acoustic-mode amplification factor
![]() $(\unicode[STIX]{x1D712}_{a^{+}}^{\pm })$
originating from an upstream acoustic perturbation by simply introducing the corresponding upstream acoustic mode in (B 5). The corresponding system, expressed in the eigenmode basis, is
$(\unicode[STIX]{x1D712}_{a^{+}}^{\pm })$
originating from an upstream acoustic perturbation by simply introducing the corresponding upstream acoustic mode in (B 5). The corresponding system, expressed in the eigenmode basis, is
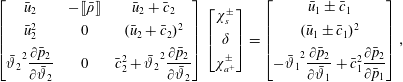 $$\begin{eqnarray}\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & -\unicode[STIX]{x27E6}\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x27E7} & \bar{u}_{2}+\bar{c}_{2}\\ \bar{u}_{2}^{2} & 0 & (\bar{u}_{2}+\bar{c}_{2})^{2}\\ {\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & \bar{c}_{2}^{2}+{\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\end{array}\right]\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}^{\pm }\\ \unicode[STIX]{x1D6FF}\\ \unicode[STIX]{x1D712}_{a^{+}}^{\pm }\end{array}\right]=\left[\begin{array}{@{}c@{}}\bar{u}_{1}\pm \bar{c}_{1}\\ (\bar{u}_{1}\pm \bar{c}_{1})^{2}\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}+\bar{c}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}ccc@{}}\bar{u}_{2} & -\unicode[STIX]{x27E6}\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x27E7} & \bar{u}_{2}+\bar{c}_{2}\\ \bar{u}_{2}^{2} & 0 & (\bar{u}_{2}+\bar{c}_{2})^{2}\\ {\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}} & 0 & \bar{c}_{2}^{2}+{\bar{\unicode[STIX]{x1D717}}_{2}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\end{array}\right]\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}^{\pm }\\ \unicode[STIX]{x1D6FF}\\ \unicode[STIX]{x1D712}_{a^{+}}^{\pm }\end{array}\right]=\left[\begin{array}{@{}c@{}}\bar{u}_{1}\pm \bar{c}_{1}\\ (\bar{u}_{1}\pm \bar{c}_{1})^{2}\\ -{\bar{\unicode[STIX]{x1D717}}_{1}}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}+\bar{c}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}\end{array}\right],\end{eqnarray}$$
where
![]() $\pm$
stand for the fast
$\pm$
stand for the fast
![]() $(+)$
or slow
$(+)$
or slow
![]() $(-)$
upstream acoustic mode. Inverting the system of (B 11) gives
$(-)$
upstream acoustic mode. Inverting the system of (B 11) gives
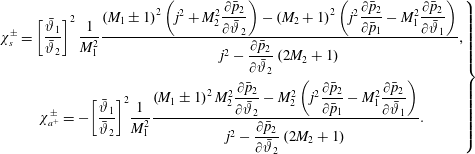 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}^{\pm }=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{1}{M_{1}^{2}}}{\displaystyle \frac{\left(M_{1}\pm 1\right)^{2}\left(j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\right)-\left(M_{2}+1\right)^{2}\left(j^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}-M_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}},\\ \unicode[STIX]{x1D712}_{a^{+}}^{\pm }=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{1}{M_{1}^{2}}}{\displaystyle \frac{\left(M_{1}\pm 1\right)^{2}M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}-M_{2}^{2}\left(j^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}-M_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}^{\pm }=\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{1}{M_{1}^{2}}}{\displaystyle \frac{\left(M_{1}\pm 1\right)^{2}\left(j^{2}+M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\right)-\left(M_{2}+1\right)^{2}\left(j^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}-M_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}},\\ \unicode[STIX]{x1D712}_{a^{+}}^{\pm }=-\left[{\displaystyle \frac{\bar{\unicode[STIX]{x1D717}}_{1}}{\bar{\unicode[STIX]{x1D717}}_{2}}}\right]^{2}{\displaystyle \frac{1}{M_{1}^{2}}}{\displaystyle \frac{\left(M_{1}\pm 1\right)^{2}M_{2}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}-M_{2}^{2}\left(j^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{p}_{1}}}-M_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)}{j^{2}-{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}}}\left(2M_{2}+1\right)}}.\end{array}\right\}\end{eqnarray}$$
Appendix C. The isothermal limits at the TCP
The transmission coefficients diverge towards singular values for the post-shock state at the TCP when the hypothetical isothermal-shock limit is considered. In this appendix, asymptotic expansions of the transmission coefficients are derived in terms of powers of
![]() $1/\bar{c}_{2}$
(with
$1/\bar{c}_{2}$
(with
![]() $\bar{c}_{2}\rightarrow 0$
at the TCP in the isothermal-shock limit), and the aforementioned singular limits are deduced.
$\bar{c}_{2}\rightarrow 0$
at the TCP in the isothermal-shock limit), and the aforementioned singular limits are deduced.
The case of incoming entropy perturbation is considered here. Given (B 10) and the isentropic limit of
![]() ${\mathcal{H}}$
-lines in the
${\mathcal{H}}$
-lines in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram (for which
$(p,\unicode[STIX]{x1D717})$
-diagram (for which
![]() $\bar{c}_{2}^{2}=-\bar{\unicode[STIX]{x1D717}}_{2}^{2}\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}$
), one can deduce that at the TCP,
$\bar{c}_{2}^{2}=-\bar{\unicode[STIX]{x1D717}}_{2}^{2}\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{2}$
), one can deduce that at the TCP,
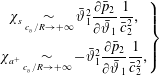 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\underset{c_{v}/R\rightarrow +\infty }{{\sim}}\bar{\unicode[STIX]{x1D717}}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}{\displaystyle \frac{1}{\bar{c}_{2}^{2}}},\\ \unicode[STIX]{x1D712}_{a^{+}}\underset{c_{v}/R\rightarrow +\infty }{{\sim}}-\bar{\unicode[STIX]{x1D717}}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}{\displaystyle \frac{1}{\bar{c}_{2}^{2}}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\underset{c_{v}/R\rightarrow +\infty }{{\sim}}\bar{\unicode[STIX]{x1D717}}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}{\displaystyle \frac{1}{\bar{c}_{2}^{2}}},\\ \unicode[STIX]{x1D712}_{a^{+}}\underset{c_{v}/R\rightarrow +\infty }{{\sim}}-\bar{\unicode[STIX]{x1D717}}_{1}^{2}{\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}{\displaystyle \frac{1}{\bar{c}_{2}^{2}}},\end{array}\right\}\end{eqnarray}$$
where
![]() $\bar{c}_{2}\rightarrow 0$
at the TCP. The isothermal nature of
$\bar{c}_{2}\rightarrow 0$
at the TCP. The isothermal nature of
![]() ${\mathcal{H}}$
-lines further provides a relationship between
${\mathcal{H}}$
-lines further provides a relationship between
![]() $\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}$
and
$\unicode[STIX]{x2202}\bar{p}_{2}/\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}$
and
![]() $\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}/\unicode[STIX]{x2202}\bar{T}_{2}$
, where
$\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}/\unicode[STIX]{x2202}\bar{T}_{2}$
, where
![]() $\bar{p}_{2}^{\text{T}}(\bar{T}_{2},\bar{\unicode[STIX]{x1D717}}_{2})$
is the isotherm map in the
$\bar{p}_{2}^{\text{T}}(\bar{T}_{2},\bar{\unicode[STIX]{x1D717}}_{2})$
is the isotherm map in the
![]() $(p,\unicode[STIX]{x1D717})$
-diagram,
$(p,\unicode[STIX]{x1D717})$
-diagram,
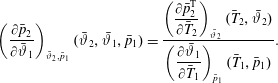 $$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)_{\bar{\unicode[STIX]{x1D717}}_{2},\bar{p}_{1}}(\bar{\unicode[STIX]{x1D717}}_{2},\bar{\unicode[STIX]{x1D717}}_{1},\bar{p}_{1})={\displaystyle \frac{\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}}{\unicode[STIX]{x2202}\bar{T}_{2}}}\right)_{\bar{\unicode[STIX]{x1D717}}_{2}}(\bar{T}_{2},\bar{\unicode[STIX]{x1D717}}_{2})}{\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}{\unicode[STIX]{x2202}\bar{T}_{1}}}\right)_{\bar{p}_{1}}(\bar{T}_{1},\bar{p}_{1})}}.\end{eqnarray}$$
$$\begin{eqnarray}\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}}{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}}\right)_{\bar{\unicode[STIX]{x1D717}}_{2},\bar{p}_{1}}(\bar{\unicode[STIX]{x1D717}}_{2},\bar{\unicode[STIX]{x1D717}}_{1},\bar{p}_{1})={\displaystyle \frac{\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}}{\unicode[STIX]{x2202}\bar{T}_{2}}}\right)_{\bar{\unicode[STIX]{x1D717}}_{2}}(\bar{T}_{2},\bar{\unicode[STIX]{x1D717}}_{2})}{\left({\displaystyle \frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}}{\unicode[STIX]{x2202}\bar{T}_{1}}}\right)_{\bar{p}_{1}}(\bar{T}_{1},\bar{p}_{1})}}.\end{eqnarray}$$
It is well known that the derivative
![]() $\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}/\unicode[STIX]{x2202}\bar{T}_{2}$
is finite and positive at the TCP (Zappoli, Beysens & Garrabos Reference Zappoli, Beysens and Garrabos2015). The derivative
$\unicode[STIX]{x2202}\bar{p}_{2}^{\text{T}}/\unicode[STIX]{x2202}\bar{T}_{2}$
is finite and positive at the TCP (Zappoli, Beysens & Garrabos Reference Zappoli, Beysens and Garrabos2015). The derivative
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}/\unicode[STIX]{x2202}\bar{T}_{1}$
is also finite and positive (for a positive coefficient of thermal expansion, see § 2.2). Therefore, at the TCP, the asymptotic limits of the entropy-mode amplification factor and the acoustic-mode generation factor originating from an incoming entropy mode are
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D717}}_{1}/\unicode[STIX]{x2202}\bar{T}_{1}$
is also finite and positive (for a positive coefficient of thermal expansion, see § 2.2). Therefore, at the TCP, the asymptotic limits of the entropy-mode amplification factor and the acoustic-mode generation factor originating from an incoming entropy mode are
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\underset{c_{v}/R\rightarrow +\infty }{\rightarrow }+\infty ,\\ \unicode[STIX]{x1D712}_{a^{+}}\underset{c_{v}/R\rightarrow +\infty }{\rightarrow }-\infty .\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D712}_{s}\underset{c_{v}/R\rightarrow +\infty }{\rightarrow }+\infty ,\\ \unicode[STIX]{x1D712}_{a^{+}}\underset{c_{v}/R\rightarrow +\infty }{\rightarrow }-\infty .\end{array}\right\}\end{eqnarray}$$